Abstract
We study non-interactive computational intractability assumptions in prime-order cyclic groups. We focus on the broad class of computational assumptions which we call target assumptions where the adversary’s goal is to compute concrete group elements.
Our analysis identifies two families of intractability assumptions, the q-Generalized Diffie-Hellman Exponent (q-GDHE) assumptions and the q-Simple Fractional (q-SFrac) assumptions (a natural generalization of the q-SDH assumption), that imply all other target assumptions. These two assumptions therefore serve as Uber assumptions that can underpin all the target assumptions where the adversary has to compute specific group elements. We also study the internal hierarchy among members of these two assumption families. We provide heuristic evidence that both families are necessary to cover the full class of target assumptions. We also prove that having (polynomially many times) access to an adversarial 1-GDHE oracle, which returns correct solutions with non-negligible probability, entails one to solve any instance of the Computational Diffie-Hellman (CDH) assumption. This proves equivalence between the CDH and 1-GDHE assumptions. The latter result is of independent interest. We generalize our results to the bilinear group setting. For the base groups, our results translate nicely and a similar structure of non-interactive computational assumptions emerges. We also identify Uber assumptions in the target group but this requires replacing the q-GDHE assumption with a more complicated assumption, which we call the bilinar gap assumption.
Our analysis can assist both cryptanalysts and cryptographers. For cryptanalysts, we propose the q-GDHE and the q-SDH assumptions are the most natural and important targets for cryptanalysis in prime-order groups. For cryptographers, we believe our classification can aid the choice of assumptions underpinning cryptographic schemes and be used as a guide to minimize the overall attack surface that different assumptions expose.
The research leading to these results has received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007–2013)/ERC Grant Agreement n. 307937 and EPSRC grant EP/J009520/1.
E. Ghadafi—Part of the work was done while at University College London.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Prime-order groups are widely used in cryptography because their clean mathematical structure enables the construction of many interesting schemes. However, cryptographers rely on an ever increasing number of intractability assumptions to prove their cryptographic schemes are secure. Especially after the rise of pairing-based cryptography, we have witnessed a proliferation of intractability assumptions. While some of those intractability assumptions, e.g. the discrete logarithm or the computational Diffie-Hellman assumptions, are well-studied, and considered by now “standard”, the rest of the assumption wilderness has received less attention.
This is unfortunate both for cryptographers designing protocols and cryptanalysts studying the security of the underpinning assumptions. Cryptographers designing protocols are often faced with a trade-off between performance and security, and it would therefore be helpful for them to know how their chosen intractability assumptions compare to other assumptions. Moreover, when they are designing a suite of protocols, it would be useful to know whether the different assumptions they use increase the attack surface or whether the assumptions are related. Cryptanalysts facing the wilderness of assumptions are also faced with a problem: which assumptions should they focus their attention on? One option is to go for the most devastating attack and try to break the discrete logarithm assumption, but the disadvantage is that this is also the hardest assumption to attack and hence the one where the cryptanalyst is least likely to succeed. The other option is to try to attack an easier assumption but the question then is which assumption is the most promising target?
Our research vision is that a possible path out of the wilderness is to identify Uber assumptions that imply all the assumptions we use. An extreme Uber assumption would be that anything that cannot trivially be broken by generic group operations is secure, however, we already know that this is a too extreme position since there are schemes that are secure against generic attacks but insecure for any concrete instantiation of the groups [18]. Instead of trying to capture all of the generic group model, we therefore ask for a few concrete and plausible Uber assumptions that capture the most important part of the assumption landscape. Such a characterization of the assumption wilderness would help both cryptographers and crypanalysts. The cryptographic designer may choose assumptions that fall under the umbrella of a few of the Uber assumptions to minimize the attack surface on her schemes. The cryptanalyst can use the Uber assumptions as important yet potentially easy targets.
Related Work. The rapid development of cryptographic schemes has been accompanied by an increase in the number and complexity of intractability assumptions. Cryptographers have been in pursuit to study the relationship among existing assumptions either by means of providing templates which encompass assumptions in the same family, e.g. [13, 14, 27], or by studying direct implications or lack thereof among the different assumptions, e.g. [3, 7, 26, 31, 32].
A particular class of assumptions which has received little attention are fractional assumptions. Those include, for example, the q-SDH assumption [8] and many of its variants, e.g. the modified q-SDH assumption [12], and the hidden q-SDH (q-HSDH) assumption [12]. As posed by, e.g. [28], a subtle question that arises is how such class of assumptions, e.g. the q-SDH assumption, relate to other existing (discrete-logarithm related) computational and decisional intractability assumptions. For instance, while it is clear that the q-SDH assumption implies the computational Diffie-Hellman assumption, it is still unclear whether the q-SDH assumption is implied by the decisional Diffie-Hellman assumption. Another intriguing open question is if there is a hierarchy between fractional assumptions or the class of assumptions is inherently unstructured.
Sadeghi and Steiner [38] introduced a new parameter for discrete-logarithm related assumptions they termed granularity which deals with the choice of the underlying mathematical group and its respective generator. They argued such a parameter can influence the security of schemes based on such assumptions and showed that such a parameter influences the implications between assumptions.
Naor [35] classified assumptions based on the complexity of falsifying them. Informally speaking, an assumption is falsifiable if it is possible to efficiently decide whether an adversary against the assumption has successfully broken it. Very recently, Goldwasser and Kalai [24] provided another classification of intractability assumptions based on their complexity. They argued that classifications based merely on falsifiability of the assumptions might be too inclusive since they do not exclude assumptions which are too dependent on the underlying cryptographic construct they support.
Boneh et al. [9] defined a framework for proving that decisional and computational assumptions are secure in the generic group model [30, 39] and formalized an Uber assumption saying that generic group security implies real security for these assumptions. Boyen [11] later highlighted extensions to the framework and informally suggested how some other families which were not encompassed by the original Uber assumption in [9] can be captured. In essence, the Uber assumption encompasses computational and decisional (discrete-logarithm related) assumptions with a fixed unique challenge. Unfortunately, the framework excludes some families of assumptions, in particular, those where the polynomial(s) used for the challenge are chosen adaptively by the adversary after seeing the problem instance. Examples of such assumptions include the q-SDH [8], the modified q-SDH [12], and the q-HSDH [12] assumptions. The statement of the assumption of the aforementioned yield exponentially many (mutually irreducible) valid solutions rather than a unique one. Another distinction, from the Uber assumption is that the exponent required for the solution involves a fraction of polynomials rather than a polynomial. Joux and Rojat [26] proved relationships between some instances of the Uber assumption [9]. In particular, they proved implications between some variants of the computational Diffie-Hellman assumption.
Cheon [17] observed that the computational complexity of the q-SDH assumption (and related assumptions) reduces by a factor of \(O(\sqrt{q})\) from that of the discrete logarithm problem if some relation between the prime group order p and the parameter q, in particular, if either \(q\mid {p-1}\) or \(q\mid {p+1}\), holds.
Chase and Meiklejohn [16] showed that in composite-order groups some of the so-called q-type assumptions can be reduced to the standard subgroup hiding assumption. More recently, Chase et al. [15] extended their framework to cover more assumptions and get tighter reductions.
Barthe et al. [4] analyzed hardness of intractability assumptions in the generic group model by reducing them to solving problems related to polynomial algebra. They also provided an automated tool that verifies the hardness of a subclass of families of assumptions in the generic group model. More recently, Ambrona et al. [2] improved upon the results of [4] by allowing unlimited oracle queries.
Kiltz [27] introduced the poly-Diffie-Hellman assumption as a generalization of the computational Diffie-Hellman assumption. Bellare et al. [6] defined the general subgroup decision problem which is a generalization of many existing variants of the subgroup decision problem in composite-order groups. Escala et al. [19] proposed an algebraic framework as a generalization of Diffie-Hellman like decisional assumptions. Analogously to [19], Morillo et al. [34] extended the framework to computational assumptions.
Our Contribution. We focus on efficiently falsifiable computational assumptions in prime-order groups. More precisely, we define a target assumption as an assumption where the adversary has a specific target element that she is trying to compute. A well-known target assumption is the Computational Diffie-Hellman (CDH) assumption over a cyclic group \(\mathbb {G}_p\) of prime order p, which states that given \(\left( G,G^a,G^b \right) \in \mathbb {G}^3_p\), it is hard to compute the target \(G^{ab}\in \mathbb {G}_p\). We define target assumptions quite broadly and also include assumptions where the adversary takes part in specifying the target to be computed. In the q-SDH assumption [8] for instance, the adversary is given \(G,G^x,\ldots ,G^{x^q}\) and has to output \((c,G^{\frac{1}{x\,{+}\,c}})\in \mathbb {Z}_p\setminus \{-x\} \times \mathbb {G}_p\). Here c selected by the adversary is part of the specification of the target \(G^{\frac{1}{x\,{+}\,c}}\). In other words, our work includes both assumptions in which the target element to be computed is either uniquely determined a priori by the instance, or a posteriori by the adversary. We note that the case of multiple target elements is also covered by our framework as long as all the target elements are uniquely determined. This is because a tuple of elements is hard to compute if any of its single elements is hard to compute.
Our main contribution is to identify two classes of assumptions that imply the security of all target assumptions. The first class of assumptions is the Generalized Diffie-Hellman Exponent (q-GDHE) assumption [9] that says given \(( G,G^x,\ldots ,G^{x^{q-1}}, G^{x^{q+1}}, \ldots , G^{x^{2q}} ) \in \mathbb {G}^{2q}_p\), it is hard to compute \(G^{x^q} \in \mathbb {G}_p\). The second class of assumptions, which is a straightforward generalization of the q-SDH assumption, we call the simple fractional (q-SFrac) assumption and it states that given \((G, G^x,\ldots , G^{x^q} ) \in \mathbb {G}^{q+1}_p\), it is hard to output polynomials \(r(X)\) and \(s(X)\) together with the target \(G^{\frac{r(x)}{s(x)}} \in \mathbb {G}_p\), where \(0\le \deg (r(X))<\deg (s(X))\le q\). We remark that the latter assumption is not totally new as variants thereof appeared in the literature. For instance, Fucshsbauer et al. [20] defined an identical variant over bilinear groups which they called the generalized \(q\text {-co-SDH}\) assumption. The assumption that the q-GDHE and q-SFrac assumptions both hold when q is polynomial in the security parameter can therefore be seen as an Uber assumption for the entire class of target assumptions.
Having identified the q-GDHE and \(q\text {-SFrac}\) assumptions as being central for the security of target assumptions in general, we investigate their internal structure. We first show that q-SFrac is unlikely to be able to serve as an Uber assumption on its own. More precisely, we show that for a generic group adversary the 2-GDHE assumption is not implied by q-SFrac assumptions. Second, we show that the q-GDHE assumptions appear to be strictly increasing as q grows, i.e., if the \((q+1)\)-GDHE holds, then so does q-GDHE, but for a generic group adversary the \((q+1)\)-GDHE may be false even though q-GDHE holds. We also analyze the particular case where \(q=1\) and prove that the 1-GDHE assumption is equivalent to the CDH assumption. We summarize the implications we prove in Fig. 1, where  denotes that \(\mathsf {B}\) is implied (in a black-box manner) by \(\mathsf {A}\), whereas
denotes that \(\mathsf {B}\) is implied (in a black-box manner) by \(\mathsf {A}\), whereas  denotes the absence of such an implication (cf. Sect. 2.1).
denotes the absence of such an implication (cf. Sect. 2.1).
Based on these results we view the q-GDHE and \(q\text {-SFrac}\) assumptions as a bulwark. Whatever type of target assumptions a cryptographer bases her schemes on, they are secure as long as neither the q-GDHE nor the \(q\text {-SFrac}\) assumptions are broken.Footnote 1 Since the attacker has less leeway in the q-GDHE assumptions, the cryptographer may choose to rely exclusively on target assumpitons that are implied by the q-GDHE assumptions, and we therefore identify a large class of target assumptions that only need the q-GDHE assumptions to hold.
We also have advice for the cryptanalyst. We believe it is better to focus on canary in a coal mine assumptions than the discrete logarithm problem that has received the most attention so far. Based on our work, the easiest target assumptions to attack in single prime-order groups are the q-GDHE assumptions and the q-SFrac assumptions. The class of q-SFrac assumptions allows more room for the adversary to maneuver in the choice of polynomials r(X) and s(X) and appears less structured than the q-GDHE assumptions. Pragmatically, we note that within the q-SFrac assumptions it is almost exclusively the q-SDH assumptions that are used. We therefore suggest the q-GDHE assumptions and the q-SDH assumptions to be the most suitable targets for cryptanalytic research.
Switching from single prime-order groups \(\mathbb {G}_p\) to groups with a bilinear map \(e:\mathbb {G}_1\times \mathbb {G}_2\rightarrow \mathbb {G}_T\), a similar structure emerges. For target assumptions in the base groups \(\mathbb {G}_1\) and \(\mathbb {G}_2\), we can again identify assumptions similar to the q-GDHE and q-SFrac assumptions that act as a joint Uber assumption. In the target group \(\mathbb {G}_T\), a somewhat more complicated picture emerges under the influence of the pairing of source group elements. However, we can replace the q-GDHE assumption with an assumption we call the q-Bilinear Gap (\(q\text {-BGap}\)) assumption, and get that this assumption together with a natural generalization of the \(q\text {-SFrac}\) assumption to bilinear groups, which we name the \(q\text {-BSFrac}\) assumption, jointly act as an Uber assumption for all target assumptions in \(\mathbb {G}_T\).
A natural question is whether our analysis extends to other assumptions as well, for instance “flexible” assumptions such as the q-HSDH assumption [12], where the adversary can choose secret exponents and therefore the target elements are no longer uniquely determined. Usually assumptions in the literature involve group elements that have discrete logarithms defined by polynomials in secret values in \(\mathbb {Z}_p\) chosen by a challenger and/or public values in \(\mathbb {Z}_p\). This gives rise to several classes of assumptions:
-
1.
Non-interactive assumptions where the adversary’s goal is to compute group elements defined by secret variables chosen by the challenger.
-
2.
Non-interactive assumptions where the adversary’s goal is to compute group elements defined by secret variables chosen by the challenger and public values chosen by the adversary.
-
3.
Non-interactive assumptions where the adversary’s goal is to compute group elements defined by secret variables chosen by the challenger, and public and secret values chosen by the adversary.
-
4.
Interactive assumptions, where the challenger and adversary interact.
Target assumptions include all assumptions in classes 1 and 2. However, class 3 includes assumptions which are not falsifiable, e.g. knowledge-of-exponent assumptions [5]. Since q-GDHE is in class 1 and q-SFrac is in class 2, both of which only have falsifiable assumptions, we cannot expect them to capture non-falsifiable assumptions in class 3. We leave it as an interesting open problem which structure, if any, can be found in classes 3 and 4, and we hope our work will inspire research on this question.
We stress that our aim is to find concrete and precise reductions and/or prove separations among the different classes of assumptions which encompass a significant portion of existing assumptions. Thus, our approach is different from previous works such as [9, 11, 19, 34] which aimed at defining algebraic frameworks or templates in generic groups to capture some families of assumptions. The closest work to ours is Abdalla et al. [1], which provided an Uber assumption for decisional assumptions in cyclic groups (without a bilinear map, which invalidates many decisional assumptions). Other works, discussed above, have mostly dealt with specific relations among assumptions, e.g., the equivalence of CDH and square-CDH as opposed to the general approach we take.
Paper Organization. Our research contribution is organized into three parts. In Sect. 3, we define our framework for target assumptions in cyclic groups, and progressively seek reductions to simpler assumptions. In Sect. 4, we study the internal structure and the relationships among the families of assumptions we identify as Uber assumptions for our framework. In Sect. 5, we provide a generalization of our framework in the bilinear setting.
2 Preliminaries
Notation. We say a function f is negligible when \(f({\kappa })={\kappa }^{-\omega (1)}\) and it is overwhelming when \(f({\kappa })=1-{\kappa }^{\omega (1)}\). We write \(f(\kappa )\approx 0\), when \(f(\kappa )\) is a negligible function. We will use \({\kappa }\) to denote a security parameter, with the intuition that as \({\kappa }\) grows we expect stronger security.
We write \(y=A(x;r)\) when algorithm A on input x and randomness r, outputs y. We write \(y\leftarrow A(x)\) for the process of picking randomness r at random and setting \(y=A(x;r)\). We also write \(y\leftarrow S\) for sampling y uniformly at random from the set S. We will assume it is possible to sample uniformly at random from sets such as \(\mathbb {Z}_p\). We write PPT and DPT for probabilistic and deterministic polynomial time respectively.
Quadratic Residuosity. For an odd prime p and an integer \(a\ne 0\), we say a is a quadratic residue modulo p if there exists a number x such that \(x^2 \equiv a ~(\text {mod}~p)\) and we say a is quadratic non-residue modulo p otherwise. We denote the set of quadratic residues modulo p by \(\mathbb {QR}(p)\) and the set of quadratic non-residues modulo p by \(\mathbb {QNR}(p)\). By Euler’s theorem, we have \(|\mathbb {QR}(p)|=|\mathbb {QNR}(p)|= {\frac{p\,{-}\,1}{2}}\).
2.1 Non-interactive Assumptions
In a non-interactive computational problem the adversary is given a problem instance and tries to find a solution. We say the adversary breaks the problem if it has non-negligible chance of finding a valid solution and we say the problem is hard if any PPT adversary has negligible chance of breaking it. We focus on non-interactive problems that are efficiently falsifiable, i.e., given the instance there is an efficient verification algorithm that decides whether the adversary won.
Definition 1 (Non-Interactive Computational Assumption)
A Non-interactive Computational Assumption consists of an instance generator \(\mathcal {I}\) and a verifier \(\mathcal {V}\) defined as follows:
- \(({pub},{priv})\leftarrow \mathcal {I}(1^{\kappa }){:}\) :
-
\(\mathcal {I}\) is a PPT algorithm that takes as input a security parameter \(1^{\kappa }\), and outputs a pair of public/private information \(({pub},{priv})\).
- \(b\leftarrow \mathcal {V}({pub},{priv},{sol}){:}\) :
-
\(\mathcal {V}\) is a DPT algorithm that receives as input \(({pub},{priv})\) and a purported solution \({sol}\) and returns 1 if it considers the answer correct and 0 otherwise.
The assumption is that for all PPT adversaries \(\mathcal {A}\), the advantage \(\mathsf {Adv}_{\mathcal {A}}\) is negligible (in \({\kappa }\)), where
Relations Among Assumptions. For two non-interactive assumptions \(\mathsf {A}\) and \(\mathsf {B}\), we will use the notation  when assumption \(\mathsf {B}\) is implied (in a black-box manner) by assumption \(\mathsf {A}\), i.e. given an efficient algorithm \(\mathcal {{B}}\) for breaking assumption \(\mathsf {B}\), one can construct an efficient algorithm \(\mathcal {{A}}\) that uses \(\mathcal {{B}}\) as an oracle and breaks assumption \(\mathsf {A}\). The absence of implication will be denoted by
when assumption \(\mathsf {B}\) is implied (in a black-box manner) by assumption \(\mathsf {A}\), i.e. given an efficient algorithm \(\mathcal {{B}}\) for breaking assumption \(\mathsf {B}\), one can construct an efficient algorithm \(\mathcal {{A}}\) that uses \(\mathcal {{B}}\) as an oracle and breaks assumption \(\mathsf {A}\). The absence of implication will be denoted by  .
.
2.2 Non-interactive Assumptions over Cyclic Groups
We study non-interactive assumptions over prime-order cyclic groups. These assumptions are defined relative to a group generator \(\mathcal {G}\).
Definition 2 (Group Generator)
A group generator is a PPT algorithm \(\mathcal {G}\), which on input a security parameter \({\kappa }\) (given in unary) outputs group parameters \((\mathbb {G}_p,{G})\), where
-
\(\mathbb {G}_p\) is cyclic group of known prime order p with bitlength \(|p|=\varTheta ({\kappa })\).
-
\(\mathbb {G}_p\) has a unique canonical representation of group elements, and polynomial time algorithms for carrying out group operations and deciding membership.
-
\({G}\) is a uniformly random generator of the group.
In non-interactive assumptions over prime-order groups the instance generator runs the group setup \((\mathbb {G}_p,{G})\leftarrow \mathcal {G}(1^{\kappa })\) and includes \(\mathbb {G}_p\) in \({pub}\). Sadeghi and Steiner [38] distinguish between group setups with low, medium and high granularity. In the low granularity setting the non-interactive assumption must hold with respect to random choices of \(\mathbb {G}_p\) and \({G}\), in the medium granularity setting it must hold for all choices of \(\mathbb {G}_p\) and a random \({G}\), and in the high granularity setting it must hold for all choices of \(\mathbb {G}_p\) and \({G}\). Our definitions always assume \({G}\) is chosen uniformly at random, so depending on \(\mathcal {G}\) we are always working in the low or medium granularity setting.
We will use [x] to denote the group element that has discrete logarithm x with respect to the group generator \({G}\). In this notation the group generator \({G}\) is [1] and the neutral element is [0]. We will find it convenient to use additive notation for the group operation, so we have \([x]+[y]=[x+y]\). Observe that given \(\alpha \in \mathbb {Z}_p\) and \([x]\in \mathbb {G}_p\) it is easy to compute \([\alpha x]\) using the group operations. For a vector \({\varvec{x}}=(x_1,\ldots ,x_n) \in \mathbb {Z}^n_p\) we use \(\left[{{\varvec{x}}}\right]\) as a shorthand for the tuple \(\left( \left[{x_1}\right],\ldots ,\left[{x_n}\right]\right) \in \mathbb {G}^n_p\). We will occasionally abuse the notation and let \(\left[{x_1,\ldots ,x_n}\right]\) denote the tuple \(\left( \left[{x_1}\right],\ldots ,\left[{x_n}\right]\right) \in \mathbb {G}^n_p\).
There are many examples of non-interactive assumptions defined relative to a group generator \(\mathcal {G}\). We list in Fig. 2 some of the existing non-interactive computational assumptions.
Generic Group Model. Obviously, if an assumption can be broken using generic-group operations, then it is false. The absence of a generic-group attack on an assumption does not necessarily mean the assumption holds [18, 25] but is a necessary precondition for the assumption to be plausible.
We formalize the generic group model [36, 39] where an adversary can only use generic group operations as follows. Given \(\mathbb {G}_p\) we let \([\cdot ]\) be a random bijection \(\mathbb {Z}_p\rightarrow \mathbb {G}_p\). We give oracle access to the addition operation, i.e., \(\mathcal {O}([x],[y])\) returns \([x+y]\). We say an assumption holds in the generic group model if an adversary with access to such an addition oracle has negligible chance of breaking the assumption. Note that the adversary gets \(\mathbb {G}_p\) as input and hence is capable of deciding group membership. Also, given an arbitrary [x], she can compute \([0]=[px]\) using the addition oracle. A generic adversary might be able to sample a random group element from \(\mathbb {G}_p\), but since they are just random encodings we may without loss of generality assume she only generates elements as linear combinations of group elements she has already seen. All the assumptions listed in Fig. 2 are secure in the generic group model.
3 Target Assumptions
The assumptions that can be defined over cyclic groups are legion. We will focus on the broad class of non-interactive computational assumptions where the adversary’s goal is to compute a particular group element. We refer to them as target assumptions.
The CDH assumption is an example of a target assumption where the adversary has to compute a specific group element. She is given \(\left( [1 ],[x ], [y ]\right) \in \mathbb {G}^3_p\) and is tasked with computing \([xy ]\in \mathbb {G}_p\).
We aim for maximal generality of the class of assumptions and will therefore also capture assumptions where the adversary takes part in specifying the target element to be computed. In the q-SDH assumption for instance the adversary is given \(\left( [1],[x],\ldots , [x^q ]\right) \in \mathbb {G}^{q+1}_p\) and is tasked with finding \(c\in \mathbb {Z}_p\) and \([\frac{1}{x\,{+}\,c}]\in \mathbb {G}_p\). Here the problem instance in itself does not dictate which group element the adversary must compute but the output of the adversary includes c, which uniquely determines the target element to be computed.
We will now define target assumptions. The class will be defined very broadly in order to capture existing assumptions in the literature such as CDH and q-SDH as well as other assumptions that may appear in future works.
In a target assumption, the instance generator outputs \({pub}\) that includes a prime-order group, a number of group elements, and possibly some additional information. Often, the group elements are of the form \([a(x)]\), where \(a\) is a polynomial and x is chosen uniformly at random from \(\mathbb {Z}_p\). We generalize this by letting the instance generator output group elements of the form \([\frac{a({\varvec{x}})}{b({\varvec{x}})}]\), where \(a({\varvec{x}})\) and \(b({\varvec{x}})\) are multi-variate polynomials and \({\varvec{x}}\) is chosen uniformly at random from \(\mathbb {Z}_p^{m}\). We will assume all the polynomials are known to the adversary, i.e., they will be explicitly given in the additional information in \({pub}\) in the form of their coefficients. The adversary will now specify a target group element. She does so by specifying polynomials \(r({\varvec{X}})\) and \(s({\varvec{X}})\) and making an attempt at computing the group element \([\frac{r({\varvec{x}})}{s({\varvec{x}})}]\).
If the target element can be computed using generic-group operations on the group elements in \({pub}\), then the problem is easy to solve and hence the assumption is trivially false. To exclude trivially false assumptions, the solution verifier will therefore check that for all fixed linear combinations \(\alpha _1,\ldots ,\alpha _n \in \mathbb {Z}_p\) there is a low probability over the choice of \({\varvec{x}}\) that \(\frac{r({\varvec{x}})}{s({\varvec{x}})}=\sum _i \alpha _i\frac{a_i({\varvec{x}})}{b_i({\varvec{x}})}\). The solution tuple output by the adversary is \({sol}= \left( r({\varvec{X}}),s({\varvec{X}}), [y], {sol}' \right) \), where \({sol}'\) is some potential extra information the verifier may need to check, for instance about how the polynomials \(r\) and \(s\) were constructed.
Definition 3 (Target Assumption)
Given polynomials \({d}({\kappa }), {m}({\kappa })\) and \({n}({\kappa })\) we say \((\mathcal {I},\mathcal {V})\) is a \(({d},{m},{n})\)-target assumption for \(\mathcal {G}\) if they can be defined by a PPT algorithm  and a DPT algorithm \(\mathcal {V}^{\mathsf {core}}\) such that
and a DPT algorithm \(\mathcal {V}^{\mathsf {core}}\) such that
- \(({pub},{priv})\leftarrow \mathcal {I}(1^{\kappa }){:}\) :
-
Algorithm \(\mathcal {I}\) proceeds as follows:
-
\((\mathbb {G}_p,[1])\leftarrow \mathcal {G}(1^{\kappa })\)
-
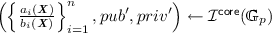
-
\({\varvec{x}}\leftarrow \mathbb {Z}_p^{{m}}\) conditioned on \(b_i({\varvec{x}})\ne 0\)
-
\({pub}:=\left( \mathbb {G}_p,\left\{ \left[ \frac{a_i({\varvec{x}})}{b_i({\varvec{x}})}\right] \right\} _{i=1}^{{n}} ,\left\{ \frac{a_i({\varvec{X}})}{b_i({\varvec{X}})} \right\} _{i=1}^{{n}} ,{pub}'\right) \)
-
Return \(\left( {pub}, {priv}= ([1], {\varvec{x}}, {priv}') \right) \)
-
 :
: -
Algorithm
 returns 1 if all of the following checks pass and 0 otherwise:
returns 1 if all of the following checks pass and 0 otherwise:
-

-
\([y ]=\frac{r({\varvec{x}})}{s({\varvec{x}})}[1]\)
-
\(\mathcal {V}^{\mathsf {core}}({pub},{priv},{sol})=1\)
We require that the number of indeterminates in \({\varvec{X}}\) is \({m}({\kappa })\) and each of the polynomials \(a_1({\varvec{X}}),b_1({\varvec{X}}),\ldots ,a_n({\varvec{X}}),b_n({\varvec{X}}),r({\varvec{X}}),s({\varvec{X}})\) has a total degree bounded by \({d}({\kappa })\), both of which can easily be checked by \(\mathcal {V}^{\mathsf {core}}\).
It is easy to see that all assumptions in Fig. 2 are target assumptions. For CDH for instance, we have \({d}=2, {m}=2, {n}=3\), \(a_1(X_1,X_2)=1, a_2(X_1,X_2)=X_1, a_3(X_1,X_2)=X_2\), and \(b_1(X_1,X_2)=b_2(X_1,X_2)=b_3(X_1,X_2)=1\). Algorithm \(\mathcal {V}^{\mathsf {core}}\) then checks that the adversary’s output is \(r(X_1,X_2)=X_1 X_2\) and \(s(X_1,X_2)=1\), which means the adverary is trying to compute the target \([x_1 x_2] \in \mathbb {G}_p\).
In q-SDH we have \({d}=q\), \({m}=1\), \({n}=q+1\), \(a_i(X)=X^{i-1}\), and \(b_i(X)=1\) for \(i=1,\ldots ,q+1\). Algorithm \(\mathcal {V}^{\mathsf {core}}\) checks that the target polynomials are of the form \(r(X)=1\) and \(s(X)=c+X\) for some \(c\in \mathbb {Z}_p\), meaning the adversary it is trying to compute the target \([\frac{1}{x\,{+}\,c} ]\in \mathbb {G}_p\).
3.1 Simple Target Assumptions
We now have a very general definition of target assumptions relating to the computation of group elements. In the following subsections, we go through progressively simpler classes of assumptions that imply the security of target assumptions. We start by defining simple target assumptions, where the divisor polynomials in the instance are trivial, i.e., \(b_1({\varvec{X}})=\cdots =b_n({\varvec{X}})=1\).
Definition 4 (Simple Target Assumption)
We say a \(({d},{m},{n})\)-target assumption  for \(\mathcal {G}\) is simple if the instance generator always picks polynomials \(b_1({\varvec{X}})=\ldots =b_n({\varvec{X}})=1\).
for \(\mathcal {G}\) is simple if the instance generator always picks polynomials \(b_1({\varvec{X}})=\ldots =b_n({\varvec{X}})=1\).
Next, we will prove that the security of simple target assumptions implies the security of all target assumptions. The idea is to reinterpret the tuple the adversary gets using the random generator [1] to having random generator \([\prod _{i=1}^{n}b_i({\varvec{x}})]\). Now all fractions of formal polynomials are scaled up by a factor \(\prod _{i=1}^{n}b_i({\varvec{X}})\) and the divisor polynomials can be cancelled out.
Theorem 1
For any \(({d},{m},{n})\)-target assumption  there exists a \((({n}+1) {d},{m},{n})\)-simple target assumption
there exists a \((({n}+1) {d},{m},{n})\)-simple target assumption  such that
such that  .
.
Proof
Given an assumption  and an adversary \(\mathcal {{A}}\) against it, we define a simple target assumption \(\mathsf {B}=(\mathcal {I}_{\mathsf {B}},\mathcal {V}_{\mathsf {B}})\) and an adversary \(\mathcal {{B}}\) (that uses adversary \(\mathcal {{A}}\) in a black-box manner) against it as illustrated in Fig. 3. The key observation is that as long as \(\prod _{i=1}^{n}b_i({\varvec{x}})\ne 0\), the two vectors of group elements \(\left( [c_1({\varvec{x}})],\ldots ,[c_{n}({\varvec{x}})]\right) \) and \(\left( [\frac{a_1({\varvec{x}})}{b_1({\varvec{x}})}],\ldots ,[\frac{a_{n}({\varvec{x}})}{b_{{n}}({\varvec{x}})}]\right) \) are identically distributed. By the specification of assumption \(\mathsf {A}\), it follows that \(b_i({\varvec{X}}) \not \equiv 0\) for all \(i\in \{1,\ldots ,{n}\}\). By the Schwartz-Zippel lemma, the probability that \(\prod _{i=1}^{{n}}b_i({\varvec{x}})=0\) is at most \(\frac{{d}{n}}{p}\). Thus, if \(\mathcal {A}\) has success probability \(\epsilon _\mathcal {A}\), then \(\mathcal {B}\) has success probability \(\epsilon _\mathcal {B}\ge \epsilon _\mathcal {A}-\frac{{d}{n}}{p}\). \(\square \)
and an adversary \(\mathcal {{A}}\) against it, we define a simple target assumption \(\mathsf {B}=(\mathcal {I}_{\mathsf {B}},\mathcal {V}_{\mathsf {B}})\) and an adversary \(\mathcal {{B}}\) (that uses adversary \(\mathcal {{A}}\) in a black-box manner) against it as illustrated in Fig. 3. The key observation is that as long as \(\prod _{i=1}^{n}b_i({\varvec{x}})\ne 0\), the two vectors of group elements \(\left( [c_1({\varvec{x}})],\ldots ,[c_{n}({\varvec{x}})]\right) \) and \(\left( [\frac{a_1({\varvec{x}})}{b_1({\varvec{x}})}],\ldots ,[\frac{a_{n}({\varvec{x}})}{b_{{n}}({\varvec{x}})}]\right) \) are identically distributed. By the specification of assumption \(\mathsf {A}\), it follows that \(b_i({\varvec{X}}) \not \equiv 0\) for all \(i\in \{1,\ldots ,{n}\}\). By the Schwartz-Zippel lemma, the probability that \(\prod _{i=1}^{{n}}b_i({\varvec{x}})=0\) is at most \(\frac{{d}{n}}{p}\). Thus, if \(\mathcal {A}\) has success probability \(\epsilon _\mathcal {A}\), then \(\mathcal {B}\) has success probability \(\epsilon _\mathcal {B}\ge \epsilon _\mathcal {A}-\frac{{d}{n}}{p}\). \(\square \)
3.2 Univariate Target Assumptions Imply Multivariate Target Assumptions
We will now show that security of target assumptions involving univariate polynomials imply security of target assumptions involving multivariate polynomials.
Theorem 2
For any \(({d},{m},{n})\)-simple target assumption \(\mathsf {A}=(\mathcal {I}_{\mathsf {A}},\mathcal {V}_{\mathsf {A}})\) there exists a \((({n}+1){d},1,{n})\)-simple target assumption \(\mathsf {B}=(\mathcal {I}_{\mathsf {B}},\mathcal {V}_{\mathsf {B}})\) where  .
.
Proof
Given \(\mathsf {A}=(\mathcal {I}_{\mathsf {A}},\mathcal {V}_{\mathsf {A}})\) and an adversary \(\mathcal {{A}}\) with success probability \(\epsilon _\mathcal {{A}}\) against it, we define a simple target assumption \((\mathcal {I}_{\mathsf {B}},\mathcal {V}_{\mathsf {B}})\) with univariate polynomials and construct an adversary \(\mathcal {{B}}\) (that uses \(\mathcal {{A}}\) in a black-box manner) against it as illustrated in Fig. 4.
Without loss of generality we can assume \(a_1({\varvec{X}}),\ldots ,a_{n}({\varvec{X}})\) are linearly independent, and therefore the polynomials \(r_{\mathsf {A}}({\varvec{X}})\) and \(s_{\mathsf {A}}({\varvec{X}})a_1({\varvec{X}}),\ldots ,s_{\mathsf {A}}({\varvec{X}})a_{n}({\varvec{X}})\) are all linearly independent. By Lemma 1 below this means that with probability \(1-\frac{d(n\,{+}\,1)}{p}\) the univariate polynomials \(r({\varvec{c}}(X))\) and \(s({\varvec{c}}(X))a_1({\varvec{c}}(X))\), \(\ldots \), \(s({\varvec{c}}(X))a_{n}({\varvec{c}}(X))\) output by \(\mathcal {B}\) are also linearly independent since the only information about \({\varvec{c}}(X)\) that \(\mathcal {B}\) passes on to \(\mathcal {A}\) can be computed from \((x,{\varvec{c}}(x))\). This means \(\mathcal {B}\) has advantage \(\epsilon _\mathcal {B}\ge \epsilon _\mathcal {A}-\frac{d(n\,{+}\,1)}{p}\) against assumption \(\mathsf {B}\). \(\square \)
Lemma 1
Let \(a_1({\varvec{X}}),\ldots ,a_n({\varvec{X}})\in \mathbb {Z}_p[{\varvec{X}}]\) be linearly independent m-variate polynomials of total degree bounded by d, and let \((x,{\varvec{x}})\in \mathbb {Z}_p\times \mathbb {Z}_p^m\). Pick a vector of m random univariate degree n polynomials \({\varvec{c}}(X)\in \left( \mathbb {Z}_p[X]\right) ^m\) that passes through \((x,\mathbf {x})\), i.e., \({\varvec{c}}(x)={\varvec{x}}\). The probability that \(a_1({\varvec{c}}(X)),\ldots ,a_n({\varvec{c}}(X))\) are linearly independent is at least \(1-\frac{dn}{p}\).
Proof
Take n random points \({\varvec{x}}_1,\ldots ,{\varvec{x}}_n\in \mathbb {Z}_p^m\) and consider the matrix
We will argue by induction that with probability \(1-\frac{dn}{p}\) the matrix is invertible. For \(n=1\) it follows from the Schwartz-Zippel lemma that the probability \(a_1({\varvec{x}}_1)=0\) is at most \(\frac{d}{p}\). Suppose now by induction hypothesis that we have probability \(1-\frac{d(n\,{-}\,1)}{p}\) that the top left \((n-1)\times (n-1)\) matrix is invertible. When it is invertible, the values \(a_n({\varvec{x}}_1),\ldots ,a_n({\varvec{x}}_{n-1})\) uniquely determine \(\alpha _1,\ldots ,\alpha _{n-1}\) such that for \(j=1,\ldots ,n-1\) we have \(a_n({\varvec{x}}_j)=\sum _{i=1}^{n-1}\alpha _ia_i({\varvec{x}}_j)\). Since the polynomials \(a_1({\varvec{X}}),\ldots ,a_n({\varvec{X}})\) are linearly independent, by the Schwartz-Zippel lemma, there is at most probability \(\frac{d}{p}\) that we also have \(a_n({\varvec{x}}_n)=\sum _{i=1}^{n-1}\alpha _ia_i({\varvec{x}}_n)\). So the row \((a_n({\varvec{x}}_1),\ldots ,a_n({\varvec{x}}_n))\) is linearly independent of the other rows, and hence we have M is invertible with at least probability \(1-\frac{d(n\,{-}\,1)}{p}-\frac{d}{p}=1-\frac{dn}{p}\).
Finally, picking a vector of m random polynomials \({\varvec{c}}(X)\) of degree n such that \({\varvec{c}}(x)={\varvec{x}}\) and evaluating it in distinct points \(x_1,\ldots ,x_n\leftarrow \mathbb {Z}_p\setminus \{x\}\) gives us n random points \({\varvec{c}}(x_j)\in \mathbb {Z}_p^m\). So the matrix
has at least probability \(1-\frac{dn}{p}\) of being invertible. If \(\sum _{i=1}^n\alpha _ia_i({\varvec{c}}(X))=0\), then it must hold in the distinct points \(x_1,\ldots ,x_n\), and we can see there is only the trivial linear combination with \(\alpha _1=\cdots = \alpha _n=0\). \(\square \)
Having reduced target assumptions to simple univariate target assumptions with \({m}=1\), we will in the next two subsections consider two separate cases. First, the case where the polynomial \(s(X)\) is fixed, i.e., it can be deterministically computed. Second, the case where the polynomial \(s(X)\) may vary.
3.3 Polynomial Assumptions
We now consider simple target assumptions with univariate polynomials where \(s(X)\) is fixed. We can without loss of generality assume this means \({priv}'\) output by the instance generator contains \(s(X)\) and the solution verifier checks whether the adversary’s solution matches \(s(X)\). There are many assumptions where \(s(X)\) is fixed, in the Diffie-Hellman inversion assumption we will for instance always have \(s(X)=X\) and in the q-GDHE assumption we always have \(s(X)=1\). When the polynomial \(s(X)\) is fixed, we can multiply it away as we did for the multivariate polynomials \(b_1({\varvec{X}}),\ldots ,b_{n}({\varvec{X}})\) when reducing target assumptions to simple target assumptions. This leads us to define the following class of assumptions:
Definition 5 (Polynomial Assumption)
We say a \(({d},1,{n})\)-simple target assumption \((\mathcal {I},\mathcal {V})\) for \(\mathcal {G}\) is a \(({d},{n})\)-polynomial assumption if \(\mathcal {V}\) only accepts a solution with \(s(X)=1\).
We leave the proof of the following theorem to the reader.
Theorem 3
For any \(({d},1,{n})\)-simple target assumption \(\mathsf {A}=(\mathcal {I}_{\mathsf {A}},\mathcal {V}_{\mathsf {A}})\) for \(\mathcal {G}\) where the polynomial \(s(X)\) is fixed, there is a \((2{d},{n})\)-polynomial assumption \(\mathsf {B}=(\mathcal {I}_{\mathsf {B}},\mathcal {V}_{\mathsf {B}})\) where  .
.
We will now show that all polynomial assumptions are implied by the generalized Diffie-Hellman exponent (q-GDHE) assumptions (cf. Fig. 2) along the lines of [22]. This means the q-GDHE assumptions are Uber assumptions that imply the security of a major class of target assumptions, which includes a majority of the non-interactive computational assumptions for prime-order groups found in the literature.
Theorem 4
For any \(({d},{n})\)-polynomial assumption \(\mathsf {A}=(\mathcal {I}_{\mathsf {A}},\mathcal {V}_{\mathsf {A}})\) for \(\mathcal {G}\) we have that  .
.
Proof
Let \(\mathcal {{A}}\) be an adversary against the \(({d},{n})\)-polynomial assumption. We show how to build an adversary \(\mathcal {{B}}\), which uses \(\mathcal {{A}}\) in a black-box manner to break the \(({d}+1)\)-GDHE assumption. Adversary \(\mathcal {{B}}\) gets \([1], \left[ {x}\right] ,\ldots , \left[ {x^{{d}}}\right] ,[x^{{d}+2}],\ldots , \left[ {x^{2{d}+2}}\right] \) from the \(({d}+1)\text {-GDHE}\) instance generator and her aim is to output the element \( \left[ {x^{{d}+1}}\right] \in \mathbb {G}_p\). Adversary \(\mathcal {{B}}\) uses algorithm  to generate a simulated polynomial problem instance as described below, which she then forwards to \(\mathcal {{A}}\).
to generate a simulated polynomial problem instance as described below, which she then forwards to \(\mathcal {{A}}\).

Assuming \(c(x)\ne 0\), which happens with probability \(1 - \frac{d\,{+}\,1}{p}\), the input to \(\mathcal {{A}}\) looks identical to a normal problem instance for assumption \(\mathsf {A}\) with generator \([c(x)]\). Furthermore, if \(\mathcal {{A}}\) finds a satisfactory solution to this problem, we then have \([y]=r(x)[c(x)]\). By Lemma 2 below there is at most \(\frac{1}{p}\) chance of returning \(r(X)\) such that \(r(X)c(X)\) has coefficient 0 for \(X^{d+1}\) and hence using the \((2d+2)\) elements from the \((d+1)\)-GDHE tuple, we can recover \([x^{d+1}]\) from [y]. We now get that if \(\mathcal {{A}}\) has advantage \(\epsilon _{\mathcal {A}}\) against \(\mathsf {A}\), then \(\mathcal {{B}}\) has advantage \(\epsilon _\mathcal {B}\ge \epsilon _\mathcal {A}-\frac{d\,{+}\,2}{p}\) against the \(({d}+1)\)-GDHE assumption. \(\square \)
Lemma 2
(Lemma 10 from [22]). Let \(\left\{ a_i(X)\right\} _{i=1}^{n}\) be polynomials of degree at most \({d}\). Pick \(x\leftarrow \mathbb {Z}_p\) and \(c(X)\) as a random degree \({d}+1\) polynomial such that all products \(b_i(X)=a_i(X)c(X)\) have coefficient 0 for \(X^{d+1}\). Given \(\left( \left\{ a_i(X)\right\} _{i=1}^{n},x,c(x)\right) \), the probability of guessing a non-trivial degree \({d}\) polynomial \(r(X)\) such that \(r(X)c(X)\) has coefficient 0 for \(X^{d+1}\) is at most \(\frac{1}{p}\).
3.4 Fractional Assumptions
We now consider the alternative case of simple target assumptions with univariate polynomials, where \(s(X)\) is not fixed. When \(s(X)|r(X)\), we can without loss of generality divide out and get \(s(X)=1\). The remaining case is when \(s(X)\not \mid r(X)\), which we now treat.
Definition 6
(
\(({d},{n})\)-Fractional Assumption). We say a \(({d},1,{n})\)-simple target assumption  for \(\mathcal {G}\) is an \(({d},{n})\)
-fractional assumption if
for \(\mathcal {G}\) is an \(({d},{n})\)
-fractional assumption if  only accepts the solution if \(s(X) \not \mid r(X)\).
only accepts the solution if \(s(X) \not \mid r(X)\).
Next we define a simple fractional assumption which we refer to for short as q-SFrac, which says given the tuple \(([1],[x],[x^2],\ldots ,[x^q])\) it is hard to compute \(\left[ \frac{r(x)}{s(x)}\right] \) when \(\deg (r)<\deg (s)\). The simple fractional assumption is a straightforward generalization of the q-SDH assumption, where \(\deg (r)=0\) since \(r(X)=1\) and \(\deg (s) =1\). A proof for the intractability of the q-SFrac assumption in the generic group model can be found in the full version [23].
Definition 7
( q-SFrac Assumption). The q-SFrac assumption is a simple target assumption where \({n}=q+1\), \(a_i(X)=X^{i-1}\), and \(0 \le \deg (r) < \deg (s) \le q\).
We now prove the following theorem.
Theorem 5
For any \(({d},{n})\)-fractional assumption \(\mathsf {A}=(\mathcal {I},\mathcal {V})\) for \(\mathcal {G}\) we have  .
.
Proof
Let \(\mathcal {{A}}\) be an adversary against a \(({d},{n})\)-fractional assumption \(\mathsf {A}\). We show how to use \(\mathcal {A}\) to construct an adversary \(\mathcal {{B}}\) against the \({d}\)-SFracassumption. Adversary \(\mathcal {{B}}\) gets \(\left( \mathbb {G}_p, [1], \left[ {x}\right] ,\ldots , \left[ {x^{d}}\right] \right) \) from her environment and her aim is to output a valid solution of the form \(\left( r'(X),s'(X),\left[ \frac{r'(x)}{s'(x)}\right] \right) \) where \(\deg (r') < \deg (s')\le {d}\). Adversary \(\mathcal {{B}}\) uses the instance generator algorithm  of the fractional assumption as described below to generate a problem instance, which she then forwards to \(\mathcal {{A}}\).
of the fractional assumption as described below to generate a problem instance, which she then forwards to \(\mathcal {{A}}\).

The advantage of adversary \(\mathcal {{B}}\) against the \({d}\)-SFracassumption is the same as that of adversary \(\mathcal {{A}}\) against the fractional assumption \(\mathsf {A}\). \(\square \)
3.5 The q-SFracand q-GDHE Assumptions Together Imply All Target Assumptions in Cyclic Groups
We now prove that the q-SFracand q-GDHE assumptions together constitute an Uber assumption for all target assumptions in prime-order cyclic groups.
Theorem 6
There is a polynomial \(q({d},{m},{n})\) such that the joint q-SFrac and q-GDHE assumption implies all \(({d},{m},{n})\)-target assumptions.
Proof
Let \(\mathsf {A}\) be a \(({d},{m},{n})\)-target assumption. By Theorem 1, for any adversary \(\mathcal {A}\) with advantage \(\epsilon _{_\mathcal {A}}\) against \(\mathsf {A}\), we can define a \(({d}({n}+1),{m},{n})\)-simple target assumption \(\mathsf {A_1}\) and an adversary \(\mathcal {A}_1\) with advantage \(\epsilon _{_{\mathcal {A}_1}} \ge \epsilon _{_\mathcal {A}} - \frac{{d}{n}}{p}\) against it. By Theorem 2, using \(\mathcal {A}_1\) against \(\mathsf {A_1}\), we can define a \(({d}({n}+1)^2, 1,{n})\)-simple target assumption \(\mathsf {A_2}\) and an adversary \(\mathcal {A}_2\) against it with advantage \(\epsilon _{_{\mathcal {A}_2}} \ge \epsilon _{_{\mathcal {A}_1}} - \frac{{d}({n}\,+\,1)^2}{p} \ge \epsilon _{_{\mathcal {A}}} - \frac{{d}({n}\,+\, ({n}\,+\,1)^2)}{p}\). We now have two cases as follows:
-
With non-negligible probability a successful solution has \(s_{\mathsf {A_2}}(X)\not \mid r_{\mathsf {A_2}}(X)\). By Theorem 5, we can use \(\mathcal {A}_2\) to construct an adversary \(\mathcal {A}_3\) against the \(({d}({n}+1)^2){\text {-SFrac}}\) assumption where advantage \(\epsilon _{_{\mathcal {A}_3}} \ge \epsilon _{_{\mathcal {A}_2}} \ge \epsilon _{_{\mathcal {A}}} - \frac{{d}({n}\, + \,({n}\,+\,1)^2)}{p}\). Since by defintion \({d},{n}\in \mathsf {Poly}({\kappa })\) and \(\log {p} \in \theta ({\kappa })\), it follows that \(\frac{{d}({n}\,+\, ({n}\,+\,1)^2)}{p}\) is negligible (in \({\kappa }\)).
-
With overwhelming probability a successful solution uses polynomials where \(s_{\mathsf {A_2}}(X)|r_{\mathsf {A_2}}(X)\) which is equivalent to the case where \(s_{\mathsf {A_2}}(X)=1\). By Theorem 3, using \(\mathcal {A}_2\) we can define a \((2 {d}({n}+ 1)^2,{n})\)-polynomial assumption \(\mathsf {A_3}\) and an adversary \(\mathcal {A}_3\) with advantage \(\epsilon _{_{\mathcal {A}_3}} \ge \epsilon _{_{\mathcal {A}_2}} - \frac{4 {d}({n}\,+\, 1)^2}{p} \ge \epsilon _{_{\mathcal {A}}} - \frac{{d}({n}\,+\, 5({n}\,+\,1)^2 )}{p}\). By Theorem 4, using adversary \(\mathcal {A}_3\), we can construct an adversary \(\mathcal {A}_4\) against the \((2{d}({n}+1)^2 + 1)\)-GDHE assumption with advantage \(\epsilon _{_{\mathcal {A}_4}} \ge \epsilon _{_{\mathcal {A}_3}} - \frac{2 {d}({n}\,+\, 1)^2 \,+\,2}{p}\). From which it follows that \(\epsilon _{_{\mathcal {A}_4}} \ge \epsilon _{_{\mathcal {A}}} - \frac{{d}(7({n}\,+\,1)^2 \,+\, {n}) + 2}{p}\). Since by defintion \({d},{n}\in \mathsf {Poly}({\kappa })\) and \(\log {p} \in \theta ({\kappa })\), it follows that \(\frac{{d}(7({n}\, +\, 1)^2 \,+\, {n}) + 2}{p}\) is negligible (in \({\kappa }\)).
\(\square \)
4 The Relationship Between the GDHE and SFrac Assumptions
Having identified the q-GDHE and q-SFrac assumptions as Uber assumptions for all target assumptions, it is natural to investigate their internal structure and their relationship to each other. One obvious question is whether a further simplification is possible and one of the assumption classes imply the other. We first analyze the case where \(q\ge 2\) and show that q-SFrac does not imply 2-GDHE for generic algorithms. This means that we need the q-GDHE assumptions to capture the polynomial target assumptions, the q-SFrac assumptions cannot act as an Uber assumption for all target assumptions on their own.
We also look at the lowest level of the q-SFrac and q-GDHE hierarchies. Observe that the 1-SFrac assumption is equivalent to the 1-SDH assumption. We prove that the 1-GDHE assumption is equivalent to the CDH assumption. This immediately also gives us that the 1-SFrac assumption implies the 1-GDHE assumption since the 1-SDH assumption implies the CDH assumption. A summary of the implications we prove can be found in Fig. 1.
4.1 The SFrac Assumptions Do Not Imply the 2-GDHE Assumption
We prove here that the i-GDHE assumption for \(i \ge 2\) is not implied by any q-SFracassumption for generic adversaries, i.e.  for all \(i \ge 2\). More precisely, we show that providing an unbounded generic adversary \(\mathcal {A}\) against a q-SFracassumption with a 2-GDHE oracle \(\mathcal {O}_{{\mathrm {\tiny 2\text {-GDHE}}}}\), which on input \((\left[{a}\right],\left[{b}\right],\left[{c}\right],\left[{d}\right])\) where \(b=az\), \(c=az^{3}\), \(d=az^4\) returns the element \(\left[{az^2}\right]\), and returns the symbol \(\perp \) if the input is malformed, does not help the adversary.
for all \(i \ge 2\). More precisely, we show that providing an unbounded generic adversary \(\mathcal {A}\) against a q-SFracassumption with a 2-GDHE oracle \(\mathcal {O}_{{\mathrm {\tiny 2\text {-GDHE}}}}\), which on input \((\left[{a}\right],\left[{b}\right],\left[{c}\right],\left[{d}\right])\) where \(b=az\), \(c=az^{3}\), \(d=az^4\) returns the element \(\left[{az^2}\right]\), and returns the symbol \(\perp \) if the input is malformed, does not help the adversary.
Theorem 7
The q-SFracassumption does not imply the 2-GDHE assumption in generic groups.
Proof
Consider a generic adversary \(\mathcal {A}\) which gets input \(\left( \left[{1}\right], \left[{x}\right], \ldots , \left[{x^q}\right] \right) \) and is tasked with outputting \(\left( \frac{r(X)}{s(X)}, \left[{\frac{r(x)}{s(x)}}\right] \right) \), where \(0 \le \deg (r) < \deg (s) \le q\). We give \(\mathcal {A}\) access to an oracle \(\mathcal {O}_{{\mathrm {\tiny 2\text{-GDHE }}}}(\cdot ,\cdot ,\cdot ,\cdot )\) as above, which can be queried polynomially many times.
Since \(\mathcal {A}\) is generic, the tuple \(\left( [a],[b],[c],[d] \right) \) she uses as input in her 1-st  query can only be linear combinations of the elements \([1],[x],\ldots ,[x^q]\). Thus, we have
query can only be linear combinations of the elements \([1],[x],\ldots ,[x^q]\). Thus, we have
for known \(\alpha _j,\beta _j,\gamma _j\). Let the corresponding formal polynomials be a(X), b(X) and c(X), respectively. We have that \(\deg (a), \deg (b), \deg (c) \in \{0,\ldots ,q\}\). By definition, for the input to the oracle  to be well-formed, we must have \(b= a z\) and \(c=a z^{3}\) for some z. In the generic group model this has negligible probability of holding unless z corresponds to some (possibly rational) function z(X) and we have \(b(X)=a(X)z(X)\) and \(c(X)=a(X)z(X)^3\) when viewed as formal polynomials.
to be well-formed, we must have \(b= a z\) and \(c=a z^{3}\) for some z. In the generic group model this has negligible probability of holding unless z corresponds to some (possibly rational) function z(X) and we have \(b(X)=a(X)z(X)\) and \(c(X)=a(X)z(X)^3\) when viewed as formal polynomials.
If the adversary submits a query where \(a(X) \equiv 0\) or \(b(X) \equiv 0\), the oracle will just return [0], which is useless to the adversary. So from now on let’s assume that \(a(X) \not \equiv 0\), \(b(X) \not \equiv 0\) and \(c(X) \not \equiv 0\).
We now have
This means \(a(X)^2|b(X)^3\), which implies \(a(X)|b(X)^2\). The answer returned by the oracle on a well-formed input corresponds to \(a(X)z(X)^2=a(X)\left( \frac{b(X)}{a(X)}\right) ^2=\frac{b(X)^2}{a(X)}\). Since \(a(X)|b(X)^2\), the answer corresponds to a proper polynomial.
If \(\deg (b)\le \deg (a)\), we have \(2\deg (b)-\deg (a)\le \deg (b)\le q\), and if \(\deg (b)\ge \deg (a)\), we have \(2\deg (b)-\deg (a)\le 3\deg (b)-2\deg (a)=\deg (c)\le q\). Thus, the answer the oracle returns corresponds to a known polynomial of degree in \(\{0,\ldots ,q\}\) which could have been computed by the adversary herself using generic group operations on the tuple \([1],[x],\ldots ,[x^q]\) without calling the oracle. \(\square \)
Since as we prove later the GDHE assumptions family is strictly increasingly stronger, we get the following corollary.
Corollary 1
For all \(i \ge 2\) it holds that  .
.
4.2 CDH Implies the 1-GDHE Assumption
Since having access to a CDH oracle allows one to compute any polynomial in the exponent [31] (in fact, such an oracle provides more power as it allows computing even rational functions in the exponent for groups with known order [31]), it is clear that  and
and  . We prove in this section the implication
. We prove in this section the implication  , which means that the assumptions CDH and 1-GDHE are equivalent. As a corollary
, which means that the assumptions CDH and 1-GDHE are equivalent. As a corollary  for all q.
for all q.
We start by proving that the square computational Diffie-Hellman assumption (SCDH) (cf. Fig. 2), which is equivalent to the CDH assumption [3, 26], implies the square root Diffie-Hellman (SRDH) assumption [29] (cf. Fig. 2)Footnote 2. Note that given a SCDH oracle, one can solve any CDH instance by making 2 calls to the SCDH oracle. Let \(([1],[a],[b])\in \mathbb {G}^3_p\) be a CDH instance, we have \([ab]=\frac{1}{4}([(a+b)^2] - ([(a-b)^2]))\).
We remark here that Roh and Hahn [37] also gave a reduction from the SCDH assumption to the SRDH assumption. However, their reduction relies on two assumptions: that the oracle will always (i.e. with probability 1) return a correct answer when queried on quadratic-residue elements and uniformly random elements when queried on quadratic non-residue elements, and that the prime order of the group p has the special form \(p=2^t q + 1\) where \(2^{t}=O({\kappa }^{O(1)})\). Our reduction is more general since we do not place any restrictions on t or q and more efficient since it uses \(4t+2|q|\) oracle queries, whereas their reduction uses \(O(t(2^t+|q|))\) oracle queries. Later on, we will also show how to boost an imperfect 1-GDHE oracle to get a SCDH oracle.
The Perfect Oracle Case. We prove that a perfect SRDH oracle  which on input a pair \(([a],[a z]) \in \mathbb {G}^2_p\) returns the symbol QNR (which for convenience we denote by [0]) if \(z \notin \mathbb {QR}(p)\) and \([\pm a\sqrt{z}]\) otherwise, leads to a break of the SCDH assumption. The role of the exponent a is to allow queries on pairs w.r.t. a different group generator than the default one.
which on input a pair \(([a],[a z]) \in \mathbb {G}^2_p\) returns the symbol QNR (which for convenience we denote by [0]) if \(z \notin \mathbb {QR}(p)\) and \([\pm a\sqrt{z}]\) otherwise, leads to a break of the SCDH assumption. The role of the exponent a is to allow queries on pairs w.r.t. a different group generator than the default one.
Let \(p=2^t q + 1\) for an odd positive integer q be the prime order of the group \(\mathbb {G}_p\). Note that when \(p \equiv 3 ~(\text {mod}~4)\) (this is the case when \(-1 \in \mathbb {QNR}(p)\)), we have \(t=1\), and in the special case where p is a safe prime, q is also a prime. On the other hand, when \(p \equiv 1 ~(\text {mod}~4)\) (this is the case when \(-1 \in \mathbb {QR}(p)\)), we have \(t>1\).
In the following let \(\omega \in \mathbb {QNR}(p)\) be an arbitrary \(2^t\)-th root of unity of \(\mathbb {Z}^\times _p\), i.e., \(\omega ^{2^{t-1}}\equiv -1 \bmod (p-1)\) and \(\omega ^{2^t}\equiv 1 \bmod (p-1)\). Note that there are \(\phi (2^t)=2^{t-1}\) roots of unity and finding one is easy since for any generator g of \(\mathbb {Z}^\times _p\), \(g^q\) is a \(2^t\)-th root of unity. Observe that all elements in \(\mathbb {Z}_p^\times \) can be written in the form \(\omega ^i\beta \), where \(\beta \) has odd order k|q. The quadratic residues are those where i is even, and the quadratic non-residues are the ones where i is odd.
Theorem 8
Given a perfect  oracle, we can solve any SCDH instance using at most \(4t+2|q|\) oracle calls when the group order is \(p=2^tq+1\) for odd q.
oracle, we can solve any SCDH instance using at most \(4t+2|q|\) oracle calls when the group order is \(p=2^tq+1\) for odd q.
Algorithms \(\mathsf {FindExpi}\) and \(\mathsf {Square}\) used in the proof of Theorem 8
Proof
Given a SCDH instance \(([1],[x]) \in \mathbb {G}^2_p\), our task is to compute \(\left[ x^2\right] \in \mathbb {G}_p\). The task is trivial when \(x=0\), so let’s from now on assume \(x\ne 0\). Since any \(x\in \mathbb {Z}^\times _p\) can be written as \(x=\omega ^i \beta \) where \(\omega \in \mathbb {Z}^\times _p\) is a \(2^t\)-th root of unity and \(\beta \in \mathbb {Z}^\times _p\) has an odd order k where k|q, our task is to compute \(\left[ x^2\right] =\left[ \omega ^{2i} \beta ^2\right] \). In the following, we will first describe an algorithm \(\mathsf {FindExpi}\) that uses the square-root oracle to determine i. Next, we describe an algorithm \(\mathsf {Square}\) that computes \([y]=\left[ \omega ^j\beta ^2\right] \) for some j, and then use \(\mathsf {FindExpi}\) to clean it up to get \(\left[ x^2\right] =\left[ \omega ^{2i-j}y]=[\omega ^{2i}\beta ^2\right] \). Both of these algorithms are given in Fig. 5.
Recall the perfect SRDH oracle responds with QNR, i.e. [0], whenever it gets a quadratic non-residue as input, i.e., whenever it gets input \(([1],[\omega ^i\beta ])\) for an odd i and \(\beta \) has an odd order. When it gets a quadratic residue as input, i.e., when i is even, it returns \(\left[ \pm \omega ^{\frac{i}{2}}\beta ^{\frac{1}{2}}\right] \). Since \(\omega ^{2^{t-1}}=-1\) this means it returns either \(\left[ \omega ^{\frac{i}{2}}\beta ^{\frac{1}{2}}\right] \) or \(\left[ \omega ^{2^{t-1}+\frac{i}{2}}\beta ^{\frac{1}{2}}\right] \).
Let the binary expansion of the exponent be \(i=i_{t-1}i_{t-2}\ldots i_0\). In the \(\mathsf {FindExpi}\) algorithm we use the oracle to learn the least significant bit and also to right-shift the bits. Consider running the oracle on ([1], [x]) and on \(([1],[\omega ^{-1}x])\). If \(i_0=0\), then i is even and on the first input the oracle returns a new element with exponent \(i_{t}i_{t-1}\ldots i_1\). If \(i_1=1\) then i is odd, and the oracle returns a new element with exponent \(i_ti_{t-1}\ldots i_1\) on the second input. Which call returns a non-trivial group element tells us what \(i_0\) is and in both cases we get a new element where the bits have been shifted right and a new most significant bit \(i_t\) has been added. Repeating t times allows us to learn all of \(i=i_{t-1}\ldots i_0\).
Next we describe the \(\mathsf {Square}\) algorithm. The idea behind this algorithm is that given \([\omega ^i\beta ]\) we want to compute \([\omega ^j\beta ^2]\) for some j, but we do not care much about the root of unity part, i.e., what j is, since we can always determine that by calling \(\mathsf {FindExpi}\) and clean it up later. As a first step one of the inputs ([1], [x]) or \(([1],[\omega x])\) will correspond to a quadratic residue and the square root oracle will return some \([y]=[\omega ^j \beta ^{\frac{1}{2}}]=[\omega ^j \beta ^{\frac{q\,+\,1}{2}}]\). Let’s define \(h=\frac{q\,+\,1}{2}\), which is a positive integer, so we have \([y]=[\omega ^j \beta ^h]\).
The idea now is that we will use repeated applications of the SRDH oracle to halve h until we get down to \(h=2\). If h is even, this works fine as one of the pairs \(([1],[\omega ^j\beta ^h])\) or \(([1],[\omega ^{j+1}\beta ^h])\) will correspond to a quadratic residue and we get a new element of the form \([\omega ^{j'}\beta ^{h'}]\), where \(h'=\frac{h}{2}\).
If h is odd, this strategy does not work directly. However, in this case we can use [x] as generator instead of [1] and have that one of the pairs \(([\omega ^i\beta ],[\omega ^j\beta ^h])\) or \(([\omega ^i\beta ],[\omega ^{j+1}\beta ^h])\) is a quadratic residue. By applying the square-root oracle, we get a new element of the form \([\omega ^{j'}\beta ^{h'}]\), where \(h'=\frac{h\,+\, 1}{2}\).
Repeated application of these two types of calls, depending on whether h is even or odd, eventually gives us an element of the form \([\omega ^j\beta ^2]\). At this stage, we can use the \(\mathsf {FindExpi}\) algorithm to determine i and j, which makes it easy to compute \([x^2]=\omega ^{2i-j}[\omega ^j\beta ^2]\).
We now analyse the time complexity of the algorithms. Algorithm \(\mathsf {FindExpi}\) makes at most 2t oracle calls, whereas \(\mathsf {Square}\) makes at most 2|q| oracle calls plus two invocations of \(\mathsf {FindExpi}\), i.e., at most \(4t+2|q|\) oracle calls in total. \(\square \)
Using an Adversarial
\(\mathcal {O}_{1{\mathbf -GDHE}}^*\) Oracle. In Theorem 8, we assumed the reduction had a perfect  oracle. Here we weaken the assumption used in the reduction and consider an
oracle. Here we weaken the assumption used in the reduction and consider an  oracle that returns a correct answer with a non-negligible probability \(\epsilon \) when queried on a quadratic residue element. More precisely, let \(([a],[b]) \in \mathbb {G}^2_p\) be the input we are about to query the \(\mathcal {O}_{{1\hbox {-GDHE}}}^*\) oracle on. Since we can easily detect if \(b=0\), we can assume that we never need to query to oracle on any input where \(b=0\). When queried on \(([a],[b]) \in \mathbb {G}^\times _p \times \mathbb {G}^\times _p\), the oracle will return either the symbol QNR, i.e. \([0] \in \mathbb {G}_p\) or \([c] \in \mathbb {G}_p\) for some \(c\in \mathbb {Z}^\times _p\). Our assumption about correctness is
oracle that returns a correct answer with a non-negligible probability \(\epsilon \) when queried on a quadratic residue element. More precisely, let \(([a],[b]) \in \mathbb {G}^2_p\) be the input we are about to query the \(\mathcal {O}_{{1\hbox {-GDHE}}}^*\) oracle on. Since we can easily detect if \(b=0\), we can assume that we never need to query to oracle on any input where \(b=0\). When queried on \(([a],[b]) \in \mathbb {G}^\times _p \times \mathbb {G}^\times _p\), the oracle will return either the symbol QNR, i.e. \([0] \in \mathbb {G}_p\) or \([c] \in \mathbb {G}_p\) for some \(c\in \mathbb {Z}^\times _p\). Our assumption about correctness is

The oracle can behave arbitrarily when it does not return a correct answer or when the input is not a quadratic residue.
We will now show that we can rectify the adversarial behaviour of the oracle so that it cannot adapt its answer based on the instance input. The idea is to randomize the inputs to be queried to the oracle so that they are uniformly distributed over the input space and we get \(\epsilon \) chance of getting a correct square-root when the input is a quadratic residue. To check the solution, we then randomize an element related to the answer, which we can use to detect when the oracle is misbehaving. The result is a Monte Carlo algorithm described in Fig. 6, which with probability \(\epsilon '\ge \epsilon ^2\) returns a correct square-root when queried on a quadratic residue and \(\bot \) in all other cases.
Lemma 3
Using \(\mathcal {O}_{{1\text {-GDHE}}}^*\) which returns a correct answer with probability \(\epsilon \), algorithm \(\mathsf {MOracle}\) returns a correct answer with probability \(\epsilon ' \ge \epsilon ^2\) when queried on a well-formed pair \(([a],[b])\in \mathbb {G}^\times _p \times \mathbb {G}^\times _p\) and \(\bot \) otherwise.
Proof
If \(\frac{b}{a} \in \mathbb {QR}(p)\), we also have \(\frac{\beta ^2 b}{a} \in \mathbb {QR}(p)\), and when \(\frac{b}{a} \notin \mathbb {QR}(p)\), we also have \(\frac{\beta ^2 b}{a} \notin \mathbb {QR}(p)\). We have probability \(\epsilon \) that the answer [y] is a correct answer when \(\frac{b}{a} \in \mathbb {QR}(p)\) in which case \(y=\pm \alpha \beta a \sqrt{\frac{b}{a}}\), we can thus recover \([\pm a \sqrt{\frac{b}{a}}= \pm \sqrt{a b}]\) by computing \(\frac{1}{\alpha \beta }[y]\). Let \(y'=\frac{y}{\alpha \beta }=\pm \sqrt{a b}\). We have probability \(\epsilon \) that [z] is a correct answer. Now let \(z' = \frac{z}{\gamma \delta }\).
Note that \(r^2 a + 2 r s y' + s^2 b=(r a + s y')^2 + s^2( b - y'^2)\) and if [z] is a correct answer then we have \(z'=\pm (r a+ s y')\). Thus, we have probability at least \(\epsilon ^2\) that algorithm \(\mathsf {MOracle}\) will return a correct square root when the input is well-formed.
We now argue that if \(y' \ne \pm \sqrt{ab}\), with overwhelming probability the algorithm will return \(\bot \). Let \(\tau =a(r^2 a + 2 r s y' + s^2 b) = r^2 a^2 + 2 a r s y' + s^2 a b\).
Since \(a(r^2 a + 2 r s y' + s^2 b) = (r a + s y')^2 + s^2 (a b - y'^2)\), the query to the oracle is determined by a and \(\tau \), and there are roughly \(p^2\) pairs (r, s) mapping into a maximum of p choices of \(\tau \). Therefore, for the same oracle query there are many possible values s could have. Now if \(y' \ne \pm \sqrt{a b }\), i.e. y is an incorrect answer, then the oracle has negligible chance of passing the test \(z'=\pm (ra + sy')\) in line 5. If the test passes, then \(z'^2=(r a + s y')^2 = r^2 a^2 + 2 a r s y' + s^2 a b= \tau - s^2(ab - y'^2)\). Since s is information-theoretically undetermined from a and \(\tau \), there is negligible chance over the choice of s that this equality holds unless \(ab - y'^2=0\). \(\square \)
Since \(\epsilon \) is non-negligible, there must be a constant \(c>0\) such that for infinitely many \({\kappa }\) we have \(\epsilon '\ge {\kappa }^{-c}\). We can use repetitions to boost the oracle to give the correct answer with overwhelming probability on these \({\kappa }\) values, i.e., on quadratic residues it returns square-roots and on quadratic non-residues it returns \(\bot \) or equivalently [0]. Chernoff-bounds ensure we only need \(\frac{{\kappa }}{\epsilon ^2}\) polynomially iterations of the Monte Carlo algorithm to build a good SRDH oracle.
4.3 The q-GDHE Family Structure
We say a family of assumptions \(\{q\text {-}\mathsf {A}\}\) is a strictly increasingly stronger family if for all polynomials \(q\le q^\prime \) it holds that  but
but  . A proof for the following theorem can be found in the full version [23].
. A proof for the following theorem can be found in the full version [23].
Theorem 9
The q-GDHE family is a strictly increasingly stronger family.
5 Target Assumptions over Bilinear Groups
We now turn our attention to prime-order bilinear groups. Our reductions from the cyclic group setting translate into a bilinear framework that captures existing computational bilinear assumptions where the adversary’s task is to compute a specific group element in the base groups or the target group. For instance, the bilinear variants of the matrix computational Diffie-Hellman assumption in [34] (which implies the (computational bilinear) k-linear assumptions), the (bilinear) q-SDH assumptions, and the bilinear assumptions studied in [26] are all examples of target assumptions in bilinear groups.
Definition 8 (Bilinear Group Generator)
A bilinear group generator is a PPT algorithm \(\mathcal {BG}\), which on input a security parameter \({\kappa }\) (given in unary) outputs bilinear group parameters \((\mathbb {G}_1,\mathbb {G}_2, \mathbb {G}_T,{G}_1,{G}_2)\), where
-
\(\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T\) are cyclic groups of prime order p with bitlength \(|p|=\varTheta ({\kappa })\).
-
\(\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T\) have polynomial-time algorithms for carrying out group operations and unique representations for group elements.
-
There is an efficiently computable bilinear map (pairing) \(e:\mathbb {G}_1\times \mathbb {G}_2\rightarrow \mathbb {G}_T\).
-
\({G}_1\) and \({G}_2\) are independently chosen uniformly random generators of \(\mathbb {G}_1\) and \(\mathbb {G}_2\), respectively, and \(e({G}_1,{G}_2)\) generates \(\mathbb {G}_T\).
Again, we will be working in the low/medium granularity setting so we always assume uniformly random generators of the base groups.
According to [21], bilinear groups of prime order can be classified into 3 main types depending on the existence of efficiently computable isomorphisms between the groups. In Type-1, \(\mathbb {G}_1= \mathbb {G}_2\). In Type-2 \(\mathbb {G}_1\ne \mathbb {G}_2\) and there is an isomorphism \(\psi : \mathbb {G}_2\rightarrow \mathbb {G}_1\) that is efficiently computable in one direction, whereas in Type-3 no efficient isomorphism between the groups in either direction exists. Type-3 bilinear groups are the most efficient and hence practically relevant and we therefore restrict our focus to this type, although much of this section also applies to Type-1 and Type-2 bilinear groups.
We will use \(\left[{x}\right]_{_{1}},\left[{y}\right]_{_{2}},\left[{z}\right]_{_{T}}\) to denote the group elements in the respective groups and as in the previous sections use additive notation for all group operations. This means the generators are \(\left[{1}\right]_1,\left[{1}\right]_2\) and \(e(\left[{1}\right]_{_{1}},\left[{1}\right]_{_{2}})=\left[{1}\right]_{_{T}}\). We will often denote the pairing with multiplicative notation, i.e., \(\left[{x}\right]_{_{1}}\cdot \left[{y}\right]_{_{2}}=\left[{xy}\right]_{_{T}}\).
A bilinear group generator can be seen as a particular example of a cyclic group generator generating \(\mathbb {G}_1, \mathbb {G}_2\) or \(\mathbb {G}_T\). All our results regarding non-interactive computational assumptions therefore still apply in the respective groups but in this section we will also cover the case where exponents are shared between the groups. The presence of the pairing \(e\) makes it possible for elements in the base groups \(\mathbb {G}_1,\mathbb {G}_2\) to combine in the target group \(\mathbb {G}_T\), so we can formulate assumptions that involve several groups, e.g., that given \(\left[{1}\right]_{_{1}},\left[{1}\right]_{_{2}},\left[{x}\right]_{_{T}}\) it is hard to compute \(\left[{x}\right]_{_{1}}\). In the following sections, we define and analyze non-interactive target assumptions in the bilinear group setting.
5.1 Target Assumptions in Bilinear Groups
We now define and analyze target assumptions, where the adversary’s goal is to compute a group element in \(\mathbb {G}_j\), where \(j\in \{1,2,T\}\). When we defined target assumptions over a single cyclic group, we gave the adversary group elements of the form \(\left[{\frac{a({\varvec{x}})}{b({\varvec{x}})}}\right]\). In the bilinear group setting, the adversary may get a mix of group elements in all three groups. We note that if the adversary has \(\left[{\frac{a^{(1)}({\varvec{x}})}{b^{(1)}({\varvec{x}})}}\right]_{_{1}}\) and \(\left[{\frac{a^{(2)}({\varvec{x}})}{b^{(2)}({\varvec{x}})}}\right]_{_{2}}\) she can obtain \(\left[{\frac{a^{(1)}({\varvec{x}})a^{(2)}({\varvec{x}})}{b^{(1)}({\varvec{x}})b^{(2)}({\varvec{x}})}}\right]_{_{T}}\) via the pairing operation. When we define target assumptions in bilinear groups, we will therefore without loss of generality assume the fractional polynomials the instance generator outputs for the target group \(\mathbb {G}_T\) include all products \(\frac{a_i^{(1)}({\varvec{X}})a_j^{(2)}({\varvec{X}})}{b_i^{(1)}({\varvec{X}})b_j^{(2)}({\varvec{X}})}\) of fractional polynomials for elements in the base groups.
Definition 9
(Bilinear Target Assumption in \(\mathbb {G}_j\) ). Given polynomials \({d}({\kappa })\), \({m}({\kappa })\), \({n}_{_1}({\kappa })\), \({n}_{_2}({\kappa })\), and \({n}_{_T}({\kappa })\) we say \((\mathcal {I},\mathcal {V})\) is a \(({d},{m},{n}_{_1},{n}_{_2},{n}_{_T})\)-bilinear target assumption in \(\mathbb {G}_j\) for \(\mathcal {BG}\) if it works as follows:
- \(({pub},{priv})\leftarrow \mathcal {I}(1^{\kappa }){:}\) :
-
There is a PPT algorithm
 defining \(\mathcal {I}\) as follows:
defining \(\mathcal {I}\) as follows:
-
1.
\(\left( \mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,\left[{1}\right]_{_{1}},\left[{1}\right]_{_{2}} \right) \leftarrow \mathcal {BG}(1^{\kappa }); \mathsf {bgp}:=(\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T)\)
-
2.

-
3.
\({\varvec{x}}\leftarrow \mathbb {Z}_p^{m}\) conditioned on \(b_i^{(j)}({\varvec{x}})\ne 0\) for all choices of i and j
-
4.
\({pub}:=\left( \mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T, \left\{ \left\{ \left[{\frac{a_i^{(j)}({\varvec{x}})}{b_i^{(j)}({\varvec{x}})}}\right]_{_{j}} \right\} _{i=1}^{{n}_{_j}},\left\{ \frac{a_i^{(j)}({\varvec{X}})}{b_i^{(j)}({\varvec{X}})} \right\} _{i=1}^{{n}_{_j}}\right\} _{j=1,2,T}, {pub}' \right) \)
-
5.
Return \(({pub},{priv}:=\left( \left[{1}\right]_{_{1}}, \left[{1}\right]_{_{2}},{\varvec{x}},{priv}' \right) )\)
-
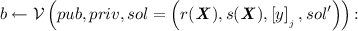 :
: -
There is a DPT algorithm
 such that
such that  returns 1 if all of the following checks pass and 0 otherwise:
returns 1 if all of the following checks pass and 0 otherwise:
-
1.

-
2.
\(\left[{y}\right]_{_{j}}= \frac{r({\varvec{x}})}{s({\varvec{x}})} \left[{1}\right]_{_{j}}\)
-
3.
\(\mathcal {V}^{\mathsf {core}}({pub},{priv},{sol})=1\)
We require that the number of variables in \({\varvec{X}}\) is \({m}({\kappa })\), the total degrees of the polynomials are bounded by \({d}({\kappa })\), and that all products of polynomial fractions in \(\mathbb {G}_1\) and \(\mathbb {G}_2\) are included in the polynomial fractions in \(\mathbb {G}_T\).
Also, since the pairing function allows one to obtain the product of any two polynomials from the opposite source groups in the target group, for assumptions where the required target element is in \(\mathbb {G}_T\), the degree of the polynomials \(r({\varvec{X}})\) and \(s({\varvec{X}})\) the adversary specifies is upper bounded by \(2 {d}\) instead of \({d}\).
Similarly to the single group setting, we can reduce any bilinear target assumption to a simple bilinear target assumption, where all \(b_i^{(1)}({\varvec{X}})=b_i^{(2)}({\varvec{X}})=b_i^{(T)}({\varvec{X}})=1\). Also, we can reduce bilinear target assumptions with multivariate polynomials to bilinear target assumptions with univariate polynomials.
We can then consider two cases depending on whether or not the polynomial \(s(X)\) divides \(r(X)\). Just as in the single cyclic group setting, we get that all bilinear target assumptions can be reduced to the following two assumptions.
Definition 10
(Bilinear Polynomial Assumption in \(\mathbb {G}_j\) ). We say a \(({d},1, {n}_{_1}, {n}_{_2}, {n}_{_T})\)-simple bilinear target assumption \((\mathcal {I},\mathcal {V})\) in \(\mathbb {G}_j\) for \(\mathcal {BG}\) is a \(({d},{n}_{_1},{n}_{_2},{n}_{_T})\)-bilinear polynomial assumption in \(\mathbb {G}_j\) if \(\mathcal {V}\) only accepts solutions where \(s(X)=1\).
Definition 11
(Bilinear Fractional Assumption in \(\mathbb {G}_j\) ( BFrac \(_j\) )). We say a \(({d},1, {n}_{_1}, {n}_{_2}, {n}_{_T})\)-simple bilinear target assumption \((\mathcal {I},\mathcal {V})\) in \(\mathbb {G}_j\) for \(\mathcal {BG}\) is a \(({d},{n}_{_1},{n}_{_2},{n}_{_T})\)-bilinear fractional assumption in \(\mathbb {G}_j\) if \(\mathcal {V}\) only accepts solutions where \(s(X) \not \mid r(X)\).
It is straightforward to prove the following theorem, which states that the \(({d},{n}_{_1},{n}_{_2},{n}_{_T})\text {-BFrac}_i\) assumption can be further simplified to only consider the target group case.
Theorem 10
If the \(({d},{n}_{_1},{n}_{_2},{n}_{_T})\text {-BFrac}_T\) assumption over \(\mathcal {BG}\) holds, then the assumptions \(({d},{n}_{_1},{n}_{_2},{n}_{_T})\text {-BFrac}_1\) and \(({d},{n}_{_1},{n}_{_2},{n}_{_T})\text {-BFrac}_2\) over \(\mathcal {BG}\) also hold.
5.2 Bilinear Target Assumptions in the Base Groups
All the results in this section are assuming a Type-3 bilinear group. Intuitively, bilinear target assumptions in \(\mathbb {G}_1\) and \(\mathbb {G}_2\) are very similar to the cyclic group case because the generic computations one can do in a base group are not affected by group elements in the other groups. We will now formalize this intuition by generalizing the q-GDHE and the q-SFrac assumptions to the bilinear setting.
Definition 12
( q-Bilinear GDHE Assumption in \(\mathbb {G}_1\) ( q-BGDHE \(_1\) )). The q-BGDHE assumption in \(\mathbb {G}_1\) over \(\mathcal {BG}\) is that for all PPT adversaries \(\mathcal {A}\)
The q-BGDHE assumption in \(\mathbb {G}_2\) (\(q\text {-BGDHE}_2\)) over \(\mathcal {BG}\) is defined similarly.
Definition 13
( q-Bilinear SFrac in \(\mathbb {G}_i\) Assumption Footnote 3 ( q \(-\mathbf{BSFrac}_i\) )). The \(q{\text {-BSFrac}}_i\) for \(i \in \{1,2,T\}\) over \(\mathcal {BG}\) is that for all PPT adversaries \(\mathcal {A}\)
Similarly to Theorem 4, we can prove that all bilinear polynomial assumptions in the base group \(\mathbb {G}_j\) for \(j\in \{1,2\}\) are implied by the \(q\hbox {-BGDHE}_j\) assumption. Also, similarly to Theorem 5, we can show that all bilinear fractional assumptions in the base group \(\mathbb {G}_j\) for \(j\in \{1,2\}\) are implied by the \(q{\text {-BSFrac}}_j\) assumption. For bilinear target assumptions in the base groups, we therefore get a situation very similar to the single cyclic group case, which we express in the following theorem:
Theorem 11
For \(j\in \{1,2\}\) there is a polynomial \(q({d},{m},{n}_1,{n}_2,{n}_T)\) such that the joint q-\(\text {BSFrac}_{j}\) and q-\(\text {BGDHE}_j\) assumption imply all \(({d},{m},{n}_1,{n}_2,{n}_T)\) bilinear target assumptions in \(\mathbb {G}_j\).
By the above theorem, the joint \(q\text {-BGDHE}_j\) and q-BSFrac\(_j\) assumption serves as an Uber assumption for all bilinear target assumptions in the base group \(\mathbb {G}_j\).
5.3 Bilinear Target Assumptions in the Target Group
We now consider bilinear target assumptions in the target group \(\mathbb {G}_T\). This is different from the case of bilinear target assumptions in the base groups since the bilinear map allow one to map elements from the base groups into the target group resulting new elements in that group.
Consider a polynomial assumption. We can use matrices \(\mathbf {A}\) and \(\mathbf {B}\) to represent the polynomials in \(\mathbb {G}_1\) and \(\mathbb {G}_2\) as \([1~X~\ldots ~X^d]_1 \mathbf {A}\) and \([X^d~\ldots ~X~1]_2 \mathbf {B}\). Given group elements with evaluations of these polynomials one may use the pairing to compute products of the polynomial evaluations in the target group \(\mathbb {G}_T\). Observe that \(\mathbf {A^T}\mathbf {B}\) represents the coefficients of the \(X^{d}\) terms in all the possible pairings of two elements in \(\mathbb {G}_1\) and \(\mathbb {G}_2\). We will use this to formulate a target group analogue of the q-\(\text {BGDHE}\) assumptions.
Definition 14
( q-Bilinear Gap Assumption ( q-BGap )). We say the q-BGapassumption holds when for all PPT \(\mathcal {A}\)

Let \(\mathbf {A}\in \mathbb {Z}_p^{(q+1) \times n_1}\) and \(\mathbf {B}\in \mathbb {Z}_p^{(q+1) \times n_2}\) where without loss of generality we can assume their ranks are \(n_1\) and \(n_2\), respectively, and \(n_1+n_2=q+1\). Note that for smaller dimensions we can always add a column in the null space of \(\mathbf {A^T}\) to \(\mathbf {B}\) and still have \(\mathbf {A^T} \mathbf {B}=\mathbf {0}\).
Theorem 12
For any \((d,n_1,n_2,n_T)\)-polynomial assumption \(\mathsf {A}=(\mathcal {I}_{\mathsf {A}},\mathcal {V}_{\mathsf {A}})\) in \(\mathbb {G}_T\) over \(\mathcal {BG}\), we have that  .
.
Proof
Let \(\mathcal {{A}}\) be an adversary against the \(({d},n_1,n_2,n_T)\)-polynomial assumption. We build an adversary \(\mathcal {{B}}\) against the \((3{d}+1){\text {-BGap}}\) assumption which uses \(\mathcal {{A}}\) in a black-box manner. Adversary \(\mathcal {{B}}\) runs  to get the tuple \(\left( \left\{ \left\{ a^{(j)}_i(X) \right\} _{i=1}^{{n}_j} \right\} _{j=1,2,T},{pub}'_{\mathsf {A}}, {priv}'_{\mathsf {A}}\right) \). Now, \(\mathcal {B}\) randomly chooses a polynomial \(c(X) \leftarrow \mathbb {Z}_p[X]\) where \(\deg (c)\le 2{d}+1\) conditioned on all \(a^{(T)}_i(X)c(X) X^{d}\) having coefficient 0 in the term for \(X^{3d+1}\). Define the following polynomials
to get the tuple \(\left( \left\{ \left\{ a^{(j)}_i(X) \right\} _{i=1}^{{n}_j} \right\} _{j=1,2,T},{pub}'_{\mathsf {A}}, {priv}'_{\mathsf {A}}\right) \). Now, \(\mathcal {B}\) randomly chooses a polynomial \(c(X) \leftarrow \mathbb {Z}_p[X]\) where \(\deg (c)\le 2{d}+1\) conditioned on all \(a^{(T)}_i(X)c(X) X^{d}\) having coefficient 0 in the term for \(X^{3d+1}\). Define the following polynomials
and define the matrices \(\mathbf {A} \in \mathbb {Z}^{(3{d}+2) \times {n}_1}_p\) and \(\mathbf {B} \in \mathbb {Z}^{(3{d}+2) \times (3{d}+2-{n}_1)}_p\) as follows:
where the values \(\beta '_{i,j}\in \mathbb {Z}_p\) are chosen as an arbitrary extension to give us \(\text {rank}(\mathbf {A})+\text {rank}(\mathbf {B})=3{d}+2\) in a way such that we still have \(\mathbf {A}^T \mathbf {B}=0\). Adversary \(\mathcal {B}\) now forwards \(\mathbf {A}\) and \(\mathbf {B}\) to her environment and gets back the tuple
using which she can compute all of the group elements \([a'^{(1)}_i(x)]_1\), \([a'^{(2)}_i(x)]_2\), and \([a'^{(T)}_i(x)]_T\). Adversary \(\mathcal {B}\) now starts \(\mathcal {A}\) on the tuple
and gets \((r(X),[y]_T,{sol}')\) as an answer, where  . Parse \(r(X) c(X) X^d\) as \(\sum _{i=0}^{5{d}+1} \gamma _{i} X^{i}\). Using the tuple available to her, \(\mathcal {B}\) can recover \([x^{3{d}+1}]_{_T}\) by computing \(\frac{1}{\gamma _{_{3{d}+1}}}([y]_{_T} - [\sum _{i \ne 3{d}+1} \gamma _{i} x^{i}]_{_T})\).
. Parse \(r(X) c(X) X^d\) as \(\sum _{i=0}^{5{d}+1} \gamma _{i} X^{i}\). Using the tuple available to her, \(\mathcal {B}\) can recover \([x^{3{d}+1}]_{_T}\) by computing \(\frac{1}{\gamma _{_{3{d}+1}}}([y]_{_T} - [\sum _{i \ne 3{d}+1} \gamma _{i} x^{i}]_{_T})\).
Assume \(c(x) \ne 0\), which happens with probability \(1 -\frac{2d\,+\,1}{p}\), and \(x^d \ne 0\), which happens with probability \(1 -\frac{d}{p}\). The instance \(\mathcal {A}\) sees is indistinguishable from an instance she gets directly from the instance generator with generators \([c(x)]_{_1}\), \([x^d]_{_2}\) and \([c(x) x^d]_{_T}\). By Lemma 2, the probability that \(r(X)c(X)X^d\) has a 0 coefficient of \(X^{3d+1}\) is \(\frac{1}{p}\). Thus, if \(\mathcal {A}\) has probability \(\epsilon _\mathcal {A}\) against assumption \(\mathsf {A}\), we have \(\epsilon _\mathcal {B}= \epsilon _\mathcal {A}- \frac{3d\,+\,2}{p}\) is the probability of \(\mathcal {B}\) against the \((3{d}+1){\text {-BGap}}\) assumption. \(\square \)
We conclude with the following theorem.
Theorem 13
There is a polynomial \(q({d},{m},{n}_1,{n}_2,{n}_T)\) such that the joint q-\(\text {BSFrac}_{T}\) and q-\(\text {BGap}\) assumption imply all \(({d},{m},{n}_1,{n}_2,{n}_T)\) bilinear target assumptions in \(\mathbb {G}_T\).
Notes
- 1.
We note the caveat that our reductions are not tight. So it may be for concrete parameters a target assumption can be broken even if q-GDHE and q-SFrac hold for the same parameters. For all reductions, the concrete loss is stated explicitly in our proofs such that a cryptographer can work out a choice of parameters that yields security from the q-GDHE and q-SFrac assumptions.
- 2.
The SRDH assumption differs from the 1-GDHE assumption in that while the former accepts either \([-x]\) or [x] as a valid answer, the latter only accepts [x] as a valid answer.
- 3.
The \(q\text {-BSFrac}_1\) assumption is the same as the \(q\text {-co-SDH}\) assumption in [20].
References
Abdalla, M., Benhamouda, F., Passelègue, A.: An algebraic framework for pseudorandom functions and applications to related-key security. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 388–409. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_19
Ambrona, M., Barthe, G., Schmidt, B.: Automated unbounded analysis of cryptographic constructions in the generic group model. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 822–851. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_29
Bao, F., Deng, R.H., Zhu, H.F.: Variations of Diffie-Hellman problem. In: Qing, S., Gollmann, D., Zhou, J. (eds.) ICICS 2003. LNCS, vol. 2836, pp. 301–312. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-39927-8_28
Barthe, G., Fagerholm, E., Fiore, D., Mitchell, J., Scedrov, A., Schmidt, B.: Automated analysis of cryptographic assumptions in generic group models. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 95–112. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_6
Bellare, M., Palacio, A.: The knowledge-of-exponent assumptions and 3-round zero-knowledge protocols. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 273–289. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_17
Bellare, M., Waters, B., Yilek, S.: Identity-based encryption secure against selective opening attack. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 235–252. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_15
Boer, B.: Diffie-Hellman is as strong as discrete log for certain primes. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 530–539. Springer, New York (1990). https://doi.org/10.1007/0-387-34799-2_38
Boneh, D., Boyen, X.: Short signatures without random oracles and the SDH assumption in bilinear groups. J. Crypt. 21(2), 149–177 (2008)
Boneh, D., Boyen, X., Goh, E.-J.: Hierarchical identity based encryption with constant size ciphertext. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 440–456. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_26
Boneh, D., Gentry, C., Waters, B.: Collusion resistant broadcast encryption with short ciphertexts and private keys. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 258–275. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_16
Boyen, X.: The Uber-assumption family. In: Galbraith, S.D., Paterson, K.G. (eds.) Pairing 2008. LNCS, vol. 5209, pp. 39–56. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85538-5_3
Boyen, X., Waters, B.: Full-domain subgroup hiding and constant-size group signatures. In: Okamoto, T., Wang, X. (eds.) PKC 2007. LNCS, vol. 4450, pp. 1–15. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71677-8_1
Bresson, E., Chevassut, O., Pointcheval, D.: The group Diffie-Hellman problems. In: Nyberg, K., Heys, H. (eds.) SAC 2002. LNCS, vol. 2595, pp. 325–338. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36492-7_21
Bresson, E., Lakhnech, Y., Mazaré, L., Warinschi, B.: A generalization of DDH with applications to protocol analysis and computational soundness. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 482–499. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_27
Chase, M., Maller, M., Meiklejohn, S.: Déjà Q all over again: tighter and broader reductions of q-type assumptions. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 655–681. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_22
Chase, M., Meiklejohn, S.: Déjà Q: using dual systems to revisit q-type assumptions. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 622–639. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_34
Cheon, J.H.: Security analysis of the strong Diffie-Hellman problem. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 1–11. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_1
Dent, A.W.: Adapting the weaknesses of the random oracle model to the generic group model. In: Zheng, Y. (ed.) ASIACRYPT 2002. LNCS, vol. 2501, pp. 100–109. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-36178-2_6
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for Diffie-Hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_8
Fuchsbauer, G., Hanser, C., Slamanig, D.: Structure-preserving signatures on equivalence classes and constant-size anonymous credentials. Cryptology ePrint Archive, Report 2014/944 (2014)
Galbraith, S.D., Paterson, K.G., Smart, N.P.: Pairings for cryptographers. Discrete Appl. Math. 156(16), 3113–3121 (2008)
Gennaro, R., Gentry, C., Parno, B., Raykova, M.: Quadratic span programs and succinct NIZKs without PCPs. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 626–645. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_37
Ghadafi, E., Groth, J.: Towards a classification of non-interactive computational assumptions in cyclic groups. Cryptology ePrint Archive, Report 2017/343 (2017). http://eprint.iacr.org/2017/343
Goldwasser, S., Tauman Kalai, Y.: Cryptographic assumptions: a position paper. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 505–522. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_21
Jager, T., Schwenk, J.: On the analysis of cryptographic assumptions in the generic ring model. J. Crypt. 26(2), 225–245 (2012)
Joux, A., Rojat, A.: Security ranking among assumptions within the Uber Assumption framework. In: Desmedt, Y. (ed.) ISC 2013. LNCS, vol. 7807, pp. 391–406. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-27659-5_28
Kiltz, E.: A tool box of cryptographic functions related to the Diffie-Hellman function. In: Rangan, C.P., Ding, C. (eds.) INDOCRYPT 2001. LNCS, vol. 2247, pp. 339–349. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45311-3_32
Koblitz, N., Menezes, A.: Another look at generic groups. Adv. Math. Commun. 1(1), 13–28 (2007)
Konoma, C., Mambo, M., Shizuya, H.: Complexity analysis of the cryptographic primitive problems through square-root exponent. IEICE Trans. E87–A(5), 1083–1091 (2004)
Maurer, U.: Abstract models of computation in cryptography. In: Smart, N.P. (ed.) Cryptography and Coding 2005. LNCS, vol. 3796, pp. 1–12. Springer, Heidelberg (2005). https://doi.org/10.1007/11586821_1
Maurer, U.M.: Towards the equivalence of breaking the Diffie-Hellman protocol and computing discrete logarithms. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 271–281. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48658-5_26
Maurer, U.M., Wolf, S.: Diffie-Hellman oracles. In: Koblitz, N. (ed.) CRYPTO 1996. LNCS, vol. 1109, pp. 268–282. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68697-5_21
Mitsunari, S., Sakai, R., Kasahara, M.: A new traitor tracing. IEICE Trans. E85–A(2), 481–484 (2002)
Morillo, P., Ràfols, C., Villar, J.L.: The kernel matrix Diffie-Hellman assumption. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10031, pp. 729–758. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53887-6_27
Naor, M.: On cryptographic assumptions and challenges. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 96–109. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_6
Nechaev, V.I.: Complexity of a determinate algorithm for the discrete logarithm. Math. Zametki 55(2), 91–101 (1994)
Roh, D., Hahn, S.G.: The square root Diffie-Hellman problem. Des. Codes Crypt. 62(2), 179–187 (2012)
Sadeghi, A.-R., Steiner, M.: Assumptions related to discrete logarithms: why subtleties make a real difference. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 244–261. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_16
Shoup, V.: Lower bounds for discrete logarithms and related problems. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 256–266. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_18
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Ghadafi, E., Groth, J. (2017). Towards a Classification of Non-interactive Computational Assumptions in Cyclic Groups. In: Takagi, T., Peyrin, T. (eds) Advances in Cryptology – ASIACRYPT 2017. ASIACRYPT 2017. Lecture Notes in Computer Science(), vol 10625. Springer, Cham. https://doi.org/10.1007/978-3-319-70697-9_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-70697-9_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70696-2
Online ISBN: 978-3-319-70697-9
eBook Packages: Computer ScienceComputer Science (R0)







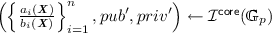
 :
: returns 1 if all of the following checks pass and 0 otherwise:
returns 1 if all of the following checks pass and 0 otherwise:

 and adversary
and adversary 



 defining
defining 
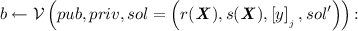 :
: such that
such that  returns 1 if all of the following checks pass and 0 otherwise:
returns 1 if all of the following checks pass and 0 otherwise:
