Abstract
OCB3 is the current version of the OCB authenticated encryption mode which is selected for the third round in CAESAR. So far the integrity analysis has been limited to an adversary making a single forging attempt. A simple extension for the best known bound establishes integrity security as long as the total number of query blocks (including encryptions and forging attempts) does not exceed the birthday-bound. In this paper we show an improved bound for integrity of OCB3 in terms of the number of blocks in the forging attempt. In particular we show that when the number of encryption query blocks is not more than birthday-bound (an assumption without which the privacy guarantee of OCB3 disappears), even an adversary making forging attempts with the number of blocks in the order of \(2^n/\ell _{\text {MAX}}\) (n being the block-size and \(\ell _{\text {MAX}}\) being the length of the longest block) may fail to break the integrity of OCB3.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Authenticated encryption schemes [Rog02], which target both data confidentiality and integrity simultaneously, have received considerable attention in recent years. The increased interest is in part due to the ongoing CAESAR competition [cae], which aims to deliver a portfolio of state-of-the-art authenticated encryption schemes covering a spectrum of security and efficiency trade-offs. While other possibilities exist, it is natural to build AE schemes from blockciphers, employing some mode of operation. Some of the known blockcipher based authenticated encryptions are OCB [RBB03, Rog04], GCM [MV04, MV05], COPA [ABL+13], ELmD [DN14] and AEZ [HKR15]. Due to the CAESAR competition, many designs have appeared in literature. Moreover, some designs have been refined for better performance and improved security. OCB3 (submitted to CAESAR and now a third round candidate) is one such example, an enhancement of the well known construction OCB.
 and
and  . OCB is a blockcipher-based mode of operation that achieves authenticated encryption in almost the same amount of time as the fastest conventional mode, CTR mode [WHF02], which achieves privacy alone in that time. Despite this, OCB is simple and clean, and easy to implement in either hardware or software. For every message, it uses two blockcipher calls to process a constant block \(0^{n}\) and a nonce, one blockcipher call for each message block and one additional blockcipher call for the checksum.
. OCB is a blockcipher-based mode of operation that achieves authenticated encryption in almost the same amount of time as the fastest conventional mode, CTR mode [WHF02], which achieves privacy alone in that time. Despite this, OCB is simple and clean, and easy to implement in either hardware or software. For every message, it uses two blockcipher calls to process a constant block \(0^{n}\) and a nonce, one blockcipher call for each message block and one additional blockcipher call for the checksum.
The refined OCB or OCB3 [KR11] aims to shave off one AES encipherment per message encrypted about \(98\%\) of the time. The nonce here is used as a counter, i.e., in a given session, its top segment (of 122 bits) stays fixed, while, with each successive message, the bottom segment (of 6 bits) gets bumped up by one. This is the approach recommended in RFC 5116 [McG08, Sect. 3.2].
Known Security Results of  . Though the original OCB has already been proved to be secure, the security bound provided by [KR11], in particular the authenticity bound, does not show the standard birthday-bound security when the adversary is allowed to make multiple verification queries. More formally, the original bound is \(O(\sigma _T^2/N) + O(1/2^{\tau })\) where \(\sigma _T\) denotes the total number of input blocks in q encryption queries and \(\tau \) denotes the tag length, if the number of verification queries is one. This bound generally implies \(O(q'\sigma _T^2/N) + O(q'/2^{\tau })\) when the number of verification queries is \(q'\ge 1\), hence the provable security is degraded.
. Though the original OCB has already been proved to be secure, the security bound provided by [KR11], in particular the authenticity bound, does not show the standard birthday-bound security when the adversary is allowed to make multiple verification queries. More formally, the original bound is \(O(\sigma _T^2/N) + O(1/2^{\tau })\) where \(\sigma _T\) denotes the total number of input blocks in q encryption queries and \(\tau \) denotes the tag length, if the number of verification queries is one. This bound generally implies \(O(q'\sigma _T^2/N) + O(q'/2^{\tau })\) when the number of verification queries is \(q'\ge 1\), hence the provable security is degraded.
Another adaptation of the proof can be applied to obtain a bound of the form \(O((\sigma _T + \sigma '_T)^2/N + q'/2^{\tau })\), where \(\sigma '_T\) is the blocks in the decryption queries. It still remains birthday-bound in \(\sigma '_T\). All known attacks exploit the collision in the input blocks for all encryption queries and hence \(\sigma ^2_T/N\) is tight. But no matching attack with advantage \(\sigma '^2_T/N\) is known. A recent collision attack on PHash [GPR17] (used to process the associated data) can be applied to obtain an integrity attack with advantage \(O(\sigma '_T/N)\). (See [BGM04].)
Our Contribution. We show that the existing attack is the best possible by improving the integrity advantage. We follow the combined AE security distinguishing game [RS06] to bound the integrity security of OCB3. We use Patarin’s coefficients H technique [Pat08] to bound the AE distinguishing game.
Theorem 1
(Main Result). Let \({\mathcal {A}}\) be an adversary that makes q encryption queries consisting of \(\sigma \) message blocks in all with at most \(\ell _{\text {MAX}}\) blocks per query, and \(\alpha \) associated data blocks in all, and \(q'\) decryption queries in a nonce-respecting authenticated encryption security game with associated data against a real oracle \({\mathcal {O}}_1\) representing \({\textsf {OCB3}}\) and an ideal oracle \({\mathcal {O}}_0\) representing an ideal nonce-based authenticated encryption function. Then

where \(\sigma _T = \sigma + \alpha + q\) is the total number of blocks queried in the encryption queries (including messages, associated data and nonces).
2 Preliminaries
\({\mathbb {N}}\) denotes the set of non-negative integers. For \(n\in {\mathbb {N}}\), [n] denotes the set \(\left\{ 1,\ldots ,n\right\} \) ([0] is thus the empty set). For \(m,n\in {\mathbb {N}}\), [m..n] denotes the set \(\left\{ m,\ldots ,n\right\} \) (which is the empty set when \(m>n\)). For a binary string  , |x| will denote the number of bits in x. We fix an arbitrary block-length \(n\in {\mathbb {N}}\setminus \left\{ 0\right\} \). If \(|x| = n\), we call x a complete block; if \(|x|<n\), we call x an incomplete block; if \(|x| = 0\) (the null string), we call x the empty block. (By convention, the empty block is also an incomplete block.) \(\oplus \) and \(\cdot \) denote the field addition (XOR) and field multiplication respectively over the finite field
, |x| will denote the number of bits in x. We fix an arbitrary block-length \(n\in {\mathbb {N}}\setminus \left\{ 0\right\} \). If \(|x| = n\), we call x a complete block; if \(|x|<n\), we call x an incomplete block; if \(|x| = 0\) (the null string), we call x the empty block. (By convention, the empty block is also an incomplete block.) \(\oplus \) and \(\cdot \) denote the field addition (XOR) and field multiplication respectively over the finite field  . During calculations, for two block x and y, we will simply write \(x+y\) to denote \(x\oplus y\).
. During calculations, for two block x and y, we will simply write \(x+y\) to denote \(x\oplus y\).
For \(i\in [|x|]\), x[i] denotes the i-th bit of x (we begin all indexing from 1, so x[1] is the first bit of x). For \(i\ge 1\) and \(j\le |x|\), x[i..j] denotes the \((j-i+1)\)-bit contiguous substring of x starting at the i-th bit when \(i\le j\), and the empty string otherwise. For two strings x and y, x||y denotes the concatenation of x and y. For a bit b, \(b^m\) denotes an m-bit string with each bit equal to b.
Any  can be mapped uniquely to a sequence \((x_1,\ldots ,x_\ell ,x_*)\), where \(\ell \in {\mathbb {N}}\), \(x_1,\ldots ,x_\ell \) are complete blocks, and \(x_*\) is an incomplete (possibly empty) block, such that
can be mapped uniquely to a sequence \((x_1,\ldots ,x_\ell ,x_*)\), where \(\ell \in {\mathbb {N}}\), \(x_1,\ldots ,x_\ell \) are complete blocks, and \(x_*\) is an incomplete (possibly empty) block, such that
For this mapping we take \(\ell = \lfloor |x|/n\rfloor \), \(x_i = x[n(i-1)+1..ni]\) for \(i\in [\ell ]\), and \(x_* = x[n\ell +1..|x|]\). For an incomplete block x, \(\mathsf {pad}(x)\) denotes the complete block
For a complete block x, \(\mathsf {chop}_k(x)\) denotes the incomplete block x[1..k]. For some \(m\in {\mathbb {N}}\), for  , \(x\gg k\) denotes x rotated b bits to the right, i.e., \(0^b||x[1..m-b]\), while \(x\ll b\) denotes x rotated b bits to the left, i.e., \(x[b+1..m]||0^b\).
, \(x\gg k\) denotes x rotated b bits to the right, i.e., \(0^b||x[1..m-b]\), while \(x\ll b\) denotes x rotated b bits to the left, i.e., \(x[b+1..m]||0^b\).
We say a function  is partially determined if we know the values of f on a strict subset of
is partially determined if we know the values of f on a strict subset of  . This subset is called \({\textsf {Dom}}(f)\). A partially determined state of f can be viewed as a restriction of f to \({\textsf {Dom}}(f)\). The range of this restricted function is called \({\textsf {Ran}}(f)\). We will treat a partially determined function as updatable: for some
. This subset is called \({\textsf {Dom}}(f)\). A partially determined state of f can be viewed as a restriction of f to \({\textsf {Dom}}(f)\). The range of this restricted function is called \({\textsf {Ran}}(f)\). We will treat a partially determined function as updatable: for some  and some
and some  , (x, y) may be added to f, so that \({\textsf {Dom}}(f)\) expands to \({\textsf {Dom}}(f)\cup \left\{ x\right\} \), and \({\textsf {Ran}}(f)\) becomes \({\textsf {Ran}}(f)\cup \left\{ y\right\} \). We say f is permutation-compatible if \(|{\textsf {Dom}}(f)| = |{\textsf {Ran}}(f)|\).
, (x, y) may be added to f, so that \({\textsf {Dom}}(f)\) expands to \({\textsf {Dom}}(f)\cup \left\{ x\right\} \), and \({\textsf {Ran}}(f)\) becomes \({\textsf {Ran}}(f)\cup \left\{ y\right\} \). We say f is permutation-compatible if \(|{\textsf {Dom}}(f)| = |{\textsf {Ran}}(f)|\).
For a set  , we write
, we write  to denote that x is sampled from S uniformly. For a given domain \({\mathcal {D}}\) and a given co-domain \({\mathcal {R}}\), \({\textsf {Func}}[{\mathcal {D}},{\mathcal {R}}]\) will denote the set of all functions from \({\mathcal {D}}\) into \({\mathcal {R}}\). We say \(f^*\) is an ideal random function from \({\mathcal {D}}\) to \({\mathcal {R}}\) to indicate that
to denote that x is sampled from S uniformly. For a given domain \({\mathcal {D}}\) and a given co-domain \({\mathcal {R}}\), \({\textsf {Func}}[{\mathcal {D}},{\mathcal {R}}]\) will denote the set of all functions from \({\mathcal {D}}\) into \({\mathcal {R}}\). We say \(f^*\) is an ideal random function from \({\mathcal {D}}\) to \({\mathcal {R}}\) to indicate that  . If \(f^*\) is an ideal random function, it can be viewed as a with-replacement sampler from \({\mathcal {R}}\): for distinct inputs \(x_1,\ldots ,x_m\in {\mathcal {D}}\),
. If \(f^*\) is an ideal random function, it can be viewed as a with-replacement sampler from \({\mathcal {R}}\): for distinct inputs \(x_1,\ldots ,x_m\in {\mathcal {D}}\),  for \(i\in [m]\), and \(f^*(x_1),\ldots ,f^*(x_m)\) are all independent. Similarly \({\textsf {Perm}}[{\mathcal {D}}]\) will denote the set of all permutations on \({\mathcal {D}}\). We say \(\pi ^*\) is an ideal random permutation on \({\mathcal {D}}\) to indicate that
for \(i\in [m]\), and \(f^*(x_1),\ldots ,f^*(x_m)\) are all independent. Similarly \({\textsf {Perm}}[{\mathcal {D}}]\) will denote the set of all permutations on \({\mathcal {D}}\). We say \(\pi ^*\) is an ideal random permutation on \({\mathcal {D}}\) to indicate that  . If \(f^*\) is an ideal random permutation, it can be viewed as a without-replacement sampler from \({\mathcal {D}}\): for distinct inputs \(x_1,\ldots ,x_m\in {\mathcal {D}}\),
. If \(f^*\) is an ideal random permutation, it can be viewed as a without-replacement sampler from \({\mathcal {D}}\): for distinct inputs \(x_1,\ldots ,x_m\in {\mathcal {D}}\),  where \({\mathcal {D}}^{{\underline{s}}}\) denotes the set of all s-tuples of distinct elements from \({\mathcal {D}}\).
where \({\mathcal {D}}^{{\underline{s}}}\) denotes the set of all s-tuples of distinct elements from \({\mathcal {D}}\).
2.1 Some Basic Results
We briefly state some results which would be used in our security analysis.
Property-1. Suppose \(X_1, \ldots , X_s\) is a random without-replacement sample from \({\mathcal {D}}\). Then for any \(1 \le i_1< \cdots < i_r \le s\), \(X_{i_1}, \ldots , X_{i_r}\) is also a random without-replacement sample from \({\mathcal {D}}\). In other words, the joint distribution of a without-replacement sample is independent of the ordering of the sample.
Property-2. Suppose A is a binary full row rank matrix of dimension \(nd \times ns\) for some positive integers n, d and s. Let \(X_1, \ldots , X_s\) be a without-replacement sample from \(\{0,1\}^n\), and X be the column vector \((X_1,\ldots ,X_n)\). Then

for any d dimensional binary vector c. Moreover if c is not in the column space of A then this probability is zero.
2.2 Distinguishing Advantage
For two oracles \({\mathcal {O}}_0\) and \({\mathcal {O}}_1\), an algorithm \({\mathcal {A}}\) trying to distinguish between \({\mathcal {O}}_0\) and \({\mathcal {O}}_1\) is called a distinguishing adversary. \({\mathcal {A}}\) plays an interactive game with \({\mathcal {O}}_b\) for some bit b unknown to \({\mathcal {A}}\), and then outputs a bit \(b_{\mathcal {A}}\). The winning event is \([b_{\mathcal {A}}= b]\). The distinguishing advantage of \({\mathcal {A}}\) is defined as

Let \({\mathbf {A}}[q,t]\) be the class of all distinguishing adversaries limited to q oracle queries and t computations. We define

When the adversaries in \({\mathbf {A}}[q,t]\) are allowed to make both encryption queries and decryption queries to the oracle, this is written as  , where q is the maximum number of encryption queries allowed and \(q'\) is the maximum number of decryption queries allowed. \({\textsf {Enc}}_b\) and \({\textsf {Dec}}_b\) denote respectively the encryption and decryption function associated with \({\mathcal {O}}_b\).
, where q is the maximum number of encryption queries allowed and \(q'\) is the maximum number of decryption queries allowed. \({\textsf {Enc}}_b\) and \({\textsf {Dec}}_b\) denote respectively the encryption and decryption function associated with \({\mathcal {O}}_b\).
\({\mathcal {O}}_0\) conventionally represents an ideal primitive, while \({\mathcal {O}}_1\) represents either an actual construction or a mode of operation built of some other ideal primitives. Typically the goal of the function represented by \({\mathcal {O}}_1\) is to emulate the ideal primitive represented by \({\mathcal {O}}_0\). We use the standard terms real oracle and ideal oracle for \({\mathcal {O}}_1\) and \({\mathcal {O}}_0\) respectively. A security game is a distinguishing game with an optional set of additional restrictions, chosen to reflect the desired security goal. When we talk of distinguishing advantage with a specific security game G in mind, we include G in the superscript, e.g.,  .
.
2.3 The Authenticated Encryption Security Game
A nonce-based authenticated encryption scheme with associated data consists of a key space \({\mathcal {K}}\), a message space \({\mathcal {M}}\), a tag space \({\mathfrak {T}}\), a nonce space \({\mathcal {N}}\) and an associated data space \({\mathfrak {A}}\), along with two functions \({\textsf {Enc}}:{\mathcal {K}}\times {\mathcal {N}}\times {\mathfrak {A}}\times {\mathcal {M}}\longrightarrow {\mathcal {M}}\times {\mathfrak {T}}\) and \({\textsf {Dec}}:{\mathcal {K}}\times {\mathcal {N}}\times {\mathfrak {A}}\times {\mathcal {M}}\times {\mathfrak {T}}\longrightarrow {\mathcal {M}}\cup \left\{ \bot \right\} \), with the correctness condition that for any \(K\in {\mathcal {K}},{\textsf {N}}\in {\mathcal {N}},{\textsf {A}}\in {\mathfrak {A}},{\textsf {M}}\in {\mathcal {M}}\), we have
In addition, in most popular authenticated encryption schemes (including \({\textsf {OCB3}}\)), the map \(p_{\mathcal {M}}\circ {\textsf {Enc}}(K,{\textsf {N}},{\textsf {A}},\cdot )\) for fixed \(K,{\textsf {N}},{\textsf {A}}\) is a length-preserving permutation, where \(p_{\mathcal {M}}:{\mathcal {M}}\times {\mathfrak {T}}\longrightarrow {\mathcal {M}}\) is the projection on \({\mathcal {M}}\).
In the nonce-respecting authenticated encryption security game with associated data \({\textsf {naead}}\), \({\textsf {Enc}}_1\) and \({\textsf {Dec}}_1\) of the real oracle are the encryption function \({\textsf {Enc}}(K,\cdot ,\cdot ,\cdot )\) and decryption function \({\textsf {Dec}}(K,\cdot ,\cdot ,\cdot ,\cdot )\) respectively of the authenticated encryption scheme under consideration for a key K randomly chosen from \({\mathcal {K}}\); in the ideal oracle, \({\textsf {Enc}}_0:{\mathcal {N}}\times {\mathfrak {A}}\times {\mathcal {M}}\longrightarrow {\mathcal {M}}\times {\mathfrak {T}}\) is an ideal random function from \({\mathcal {N}}\times {\mathfrak {A}}\times {\mathcal {M}}\) to \({\mathcal {M}}\times {\mathfrak {T}}\), and \({\textsf {Dec}}_0:{\mathcal {N}}\times {\mathfrak {A}}\times {\mathcal {M}}\times {\mathfrak {T}}\longrightarrow {\mathcal {M}}\cup \left\{ \bot \right\} \) is the constant function that returns \(\bot \) irrespective of the input. We henceforth refer to \(({\textsf {Enc}}_0,{\textsf {Dec}}_0)\) as the ideal nonce-based authenticated encryption scheme. The distinguishing adversary operates under the following restrictions:
-
no two encryption queries can have the same nonce;
-
if an encryption query \(({\textsf {N}},{\textsf {A}},{\textsf {M}})\) yields \(({\textsf {C}},{\textsf {T}})\), a decryption query \(({\textsf {N}},{\textsf {A}},{\textsf {C}},{\textsf {T}})\) is not allowed.
The distinguishing advantage of the adversary in the nonce-respecting authenticated encryption security game with associated data will be denoted  . Note that security under this formulation covers the two standard security goals of authenticated encryption:
. Note that security under this formulation covers the two standard security goals of authenticated encryption:
-
(Privacy) Security against an adversary who tries to distinguish the construction from an ideal prf \(f^*:{\mathcal {M}}\longrightarrow {\mathcal {M}}\times {\mathfrak {T}}\), and
-
(Integrity) Security against an adversary who tries to make a successful forging attempt on the construction.
2.4 Coefficients H Technique
Consider a security game G where the adversary can make both encryption queries and decryption queries. The part of the computation visible to the adversary at the time of choosing its final response is known as a view. This includes the queries and the responses, and may also include any additional information the oracle chooses to reveal to the adversary at the end of the query-response phase of the game. The probability of the security game with an oracle \({\mathcal {O}}\) resulting in a given view V is known as the interpolation probability of V, denoted  .
.
Note that for a view to be realised, two things need to happen:
-
The adversary needs to make the queries listed in the view;
-
The oracle needs to make the corresponding responses.
Of these, the former is deterministic; the latter, probabilistic. Thus when we talk of interpolation probability, we are only concerned with the oracle responses, with the assumption that the adversary’s queries are consistent with the view. For any other adversary, the interpolation probability is trivially 0. Thus  depends only on the oracle \({\mathcal {O}}\) and the view V and not on the adversary; hence the notation.
depends only on the oracle \({\mathcal {O}}\) and the view V and not on the adversary; hence the notation.
We extend the notation of interpolation probability to a set \({\mathcal {V}}\) of views:  denotes the probability that the security game with \({\mathcal {O}}\) results in a view \(V\in {\mathcal {V}}\). Now we state a theorem, due to Jacques Patarin, known as the Coefficient H Technique.
denotes the probability that the security game with \({\mathcal {O}}\) results in a view \(V\in {\mathcal {V}}\). Now we state a theorem, due to Jacques Patarin, known as the Coefficient H Technique.
Theorem 2
(Coefficient H Technique). [Pat08] Suppose there is a set \({\mathcal {V}}_{{\textsf {bad}}}\) of views satisfying the following:
-
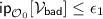 ;
; -
For any \(V\notin {\mathcal {V}}_{{\textsf {bad}}}\),

Then for an adversary \({\mathcal {A}}\) trying to distinguish between \({\mathcal {O}}_1\) and \({\mathcal {O}}_0\), we have the following bound on its distinguishing advantage:

3 \({\textsf {OCB3}}\) Construction
The \({\textsf {OCB3}}\) encryption and decryption algorithms are described in Algorithm 1. We take block length \(n = 128\). \(E_K\) denotes a call to blockcipher, and \({\mathcal {H}}_K\) denotes a call to a hash function based on the stretch-then-shift xor-universal hash \(H_\kappa \), as described below in Subsect. 3.1. Note that they share the same key K. Hashing of associated data \({\textsf {A}}\) is done through parallel masked calls to \(E_K\), which are added to get the authentication key \({\textsf {auth}}\). The message space \({\mathcal {M}}\) consists of all messages with at least one full block, i.e., all strings of 128 bits or more, and the nonce space \({\textsf {N}}\) consists of all 128-bit strings whose first 122 bits are not all 0. The message \({\textsf {M}}\) is encrypted in ECB mode, with masking that incorporates the nonce \({\textsf {N}}\). If there is an incomplete block at the end, it is added after a \(10^*\) padding to an encrypted masking key. Finally, a checksum of the message blocks is masked and encrypted through \(E_K\), and \({\textsf {auth}}\) is added to it to produce the authentication tag \({\textsf {T}}\). We ignore here the last step of \({\textsf {OCB3}}\), where a tag of a desired length \(\tau \) is obtained by chopping \({\textsf {T}}\) as required. A schematic view of the encryption is illustrated in Fig. 1, which treats each masked blockcipher call as a call to a tweakable blockcipher. The masking scheme corresponding to the various tweakable blockcipher calls is given in Table 1. The important thing to note here is that all the masking coefficients are distinct.
3.1 Stretch-then-Shift Hash
In this subsection we describe the hash function \({\mathcal {H}}_K\) used in \({\textsf {OCB3}}\) to process the nonce \({\textsf {N}}\). It is based on an xor-universal hash function \(H_\kappa \) with a 128-bit key and a 6-bit input, defined as
This is a linear function of \(\kappa \), and thus can be described as left multiplication with a matrix \({\mathbf {H}}[x]\) as
It is easy to show that when  , for any
, for any  , we have
, we have  . The authors show with a computer-aided exhaustive search that when \(\kappa \) is uniform over
. The authors show with a computer-aided exhaustive search that when \(\kappa \) is uniform over  , for any
, for any  and any
and any  , we have
, we have

We describe here a generalised hash \({\mathcal {H}}[\pi ]\), based on an arbitrary permutation \(\pi \). We begin by splitting \({\textsf {N}}\) into two parts:
so as \({\textsf {BN}}\) denotes the last 6 bits of \({\textsf {N}}\), and \({\textsf {TN}}\) denotes the first 122 bits, with 6 0’s appended at the end (Note that as long as \({\textsf {N}}\in {\mathcal {N}}\), \({\textsf {TN}}\) cannot be 0). Next we define
Finally, we define
The \({\mathcal {H}}_K\) used in \({\textsf {OCB3}}\) is an instantiation \({\mathcal {H}}[\pi ]\) with \(\pi = E_K\), i.e.,

4 Security Result
We present the main security result of the paper, along with an overview of our proof approach. Consider a nonce-based authenticated encryption security game with associated data involving \({\textsf {OCB3}}[\pi ]\), an ideal version of \({\textsf {OCB3}}\) where \(E_K\) is replaced by a random permutation \(\pi \). Recall Theorem 1 from Sect. 1.
Theorem 1
Let \({\mathcal {A}}\) be an adversary that makes q encryption queries consisting of \(\sigma \) message blocks in all with at most \(\ell _{\text {MAX}}\) blocks per query, and \(\alpha \) associated data blocks in all, and \(q'\) decryption queries in a nonce-respecting authenticated encryption security game with associated data against the oracles \({\mathcal {O}}_1\) and \({\mathcal {O}}_0\), where \({\mathcal {O}}_1\) simulates \({\textsf {OCB3}}[\pi ]\), and \({\mathcal {O}}_0\) simulates an ideal nonce-based authenticated encryption scheme with associated data. Then

where \(\sigma _T = \sigma + \alpha + q\) is the total number of blocks queried in the encryption queries (including messages, associated data and nonces).
4.1 Proof Approach
Before delving into the details of the proof, we give an overview of it. There are two parts to this security bound: the privacy bound, represented by the term \(5\sigma _T^2/N +2\sigma ^4/N^2\), and the integrity bound, represented by the term \((64q'\ell _{\text {MAX}}+15q')/N\). The privacy bound is birthday in the number of encryption-query blocks, and and relies on the simple requirement that every blockcipher output is distinct. The integrity bound, being beyond-birthday in the number of decryption-query blocks (as long as \(\ell _{\text {MAX}}\) is within a reasonable bound) is trickier to obtain, and is the main contribution of the paper.
We consider a slightly modified game where we let the real oracle \({\mathcal {O}}_1\) reveal the inputs and outputs of all internal blockcipher calls in the encryption queries at the end of the query phase. Thus, it becomes necessary for the ideal oracle \({\mathcal {O}}_0\) to sample these values. In Subsect. 4.3, we describe the sampling order for \({\mathcal {O}}_0\), which proceeds in four steps. Step 1 takes place during the encryption-query phase itself, when \({\mathcal {O}}_0\) behaves as in a standard \({\textsf {naead}}\) game, sampling the ciphertext and tag blocks on the fly. (In the decryption query phase, \({\mathcal {O}}_0\) always outputs \(\bot \).) After the query phase, in Step 2 and Step 3, the inputs and outputs of the internal blockcipher calls in all the encryption queries are sampled. Finally, in Step 4, the inputs and outputs of the internal blockcipher calls in the decryption queries which are not yet determined are sampled, completing the sampling process.
During this sampling process, we keep checking the sampled values for various bad events. \({\textsf {badA}}\) occurs at the end of Step 1 if there are certain undesirable collisions or multicollisions in the sampled ciphertext and tag blocks. \({\textsf {badB}}\) or \({\textsf {badC}}\) occurs at the end of Step 2 or Step 3 respectively if there are certain collisions in the inputs or sampled outputs of the internal blockcipher calls. Finally, \({\textsf {badD}}[i]\) occurs at the end of Step 4 if after sampling the inputs and outputs of the internal blockcipher calls in the i-th decryption query it turns out that the correct output of \({\mathcal {O}}_0\) should not have been \(\bot \). \({\textsf {badD}}[i]\) corresponds to the violation of integrity security, and the bounding of the probability of \({\textsf {badD}}[i]\), which is done by carefully selecting the specific collisions we need to ban, forms the heart of this paper.
In Subsect. 4.5, we calculate the probabilities of the various bad cases. The calculations for \({\textsf {badA}}\), \({\textsf {badB}}\) and \({\textsf {badC}}\) are straightforward. For \({\textsf {badD}}[i]\), we look at several cases, and establish a bound for \({\textsf {badD}}[i]\) based on some lemmas the proof of which we defer to Sect. 5. By Property-1 in Subsect. 2.1, we can reorder the sampling phase in Step 4 to first sample the blockcipher outputs required for \({\textsf {badD}}[i]\). Finally, we bound the probability of \(\cup _{i=1}^{q'}{\textsf {badD}}[i]\) by the union-bound. In Sect. 5, we prove the lemmas through an exhaustive case-analysis.
The \({\textsf {OCB3}}[\pi ]\) construction: notation for the i-th encryption query. \({\textsf {L}}\) denotes \(\pi (0)\) and \({\textsf {Q}}^i\) denotes \({\mathcal {H}}[\pi ]({\textsf {N}}^i)\). Top to Bottom: encrypting \({\textsf {M}}^i\) when  ; encrypting \({\textsf {M}}^i\) when
; encrypting \({\textsf {M}}^i\) when  ; hashing \({\textsf {A}}^i\) when
; hashing \({\textsf {A}}^i\) when  ; hashing \({\textsf {A}}^i\) when
; hashing \({\textsf {A}}^i\) when  .
.
4.2 Notation for Adversary Interactions
First we set up the notation for the adversary interactions in the game described in Theorem 1. The i-th encryption query consists of
-
a message \({\textsf {M}}^{i}\), consisting of \(\ell ^i\ge 1\) complete blocks and an incomplete (possibly empty) block
 at the end;
at the end; -
associated data \({\textsf {A}}^i\), consisting of \(k^i\ge 1\) blocks and an incomplete (possibly empty) block
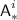 at the end;
at the end; -
a nonce block \({\textsf {N}}^i\), with the first 122 bits not all zero, such that for any \(i'\in [i-1]\), \({\textsf {N}}^i\ne {\textsf {N}}^{i'}\).
Following the notation for \({\mathcal {H}}[\pi ]\) described in Subsect. 3.1, we define \({\textsf {TN}}^i:= \tau ({\textsf {N}}^i), {\textsf {BN}}^i:= \beta ({\textsf {N}}^i),{\mathbf {H}}^i:= {\mathbf {H}}[{\textsf {BN}}^i]\). The corresponding output consists of
-
a ciphertext \({\textsf {C}}^{i}\), consisting of \(\ell ^{i}\) complete blocks and an incomplete block
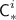 at the end, with
at the end, with 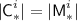 ;
; -
a tag block \({\textsf {T}}^{i}\).
The i-th decryption query consists of
-
a ciphertext \({\textsf {C'}}^{i}\), consisting of \(\ell '^{i}\ge 1\) complete blocks and an incomplete (possibly empty) block
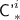 at the end;
at the end; -
a tag block \({\textsf {T'}}^i\);
-
associated date \({\textsf {A'}}^i\), consisting of \(k'^i\) blocks and an incomplete (possibly empty) block
 at the end;
at the end; -
a nonce block \({\textsf {N'}}^i\), with the first 122 bits not all zero.
(Note that in the decryption queries, nonces are allowed to repeat.) Again, as in the i-th encryption query, we define \({\textsf {TN'}}^i:= \tau ({\textsf {N'}}^i),{\textsf {BN'}}^i:= \beta ({\textsf {N'}}^i), \mathbf {H'}^i:= {\mathbf {H}}[{\textsf {BN'}}^i]\). The response is either \(\bot \), or a message \({\textsf {M}}'^i\) consisting of \(\ell '^i\) complete blocks and an incomplete block  at the end, with
at the end, with  .
.
The \({\textsf {OCB3}}[\pi ]\) construction: notation for the i-th decryption query. \({\textsf {L}}\) denotes \(\pi (0)\) and \({\textsf {Q'}}^i\) denotes \({\mathcal {H}}[\pi ]({\textsf {N'}}^i)\). Top to Bottom: decrypting \({\textsf {C'}}^i\) when  ; decrypting \({\textsf {C'}}^i\) when
; decrypting \({\textsf {C'}}^i\) when  ; hashing \({\textsf {A'}}^i\) when
; hashing \({\textsf {A'}}^i\) when  ; hashing \({\textsf {A'}}^i\) when
; hashing \({\textsf {A'}}^i\) when  .
.
4.3 Oracle Behaviour
Now we describe the oracles involved in the game in greater detail. Let \({\mathcal {I}}\) (resp. \({\mathcal {I}}'\)) denote the indices for the encryption (resp. decryption) queries with incomplete-block messages, and let \({\mathcal {J}}\) (resp. \({\mathcal {J}}'\)) denote the indices for the encryption (resp. decryption) queries with incomplete-block associated data. Let
be the set of first-appearance indices of the distinct values taken by \({\textsf {TN}}^i\).
Real Oracle. \({\textsf {Enc}}_1\) and \({\textsf {Dec}}_1\) of the real oracle \({\mathcal {O}}_1\) represent the encryption and decryption functions of \({\textsf {OCB3}}[\pi ]\) respectively. The notation we use for the internal computations of \({\mathcal {O}}_1\) while responding to the i-th encryption (resp. decryption) query is illustrated in Fig. 2 (resp. Fig. 3). In addition, still following the notation from Subsect. 3.1, for \(i\in [q]\) we define \({\textsf {KN}}^i:= \pi ({\textsf {TN}}^i), {\textsf {Q}}^i:= {\mathbf {H}}^i\cdot {\textsf {KN}}^i\), and for \(i\in [q']\) we define \({\textsf {KN'}}^i:= \pi ({\textsf {TN'}}^i), {\textsf {Q'}}^i:= \mathbf {H'}^i\cdot {\textsf {KN'}}^i\). We keep track of \({\textsf {Dom}}(\pi )\), the set of inputs to \(\pi \), and \({\textsf {Ran}}(\pi )\), the set of outputs from \(\pi \). At the end of the query phase, the partially determined \(\pi \) is also revealed to the adversary.
Ideal Oracle. \({\textsf {Dec}}_0\) of the ideal oracle is the constant function returning \(\bot \). \({\textsf {Enc}}_0\) samples and returns \(({\textsf {C}}^i,{\textsf {T}}^i)\) for the i-th query. At the end of the query phase, the \({\mathcal {O}}_0\) partially samples \(\pi \) and gives it to the adversary. The sampling behaviour followed by \({\mathcal {O}}_0\) is described in the subsequent paragraphs. (Note that if one of the bad events \({\textsf {badA}}\), \({\textsf {badB}}\), \({\textsf {badC}}\), or \({\textsf {badD}}[i]\) for some \(i\in [q']\) is encountered by \({\mathcal {O}}_0\), its behaviour thereafter is undefined.)
Step 1 and  . This step is online—it takes place during the query phase. For \(i\in [q]\), on the i-th encryption query, for each \(j\in [\ell ^i]\), sample \({\textsf {C}}^{i}_{j}\) uniformly with replacement from
. This step is online—it takes place during the query phase. For \(i\in [q]\), on the i-th encryption query, for each \(j\in [\ell ^i]\), sample \({\textsf {C}}^{i}_{j}\) uniformly with replacement from  and return \({\textsf {C}}^{i}_{j}\) to the adversary; sample \({\textsf {T}}^i\) uniformly with replacement from
and return \({\textsf {C}}^{i}_{j}\) to the adversary; sample \({\textsf {T}}^i\) uniformly with replacement from  and return \({\textsf {T}}^i\) to the adversary; and if \(i\in {\mathcal {I}}\), sample \(\overline{{\textsf {C}}^{i}_*}\) uniformly with replacement from
and return \({\textsf {T}}^i\) to the adversary; and if \(i\in {\mathcal {I}}\), sample \(\overline{{\textsf {C}}^{i}_*}\) uniformly with replacement from  , set
, set  ; and return
; and return  to the adversary.
to the adversary.
\({\textsf {badA}}\) occurs when we have

for some \(i_{1}, i_{2}, i_{3}\in [q]\) and three distinct pairs \((j_1,j'_1),(j_2,j'_2),(j_3,j'_3)\) satisfying

This restriction on certain multi-collisions over the ciphertexts is required in the proof of Lemma 5 in Sect. 5. The remaining steps of the simulation take place after the query phase is over.
Step 2 and  . Begin with \(\pi = \left\{ \right\} \) (so that \({\textsf {Dom}}(\pi )= {\textsf {Ran}}(\pi )= \left\{ \right\} \)). Sample \({\textsf {L}}\) uniformly from
. Begin with \(\pi = \left\{ \right\} \) (so that \({\textsf {Dom}}(\pi )= {\textsf {Ran}}(\pi )= \left\{ \right\} \)). Sample \({\textsf {L}}\) uniformly from  . For \(i\in {\mathcal {F}}\), sample \({\textsf {KN}}^i\) uniformly without replacement from
. For \(i\in {\mathcal {F}}\), sample \({\textsf {KN}}^i\) uniformly without replacement from  . Next set the following values:
. Next set the following values:
-
for \(i\in [q]\), set
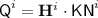 ;
; -
for \(i\in [q],j\in [\ell ^i]\) set
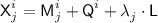 and
and 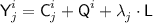 ;
; -
for \(i\in {\mathcal {I}}\) set
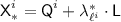 and
and 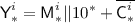 ;
; -
for \(i\in [q]\setminus {\mathcal {I}}\) set
 and
and  ;
; -
for \(i\in {\mathcal {I}}\) set
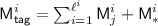 and
and  ;
; -
for \(i\in [q],j\in [k^i]\) set
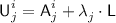 ;
; -
for \(i\in {\mathcal {J}}\) set
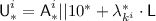 .
.
\({\textsf {badB}}\) occurs when:
-
there are collisions in the values 0, \({\textsf {TN}}^i\) for \(i\in {\mathcal {F}}\), \({\textsf {X}}^{i}_{j}\) for \(i\in [q],j\in [\ell ^i]\),
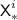 for \(i\in {\mathcal {I}}\),
for \(i\in {\mathcal {I}}\), 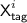 for \(i\in [q]\), \({\textsf {U}}^{i}_{j}\) for \(i\in [q],j\in [k^i]\),
for \(i\in [q]\), \({\textsf {U}}^{i}_{j}\) for \(i\in [q],j\in [k^i]\), 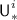 for \(i\in {\mathcal {J}}\), not counting the trivial collisions \({\textsf {U}}^{i}_{j}= {\textsf {U}}^{i'}_{j}\) when \({\textsf {A}}^{i}_{j}= {\textsf {A}}^{i'}_{j}\); or
for \(i\in {\mathcal {J}}\), not counting the trivial collisions \({\textsf {U}}^{i}_{j}= {\textsf {U}}^{i'}_{j}\) when \({\textsf {A}}^{i}_{j}= {\textsf {A}}^{i'}_{j}\); or -
there are collisions in the values \({\textsf {L}}\), \({\textsf {KN}}^i\) for \(i\in {\mathcal {F}}\), \({\textsf {Y}}^{i}_{j}\) for \(i\in [q],j\in [\ell ^i]\),
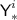 for \(i\in {\mathcal {I}}\).
for \(i\in {\mathcal {I}}\).
Add the following to \(\pi \):
-
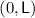 ;
; -
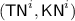 for \(i\in {\mathcal {F}}\);
for \(i\in {\mathcal {F}}\); -
\(({\textsf {X}}^{i}_{j},{\textsf {Y}}^{i}_{j})\) for \(i\in [q],j\in [\ell ^i]\);
-
 for \(i\in {\mathcal {I}}\);
for \(i\in {\mathcal {I}}\);
Note that the \(\pi \) sampled thus far remains permutation-compatible as long as \({\textsf {badB}}\) does not occur.
Step 3 and  . For each distinct \({\textsf {U}}^{i}_{j}, i\in [q],j\in [k^i]\), sample \({\textsf {V}}^{i}_{j}\) uniformly without replacement from
. For each distinct \({\textsf {U}}^{i}_{j}, i\in [q],j\in [k^i]\), sample \({\textsf {V}}^{i}_{j}\) uniformly without replacement from  . For each distinct
. For each distinct  for \(i\in {\mathcal {J}}\), sample
for \(i\in {\mathcal {J}}\), sample  uniformly without replacement from
uniformly without replacement from  . Next set the following values:
. Next set the following values:
-
for \(i\in [q]\setminus {\mathcal {J}}\) set \({\textsf {auth}}^i = \sum _{j=1}^{k^i}{\textsf {V}}^{i}_{j}\);
-
for \(i\in {\mathcal {J}}\) set
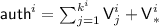 ;
; -
for \(i\in [q]\) set
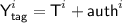 .
.
\({\textsf {badC}}\) occurs when:
-
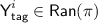 for some \(i\in [q]\);
for some \(i\in [q]\); -
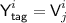 for some \(i\in [q],j\in [k^i]\);
for some \(i\in [q],j\in [k^i]\); -
 for some \(i\in {\mathcal {I}}\); or
for some \(i\in {\mathcal {I}}\); or -
 for some \(i,i'\in [q]\).
for some \(i,i'\in [q]\).
Add the following to \(\pi \):
-
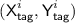 for \(i\in [q]\);
for \(i\in [q]\); -
\(({\textsf {U}}^{i}_{j},{\textsf {V}}^{i}_{j})\) for \(i\in [q],j\in [k^i]\);
-
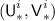 for \(i\in {\mathcal {J}}\);
for \(i\in {\mathcal {J}}\);
Note that the \(\pi \) sampled thus far remains permutation-compatible as long as neither of \({\textsf {badB}}\) and \({\textsf {badC}}\) occurs.
Step 4 and  . In this step we keep updating \(\pi \) (and hence \({\textsf {Dom}}(\pi )\) and \({\textsf {Ran}}(\pi )\)) on the fly. For each \(i\in [q']\), set
. In this step we keep updating \(\pi \) (and hence \({\textsf {Dom}}(\pi )\) and \({\textsf {Ran}}(\pi )\)) on the fly. For each \(i\in [q']\), set  and
and  as follows:
as follows:
-
If \({\textsf {TN'}}^i\in {\textsf {Dom}}(\pi )\), set \({\textsf {KN'}}^i = \pi ({\textsf {TN'}}^i)\), otherwise sample \({\textsf {KN'}}^i\) uniformly without replacement from
 , and add \(({\textsf {TN'}}^i,{\textsf {KN'}}^i)\) to \(\pi \);
, and add \(({\textsf {TN'}}^i,{\textsf {KN'}}^i)\) to \(\pi \); -
For \(j\in [\ell '^i]\), set
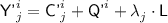 ; if \({\textsf {Y'}}^{i}_{j}\in {\textsf {Ran}}(\pi )\), set \({\textsf {X'}}^{i}_{j}= \pi ^{-1}({\textsf {Y'}}^{i}_{j})\), otherwise sample \({\textsf {X'}}^{i}_{j}\) uniformly without replacement from
; if \({\textsf {Y'}}^{i}_{j}\in {\textsf {Ran}}(\pi )\), set \({\textsf {X'}}^{i}_{j}= \pi ^{-1}({\textsf {Y'}}^{i}_{j})\), otherwise sample \({\textsf {X'}}^{i}_{j}\) uniformly without replacement from 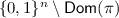 , and add \(({\textsf {X'}}^{i}_{j},{\textsf {Y'}}^{i}_{j})\) to \(\pi \); finally, set
, and add \(({\textsf {X'}}^{i}_{j},{\textsf {Y'}}^{i}_{j})\) to \(\pi \); finally, set 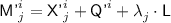 ;
; -
If \(i\in {\mathcal {I}}'\), set
 ; if
; if 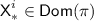 , set
, set 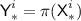 , otherwise sample
, otherwise sample 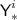 uniformly without replacement from
uniformly without replacement from 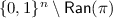 , and add
, and add 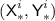 to \(\pi \); finally, set
to \(\pi \); finally, set 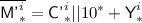 ;
; -
If \(i\notin {\mathcal {I}}'\), set
 ;
; -
If \(i\in {\mathcal {I}}'\), set
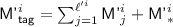 ;
; -
For \(j\in [k'^i]\), set
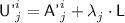 ; if \({\textsf {U'}}^{i}_{j}\in {\textsf {Dom}}(\pi )\), set \({\textsf {V'}}^{i}_{j}= \pi ({\textsf {U'}}^{i}_{j})\), otherwise sample \({\textsf {V'}}^{i}_{j}\) uniformly without replacement from
; if \({\textsf {U'}}^{i}_{j}\in {\textsf {Dom}}(\pi )\), set \({\textsf {V'}}^{i}_{j}= \pi ({\textsf {U'}}^{i}_{j})\), otherwise sample \({\textsf {V'}}^{i}_{j}\) uniformly without replacement from  , and add \(({\textsf {U'}}^{i}_{j},{\textsf {V'}}^{i}_{j})\) to \(\pi \);
, and add \(({\textsf {U'}}^{i}_{j},{\textsf {V'}}^{i}_{j})\) to \(\pi \); -
If \(i\in {\mathcal {J}}'\), set
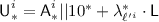 ; if
; if 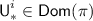 , set
, set  , otherwise sample
, otherwise sample 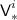 uniformly without replacement from
uniformly without replacement from 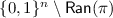 , and add
, and add 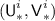 to \(\pi \);
to \(\pi \); -
If \(i\notin {\mathcal {J}}'\), set \({\textsf {auth'}}^i = \sum _{j=1}^{k'^i}{\textsf {V'}}^{i}_{j}\);
-
If \(i\in {\mathcal {J}}'\), set
 ;
; -
Set
 ; if
; if 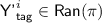 , set
, set  , otherwise sample
, otherwise sample  uniformly without replacement from
uniformly without replacement from 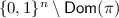 , and add
, and add 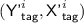 to \(\pi \); finally, set
to \(\pi \); finally, set  ;
; -
Return \(\pi \) to the adversary.
\({\textsf {badD}}[i]\) occurs when 
4.4 Notation for the Proof
Before we begin the proof, we introduce some more notation. Let \({\mathcal {P}}'^i\) denote the set of positions for the i-th decryption query, defined as

Further, let \({\mathcal {P}}'^i(-):= {\mathcal {P}}'^i\setminus \left\{ {\textsf {tag}}\right\} \). For \(p\in {\mathcal {P}}'^i\), let  denote the masking key for position p in i-th decryption query, defined as
denote the masking key for position p in i-th decryption query, defined as

where

For convenience, we will abuse the notation of set membership and extend it to sequences. Thus, for a sequence \({\textsf {S}}\) and a block \({\textsf {Z}}\), \({\textsf {Z}}\in {\textsf {S}}\) will imply that \({\textsf {Z}}\) occurs somewhere in \({\textsf {S}}\).
4.5 Proof of Theorem
Let \({\mathcal {V}}_{{\textsf {bad}}}\) consist of all those transcripts where one of \({\textsf {badA}}\), \({\textsf {badB}}\), \({\textsf {badC}}\) or \({\textsf {badD}}[i]\) for some \(i\in [q']\) has been encountered. Then

We make the following claim:
Claim
We have the following bounds on the bad events under \({\mathcal {O}}_0\):




From the claim we have

Consider a view \(V\notin {\mathcal {V}}_{{\textsf {bad}}}\). In the real oracle, to obtain V, exactly \(\sigma _T + |{\mathcal {F}}| + 1\) calls are made to \(\pi \): one for each message block, one for each position-wise distinct associated data block, one for each distinct \({\textsf {TN}}^i\), one for 0, and one for each tag. We know that these are all distinct because neither of \({\textsf {badB}}\) and \({\textsf {badC}}\) has been encountered. Hence

In the ideal oracle, in Step 1, the \(\sigma +q\) online outputs are sampled uniformly with replacement. In Steps 2 and 3, \(|{\mathcal {F}}| + 1 + \alpha \) outputs are sampled uniformly without replacement. Finally, since \({\textsf {badD}}[i]\) was not encountered for any \(i\in [q']\), all decryption queries in V must have returned \(\bot \), which \({\mathcal {O}}_0\) always returns. Hence

Theorem 2 then gives us the required result. \(\square \)
Proof of Claim. Suppose \({\textsf {badA}}\) is encountered. Then we have

for some \(i_1, i_2, i_3\in [q]\) and three distinct pairs \((j_1,j'_1),(j_2,j'_2),(j_3,j'_3)\). Now for fixed \(i_1, i_2, i_3,j_1,j'_1,j_2,j'_2,j_3,j'_3\), this probability is at most \(1/N^2\). Notice that if for any choice of \((j_1,j_2,j_3,j'_1)\), there is at most one choice of \(j'_2\) and at most one choice of \(j'_3\). For any choice of \(i_1\), there are at most \(\sigma ^2\) choices for \((i_2,j_2)\) and \((i_3,j_3)\), and at most \((\ell ^i)^2\) choices for \((j_1,j'_1)\). Summing over i gives us

establishing (1). For \({\textsf {badB}}\), since we are now sampling without replacement, each collision event has probability at most \(1/(N-1)\). There are at most \((q+1)\) values among 0, \({\textsf {TN}}^i\) for \(i\in {\mathcal {F}}\), and they are all distinct by sampling; there are at most \(\alpha \) distinct values among \({\textsf {U}}^{i}_{j}\) for \(i\in [q],j\in [k^i]\),  for \(i\in {\mathcal {J}}\); and there are \(\sigma +q\) values among \({\textsf {X}}^{i}_{j}\) for \(i\in [q],j\in [\ell ^i]\),
for \(i\in {\mathcal {J}}\); and there are \(\sigma +q\) values among \({\textsf {X}}^{i}_{j}\) for \(i\in [q],j\in [\ell ^i]\),  for \(i\in {\mathcal {I}}\) and
for \(i\in {\mathcal {I}}\) and  for \(i\in [q]\). These give us at most \((q+1)(\sigma +\alpha +q) + (\sigma +\alpha +q)^2/2\) possible collision pairs. Similarly, among \({\textsf {L}}\), \({\textsf {KN}}^i\) for \(i\in {\mathcal {F}}\), \({\textsf {Y}}^{i}_{j}\) for \(i\in [q],j\in [\ell ^i]\), and
for \(i\in [q]\). These give us at most \((q+1)(\sigma +\alpha +q) + (\sigma +\alpha +q)^2/2\) possible collision pairs. Similarly, among \({\textsf {L}}\), \({\textsf {KN}}^i\) for \(i\in {\mathcal {F}}\), \({\textsf {Y}}^{i}_{j}\) for \(i\in [q],j\in [\ell ^i]\), and  for \(i\in {\mathcal {I}}\), there are at most \((q+1)\sigma + \sigma ^2/2\) possible collision pairs. Thus we have
for \(i\in {\mathcal {I}}\), there are at most \((q+1)\sigma + \sigma ^2/2\) possible collision pairs. Thus we have

establishing (2). For \({\textsf {badC}}\), since at this point \(|{\textsf {Ran}}(\pi )|= \rho := \sigma +|{\mathcal {F}}|+1\), the probability of each collision event is at most \(1/(N-\rho -1)\). Since there are at most \(q\rho +q\alpha +q^2/2\) possible collision pairs, we have

establishing (3). To prove (4) we need to bound the probability of \({\textsf {badD}}[i]\), and for that we consider several cases. For now we assume that \(i\in {\mathcal {I}}'\). Then \({\mathcal {P}}'^i(-)\) is simply \([\ell '^i]\). For some \(p\in {\mathcal {P}}'^i\), we say  is trivially determined if the adversary can deduce the value of
is trivially determined if the adversary can deduce the value of  from the transcript of the encryption queries. This can happen in two ways:
from the transcript of the encryption queries. This can happen in two ways:
-
When \(p\in [\ell '^i]\),
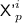 is trivially determined if for some \(i'\) we have \({\textsf {N'}}^i = {\textsf {N}}^{i'}\) and
is trivially determined if for some \(i'\) we have \({\textsf {N'}}^i = {\textsf {N}}^{i'}\) and 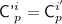 , which forces
, which forces  to equal
to equal 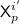 — then we say
— then we say 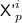 is \(i'\)-trivial;
is \(i'\)-trivial; -
 is trivially determined if for some j we have \({\textsf {A'}}^i = {\textsf {A}}^j\) and
is trivially determined if for some j we have \({\textsf {A'}}^i = {\textsf {A}}^j\) and 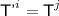 , which forces
, which forces  to equal
to equal  — then we say
— then we say 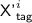 is j-trivial.
is j-trivial.
We look at five cases:
-
Case 1.
 is trivially determined for all \(p\in {\mathcal {P}}'^i\);
is trivially determined for all \(p\in {\mathcal {P}}'^i\); -
Cases 2 and 3. For some \(p_0\in {\mathcal {P}}'^i\),
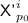 is not trivially determined, and
is not trivially determined, and  is trivially determined for all \(p\in {\mathcal {P}}'^i\setminus \left\{ p_0\right\} \):
is trivially determined for all \(p\in {\mathcal {P}}'^i\setminus \left\{ p_0\right\} \):-
Case 2. \(p_0\in [\ell '^i]\);
-
Case 3. \(p_0 = {\textsf {tag}}\);
-
-
Case 4. For some \(p_0\in [\ell '^i]\),
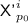 and
and  are not trivially determined, and
are not trivially determined, and 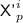 is trivially determined for all \(p\in [\ell '^i]\setminus \left\{ p_0\right\} \);
is trivially determined for all \(p\in [\ell '^i]\setminus \left\{ p_0\right\} \); -
Case 5. For some distinct \(p_0,p_1\in [\ell '^i]\),
 and
and 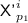 are not trivially determined.
are not trivially determined.
Note that the decryption query satisfies one of the five cases above, and moreover that this case can be chosen in advance by the adversary, by appropriately setting the query parameters. Accordingly, we can divide \([q']\) into five disjoint subsets  , such that for \(k\in [5]\),
, such that for \(k\in [5]\),  denotes the set of decryption queries which fall under Case \(\langle k\rangle \) above.
denotes the set of decryption queries which fall under Case \(\langle k\rangle \) above.
We now state five lemmas for the five separate cases, the proofs of which we defer to Sect. 5.
Lemma 1
For  ,
,  .
.
Lemma 2
For  ,
,  , as long as \(2\sigma _T\le N\).
, as long as \(2\sigma _T\le N\).
Lemma 3
For  ,
,  , as long as \(2\sigma _T\le N\).
, as long as \(2\sigma _T\le N\).
Lemma 4
For  ,
,  .
.
Lemma 5
For  ,
,  .
.
Taking the maximum over these bounds gives (4), and completes the proof of the claim. \(\square \)
5 Proof of Lemmas
We recall that for the i-th decryption query, we first sample/set the inputs and outputs of \(\pi \), and then define \({\textsf {M}}'^{i}_{p}\) as

Finally, we set

and \({\textsf {badD}}[i]\) is triggered when  .
.
The Subcase Tree. In Subsect. 4.5, we divide the set [q’] of decryption queries into five subsets  , depending on which of five cases a particular decryption query satisfies. We divide each of the cases, except Case 1, into various sub-cases. Whenever a
, depending on which of five cases a particular decryption query satisfies. We divide each of the cases, except Case 1, into various sub-cases. Whenever a  is trivially determined for
is trivially determined for  , we let \(i^{\prime }\) be such that
, we let \(i^{\prime }\) be such that  is \(i'\)-trivial, and whenever
is \(i'\)-trivial, and whenever  is trivially determined, we let j be such that
is trivially determined, we let j be such that  is j-trivial. (Note that there can be exactly one choice for each of \(i'\) and \(j\).)
is j-trivial. (Note that there can be exactly one choice for each of \(i'\) and \(j\).)
-
Case 2. Here
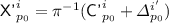 , so we branch based on
, so we branch based on 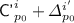 :
: - \(\bullet \) :
-
Subcase 2(a).
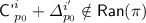 ;
; - \(\bullet \) :
-
Subcase 2(b).
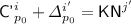 for some \(j'\in [q]\);
for some \(j'\in [q]\); - \(\bullet \) :
-
Subcase 2(c).
 for some \(j'\in [q],s_0\in [k^{j'}]\);
for some \(j'\in [q],s_0\in [k^{j'}]\); - \(\bullet \) :
-
Subcase 2(d).
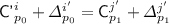 for some
for some 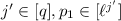 ;
; - \(\bullet \) :
-
Subcase 2(e).
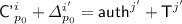 for some \(j'\in [q]\).
for some \(j'\in [q]\).
-
Case 3. Here
 , so we branch based on \({\textsf {auth'}}^i + {\textsf {T'}}^i\):
, so we branch based on \({\textsf {auth'}}^i + {\textsf {T'}}^i\):-
Subcase 3(a). \({\textsf {auth'}}^i + {\textsf {T'}}^i\notin {\textsf {Ran}}(\pi )\);
-
Subcase 3(b). \({\textsf {auth'}}^i + {\textsf {T'}}^i = {\textsf {KN}}^{j'}\) for some \(j'\in [q]\);
-
Subcase 3(c).
 for some \(j'\in [q],s_0\in [k^{j'}]\);
for some \(j'\in [q],s_0\in [k^{j'}]\); -
Subcase 3(d).
 for some
for some  ;
; -
Subcase 3(e). \({\textsf {auth'}}^i + {\textsf {T'}}^i = {\textsf {auth}}^{j'} + {\textsf {T}}^{j'}\) for some \(j'\in [q]\).
-
-
Case 4. Here
 and
and 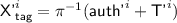 , so we can branch based on
, so we can branch based on 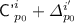 and \({\textsf {auth'}}^i + {\textsf {T'}}^i\) and get seventeen cases here: one covering either of them being randomly sampled, and the other sixteen a Cartesian product between Subcases 2(b)–2(e) and Subcases 3(b)–3(e). However, most of this cases can be settled using near-identical arguments, so we make the case division to reflect the interesting cases:
and \({\textsf {auth'}}^i + {\textsf {T'}}^i\) and get seventeen cases here: one covering either of them being randomly sampled, and the other sixteen a Cartesian product between Subcases 2(b)–2(e) and Subcases 3(b)–3(e). However, most of this cases can be settled using near-identical arguments, so we make the case division to reflect the interesting cases:-
Subcase 4(a).
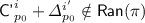 or \({\textsf {auth'}}^i + {\textsf {T'}}^i\notin {\textsf {Ran}}(\pi )\);
or \({\textsf {auth'}}^i + {\textsf {T'}}^i\notin {\textsf {Ran}}(\pi )\); -
Subcase 4(b).
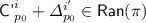 ,
,  for some \(j'\in [q],s_0\in [k^{j'}]\);
for some \(j'\in [q],s_0\in [k^{j'}]\); -
Subcase 4(c).
 , \({\textsf {auth'}}^i + {\textsf {T'}}^i\in {\textsf {Ran}}(\pi )\),
, \({\textsf {auth'}}^i + {\textsf {T'}}^i\in {\textsf {Ran}}(\pi )\),  for all \(j'\in [q],s_0\in [k^{j'}]\).
for all \(j'\in [q],s_0\in [k^{j'}]\).
-
-
Case 5. Here
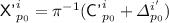 and
and  , so we can branch based on
, so we can branch based on 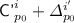 and
and 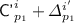 :
:-
Subcase 5(a).
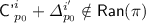 or
or 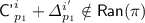 ;
; -
Subcase 5(b).
 for some \(j',j''\in [q],j'\ne j'',p_2\in [\ell ^{j'}],p_3\in [\ell ^{j''}]\);
for some \(j',j''\in [q],j'\ne j'',p_2\in [\ell ^{j'}],p_3\in [\ell ^{j''}]\); -
Subcase 5(c).
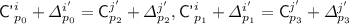 for some \(j'\in [q],p_2,p_3\in [\ell ^{j'}]\);
for some \(j'\in [q],p_2,p_3\in [\ell ^{j'}]\); -
Subcase 5(d).
 and
and 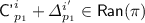 , either
, either 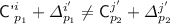 for any \(j'\in [q],p_2\in [\ell ^{j'}]\) or
for any \(j'\in [q],p_2\in [\ell ^{j'}]\) or  for any \(j'\in [q],p_2\in [\ell ^{j'}]\).
for any \(j'\in [q],p_2\in [\ell ^{j'}]\).
-
Now we turn to the proof of the lemmas. We make the following observations:
-
When
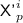 is \(i'\)-trivial for some \(p\in [\ell '^i]\),
is \(i'\)-trivial for some \(p\in [\ell '^i]\),  ;
; -
When
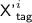 is j-trivial,
is j-trivial, 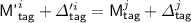 .
.
For brevity, when we write the collision equation(s) that need to be satisfied for \({\textsf {badD}}[i]\) to occur, the random variables that contribute to the subsequent probability calculation are indicated  .
.
5.1 Proof of Lemma 1
Lemma 1
For  ,
,  .
.
Proof
When  ,
,  is trivially determined for all \(p\in {\mathcal {P}}'^i\). From observations above, for \({\textsf {badD}}[i]\) to occur, we must have
is trivially determined for all \(p\in {\mathcal {P}}'^i\). From observations above, for \({\textsf {badD}}[i]\) to occur, we must have

If \(\ell ^j\ne \ell '^i\), the equation is

where the coefficient of \({\textsf {L}}\) is non-zero. The probability of this \(\le 1/(N-2)\le 1/2N\). If \(\ell ^j = \ell '^i\), so \(j\ne i'\) (the decryption query has to be non-trivial), but \({\textsf {TN}}^j = {\textsf {TN}}^{i'}\), then \({\mathbf {H}}^j + {\mathbf {H}}^{i'}\) is full-rank, so

The probability of this \(\le 1/N\). And finally when \(\ell ^j = \ell '^i\) and \({\textsf {TN}}^j\ne {\textsf {TN}}^{i'}\), we have

The probability of this \(\le 1/(N-1)\le 2/N\). This completes the proof. \(\square \)
5.2 Proof of Lemma 2
Lemma 2
For  ,
,  , as long as \(2\sigma _T\le N\).
, as long as \(2\sigma _T\le N\).
Proof
When  , for some \(p_0\in [\ell '^i]\),
, for some \(p_0\in [\ell '^i]\),  is trivially determined for all \(p\in {\mathcal {P}}'^i\setminus \left\{ p_0\right\} \), but
is trivially determined for all \(p\in {\mathcal {P}}'^i\setminus \left\{ p_0\right\} \), but  is not trivially determined . The equation for \({\textsf {badD}}[i]\) becomes
is not trivially determined . The equation for \({\textsf {badD}}[i]\) becomes

where

Based on the value of  , we look at the subcases listed in the tree at the beginning of this section. Note that
, we look at the subcases listed in the tree at the beginning of this section. Note that

-
Subcase 2(a).
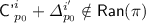 , so
, so  is sampled. The equation for \({\textsf {badD}}[i]\) is
is sampled. The equation for \({\textsf {badD}}[i]\) is 
The probability of this \(\le 1/(N-2)\le 2/N\).
-
Subcase 2(b).
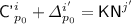 for some \(j'\in [q]\), so
for some \(j'\in [q]\), so  , and a second equation comes from the condition for \({\textsf {badD}}[i]\). When \(\ell ^{i'} = \ell ^j\) and \({\textsf {TN}}^{i'} = {\textsf {TN}}^{j'}\), these two equations become
, and a second equation comes from the condition for \({\textsf {badD}}[i]\). When \(\ell ^{i'} = \ell ^j\) and \({\textsf {TN}}^{i'} = {\textsf {TN}}^{j'}\), these two equations become 
Since there are at most \(2^6\) choices for \(j'\), this probability \(\le 64/(N-1)(N-2)\le 256/N^2\le 1/N\). When \(\ell ^{i'} = \ell ^j\) and \({\textsf {TN}}^{i'}\ne {\textsf {TN}}^{j'}\), the two equations become

Here there are q choices for \(j'\), and this probability \(\le q(N-2)(N-3)\le 4q/N^2\). When \(\ell ^{i'}\ne \ell ^j\), the two equations become

Here too there are q choices for \(j'\), and this probability \(\le q/(N-2)(N-3)\le 4q/N^2\). Thus, the probability of \({\textsf {badB}}\) and Subcase 2(b) simultaneously happening is at most 2 / N, as long as \(2q\le N\).
-
Subcase 2(c).
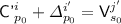 for some \(j'\in [q],s_0\in [k^{j'}]\), so
for some \(j'\in [q],s_0\in [k^{j'}]\), so 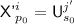 , and a second equation comes from the condition for \({\textsf {badD}}[i]\). Here the two equations are
, and a second equation comes from the condition for \({\textsf {badD}}[i]\). Here the two equations are 
There are \(\alpha \) choices for \((j',s_0)\), so the probability of this \(\le \alpha /(N-2)(N-3) \le 4\alpha /N^2\le 2/N\), as long as \(2\alpha \le N\).
-
Subcase 2(d).
 for some \(j'\in [q],p_1\in [\ell ^{j'}]\), so
for some \(j'\in [q],p_1\in [\ell ^{j'}]\), so 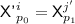 , and a second equation comes from the condition for \({\textsf {badD}}[i]\). The two equations are
, and a second equation comes from the condition for \({\textsf {badD}}[i]\). The two equations are 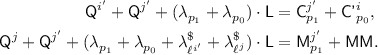
When \(i' = j\), the two equations become
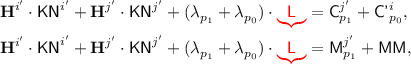
which is actually a single equation with the constraint that
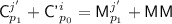 , which implies that \(j'\) must satisfy
, which implies that \(j'\) must satisfy 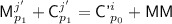 . Since there are no collisions on
. Since there are no collisions on  over all pairs \((j',p_1)\), there is at most one choice of \((j',p_1)\) satisfying this. Thus, the probability of this \(\le 1/(N-2)\le 2/N\). When \(i\ne j'\) but \({\textsf {KN}}^{i'} = {\textsf {KN}}^j\) and \(\ell ^{i'} = \ell ^j\), the two equations become
over all pairs \((j',p_1)\), there is at most one choice of \((j',p_1)\) satisfying this. Thus, the probability of this \(\le 1/(N-2)\le 2/N\). When \(i\ne j'\) but \({\textsf {KN}}^{i'} = {\textsf {KN}}^j\) and \(\ell ^{i'} = \ell ^j\), the two equations become 
There are at most \(\sigma \) choices for \((j',p_1)\), so the probability \(\le \sigma /(N-1)(N-2)\le 4\sigma /N^2.\) When \(i\ne j'\), \({\textsf {KN}}^{i'} = {\textsf {KN}}^j\ne {\textsf {KN}}^{j'}\), \(\ell ^{i'}\ne \ell ^j\), the two equations become
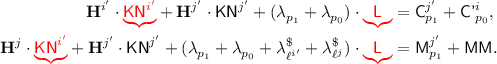
There are at most \(\sigma \) choices for \((j',p_1)\), so the probability of this \(\le \sigma /(N-1)(N-2)\le 4\sigma /N^2\). When \(i\ne j'\), \({\textsf {KN}}^{i'} = {\textsf {KN}}^j = {\textsf {KN}}^{j'}\), \(\ell ^{i'}\ne \ell ^j\), the two equations become
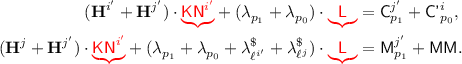
They may be multiples of the same equation, in which case we have at most 64 choices for \(j'\) and at most \(\ell _{\text {MAX}}\) choices for \(p_1\). Then this probability \(\le 64\ell _{\text {MAX}}/N\). When they are different equations, this probability \(\le \sigma /N(N-1)\le 2\sigma /N^2\). So the probability of \({\textsf {badD}}[i]\) and Subcase 2(d) simultaneously happening is at most \((64\ell _{\text {MAX}}+7)/N\) as long as \(2\sigma \le N\).
-
Subcase 2(e).
 for some \(j'\in [q]\), so
for some \(j'\in [q]\), so  , and a second equation comes from the condition for \({\textsf {badD}}[i]\). When \(j = j'\), the two equations become
, and a second equation comes from the condition for \({\textsf {badD}}[i]\). When \(j = j'\), the two equations become 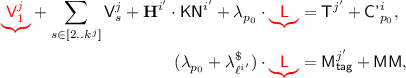
and the probability of this \(\le 1/(N-k^j-1)(N-k^j-2) \le 4/N^2\). When \(j\ne j'\), the two equations become
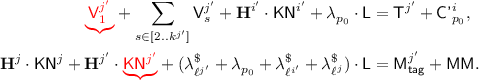
and the probability of this \(\le q/(N-k^{j'}-3)(N-k^{j'}-4)\le 4q/N^2\). Thus, the probability of \({\textsf {badB}}\) and Subcase 2(e) simultaneously happening is at most 2 / N, as long as \(2q\le N\).
Summing over the subcases completes the proof. \(\square \)
5.3 Proof of Lemma 3
Lemma 3
For  ,
,  , as long as \(2\sigma _T\le N\).
, as long as \(2\sigma _T\le N\).
Proof
When  ,
,  is trivially determined for all \(p\in [\ell '^i]\), but
is trivially determined for all \(p\in [\ell '^i]\), but  is not trivially determined. The equation for \({\textsf {badD}}[i]\) becomes
is not trivially determined. The equation for \({\textsf {badD}}[i]\) becomes

Based on the value of \({\textsf {auth'}}^i + {\textsf {T'}}^i\), we look at the subcases listed in the tree at the beginning of this section.
-
Subcase 3(a). \({\textsf {auth'}}^i + {\textsf {T'}}^i\notin {\textsf {Ran}}(\pi )\), so
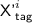 is sampled. The equation for \({\textsf {badD}}[i]\) is
is sampled. The equation for \({\textsf {badD}}[i]\) is 
The probability of this \(\le 1/(N-2)\le 2/N\).
-
Subcase 3(b). \({\textsf {auth'}}^i + {\textsf {T'}}^i = {\textsf {KN}}^{j'}\) for some \(j'\in [q]\), so
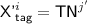 , and a second equation comes from the condition for \({\textsf {badD}}[i]\). The two equations are
, and a second equation comes from the condition for \({\textsf {badD}}[i]\). The two equations are 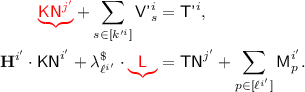
The probability of this \(\le 4q/N^2\le 2/N\), as long as \(2q\le N\).
-
Subcase 3(c).
 for some \(j'\in [q],s_0\in [k^{j'}]\), so
for some \(j'\in [q],s_0\in [k^{j'}]\), so 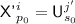 , and a second equation comes from the condition for \({\textsf {badD}}[i]\). The two equations are
, and a second equation comes from the condition for \({\textsf {badD}}[i]\). The two equations are 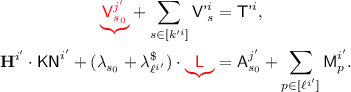
When the top equation vanishes, the probability of this \(\le 1/(N-1)\le 2/N\). When both equations are there, the probability of this \(\le 4\alpha /N^2\). So the probability of \({\textsf {badD}}[i]\) and Subcase 3(c) simultaneously happening is at most 2 / N, as long as \(2\alpha \le N\).
-
Subcase 3(d).
 for some \(j'\in [q],p_1\in [\ell ^{j'}]\), so
for some \(j'\in [q],p_1\in [\ell ^{j'}]\), so 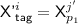 , and a second equation comes from the condition for \({\textsf {badD}}[i]\). The two equations are
, and a second equation comes from the condition for \({\textsf {badD}}[i]\). The two equations are 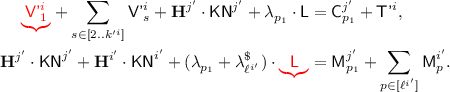
The probability of this \(\le 4\sigma /N^2\le 2/N\), as long as \(2\sigma \le N\).
-
Subcase 3(e). \({\textsf {auth'}}^i + {\textsf {T'}}^i = {\textsf {auth}}^{j'} + {\textsf {T}}^{j'}\) for some \(j'\in [q]\), so
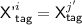 , and a second equation comes from the condition for \({\textsf {badD}}[i]\). If \({\textsf {A}}^{j'} = {\textsf {A'}}^i\), we have \({\textsf {T}}^{j'}\ne {\textsf {T'}}^i\) (by definition of this case), or \({\textsf {auth}}^{j'}\ne {\textsf {auth'}}^i\), a contradiction. So \({\textsf {A}}^{j'}\ne {\textsf {A'}}^i\). If we can find \(s_0\le k^{j'}\) such that either \(s_0>k'^i\), or
, and a second equation comes from the condition for \({\textsf {badD}}[i]\). If \({\textsf {A}}^{j'} = {\textsf {A'}}^i\), we have \({\textsf {T}}^{j'}\ne {\textsf {T'}}^i\) (by definition of this case), or \({\textsf {auth}}^{j'}\ne {\textsf {auth'}}^i\), a contradiction. So \({\textsf {A}}^{j'}\ne {\textsf {A'}}^i\). If we can find \(s_0\le k^{j'}\) such that either \(s_0>k'^i\), or 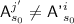 , then the equations are
, then the equations are 
Otherwise we can find \(s_0\le k'^i\) such that either \(s_0>k^{j'}\), or
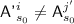 , then the equations are
, then the equations are 
The probability of either of these does not exceed 2 / N as long as \(2\sigma \le N\).
Summing over the subcases completes the proof. \(\square \)
5.4 Proof of Lemma 4
Lemma 4
For  ,
,  .
.
Proof
The bounds for Case 4 are simple to derive:
-
Subcase 4(a). We get a bound of 2 / N on the probability as in Subcase 2(a) or Subcase 3(a).
-
Subcase 4(b). We treat this separately because the equation
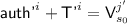
can vanish. When it does not vanish, we can find two independent collision equations that need to be satisfied, which can occur together with a probability of at most \(2/N^2\). When it does vanish, we proceed as in Subcase 3(c) and use instead the equation where
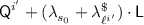 is equated to a constant. There are four possibilities here based on Subcases 2(b)-2(e). In each possibility, there are at most \(\sigma _T^2\) choices for these collision indices. Thus, each possibility with \({\textsf {badD}}[i]\) has a probability of at most \(2\sigma _T^2/N^2\), and Subcase 4(b) has a probability of at most \(8\sigma _T^2/N^2\).
is equated to a constant. There are four possibilities here based on Subcases 2(b)-2(e). In each possibility, there are at most \(\sigma _T^2\) choices for these collision indices. Thus, each possibility with \({\textsf {badD}}[i]\) has a probability of at most \(2\sigma _T^2/N^2\), and Subcase 4(b) has a probability of at most \(8\sigma _T^2/N^2\). -
Subcase 4(c). There are twelve possibilites here, based on various combinations of Subcases 2(b)-2(e) and Subcases 3(b),3(d),3(e). In each of these possibilities, we can find two independent collision equations that need to be satisfied, which can occur together with a probability of at most \(2/N^2\). There are at most \(\sigma _T^2\) choices for these collision indices. Thus, each possibility with \({\textsf {badD}}[i]\) has a probability of at most \(2\sigma _T^2/N^2\), and Subcase 4(c) has a probability of at most \(24\sigma _T^2/N^2\).
Summing over the three subcases completes the proof. \(\square \)
5.5 Proof of Lemma 5
Lemma 5
For  ,
,  .
.
Proof
We look one by one at the subcases listed in the tree at the beginning of this section.
-
Subcase 5(a). Here we get a bound of 2 / N on the probability as in Subcase 2(a).
-
Subcase 5(b). This is the case when
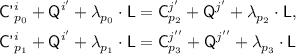
for some \(j',j''\in [q],p_2\in [\ell ^{j'}],p_3\in [\ell ^{j''}]\) with \(j'\ne j''\). If \({\textsf {TN}}^{j'} = {\textsf {TN}}^{i'}\), the equations may become dependent on each other. But here there are at most 64 choices for \(j'\), since the nonce is distinct in every encryption query, and only 64 distinct values of \({\textsf {N}}^{j'}\) can yield the same \({\textsf {TN}}^{j'}\). Thus the probability of this does not exceed \(64\ell _{\text {MAX}}/N\). Otherwise, we always get two independent equations, and the bound of \(2\sigma _T^2/N^2\) holds. Thus, the probability of Subcase 5(b) with \({\textsf {badD}}[i]\) does not exceed \(64\ell _{\text {MAX}}/N + 2\sigma _T^2/N^2\).
-
Subcase 5(c). This is trickier. Here too these two equations may become the same equation. Since the equations can be rewritten as

they become the same equation when \(\lambda _{p_0} + \lambda _{p_2} = \lambda _{p_1} + \lambda _{p_3}\) and
 . Thus any valid choice of \((p_2,p_3)\) must satisfy
. Thus any valid choice of \((p_2,p_3)\) must satisfy 
i.e., for each such choice of \((p_2,p_3)\), \(\lambda _{p_2} + \lambda _{p_3}\) takes the same fixed value, and
 take the same fixed value. Since \({\textsf {badA}}\) has not occurred, we know there are at most 2 such choices of \((p_2,p_3)\). Thus the probability of this does not exceed 2 / N.
take the same fixed value. Since \({\textsf {badA}}\) has not occurred, we know there are at most 2 such choices of \((p_2,p_3)\). Thus the probability of this does not exceed 2 / N. -
Subcase 5(d). There can be fifteen possibilities, depending on various combinations of the subcases of Case 2. In each of these, we can find two independent collision equations that need to be satisfied, which can occur together with a probability of at most \(2/N^2\). There are at most \(\sigma _T^2\) choices for these collision indices. Thus, each of those possibilities with \({\textsf {badD}}[i]\) has a probability of at most \(2\sigma _T^2/N^2\), and Subcase 5(d) has a probability of at most \(30\sigma _T^2/N^2\).
Summing over the four subcases completes the proof. \(\square \)
More detailed proofs of Lemmas 4 and 5 can be found in the full version of the paper at the IACR eprint archive, at the url https://eprint.iacr.org/2017/845.pdf.
References
Andreeva, E., Bogdanov, A., Luykx, A., Mennink, B., Tischhauser, E., Yasuda, K.: Parallelizable and authenticated online ciphers. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 424–443. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_22
Bellare, M., Goldreich, O., Mityagin, A.: The power of verification queries in message authentication and authenticated encryption. Cryptology ePrint Archive, Report 2004/309 (2004). http://eprint.iacr.org/2004/309
Caesar competition (2013). https://competitions.cr.yp.to/caesar.html
Datta, N., Nandi, M.: ELmE: A misuse resistant parallel authenticated encryption. In: Susilo, W., Mu, Y. (eds.) ACISP 2014. LNCS, vol. 8544, pp. 306–321. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08344-5_20
Gaži, P., Pietrzak, K., Rybár, M.: The exact security of PMAC. IACR Trans. Symmetric Cryptol. 2016(2), 145–161 (2017)
Hoang, V.T., Krovetz, T., Rogaway, P.: Robust authenticated-encryption AEZ and the problem that it solves. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 15–44. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_2
Krovetz, T., Rogaway, P.: The software performance of authenticated-encryption modes. In: Joux, A. (ed.) FSE 2011. LNCS, vol. 6733, pp. 306–327. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21702-9_18
McGrew, D.: An interface and algorithms for authenticated encryption (2008). https://buildbot.tools.ietf.org/html/rfc5116
McGrew, D., Viega, J.: The security and performance of the galois/counter mode (GCM) of operation. In: Canteaut, A., Viswanathan, K. (eds.) INDOCRYPT 2004. LNCS, vol. 3348, pp. 343–355. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30556-9_27
McGrew, D., Viega, J.: The galois/counter mode of operation (gcm). In: NIST Modes Operation Symmetric Key Block Ciphers (2005)
Patarin, J.: The “Coefficients H” technique. In: Avanzi, R.M., Keliher, L., Sica, F. (eds.) SAC 2008. LNCS, vol. 5381, pp. 328–345. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04159-4_21
Rogaway, P., Bellare, M., Black, J.: OCB: A block-cipher mode of operation for efficient authenticated encryption. ACM Trans. Inf. Syst. Secur. 6(3), 365–403 (2003)
Rogaway, P.: Authenticated-encryption with associated-data. In: Proceedings of the 9th ACM Conference on Computer and Communications Security, CCS 2002, NY, USA, pp. 98–107. ACM, New York (2002)
Rogaway, P.: Efficient instantiations of tweakable blockciphers and refinements to modes OCB and PMAC. In: Lee, P.J. (ed.) ASIACRYPT 2004. LNCS, vol. 3329, pp. 16–31. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30539-2_2
Rogaway, P., Shrimpton, T.: A provable-security treatment of the key-wrap problem. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 373–390. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_23
Whiting, D., Housley, R., Ferguson, N.: AES encryption & authentication using CTR mode & CBC-MAC. IEEE P802, 11 (2002)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Bhaumik, R., Nandi, M. (2017). Improved Security for OCB3. In: Takagi, T., Peyrin, T. (eds) Advances in Cryptology – ASIACRYPT 2017. ASIACRYPT 2017. Lecture Notes in Computer Science(), vol 10625. Springer, Cham. https://doi.org/10.1007/978-3-319-70697-9_22
Download citation
DOI: https://doi.org/10.1007/978-3-319-70697-9_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70696-2
Online ISBN: 978-3-319-70697-9
eBook Packages: Computer ScienceComputer Science (R0)





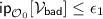 ;
;

 ; encrypting
; encrypting  ; hashing
; hashing  ; hashing
; hashing  .
.
 at the end;
at the end;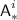 at the end;
at the end;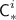 at the end, with
at the end, with 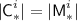 ;
;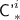 at the end;
at the end; at the end;
at the end;
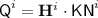 ;
;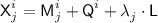 and
and 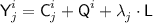 ;
;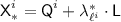 and
and 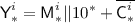 ;
; and
and  ;
;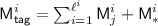 and
and  ;
;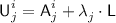 ;
;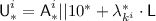 .
.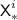 for
for 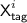 for
for 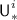 for
for 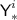 for
for 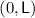 ;
;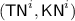 for
for  for
for 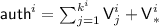 ;
;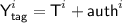 .
.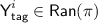 for some
for some 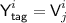 for some
for some  for some
for some  for some
for some 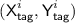 for
for 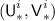 for
for  , and add
, and add 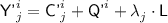 ; if
; if 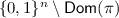 , and add
, and add 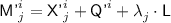 ;
; ; if
; if 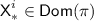 , set
, set 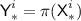 , otherwise sample
, otherwise sample 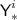 uniformly without replacement from
uniformly without replacement from 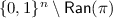 , and add
, and add 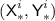 to
to 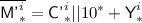 ;
; ;
;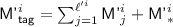 ;
;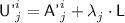 ; if
; if  , and add
, and add 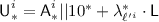 ; if
; if 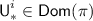 , set
, set  , otherwise sample
, otherwise sample 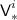 uniformly without replacement from
uniformly without replacement from 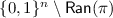 , and add
, and add 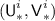 to
to  ;
; ; if
; if 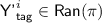 , set
, set  , otherwise sample
, otherwise sample  uniformly without replacement from
uniformly without replacement from 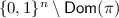 , and add
, and add 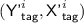 to
to  ;
;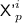 is trivially determined if for some
is trivially determined if for some 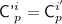 , which forces
, which forces  to equal
to equal 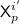 — then we say
— then we say 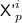 is
is  is trivially determined if for some j we have
is trivially determined if for some j we have 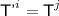 , which forces
, which forces  to equal
to equal  — then we say
— then we say 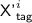 is j-trivial.
is j-trivial. is trivially determined for all
is trivially determined for all 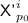 is not trivially determined, and
is not trivially determined, and  is trivially determined for all
is trivially determined for all 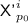 and
and  are not trivially determined, and
are not trivially determined, and 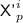 is trivially determined for all
is trivially determined for all  and
and 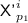 are not trivially determined.
are not trivially determined.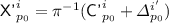 , so we branch based on
, so we branch based on 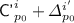 :
: 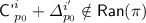 ;
;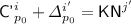 for some
for some  for some
for some 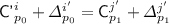 for some
for some 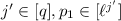 ;
;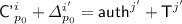 for some
for some  , so we branch based on
, so we branch based on  for some
for some  for some
for some  ;
; and
and 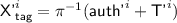 , so we can branch based on
, so we can branch based on 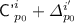 and
and 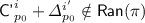 or
or 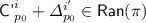 ,
,  for some
for some  ,
,  for all
for all 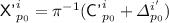 and
and  , so we can branch based on
, so we can branch based on 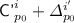 and
and 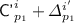 :
: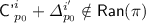 or
or 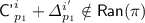 ;
; for some
for some 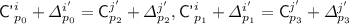 for some
for some  and
and 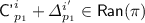 , either
, either 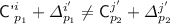 for any
for any  for any
for any 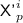 is
is  ;
;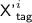 is j-trivial,
is j-trivial, 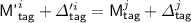 .
.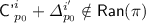 , so
, so  is sampled. The equation for
is sampled. The equation for 
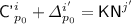 for some
for some  , and a second equation comes from the condition for
, and a second equation comes from the condition for 


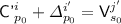 for some
for some 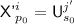 , and a second equation comes from the condition for
, and a second equation comes from the condition for 
 for some
for some 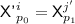 , and a second equation comes from the condition for
, and a second equation comes from the condition for 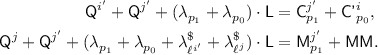
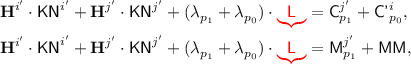
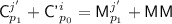 , which implies that
, which implies that 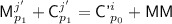 . Since there are no collisions on
. Since there are no collisions on  over all pairs
over all pairs 
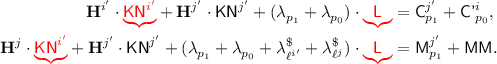
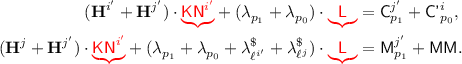
 for some
for some  , and a second equation comes from the condition for
, and a second equation comes from the condition for 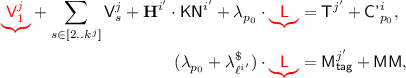
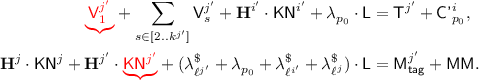
 is sampled. The equation for
is sampled. The equation for 
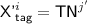 , and a second equation comes from the condition for
, and a second equation comes from the condition for 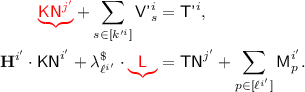
 for some
for some 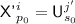 , and a second equation comes from the condition for
, and a second equation comes from the condition for 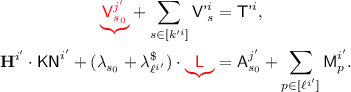
 for some
for some 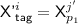 , and a second equation comes from the condition for
, and a second equation comes from the condition for 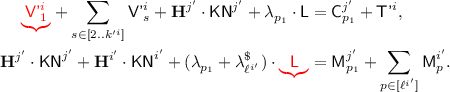
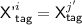 , and a second equation comes from the condition for
, and a second equation comes from the condition for 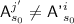 , then the equations are
, then the equations are 
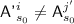 , then the equations are
, then the equations are 
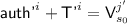
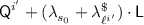 is equated to a constant. There are four possibilities here based on Subcases 2(b)-2(e). In each possibility, there are at most
is equated to a constant. There are four possibilities here based on Subcases 2(b)-2(e). In each possibility, there are at most 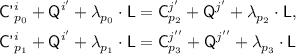

 . Thus any valid choice of
. Thus any valid choice of 
 take the same fixed value. Since
take the same fixed value. Since 