Identification Protocols and Signature Schemes Based on Supersingular Isogeny Problems

Abstract

We provide a new identification protocol and new signature schemes based on isogeny problems. Our identification protocol relies on the hardness of the endomorphism ring computation problem, arguably the hardest of all problems in this area, whereas the only previous scheme based on isogenies (due to De Feo, Jao and Plût) relied on potentially easier problems. The protocol makes novel use of an algorithm of Kohel-Lauter-Petit-Tignol for the quaternion version of the $\ell$-isogeny problem, for which we provide a more complete description and analysis. Our new signature schemes are derived from the identification protocols using the Fiat-Shamir (respectively, Unruh) transforms for classical (respectively, post-quantum) security. We study their efficiency, highlighting very small key sizes and reasonably efficient signing and verification algorithms.

1 Introduction

A recent research area is cryptosystems whose security is based on the difficulty of finding a path in the isogeny graph of supersingular elliptic curves [6, 8, 14, 21, 22]. Unlike other elliptic curve cryptosystems, the only known quantum algorithm for these problems, due to Biasse-Jao-Sankar [4], has exponential complexity. Hence, additional motivation for the study of these cryptosystems is that they are possibly suitable for post-quantum cryptography.

A large range of cryptographic primitives can now be based on isogeny assumptions. The work of Charles-Goren-Lauter [6] gave a collision-resistant hash function. Jao-De Feo [21] gave a key exchange protocol, De Feo-Jao-Plût [14] gave a public key encryption scheme and an interactive identification protocol, Jao-Soukharev [22] gave an undeniable signature, and Xi-Tian-Wang [41] gave a designated verifier signature. In this paper we focus on identification protocols and signature schemes.

A first identification protocol based on isogeny problems was proposed by De Feo-Jao-Plût [14], as an extension of the key exchange protocol of Jao-De Feo [21]. This scheme has the advantage of being simple to describe and easy to implement. On the other hand, it inherits the disadvantages of [21], in particular it relies on a non-standard isogeny problem using small isogeny degrees, reveals auxiliary points, and uses special primes.

The fastest classical attack on this scheme has heuristic running time of $\tilde{O}( p^{1/4} )$ bit operations, and the fastest quantum attack has running time of $\tilde{O}( p^{1/6} )$. Several recent papers [17, 19, 29, 32] have shown that revealing auxiliary points may be dangerous in certain contexts. It is therefore highly advisable to build cryptographic schemes on the most general, standard and potentially hardest isogeny problems.

Our main contribution in this paper is a new identification protocol with statistical zero-knowledge and computational soundness based on the endomorphism ring computation problem. The latter problem has been studied for some time in computational number theory, and is equivalent to computing an isogeny between two arbitrary given elliptic curves, without any restriction on the parameters and no extra information revealed. In contrast to the problem used in De Feo-Jao-Plût’s protocol, this problem has heuristic classical complexity of $\tilde{O}( p^{1/2} )$ bit operations, and quantum complexity $\tilde{O}( p^{1/4} )$.

Our identification protocol is very similar to the standard sigma protocol for graph isomorphism.

The public key is a pair of elliptic curves $(E_0, E_1)$ and the private key is an isogeny $\phi : E_0 \rightarrow E_1$. To interactively prove knowledge of $\phi$ one chooses a random isogeny $\psi : E_1 \rightarrow E_2$ and sends $E_2$ to the verifier. The verifier sends a bit b. If $b=0$ the prover reveals $\psi$. If $b=1$ the prover reveals an isogeny $\mu : E_0 \rightarrow E_2$. In either case, the verifier checks that the response is correct. The interaction is repeated a number of times until the verifier is convinced that the prover knows an isogeny from $E_0$ to $E_1$. However, the subtlety is that we cannot just set $\mu = \psi \circ \phi$, as then $E_1$ would appear on the path in the isogeny graph from $E_0$ to $E_2$ and so we would have leaked the private key. The crucial idea is to use the algorithm of Kohel-Lauter-Petit-Tignol [26] to produce an isogeny $\mu : E_0 \rightarrow E_2$ that is completely independent of $\phi$. The mathematics behind the algorithm of Kohel-Lauter-Petit-Tignol goes beyond what usually arises in elliptic curve cryptography.

Our second contribution are secure digital signatures based on isogeny problems, which we construct using generic transforms from identification protocols. We use the well-known Fiat-Shamir transform [15] to obtain security against classical adversaries in the random oracle model. This is not known to be secure against quantum adversaries¹ so for post-quantum security we use another transform due to Unruh [33]. We provide a full description of the two resulting signature schemes. Our signatures have very small key sizes, and reasonably efficient signing and verification procedures. The full version of the paper also contains two signature schemes based on the De Feo-Jao-Plût ID-scheme.²

As an additional contribution, we carefully analyse the complexity of the quaternion isogeny algorithm of Kohel-Lauter-Petit-Tignol [26] for powersmooth norms, and we highlight a property of its output distribution (under a minor change) that had remained unnoticed until now. This contribution is of independent interest, and it might be useful for other schemes based on similar isogeny problems.

Outline. The paper is organized as follows. In Sect. 2 we give preliminaries on isogeny problems and random walks in isogeny graphs, as well as security definitions for identification protocols. In Sect. 3 we describe our new identification protocol based on the endomorphism ring computation problem. In Sect. 4 we present our signature schemes and summarize their main efficiency features. A full version of this paper is available on the IACR eprint server [18].

2 Preliminaries

2.1 Hard Problem Candidates Related to Isogenies

We summarize the required background on elliptic curves. For a more detailed exposition of the theory, see [31]. Let $E,E'$ be two elliptic curves over a finite field $\mathbb {F} _q$. An isogeny $\varphi :E\rightarrow E'$ is a non-constant morphism from E to $E'$ that maps the neutral element into the neutral element. The degree of an isogeny $\varphi$ is the degree of $\varphi$ as a morphism. An isogeny of degree $\ell$ is called an $\ell$-isogeny. If $\varphi$ is separable, then $\deg \varphi =\#\ker \varphi$. If there is a separable isogeny between two curves, we say that they are isogenous. Tate’s theorem is that two curves $E,E'$ over $\mathbb {F} _q$ are isogenous over $\mathbb {F} _q$ if and only if $\#E(\mathbb {F} _q)=\#E'(\mathbb {F} _q)$.

A separable isogeny can be identified with its kernel [40]. Given a subgroup G of E, we can use Vélu’s formulae [39] to explicitly obtain an isogeny $\varphi :E\rightarrow E'$ with kernel G and such that $E'\cong E/G$. These formulas involve sums over points in G, so using them is efficient as long as $\#G$ is small. Kohel [25] and Dewaghe [12] have (independently) given formulae for the Vélu isogeny in terms of the coefficients of the polynomial defining the kernel, rather than in terms of the points in the kernel. Given a prime $\ell$, the torsion group $E[\ell ]$ contains exactly $\ell +1$ cyclic subgroups of order $\ell$, each one corresponding to a different isogeny.

A composition of n separable isogenies of degrees $\ell _i$ for $1 \le i \le n$ gives an isogeny of degree $N = \prod _i \ell _i$ with kernel a group G of order N. Conversely any isogeny whose kernel is a group of smooth order can be decomposed as a sequence of isogenies of small degree, hence can be computed efficiently. For any permutation $\sigma$ on $\{ 1, \dots , n \}$, by considering appropriate subgroups of G, one can write the isogeny as a composition of isogenies of degree $\ell _{\sigma (i)}$. Hence, there is no loss of generality in the protocols in our paper of considering chains of isogenies of increasing degree.

For each isogeny $\varphi :E\rightarrow E'$, there is a unique isogeny $\hat{\varphi }:E'\rightarrow E$, which is called the dual isogeny of $\varphi$, and which satisfies $\varphi \hat{\varphi }=\hat{\varphi }\varphi =[\deg \varphi ]$. If we have two isogenies $\varphi :E\rightarrow E'$ and $\varphi ':E'\rightarrow E$ such that $\varphi \varphi '$ and $\varphi '\varphi$ are the identity in their respective curves, we say that $\varphi ,\varphi '$ are isomorphisms, and that $E,E'$ are isomorphic. Isomorphism classes of elliptic curves over $\mathbb {F} _q$ can be labeled with their j-invariant [31, III.1.4(b)]. An isogeny $\varphi :E\rightarrow E'$ such that $E=E'$ is called an endomorphism. The set of endomorphisms of an elliptic curve, denoted by $\text {End}(E)$, has a ring structure with the operations point-wise addition and function composition.

Elliptic curves can be classified according to their endomorphism ring. Over the algebraic closure of the field, $\text {End}(E)$ is either an order in a quadratic imaginary field or a maximal order in a quaternion algebra. In the first case, we say that the curve is ordinary, whereas in the second case we say that the curve is supersingular. The endomorphism ring of a supersingular curve over a field of characteristic p is a maximal order $\mathcal {O}$ in the quaternion algebra $B_{p,\infty }$ ramified at p and $\infty$.

In the case of supersingular elliptic curves, there is always a curve in the isomorphism class defined over $\mathbb {F} _{p^2}$, and the j-invariant of the class is also an element of $\mathbb {F} _{p^2}$. A theorem by Deuring [11] gives an equivalence of categories between the j-invariants of supersingular elliptic curves over $\mathbb {F} _{p^2}$ up to Galois conjugacy in $\mathbb {F} _{p^2}$, and the maximal orders in the quaternion algebra $B_{p,\infty }$ up to the equivalence relation given by $\mathcal {O}\sim \mathcal {O}'$ if and only if $\mathcal {O}=\alpha ^{-1}\mathcal {O}'\alpha$ for some $\alpha \in B_{p,\infty }^*$. Specifically, the equivalence of categories associates to every j-invariant a maximal order that is isomorphic to the endomorphism ring of any curve with that j-invariant. Furthermore, if $E_0$ is an elliptic curve with $\text {End}(E_0) = \mathcal {O}_0$, there is a one-to-one correspondence (which we call the Deuring correspondence) between isogenies $\psi : E_0 \rightarrow E$ and left $\mathcal {O}_0$-ideals I. More details on the Deuring correspondence can be found in Chap. 41 of [37].

We now present some hard problem candidates related to supersingular elliptic curves, and discuss the related algebraic problems in the light of the Deuring correspondence.

Problem 1

Let $p,\ell$ be distinct prime numbers. Let $E,E'$ be two supersingular elliptic curves over $\mathbb {F} _{p^2}$ with $\#E(\mathbb {F} _{p^2})=\#E'(\mathbb {F} _{p^2})=(p+1)^2$, chosen uniformly at random. Find $k\in \mathbb {N}$ and an isogeny of degree $\ell ^k$ from E to $E'$.

Problem 2

Let $p,\ell$ be distinct prime numbers. Let E be a supersingular elliptic curve over $\mathbb {F} _{p^2}$, chosen uniformly at random. Find $k_1,k_2\in \mathbb {N}$, a supersingular elliptic curve $E'$ over $\mathbb {F} _{p^2}$, and two distinct isogenies of degrees $\ell ^{k_1}$ and $\ell ^{k_2}$, respectively, from E to $E'$.

The hardness assumption of both problems has been used in [6] to prove preimage and collision-resistance of a proposed hash function. Variants of the first problem, in which some extra information is provided, were used by De Feo-Jao-Plût [14] to build an identification scheme, a key exchange protocol and a public-key encryption scheme. More precisely, the identification scheme in [14] relies on Problems 3 and 4 below (which De Feo, Jao and Plût call the Computational Supersingular Isogeny and Decisional Supersingular Product problems). In order to state them we need to introduce some notation. Let p be a prime of the form $\ell _1^{e_1}\ell _2^{e_2}\cdot f\pm 1$, and let E be a supersingular elliptic curve over $\mathbb {F} _{p^2}$. Let $\{R_1,S_1\}$ and $\{R_2,S_2\}$ be bases for $E[\ell _1^{e_1}]$ and $E[\ell _2^{e_2}]$, respectively.

Problem 3

(Computational Supersingular Isogeny). Let $\phi _1:E\rightarrow E'$ be an isogeny with kernel $\langle [m_1]R_1+[n_1]S_1\rangle$, where $m_1,n_1$ are chosen uniformly at random from $\mathbb {Z}/\ell _1^{e_1}\mathbb {Z}$, and not both divisible by $\ell _1$. Given $E'$ and the values $\phi _1(R_2), \phi _1(S_2)$, find a generator of $\langle [m_1]R_1+[n_1]S_1\rangle$.

The fastest known algorithms for this problem use a meet-in-the-middle argument. The classical and quantum algorithm have heuristic running time respectively of $\tilde{O}( \ell _1^{e_1/2} )$ and $\tilde{O}( \ell _1^{e_1/3} )$ bit operations, which is respectively $\tilde{O}( p^{1/4} )$ and $\tilde{O}( p^{1/6} )$ in the context of De Feo-Jao-Plût [14].

Problem 4

(Decisional Supersingular Product). Let $E, E'$ be supersingular elliptic curves over $\mathbb {F} _{p^2}$ such that there exists an isogeny $\phi :E\rightarrow E'$ of degree $\ell _1^{e_1}$. Fix generators $R_2, S_2 \in E[ \ell _2^{e_2} ]$ and suppose $\phi ( R_2)$ and $\phi (S_2)$ are given. Consider the two distributions of pairs $(E_2,E_2')$ as follows:

• $(E_2 , E_2')$ such that there is a cyclic group $G \subseteq E[ \ell _2^{e_2} ]$ of order $\ell _2^{e_2}$ and $E_2 \cong E/G$ and $E_2' \cong E' / \phi (G)$.

• $(E_2,E_2')$ where $E_2$ is chosen at random among the curves having the same cardinality as $E_0$, and $\phi ':E_2\rightarrow E_2'$ is a random $\ell _1^{e_1}$-isogeny.

The problem is, given $(E, E' )$ and the auxiliary points $(R_2, S_2, \phi ( R_2), \phi (S_2))$, plus a pair $(E_2, E_2')$, to determine from which distribution the pair is sampled.

We stress that Problems 3 and 4 are potentially easier than Problems 1 and 2 because special primes are used and extra points are revealed. Furthermore, it is shown in Sect. 4 of [17] that if $\text {End}(E)$ is known and one can find any isogeny from E to $E'$ then one can compute the specific isogeny of degree $\ell _1^{e_1}$. The following problem, on the other hand, offers better foundations for cryptography based on supersingular isogeny problems.

Problem 5

Let p be a prime number. Let E be a supersingular elliptic curve over $\mathbb {F} _{p^2}$, chosen uniformly at random. Determine the endomorphism ring of E.

Note that it is essential that the curve is chosen randomly in this problem, as for special curves the endomorphism ring is easy to compute. Essentially, Problem 5 is the same as explicitly computing the forward direction of Deuring’s correspondence. This problem was studied by Kohel in [25], in which an algorithm to solve it was obtained, but with expected running time $\tilde{O}(p)$. It was later improved by Galbraith to $\tilde{O}(p^{\frac{1}{2}})$, under heuristic assumptions [16]. Interestingly, the best quantum algorithm for this problem runs in time $\tilde{O}(p^\frac{1}{4})$, only providing a quadratic speedup over classical algorithms [4]. This has largely motivated the use of supersingular isogeny problems in cryptography.

Problem 6

Let p be a prime number. Let $E, E'$ be supersingular elliptic curves over $\mathbb {F} _{p^2}$, chosen uniformly at random.³ Find an isogeny $E \rightarrow E'$.

Heuristically, if we can solve Problem 1 or Problem 6, then we can solve Problem 5. To compute an endomorphism of E, we take two random walks $\phi _1:E\rightarrow E_1$ and $\phi _2:E\rightarrow E_2$, and solve Problem 6 on the pair $E_1,E_2$, obtaining an isogeny $\psi :E_1\rightarrow E_2$. Then the composition $\hat{\phi }_2\psi \phi _1$ is an endomorphism of E. Repeating the process, it is easy to find four endomorphisms that are linearly independent, thus generating a subring of $\text {End}(E)$, and this subring is likely to be of small index so that the full ring can be recovered.

For the converse, suppose that we can compute the endomorphism rings of both E and $E'$. The strategy is to compute a module I that is a left ideal of $\text {End}(E)$ and a right ideal of $\text {End}(E')$ of appropriate norm, and to translate it back to the geometric setting to obtain an isogeny. This approach motivated the quaternion $\ell$-isogeny algorithm of Kohel-Lauter-Petit-Tignol [26, 28], which solves the following problem:

Problem 7

Let $p,\ell$ be distinct prime numbers. Let $\mathcal {O}_0,\mathcal {O}_1$ be two maximal orders in $B_{p,\infty }$, chosen uniformly at random. Find $k\in \mathbb {N}$ and an ideal I of norm $\ell ^k$ such that I is a left $\mathcal {O}_0$-ideal and its right order is isomorphic to $\mathcal {O}_1$.

The algorithm can be adapted to produce ideals of B-powersmooth norm (meaning the norm is $\prod _i\ell _i^{e_i}$ where the $\ell _i$ are distinct primes and $\ell _i^{e_i} \le B$) for $B\approx \frac{7}{2}\log p$ and using $O(\log p)$ different primes, instead of ideals of norm a power of $\ell$. We will use that version in our signature scheme.

For completeness we mention that ordinary curve versions of Problems 1 and 5 are not known to be equivalent, and in fact there is a subexponential algorithm for computing the endomorphism ring of ordinary curves [5], whereas the best classical algorithm known for computing isogenies is still exponential. There is, however, a subexponential quantum algorithm for computing an isogeny between ordinary curves [7], which is why the main interest in cryptography is the supersingular case.

2.2 Random Walks in Isogeny Graphs

Let $p\ge 5$ be a prime number. There are $N_p:=\lfloor \frac{p}{12}\rfloor +\epsilon _p$ supersingular j-invariants in characteristic p, with $\epsilon _p=0,1,1,2$ when $p=1,5,7,11\bmod 12$ respectively. For any prime $\ell \ne p$, one can construct a so-called isogeny graph, where each vertex is associated to a supersingular j-invariant, and an edge between two vertices is associated to a degree $\ell$ isogeny between the corresponding vertices.

Isogeny graphs are regular⁴ with regularity degree $\ell +1$; they are undirected since to any isogeny from $j_1$ to $j_2$ corresponds a dual isogeny from $j_2$ to $j_1$. Isogeny graphs are also very good expander graphs [20]; in fact they are optimal expander graphs in the following sense:

Definition 1

(Ramanujan graph). Let G be a k-regular graph, and let $k,\lambda _2,\cdots ,\lambda _r$ be the eigenvalues of the adjacency matrix sorted by decreasing order of the absolute value. Then G is a Ramanujan graph if

$$\begin{aligned} \lambda _2\le 2\sqrt{k-1}. \end{aligned}$$

This is optimal by the Alon-Boppana bound: given a family $\{G_N\}$ of k-regular graphs as above, and denoting by $\lambda _{2,N}$ the corresponding second eigenvalue of each graph $G_N$, we have $\liminf _{N\rightarrow \infty }\lambda _{2,N}\ge 2\sqrt{k-1}$. The Ramanujan property of isogeny graphs follows from the Weil conjectures proved by Deligne [10, 30].

Let p and $\ell$ be as above, and let j be a supersingular invariant in characteristic p. We define a random step of degree $\ell$ from j as the process of randomly and uniformly choosing a neighbour of j in the $\ell$-isogeny graph, and returning that vertex. For a composite degree $n=\prod _i\ell _i$, we define a random walk of degree n from $j_0$ as a sequence of j-invariants $j_i$ such that $j_i$ is a random step of degree $\ell _i$ from $j_{i-1}$. We do not require the primes $\ell _i$ to be distinct.

The output of random walks in expander graphs converge quickly to a uniform distribution. In our signature scheme we will be using random walks of B-powersmooth degree n, namely $n=\prod _i\ell _i^{e_i}$, with all prime powers $\ell _i^{e_i}$ smaller than some bound B, with B as small as possible. To analyse the ouptut distribution of these walks we will use the following generalization⁵ of classical random walk theorems [20]:

Theorem 1

(Random walk theorem). Let p be a prime number, and let $j_0$ be a supersingular invariant in characteristic p. Let j be the final j-invariant reached by a random walk of degree $n=\prod _i\ell _i^{e_i}$ from $j_0$. Then for every j-invariant $\tilde{j}$ we have

$$\left| \Pr [j=\tilde{j}]-\frac{1}{N_p}\right| \le \prod _i\left( \frac{2\sqrt{\ell _i}}{\ell _i+1}\right) ^{e_i}.$$

Proof:

Let $v_{tj}$ be the probability that the outcome of the first t random steps is a given vertex j, and let $v_t=(v_{tj})_j$ be vectors encoding these probabilities. Let $v_0$ correspond to an initial state of the walk at $j_0$ (so that $v_{0j_0} = 1$ and $v_{0j} = 0$ for all $i \ne j_0$). Let $A_{\ell _i}$ be the adjacency matrix of the $\ell _i$-isogeny graph. Its largest eigenvalue is k. By the Ramanujan property the second largest eigenvalue is smaller than k in absolute value, so the eigenspace associated to $\lambda _1=k$ is of dimension 1 and generated by the vector $u:=(N_p^{-1})_j$ corresponding to the uniform distribution. Let $\lambda _{2i}$ be the second largest eigenvalue of $A_{\ell _i}$ in absolute value.

If step t is of degree $\ell _i$ we have $v_{t}= \tfrac{1}{k} A_{\ell _i}v_{t-1}$. Moreover we have $||v_t-u||_2\le \tfrac{1}{k} \lambda _{2i}||v_{t-1}-u||_2$ since the eigenspace associated to k is of dimension 1. Iterating on all steps we deduce

$$||v_t-u||_2\le \prod _i| \tfrac{1}{k} \lambda _{2i}|^{e_i}||v_0-u||_2\le \prod _i| \tfrac{1}{k} \lambda _{2i}|^{e_i}$$

since $||v_0-u||_2^2=(1-\frac{1}{N_p})^2+\frac{N_p-1}{N_p}(\frac{1}{N_p})^2\le 1-\frac{2}{N_p}+\frac{2}{N_p^2}<1$. Finally we have

$$\left| \Pr [j=\tilde{j}]-\frac{1}{N_p}\right| =||v_t-u||_\infty \le ||v_t-u||_2\le \prod _i| \tfrac{1}{k}\lambda _{2i}|^{e_i}\le \prod _i\left( \frac{2\sqrt{\ell _i}}{\ell _i+1}\right) ^{e_i},$$

where we have used the Ramanujan property to bound the eigenvalues.     $\Box$

In our security proof we will want the right-hand term to be smaller than $(p^{1+\epsilon })^{-1}$ for an arbitrary positive constant $\epsilon$, and at the same time we will want the powersmooth bound B to be as small as possible. The following lemma shows that taking $B\approx 2(1+\epsilon )\log p$ suffices asymptotically.

Lemma 1

Let $\epsilon >0$. There is a function $c_p=c(p)$ such that $\lim _{p\rightarrow \infty }c_p=2(1+\epsilon )$, and, for each p,

$$\prod _{\begin{array}{c} \ell _i \text { prime}\\ e_i:= \max \{e | \ell _i^{e}<c_p\log p\} \end{array}}\left( \frac{\ell _i+1}{2\sqrt{\ell _i}}\right) ^{e_i}>p^{1+\epsilon }.$$

Proof:

Let B be an integer. We have

$$ \prod _{\begin{array}{c} \ell _i^{e_i}<B \\ \ell _i \text { prime}\\ e_i \text { maximal} \end{array}}\left( \frac{\ell _i+1}{2\sqrt{\ell _i}}\right) ^{e_i}> \prod _{\begin{array}{c} \ell _i<B \\ \ell _i \text { prime} \end{array}}\left( \frac{\ell _i+1}{2\sqrt{\ell _i}}\right) > \prod _{\begin{array}{c} \ell _i<B \\ \ell _i \text { prime} \end{array}}\left( \frac{\sqrt{\ell _i}}{2}\right) . $$

Taking logarithms, using the prime number theorem and replacing the sum by an integral we have

$$\begin{aligned} \log \prod _{\begin{array}{c} \ell _i<B \\ \ell _i \text { prime} \end{array}}\left( \frac{\sqrt{\ell _i}}{2}\right)&= \sum _{\begin{array}{c} \ell _i<B \\ \ell _i \text { prime} \end{array}}\frac{1}{2}\log \ell _i-\sum _{\begin{array}{c} \ell _i<B \\ \ell _i \text { prime} \end{array}}\log 2 \approx \frac{1}{2}\int _{1}^B\log x\frac{1}{\log x}dx - \frac{B}{\log B} =\\&= \frac{1}{2}B-\frac{B}{\log B}\approx \frac{1}{2}B. \end{aligned}$$

if B is large enough. Taking $B = c \log (p)$ where $c=2(1+\epsilon )$ gives $\frac{1}{2}B = (1+\epsilon ) \log p = \log ( p^{1+\epsilon } )$ which proves the lemma.     $\Box$

2.3 Identification Schemes

In this section we recall the standard cryptographic notions of identification schemes. A good general reference is Chap. 8 of Katz [23]. A sigma-protocol is a three-move proof of knowledge of a relation. The notions of honest verifier zero-knowledge (HVZK) and 2-special soundness are standard and due to lack of space we do not recall them. In the special case of “hard relations” (see Definition 3 below), one can interpret a sigma-protocol as a public key identification scheme. Good general references are the lecture notes of Damgård [9] and Venturi [35]. All algorithms below are probabilistic polynomial-time (PPT) unless otherwise stated.

An identification scheme is an interactive protocol between two parties (a Prover and a Verifier), where the Prover aims to convince the Verifier that it knows some secret key without revealing anything about it. This is achieved by the Prover first committing to some value, then the Verifier sending a challenge, and finally the Prover providing some answer in accordance to the commitment, the challenge and the secret. We use the terminology and notation of Abdalla-An-Bellare-Namprempre [1] (also see Bellare-Poettering-Stebila [3]). We also introduce a notion of “recoverability” which is implicit in the Schnorr signature scheme and seems to be folklore in the field.

Definition 2

A canonical identification scheme is $\mathcal {ID}= ( K, \mathcal {P}, \mathcal {V}, c )$ where: K is a PPT algorithm (key generation) that on input a security parameter $\lambda$ outputs a pair $( {\textsc {pk}}, {\textsc {sk}})$; $\mathcal {P}$ is a PPT algorithm taking input ${\textsc {sk}}$ and outputting a message; $c \ge 1$ is the (integer) bitlength of the challenge (a function of the security parameter $\lambda$); $\mathcal {V}$ is a deterministic polynomial-time verification algorithm that takes as input ${\textsc {pk}}$ and a transcript and outputs 0 or 1. A transcript of an honest execution of the scheme $\mathcal {ID}$ is the sequence: ${\textsc {cmt}}\leftarrow \mathcal {P}( {\textsc {pk}}, {\textsc {sk}})$, ${\textsc {ch}}\leftarrow \{ 0,1 \}^c$, ${\textsc {rsp}}\leftarrow \mathcal {P}( {\textsc {pk}}, {\textsc {sk}}, {\textsc {cmt}}, {\textsc {ch}})$. On an honest execution we require that $\mathcal {V}( {\textsc {pk}}, {\textsc {cmt}}, {\textsc {ch}}, {\textsc {rsp}}) = 1$.

An impersonator for $\mathcal {ID}$ is an algorithm $\mathcal {I}$ that plays the following game: $\mathcal {I}$ takes as input a public key ${\textsc {pk}}$ and a set of transcripts of honest executions of the scheme $\mathcal {ID}$; $\mathcal {I}$ outputs ${\textsc {cmt}}$, receives ${\textsc {ch}}\leftarrow \{ 0,1 \}^c$ and outputs ${\textsc {rsp}}$. We say that $\mathcal {I}$ wins if $\mathcal {V}( {\textsc {pk}}, {\textsc {cmt}}, {\textsc {ch}}, {\textsc {rsp}}) = 1$. The advantage of $\mathcal {I}$ is $| \Pr ( \mathcal {I}\text { wins} ) - \tfrac{1}{2^c} |$. We say that $\mathcal {ID}$ is secure against impersonation under passive attacks if the advantage is negligible for all PPT adversaries.

An ID-scheme $\mathcal {ID}$ is non-trivial if $c \ge \lambda$.

An ID-scheme is recoverable if there is a deterministic polynomial-time algorithm ${Rec}$ such that for any transcript $({\textsc {cmt}}, {\textsc {ch}}, {\textsc {rsp}})$ of an honest execution we have

$$\begin{aligned} {Rec}( {\textsc {pk}}, {\textsc {ch}}, {\textsc {rsp}}) = {\textsc {cmt}}. \end{aligned}$$

One can transform any 2-special sound ID scheme into a non-trivial scheme by running t sessions in parallel, and this is secure for classical adversaries (see Sect. 8.3 of [23]). We will not need this result in the quantum case. One first generates ${\textsc {cmt}}_i \leftarrow \mathcal {P}( {\textsc {pk}}, {\textsc {sk}})$ for $1 \le i \le t$. One then samples ${\textsc {ch}}\leftarrow \{ 0,1 \}^{ct}$ and parses it as ${\textsc {ch}}_i \in \{ 0,1 \}^c$ for $1 \le i \le t$. Finally one computes ${\textsc {rsp}}_i \leftarrow P( {\textsc {pk}}, {\textsc {sk}}, {\textsc {cmt}}_i , {\textsc {ch}}_i )$. We define

$$ \mathcal {V}( {\textsc {pk}}, {\textsc {cmt}}_1 , \cdots , {\textsc {cmt}}_t , {\textsc {ch}}, {\textsc {rsp}}_1 , \cdots , {\textsc {rsp}}_t ) = 1 $$

if and only if $\mathcal {V}( {\textsc {pk}}, {\textsc {cmt}}_i , {\textsc {ch}}_i , {\textsc {rsp}}_i ) = 1$ for all $1 \le i \le t$. The successful cheating probability is then improved to $1/2^{ct}$, which is non-trivial when $t \ge \lambda /c$.

An ID-scheme is a special case of a sigma-protocol with respect to the relation defined by the instance generator K as $({\textsc {pk}},{\textsc {sk}}) \leftarrow K$, where we think of ${\textsc {sk}}$ as a witness for ${\textsc {pk}}$. More generally, any sigma-protocol for a relation of a certain type can be turned into an identification scheme.

Definition 3

(Definition 6 of [35]; Sect. 6 of [9]; Definition 15 of [33], where it is called “hard instance generator”) A hard relation R on $Y \times X$ is one where there exists a PPT algorithm K that outputs pairs $(y,x) \in Y \times X$ such that $R( y,x ) = 1$, but for all PPT adversaries $\mathcal {A}$

$$ \Pr [ (y,x) \leftarrow K(1^\lambda ); x' \leftarrow \mathcal {A}( y ) : R( y,x' ) = 1 ] \le {{\mathrm{negl}}}(\lambda ). $$

The following result is essentially due to Feige, Fiat and Shamir [13] and has become folklore in this generality. For the proof see Theorem 5 of [35].

Theorem 2

Let R be a hard relation with generator K and let $( \mathcal {P}, \mathcal {V})$ be the prover and verifier in a sigma-protocol for R with c-bit challenges for some integer $c \ge 1$. Suppose the sigma-protocol is complete, 2-special sound, and honest verifier zero-knowledge. Then $( K, \mathcal {P}, \mathcal {V}, c )$ is a canonical identification scheme that is secure against impersonation under (classical) passive attacks.

There are standard constructions to construct signature schemes from identification protocols. Due to lack of space we refer to Abdalla-An-Bellare-Namprempre [1] (also see Bellare-Poettering-Stebila [3]). As discussed in the full version of the paper, our ID-schemes are recoverable, and this allows us to reduce the signature size compared with general constructions.

3 New Identification Protocol Based Endomorphism Ring Computation

We now present our main result. The main advantage of our identification protocol compared with De Feo-Jao-Plût’s one is that security is based on the general problem of computing the endomorphism ring of a supersingular elliptic curve, or equivalently on computing an isogeny between two supersingular curves. In particular, the prime has no special property and no auxiliary points are revealed.

3.1 High Level Description

Our identification protocol is similar to the graph isomorphism zero-knowledge protocol, in which one reveals one of two graph isomorphisms, but never enough information to deduce the secret isomorphism.

As recalled in Sect. 2.1, although it is believed that computing endomorphism rings of supersingular elliptic curves is a hard computational problem in general, there are some particular curves for which it is easy. The following construction is explained in Lemma 2 of [26]. We choose $E_0 : y^2 = x^3 + Ax$ over a field $\mathbb {F}_{p^2}$ where $p \equiv 3 (\text {mod}\;{4})$ and $\#E_0( \mathbb {F}_{p^2} ) = (p+1)^2$. We have $j(E_0) = 1728$. When $p=3\bmod 4$, the quaternion algebra $B_{p,\infty }$ ramified at p and $\infty$ can be canonically represented as $\mathbb {Q}\langle \mathbf{i},\mathbf{j}\rangle = \mathbb {Q}+ \mathbb {Q}\mathbf{i}+ \mathbb {Q}\mathbf{j}+ \mathbb {Q}\mathbf{k}$, where $\mathbf{i}^2=-1$, $\mathbf{j}^2=-p$ and $\mathbf{k}:=\mathbf{i}\mathbf{j}=-\mathbf{j}\mathbf{i}$. The endomorphism ring of $E_0$ is isomorphic to the maximal order $\mathcal {O}_0$ with $\mathbb {Z}$-basis $\{1,\mathbf{i},\frac{1+\mathbf{k}}{2},\frac{\mathbf{i}+\mathbf{j}}{2}\}$. Indeed, there is an isomorphism of quaternion algebras $\theta :B_{p,\infty }\rightarrow \text {End}(E_0)\otimes \mathbb {Q}$ sending $(1,\mathbf{i},\mathbf{j},\mathbf{k})$ to $(1,\phi ,\pi ,\pi \phi )$ where $\pi :(x,y)\rightarrow (x^p,y^p)$ is the Frobenius endomorphism, and $\phi :(x,y)\rightarrow (-x,\iota y)$ with $\iota ^2=-1$.

To generate the public and private keys, we take a random isogeny (walk in the graph) $\varphi : E_0\rightarrow E_1$ and, using this knowledge, compute $\text {End}(E_1)$. The public information is $E_1$. The secret is $\text {End}(E_1)$, or equivalently a path from $E_0$ to $E_1$. Under the assumption that computing the endomorphism ring is hard, the secret key cannot be computed from the public key only.

Our scheme will require three algorithms, that are explained in detail in later sections.

• Translate isogeny path to ideal: Given $E_0, \mathcal {O}_0= \text {End}(E_0)$ and a chain of isogenies from $E_0$ to $E_1$, to compute $\mathcal {O}_1 = \text {End}(E_1)$ and a left $\mathcal {O}_0$-ideal I whose right order is $\mathcal {O}_1$.

• Find new path: Given a left $\mathcal {O}_0$-ideal I corresponding to an isogeny $E_0 \rightarrow E_2$, to produce a new left $\mathcal {O}_0$-ideal J corresponding to an “independent” isogeny $E_0 \rightarrow E_2$ of powersmooth degree.

• Translate ideal to isogeny path: Given $E_0, \mathcal {O}_0, E_2, I$ such that I is a left $\mathcal {O}_0$-ideal whose right order is isomorphic to $\text {End}(E_2)$, to compute a sequence of prime degree isogenies giving the path from $E_0$ to $E_2$.

Figure 1 gives the interaction between the prover and the verifier. We define L to be the product of all prime powers $\ell ^e$ such that $\ell ^e \le B = 2(1+\epsilon ) \log p$ for an arbitrary $\epsilon >0$. In other words, let $\ell _1, \dots , \ell _r$ be the list of all primes up to B and let $L = \prod _{i=1}^r \ell _i^{e_i}$ where $\ell _i^{e_i} \le B < \ell _i^{e_i + 1}$. Note that $r \approx B/\log (B)$ and so $L \approx p^{2(1 + \epsilon )}$.

One can see that Fig. 1 gives a canonical, recoverable identification protocol, but it is not non-trivial as the challenge is only one bit.

Fig. 1.

New identification scheme

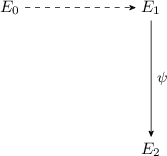
The isogenies involved in this protocol are summarised in the following diagram:

The two translation algorithms mentioned above in the $b=1$ case will be described in Sect. 3.4. They rely on the fact that $\text {End}(E_0)$ is known. The algorithms are efficient when the degree of the random walk is powersmooth, and for this reason all isogenies in our protocols will be of powersmooth degree. The powersmooth version of the quaternion isogeny algorithm of Kohel-Lauter-Petit-Tignol will be described and analysed in Sect. 3.3. The random walks are taken of sufficiently large degree such that their output has close to uniform distribution, by Theorem 1 and Lemma 1.

We repeat the process to reduce the cheating probability. The computational hardness of Problem 5 remains essentially the same if the curves are chosen according to a distribution that is close to uniform. We can then prove:

Theorem 3

Let $\lambda$ be a security parameter and $t \ge \lambda$. If Problem 6 is computationally hard, then the identification scheme obtained from t parallel executions of the protocol in Fig. 1 is a non-trivial, recoverable canonical identification scheme that is secure against impersonation under (classical) passive attacks.

The advantage of this protocol over De Feo-Jao-Plût’s protocol is that it relies on a more standard and potentially harder computational problem. In the rest of this section we first give a proof of Theorem 3, then we provide details of the algorithms involved in our scheme.

3.2 Proof of Theorem 3

We shall prove that the sigma protocol in Fig. 1 is complete, 2-special sound and honest verifier zero-knowledge. It follows that t parallel executions of the protocol is non-trivial as well as being 2-special sound and HVZK. The theorem will then follow from Theorem 2 and Problem 6 (which implies that the relation being proved is a hard relation).

Completeness. Let $\varphi$ be an isogeny between $E_0$ and $E_1$ of B-powersmooth degree, for $B=O(\log p)$. If the challenge received is $b=0$, it is clear that the prover knows a valid isogeny $\psi : E_1\rightarrow E_2$, so the verifier accepts the proof. If $b=1$, the prover follows the procedure described above and the verifier accepts. In the next subsections we will show that this procedure is polynomial time.

2-special soundness. Let $(E_0, E_1)$ be a public key for the scheme. Suppose we are given transcripts $( {\textsc {cmt}}, \{ {\textsc {ch}}_1, {\textsc {ch}}_2 \}, \{ {\textsc {rsp}}_1, {\textsc {rsp}}_2 \} )$ for the single-bit scheme such that $\mathcal {V}( {\textsc {pk}}, {\textsc {cmt}}, {\textsc {ch}}_i , {\textsc {rsp}}_i ) = 1$ for all $i \in \{1, 2 \}$. Let $E_2 = {\textsc {cmt}}$. Since ${\textsc {ch}}_1 \ne {\textsc {ch}}_2$ the responses ${\textsc {rsp}}_1$ and ${\textsc {rsp}}_2$ therefore give two isogenies $\psi :E_1\rightarrow E_{2}$, $\eta :E_0\rightarrow E_{2}$.

Given these two valid answers an extraction algorithm can compute an isogeny $\phi :E_0\rightarrow E_1$ as $\phi =\hat{\psi }\circ \eta$, where $\hat{\psi }$ is the dual isogeny of $\psi$. The extractor outputs $\phi$, which is a solution to Problem 6. This is summarized in the following diagram.

Honest verifier zero-knowledge. We shall prove that there exists a probabilistic polynomial time simulator $\mathcal {S}$ that outputs transcripts indistinguishable from transcripts of interactions with an honest verifier, in the sense that the two distributions are statistically close. Note that $\mathcal {O}_0 = \text {End}( E_0 )$ is public information so is known to the simulator. The simulator starts by taking a random coin $b\leftarrow \{0,1\}$.

• If $b=0$, take a random walk from $E_1$ of powersmooth degree L, as in the real protocol, obtaining a curve $E_2$ and an isogeny $\psi :E_1\rightarrow E_2$. The simulator outputs the transcript $(E_2,0,\psi )$.

  

  In this case, it is clear that the distributions of every element in the transcript are the same as in the real interaction, as they are generated in the same way. This is possible because, when $b=0$, the secret is not required for the prover to answer the challenge.

• If $b=1$, take a random walk from $E_0$ of powersmooth degree L to obtain a curve $E_2$ and an isogeny $\mu :E_0\rightarrow E_2$, then proceed as in Step 3 of Fig. 1 to produce another isogeny $\eta :E_0\rightarrow E_2$. The simulator outputs the transcript $(E_2,1,\eta )$.

The reason to output $\eta$ instead of $\mu$ is to ensure that the transcript distributions are indistinguishable from the distributions in the real scheme.

We first study the distribution of $E_2$ up to isomorphism. Let $X_r$ be the output of the random walk from $E_1$ to produce $j(E_2)$ in the real interaction, and let $X_s$ be the output of the random walk from $E_0$ to produce $j(E_2)$ in the simulation.

Let $\mathcal {G}$ be the set of all supersingular j-invariants, namely the vertex set of the isogeny graph. Note that $\#\mathcal {G}= N_p\approx p/12$. By Theorem 1 and Lemma 1, since the isogeny walks have degree L, we have, for any $j \in \mathcal {G}$

$$ \left| \Pr (X_r= j )-\frac{1}{N_p}\right| \le \frac{1}{p^{1+\epsilon }},\qquad \quad \left| \Pr (X_s= j )-\frac{1}{N_p}\right| \le \frac{1}{p^{1+\epsilon }}.$$

Therefore

$$\begin{aligned} \sum _{j \in \mathcal {G}} \left| \Pr (X_r=j)-\Pr (X_s=j)\right|&\le N_p\cdot \max _i\left| \Pr (X_r=j)-\Pr (X_s=j)\right| \\&\le N_p\cdot \left( \frac{1}{p^{1+\epsilon }}+\frac{1}{p^{1+\epsilon }}\right) \approx \frac{1}{6p^{\epsilon }} \end{aligned}$$

which is a negligible function of $\lambda$ for any constant $\epsilon >0$. In other words, the statistical distance, between the distribution of $j(E_2)$ in the real signing algorithm and the simulation, is negligible. Now, since $\eta$ is produced in the same way from $E_0$ and $E_2$ in the simulation and in the real protocol execution, we have that the statistical distance between the distributions of $\eta$ is also negligible. This follows from Lemma 2 in Sect. 3.3, which states that the output of the quaternion path algorithm does not depend on the input ideal, only on its ideal class.

3.3 Quaternion Isogeny Path Algorithm

In this section we sketch the quaternion isogeny algorithm from Kohel-Lauter-Petit-Tignol [26] and we evaluate its complexity when $p=3\bmod 4$. (The original paper does not give a precise complecity analysis; it is only claimed that the algorithm runs in heuristic probabilistic polynomial time.) This is the algorithm used for the Find new path procedure in the identification scheme.

The algorithm takes as input two maximal orders $\mathcal {O},\mathcal {O}'$ in the quaternion algebra $B_{p,\infty }$, and it returns a sequence of left $\mathcal {O}$-ideals $I_0=\mathcal {O}\supset I_1\supset \ldots \supset I_e$ such that the right order of $I_e$ is in the same equivalence class as $\mathcal {O}'$. In addition, the output is such that the index of $I_{i+1}$ in $I_i$ is a small prime for all i. The paper [26] focusses on the case where the norm of $I_e$ is $\ell ^e$ for some integer e, but it mentions that the algorithm can be extended to the case of powersmooth norms. We will only describe and use the powersmooth version. In our application there are some efficiency advantages from using isogenies whose degree is a product of small powers of distinct primes, rather than a large power of a small prime.

Note that the ideals returned by the quaternion isogeny path algorithm (or equivalently the right orders of these ideals) correspond to vertices of the path in the quaternion algebra graph, and to a sequence of j-invariants by Deuring’s correspondence. In the next subsection we will describe how to make this correspondence explicit; here we focus on the quaternion algorithm itself.

An important feature of the algorithm is that paths between two arbitrary maximal orders $\mathcal {O}$ and $\mathcal {O}'$ are always constructed as a concatenation of two paths from each maximal order to a special maximal order. As mentioned above, in our protocol and the discussion below we fix $\mathcal {O}_0=\langle 1,\mathbf{i},\frac{1+\mathbf{k}}{2},\frac{\mathbf{i}+\mathbf{j}}{2}\rangle$ where $\mathbf{i}^2 = -1$ and $\mathbf{j}^2 = -p$. General references for maximal orders and ideals in quaternion algebras are [36, 37].

We focus on the case where $\mathcal {O}=\mathcal {O}_0$, and assume that instead of a second maximal $\mathcal {O}'$ we are given the corresponding left $\mathcal {O}_0$-ideal I as input (the two variants of the problem are equivalent). This will be sufficient for our use of the algorithm. We assume that I is given by a $\mathbb {Z}$ basis of elements in $\mathcal {O}_0$. Denote by $n( \alpha )$ and n(I) the norm of an element or ideal respectively. The equivalence class of maximal orders defines an equivalence class of $\mathcal {O}_0$-ideals, where two ideals I and J are in the same class if and only if $I=Jq$ with $q\in B_{p,\infty }^*$. Therefore our goal is, given a left $\mathcal {O}_0$-ideal I, to compute another left $\mathcal {O}_0$-ideal J with powersmooth norm in the same ideal class. Further, in order to be able to later apply Algorithm 2, we require the norm of I to be odd (but the Find new path algorithm also allows to find even norm ideals if desired). Without loss of generality we assume there is no integer $s>1$ such that $I\subset s\mathcal {O}_0$, and that $I\ne \mathcal {O}_0$. The algorithm proceeds as follows:

• 1. Compute an element $\delta \in I$ and an ideal $I' = I\bar{\delta }/n(I)$ of prime norm N.

• 2. Find $\beta \in I'$ with norm NS where S is powersmooth and odd.

• 3. Output $J = I'\bar{\beta }/N$.

Steps 1 and 3 of this algorithm rely on the following simple result [26, Lemma 5]: if I is a left $\mathcal {O}$-ideal of reduced norm N and $\alpha$ is an element of I, then $I\bar{\alpha }/N$ is a left $\mathcal {O}$-ideal of norm $n(\alpha )/N$. Clearly, I and J are in the same equivalence class.

To compute $\delta$ in Step 1, first a Minkowski-reduced basis $\{\alpha _1,\alpha _2,\alpha _3,\alpha _4\}$ of I is computed. To obtain Lemma 2 below we make sure that the Minkowski basis is uniformly randomly chosen among all such bases⁶. Then random elements $\delta =\sum _ix_i\alpha _i$ are generated with integers $x_i$ in an interval $[-m,m]$, where m is determined later, until the norm of $\delta$ is equal to n(I) times a prime. A probable prime suffices in this context (actually Step 1 is not strictly needed but aims to simplify Step 2), so we can use the Miller-Rabin test to discard composite numbers with a large probability.

Step 2 is the core of the algorithm and actually consists of the following substeps:

• 2a. Find $\alpha$ such that $I'=\mathcal {O}_0N+\mathcal {O}_0\alpha$.

• 2b. Find $\beta _1\in \mathcal {O}_0$ with odd powersmooth norm $NS_1$.

• 2c. Find $\beta _2\in \mathbb {Z}\mathbf{j}+ \mathbb {Z}\mathbf{k}$ such that $\alpha =\beta _1\beta _2\bmod N\mathcal {O}_0$.

• 2d. Find $\beta _2' \in \mathcal {O}_0$ with odd powersmooth norm $S_2$ and $\lambda \in \mathbb {Z}_N^*$ such that $\beta _2'=\lambda \beta _2\bmod N\mathcal {O}_0$.

• 2e. Set $\beta =\beta _1\beta _2'$.

In Step 2a we need $\alpha \in I'$ such that $\gcd (n(\alpha ),N^2)=N$. This is easily achieved by taking $\alpha$ as a random small linear combination of a Minkowski basis, until the condition is met. Note that if $\alpha \in I'$ is such that $\gcd (n(\alpha ),N^2)=N$ then $J := \mathcal {O}_0 N + \mathcal {O}_0 \alpha \subseteq I'$ and $J \ne \mathcal {O}_0 N$. Since the norm of $\mathcal {O}_0 N$ is $N^2$ and N is prime it follows that the norm of J is N and so $J = I'$.

In Step 2b the algorithm actually searches for $\beta _1=a+b\mathbf{i}+c\mathbf{j}+d\mathbf{k}$. A large enough powersmooth number $S_1$ is fixed a priori, then the algorithm generates small random values of c, d until the norm equation $a^2+b^2=S_1-p(c^2+d^2)$ can be solved efficiently using Cornacchia’s algorithm (for example, until the right hand side is a prime equal to 1 modulo 4).

Step 2c is just linear algebra modulo N. As argued in [26] it has a negligible chance of failure, in which case one can just go back to Step 2b.

In Step 2d the algorithm a priori fixes $S_2$ large enough, then searches for integers $a,b,c,d,\lambda$ with $\lambda \notin N\mathbb {Z}$ such that $N^2(a^2+b^2)+p\left( (\lambda C+cN)^2+(\lambda D+dN)^2\right) =S_2$ where we have $\beta _2=C\mathbf{j}+D\mathbf{k}$. If necessary $S_2$ is multiplied by a small prime such that $p(C^2+D^2)S_2$ is a square modulo N, after which the equation is solved modulo N, leading to two solutions for $\lambda$. An arbitrary solution is chosen, and then looking at the equation modulo $N^2$ leads to a linear space of solutions for $(c,d)\in \mathbb {Z}_N$. The algorithm chooses random solutions until the equation

$$ a^2+b^2=\left( S_2-p^2\left( (\lambda C+cN)^2+(\lambda D+dN)^2\right) \right) /N^2 $$

can be efficiently solved with Cornacchia’s algorithm.

The overall algorithm is summarized in Algorithm 1. We now prove two lemmas on this algorithm. The first lemma shows that the output of this algorithm only depends on the ideal class of I but not on I itself. This is important in our identification protocol, as otherwise part of the secret isogeny $\varphi$ could potentially be recovered from $\eta$. The second lemma gives a precise complexity analysis of the algorithm, where [26] only showed probabilistic polynomial time complexity. Both lemmas are of independent interest.

Lemma 2

The output distribution of the quaternion isogeny path algorithm only depends on the equivalence class of its input. (In particular, the output distribution does not depend on the particular ideal class representative chosen for this input.)

Proof:

Let $I_1$ and $I_2$ be two left $\mathcal {O}_0$-ideals in the same equivalence class, namely there exists $q\in B_{p,\infty }^*$ such that $I_2=I_1q$. We show that the distribution of the ideal $I'$ computed in Step 1 of the algorithm is identical for $I_1$ and $I_2$. As the inputs are not used anymore in the remaining of the algorithm this will prove the lemma.

In the first step the algorithm computes a Minkowski basis of its input, uniformly chosen among all possible Minkowski bases. Let $B_1=\{\alpha _{11},\alpha _{12},\alpha _{13},\alpha _{14}\}$ be a Minkowski basis of $I_1$. Then by multiplicativity of the norm we have that $B_2=\{\alpha _{11}q,$ $\alpha _{12}q, \alpha _{13}q, \alpha _{14}q \}$ is a Minkowski basis of $I_2$. The algorithm then computes random elements $\delta =\sum _ix_i\alpha _i$ for integers $x_i$ in an interval $[-m,m]$. Clearly, for any element $\delta _1$ computed when the input is $I_1$, there corresponds an element $\delta _2=\delta _1q$ computed when the input is $I_2$. This is repeated until the norm of $\delta$ is a prime times n(I). As $n(I_2)=n(I_1)n(q)$ the stopping condition is equivalent for both. Finally, an ideal I of prime norm is computed as $I\bar{\delta }/n(I)$. Clearly when $\delta _2=\delta _1q$ we have $\frac{I_2\bar{\delta }_2}{n(I_2)}=\frac{I_1q\bar{q}\bar{\delta }_1}{n(q)n(I_1)}=\frac{I_1\bar{\delta }_1}{n(I_1)}$. This shows that the prime norm ideal computed in Step 1 only depends on the equivalence class of the input.     $\Box$

The expected running time given in the following lemma relies on several heuristics related to the factorization of numbers generated following certain distributions. Intuitively all these heuristics say that asymptotically those numbers behave in the same way as random numbers of the same size.

Lemma 3

Let $X:=\max \left| c_{ij}\right|$ where $c_{ij}\in \mathbb {Z}$ are integers such that $c_{i1}+c_{i2} \mathbf{i}+c_{i3}\frac{1+\mathbf{k}}{2}+c_{i4}\frac{\mathbf{i}+\mathbf{j}}{2}$ for $1 \le i \le 4$ forms a $\mathbb {Z}$-basis for I. If $\log X =O(\log p)$ then Algorithm 1 heuristically runs in time $\tilde{O}(\log ^3p)$, and produces an output of norm S with $\log (S)\approx \tfrac{7}{2} \log (p)$ which is $(\frac{7}{2} + o(1))\log p$-powersmooth.

Proof:

The Minkowski basis can be computed in $O(\log ^2 X)$, for example using the algorithm of [27].

For generic ideals the reduced norms of all Minkowski basis elements⁷ are in $O(\sqrt{p})$ (see [26, Sect. 3.1]). In the first loop we initially set $m=\lceil \log p\rceil$. Assuming heuristically that the numbers N generated behave like random numbers we expect the box to produce some prime number. The resulting N will be in $\tilde{O}(\sqrt{p})$. For some non generic ideals the Minkowski basis may contain two pairs of elements with norms respectively significantly smaller or larger than $O(\sqrt{p})$; in that case we can expect to finish the loop for smaller values of m by setting $x_3=x_4=0$, and to obtain some N of a smaller size.

Rabin’s pseudo-primality test performs a single modular exponentiation (modulo a number of size $\tilde{O}(\sqrt{p})$), and it is passed by composite numbers with a probability at most 1 / 4. The test can be repeated r times to decrease this probability to $1/4^r$. Assuming heuristically that the numbers tested behave like random numbers the test will only be repeated a significant amount of times on actual prime numbers, so in total it will be repeated $O(\log p)$ times. This leads to a total complexity of $\tilde{O}(\log ^3p)$ bit operations for the first loop using fast (quasi-linear) modular multiplication.

The other two loops involve solving equations of the form $x^2+y^2=M$. For such an equation to have solutions it is sufficient that M is a prime with $M=1\bmod 4$, a condition that is heuristically satisfied after $2\log M$ random trials. Choosing $S_1$ and $S_2$ as in the algorithm ensures that the right-hand term of the equation is positive, and (assuming this term behaves like a random number of the same size) is of the desired form for some choices (c, d), at least heuristically. Cornacchia’s algorithm runs in time $\tilde{O}(\log ^2 M)$, which is also $\tilde{O}(\log ^2 p)$ in the algorithm. The pseudo-primality tests will require $\tilde{O}(\log ^3p)$ operations in total, and their cost will dominate both loops.

Computing $\beta _2$ is just linear algebra modulo $N\approx \tilde{O}(\sqrt{p})$ and this cost can be neglected. The last two steps can similarly be neglected.

As a result, we get an overall cost of $\tilde{O}(\log ^3p)$ bit operations for the whole algorithm.

Let $s=\frac{7}{2}\log p$. We have $n(J)=n(I')n(\beta _1)n(\beta _2')/N^2$ so neglecting $\log \log$ factors $\log n(J)\approx \frac{1}{2}\log p+\log p+3\log p-\log p=\frac{7}{2}\log p$. We make the heuristic assumption that $\log n(J) = (\frac{7}{2} + o(1))\log p$. Moreover heuristically $\prod _{p_i^{e_i}<s} p_i^{e_i}\approx (s)^{s/\log s}\approx p^{7/2 + o(1)}$ so we can expect to find $S_1S_2$ that is s-powersmooth and of the correct size.     $\Box$

3.4 Step-by-Step Deuring Correspondence

We now discuss algorithms to convert isogeny paths into paths in the quaternion algebra, and vice versa. This will be necessary in our protocols as we are sending curves and isogenies, whereas the process uses the quaternion isogeny algorithm.

All the isogeny paths that we will need to translate in our signature scheme will start from the special j-invariant $j_0=1728$. We recall (see beginning of Sect. 3.1) that this corresponds to the curve $E_0$ with equation $y^2=x^3+x$ and endomorphism ring $\text {End}(E_0):=\langle 1,\phi , \frac{1+\pi \phi }{2},\frac{\pi + \phi }{2}\rangle$. Moreover there is an isomorphism of quaternion algebras sending $(1,\mathbf{i},\mathbf{j},\mathbf{k})$ to $(1,\phi ,\pi ,\pi \phi )$.

For any isogeny $\varphi :E_0\rightarrow E_1$ of degree n, we can associate a left $\text {End}(E_0)$-ideal $I = \mathrm {Hom}(E_1,E_0) \varphi$ of norm n, corresponding to a left $\mathcal {O}_0$-ideal with the same norm in the quaternion algebra $B_{p,\infty }$. Conversely every left $\mathcal {O}_0$-ideal arises in this way [25, Section 5.3]. In our protocol we will need to make this correspondence explicit, namely we will need to pair up each isogeny from $E_0$ with the correct $\mathcal {O}_0$-ideal. Moreover we need to do this for “large” degree isogenies to ensure a good distribution via our random walk theorem.

Translating an Ideal to an Isogeny Path. Let $E_0$ and $\mathcal {O}_0 = \text {End}(E_0)$ be given, together with a left $\mathcal {O}_0$-ideal I corresponding to an isogeny of degree n. We assume I is given as a $\mathbb {Z}$-basis $\{ \alpha _1, \dots , \alpha _4 \}$. The main idea to determine the corresponding isogeny explicitly is to determine its kernel [40].

Assume for the moment that n is a small prime. One can compute generators for all cyclic subgroups of $E_0[n]$, each one uniquely defining a degree n isogeny which can be computed with Vélu’s formulae. A generator P then corresponds to the basis $\{ \alpha _1, \dots , \alpha _4 \}$ if and only if $\alpha _j(P) = 0$ for all $1 \le j \le 4$. To evaluate $\alpha (P)$ with $\alpha \in I$ and $P\in E_0[n]$, we first write $\alpha =(u + v\mathbf{i}+ w\mathbf{j}+ x\mathbf{k})/2$, then we compute $P'$ such that $[2]P'=P$ and finally we evaluate $[u]P' + [v] \phi (P') + [w] \pi (P') + [x] \pi ( \phi (P'))$.

An alternative to trying all subgroups is to choose a pair $\{ P_1, P_2 \}$ of generators for $E_0[n]$ and, for some $\alpha \in I$, solve the discrete logarithm instance (if possible) $\alpha (P_2) = [x] \alpha (P_1)$. It follows that $\alpha ( P_2 - [x] P_1 ) = 0$ and so we have determined a candidate point in the kernel of the isogeny. Both solutions are too expensive for large n.

When $n=\ell ^e$ the degree n isogeny can be decomposed into a composition of e degree $\ell$ isogenies. If I is the corresponding left $\mathcal {O}_0$-ideal of norm $\ell ^e$, then $I_i:=I\bmod \mathcal {O}_0\ell ^i$ is a left $\mathcal {O}_0$-ideal of norm $\ell ^i$ corresponding to the first i isogenies. Similarly if P is a generator for the kernel of the degree $\ell ^e$ isogeny then $\ell ^{e-i+1}P$ is the kernel of the degree $\ell ^i$ isogeny corresponding to the first i steps. One can therefore perform the matching of ideals with kernels step-by-step with successive approximations of I or P respectively. This algorithm is more efficient than the previous one, but it still requires to compute $\ell ^e$ torsion points, which in general may be defined over a degree $\ell ^e$ extension of $\mathbb {F}_{p^2}$. To ensure that the $\ell ^e$ torsion is defined over $\mathbb {F}_{p^2}$ one can choose p such that $\ell ^e \mid (p \pm 1)$ as in the De Feo-Jao-Plût protocols; however for general p this translation algorithm will still be too expensive.

We solve this efficiency issue by using powersmooth degree isogenies in our protocols. When $n=\prod _i\ell _i^{e_i}$ with distinct primes $\ell _i$, one reduces to the prime power case as follows. For simplicity we assume that 2 does not divide n. The isogeny of degree n can be decomposed into a sequence of prime degree isogenies. For simplicity we assume the isogeny steps are always performed in increasing degree order; we can require that this is indeed the case in our protocols. Let $n_i:=\prod _{j\le i}\ell _j^{e_j}$. Using a Chinese Remainder Theorem-like representation, points in $E_0[n]$ can be represented as a sequence of points in $E_0[\ell _i^{e_i}]$. If I is a left $\mathcal {O}_0$-ideal of norm n and $\varphi$ is the corresponding isogeny, then the kernel of $I\bmod \mathcal {O}_0\ell _i^{e_i}$ is the $\ell _i^{e_i}$ part of the kernel of $\varphi$, namely $\ker (I\bmod \mathcal {O}_0\ell _i^{e_i})=\left[ {n}/{\ell _i^{e_i}}\right] \ker \varphi$. Given a left $\mathcal {O}_0$-ideal I, Algorithm 2 progressively identifies the corresponding isogeny sequence.

In our protocols we will have $\ell _i^{e_i}=O(\log n)=O(\log p)$; moreover we will be using $O(\log p)$ different primes. The complexity of Algorithm 2 under these assumptions is given by the following lemma. Note that almost all primes $\ell _i$ are such that $\sqrt{B} < \ell _i \le B$ and so $e_i = 1$, hence we ignore the obvious $\ell$-adic speedups that can be obtained in the rare cases when $\ell _i$ is small.

Lemma 4

Let $n=\prod \ell _i^{e_i}$ with $\log n =O(\log p)$ and $\ell _i^{e_i}=O(\log p)$. Then Algorithm 2 can be implemented to run in time $\tilde{O}(\log ^6 p)$ bit operations for the first loop, and $\tilde{O}(\log ^4 p)$ for the rest of the algorithm.

Proof:

Without any assumption on p the $\ell _i^{e_i}$ torsion points will generally be defined over $\ell _i^{e_i}$ degree extension fields, hence they will be of $O(\log ^2p)$ size. However the isogenies themselves will be rational, i.e. defined over $\mathbb {F}_{p^2}$. This means their kernel is defined by a polynomial over $\mathbb {F}_{p^2}$. Isogenies over $\mathbb {F}_{p^2}$ of degree d can be evaluated at any point in $\mathbb {F}_{p^2}$ using O(d) field operations in $\mathbb {F}_{p^2}$.

Let $d=\ell _i^{e_i}$. To compute a basis of the d-torsion, we first factor the division polynomial over $\mathbb {F}_{p^2}$. This polynomial has degree $O( d^2 ) = O( \log (p)^2 )$. Using the algorithm in [24] this can be done in $\tilde{O}(\log ^4p)$ bit operations. Since the isogenies are defined over $\mathbb {F}_{p^2}$, this will give factors of degree at most $(d-1)/2$, each one corresponding to a cyclic subgroup. We then randomly choose some factor with a probability proportional to its degree, and we factor it over its splitting field, until we have found a basis of the d-torsion. After O(1) random choices we will have a basis of the d-torsion. Each factorization costs $\tilde{O}(\log ^5p)$ using the algorithm in [38], and verifying that two points generate the d-torsion can be done with O(d) field operations. It then takes O(d) field operations to compute generators for all kernels. As $r=O(\log p)$ we deduce that the first loop requires $\tilde{O}(\log ^6p)$ bit operations.

Computing $P_{ijk}$ involves Frobenius operations and multiplications by scalars bounded by d (and so $O(\log \log p)$ bits). This requires $O(\log p)$ field operations, that is a total of $\tilde{O}(\log ^3p)$ bit operations. Any cyclic subgroup of order $\ell _i^{e_i}$ is generated by a point $Q_i = aP_{i1}+bP_{i2}$, and the image of this point by $\alpha _{ik}$ is $aP_{i1k}+bP_{i2k}$. One can determine the integers a, b by an ECDLP computation or by testing random choices. There are roughly $\ell _i^{e_i}=O(\log p)$ subgroups, and testing each of them requires at most $O(\log \log p)$ field operations, so finding $Q_i$ requires $\tilde{O}(\log p)$ field operations. Evaluating $\varphi _{i-1}(Q_i)$ requires $O(\log ^2p)$ field operations. Computing the isogeny $\phi _i$ can be done in $O(\log p)$ field operations using Vélu’s formulae. As $r=O(\log p)$ we deduce that the second loop requires $\tilde{O}(\log ^4p)$ bit operations.     $\Box$

We stress that in our signature algorithm, Algorithm 2 will be run $O(\log p)$ times. However the torsion points are independent of both the messages and the keys, so they can be precomputed. Hence the “online” running time of Algorithm 2 is $\tilde{O}( \log ^4p)$ bit operations per execution.

Translating an Isogeny Path to an Ideal. Let $E_0, E_1, \dots , E_r$ be an isogeny path and suppose $\varphi _{i} : E_0 \rightarrow E_i$ is of degree $n_i = \prod _{j \le i} \ell _j^{e_j}$. We define $I_0=\mathcal {O}_0$. Then for $i=1,\ldots ,r$ we compute an element $\alpha _i\in I_{i-1}$ and an ideal $I_i=I_{i-1}\ell _i^{e_i}+I_{i-1}\alpha _i$ that corresponds to the isogeny $\varphi _i=\phi _i\circ \ldots \circ \phi _1$. (We stress that the definition of $I_i$ here differs from the previous subsection.) At step i, we use a basis of $I_{i-1}$ to compute a quadratic form $f_i$ that is the norm form of the ideal $I_{i-1}$. The roots of this quadratic form modulo $\ell _i^{e_i}$ correspond to candidates for $\alpha _i$ and hence $I_i$. Note that this correspondence is not injective: a priori there will be $O((\ell _i^{e_i})^3)$ roots but there are only $O(\ell _i^{e_i})$ corresponding ideals including the correct one. Our strategy is to pick random solutions to the quadratic form until the maps $\alpha _i$ and $\phi _i$ have the same kernels.

In our protocols we will have $\ell _i^{e_i}=O(\log n)=O(\log p)$; moreover we will be using $O(\log p)$ different primes. The complexity of Algorithm 3 under these assumptions is given by the following lemma.

Lemma 5

Let $n=\prod _{i=1}^r \ell _i^{e_i}$ with $\log n=O(\log p)$ and $\ell _i^{e_i}=O(\log p)$, and assume all the isogenies are defined over $\mathbb {F}_{p^2}$. Then Algorithm 3 can be implemented to run in expected time $\tilde{O}(\log ^4 p)$ and the output is a $\mathbb {Z}$-basis with integers bounded by X such that $\log X = O( \log p )$.

Proof:

We remind that without any assumption on p the $\ell _i^{e_i}$ torsion points will generally be defined over $\ell _i^{e_i}$ degree extension fields, hence they will be of $O(\log ^2p)$ size. Isogenies of degree d can be evaluated at any point using O(d) field operations.

When the degree is odd the isogeny $\phi _i$ is naturally given by a polynomial $\psi _i$ such that the roots of $\psi _i$ correspond to the x-coordinates of affine points in $\ker \varphi _i$. To identify a generator $Q_i$ we first factor $\psi _i$ over $\mathbb {F}_{p^2}$. Using the algorithm in [38] this can be done with $\tilde{O}(\log ^3p)$ bit operations. We choose a random irreducible factor with a probability proportional to its degree, we use this polynomial to define a field extension of $\mathbb {F}_{p^2}$, and we check whether the corresponding point is of order $\ell _i^{e_i}$. If not we choose another irreducible factor and we repeat. We expect to only need to repeat this O(1) times, and each step requires $\tilde{O}(\log p)$ bit operations. So the total cost for line 3 is $\tilde{O}(\log ^3p)$.

Step 4 requires $O(\log \log p)$ field operations to compute a point $Q_i'$ such that $[2]Q_i'=Q_i$. After that it mostly requires $O(\log p)$ field operations to compute the Frobenius map. The total cost of this step is therefore $\tilde{O}(\log ^3p)$.

Basis elements for all the ideals $I_i$ appearing in the algorithm can be reduced modulo $\mathcal {O}_0n$, hence their coefficients are of size $\log n=O(\log p)$.

To compute a random solution to $f_i$ modulo $\ell _i^{e_i}$, we choose uniformly random values for w, x, y, and when the resulting quadratic equation in z has solutions modulo $\ell _i^{e_i}$ we choose a random one. As $\ell _i^{e_i}=O(\log p)$ the cost of this step can be neglected. Computing $[\alpha _i](Q_i)$ requires $O(\log \log p)$ operations over a field of size $O(\log ^2p)$. On average we expect to repeat the loop $O(\ell _i^{e_i})=O(\log p)$ times, resulting in a total cost of $\tilde{O}(\log ^3p)$. Computing each $f_i$ costs $\tilde{O}(\log p)$ bit operations.

As $r=O(\log p)$ the total cost of the algorithm is $\tilde{O}(\log ^4p)$.

One can check that all integers in the algorithm are bounded in terms of n, and so coefficients are of size X where $\log X = O( \log n ) = O( \log p )$.     $\Box$

Recall that the condition $\log X = O( \log p )$ is needed in Lemma 3.

4 Classical and Post-Quantum Signature Schemes

Digital signatures are one of the most fundamental cryptographic primitives. It is well-known that they can be built from identification protocols using the Fiat-Shamir transform [15]. The resulting signatures are existentially unforgeable under adaptive chosen-message attacks (the standard security definition for signatures) with respect to classical adversaries, in the random oracle model. The transform is also secure against quantum adversaries under certain conditions [34], however these conditions are met by neither De Feo-Jao-Plût’s protocol nor ours. In particular, soundness relies on computational assumptions in both protocols. However, one can replace the Fiat-Shamir transform with an alternative transform due to Unruh to achieve security against quantum adversaries [33].

This section explains the two signature schemes obtained from our new identification protocol. Due to lack of space we refer to Yoo et al. [42] and the full version of the paper [18] for the two signature schemes obtained from the De Feo-Jao-Plût ID-scheme.

4.1 Classical Signature Scheme Based on Endomorphism Ring Computation

In this section we fully specify the signature scheme resulting from applying a variant of the Fiat-Shamir transform to our new identification scheme based on the endomorphism ring computation problem, and we analyse its efficiency.

Key Generation Algorithm: On input a security parameter $\lambda$ generate a prime p with $2\lambda$ bits, which is congruent to 3 modulo 4. Let $E_0 : y^2 = x^3 + Ax$ over $\mathbb {F}_p$ be supersingular, and let $\mathcal {O}_0 = \text {End}( E_0 )$. Fix B, $S_1$, $S_2$ as small as possible⁸ such that $S_{k}:=\prod _i\ell _{k,i}^{e_{k,i}}$, $\ell _{k,i}^{e_{k,i}}<B$, $\gcd (S_1,S_2)=1$, and $\prod \left( \frac{2\sqrt{\ell _{k,i}}}{\ell _{k,i}+1}\right) ^{e_{k,i}}<(p^{1+\epsilon })^{-1}$. Perform a random isogeny walk of degree $S_1$ from the curve $E_0$ with j-invariant $j_0=1728$ to a curve $E_1$ with j-invariant $j_1$. Compute $\mathcal {O}_1 = \text {End}( E_1 )$ and the ideal I corresponding to this isogeny. Choose a hash function H with $t= 2\lambda$ bits of output. The public key is ${\textsc {pk}}= (p, j_1, H )$ and the secret key is ${\textsc {sk}}= \mathcal {O}_1$, or equivalently I.

Signing Algorithm: On input a message m and keys $({\textsc {pk}}, {\textsc {sk}})$, recover the parameters p and $j_1$. For $i=1,\ldots ,t$, generate a random isogeny walk $w_{i}$ of degree $S_2$, ending at a j-invariant $j_{2,i}$. Compute $h:=H(m,j_{2,1},\ldots ,j_{2,t})$ and parse the output as t challenge bits $b_i$. For $i=1,\ldots ,t$, if $b_i=1$ use $w_i$ and Algorithm 3 of Sect. 3.4 to compute the corresponding ideal $I_i$ and hence its right order $\mathcal {O}_{2,i} = \text {End}( E_{2,i} )$, then use the algorithm of Sect. 3.3 on input $I I_i$ to compute a “fresh” path between $\mathcal {O}_0$ and $\mathcal {O}_{2,i}$, and finally use Algorithm 2 to compute an isogeny path $w_i'$ from $j_0$ to $j_{2,i}$. If $b_i=0$ set $z_i:=w_i$, otherwise set $z_i:=w_i'$. Return the signature $\sigma =(h,z_1,\ldots ,z_{t})$.

Verification Algorithm: On input a message m, a signature $\sigma$ and a public key ${\textsc {pk}}$, recover the parameters p and $j_1$. For each $1 \le i \le t$ one uses $z_i$ to compute the image curve $E_{2,i}$ of the isogeny. Hence the verifier recovers the signature components $j_{2,i}$ for $1 \le i \le t$. The verifier then recomputes the hash $H(m,j_{2,1},\ldots ,j_{2,t})$ and checks that the value is equal to h, accepting the signature if this is the case and rejecting otherwise.

We now show that this scheme is a secure signature.

Theorem 4

If Problem 6 is computationally hard then the signature scheme is secure in the random oracle model under a chosen message attack.

Proof:

As shown in Sect. 3.2, if Problem 6 is computationally hard then the identification scheme (sigma protocol) has 2-special soundness and honest verifier zero-knowledge. Theorem 2 therefore implies that the identification scheme is secure against impersonation under passive attacks. It follows from Abdalla et al. [1] that the signature scheme is secure in the random oracle model.     $\Box$

Efficiency: As the best classical algorithm for computing the endomorphism ring of a supersingular elliptic curve runs in time $\tilde{O}(\sqrt{p})$ one can take $\log p=2\lambda$. By Theorem 1 and Lemma 1, taking $B\approx 2(1+\epsilon )\log p$ ensures that the outputs of random walks are distributed uniformly enough. Random walks then require $2(1+\epsilon )\log p$ bits to represent, so signatures are

$$\begin{aligned} t+\frac{t}{2}\left( 2(1+\epsilon )\lceil \log p\rceil +\frac{7}{2}\lceil \log p\rceil \right) \end{aligned}$$

bits on average, depending on the challenge bits. For $\lambda$ bits of security, we choose $t=2\lambda$, so the average signature length is approximately $2\lambda +(\lambda )(4(1+\epsilon )\lambda +7\lambda )\approx (11+4\epsilon )\lambda ^2\approx 11\lambda ^2$.

Private keys are $2(1+\epsilon )\log p\approx 4\lambda$ bits if a canonical representation of the kernel of the isogeny between $E_0$ and $E_1$ is stored. This can be reduced to $2\lambda$ bits for generic $E_1$: if I is the ideal corresponding to this isogeny, it is sufficient to store another ideal J in the same class, and for generic $E_1$ there exists one ideal of norm $n\approx \sqrt{p}$. To represent this ideal in the most efficient way, it is sufficient to give n and a second integer defining the localization of I at every prime factor $\ell$ of n, for canonical embeddings of $B_{p,\infty }$ into $M_2(\mathbb {Q}_\ell )$. This reduces storage costs to roughly $2\lambda$ bits. Public keys are $3\log p=6\lambda$ bits. A signature mostly requires t calls to the Algorithms of Sects. 3.3 and 3.4, for a total cost of $\tilde{O}(\lambda ^5)$. Verification requires to check $O(\lambda )$ isogeny walks, each one comprising $O(\lambda )$ steps with a cost $\tilde{O}(\lambda ^3)$ each when modular polynomials are precomputed, hence a total cost of $\tilde{O}(\lambda ^5)$ bit operations (under the same heuristic assumptions as in Lemma 3).

Optimization with Non Backtracking Walks: In our description of the signature scheme we have allowed isogeny paths to “backtrack”. We made this choice to simplify the convergence analysis of random walks and because it does not affect the asymptotic complexity of our schemes significantly. However in practice at any concrete security parameter, it will be better to use non-backtracking random walks as they will converge more quickly to a uniform distribution [2].

4.2 Post-Quantum Signature Scheme Based on Endomorphism Ring Computation

We briefly describe the signature scheme arising from applying Unruh’s transform to the identification protocol of Sect. 3.

Key Generation Algorithm: On input a security parameter $\lambda$ generate a prime p with $4\lambda$ bits, which is congruent to 3 modulo 4. Let $E_0 : y^2 = x^3 + Ax$ over $\mathbb {F}_p$ be supersingular, and let $\mathcal {O}_0 = \text {End}( E_0 )$. Set $t= 3\lambda$. Fix B, $S_1$, $S_2$ as in the key generation algorithm of Sect. 4.1. Perform a random isogeny walk of degree $S_1$ from the curve $E_0$ with j-invariant $j_0=1728$ to a curve $E_1$ with j-invariant $j_1$. Compute $\mathcal {O}_1 = \text {End}( E_1 )$ and the ideal I corresponding to this isogeny.

Choose a hash function $H : \{ 0,1 \}^* \rightarrow \{0,1\}^t$. Let $N \approx \tfrac{7}{2} \log p$ be an upper bound for the bitlength of the representation of any isogeny path in the algorithm. Let $G : \{ 0,1 \}^N \rightarrow \{ 0,1 \}^N$ be a hash function such that every element has polynomially many preimages. The public key is ${\textsc {pk}}= (p, j_1, H, G )$ and the secret key is ${\textsc {sk}}= \mathcal {O}_1$, or equivalently I.

Signing Algorithm: On input a message m and keys $({\textsc {pk}}, {\textsc {sk}})$, recover the parameters p and $j_1$. For $i=1,\ldots ,t$ generate a random isogeny walk $w_{i}$ of degree $S_2$, ending at a j-invariant $j_{2,i}$.

For $i=1,\ldots ,t$ apply Algorithm 3 of Sect. 3.4 to compute the ideal $I_i$ corresponding to the isogeny path $w_i$, then use the algorithm of Sect. 3.3 on input $I I_i$ to compute a “fresh” ideal corresponding to a path between $\mathcal {O}_0$ and $\mathcal {O}_{2,i}$, and finally use Algorithm 2 to compute an isogeny path $w_i'$ from $j_0$ to $j_{2,i}$.

Compute $g_{i,0} = G( w_i )$ and $g_{i,1} = G( w_i' )$ for $1 \le i \le t$, where the bitstrings $w_i$ and $w_i'$ are padded with zeroes to become binary strings of length N. Compute $h:=H(m,j_1,j_{2,1},\ldots ,j_{2,t}, g_{1,0}, g_{1,1}, \dots , g_{t,0}, g_{t,1} )$ and parse the output as t challenge bits $h_i$. For $i=1,\ldots ,t$, if $h_i=0$ then set ${\textsc {rsp}}_i = w_i$ and if $h_i = 1$ then set ${\textsc {rsp}}_i = w_i'$. Return the signature $\sigma =(h,{\textsc {rsp}}_1,\ldots ,{\textsc {rsp}}_{t}, g_{1,1-h_1}, \dots , g_{t, 1-h_t})$.

Verification Algorithm: On input a message m, a signature $\sigma$ and a public key ${\textsc {pk}}$, recover the parameters p and $j_1$.

For each $1 \le i \le t$ one uses ${\textsc {rsp}}_i$ to compute the image curve $E_{2,i}$ of the isogeny (if $h_i=0$ then ${\textsc {rsp}}_i$ is a path from $E_1$ and if $h_i = 1$ then it is a path from $E_0$). Hence the verifier recovers the j-invariants $j_{2,i}$ for $1 \le i \le t$.

The verifier then computes $g_{i,h_i} = G( {\textsc {rsp}}_i )$ for $1 \le i \le t$ (again padding to N bits using zeros). Finally the verifier computes the hash value

$$\begin{aligned} h' = H(m,j_1, j_{2,1},\ldots ,j_{2,t}, g_{1,0}, g_{1,1}, \dots , g_{t,0}, g_{t,1}). \end{aligned}$$

If $h' = h$ then the verifier accepts the signature and otherwise rejects.

We now show that this scheme is a secure signature.

Theorem 5

If Problem 6 is computationally hard then the signature scheme is secure in the quantum random oracle model under a chosen message attack.

Proof:

As shown in Sect. 3.2, if Problem 6 is computationally hard then the identification scheme (sigma protocol) has 2-special soundness and honest verifier zero-knowledge. A result of Unruh [33] then implies that the signature scheme is secure in the quantum random oracle model.     $\Box$

Efficiency: For the same reasons as in the application of the Unruh transform applied to the De Feo-Jao-Plût scheme, this signature scheme is less efficient than its classical counterpart. Again, we only send half the values $g_{i,j}$, since the missing values can be recomputed by the signer.

The average signature size is $t + t( (\log S_1 + N)/2 ) + t N$, on the basis that half the responses ${\textsc {rsp}}_i$ can be represented using $\log S_1$ bits and half of them require N bits. For $\lambda$ bits of security, we choose $\log p = 4 \lambda$ and $t=3\lambda$, so that $N = 14 \lambda$ and $\log S_1 = (8 + \epsilon )\lambda$. Then the average signature size is approximately $75 \lambda ^2$.

4.3 Comparison

Tables 1 and 2 summarize the main efficiency features of four signature schemes based either on De Feo-Jao-Plût or on our new identification scheme, and on Fiat-Shamir or Unruh transforms. The numbers provided were obtained by optimizing signature sizes first, then signing and verification time and finally key sizes; other trade-offs are of course possible. The scheme based on the De Feo-Jao-Plût identification protocol and Unruh transform was discovered independently in [42]; the version we give incorporates optimizations that reduce the signature sizes for the same security guarantees⁹. Signatures based on De Feo-Jao-Plût identification protocol are simpler and somewhat more efficient than signatures based on our new identification protocol; however the latter have the advantage to rely on more standard and potentially harder computational problems. Schemes based on the Fiat-Shamir transform are more efficient than schemes based on Unruh’s transform; however the latter provide security guarantees against quantum adversaries.

Table 1. Asymptotic efficiency of four signature schemes using De Feo-Jao-Plût and our identification protocol, and Fiat-Shamir and Unruh transform, as a function of the security parameter $\lambda$. All sizes are in bits and computation costs are in bit operations.

Table 2. Concrete efficiency of our signature schemes at security levels of 128 and 256 bits. Security level provided are against classical or quantum adversaries for schemes based on the Fiat-Shamir or Unruh transforms respectively. All sizes are in bits.

Table 1 and a quick comparison with RSA signatures suggest that isogeny-based signatures schemes may be efficiency enough for practical use. Indeed for RSA signatures, key sizes are cubic in the security parameter, and signing and verification times are respectively quasi-quadratic and quasi-linear in the key sizes (the latter assuming a small public key exponent is used), amounting to $\tilde{O}(\lambda ^3)$ and $\tilde{O}(\lambda ^6)$. As for concrete parameters, key sizes are much smaller for isogeny-based signatures than for RSA signatures and comparable to ECDSA signatures. Further work in this area should aim at decreasing signature sizes.

5 Conclusion

We provided both a new identification protocol and new signature schemes based on isogeny problems. While the only previous identification protocol based on isogeny problems relied on special and potentially easier variants of these problems [14], our protocol is based on what is arguably the hardest problem in this area, namely the endomorphism ring computation problem. A crucial ingredient for our protocol is the quaternion isogeny algorithm of Kohel-Lauter-Petit-Tignol [26] in the powersmooth case, for which we provide a more complete description and analysis. The signature schemes are derived using the Fiat-Shamir and Unruh transforms, respectively for classical and post-quantum security. We showed that they can have very small key sizes and reasonably efficient signing and verification algorithms compared to RSA signatures.

Isogeny problems are interesting in cryptography for their potential resistance to quantum algorithms, but they are also rather new in cryptography. Among all isogeny problems, the problem of computing the endomorphism ring of a supersingular elliptic curve is the most natural one to consider from an algorithmic number theory point of view, and it has in fact been studied since Kohel’s PhD thesis in 1996. Yet, even this problem is far from having received the same scrutiny as more established cryptography problems like discrete logarithms or integer factoring. We hope that this paper will encourage the community to study its complexity.

A Efficient Representations of Isogeny Paths and Other Data

Our schemes require representing/transmitting elliptic curves and isogenies. In this section we briefly explain how to represent certain mathematical objects appearing in our protocol as bitstrings in a canonical way so that minimal data needs to be sent and stored.

Let p be a prime number. Every supersingular j-invariant is defined over $\mathbb {F}_{p^2}$. A canonical representation of $\mathbb {F}_{p^2}$-elements is obtained via a canonical choice of degree 2 irreducible polynomial over $\mathbb {F}_p$. Canonical representations in any other extension fields are defined in a similar way. Although there are only about p / 12 supersingular j-invariants in characteristic p, we are not aware of an efficient method to encode these invariants into $\log p$ bits, so we represent supersingular j-invariants with the $2\log p$ bits it takes to represent an arbitrary $\mathbb {F}_{p^2}$-element.

Elliptic curves are defined by their j-invariant up to isomorphism. Hence, rather than sending the coefficients of the elliptic curve equation, it suffices to send the j-invariant. For any invariant j there is a canonical elliptic curve equation $E_j : y^2=x^3+\frac{3j}{1728-j}x+\frac{2j}{1728-j}$ when $j\ne 0,1728$, $y^2=x^3+1$ when $j=0$, and $y^2=x^3+x$ when $j=1728$. The last one is used in our main signature scheme.

We now turn to representing chains $E_0, E_1, \dots , E_n$ of isogenies $\phi _i : E_{i-1} \rightarrow E_i$ each of prime degree $\ell _i$ where $1 \le i \le n$. Here $\ell _i$ are always very small primes. A useful feature of our protocols is that isogeny chains can always be chosen such that the isogeny degrees are increasing $\ell _{i} \ge \ell _{i-1}$. First we need to discuss how to represent the sequence of isogeny degrees. If all degrees are equal to a fixed constant $\ell$ (e.g., $\ell = 2$) and if the length n is a fixed system parameter, then there is nothing to send. If the degrees are different then the most compact representation seems to be to compute and send

$$ N = \prod _{i=1}^n \ell _i. $$

The receiver can recover the sequence of isogeny degrees from N by factoring using trial division and ordering the primes by size. This representation is possible due to our convention that the isogeny degrees are increasing and since the degrees are all small.

To represent the curves themselves in the chain of isogenies the simplest method is to send all the j-invariants $j_i = j( E_i ) \in \mathbb {F}_{p^2}$ for $0 \le i \le n$. This requires $2(n+1) \log _2( p )$ bits. Note that the verifier is able to check the correctness of the isogeny chain by checking that $\varPhi _{\ell _i}( j_{i-1}, j_i ) = 0$ for all $1 \le i \le n$, where $\varPhi _{\ell _i}$ is the $\ell _i$-th modular polynomial. The advantage of this method is that verification is relatively quick (just evaluating a polynomial that can be precomputed and stored).

The other naive method is to send the x-coordinate of a kernel point $P_i \in E_{j_i}$ on the canonical curve. This requires large bandwidth.

A refinement of the second method is used in our signature scheme based on the De Feo-Jao-Plût identification protocol, where $\ell$ is fixed and one can publish a point that defines the kernel of the entire isogeny chain. Precisely a curve E and points $R, S \in E[ \ell ^n ]$ are fixed. Each integer $0 \le \alpha < \ell ^n$ defines a subgroup $\langle R + [\alpha ] S \rangle$ and hence an $\ell ^n$ isogeny. It suffices to send $\alpha$, which requires $\log _2( \ell ^n )$ bits. In the case $\ell = 2$ this is just n bits, which is smaller than all the other suggestions in this section.

The full version of the paper contains a more thorough discussion of optimisations and also an analysis of the complexity of computing isogeny chains.