Abstract
Realizing indistinguishablility obfuscation (IO) based on well understood computational assumptions is an important open problem. Recently, realizing functional encryption (FE) has emerged as a promising direction towards that goal. This is because: (1) compact single-key FE (where the functional secret-key is of length double the ciphertext length) is known to imply IO [Anath and Jain, CRYPTO 2015; Bitansky and Vaikuntanathan, FOCS 2015] and (2) several strong variants of single-key FE are known based on various standard computation assumptions.
In this work, we study when FE can be used for obtaining IO. We show any single-key FE for function families with “short” enough outputs (specifically the output is less than ciphertext length by a value at least \(\omega (n + \mathrm {\kappa })\), where n is the message length and \(\mathrm {\kappa }\) is the security parameter) is insufficient for IO even when non-black-box use of the underlying FE is allowed to some degree. Namely, our impossibility result holds even if we are allowed to plant FE sub-routines as gates inside the circuits for which functional secret-keys are issued (which is exactly how the known FE to IO constructions work).
Complementing our negative result, we show that our condition of “short” enough is almost tight. More specifically, we show that any compact single-key FE with functional secret-key output length strictly larger than ciphertext length is sufficient for IO. Furthermore, we show that non-black-box use of the underlying FE is necessary for such a construction, by ruling out any fully black-box construction of IO from FE even with arbitrary long output.
S. Garg—University of California, Berkeley. Research supported in part from 2017 AFOSR YIP Award, DARPA/ARL SAFEWARE Award W911NF15C0210, AFOSR Award FA9550-15-1-0274, NSF CRII Award 1464397, and research grants by the Okawa Foundation, Visa Inc., and Center for Long-Term Cybersecurity (CLTC, UC Berkeley). The views expressed are those of the author and do not reflect the official policy or position of the funding agencies.
M. Mahmoody—Supported by NSF CAREER award CCF-1350939.
A. Mohammed—Supported by University of Kuwait.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
The goal of program obfuscation is to make computer programs “unintelligible” while preserving their functionality. Over the past four years, we have come a long way from believing that obfuscation is impossible [BGI+01, GK05] to having plausible candidate constructions [GGH+13b, BR14, BGK+14, AGIS14, MSW14, AB15, GGH15, Zim15, GLSW15, BMSZ16, GMM+16, DGG+16, Lin16a, LV16, AS16, Lin16b, LT17]. Furthermore, together with one-way functions, obfuscation has been shown to have numerous consequences, e.g. [GGH+13b, SW14, GGHR14, BZ14, BPR15].
However, all these constructions are based on the conjectured security of new computational assumptions [GGH13a, CLT13, GGH15] the security of which is not very well-understood [GGH13a, CHL+15, CGH+15, CLLT15, HJ16, MSZ16, CGH16, CLLT16, ADGM16]. In light of this, it is paramount that we base security of IO on better understood assumptions. Towards this goal, one of the suggested approaches is to first realize some kind of a Functional Encryption (FE) scheme based on standard computational assumptions and then use that to realize IO. This directions is particularly promising because of the following.
-
1.
Compact single-key FE is known to imply IO. Recent results by Ananth and Jain [AJ15] and Bitansky and Vaikuntanathan [BV15] show how to base IO on a compact FE scheme — namely, a single-key FE scheme for which the encryption circuit is independent of the function circuit for which the functional secret-key is given out. Furthermore, these results can even be realized starting with FE for which at most one functional secret-key can be given out (i.e., the functional encryption scheme is single-key secure, and this is what we refer to by FE all along this paper). Furthermore, the construction works even if the ciphertext is weakly compact, i.e. the length of the ciphertext grows sub-linearly in the circuit size but is allowed to grow arbitrarily with the depth of the circuit.
-
2.
Positive results on single-key FE. The construction of IO from compact single-key FE puts us in close proximity to primitives known from standard assumptions. One prominent work, is the single-key functional encryption scheme of Goldwasser et al. [GKP+13] that is based on LWE. Interestingly, this encryption scheme is weakly compact for boolean circuits. However, in this scheme the ciphertext grows additionally with the output length of the circuit for which the functional secret-key is given out. Hence, it doesn’t imply IO.
In summary, the gap between the known single-key FE constructions from LWE and the single-key FE schemes known to imply IO (for the same ciphertext length properties) is only in the output length of circuit for which the functional secret-key is issued. In light of this, significant research continues to be invested towards realizing IO starting with various kinds of FE schemes (e.g. [BNPW16, BLP16]). This brings us to the following question.
Main Question: What kind of FE schemes are sufficient for IO?
1.1 Our Results
The main result of this work is to show that single-key FE schemes that support only functions with ‘short output’ are incapable of producing IO even when non-black-box use of the FE scheme is allowed in certain ways. The non-black-box use of FE is modeled in a way similar to prior works by Brakerski et al. [BKSY11], Asharov and Segev [AS15], and Garg et al. [GMM17]. We specifically use the monolithic framework of [GMM17] which is equivalent to the fully black-box framework of [IR89, RTV04] applied to monolithic primitives (that can include all of their subroutines as gates inside circuits given to them as input). This monolithic model captures the most commonly used non-black-box techniques in cryptography, including the ones used by Ananth and Jain [AJ15] and Bitansky and Vaikunthanathan [BV15] for realizing IO from FE. More formally, we prove the following theorem.
Theorem 1
(Main Result–Informal). Assuming one-way functions exist and \(\mathbf {NP}\not \subseteq \mathbf {coAM}\), there is no construction of IO from “short” output single-key FE where one is allowed to plant FE gates arbitrarily inside the circuits that are given to FE as input. An FE scheme is said to be “short” output if
where n is the plaintext length, \(\mathrm {\kappa }\) is the security parameter, p is the ciphertext length (for messages of length n) and t is the output length of the functions evaluated on messages of length n.
As a special case, the above result implies that single-key FE for boolean circuits and other single-key FE schemes known from standard assumptions are insufficient for IO in an monolithic black-box way.
“Long-output” FE implies IO. Complementing this negative result, we show that above condition on ciphertext length t is almost tight. In particular, we show that a “long output” single-key FE — namely, a single-key FE scheme with \(t = p +1\) (supporting an appropriate class of circuits) is sufficient for realizing IO. This construction is non-black-box (or, monolithic to be precise) and is obtained as a simple extension of the previous results of Ananth and Jain [AJ15] and Bitansky and Vaikuntanathan [BV15]. We refer the reader to the full version of this paper for this result.
Fully Black-Box Separation of IO from FE. Finally, we show that some form of non-black-box techniques (beyond the fully black-box framework of [RTV04]) is necessary for getting IO from FE, regardless of the output lengths. Namely, we prove a fully black-box separation from FE to IO. Previously, Lin [Lin16a] (Corollary 1 there) showed that the existence of such fully black-box construction from FE to IO would imply a construction of IO from LWE and constant-degree PRGs. Our result shows that no such fully black-box construction exists (but the possibility of IO from LWE and constant-degree PRGs remains open). We refer the reader to the full version of this paper for this result.
1.2 Comparison with Known Lower Bounds on IO
Sequence of works [AS15, CKP15, Pas15, MMN15, BBF16, MMN+16a, MMN+16b], under reasonable complexity assumptions,Footnote 1 proved lower bounds for building IO in a black-box manner from one-way functions, collision resistant hash functions, trapdoor permutations or even constant degree graded encoding oracles. Building on these work, authors [GMM17] showed barriers to realizing IO based on non-black-box use of “all-or-nothing encryption” primitives — namely, encryption primitives where the provided secret-keys either allow for complete decryption, or keep everything hidden. This includes encryption primitives such as attribute-based encryption [GVW13], predicate encryption [GVW15], and fully homomorphic encryption [Gen09, BV11b, BV11a, GSW13]. In comparison, this work aims to show barriers to getting IO through a non-black-box use of single-key FE, an encryption primitive that is not all-or-nothing, but has been previously shown to imply IO in certain settings. The work of Asharov and Segev [AS15] proved lower bounds on the complexity of assumptions behind IO with oracle gates (in our terminology, restricted monolithic) which is a stronger primitive than IO.Footnote 2
On the Relation to [GMM17, GKP+13]. Note that, as mentioned above, the work [GMM17] rules out the existence of monolithic IO constructions from attribute-based encryption (ABE) and the existence of monolithic IO constructions from fully homomorphic encryption (FHE). Furthermore, this result can be further broadened to separate IO from ABE and FHE in a monolithic way. One can then ask why the result in this paper does not follow as a corollary from [GMM17, GKP+13], where they construct single-key (non-compact) FE for general circuits from ABE and FHE.
We note that our result does not follow from the above observation for two reasons. First, the single-key FE construction of [GKP+13] also uses a garbling scheme in order to garble circuits with FHE decryption gates, whereas the impossibility of [GMM17] does not capture such garbling mechanisms in the monolithic model. However, if one could improve the result of [GMM17] in the monolithic model by adding a garbling subroutine that can accept ABE and FHE gates, then we can compose the results of [GMM17, GKP+13] and obtain an impossibility of IO from t-bit output (non-compact) FE. Secondly, we note that this resulting t-bit output FE scheme has the property that \(t \le p/{\text {poly}}(\mathrm {\kappa })\) (i.e. the ciphertext size is a (polynomial) multiplicative factor of the output length of the function), whereas in this work we show the stronger impossibility of basing IO on single-key FE for output-length \(t \le p - \omega (\mathrm {\kappa })\).
Other Non-Black-Box Separations. Proving separations for non-black-box constructions are usually very hard. However, there are several works that go done this line. The work of Pass et al. [PTV11] showed that, under believable assumptions, there are no non-black-box constructions of certain cryptographic primitives (e.g., one-way permutations) from one-way functions, as long as the security reductions are black-box. Pass [Pas11] and Gentry and Wichs [GW11] proved further separations in this model by separating certain primitives from any falsifiable assumptions [Nao03], again, as long as the security proof is black-box. Finally, the recent work of Dachman-Soled [Dac16] showed that certain classes of constructions with some carefully defined non-black-box power are not capable of basing public-key encryption on one way functions.
1.3 Technical Overview
In order to demonstrate the ideas behind our impossibility, we start by recalling the constructions of IO from FE [AJ15, BV15]. The key point here is that their IO constructions crucially rely on the ability of the underlying FE scheme to generate functional secret keys for functions that generate outputs of sizes that are larger than the ciphertexts that are decrypted using these functional secret keys. In particular, when evaluating the obfuscation of some circuit C on some input \(x = (x_1,...,x_n)\), they would need to decrypt a ciphertext using a functional secret key for a function that generates two ciphertexts – which is an output that is double the size of the input. Then, by successively decrypting \(c_{x_1,...,x_i}\) for all i under a functional secret key that has the property described above to get two encryptions \((c_{x_1,...,x_i,0},c_{x_1,...,x_i,1})\) where \(c_{y}\) is an encryption of y, the evaluator will obtain a ciphertext of the entire input x that it wants to evaluate the obfuscated circuit on. The obtained \(c_{x_1,...,x_n}\) is then decrypted using one final functional secret key that corresponds to the circuit C to get C(x).
On the other hand, in case the output of a functional secret key is “sufficiently smaller” than a ciphertext, then this explosion in number of ciphertexts does not seem possible anymore. This is also the key to our impossibility. Roughly speaking, at the core of the proof of our impossibility result is to show that in this “small” output setting, the total number of ciphertexts that an evaluator can compute remains polynomially bounded. Turning this high level intuition into an impossibility proof requires several new ideas that we now elaborate upon below.
The Details of the Proof of Separation. As mentioned before, monolithic constructions of IO from FE are the same as fully black-box constructions of IO from monolithic FE which is a primitive that is similar to FE but it allows FE gates to be used in the circuits for which keys are issued. Therefore, to prove the separation, we can still use oracle separation techniques from the literature on black-box constructions [IR89].
In fact, for any candidate construction \(\mathrm {IO}^{(\cdot )}\) of indistinguishability obfuscation from monolithic FE, we construct an oracle O relative to which secure monolithic FE exists but the construction \(\mathrm {IO}^{O}\) becomes insecure (against polynomial-query attackers). In order to do this, we will employ an intermediate primitive: a variant of functional witness encryption defined by Boyle et al. [BCP14]. We call this variant customized FWE (cFWE for short) and show that (1) relative to our oracle cFWE exists, (2) cFWE implies monolithic FE in a black-box way, and that (3) the construction \(\mathrm {IO}^{O}\) is insecure. We opted to work with this intermediate primitive of cFWE since it is conceptually easier to work with than an ideal FE oracle and allows us to leverage the previous results of [GMM17] to prove our separation in a modular way. Now in order to get (1) we directly define our oracle O to be an idealized version of cFWE. To get (2) we use the power of cFWE.Footnote 3 To get (3) we rely on the fact that cFWE is weakened in a careful way so that it does not imply IO. Below, we describe more details about our idealized oracle for cFWE and how to break the security of a given candidate IO construction relative to this oracle. We first recap the general framework for proving separations for IO.
General Recipe for Proving Separations for IO. Let \({\mathcal I}\) be our idealized cFWE oracle. A general technique developed over the last few years [CKP15, MMN+16b, GMM17] for breaking \(\mathrm {IO}^{\mathcal I}\) using a polynomial number of queries to the oracle (i.e. the step (3) above) is to “compile out” the oracle \({\mathcal I}\) from the obfuscation scheme and get a new secure obfuscator \(\mathrm {IO}' = (\mathrm {iO}',\mathrm {Ev}')\) in the plain-model that is only approximately-correct. Namely, by obfuscating \(\mathrm {iO}'(C)=B\) and running B over a random input we get the correct answer with probability 99/100. By the result of [BBF16], doing so implies a polynomial query attacker against \(\mathrm {IO}^{\mathcal I}\) in model \({\mathcal I}\). Note that this compiling out process (of \({\mathcal I}\) from \(\mathrm {IO}^{\mathcal I}\)) is not independent of the oracle being removed since different oracles may require different approaches to be emulated. However, the general high-level of the compiler that is used in previous work [CKP15, MMN+16b, GMM17], and we use as well, is the same: The new plain-model obfuscator \(\mathrm {iO}'\), given a circuit C to obfuscate would work in two steps. The first step of \(\mathrm {iO}'\) is to emulate \(\mathrm {iO}^{{\mathcal I}}(C)\) (by simulating the oracle \({\mathcal I}\)) to get an ideal-model obfuscation B, making sure to ‘lazily’ evaluate (emulate) any queries issued to \({\mathcal I}\). The second step of the compiler is to learn the queries that are likely to be asked by \(\mathrm {Ev}^{{\mathcal I}}(B,x)\) for a uniformly random input x, denote by \(Q_B\), which can be found by by emulating \(\mathrm {Ev}^{{\mathcal I}}(B,x_i)\) enough number of times for different uniformly random \(x_i\). Finally, the output of \(\mathrm {iO}'\) is the plain-model obfuscation \(B' = (B,Q_B)\), where B is the ideal-model obfuscation and \(Q_B\) is the set of learned queries. To evaluate the obfuscation over a new random input x, we simply execute \(\mathrm {Ev}'(B,x) = \mathrm {Ev}^{{\mathcal I}}(B,x)\) while emulating any queries to \({\mathcal I}\) consistently relative to \(Q_B\). Any compiler (for removing \({\mathcal I}\) from IO) that uses the approach describe above is in fact secure, because we only send emulated queries to the evaluator that could be simulated in the ideal world \({\mathcal I}\). The challenge, however, is to prove the correctness of the new obfuscator. So we shall prove that, by having enough iterations of the learning process (in the learning step of \(\mathrm {iO}'\)), the probability that we ask an unlearned emulation query occurs with sufficiently small probability.
The Challenge Faced for Compiling Out Our Customized Functional Witness Encryption Oracle. When \({\mathcal I}\) is defined to be our idealized cFWE oracle, in order to prove the approximate correctness of the plain-model obfuscator, we face two problems.
-
1.
The Fuzzy Nature of FWE: Unlike ‘all-or-nothing’ primitives such as witness encryption and predicate encryption, functional witness encryption mechanisms allow for more relaxed decryption functionalities. In particular, decrypting a ciphertext does not necessarily reveal the whole message m. In fact, the decryptor will learn only f(w, m), which is a function of the encrypted message and witness. As a result, even after many learning steps, when the actual execution of the obfuscated circuit starts, we might aim for evaluating a ciphertext (generated during the obfuscation phase) on a new function. This challenge did not exist in the previous separations of [GMM17] that deals with the ‘all-or-nothing’ primitives, because the probability of not decrypting a ciphertext during all the learning steps and then suddenly trying to decrypt it during the final evaluation phase could be bounded to be arbitrary small. However, here we might try to decrypt this ciphertext in all these steps, every time with a different function, which could make the information gathered during the learning step useless for the final evaluation.
-
2.
Unlearnable Hidden Queries: To get monolithic FE from our cFWE (step (2) above), our cFWE needs to be restricted monolithic. Namely, we allow the functions evaluated by cFWE to accept circuits with all possible gates that compute the subroutines of cFWE itself. However, for technical reasons, we limit how the witness verification is done in cFWE to only accept one-way function gates. Now, since we are dealing with an oracle that is an ideal version of our cFWE primitive, the function \(f^{\mathrm {cFWE}}(m,w)\) may also issue queries of their own. The challenge is that there could be many such indirect/hidden queries asked during the obfuscation phase (in particular during the learning step) that we cannot send over to the final evaluator simply because these queries are not suitable in the ideal world.
Resolving Challenges. Here we describe main ideas to resolve the challenges above.
-
1.
To resolve the first challenge, we add a specific feature to cFWE so that no ciphertext \(c={\text {Enc}}(x=(a,m))\) would be decrypted more than once by the same person. More formally, we add a subroutine to FWE (as part of our cFWE) that reveals the message \(x=(a,m)\) fully, if one can provide two correct witnesses \(w_1 \ne w_2\) for the attribute a. This way, the second time that we want to decrypt c, instead we can recover the whole message x and run the function f on our own! By this trick, we will not have to worry about the fuzzy nature of FWE, as each message is now decryped at most once. In fact, adding this subroutine is the exact reason that cFWE is a weaker primitive than FWE
-
2.
To resolve the second challenge, we rely on an information theoretic argument. Suppose for simplicity that the encryption algorithm does not take an input other than the messageFootnote 4 x. Suppose we use a random (injective) function \({\text {Enc}}:x \mapsto c\) for encryption, mapping strings of length n to strings of length \(p=p(n)\). Then, if \(p \gg n\), information theoretically, any q query algorithm who has no special advice about the oracle has a chance of \(\approx q \cdot 2^{n-p}\) to find a valid ciphertext. If \(p \gg n\) this probability is very small, so intuitively we would need about \(p-n-\log (q)\) bits of advice to find such ciphertext. On the other hand, any decryption query over a ciphertext c will only return \(t=t(n)\) bits, which in our paper is assumed to be \(t \ll p-n\). Therefore, if we interpret the decryption like a ‘trade’ of information, we need to spend \(\approx \varOmega (p-n)\) bits to get back only \(s \le o(p-n)\) bits. This is the main idea behind our argument showing that during the learning phase, we will not discover more than a polynomial number of new ciphertexts, unless we have encrypted them! By running the learning step of the compiler enough number of times, we will learn all such queries and can successfully finish the final evaluation.
By the using above two ideas, we can successfully compile out our oracle \({\mathcal I}\) from any \(\mathrm {IO}^{\mathcal I}\) construction. The compilation process itself consists of two steps. The first step being compiling out just the decryption queries where we face and resolve the challenges that we described above. Once we do that, we get an approximate obfuscator in a new oracle model \({\mathcal I}'\) that is actually a variant of an idealized witness encryption oracle. The second step would be to compile out the oracle \({\mathcal I}'\), which was already shown by [GMM17], to get the desired approximate obfuscator in the plain model.
2 Preliminaries
In this section we define the primitives that we deal with in this work and are defined prior to our work. We also give a brief background on black-box constructions and their monolithic variants.
Notation. We use “|” to concatenate strings and we use “,” for attaching strings in a way that they could be retrieved. Namely, one can uniquely identify x and y from (x, y). For example \((00|11) = (0011)\), but \((0,011) \ne (001,1)\). When writing the probabilities, by putting an algorithm A in the subscript of the probability (e.g., \(\Pr _A[\cdot ]\)) we mean the probability is over A’s randomness. We will use n or \(\kappa \) to denote the security parameter. We call an efficient algorithm \(\mathsf {V}\) a verifier for an \(\mathbf {NP}\) relation R if \(\mathsf {V}(w,a)=1\) iff \((w,a) \in R\). We call \(L_R = L_\mathsf {V}= \{ a \mid \exists w, (a,w) \in R \}\) the corresponding \(\mathbf {NP}\) language. By PPT we mean a probabilistic polynomial time algorithm. By an oracle PPT/algorithm we mean a PPT that might make oracle calls.
2.1 Obfuscation
The definition of IO below has a subroutine for evaluating the obfuscated code. The reason for defining the evaluation as a subroutine of its own is that when we want to construct IO in oracle/idealized models, we allow the obfuscated circuit to call the oracle as well. Having an evaluator subroutine to run the obfuscated code allows to have such oracle calls in the framework of black-box constructions of [RTV04] where each primitive \({\mathcal Q}\) is simply a class of acceptable functions that we (hope to) efficiently implement given oracle access to implementations of another primitive \({\mathcal P}\) (see Definition 12).
Definition 1
(Indistinguishability Obfuscation (IO)). An Indistinguishability Obfuscation (IO) scheme consists of two subroutines:
-
Obfuscator \(\mathrm {iO}\) is a PPT that takes as inputs a circuit C and a security parameter \(1^\mathrm {\kappa }\) and outputs a “circuit” B.
-
Evaluator \(\mathrm {Ev}\) takes as input (B, x) and outputs y (supposedly, equal to C(x)).
The completeness and soundness conditions assert that:
-
Completeness: For every C, with probability 1 over the randomness of O, we get \(B \leftarrow \mathrm {iO}(C,1^\mathrm {\kappa })\) such that: For all x it holds that \(\mathrm {Ev}(B,x)=C(x)\).
-
Security: For every distinguisher D there exists a negligible function \(\mu (\cdot )\) such that for every two circuits \(C_0,C_1\) that are of the same size and compute the same function, we have:
$$ | \mathop {\Pr }\limits _{\mathrm {iO}}[D(\mathrm {iO}(C_0,1^\mathrm {\kappa })=1] - \mathop {\Pr }\limits _{\mathrm {iO}}[D(\mathrm {iO}(C_1,1^\mathrm {\kappa })=1] | \le \mu (\mathrm {\kappa }) $$
Definition 2
(Approximate IO). For function \(0<\varepsilon (n)\le 1\), an \(\varepsilon \)-approximate IO scheme is defined similarly to an IO scheme with a relaxed completeness condition:
-
\(\varepsilon \)-Approximate Completeness. For every C and n we have:
$$ \mathop {\Pr }\limits _{x,\mathrm {iO}}[B=\mathrm {iO}(C,1^\mathrm {\kappa }), \mathrm {Ev}(B,x)=C(x)] \ge 1-\varepsilon (\mathrm {\kappa })$$
2.2 Functional Encryption
We will mainly be concerned with single-key functional encryption schemes which we define below so in the rest of this work whenever we refer to functional encryption, it is of the single-key type. We define a single-key functional encryption for function family \(\mathsf {F}= \{ \mathsf {F}_n \}_{n \in {\mathbb N}}\) (represented as a circuit family) as follows:
Definition 3
(Single-Key Functional Encryption [BV15]). A single-key functional encryption (FE) for function family \(\mathsf {F}\) consists of three PPT algorithms \(({\text {Setup}}, {\text {Enc}},{\text {Dec}})\) defined as follows:
-
\({\text {Setup}}(1^\mathrm {\kappa })\): Given as input the security parameter \(1^\mathrm {\kappa }\), it outputs a master public key and master secret key pair \((\mathsf {MPK},\mathsf {MSK})\).
-
\({\text {KGen}}(\mathsf {MSK},f)\): Given master secret key \(\mathsf {MSK}\) and function \(f \in \mathsf {F}\), outputs a decryption key \(\mathsf {SK}_f\).
-
\({\text {Enc}}(\mathsf {MPK}, x)\): Given the master public key \(\mathsf {MPK}\) and message x, outputs ciphertext \(c \in \{0,1\}^p\).
-
\({\text {Dec}}(\mathsf {SK}_f, c)\): Given a secret key \(\mathsf {SK}_f\) and a ciphertext \(c \in \{0,1\}^m\), outputs a string \(y \in \{0,1\}^s\).
The following completeness and security properties must be satisfied:
-
Completeness: For any security parameter \(\mathrm {\kappa }\), any \(f \in \mathsf {F}\) with domain \(\{0,1\}^n\) and message \(x \in \{0,1\}^n\), the following holds:
$$\begin{aligned} {\text {Dec}}(\mathsf {SK}_f, {\text {Enc}}(\mathsf {MPK}, x)) = f(x) \end{aligned}$$where \((\mathsf {MPK},\mathsf {MSK}) \leftarrow {\text {Setup}}(1^\mathrm {\kappa })\) and \(\mathsf {SK}_f \leftarrow {\text {KGen}}(\mathsf {MSK},f)\)
-
Security: For any PPT adversary A, there exists a negligible function \({\text {negl}}(\cdot )\) such that:
$$\Pr [{IND}_{A}^{{1FE}}(1^\mathrm {\kappa }) = 1] \le \dfrac{1}{2} + {\text {negl}}(\mathrm {\kappa }),$$where \({IND}_{A}^{{1FE}}\) is the following experiment.
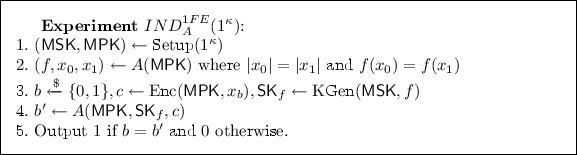
-
Efficiency: We define two notions of efficiency for single-key FE supporting the function family \(\mathsf {F}\):
-
Compactness: An FE scheme is said to be compact if the size of the encryption circuit is bounded by some fixed polynomial \({\text {poly}}(n,\mathrm {\kappa })\) where n is the size of the message, independent of the function f chosen by the adversary.Footnote 5
-
Function Output Length: An FE scheme is said to be t-bit-output if \(\mathsf {outlen}(f) \le t(n,\mathrm {\kappa })\) for any \(f \in \mathsf {F}\), where \(\mathsf {outlen}(f)\) denotes the output length of f. Given ciphertext length \(p(n,\mathrm {\kappa })\), we say an FE scheme is long-output if it is \((p+i)\)-bit-output for some \(i \ge 1\) and short-output if it is only \((p-\omega (n+\mathrm {\kappa }))\)-bit-output where n is the size of the message.
-
Definition 4
(Functional Witness Encryption (FWE) [BCP14]). Let \(\mathsf {V}\) be a PPT algorithm that takes as input an instance-message pair \(x = (a,m)\) and witness w then outputs a bit. Furthermore, let \(\mathsf {F}\) be a PPT Turing machine that accepts as input a witness w and a message m then outputs a string \(y \in \{0,1\}^s\). For any given security parameter \(\mathrm {\kappa }\), a functional witness encryption scheme consists of two PPT algorithms \(P = ({\text {Enc}},{\text {Dec}}_{\mathsf {V},\mathsf {F}})\) defined as follows:
-
\({\text {Enc}}(1^\mathrm {\kappa },a,m):\) given an instance \(a \in \{0,1\}^*\), message \(m \in \{0,1\}^*\), and security parameter \(\mathrm {\kappa }\), outputs \(c \in \{0,1\}^*\).
-
\({\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,c):\) given ciphertext c and “witness” string \(w \in \{0,1\}^*\), outputs a message \(m' \in \{0,1\}^*\).
A functional witness encryption scheme satisfies the following completeness and security properties:
-
Correctness: For any security parameter \(\mathrm {\kappa }\), any \(m \in \{0,1\}^*\), and any (w, (a, m)) such that \(\mathsf {V}^P(w,a)=1\), it holds that
$$\mathop {\Pr }\limits _{{\text {Enc}},{\text {Dec}}}[{\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,{\text {Enc}}(1^\mathrm {\kappa },a,m)) = \mathsf {F}^P(w,m)] = 1$$ -
Extractability: For any PPT adversary A and polynomial \(p_1(.)\), there exists a PPT extractor E and a polynomial \(p_2(.)\) such that for any security parameter \(\mathrm {\kappa }\), any a for which \(\mathsf {V}^P(w,a) = 1\) for some w, and any \(m_0,m_1\) where \(|m_0| = |m_1|\), if:
$$\Pr \left[ A(1^\mathrm {\kappa },c) = b \; | \; b \xleftarrow {\$} \{0,1\}, c \leftarrow {\text {Enc}}(1^\mathrm {\kappa },a, m_b) \right] \ge \dfrac{1}{2} + p_1(\mathrm {\kappa })$$Then:
$$\begin{aligned} \Pr \left[ \begin{array}{c} E^A(1^\mathrm {\kappa },a,m_0,m_1) = w : \mathsf {V}^P(w,a) = 1 \wedge \mathsf {F}^P(w,m_0) \ne \mathsf {F}^P(w,m_1) \end{array} \right] \ge p_2(\mathrm {\kappa }) \end{aligned}$$
2.3 Background on Black-Box Constructions
Definition 5
(Cryptographic Primitive [RTV04]). A primitive \({\mathcal P}= ({\mathcal F},{\mathcal R})\) is defined as set of functions \({\mathcal F}\) and a relation \({\mathcal R}\) between functions. A (possibly inefficient) function \(F \in \{0,1\}^* \rightarrow \{0,1\}^*\) is a correct implementation of \({\mathcal P}\) if \(F \in {\mathcal F}\), and a (possibly inefficient) adversary A breaks an implementation \(F \in {\mathcal F}\) if \((A,F) \in {\mathcal R}\). We sometimes refer to an implementation \(F \in {\mathcal F}\) as a set of t functions (or subroutines) \(F = \{ F_1,...,F_t \}\).
Definition 6
(Indexed primitives). Let \({\mathcal W}\) be a set of (possibly inefficient) functions. An \({\mathcal W}\) -indexed primitive \({\mathcal P}[{\mathcal W}]\) is indeed a set of primitives \(\{{\mathcal P}[W]\}_{W \in {\mathcal W}}\) indexed by \(W \in {\mathcal W}\) where, for each \(W \in {\mathcal W}\), \({\mathcal P}[W] = ({\mathcal F}[W],{\mathcal R}[W])\) is a primitive according to Definition 5.
Definition 7
(Restrictions of indexed primitives). For \({\mathcal P}[{\mathcal W}]= \{ ({\mathcal F}[W], {\mathcal R}[W]) \}_{W \in {\mathcal W}}\) and \({\mathcal P}'[{\mathcal W}']=\{ ({\mathcal F}'[W],{\mathcal R}'[W]) \}_{W \in {\mathcal W}'}\), we say \({\mathcal P}'[{\mathcal W}']\) is a restriction of \({\mathcal P}[{\mathcal W}]\) if the following conditions hold: (1) \({\mathcal W}' \subseteq {\mathcal W}\), and (2) for all \(W \in {\mathcal W}'\), \({\mathcal F}'[W] \subseteq {\mathcal F}[W]\), and (3) for all \(W \in {\mathcal W}'\), \({\mathcal R}'[W] = {\mathcal R}[W]\).
We now proceed to apply the above definition of restrictions on indexed primitives to give the definition of monolithic (and restricted monolithic) primitives. We will then apply them to the case of functional encryption. We refer the reader to [GMM17] for a more in-depth study of the monolithic framework.
Definition 8
(Universal Circuit Evaluator). We call an oracle algorithm \(w^{(\cdot )}\) a universal circuit evaluator if it accepts a pair of inputs (C, x) where \(C^{(\cdot )}\) is an oracle-aided circuit and x is a string in the domain of C then outputs \(C^{(\cdot )}(x)\) by forwarding all of C’s oracle queries to its own oracle.
Definition 9
(Monolithic Primitive [GMM17]). We call the restricted primitive \({\mathcal P}'[{\mathcal W}'] =\) \( \{ ({\mathcal F}'[W],{\mathcal R}[W]) \}_{W \in {\mathcal W}'}\) the monolithic variant of \({\mathcal P}[{\mathcal W}]=\{ ({\mathcal F}[W],{\mathcal R}[W]) \}_{W \in {\mathcal W}}\) if the following holds:
-
For any F and \(W \in {\mathcal W}\), if \(W = w^F\) for some universal circuit evaluator \(w^{(\cdot )}\) and \(F \in {\mathcal F}[W]\) then \(W \in {\mathcal W}'\) and \(F \in {\mathcal F}'[W]\).
Definition 10
(Restricted Monolithic Primitive [GMM17]). We call the restricted primitive \({\mathcal P}'[{\mathcal W}'] = \{ ({\mathcal F}'[W],{\mathcal R}[W]) \}_{W \in {\mathcal W}'}\) the restricted monolithic variant of \({\mathcal P}[{\mathcal W}]=\{ ({\mathcal F}[W],{\mathcal R}[W]) \}_{W \in {\mathcal W}}\) if is satisfies Definition 9 but the condition is replaced with the following:
-
For any F and \(W \in {\mathcal W}\), if \(W = w^{F'}\) for some universal circuit evaluator \(w^{(\cdot )}\), \(F' \subset F \in {\mathcal F}[W]\) then \(W \in {\mathcal W}'\) and \(F \in {\mathcal F}'[W]\).
That is, the subroutines of F that \(w^{(\cdot )}\) may call are a strict subset of all the subroutines contained in implementation F.
Definition 11
(Monolithic Functional Encryption). A monolithic functional encryption scheme \(\mathrm {FE} = ({\text {FE.Setup}}, \) \({\text {FE.Enc}}, {\text {FE.Keygen}}, {\text {FE.Dec}})\) for the function family \(\mathsf {F}\) is defined the same as Definition 3 except that, for any \(f \in \mathsf {F}\), f is an oracle-aided circuit that can call any subroutine of \(\mathrm {FE}\).
Definition 12
(Black-box Construction [RTV04]). A (fully) black-box construction of a primitive \({\mathcal Q}\) from a primitive \({\mathcal P}\) consists of two PPT algorithms (Q, S):
-
1.
Implementation: For any oracle P that implements \({\mathcal P}\), \(Q^P\) implements \({\mathcal Q}\).
-
2.
Security reduction: for any oracle P implementing \({\mathcal P}\) and for any (computationally unbounded) oracle adversary A successfully breaking the security of \(Q^P\), it holds that \(S^{P,A}\) breaks the security of P.
Definition 13
(Monolithic Construction of IO from FE). A monolithic construction of IO from FE is a fully black-box construction of IO from monolithic FE.
2.4 Tools for Lower Bounds of IO
Definition 14
(Sub-models). We call the idealized model/oracle \({\mathcal O}\) a sub-model of the idealized oracle \({\mathcal I}\) with subroutines \(({\mathcal I}_1,\dots ,{\mathcal I}_k)\), denoted by \({\mathcal O}\sqsubseteq {\mathcal I}\), if there is a (possibly empty) \(S \subseteq \{ 1,\dots ,k \}\) such that the idealized oracle \({\mathcal O}\) works as follows:
-
First sample \(I \leftarrow {\mathcal I}\) where the subroutines are \(I=(I_1,\dots ,I_k)\).
-
Provide access to subroutine \(I_i\) iff \(i \in S\).
If \(S=\varnothing \) then the oracle \({\mathcal O}\) will be empty and we will be back to the plain model.
Definition 15
(Simulatable Compiling Out Procedures for IO). Suppose \({\mathcal O}\sqsubset {\mathcal I}\). We say that there is a simulatable compiler from IO in idealized model \({\mathcal I}\) into idealized model \({\mathcal O}\) with correctness error \(\varepsilon \) if the following holds.
For every implementation \(P_{\mathcal I}=(\mathrm {iO}_{\mathcal P},\mathrm {Ev}_{\mathcal P})\) of \(\delta \)-approximate IO in idealized model \({\mathcal I}\) there is a implementation \(P_{\mathcal O}=(\mathrm {iO}_{\mathcal O},\mathrm {Ev}_{\mathcal O})\) of \((\delta +\varepsilon )\)-approximate IO in idealized model \({\mathcal O}\) such that the security of the two are related as follows:
Simulation: There is an efficient PPT simulator S and a negligible function \(\mu (\cdot )\) such that for any C:
where \(\varDelta (.,.)\) denotes the statistical distance between any two given random variables.
Lemma 1
(Lower Bounds for IO using Oracle Compilers [GMM17]). Suppose \(\varnothing ={\mathcal I}_0 \sqsubseteq {\mathcal I}_1 \dots \sqsubseteq {\mathcal I}_k = {\mathcal I}\) for constant \(k=O(1)\) are a sequence of idealized models. Suppose for every \(i \in [k]\) there is a simulatable compiler for IO in model \({\mathcal I}_i\) into model \({\mathcal I}_{i-1}\) with correctness error \(\varepsilon _i < 1/(100 k)\). Also suppose primitive \({\mathcal P}\) can be black-box constructed in the idealized model \({\mathcal I}\). Then there is no fully black-box construction of IO from \({\mathcal P}\).
3 Monolithic Separation of IO from Short-Output FE
In this section, we prove our main impossibility result which states that we cannot construct an IO scheme in a monolithic way from any single-key functional encryption scheme that is restricted to handling only functions of “short” output length. More formally, we prove the following theorem.
Theorem 2
Assume the existence of one-way functions and that \(\mathbf {NP}\not \subseteq \mathbf {co\text{- }NP}\). Then there exists no monolithic construction of IO from any single-key t-bit-output functional encryption scheme where \(t(n,\mathrm {\kappa }) \le p(n,\mathrm {\kappa }) - \omega (n+\mathrm {\kappa })\), n is the message length, p is the ciphertext length, and \(\mathrm {\kappa }\) is the security parameter of the functional encryption scheme.
To prove Theorem 2, we will apply Lemma 1 for the idealized functional witness encryption model \(\varGamma \) (formally defined in Sect. 3.1) to prove that there is no black-box construction of IO from any primitive \({\mathcal P}\) that can be black-box constructed from the \(\varGamma \). In particular, we will do so for \({\mathcal P}\) that is the monolithic functional encryption primitive. Our task is thus twofold: (1) to prove that \({\mathcal P}\) can black-box constructed from \(\varGamma \) and (2) to show a simulatable compilation procedure that compiles out \(\varGamma \) from any IO construction. The first task is proven in Sect. 3.2 and the second task is proven in Sect. 3.3. By Lemma 1, this would imply the separation result of IO from \({\mathcal P}\) and prove Theorem 2.
Our oracle, which is more formally defined in Sect. 3.1, acts an idealized version of a single-key short-output functional encryption scheme, which makes the construction of secure FE quite straightforward. As a result, the main challenge lies in showing a simulatable compilation procedure for IO that satisfies Definition 15 in this idealized model, and therefore, it is instructive to look at how the compilation process works and what challenges are faced with dealing with oracle \(\varGamma \).
3.1 The Ideal Model
In this section, we define the distribution of our idealized (randomized) oracle that can be used to realize (restricted-monolithic) functional witness encryption. We also provide several definitions regarding the algorithms in this model and the types of queries that these algorithms can make.
Definition 16
(Randomized Functional Witness Encryption Oracle). Let \(\mathsf {V}\) be a PPT algorithm that takes as input (w, a), outputs \(b \in \{0,1\}\) and runs in time \({\text {poly}}(|a|)\). Also, let \(\mathsf {F}\) be a PPT algorithm that accepts as input a witness w and a message m then outputs a string \(y \in \{0,1\}^s\). We denote the random \((\mathsf {V},\mathsf {F},p)\) -functional witness encryption (rFWE) oracle as \(\overline{\varGamma }_{\mathsf {V},\mathsf {F},p} = \{\overline{\varGamma }_{\mathsf {V},\mathsf {F},p}\}_{n \in {\mathbb N}}\) where \(\overline{\varGamma }_{\mathsf {V},\mathsf {F},p} = ({\text {Enc}}, {\text {Dec}}_{\mathsf {V},\mathsf {F}}, {\text {RevAtt}}, {\text {RevMsg}}_\mathsf {V})\) is defined as follows:
-
\({\text {Enc}}{:}~\{0,1\}^{n} \mapsto \{0,1\}^{p(n)} \) is a random injective function mapping strings \(x \in \{0,1\}^n\) to “ciphertexts” \(c \in \{0,1\}^p\) where \(p(n) \ge n\).
-
\({\text {Dec}}_{\mathsf {V},\mathsf {F}}{:}~\{0,1\}^{\ell } \mapsto \{0,1\}^n \cup \{ \bot \}\): Given \((w,c) \in \{0,1\}^\ell \) as input where \(c\in \{0,1\}^{p(n)}\), \({\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,c)\) allows us to decrypt the ciphertext \(c = {\text {Enc}}(x)\) to get back x, parse it as \(x = (a,m)\), then get \(\mathsf {F}(w,m)\) as long as the predicate test is satisfied on (w, a). More formally, the following steps are performed:
-
1.
If \(\not \exists \; x\) such that \({\text {Enc}}(x) = c\), output \(\bot \). Otherwise, continue to the next step.
-
2.
Find x such that \({\text {Enc}}(x) = c\), and parse it as \(x = (a,m)\).
-
3.
If \(\mathsf {V}^{}(w,a)=1\), output \(\mathsf {F}^{}(w,m)\). Otherwise, output \(\bot \).
-
1.
-
\({\text {RevAtt}}{:}~\{0,1\}^{p(n)} \mapsto \{0,1\}^{*} \cup \{ \bot \}\) is a function that, given an input \(c \in \{0,1\}^{p(n)}\), would output the corresponding attribute \(a \in \{0,1\}^*\) for which \({\text {Enc}}((a,m)) = c\). If there is no such a then output \(\bot \).
-
\({\text {RevMsg}}_\mathsf {V}{:}~\{0,1\}^{\ell '} \mapsto \{0,1\}^{*} \cup \{ \bot \}\): Given \((w_1,w_2,c)\) where \(w_1 \ne w_2\) and \(c \in \{0,1\}^{p(n)}\), if there exist \(x = (a,m)\) such that \({\text {Enc}}(x) = c\) and \(\mathsf {V}^{}(w_i,a) = 1\) for \(i \in \{ 1,2 \}\) then reveal m. Otherwise, output \(\bot \).
When it is clear from context, we sometimes omit the subscripts from \({\text {Dec}}_{\mathsf {V},\mathsf {F}}\), \({\text {RevMsg}}_\mathsf {V}\), and \(\overline{\varGamma }_{\mathsf {V},\mathsf {F}}\) and simply write them as \({\text {Dec}}\), \({\text {RevMsg}}\), and \(\overline{\varGamma }\), respectively. Furthermore, we denote any query-answer pair \((q,\beta )\) asked by some oracle algorithm A to a subroutine \(T \in \{ {\text {Enc}},{\text {Dec}},{\text {RevAtt}},{\text {RevMsg}} \}\) as \((q \mapsto \beta )_{T}\).
Definition 17
(Restricted-Monolithic Randomized Functional Witness Encryption Oracle). We define a randomized restricted-monolithic functional witness encryption oracle \(\varGamma _{\mathsf {V},\mathsf {F},p}\) as an rFWE oracle \(\overline{\varGamma }_{\mathsf {V},\mathsf {F},p} = ({\text {Enc}},{\text {Dec}}_{\mathsf {V},\mathsf {F}},{\text {RevAtt}},{\text {RevMsg}})\) where \(\mathsf {V}\) and \(\mathsf {F}\) satisfy the following properties:
-
\(\mathsf {V}\) is a PPT oracle algorithm that takes as input (w, a), interprets \(a^{(\cdot )}\) as an oracle-aided circuit that can only make \({\text {Enc}}\) calls, then outputs \(a^{{\text {Enc}}}(w)\).
-
\(\mathsf {F}\) is a PPT oracle algorithm that takes as input (w, m), parses \(w = (z_1,z_2)\), interprets \(z_1^{(\cdot )}\) as an oracle-aided circuit that can make calls to any subroutine in \(\varGamma = ({\text {Enc}},{\text {Dec}},{\text {RevAtt}},\) \({\text {RevMsg}})\), then outputs \(z_1^{\varGamma }(m)\).
While the above oracle shares similar traits to a restricted-monolithic primitive (see Definition 10), the actual functionality of \(\mathsf {F}\) is slightly modified to simplify the notion of using only part of w. For the purposes of this section, we will use the restricted-monolithic rFWE \(\varGamma \) in order to prove our separation result of IO from monolithic functional encryption - mainly because this oracle is sufficient for getting monolithic FE. Nevertheless, we will still make use of \(\overline{\varGamma }\) later on in in the full version of this paper to prove the fully black-box separation of IO from (non-monolithic) functional encryption.
Next, we present the following definition of canonical executions that is a property of algorithms in this ideal model. This normal form of algorithms helps us in reducing the query cases to analyze since there are useless queries whose answers can be computed without needing to ask the oracle.
Definition 18
(Canonical executions). We define an oracle algorithm \(A^{\varGamma }\) relative to the restricted-monolithic rFWE oracle to be in canonical form if the following conditions are satisfied:
-
If A has issued a query of the form \({\text {Enc}}(x) = c\), then it will not ask \({\text {Dec}}_{\mathsf {V},\mathsf {F}}(.,c)\), \({\text {RevAtt}}(c)\), or \({\text {RevMsg}}_\mathsf {V}(.,.,c)\) as it can compute the answers of these queries on its own. In particular, for \({\text {Dec}}_{\mathsf {V},\mathsf {F}}\) and \({\text {RevMsg}}_\mathsf {V}\) queries, it would run \(\mathsf {V}\) and \(\mathsf {F}\) directly to compute the query answers correctly.
-
Before asking any \({\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,c)\) query where \({\text {Enc}}(x) = c\) for some \(x = (a,m)\), A would go through the following steps first:
-
A would get \(a \leftarrow {\text {RevAtt}}(c)\) then run \(\mathsf {V}^{{\text {Enc}}}(w,a)\) on its own, making sure to answer any queries of \(\mathsf {V}\) using \({\text {Enc}}\). If \(\mathsf {V}^{{\text {Enc}}}(w,a) = 0\) then do not issue \({\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,c)\) to \(\varGamma \) and use \(\bot \) as the answer instead. Otherwise, continue to the next step.
-
If A has beforehand ran \(\mathsf {V}^{{\text {Enc}}}(w',a) = 1\) for some \(w' \ne w\) then it does not ask \({\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,c)\) and instead computes the answer to this query on its own. That is, it first gets \(m \leftarrow {\text {RevMsg}}(w,w',c)\), computes on its own \(\mathsf {F}^\varGamma (w,m)\) and outputs \(\mathsf {F}^\varGamma (w,m)\) if \(\mathsf {V}^{{\text {Enc}}}(w,a) = 1\) or otherwise \(\bot \).
-
If A has not asked \({\text {Dec}}_{\mathsf {V},\mathsf {F}}(w',c)\) for any \(w' \ne w\) (or did but it received \(\bot \) as the answer) then it directly asks \({\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,c)\) from the oracle.
-
-
Before asking any \({\text {RevMsg}}_\mathsf {V}(w_1,w_2,c)\) query where \({\text {Enc}}(x) = c\) for some \(x = (a,m)\), A would go through the following steps first:
-
A would get \(a \leftarrow {\text {RevAtt}}(c)\) then run \(\mathsf {V}^{{\text {Enc}}}(w_i,a)\) for all \(i \in \{1,2\}\) on its own, making sure to answer any queries of \(\mathsf {V}\) using \({\text {Enc}}\). If \(\mathsf {V}^{{\text {Enc}}}(w_i,a) = 0\) for some i then do not issue \({\text {RevMsg}}_\mathsf {V}(w_1,w_2,c)\) to \(\varGamma \) and use \(\bot \) as the answer instead. Otherwise, continue to the next step.
-
After issuing \({\text {RevMsg}}_\mathsf {V}(w_1,w_2,c)\) to \(\varGamma \) and getting back an answer \(m \ne \bot \), ask the query \({\text {Enc}}(x)\) where \(x = (a,m)\) then run \(\mathsf {F}^\varGamma (w_1,m)\) and \(\mathsf {F}^\varGamma (w_2,m)\).
-
Note that any oracle algorithm A can be easily modified into a canonical form by increasing its query complexity by at most a polynomial factor assuming that \(\mathsf {F}\) has extended polynomial query complexity.
Remark 1
We observe the following useful property regarding the number of queries of a specific type that a canonical algorithm in the \(\varGamma \) oracle model can make. Namely, given a canonical A, for any ciphertext \(c = {\text {Enc}}(x)\) where \(x = (a,m)\) for which A has not asked \({\text {Enc}}(x)\) before, A would ask at most one query of the form \({\text {RevAtt}}(c)\), at most one query of the form \({\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,c)\) for which \(\mathsf {V}^{{\text {Enc}}}(w,a) = 1\), and at most one query of the form \({\text {RevMsg}}_\mathsf {V}(w_1,w_2,c)\) for which \(\mathsf {V}^{{\text {Enc}}}(w_i,a) = 1\) where \(i \in \{1,2\}\). Furthermore, A would never ask a query if \(\mathsf {V}^{{\text {Enc}}}(w,a) = 0\) since this condition can be verified independently by A and the answer can be simulated as it would invariably be \(\bot \).
Looking ahead, we will use this property later on to prove an upper bound on the number of ciphertexts that an adversary can decrypt without knowing the underlying message. Furthermore, we stress that this property holds specifically due to the presence of the \({\text {RevMsg}}\) subroutine which leaks the entire message of a given ciphertext once two different valid witnesses are provided. As a result, this shows that decrypting a ciphertext more than once (under different witnesses) does not help as the message could be revealed instead.
We also provide the following definitions to classify the ciphertext and query types. This would simplify our discussion and clarify some aspects of the details later in the proof.
Definition 19
(Ciphertext Types). Let A be a canonical algorithm in the \(\varGamma \) ideal model and suppose that \(Q_A\) is the set of query-answer pairs that A asks during its execution. For any q of the form \({\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,c)\), \({\text {RevAtt}}(c)\), or \({\text {RevMsg}}_\mathsf {V}(w_1,w_2,c)\), we say that c is valid if there exists x such that \(c = {\text {Enc}}(x)\), and we say that c is unknown if the query-answer pair \((x \mapsto c)_{{\text {Enc}}}\) is not in \(Q_A\).
Definition 20
(Query Types). Let A be a canonical algorithm in the \(\varGamma \) ideal model and let \(Q_A\) be the query-answer pairs that it has asked so far. For any query new query q issued to \(\varGamma \), we define several properties that such a query might have:
-
Determined: We say q is determined with respect to \(Q_A\) if there exists \((q \mapsto \beta )_{T} \in Q_A\) for some answer \(\beta \) or there exists some query \((q' \mapsto \beta ')_{T} \in Q_A\) that determines that answer of q without needing to issue q to \(\varGamma \).
-
Direct: We say q is a direct query if A issues this query to \(\varGamma \) to get back some answer \(\beta \). The answers to such queries are said to be visible to A.
-
Indirect: We say q is an indirect query if q is issued by \(\mathsf {F}^\varGamma \) during a \({\text {Dec}}\) query that was issued by A. The answers to such queries are said to be hidden from A.
3.2 Monolithic Functional Encryption Exists Relative to \(\varGamma \)
In this section, we show how to construct a semantically-secure monolithic FE scheme. Namely, we prove the following:
Lemma 2
There exists a correct and subexponentially-secure implementation of monolithic functional encryption in the \(\varGamma \) oracle model with measure one of oracles.
We do this in two steps: we first show how to construct a restricted-monolithic variant of a functional witness encryption from the ideal oracle \(\varGamma \) and then show how to use it to construct the desired functional encryption scheme. Our variant of FWE that we will construct is defined as follows.
Definition 21
(Customized Functional Witness Encryption (CFWE)). Given any one-way function R, let \(\mathsf {V}\) be a PPT oracle algorithm that takes as input an instance-message pair \(x = (a,m)\) and witness w, interprets a as an oracle circuit then outputs \(a^R(w)\) while only making calls to R. Furthermore, let \(\mathsf {F}\) be a PPT oracle algorithm that accepts as input a string \(w = (z_1,z_2)\) and a message m, interprets \(z_1\) as a circuit then outputs a string \(y = z_1(m)\). For any given security parameter \(\mathrm {\kappa }\), a customized functional witness encryption scheme defined by \(\mathsf {V}\) and \(\mathsf {F}\) consists of three PPT algorithms \(P = ({\text {Enc}},{\text {Dec}}_{\mathsf {V},\mathsf {F}},{\text {RevAtt}})\) defined as follows:
-
\({\text {Enc}}(1^\mathrm {\kappa },a,m)\): given an instance \(a \in \{0,1\}^*\), message \(m \in \{0,1\}^*\), and security parameter \(\mathrm {\kappa }\), outputs \(c \in \{0,1\}^*\).
-
\({\text {RevAtt}}(c)\): given a ciphertext c, outputs the corresponding attribute a under which the message is encrypted.
-
\({\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,c)\): given ciphertext c and “witness” string \(w \in \{0,1\}^*\), outputs a message \(m' \in \{0,1\}^*\).
A customized functional witness encryption scheme satisfies the following completeness and security properties:
-
Correctness: For any security parameter \(\mathrm {\kappa }\), any \(m \in \{0,1\}^*\), and any (w, (a, m)) such that w and \(\mathsf {V}^R(w,a)=1\), it holds that
$$\mathop {\Pr }\limits _{{\text {Enc}},{\text {Dec}}}[{\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,{\text {Enc}}(1^\mathrm {\kappa },a,m)) = \mathsf {F}^P(w,m)] = 1$$ -
Instance-Revealing: For any security parameter \(\mathrm {\kappa }\), any \(m \in \{0,1\}^*\), and any (w, (a, m)) such that \(\mathsf {V}^R(w,a)=1\), it holds that
$$\Pr [{\text {RevAtt}}({\text {Enc}}(1^\mathrm {\kappa },a,m)) = a] = 1$$ -
Weak Extractability: For any PPT adversary A and polynomial \(p_1(.)\), there exists a PPT extractor E and a polynomial \(p_2(.)\) such that for any security parameter \(\mathrm {\kappa }\), any a for which \(\mathsf {V}^R(w,a) = 1\) for some w, and any \(m_0,m_1\) where \(|m_0| = |m_1|\), if:
$$\Pr \left[ A(1^\mathrm {\kappa },c) = b \; | \; b \xleftarrow {\$} \{0,1\}, c \leftarrow {\text {Enc}}(1^\mathrm {\kappa },a, m_b) \right] \ge \dfrac{1}{2} + p_1(\mathrm {\kappa })$$Then:
$$\begin{aligned} \Pr \left[ \begin{array}{c} E^A(1^\mathrm {\kappa },a,m_0,m_1) = w : \mathsf {V}^R(w,a) = 1 \wedge \mathsf {F}^P(w,m_0) \ne \mathsf {F}^P(w,m_1) \\ \vee \\ E^A(1^\mathrm {\kappa },a,m_0,m_1) = (w_1,w_2) : w_1 \ne w_2 \wedge \mathsf {V}^R(w_1,a) = 1 \wedge \mathsf {V}^R(w_2,a) = 1 \end{array} \right] \ge p_2(\mathrm {\kappa }) \end{aligned}$$
Customized FWE in the \(\varGamma \) Ideal Model. Here we provide the construction of customized FWE using the \(\varGamma _{\mathsf {V},\mathsf {F}}\) oracle. We note that \(\varGamma \) can be thought of as an ideal customized FWE and hence the construction of the CFWE primitive is straightforward.
Construction 3
(Customized Functional Witness Encryption). Let \(\mathsf {V}\) and \(\mathsf {F}\) be as defined in Definition 21. For any security parameter \(\mathrm {\kappa }\) and oracle \(\varGamma _{\mathsf {V},\mathsf {F}}\) sampled according to Definition 17, we will implement a customized FWE scheme P defined by \(\mathsf {V}\) and function class \(\mathsf {F}\) as follows:
-
\(\mathrm {CFWE{.}Enc}(1^\mathrm {\kappa },a, m)\mathrm{:}\) Given \(a \in \{0,1\}^*\), message \(m \in \{0,1\}^{n'}\) and security parameter \(1^\mathrm {\kappa }\), let \(n = \varTheta (n' + |a| + \mathrm {\kappa })\). Sample \(r \leftarrow \{0,1\}^{\mathrm {\kappa }}\) uniformly at random then output \(c = {\text {Enc}}(x)\) where \(x = (a,(m,r))\).
-
\(\mathrm {CFWE{.}Dec}(w,c)\mathrm{:}\) Given string w and ciphertext \(c \in \{0,1\}^p\), get \(y \leftarrow {\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,c)\), then output y.
-
\(\mathrm {CFWE{.}Rev}(c)\mathrm{:}\) Given ciphertext \(c \in \{0,1\}^p\), outputs \({\text {RevAtt}}(c)\).
Lemma 3
Construction 3 is a correct and subexponentially-secure implementation of customized functional witness encryption in the \(\varGamma \) oracle model with measure one.
For the proof of correctness and security for this construction, we refer the reader to the full version of this paper.
From CFWE to Functional Encryption
Construction 4
(Functional Encryption). Let \(P_{\mathsf {F}}= ({\text {FE.Setup}},{\text {FE.Keygen}},{\text {FE.Enc}},\) \({\text {FE.Dec}})\) be the functional encryption scheme for the function family \(\mathsf {F}\) that we would like to construct. Suppose \(\mathrm {Sig}=(\mathrm {Sig{.}Gen},\mathrm {Sig{.}Sign},\mathrm {Sig{.}Ver})\) is a secure signature scheme.
Define a language L with an associated PPT verifier \(\mathsf {V}\) such that an instance a of the language corresponds to the signature verification circuit \(\mathrm {Sig{.}Ver}(vk,.)\) that takes as input \(w = (f,\mathsf {sk}_f)\) so that \(\mathsf {V}(w,a) = a(w) = 1\) if and only if \(\mathrm {Sig{.}Ver}(vk,w) = 1\) for some oracle-aided \(f \in \mathsf {F}\), \(\mathsf {sk}_f \leftarrow \mathrm {Sig{.}Sign}(sk,f)\), and \((sk,vk) \leftarrow \mathrm {Sig{.}Gen}(1^\mathrm {\kappa })\). Furthermore, let \(\mathsf {F}'\) be a PPT algorithm that takes as input \(w = (f,\mathsf {sk}_f)\) and a message m then outputs \(y = \mathsf {F}'(w,m) = f(m)\).
Given a customized functional witness encryption scheme \(\mathrm {CFWE} = (\mathrm {CFWE{.}Enc},\) \(\mathrm {CFWE{.}Dec}_{\mathsf {V},\mathsf {F}'},\) \(\mathrm {CFWE{.}Rev})\) for \(\mathsf {V}\) and \(\mathsf {F}'\) defined above, signature scheme \(\mathrm {Sig}\), and security parameter \(\mathrm {\kappa }\), we implement the monolithic FE scheme \(P_{\mathsf {F}}\) as follows:
-
\({\text {FE.Setup}}(1^\mathrm {\kappa })\mathrm{:}\) Generate \((sk,vk) \leftarrow \mathrm {Sig{.}Gen}(1^\mathrm {\kappa })\). Output \((\mathsf {MPK},\mathsf {MSK})\) where \(\mathsf {MPK}= vk\) and \(\mathsf {MSK}= sk\).
-
\({\text {FE.Keygen}}(\mathsf {MSK},f)\mathrm{:}\) Given \(\mathsf {MSK}= sk\) and \(f \in \mathsf {F}\), output \(\mathsf {SK}_{f} = (f,sk_{f})\) where \(sk_{f} \leftarrow \mathrm {Sig{.}Sign}(\mathsf {MSK},f)\).
-
\({\text {FE.Enc}}(\mathsf {MPK},m)\mathrm{:}\) Given \(\mathsf {MPK}\in \{0,1\}^{\mathrm {\kappa }}\) and message \(m \in \{0,1\}^{n'}\), output ciphertext \(c = \mathrm {CFWE{.}Enc}(1^\mathrm {\kappa },\mathsf {MPK},m)\).
-
\({\text {FE.Dec}}(\mathsf {SK}_{f},c)\mathrm{:}\) Given \(\mathsf {SK}_{f} = (f,sk_{f})\) and ciphertext \(c \in \{0,1\}^p\), call and output the value returned by \(\mathrm {CFWE{.}Dec}_{\mathsf {V},\mathsf {F}'}(\mathsf {SK}_{f},c)\).
Lemma 4
Construction 4 is a fully black-box construction of monolithic functional encryption from customized FWE.
Proof
We first show that the construction is correct. Given \((\mathsf {MPK},\mathsf {MSK}) \leftarrow {\text {FE.Setup}}(1^\mathrm {\kappa })\), for any encryption \(c \leftarrow {\text {FE.Enc}}(\mathsf {MPK},m)\) of a message \(m \in \{0,1\}^{n'}\) and functional decryption key \(\mathsf {SK}_{f} \leftarrow {\text {FE.Keygen}}(\mathsf {MSK},f)\) for a function \(f \in {\mathcal F}\), we get that, if \(\mathsf {V}(w,a) = a^{\mathrm {Sig}}(w) = \mathrm {Sig{.}Ver}(vk,(f,sk_f)) = 1\) then:
Note that, since this is an monolithic construction, f can have oracle gates to any subroutine in \(P_{\mathsf {F}}\). As a result, we need to make sure that \(\mathsf {V}\) are \(\mathsf {F}'\) are specified in a way so that all monolithic computations are valid. First, \(\mathsf {V}\) only has one \(\mathrm {Sig{.}Ver}\) gate which is supported by OWFs. Furthermore, \(\mathsf {F}'\) calls f which has oracle gates to any subroutine in \(P_{\mathsf {F}}\). Nevertheless, we can reduce each gate to \(P_{\mathsf {F}}\) to CFWE or OWF gates. In particular, \({\text {FE.Setup}}\) can be reduced to \(\mathrm {Sig{.}Gen}\) gates, \({\text {FE.Keygen}}\) can be reduced to \(\mathrm {Sig{.}Sign}\) gates, \({\text {FE.Enc}}\) can be reduced to \(\mathrm {CFWE{.}Enc}\) gates, and \({\text {FE.Dec}}\) can be reduced to \(\mathrm {CFWE{.}Dec}\) gates. Thus, all gates in \(\mathsf {F}'\) can be reduced to those in FWE or one-way functions.
Next, we prove the security of the scheme by reducing it to the underlying security of CFWE and Sig. Let A be a computationally bounded adversary that asks one functional secret key query and breaks the security of the FE scheme. That is, for some non-negligible \(\varepsilon (.)\):
where \(\text {IND}_{A}^{\text {1FE}}\) is the experiment of Definition 3.
Towards contradiction, we will now show that, given A, we can build an attacker B that can break the strong existential unforgeability of the signature scheme under chosen message attack. On receiving the public-key \(\mathsf {MPK}\) from the (signature game) challenger, B forwards \(\mathsf {MPK}\) to A and upon receiving \((f,m_0,m_1)\), requests the signature for f and then randomly chooses a message to encrypt. Note that, since \({\text {FE.Enc}}(\mathsf {MPK},m_b) = \mathrm {CFWE{.}Enc}(1^\mathrm {\kappa },\mathsf {MPK},m_b)\), B can use A to build a distinguisher \(A'\) against CFWE. B then runs the black-box straight-line extractor \(E^{A'}\) (guaranteed to exist by the security definition of CFWE) where at least one of the following events will happen with non-negligible probability:
-
The extractor returns a single witness \(w^* = (f^*,sk_{f^*})\) such that \(\mathsf {V}(w^*,\mathsf {MPK})\) outputs 1 and \(\mathsf {F}'(w^*,m_0) \ne \mathsf {F}'(w^*,m_1) \implies f^*(m_0) \ne f^*(m_1)\). Note that this implies that \(sk_{f^*}\) is a valid forgery since \(f^*\) cannot be the function f that A requests the signature for (because \(f(m_0) = f(m_1)\) in that case) and \(w^*\) passed verification thus violating the security of the signature scheme.
-
The extractor returns a pair of witnesses \((w^*_1,w^*_2)\) such that \(w^*_1 \ne w^*_2\) and \(\mathsf {V}(w^*_1,\mathsf {MPK})\) = \(\mathsf {V}(w^*_2,\mathsf {MPK})\) = 1. This either implies that \(w^*_i = (f^*,sk_{f^*})\) for some \(i \in \{ 1,2 \}\) is a valid witness and \(f^* \ne f\) in which case we have a signature forgery, or it implies that \(w^*_i = (f,sk'_{f})\) for some \(i \in \{ 1,2 \}\) and hence \(sk'_{f} \ne sk_f\) (since even if \(w^*_{i-1} = (f,sk_f)\) we have that \(w^*_{i} \ne w^*_{i-1}\)) which is also signature forgery.
In both of the above cases, an attack against the FE scheme results in an attack against the underlying signature scheme.
3.3 Compiling Out \(\varGamma \) from IO
In this section, we show a simulatable compiler for compiling out \(\varGamma _{\mathsf {V},\mathsf {F}}\) when \(\mathsf {F}\) is short-output. We adapt the approach outlined in Sect. 2 to the restricted-monolithic rFWE oracle \(\varGamma _{\mathsf {V},\mathsf {F}} = ({\text {Enc}}, {\text {Dec}}_{\mathsf {V},\mathsf {F}},\) \({\text {RevAtt}},{\text {RevMsg}}_\mathsf {V})\) while making use of Lemma 1, which allows us to compile out \(\varGamma _{\mathsf {V},\mathsf {F}}\) in two phases: we first compile out part of \(\varGamma _{\mathsf {V},\mathsf {F}}\) to get an approximately-correct obfuscator \(\widehat{O}^\varTheta \) in the random instance-revealing witness encryption model (that produces an obfuscation \(\widehat{B}^\varTheta \) in the \(\varTheta \)-model), and then use the previous result of [GMM17] to compile out \(\varTheta \) and get an obfuscator \(O'\) in the plain-model. Since we are applying this lemma only a constant number of times, security should still be preserved. Specifically, we will prove the following lemma:
Lemma 5
Let \(\mathsf {F}\) be a PPT oracle Turing machine that accepts as input a witness w and a message m then outputs a string \(y \in \{0,1\}^s\) where \(s(n) \le t(n)\). Let \(\varTheta \) be a random instance-revealing witness encryption oracle. Then for any \(\varGamma _{\mathsf {V},\mathsf {F},p}\) satisfying \(t(n) \le p(n) - \omega (n)\) and for \(\varTheta \sqsubseteq \varGamma _{\mathsf {V},\mathsf {F},p}\), the following holds:
-
For any IO in the \(\varGamma _{\mathsf {V},\mathsf {F},p}\) ideal model, there exists a simulatable compiler with correctness error \(\varepsilon < 1/200\) for it that outputs a new obfuscator in the random instance-revealing witness encryption oracle \(\varTheta \) model.
-
[GMM17] For any IO in the \(\varTheta \) oracle model, there exists a simulatable compiler with correctness error \(\varepsilon < 1/200\) for it that outputs a new obfuscator in the plain model.
We observe that by compiling out only the \({\text {Dec}}\) queries of \(\varGamma \), we will end up with queries only to \({\text {Enc}},{\text {RevAtt}}\), and \({\text {RevMsg}}\). However, we note that \({\text {Enc}}\) and \({\text {RevAtt}}\) already are part of \(\varTheta \) and \({\text {RevMsg}}\) can in fact be interpreted as the decryption subroutine of \(\varTheta \) where \(w' = (w_1,w_2)\) is defined as the witness to the decryption subroutine. Therefore, the second part of Lemma 5 follows directly by [GMM17], where they showed how to compile out the ideal witness encryption oracle from any IO scheme, and thus we focus on proving the first part of the lemma. We will present the construction of the obfuscator in the random instance-revealing witness encryption model that, given an obfuscator in the \(\varGamma \) model, would compile out and emulate queries to \({\text {Dec}}\), while forwarding any \({\text {Enc}},{\text {RevAtt}},{\text {RevMsg}}\) queries to \(\varTheta \). Throughout this section, for simplicity of notation, we will denote \(\varGamma = \varGamma _{\mathsf {V},\mathsf {F},p}\) to be the oracle satisfying \(t(n) \le p(n) - \omega (n)\).
Remark 2
For simplicity of exposition, we assume that the compiler only asks the oracle for queries from \(\varGamma _n\). However, our argument directly extends to handle arbitrary calls to the oracle \(\varGamma \) using the following standard technique. As we will show, the “error” in our poly-query compiler in the ideal model will be at most \({\text {poly}}(q)/2^n\) (where \(q={\text {poly}}(\mathrm {\kappa })\) is a fixed polynomial over the security parameter \(\mathrm {\kappa }\) of the IO construction) when we only call \(\varGamma _n\). It is also the case that this error adds up when we work with several input lengths \(n_1,n_2,\dots \), but it is still bounded by union bound. Therefore, the total error of the transformation will be at most \(O({\text {poly}}(n_1)/2^{n_1})\) where \(n_1\) is the smallest integer for which \(\varGamma _{n_1}\) is queried at some point. To make \(n_1\) large enough (to keep the error small enough) we can modify all the parties to query \(\varGamma \) on all oracle queries up to input parameter \(n_1=c (\log (\mathrm {\kappa }))\) for sufficiently large c. (Note that this will be a polynomial number of queres in total.)

The new obfuscator \(\varvec{\widehat{O}^\varTheta }\) in the instance-revealing witness encryption model. Given a \(\delta \)-approximate obfuscator \(O = (\mathrm {iO},\mathrm {Ev})\) in the rFWE oracle model, we construct an \((\delta + \varepsilon )\)-approximate obfuscator \(\widehat{O} = (\widehat{\mathrm {iO}}, \widehat{\mathrm {Ev}})\) in the \(\varTheta \) oracle model. Throughout this process, we can assume that \(\mathrm {iO}\) and \(\mathrm {Ev}\) are in their canonical form as in Definition 18.
Subroutine \(\widehat{\mathrm {iO}}^\varTheta (C)\) :
-
1.
Emulation phase: Emulate \(\mathrm {iO}^{\varGamma }(C)\). Initialize \(Q_O = \varnothing \) to be the set of query-answer pairs asked by the obfuscation algorithm \(\mathrm {iO}\). For every query q asked by \(\mathrm {iO}^{\varGamma }(C)\), call \((\rho _q,W) \leftarrow \mathtt {EmulateCall}^\varTheta (Q_O,q)\) and add \(\rho _q\) to \(Q_O\).
-
2.
Learning phase: Set \(Q_B = \varnothing \) to be the set of direct (visible) query-answer pairs asked during this phase (so far) and \(Q^h_B = \varnothing \) to be the set of indirect (hidden) query-answer pairs (see Definition 20). Let \(k = (\ell _{O}+\mathrm {\kappa })/\varepsilon \) where \(\ell _{O} \le |\mathrm {iO}|\) represents the number of queries asked by \(\mathrm {iO}\). Choose \(\lambda \xleftarrow {\$} [k]\) uniformly at random then for \(i = \{1,...,\lambda \}\) do the following:
-
Choose \(z_i \xleftarrow {\$} \{0,1\}^{|C|}\) uniformly at random
-
Run \(\mathrm {Ev}^{\varGamma }(B,z_i)\). For every query q asked by \(\mathrm {Ev}^{\varGamma }(B,z_i)\), run \((\rho _q,W) \leftarrow \mathtt {EmulateCall}^\varTheta (Q_O \cup Q_B \cup Q^h_B,q)\), then add \(\rho _q\) to \(Q_B\) and W to \(Q^h_B\).
-
-
3.
The output of the \(\varTheta \)-model obfuscation algorithm \(\widehat{\mathrm {iO}}^\varTheta (C)\) will be \(\widehat{B} = (B,Q_B)\).
Subroutine \(\widehat{\mathrm {Ev}}^\varTheta (\widehat{B},z)\) : Initialize \(Q_{\widehat{B}} = \varnothing \) to be the set of queries asked when evaluating \(\widehat{B}\). To evaluate \(\widehat{B} = (B,Q_B)\) on a new random input z we simply emulate \(\mathrm {Ev}^\varGamma (B,z)\) as follows. For every query q asked by \(\mathrm {Ev}^\varGamma (B,z)\), run and set \((\rho _q,W) = \mathtt {EmulateCall}^\varTheta (Q_B \cup Q_{\widehat{B}}, q)\) then add \((\rho _q \cup W)\) to \(Q_{\widehat{B}}\).
The running time of \(\widehat{iO}\) . We note that the running time of the new obfuscator \(\widehat{iO}\) remains polynomial time since we are emulating the original obfuscation once followed by a polynomial number \(\lambda \) of learning iterations. Furthermore, since we are working with the restricted-monolithic oracle (see Definition 17), the way that \(\mathsf {F}\) is defined (as a universal circuit evaluator) makes it so that the number of recursive calls that appear due to emulating \(\mathsf {F}^\varGamma \) is upper-bounded by some polynomial (in fact even quadratic).
Proving Approximate Correctness. Define \(Q^h_{\widehat{B}}\) to be the set of hidden queries asked during the final execution phase. Set \(Q_T = Q_O\,\cup \,Q_B\,\cup \,Q^h_B \cup Q_{\widehat{B}}\,\cup \,Q^h_{\widehat{B}}\) to be the set of all (visible and hidden) query-answer pairs asked during all the phases. We consider two distinct experiments that construct the \(\varTheta \) oracle model obfuscator exactly as described above but differ when evaluating \(\widehat{B}\):
-
Real Experiment: \(\widehat{Ev}^\varTheta (\widehat{B},z)\) emulates \(\mathrm {Ev}^\varGamma (B,z)\) on a random input z and answers any queries using \(\mathtt {EmulateCall}\).
-
Ideal Experiment: \(\widehat{\mathrm {Ev}}^\varGamma (\widehat{B},z)\) executes \(\mathrm {Ev}^\varGamma (B,z)\) and answers all the queries of \(\mathrm {Ev}^\varGamma (B,z)\) using the actual oracle \(\varGamma \).
Note that the actual emulation of the new obfuscator is statistically close to an ideal emulation of the obfuscation and learning phases using \(\varGamma \) and so it suffices to compare only the real and ideal final execution phases. In essence, in the real experiment, we can think of the execution as \(\mathrm {Ev}^{\widehat{\varGamma }}(B,z)\) where \(\widehat{\varGamma }\) is the oracle simulated using the learned query-answer pairs \(Q_B\) and oracle \(\varTheta \). We will compare the real experiment with the ideal experiment and show that the statistical distance between these two executions is at most \(\varepsilon \). In order to achieve this, we will identify the events that make the executions \(\mathrm {Ev}^{\varGamma }(B,z)\) and \(\mathrm {Ev}^{\widehat{\varGamma }}(B,z)\) diverge (i.e. without them happening, they proceed statistically the same).
Let q be a new query that is being asked by \(\mathrm {Ev}^{\widehat{\varGamma }}(B,z)\) (i.e. in the real experiment) and handled using \(\mathtt {EmulateCall}^\varTheta (Q_B \cup Q_{\widehat{B}},q)\). The following are the cases that should be handled:
-
1.
If q is a query of type \({\text {Enc}}(x)\), then the answer to q will be distributed the same in both experiments as they will be both answered using the subroutine \({\text {WEnc}}(c)\) of \(\varTheta \).
-
2.
If q is a query of type \({\text {RevAtt}}(c)\), then the answer to q will be distributed the same in both experiments as they will be both answered using the subroutine \({\text {WRevAtt}}(c)\) of \(\varTheta \).
-
3.
If q is a query of type \({\text {RevMsg}}_\mathsf {V}(w_1,w_2,c)\), then the answer to q will be distributed the same in both experiments as they will be both answered using the subroutine \({\text {WDec}}_{\mathsf {V}'}(w',c)\) where \(w' = (w_1,w_2)\).
-
4.
If q is a query of type \({\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,c)\) whose answer is determined by \(Q_B \cup Q_{\widehat{B}}\) in the real experiment then it is also determined by \(Q_T \supseteq (Q_B \cup Q_{\widehat{B}})\) in the ideal experiment and the answers are therefore distributed the same.
-
5.
Suppose q is a query of type \({\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,c)\) that is not determined by \(Q_B \cup Q_{\widehat{B}}\) in the real experiment. Then the answer returned by \(\mathtt {EmulateCall}\) is \(\bot \) since the underlying encryption query \(((a,m) \mapsto c)_{{\text {Enc}}}\) is not known. In that case, we have to consider three different counterparts in the ideal experiment:
-
(a)
Bad Event 1: If q is not determined by \(Q_T\) in the ideal experiment then this implies that the ideal execution \(\mathrm {Ev}^{\varGamma }(B,z)\) is for the first time hitting a valid ciphertext that was never generated by an encryption query asked during any of the phases. In that case, since \({\text {Enc}}\) is injective, the answer returned by \(\varGamma \) would be \(\bot \) with overwhelming probability.
-
(b)
Bad Event 2: The query q is determined by \(Q_T \setminus (Q_B \cup Q_{\widehat{B}})\) in the ideal experiment and the ideal execution \(\mathrm {Ev}^{\varGamma }(B,z)\) has hit a valid unknown ciphertext that was generated by an encryption query in the obfuscation phase that was never learned. In this case, the answer will be \(\mathsf {F}^\varGamma (w,m)\) if the verification passes and \(\bot \) otherwise.
-
(c)
Bad Event 3: The query q is determined by \(Q_T \setminus (Q_B \cup Q_{\widehat{B}})\) in the ideal experiment then and the ideal execution \(\mathrm {Ev}^{\varGamma }(B,z)\) has hit a valid unknown ciphertext that was generated as a hidden query (i.e. issued by inner \(\mathsf {F}\) executions) during the learning or evaluation phases. In this case, the answer will be \(\mathsf {F}^\varGamma (w,m)\) if the verification passes and \(\bot \) otherwise.
Notice that the answer to such a query in the ideal experiment differs from that in the real experiment (which always outputs \(\bot \)). However, we will show below that such an event is unlikely to occur.
-
(a)
For circuit input z, let E(z) be the event that either one of Cases 5a, 5b, or 5c happen. More specifically, this is the event that \(\mathrm {Ev}^{\widehat{\varGamma }}(B,z)\) asks a query q of the form \({\text {Dec}}_{\mathsf {V},\mathsf {F}}(w,c)\) where c is a valid ciphertext that was either (i) never generated before during any of the phases, (ii) generated during the obfuscation phase, or (iii) generated by a hidden query in the learning and/or final evaluation phases. Assuming that event E(z) does not happen, both experiments will proceed identically the same and the output distributions of \(\mathrm {Ev}^{\varGamma }(B,z)\) and \(\mathrm {Ev}^{\widehat{\varGamma }}(B,z)\) will be statistically close. More formally, the probability of correctness for \(\widehat{iO}\) is:
By the approximate functionality of \(\mathrm {iO}\), we have that:
Therefore,
We are thus left to show that \(\Pr [E(z)] \le \varepsilon \). Since both experiments proceed the same up until E happens, the probability of E happening is the same in both worlds and we will thus choose to bound this bad event in the ideal world.
Proof Intuition. At a high-level, in order to show that E is unlikely, we will show that the learning procedure and final execution phases, when treated as a single non-uniform query-adaptive algorithm A, will only ask a bounded number of queries for valid ciphertexts whose corresponding underlying message is unknown to this algorithm. Then, given this upper bound on such queries, we ensure that by running the learning procedure for sufficient number of times, the final execution phase will not ask such queries to unknown ciphertexts with high probability and we maintain the approximate correctness of the obfuscation.
In order to prove this upper bound on the number of ciphertexts that will be hit, we start with the query-adaptive A which consists of the combination of the learning and final execution phases that accepts as input an obfuscation B in the \(\varGamma \) oracle model and is able to adaptively query \(\varGamma \) when running B on multiple randomly chosen inputs. We then show through a sequence of reductions to other adversaries that the advantage of such an attacker in hitting a specific number of unknown ciphertexts is upper bounded by the advantage of a different non-adaptive attacker \(\widehat{A}\) in hitting the same number of ciphertexts (up to some factor). We then finally show that \(\widehat{A}\) has a negligible advantage in succeeding.
We begin by defining the notion of query adaptivity for oracle algorithms and specify what it means for an adversary to hit a ciphertext.
Definition 22
(Query Adaptivity). Let A be a poly-query randomized oracle algorithm that asks \(\tau \) queries to some idealized oracle \({\mathcal I}\). Suppose Q is the set of queries that A will ask. We define the level of query adaptivity of A as being one of two possible levels:
-
Non-adaptive: Q consists of \(\tau \) queries, possibly from different domains, and chosen by A before it issues any query and/or independently of the answers of any previous query.
-
Fully adaptive: \(Q = (q_1,...,q_\tau )\) consists of \(\tau \) queries possibly from different domains where, for each \(i \in [\tau ]\), \(q_{i+1}\) is determined by the answer returned by \(q_i\).
Definition 23
(Ciphertext Hit). Let A be a \(\tau \)-query oracle algorithm that has access to \(\varGamma \). We say that A has hit a ciphertext c if it queries \({\text {Dec}}(.,c)\), \({\text {RevAtt}}(c)\), or \({\text {RevMsg}}(.,.,c)\) and c is a valid unknown ciphertext (that is, A has never asked \({\text {Enc}}(x) = c\)). We denote the set of ciphertexts that A has hit by \(H_A\).
Our goal is to prove the following lemma which provides the desired upper bound on the number of ciphertexts that an attacker A can hit.
Lemma 6
(Hitting Ciphertexts). Let \(\varGamma _{\mathsf {V},\mathsf {F}}\) be as in Definition 17, n be a fixed number, and \(t(n) \le p(n) - \omega (n)\), where t is the upper bound on the output length of \(\mathsf {F}\) and p is the ciphertext length. Let A be an adaptive \(\tau \)-query oracle algorithm that takes as input z and has access to \(\varGamma _{\mathsf {V},\mathsf {F}}\). Let \(H_A\) be the set of unknown valid ciphertexts that A hits. Then for security parameter (of the obfuscation scheme) \(\mathrm {\kappa }\), \(n \ge \lg \mathrm {\kappa }\), \(\tau \le {\text {poly}}(\mathrm {\kappa }) \le \mathrm {\kappa }^{O(1)}\) we have that for any \(s \le \tau \):
where \(\alpha = |z| + (t+2n)s\).
Proof
We will define a sequence of adversaries and show reductions between them in order to prove the upper bound stated above. Throughout, we assume that the algorithms are in canonical form (see Definition 18).
-
1.
Attacker A: This is the original adaptive \(\tau \)-query attacker as defined in the statement of the lemma where it will receive some input z and can ask \(\tau \) queries to \(\varGamma \). The goal of the adversary is to hit at least s unknown valid ciphertexts via queries to \({\text {Dec}},{\text {RevAtt}}\) or \({\text {RevMsg}}\).
-
2.
Attacker \(A_u\): This is the same attacker as A but does not accept any input and is modified as follows. For any \({\text {Dec}}, {\text {RevAtt}}\) or \({\text {RevMsg}}\) queries asked to \(\varGamma \) with some answer \(y \ne \bot \), \(A_u\) will instead use an answer that is part of some fixed string \(u \in \{0,1\}^\alpha \) hardcoded within \(A_u\) where \(\alpha = |z| + (t+2n)s\). The \({\text {Enc}}\) queries are handled normally as before. The goal of this adversary is to hit at least s unknown valid ciphertexts via queries to \({\text {Dec}},{\text {RevAtt}}\) or \({\text {RevMsg}}\).
-
3.
Attacker \(A'\): This is the same attacker as \(A_u\) for any fixed u. However, aside from \({\text {Enc}}\) queries which are handled normally using \(\varGamma \), the other query types are instead replaced with a single subroutine \({\text {Test}}\) that takes as input a ciphertext c and outputs 1 if c is valid, and 0 otherwise. The goal of this adversary is to hit at least s unknown valid ciphertexts via queries to \({\text {Test}}\).
-
4.
Attacker \(\widehat{A}\): This is the non-adaptive attacker where it will ask all its queries at once at the start of the experiment. Furthermore, it will not ask any \({\text {Enc}}\) queries but will be constrained to asking only \({\text {Test}}\) queries. The goal of this adversary is to hit at least s unknown valid ciphertexts via queries to \({\text {Test}}\).
Lemma 7
For every A, there exists some \(u \in \{0,1\}^\alpha \) such that \(\Pr [\left| H_A\right| \ge s] \le 2^\alpha \Pr [\left| H_{A_u}\right| \ge s]\)
Proof
Recall that A accepts z as input and, when it hits s ciphertexts, it would receive back at most \((t+2n)\) since we can either get back t bits information as a result of getting back an answer from \({\text {Dec}}_{\mathsf {V},\mathsf {F}}\) or at most n bits of information from queries of \({\text {RevAtt}}\) and \({\text {RevMsg}}_{\mathsf {V}}\). Furthermore, by the canonicalization of A, it can ask for any c at most one query of each type \({\text {Dec}}_{\mathsf {V},\mathsf {F}}\), \({\text {RevAtt}}\), and \({\text {RevMsg}}_\mathsf {V}\). Thus, in order to say that \(A_u\) would succeed at hitting s with the same amount of information, the length of u has to be \(\alpha = |z| + (t+2n)s\). Now, by a union bound over all u, the probability of success for A is given as follows:
Lemma 8
For any \(u \in \{0,1\}^\alpha \), \(\Pr [\left| H_{A_u}\right| \ge s] = \Pr [\left| H_{A'}\right| \ge s]\)
Proof
Since \(A_u\) does not obtain any information regarding the actual answers to the \({\text {Dec}},{\text {RevAtt}}\) and \({\text {RevMsg}}\) queries that it asks, we can think of these subroutines simply as a testing procedure that \(A_u\) can use to determine whether any given ciphertext c is valid or not, and this is signaled by whether the oracle returns \(\bot \) or not to any of these queries. Therefore, we can interpret \(A_u\) as an adversary \(A'\) that simply calls \({\text {Test}}\) instead of \({\text {Dec}},{\text {RevAtt}}\) and \({\text {RevMsg}}\) queries as this yields the same result.
Lemma 9
\(\Pr [\left| H_{A'}\right| \ge s] \le \Pr [\left| H_{\widehat{A}}\right| \ge s]\)
Proof
Given attacker \(A'\) we can define \(\widehat{A}\) that uses \(A'\) and only issues \({\text {Test}}\) queries (non-adaptively). Any \({\text {Enc}}\) queries that \(A'\) asks (from a specific \({\text {Enc}}\) domain of size n) can be lazily evaluated (emulated) by \(\widehat{A}\). Furthermore, any \({\text {Test}}\) queries that \(A'\) asks will be answered using one of \(\widehat{A}\)’s pre-issued \({\text {Test}}\) queries while remaining consistent with the previous \({\text {Enc}}\) queries that were issued.
Lastly, we state and prove the following lemma which will be used to bound the number of ciphertexts that any (poly-query) non-adaptive algorithm might obtain and use for its decryption and/or reveal queries.
Lemma 10
(Hitting Ciphertexts for Non-Adaptive Learners). Let \(\varGamma \) be as in Definition 16 and \(t(n) \le p(n) - \omega (n)\) where t is an upper bound on the output length of \(\mathsf {F}\) and p is the ciphertext length. Let \(\widehat{A}\) be a non-adaptive \(\tau \)-query canonical algorithm as defined above and \(H_{\widehat{A}}\) be the set of unknown valid ciphertexts that \(\widehat{A}\) hits via \({\text {Test}}\) queries. Then for security parameter \(\mathrm {\kappa }\), fixed \(n \ge \lg \mathrm {\kappa }\), \(\tau \le {\text {poly}}(\mathrm {\kappa })\), we have that for any \(s \le \tau \):
Proof
Suppose \(t \le p - dn\) for \(d = \omega (1)\) and let \(\tau \le \mathrm {\kappa }^{d'} = 2^{d'\lg \mathrm {\kappa }} \le 2^{d'n}\) where \(d' = d/2 = \omega (1)\) for the purposes of upper-bounding the probability for all poly-query algorithms \(\widehat{A}\). Recall that the function \({\text {Enc}}(.)\) is injective and maps messages \(x \in \{0,1\}^n\) to ciphertexts \(c \in \{0,1\}^{p(n)}\). For simplicity, assume that we want to compute the probability that \(|H_{\widehat{A}}| = s\). For any set of s ciphertexts that are in the image of some fixed s-sized set of the domain \({\text {Enc}}(.)\), the probability that the \(\tau \) queries will hit these s ciphertexts is given by \({\tau \atopwithdelims ()s}/{2^{p} \atopwithdelims ()s}\). By a union bound over all the different s-sized sub-domains of \({\text {Enc}}(.)\), we find that for sufficiently large security parameter \(\mathrm {\kappa }\):
The last inequality follows from the short-output property, that is \(t \le p - d\cdot n\) for some \(d = \omega (1)\). Note that \(\Pr [|H_{\widehat{A}}| = s+1] \le \Pr [|H_{\widehat{A}}| = s]\) and therefore \(\Pr [|H_{\widehat{A}}| \ge s]\) is dominated by the largest term represented by \(\Pr [|H_{\widehat{A}}| = s]\).
Putting things together. By Lemmas 7, 8, and 9, and using Lemma 10, we find that:
Note that, for simplicity, Lemma 6 only considers hitting unknown ciphertexts from some fixed domain of size n. However, we observe that this argument can be extended for learners that can ask queries for different domain sizes as well.
Lemma 11
\(\Pr [E(x)] \le \varepsilon + {\text {negl}}(\mathrm {\kappa })\)
Proof
Let A to be an adaptive non-uniform oracle algorithm in the ideal hybrid that has access to \(\varGamma \) and works as follows:
-
Initialize the query-answer set \(Q_A = \varnothing \)
-
For \(i = \{1,...,k\}\), run \(\mathrm {Ev}^\varGamma (B,z_i)\). For any query q asked by \(\mathrm {Ev}^\varGamma (B,z_i)\), if \((q \mapsto a)_{T} \in Q_A\) for subroutine T then answer with a. Otherwise, handle the query in the canonical form as in Definition 18, and if a query was sent to \(\varGamma \), add the new query-answer pair \((q \mapsto a)_{T}\) to \(Q_A\).
-
Output \(\mathrm {Ev}^\varGamma (B,z_k)\)
In essence, A would run the learning and final execution phases (in total k executions) making sure to only forward to \(\varGamma \) the queries that are distinct and which cannot be computed from \(Q_A\) so far. Given the above canonical A, we observe that for any unknown valid ciphertext \(c = {\text {Enc}}(x)\) where \(x = (a,m)\), A would ask at most one query of the form \({\text {RevAtt}}(c)\), at most one query of the form \({\text {Dec}}(w,c)\) for which \(\mathsf {V}^{{\text {Enc}}}(w,a) = 1\), and at most one query of the form \({\text {RevMsg}}(w_1,w_2,c)\) for which \(\mathsf {V}^{{\text {Enc}}}(w_i,a) = 1\) where \(i \in \{1,2\}\). Furthermore, A would never ask a query if \(\mathsf {V}^{{\text {Enc}}}(w,a) = 0\) since this condition can be verified independently by A and the answer can be simulated as it would invariably be \(\bot \).
Given A, we can bound the number of distinct unknown ciphertexts that the k executions will hit, which we denote by \(|H_B| = \left| \bigcup _{i=1}^k H_{B_i}\right| \) where \(H_{B_i}\) is the set of ciphertexts hit by the ith evaluation \(\mathrm {Ev}^\varGamma (B,z_i)\). Note that the total number of queries that will be asked across all executions is \(k\ell _B = {\text {poly}}(\mathrm {\kappa })\) where \(\ell _B\) is the circuit size of \(\mathrm {Ev}(B,.)\). It is straightforward to see that, for any s, \(\Pr [|H_A| \ge s] = \Pr [|H_B| \ge s]\) since whenever one of the k executions hits an unknown ciphertext c for this first time, A will also forward it to the oracle and hit it for the first time as well.
Since A accepts as input the obfuscated circuit of size \(|iO| = \ell _O\), by Lemma 6, the probability that A hits at least \(s = (\ell _O + \mathrm {\kappa })\) ciphertexts is at most \(2^{\ell _O - \omega (n)s} \le 2^{-\omega (n)\mathrm {\kappa }} = {\text {negl}}(\mathrm {\kappa })\). Therefore, the \(k\ell _B\)-query algorithm A will hit at most \(s = (\ell _O + \mathrm {\kappa })\) new unknown ciphertexts with overwhelming probability. Therefore we have that,
Since the maximum possible number of learning iterations \(k > s\) and \(\bigcup _{j=1}^i H_{B_j} \subseteq \bigcup _{j=1}^{i+1} H_{B_j}\) for any i, the number of learning iterations that increase the size of the set \(H_B\) of unknown ciphertext hits (via one of the bad event queries) is at most s. A ciphertext that was hit could have its encryption query generated during the obfuscation phase or as one of the hidden queries issued by \(\mathsf {F}\) during one of the k executions. We say \(\lambda \xleftarrow {\$} [k]\) is bad if it is the case that \(\bigcup _{j=1}^\lambda H_{B_j} \subseteq \bigcup _{j=1}^{\lambda +1} H_{B_j}\) (i.e. \(\lambda \) is an index of a learning iteration that increases the size of the hit ciphertexts). This would imply that after \(\lambda \) learning iterations in the ideal experiment, the final execution with \(H_{\widehat{B}} := \bigcup _{j=1}^{\lambda +1} H_{B_j}\) would contain an unknown ciphertext that it we will hit for this first time and for which we cannot consistently answer the queries that reference it. Thus, given that we have set \(k = (\ell _O + \mathrm {\kappa })/\varepsilon \), the probability (over the selection of \(\lambda \)) that \(\lambda \) is bad is at most \(s/k < \varepsilon \).
Proving Security. To show that the resulting obfuscator is secure, it suffices to show that the compilation process represented as the new obfuscator’s construction is simulatable. We show a simulator \(\mathsf {Sim}\) (with access to \(\varGamma \)) that works as follows: given an obfuscated circuit B in the \(\varGamma \) ideal model, it runs the learning procedure as shown in Step 2 of the new obfuscator \(\widehat{\mathrm {iO}}\) to learn the heavy queries \(Q_B\) then outputs \(\widehat{B} = (B,Q_B)\). Note that this distribution is statistically close to the output of the real execution of \(\widehat{\mathrm {iO}}\) and, therefore, security follows.
Notes
- 1.
Note that since statistically secure IO exists if \(\mathbf {P}=\mathbf {NP}\), therefore we need computational assumptions for proving lower bounds for assumptions implying IO.
- 2.
In fact, their separation is unconditional, while statistical IO can be built if \(\mathbf {P}=\mathbf {NP}\). So any separation for IO needs to rely on computational assumptions before proving \(\mathbf {P}\ne \mathbf {NP}\).
- 3.
In fact, as shown in [BCP14], without our customization, the original FWE implies, not just IO itself, but even di-IO.
- 4.
This is not true as the encryption is randomized, but allows us to explain the idea more easily.
- 5.
A couple of other weaker notions of compactness for FE have also been considered in the literature. However, all these notions are known to be monolithically equivalent to compact single-key FE. Therefore, we restrict our discussion just to compact single-key FE.
References
Applebaum, B., Brakerski, Z.: Obfuscating circuits via composite-order graded encoding. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 528–556. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_21
Apon, D., Döttling, N., Garg, S., Mukherjee, P.: Cryptanalysis of indistinguishability obfuscations of circuits over ggh13. Cryptology ePrint Archive, Report 2016/1003 (2016). http://eprint.iacr.org/2016/1003
Ananth, P.V., Gupta, D., Ishai, Y., Sahai, A.: Optimizing obfuscation: avoiding Barrington’s theorem. In: Ahn, G.-J., Yung, M., Li, N. (eds.) ACM CCS 2014: 21st Conference on Computer and Communications Security, Scottsdale, AZ, USA, 3–7 November 2014, pp. 646–658. ACM Press (2014)
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_15
Asharov, G., Segev, G.: Limits on the power of indistinguishability obfuscation and functional encryption. In: 2015 IEEE 56th Annual Symposium on Foundations of Computer Science (FOCS), pp. 191–209. IEEE (2015)
Ananth, P., Sahai, A.: Projective arithmetic functional encryption and indistinguishability obfuscation from degree-5 multilinear maps. Cryptology ePrint Archive, Report 2016/1097 (2016). http://eprint.iacr.org/2016/1097
Brakerski, Z., Brzuska, C., Fleischhacker, N.: On statistically secure obfuscation with approximate correctness. Cryptology ePrint Archive, Report 2016/226 (2016). http://eprint.iacr.org/
Boyle, E., Chung, K.-M., Pass, R.: On extractability obfuscation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 52–73. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_3
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S., Yang, K.: On the (im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_1
Barak, B., Garg, S., Kalai, Y.T., Paneth, O., Sahai, A.: Protecting obfuscation against algebraic attacks. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 221–238. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_13
Brakerski, Z., Katz, J., Segev, G., Yerukhimovich, A.: Limits on the power of zero-knowledge proofs in cryptographic constructions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 559–578. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_34
Bitansky, N., Lin, H., Paneth, O.: On removing graded encodings from functional encryption. Cryptology ePrint Archive, Report 2016/962 (2016). http://eprint.iacr.org/2016/962
Badrinarayanan, S., Miles, E., Sahai, A., Zhandry, M.: Post-zeroizing obfuscation: new mathematical tools, and the case of evasive circuits. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 764–791. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_27
Bitansky, N., Nishimaki, R., Passelègue, A., Wichs, D.: From cryptomania to obfustopia through secret-key functional encryption. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 391–418. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_15
Bitansky, N., Paneth, O., Rosen, A.: On the cryptographic hardness of finding a Nash equilibrium. In: Guruswami, V. (ed.) 56th Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, 17–20 October 2015, pp. 1480–1498. IEEE Computer Society Press (2015)
Brakerski, Z., Rothblum, G.N.: Virtual black-box obfuscation for all circuits via generic graded encoding. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 1–25. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_1
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. In: Ostrovsky, R. (ed.) 52nd Annual Symposium on Foundations of Computer Science, Palm Springs, CA, USA, 22–25 October 2011, pp. 97–106, IEEE Computer Society Press (2011)
Brakerski, Z., Vaikuntanathan, V.: Fully homomorphic encryption from ring-LWE and security for key dependent messages. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 505–524. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_29
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: Guruswami, V. (ed.) 56th Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, 17–20 October 2015, pp. 171–190. IEEE Computer Society Press (2015)
Boneh, D., Zhandry, M.: Multiparty key exchange, efficient traitor tracing, and more from indistinguishability obfuscation. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 480–499. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_27
Coron, J.-S., Gentry, C., Halevi, S., Lepoint, T., Maji, H.K., Miles, E., Raykova, M., Sahai, A., Tibouchi, M.: Zeroizing without low-level zeroes: new MMAP attacks and their limitations. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 247–266. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_12
Chen, Y., Gentry, C., Halevi, S.: Cryptanalyses of candidate branching program obfuscators. Cryptology ePrint Archive, Report 2016/998 (2016). http://eprint.iacr.org/2016/998
Cheon, J.H., Han, K., Lee, C., Ryu, H., Stehlé, D.: Cryptanalysis of the multilinear map over the integers. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 3–12. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_1
Canetti, R., Kalai, Y.T., Paneth, O.: On obfuscation with random oracles. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 456–467. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_18
Coron, J.-S., Lee, M.S., Lepoint, T., Tibouchi, M.: Cryptanalysis of GGH15 multilinear maps. Cryptology ePrint Archive, Report 2015/1037 (2015). http://eprint.iacr.org/2015/1037
Coron, J.-S., Lee, M.S., Lepoint, T., Tibouchi, M.: Zeroizing attacks on indistinguishability obfuscation over clt13. Cryptology ePrint Archive, Report 2016/1011 (2016). http://eprint.iacr.org/2016/1011
Coron, J.-S., Lepoint, T., Tibouchi, M.: Practical multilinear maps over the integers. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 476–493. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_26
Dachman-Soled, D.: Towards non-black-box separations of public key encryption and one way function. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 169–191. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_7
Döttling, N., Garg, S., Gupta, D., Miao, P., Mukherjee, P.: Obfuscation from low noise multilinear maps. Cryptology ePrint Archive, Report 2016/599 (2016). http://eprint.iacr.org/2016/599
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: Mitzenmacher, M. (ed.) 41st Annual ACM Symposium on Theory of Computing, Bethesda, MD, USA, 31 May–2 June 2009, pp. 169–178. ACM Press (2009)
Garg, S., Gentry, C., Halevi, S.: Candidate multilinear maps from ideal lattices. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 1–17. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_1
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, 26–29 October 2013, pp. 40–49. IEEE Computer Society Press (2013)
Gentry, C., Gorbunov, S., Halevi, S.: Graph-induced multilinear maps from lattices. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 498–527. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_20
Garg, S., Gentry, C., Halevi, S., Raykova, M.: Two-round secure MPC from indistinguishability obfuscation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 74–94. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_4
Goldwasser, S., Kalai, Y.T.: On the impossibility of obfuscation with auxiliary input. In: 46th Annual Symposium on Foundations of Computer Science, Pittsburgh, PA, USA, 23–25 October 2005, pp. 553–562. IEEE Computer Society Press (2005)
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th Annual ACM Symposium on Theory of Computing, Palo Alto, CA, USA, 1–4 June 2013, pp. 555–564. ACM Press (2013)
Gentry, C., Lewko, A.B., Sahai, A., Waters, B.: Indistinguishability obfuscation from the multilinear subgroup elimination assumption. In: Guruswami, V. (ed.) 56th Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, 17–20 October 2015, pp. 151–170. IEEE Computer Society Press (2015)
Garg, S., Miles, E., Mukherjee, P., Sahai, A., Srinivasan, A., Zhandry, M.: Secure obfuscation in a weak multilinear map model. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 241–268. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_10
Garg, S., Mahmoody, M., Mohammed, A.: Lower bounds on obfuscation from all-or-nothing encryption primitives. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 661–695. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_22
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_5
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute based encryption for circuits. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th Annual ACM Symposium on Theory of Computing, Palo Alto, CA, USA, 1–4 June 2013, pp. 545–554. ACM Press (2013)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Predicate encryption for circuits from LWE. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 503–523. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_25
Gentry, C., Wichs, D.: Separating succinct non-interactive arguments from all falsifiable assumptions. In: Fortnow, L., Vadhan, S.P. (eds.) STOC. ACM (2011)
Hu, Y., Jia, H.: Cryptanalysis of GGH map. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 537–565. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_21
Impagliazzo, R., Rudich, S.: Limits on the provable consequences of one-way permutations. In: 21st Annual ACM Symposium on Theory of Computing, Seattle, WA, USA, 15–17 May 1989, pp. 44–61. ACM Press (1989)
Lin, H.: Indistinguishability obfuscation from constant-degree graded encoding schemes. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 28–57. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_2
Lin, H.: Indistinguishability obfuscation from ddh on 5-linear maps and locality-5 prgs. Cryptology ePrint Archive, Report 2016/1096 (2016). http://eprint.iacr.org/2016/1096
Lin, H., Tessaro, S.: Indistinguishability obfuscation from bilinear maps and block-wise local prgs. Cryptology ePrint Archive, Report 2017/250 (2017). http://eprint.iacr.org/2017/250
Lin, H., Vaikuntanathan, V.: Indistinguishability obfuscation from DDH-like assumptions on constant-degree graded encodings. In: Dinur, I. (ed.) 57th Annual Symposium on Foundations of Computer Science, New Brunswick, NJ, USA, 9–11 October 2016, pp. 11–20. IEEE Computer Society Press (2016)
Mahmoody, M., Mohammed, A., Nematihaji, S.: More on impossibility of virtual black-box obfuscation in idealized models. Cryptology ePrint Archive, Report 2015/632 (2015). http://eprint.iacr.org/
Mahmoody, M., Mohammed, A., Nematihaji, S., Pass, R., Shelat, A.: A note on black-box separations for indistinguishability obfuscation. Cryptology ePrint Archive, Report 2016/316 (2016). http://eprint.iacr.org/2016/316
Mahmoody, M., Mohammed, A., Nematihaji, S., Pass, R., Shelat, A.: Lower bounds on assumptions behind indistinguishability obfuscation. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 49–66. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_3
Miles, E., Sahai, A., Weiss, M.: Protecting obfuscation against arithmetic attacks. Cryptology ePrint Archive, Report 2014/878 (2014). http://eprint.iacr.org/2014/878
Miles, E., Sahai, A., Zhandry, M.: Annihilation attacks for multilinear maps: cryptanalysis of indistinguishability obfuscation over GGH13. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 629–658. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_22
Naor, M.: On cryptographic assumptions and challenges. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 96–109. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_6
Pass, R.: Limits of provable security from standard assumptions. In: Proceedings of the Forty-third Annual ACM Symposium on Theory of Computing, pp. 109–118. ACM (2011)
Pass, R., Shelat, A.: Impossibility of VBB obfuscation with ideal constant-degree graded encodings. Cryptology ePrint Archive, Report 2015/383 (2015). http://eprint.iacr.org/
Pass, R., Tseng, W.-L.D., Venkitasubramaniam, M.: Towards non-black-box lower bounds in cryptography. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 579–596. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_35
Reingold, O., Trevisan, L., Vadhan, S.: Notions of reducibility between cryptographic primitives. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 1–20. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_1
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: Shmoys, D.B. (ed.) 46th Annual ACM Symposium on Theory of Computing, New York, NY, USA, 31 May–June 3 2014, pp. 475–484. ACM Press (2014)
Zimmerman, J.: How to obfuscate programs directly. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 439–467. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_15
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Garg, S., Mahmoody, M., Mohammed, A. (2017). When Does Functional Encryption Imply Obfuscation?. In: Kalai, Y., Reyzin, L. (eds) Theory of Cryptography. TCC 2017. Lecture Notes in Computer Science(), vol 10677. Springer, Cham. https://doi.org/10.1007/978-3-319-70500-2_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-70500-2_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70499-9
Online ISBN: 978-3-319-70500-2
eBook Packages: Computer ScienceComputer Science (R0)