Abstract
We study the security of symmetric encryption schemes in settings with multiple users and realistic adversaries who can adaptively corrupt encryption keys. To avoid confinement to any particular definitional paradigm, we propose a general framework for multi-key security definitions. By appropriate settings of the parameters of the framework, we obtain multi-key variants of many of the existing single-key security notions.
This framework is instrumental in establishing our main results. We show that for all single-key secure encryption schemes satisfying a minimal key uniqueness assumption and almost any instantiation of our general multi-key security notion, any reasonable reduction from the multi-key game to a standard single-key game necessarily incurs a linear loss in the number of keys. We prove this result for all three classical single-key security notions capturing confidentiality, authenticity and the combined authenticated encryption notion.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
In theory, most symmetric and public key cryptosystems are considered by default in a single-key setting, yet in reality cryptographic ecosystems provide an abundance of keys—and hence targets—for an adversary to attack. Often one can construct a reduction that shows that single-key security implies multi-key security, but typically such a reduction is lossy: an adversary’s multi-key advantage is roughly bounded by the single-key advantage times the number of keys n in the ecosystem. The ramifications of such a loss can be debated [16], but undeniably in a concrete setting with perhaps \(2^{30}\) to \(2^{40}\) keys in circulation, an actual loss of 30 to 40 bits of security would be considerable. Therefore the natural question arises to what extent this loss in the reduction is inevitable.
This inevitable loss of reductions from multi-key to single-key has previously been addressed by Bellare et al. [6] when introducing multi-key security for public key schemes. Specifically, they provided a counterexample: namely a pathological encryption scheme that has a small chance (about \(\frac{1}{n}\), where n is a parameter) of leaking the key when used in a single-key environment. In a multi-key scenario, where there are n key pairs, insecurity of the scheme is amplified to the point where it becomes a constant. It follows that any generic reduction, i.e. a reduction that works for any scheme, from the multi-key to single-key security must lose a factor of about n. A similar example can be concocted for symmetric schemes to conclude that there cannot be a tight generic reduction from a multi-key game to a single-key game for symmetric encryption, i.e. a reduction that works for all encryption schemes, since the reduction will not be tight when instantiated by the pathological scheme. However, this does not rule out all reductions, since a tighter reduction could exist that exploits specific features of a certain class of (non-pathological) schemes.
Consider a setting with a security notion \({\mathsf {G}}\) for primitives (e.g. pseudorandomness for blockciphers), a security notion \({\mathsf {H}}\) for constructions (e.g. ciphertext integrity for authenticated encryption), and suppose we are given a specific construction \(C[\mathcal {E}]\) building on any instantiation \(\mathcal {E}\) of the primitive. A reduction \(\mathcal {R}\) would take adversary \(\mathcal {A}\) against the \({\mathsf {H}}\) property of the construction and turn it into one against the \({\mathsf {G}}\) property of the primitive. To be black-box, the reduction \(\mathcal {R}\) should not depend on \(\mathcal {A}\), but instead only use \(\mathcal {A}\)’s input/output behaviour. However, when considering black-box reductions, it turns out there are many shades of black. Baecher et al. [4] presented a taxonomy of black-box reductions; the shades of black emerge when considering whether \(\mathcal {R}\) may depend on the construction C and/or the primitive \(\mathcal {E}\) or not. A fully black-box (BBB) reduction works for all C and \(\mathcal {E}\), while partially black-box (NBN) reductions can depend on the specific choice of C and \(\mathcal {E}\).
The pathological encryption schemes used as counterexamples are by nature rather contrived and the one used by Bellare et al. is of dubious security even in the single-key setting [6]. The counterexamples suffice to rule out tight BBB reductions, but they do not rule out the existence of potentially large classes of encryption schemes—perhaps practical ones, or even all secure ones—for which a tight NBN reduction does exist. Clearly, such an NBN reduction could not be generic, but instead would have to exploit some feature of the specific primitive or construction under consideration. Even when the primitive is assumed ‘ideal’ as is common in symmetric cryptology, the relevant reductions typically still depend on the details of the construction at hand, and are therefore not fully (BBB) black-box. Concluding, for secure schemes the relation between single-key and multi-key security is still largely unsettled.
Our Contribution. Focusing on authenticated encryption (AE) schemes, we make two main contributions: a general multi-key security definition including corruptions and lower-bounds on the tightness of black-box (NBN) reductions from the multi-key security to the single-key security of AE schemes.
General Security Definition. The first complication we face is the choice of security notions. As we recall in more detail in Sect. 2.1, there are many different ways of defining single-key security for AE. For instance, confidentiality can be expressed in several (not necessarily equivalent) ways, including left-or-right indistinguishability (\({\mathsf {LRIND}}\)) and ciphertexts being indistinguishable from random strings (\(\mathsf {IND}\)). Moreover there are different ways of treating nonces; each defines a slightly different security notion.
When moving to a multi-key setting, the water becomes even more muddied, especially when considering adaptive corruptions as we do. Adaptive corruptions allow an adversary to learn some of the keys during the course of the multi-key game; it models the real-life circumstance that not all keys will remain secret and some will leak. In this setting, security can be formulated in (at least) two ways: firstly using a hidden bit \(b_i\) for each key \(K_i\), with the adversary having to guess the bit \(b_i\) for a key \(K_i\) that has not been corrupted; and secondly, using a single hidden bit b determining the ‘challenge’ oracles for all n keys (e.g. left or right, real or random) with the adversary having to guess this bit b, under the restriction that no single key gets both corrupted and challenged.
As we explain in the full version of the paper [31], these two approaches do not appear to be tightly equivalent to each other. Furthermore, notions that used to be equivalent in the single-key setting suddenly start drifting apart, something previously observed in the multi-instance setting [8]. Again, this creates a bit of a conundrum as to what is the ‘right’ multi-key security notion, where we want to avoid a situation where we show that a reduction loss targeting one security notion is inevitable, while leaving the door open for tight reductions targeting another.
To avoid having to make a choice, we instead provide a general definition for multi-key security game (Definition 7) that allows us to plug in the ‘flavour’ of AE security we desire, and of which the two approaches for dealing with corruptions in a multi-key setting are special cases.
Lower Bounds on the Loss for Simple Reductions. Roughly speaking, we show that for any member \({\mathsf {G}}^n\) of a large class of n-key security games that allow for adaptive corruptions and for most AE schemes \(C[\mathcal {E}]\) built on a single-key secure AE scheme \(\mathcal {E}\) (including \(C[\mathcal {E}] = \mathcal {E}\)), any black-box reduction from \({\mathsf {G}}^n\) for \(C[\mathcal {E}]\) to a standard single-key security game \({\mathsf {H}}^1\) for \(\mathcal {E}\) incurs a loss that is close to n. By ‘black-box’, we mean at least NBN: the reduction must be black-box with respect to the adversary against \({\mathsf {G}}^n\) but can depend on C and \(\mathcal {E}\).
A roadmap of our results, showing that some reductions between the security notions for authenticated encryption are necessarily lossy. A green arrow \(G \rightarrow G'\) indicates that there is a non-lossy reduction from \(G'\) to G (so security in the sense of G implies security in the sense of \(G'\)). A red arrow \(G \rightarrow G'\) indicates that all reductions from \(G'\) to G have a loss that is linear in n. Theorem 15 and Corollary 18 concern \({\mathsf {H}}^1 = {\mathsf {AE}}{-}\mathsf {PAS}_\mathcal {E}^{X,1}\); the other choices of \({\mathsf {H}}^1\) are treated in the full version of the paper [31]. (Color figure online)
Figure 1 shows both the logic of our approach and the overall results. The main idea is to first consider a very weak n-key security game, \({\mathsf {K}}^n\), and show that reductions from \({\mathsf {K}}^n\) to \({\mathsf {H}}^1\) are lossy. Then, for any n-key game \({\mathsf {G}}^n\) that tightly implies \({\mathsf {K}}^n\), the loss from \({\mathsf {G}}^n\) to \({\mathsf {H}}^1\) will have to match that from \({\mathsf {K}}^n\) to \({\mathsf {H}}^1\) (or a contradiction would appear when composing the reduction from \({\mathsf {K}}^n\) to \({\mathsf {G}}^n\) with that from \({\mathsf {G}}^n\) to \({\mathsf {H}}^1\)). Our weak security notion \({\mathsf {K}}^n\) is a 1-out-of-n key recovery game where the adversary first sees encryptions of fixed messages under all n keys, then corrupts all but one key and must try to guess the uncorrupted key. The choice for the three \({\mathsf {H}}^1\) notions \({\mathsf {AE}}{-}\mathsf {PAS}\), \(\mathsf {IND}{-}\mathsf {PAS}\), and \({\mathsf {CTI}}{-}{\mathsf {CPA}}\) is inspired by their ubiquity in current AE literature (the naming convention is clarified in Sect. 2.1).
To show for each choice of \({\mathsf {H}}^1\) that reductions from \({\mathsf {K}}^n\) for \(C[\mathcal {E}]\) to \({\mathsf {H}}^1\) for \(\mathcal {E}\) are lossy, we use three meta-reductions. Unlike using pathological schemes as counterexamples, meta-reductions can easily deal with NBN reductions that depend on the construction C and scheme \(\mathcal {E}\): a meta-reduction \(\mathcal {M}\) simulates an ideal adversary \(\mathcal {A}\) against \(C[\mathcal {E}]\) for a reduction \(\mathcal {R}\) and then uses \(\mathcal {R}\) to break \(\mathcal {E}\) [3, 14, 19]. Then one finds the inevitable loss factor of \(\mathcal {R}\) by bounding the advantage of \(\mathcal {M}\) (in its interaction with \(\mathcal {R}\)) by the advantage of the best possible adversary against \(\mathcal {E}\). We remark that this technique is vacuous for insecure schemes \(\mathcal {E}\) as the resulting bound on the advantage of \(\mathcal {M}\) is not meaningful.
More precisely, we show that for the three choices of \({\mathsf {H}}^1\), any black-box reduction running in time at most t from \({\mathsf {K}}^n\) for \(C[\mathcal {E}]\) to \({\mathsf {H}}^1\) for \(\mathcal {E}\) must lose \(\left( \frac{1}{n} + \epsilon \right) ^{-1}\), where \(\epsilon \) is essentially the maximum advantage in \({\mathsf {H}}^1\) of an adversary running in time \(n\cdot t\). These results hold provided that \(C[\mathcal {E}]\) is key-unique: given sufficient plaintext–ciphertext pairs the key is always uniquely determined. For almost all variants \({\mathsf {G}}^n\) of our general n-key security game, there is a tight reduction from \({\mathsf {K}}^n\) to \({\mathsf {G}}^n\) (Lemma 12); combining this tight reduction with the unavoidable loss from \({\mathsf {K}}^n\) to \({\mathsf {H}}^1\) shows that any black-box reduction from \({\mathsf {G}}^n\) to \({\mathsf {H}}^1\) is lossy.
In summary, we show that for almost any variant \({\mathsf {G}}^n\) of the general n-key security game and for \({\mathsf {H}}^1 \in \left\{ {\mathsf {AE}}{-}\mathsf {PAS}_\mathcal {E}^{X,1}, \mathsf {IND}{-}\mathsf {PAS}_\mathcal {E}^{X,1}, {\mathsf {CTI}}{-}{\mathsf {CPA}}_\mathcal {E}^{X,1}\right\} \), if \(\mathcal {E}\) is “secure” in the sense of \({\mathsf {H}}^1\) and \(C[\mathcal {E}]\) is key-unique, then any black-box reduction from \({\mathsf {G}}^n\) to \({\mathsf {H}}^1\) with a “reasonable” runtime loses approximately n.
Related Work. The idea of using a weak auxiliary security game to prove that reductions are lossy for more meaningful games was pioneered by Bader et al. for public key primitives [3]. Bader et al. considered as their \({\mathsf {H}}^1\) notion a non-interactive assumption, whereas our \({\mathsf {H}}^1\) games are highly interactive. The main obstacle here is that our meta-reduction needs to simulate an appropriate environment towards n copies of the reduction, while having access only to a single set of oracles for the considered single-key game. Thus we are forced to devise an additional mechanism that allows the meta-reduction to simulate responses to the oracle queries made by \(\mathcal {R}\) and prove that \(\mathcal {R}\) cannot distinguish this simulation from the real oracles in its game.
Multi-key security was first considered in the public key setting [6], extending the \({\mathsf {LRIND}}{-}{\mathsf {CCA}}\) notion to a single-bit multi-key setting without corruptions. A simple hybrid argument shows the loss of security is at most linear in the number of keys; furthermore this loss is inevitable as demonstrated by a counterexample. Relatedly, for many schemes a generic key recovery attack exists whose success probability is linear in both time and the number of keys n [10, 11, 22]. For schemes where this generic key recovery attack is actually the best attack (in both the single-key and n-key games), this shows that security in the n-key setting is indeed n times less than in the single-key setting. However, even for very secure schemes it is unlikely that key recovery is the optimum strategy for e.g. distinguishing genuine ciphertexts from random strings.
The danger of ignoring the loss in reductions between security notions is by now widely understood [15, 16] and has served as motivation for work on improved security analysis that avoid the loss of generic reductions. Recent results include multi-user security for Even–Mansour [34], AES-GCM with nonce randomisation [9], double encryption [26], and block ciphers [42].
Tightness is better understood in the public key setting than in the symmetric setting. There are, for instance, many constructions of (identity-based) public-key encryption [6, 13, 17, 24, 28], digital signatures [1, 12, 27, 32, 33, 40], key exchange protocols [2], as well as several different types of lower bounds and impossibility results [18, 21, 23, 29, 36]. We emphasise that, for signature schemes and public key encryption schemes, ‘tightly secure’ means that the reduction from the scheme to some complexity assumption does not incur a multiplicative loss equal to the number of signing or encryption queries.
There exist several other previous works describing meta-reductions from interactive problems, such as the one-more discrete logarithm (OMDL) problem [19, 23, 36, 41]. However, all these works have in common that they consider a significantly simpler setting, where the reduction is rewound a much smaller number of times (typically only once), and with only a single oracle (the discrete logarithm oracle).
2 Preliminaries
Notation. For any integer \(n \ge 1\) we use [n] to denote the set \(\{1, \dots , n\}\) and for any \(i \in [n]\) we use \([n \setminus i]\) to denote the set \([n] \setminus \{i\}\). For any finite set S we write  to indicate that x is drawn uniformly at random from S. In any security experiment, if an adversary \(\mathcal {A}\) has worst-case runtime t, then we say \(\mathcal {A}\) is a t-adversary. When \(\mathcal {A}\) is clear from the context, we write \(t_\mathcal {A}\) for its worst case runtime. Since our security notions are concrete, rather than asymptotic (as is standard for symmetric cryptography), we loosely use the term “secure” to mean that, for all reasonable values of t, the advantage of any t-adversary in the relevant security game is close to 0. Of course, what constitutes a “reasonable” runtime depends on the model of computation and is beyond the scope of this work.
to indicate that x is drawn uniformly at random from S. In any security experiment, if an adversary \(\mathcal {A}\) has worst-case runtime t, then we say \(\mathcal {A}\) is a t-adversary. When \(\mathcal {A}\) is clear from the context, we write \(t_\mathcal {A}\) for its worst case runtime. Since our security notions are concrete, rather than asymptotic (as is standard for symmetric cryptography), we loosely use the term “secure” to mean that, for all reasonable values of t, the advantage of any t-adversary in the relevant security game is close to 0. Of course, what constitutes a “reasonable” runtime depends on the model of computation and is beyond the scope of this work.
2.1 Authenticated Encryption
Syntax. Both the syntax and security definitions for symmetric and then authenticated encryption have evolved over the years. We will use the modern perspective where encryption is deterministic and takes in not just a key and a message, but also a nonce, which could be used to provide an explicit form of randomization. Our syntax is summarised in Definition 1 and is a simplification of that used for subtle authenticated encryption [5]. For simplicity, we omit any associated data, though our later results could be extended to that setting; moreover we are not interested in the ‘subtle’ aspect, where decryption might ‘leak’, e.g. unverified plaintext or multiple error symbols.
Definition 1
(Authenticated Encryption). An authenticated encryption scheme is a pair of deterministic algorithms \(\left( \mathcal {E}, \mathcal {D}\right) \) satisfying
where \(\mathsf {K}\), \({\mathsf {M}}\), \({\mathsf {N}}\) and \({\mathsf {C}}\) are subsets of \(\{0,1\}^*\) whose elements are called keys, messages, nonces and ciphertexts respectively. The unique failure symbol \(\bot \) indicates that C was not a valid encryption under the key K with nonce N.
As is customary, we abbreviate \(\mathcal {E}(K,N,M)\) by \(\mathcal {E}_K^N(M)\) and \(\mathcal {D}(K,N,C)\) by \(\mathcal {D}_K^N(C)\) and assume throughout that all authenticated encryption schemes satify, for all \(K \in \mathsf {K}, N \in {\mathsf {N}}, M \in {\mathsf {M}}\) and all \(C \in {\mathsf {C}}\), the following three properties:
-
1.
(correctness) \( \mathcal {D}_K^N\left( \mathcal {E}_K^N(M) \right) = M\),
-
2.
(tidiness) \(\mathcal {D}_K^N(C) \ne \bot \Rightarrow \mathcal {E}_K^N\left( \mathcal {D}_K^N(C) \right) = C\),
-
3.
(length-regularity) \(| \mathcal {E}_K^N(M) | = {\mathsf {enclen}}( | M | )\) for some fixed function \({\mathsf {enclen}}\).
Correctness and tidiness together imply that \(\mathcal {D}\) is uniquely determined by \(\mathcal {E}\), allowing us to refer to the pair \((\mathcal {E}, \mathcal {D})\) simply by \(\mathcal {E}\) [35].
Single-key Security Notions. An authenticated encryption scheme should provide both confidentiality and authenticity. When defining an adversary’s advantage, we separate these orthogonal properties by looking at the \(\mathsf {IND}{-}\mathsf {PAS}\) and \({\mathsf {CTI}}{-}{\mathsf {CPA}}\) security games, while also considering their combination \({\mathsf {AE}}{-}\mathsf {PAS}\) in a single game [38]. Below we discuss these notions in more detail, however we defer formal definitions of the relevant games and advantages to the next section, where they will be viewed as a special case of the multi-key games given in Definition 7 (cf. Remark 9).
The notions \(\mathsf {IND}{-}\mathsf {PAS}\), \({\mathsf {CTI}}{-}{\mathsf {CPA}}\) and \({\mathsf {AE}}{-}\mathsf {PAS}\) are commonly called \(\mathsf {IND{-}CPA}\), for indistinguishability under chosen plaintext attack; \(\mathsf {INT{-}CTXT}\), for integrity of ciphertexts; and \(\mathsf {AE}\), for authenticated encryption (respectively). However, we adhere to the \({\mathsf {GOAL}}{-}{\mathsf {POWER}}\) naming scheme [5]. It makes explicit that, in the first case, the adversary’s goal is to distinguish between real ciphertexts and random strings (\(\mathsf {IND}\), for indistinguishability) without access to any additional oracles (\(\mathsf {PAS}\), for passive); in the second case, the adversary’s goal is to forge a well-formed ciphertext (\({\mathsf {CTI}}\), for ciphertext integrity) and has access to an ‘always-real’ encryption oracle (\({\mathsf {CPA}}\), for chosen plaintext attack); and in the third case, the adversary tries to either distinguish real ciphertexts from random strings or forge a well-formed ciphertext (\({\mathsf {AE}}\), for authenticated encryption), without having access to any additional oracles (\(\mathsf {PAS}\)). For the notions above, we opted for minimal adversarial powers: it is often possible to trade queries to additional oracles (such as a true encryption oracle) for queries to the challenge oracle. We refer to Barwell et al. [5] for an overview of known relations between various notions.
Nonce Usage Convention. All three of the games above have variants according to how nonces may be used by the adversary in the game:
-
1.
In the IV-based setting, denoted \({\mathsf {IV}}\), the adversary is required to choose nonces uniformly at random for each encryption query.
-
2.
In the nonce-respecting setting, denoted \({\mathsf {NR}}\), the adversary chooses nonces adaptively for each encryption query, but may never use the same nonce in more than one encryption query.
-
3.
In the misuse-resistant setting, denoted \({\mathsf {MR}}\), the adversary chooses nonces adaptively for each encryption query and may use the same nonce in more than one encryption query.
Remark 2
The customary definition for IV-based security lets the game select the IVs [35]. We prefer the recent alternative [5] that provides the same interface across the various notions by restricting the class of valid adversaries in the IV-based setting to those who always provide uniformly random nonces in encryption queries. (Note that there is no need to check the distribution of nonces). This gives a subtly stronger notion, as a reduction will no longer be able to ‘program’ the IV, which it would be allowed to do in the classical definition (cf. [20, 30]).
The results in this paper hold with the alternative, customary formulation of IV-based encryption, with only cosmetic changes to the proof (to take into account the changed interface).
Different Confidentiality Goals. Above we captured the confidentiality goal \(\mathsf {IND}\) as distinguishing between real ciphertexts and random strings of the appropriate length. However, there are several competing notions to capture confidentiality, all captured by considering a different challenge encryption oracle:
-
In left-or-right indistinguishability (\({\mathsf {LRIND}}\)) the challenge oracle is \(\mathrm {LR}\); on input \((M_0, M_1, N)\), this oracle returns \(\mathcal {E}_K^N(M_b)\) (here b is the hidden bit that the adversary must try to learn).
-
In real-or-random indistinguishability the challenge oracle, on input (M, N), returns either \(\mathcal {E}_K^N(M)\) or \(\mathcal {E}_K^N(\$)\), where \(\$ \) is a random string of the same length as M.
-
In pseudorandom-injection indistinguishability the challenge oracle, on input (M, N), returns either \(\mathcal {E}_K^N(M)\) or \(\rho ^N(M)\), where \(\rho \) is a suitably sampled family of random injections [25, 38].
In the single-key setting, these four notions can be partitioned into two groups of two each, namely left-or-right and real-or-random on the one hand and \(\mathsf {IND}\) and pseudorandom-injection indistinguishability on the other. Within each group, the two notions can be considered equivalent, as an adversary against one can be turned into an adversary against the other with the same resources and a closely related advantage. Furthermore, security in the \(\mathsf {IND}\) setting trivially implies security in the \({\mathsf {LRIND}}\) setting, but not vice versa.
Summary. Thus, for each authenticated encryption scheme \(\mathcal {E}\), we potentially obtain \(5\times 4 = 20\) security games (see Fig. 2) and for each we need to consider three classes of adversary depending on nonce usage behaviour. However, for single-key security, we will concentrate on nine notions only, namely \({\mathsf {G}}^{X,1}_{\mathcal {E}}\), where
and where the 1 in the superscript indicates that these are single-key security games.
Remark 3
In this paper we use meta-reductions to analyse reductions from multi-key games to single-key games for authenticated encryption. We show that, for any AE scheme that is secure in a single-key sense, any reduction from the multi-key game to the single-key game is lossy. We do not need to consider equivalent single-key notions separately, as any scheme that is secure according to one notion will be secure according to the other, and one can convert between the single-key games without (significant) additional loss. From this perspective, we can leverage known equivalences as mentioned above. However, the set \(\{{\mathsf {AE}}{-}\mathsf {PAS}, \mathsf {IND}{-}\mathsf {PAS}, {\mathsf {CTI}}{-}{\mathsf {CPA}}\}\) does not provide a comprehensive set of meta-reduction results; for that we would have to consider for example \({\mathsf {LRIND}}{-}\mathsf {PAS}\) and \(\mathsf {IND}{-}{\mathsf {CCA}}\) as well (the full set would contain eight games). Nevertheless, our results capture the single-key notions that are most commonly used.
The oracles available to the adversary for each \({\mathsf {GOAL}}{-}{\mathsf {POWER}}\) security notion. Formal definitions of each oracle are given in Fig. 4. (Many thanks to Guy Barwell for providing this diagram.)
2.2 Black-Box Reductions
Informally, a reduction \(\mathcal {R}\) is an algorithm that transforms an adversary \(\mathcal {A}\) in some security game \({\mathsf {G}}\) into an adversary \(\mathcal {R}(\mathcal {A})\) in a different security game \({\mathsf {G}}'\). One hopes that, if the advantage \(\mathsf {Adv}^{\mathsf {G}}(\mathcal {A})\) of \(\mathcal {A}\) in \({\mathsf {G}}\) is high, then the advantage \(\mathsf {Adv}^{{\mathsf {G}}'}(\mathcal {R}(\mathcal {A}))\) is also high. Here \(\mathcal {R}\) breaks some scheme \(\mathcal {E}\), given an adversary \(\mathcal {A}\) that breaks a construction \(C[\mathcal {E}]\) that uses \(\mathcal {E}\). The construction C is typically fixed, so the reduction \(\mathcal {R}\) may depend on it (though to unclutter notation we leave this dependency implicit). On the contrary, when discussing the reduction \(\mathcal {R}\), \(\mathcal {E}\) is crucially quantified over some class of schemes \({\mathcal {C}}\).
Three properties of a reduction \(\mathcal {R}\) are usually of interest: how the resources, specifically run-time, of the resulting adversary \(\mathcal {R}(\mathcal {A})\) relate to those of \(\mathcal {A}\); how the reduction translates the success of \(\mathcal {A}\) to that of \(\mathcal {R}(\mathcal {A})\); and how ‘lossy’ this translation is, i.e. how \(\mathsf {Adv}^{{\mathsf {G}}'}(\mathcal {R}(\mathcal {A}))\) compares to \(\mathsf {Adv}^{\mathsf {G}}(\mathcal {A})\). The overall picture for a reduction, especially its loss, strongly depends on the class \({\mathcal {C}}\) of schemes considered.
Formally, we take into account both the translation \(\mathbb {S}\) and the relation \(\mathbb {T}\) in runtime into account by considering the quotient of \(\mathcal {A}\) and \(\mathcal {R}(\mathcal {A})\)’s work factors, themselves defined as the quotient of time over success probability (cf. [3]).
Definition 4
We say that \(\mathcal {R}\) is a \((\mathbb {S},\mathbb {T})\) reduction from \({\mathsf {G}}\) to \({\mathsf {G}}'\) if for every \(t_A\)-adversary \(\mathcal {A}\) against \({\mathsf {G}}\), \(\mathcal {R}_\mathcal {A}\) is an \(\mathbb {T}(t_\mathcal {A})\)-adversary against \({\mathsf {G}}'\) and \(\mathsf {Adv}^{{\mathsf {G}}'}(\mathcal {R}(\mathcal {A}))=\mathbb {S}(\mathsf {Adv}^{{\mathsf {G}}}(\mathcal {A}))\). Furthermore, the tightness of a reduction \(\mathcal {R}\) relative to the class of schemes \({\mathcal {C}}\) is defined as
where the supremum is taken over all schemes \(\mathcal {E}\) in \({\mathcal {C}}\) and all (valid) adversaries \(\mathcal {A}\) against \(\mathcal {E}\).
Remark 5
Our quantification over valid adversaries only is inspired by the AE literature’s reliance on only considering adversaries satisfying certain behaviour (e.g. to avoid trivial wins, or distinguish between \({\mathsf {IV}}\), \({\mathsf {NR}}\), and \({\mathsf {MR}}\) settings). In all cases, one can recast to a security game that incorporates checks and balances to deal with arbitrary adversarial behaviour. This recasting is without loss of generality as an adversary in this more general game will be ‘aware’ that it is making a ‘bad’ query and this bad behaviour does not influence the state of the game (cf. [7]). Of course, when determining \(\mathbb {S}\) we do need to take into account whether the reduction \(\mathcal {R}\) preserves validity.
In this paper we are concerned with simple, black-box reductions: these are reductions that have only black-box access to adversary \(\mathcal {A}\), and that run \(\mathcal {A}\) precisely once (without rewinding). For a \((\mathbb {S},\mathbb {T})\) simple reduction \(\mathcal {R}\) we have that \(\mathbb {T}(t_\mathcal {A})=t_\mathcal {A}+t_\mathcal {R}\), where \(t_\mathcal {R}\) is the time taken for whatever additional work \(\mathcal {R}\) does. Henceforth, we write \(t_\mathcal {R}\) for this quantity, whenever \(\mathcal {R}\) is a simple reduction.
These reductions compose in the obvious way: if \(\mathcal {R}_1\) is a simple \((\mathbb {S}_1,\mathbb {T}_1)\) reduction from \({\mathsf {G}}_1\) to \({\mathsf {G}}_2\) and \(\mathcal {R}_2\) is a simple \((\mathbb {S}_2,\mathbb {T}_2)\) reduction from \({\mathsf {G}}_2\) to \({\mathsf {G}}_3\), then we can construct a simple \((\mathbb {S}_3,\mathbb {T}_3)\) reduction \(\mathcal {R}_3\) from \({\mathsf {G}}_1\) to \({\mathsf {G}}_3\), where \(\mathbb {S}_3(\epsilon )=\mathbb {S}_2(\mathbb {S}_1(\epsilon ))\) and \(\mathbb {T}_3(t)=\mathbb {T}_2(\mathbb {T}_1(t))\).
Bounding Tightness. Precisely evaluating the tightness of a reduction can be difficult, yet to show that for schemes in \({\mathcal {C}}\) any simple reduction \(\mathcal {R}\) loses at least some factor L, it suffices to show that for any \(\mathcal {R}\) there exists a scheme \(\mathcal {E}\in {\mathcal {C}}\) and a valid adversary \(\mathcal {A}\) such that
Indeed, the desired lower bound follows since, for simple reductions, \(\mathbb {T}(t_\mathcal {A})\ge t_A\).
We briefly discuss two distinct techniques to establish a bound such as the one above, in which the order of quantifiers is (\(\forall \mathcal {R}\exists \mathcal {E}\exists \mathcal {A}\)):
-
Counterexample ( \(\exists \mathcal {E}\forall \mathcal {A}\forall \mathcal {R}\) ). Here, one shows that there exists a scheme \(\mathcal {E}\in {\mathcal {C}}\) such that for any adversary \(\mathcal {A}\) and any reduction \(\mathcal {R}\), inequality 1 is satisfied. One drawback of such results is that they only imply the desired lowerbound for a class of schemes \({\mathcal {C}}\) containing \(\mathcal {E};\) tighter reductions might be possible in the class \({\mathcal {C}}':= {\mathcal {C}}\setminus \{\mathcal {E}\}\). Moreover, if the counterexample scheme \(\mathcal {E}\) is an artificially insecure scheme (e.g. the one used by Bellare et al. [6]), then the lowerbound might not hold within the class of secure schemes, which are obviously of greater significance in practice.
-
Meta-reduction Lowerbound ( \(\forall \mathcal {E}\exists \mathcal {A}\forall \mathcal {R}\) ). For any \(\mathcal {E}\in {\mathcal {C}}\), this technique constructs an idealised adversary \(\mathcal {A}\) with advantage 1 and then shows, via a meta-reduction simulating \(\mathcal {A}\), that any simple reduction interacting with \(\mathcal {A}\) must have advantage at most \(L^{-1}\), yielding inequality 1. Thus we show that the loss is a property of the reduction \(\mathcal {R}\), and not of the particular choice of \(\mathcal {E}\in {\mathcal {C}}\). The results in this paper, using the meta-reduction approach, hold when \({\mathcal {C}}\) is any non-empty subset of the class of secure schemes that satisfy the key uniqueness assumption. Since \({\mathcal {C}}\) could contain just one element \(\mathcal {E}\), our results show that even a reduction that is tailored to the specific details of \(\mathcal {E}\) cannot be tight. On the other hand, our results are not directly comparable to those of Bellare et al. [6], since the artificially insecure scheme used in their counterexample does not belong to any class \({\mathcal {C}}\) we consider here.
Remark 6
An alternative definition of tightness might consider only ‘reasonable’ adversaries \(\mathcal {A}\) in the supremum, namely those for which \(t_\mathcal {A}\) is not too large. Our meta-reduction approach would not work in this setting, since the idealised adversary \(\mathcal {A}\) we construct has an extremely large (and wholly unfeasible) runtime as it performs an exhaustive search over all possible keys. Nevertheless, reductions \(\mathcal {R}\) that are black-box with respect to \(\mathcal {A}\) have no way of ‘excluding’ such unrealistic adversaries and so we feel it is not reasonable to exclude them in the definition of tightness. We remark that unrealistic adversaries are not uncommon in the meta-reduction literature [3].
3 Multi-key Security Notions
Multi-key Security with Adaptive Corruptions. In the single-key case, the challenge oracles depend on a single hidden bit b and it is the job of the adversary to try and learn b. The straightforward generalization [6] to a multi-key setting (with n keys) is to enrich all the oracles to include the index \(i\in [n]\) of the key \(K_i\) that will then be used by the oracle. Thus the challenge oracles for distinct keys will all depend on the same single hidden bit b.
However, in a realistic multi-key setting, an adversary might well learn some of the keys. For instance, consider the situation where an attacker passively monitors millions of TLS connections and adaptively implants malware on particular endpoint devices in order to recover the session keys for those devices. We still want security for those keys that have not been compromised; the question is how to appropriately model multi-key security.
There are two natural approaches to model multi-key security games in the presence of an adaptive corruption oracle \(\mathrm {Cor}\) that, on input \(i \in [n]\), returns the key \(K_i\). The approaches differ in how they avoid trivial wins that occur when the adversary corrupts a key that was used for a challenge query. In one approach, the same bit is used for the challenge queries throughout, but the adversary is prohibited from using the same index i for both a corruption and challenge query (cf. [37]). In another approach, for each index i there is an independent hidden bit \(b_i\) to guess and the adversary has to specify for which uncorrupted index its guess \(b'\) is intended (cf. [8]).
As far as we are aware, these two approaches have not been formally compared; moreover we could not easily establish a tight relationship between them. However, as we show, both options lead to a reduction loss linear in n. To do so, we will use a novel way of formalizing a multi-key security game with adaptive corruptions that encompasses both options mentioned above.
In our generalised game (Definition 7) there are n independently, uniformly sampled random bits \(b_1, \dots , b_n\). Each challenge query from the adversary must specify two indices, \(i,j \in [n]\), such that the response to the query depends on key \(K_i\) and hidden bit \(b_j\). The two ‘natural’ multi-key games are special cases of this general game: in the single-bit game the adversary is restricted to challenge queries with \(j=1\), whereas in the multi-bit game only challenge queries with \(i=j\) are allowed.
Our impossibility results hold regardless how the hidden bits are used: we only require that for any \(i \in [n]\) there exists some \(j \in [n]\) such that the adversary can make a challenge query corresponding to \(K_i\) and \(b_j\). In other words, our impossibility results hold provided that the adversary can win the game by ‘attacking’ any of the n keys in the game, not just some subset of the keys.
Definition 7
(Security of AE). Let \({\mathsf {GOAL}}\in \{{\mathsf {AE}}, {\mathsf {LRAE}}, \mathsf {IND}, {\mathsf {LRIND}}, {\mathsf {CTI}}\}\), \({\mathsf {POWER}}\in \left\{ {\mathsf {CCA}}, {\mathsf {CPA}}, \mathsf {CDA}, \mathsf {PAS}\right\} \), \(X \in \{{\mathsf {IV}}, {\mathsf {NR}}, {\mathsf {MR}}\}\) and \(n \ge 1\). Then for any authenticated encryption scheme \(\mathcal {E}\) and adversary \(\mathcal {A}\), the advantage of \(\mathcal {A}\) against \(\mathcal {E}\) with respect to \({\mathsf {GOAL}}{-}{\mathsf {POWER}}^{X,n}\) is defined as
where the experiment \({\mathsf {GOAL}}{-}{\mathsf {POWER}}^{X,n}_{\mathcal {E}}(\mathcal {A})\) is defined in Fig. 3, with the oracles’ behaviour shown in Fig. 4 and their \({\mathsf {GOAL}}{-}{\mathsf {POWER}}\)-dependent availability in Fig. 2 (all games have access to \(\mathrm {Cor}\)).
Whenever the experiment \({\mathsf {G}}={\mathsf {GOAL}}{-}{\mathsf {POWER}}^{X,n}_{\mathcal {E}}(\mathcal {A})\) is clear from the context, we write \(\mathsf {Adv}^{{\mathsf {G}}}(\mathcal {A})\) for the advantage of \(\mathcal {A}\) in experiment \({\mathsf {G}}\).
The \({\mathsf {GOAL}}{-}{\mathsf {POWER}}^{X,n}_{\mathcal {E}}\) games, where \(X \in \{{\mathsf {IV}}, {\mathsf {NR}}, {\mathsf {MR}}\}\), \(n \ge 1\), \({\mathsf {GOAL}}\in \{{\mathsf {AE}}, {\mathsf {LRAE}}, \mathsf {IND}, {\mathsf {LRIND}}, {\mathsf {CTI}}\}\) and \({\mathsf {POWER}}\in \{{\mathsf {CCA}}, {\mathsf {CPA}}, \mathsf {CDA}, \mathsf {PAS}\}\). The oracles \(\mathcal {O}\) available to the adversary always include the corruption oracle \(\mathrm {Cor}\); the other oracles depend on \({\mathsf {GOAL}}\) and \({\mathsf {POWER}}\), as indicated in Fig. 2.
Oracles for the \({\mathsf {GOAL}}{-}{\mathsf {POWER}}^{X,n}_\mathcal {E}\) security games. Without loss of generality, we assume that all oracles return  if the input arguments do not belong to the relevant sets. For example, the \(\mathcal {E}\) oracle will return
if the input arguments do not belong to the relevant sets. For example, the \(\mathcal {E}\) oracle will return  on any input (i, M, N) that is not a member of \([n] \times {\mathsf {M}}\times {\mathsf {N}}\).
on any input (i, M, N) that is not a member of \([n] \times {\mathsf {M}}\times {\mathsf {N}}\).
The outline games are deliberately kept simple, but are trivial to win: if \(\mathcal {A}\) corrupts a key \(K_i\) and then issues a challenge query corresponding to \(K_i\) and a hidden bit \(b_j\), then it is trivial for \(\mathcal {A}\) to compute \(b_j\) from the response to the query; successfully ‘guessing’ \(b_j\) does not represent a meaningful attack. In our formal syntax, we say j is compromised iff there is some \(i \in [n]\) such that \(\mathcal {A}\) has issued a query \(\mathrm {Cor}(i)\) and \(\mathcal {A}\) has also issued some challenge query of the form \(\mathrm {Enc}(i,j,-,-)\), \(\mathrm {LR}(i,j,-,-,-)\) or \(\mathrm {Dec}(i,j,-,-)\). We disallow such trivial wins.
Relatedly, we follow the AE literature in disallowing certain combinations of queries that lead to trivial wins (prohibited queries), or that are inconsistent with the nonce notion under consideration. Without loss of generality, we also disallow queries where the response from the oracle can be computed by the adversary directly without making the query, e.g. using correctness (pointless queries). The relevant—and standard—definitions are given in Combining the various restrictions leads to the notion of valid adversaries (cf. Remark 5), as summarised in Definition 8 below.
Definition 8
(Valid Adversaries). An adversary against \({\mathsf {GOAL}}{-}{\mathsf {POWER}}^{X,n}_{\mathcal {E}}\) is valid iff:
-
1.
it does not output \(\left( j, b'_j \right) \) where j was compromised;
-
2.
it does not make pointless or prohibited queries;
-
3.
it uses nonces correctly with respect to X.
Remark 9
(Recovering the Single-Key Security Notions). Setting \(n=1\) in Definition 7 yields formal definitions of the single-key security games for authenticated encryption, albeit with a more complicated interface than one is used to: the specification of i and j becomes redundant, as does the corruption oracle for valid adversaries. Indeed, to simplify notation in the case \(n=1\), we often omit i and j from the queries made, refer to the hidden bit \(b_1 \) as b, and only expect a simple guess \(b'\) by an adversary.
Relations Among Multi-key Notions. We discuss the relations between different single-user and multi-user security notions in the full version of the paper [31].
Key Recovery Notions. For our meta-reduction, we use an auxiliary, key recovery game \({\mathsf {KEYREC}}_\mathcal {E}^{\varvec{M},n}\) (Definition 10). Here there are n unknown keys and the adversary is provided with encryptions under each of the keys of the hard-coded (and hence known) messages \(\varvec{M} \in {\mathsf {M}}^l\), using known, yet random, nonces. Then the adversary provides an index \(i^* \in [n]\), learns the \(n-1\) keys \(\left( K_i\right) _{i \in [n \setminus i^*]}\) and tries to guess the uncorrupted key.
Definition 10
For any integers \(n,\ell \ge 1\), messages \(\varvec{M} = \left( M_1, \dots , M_\ell \right) \in {\mathsf {M}}^\ell \), AE scheme \(\mathcal {E}\) and any adversary \(\mathcal {A}= (\mathcal {A}_1, \mathcal {A}_2)\), the advantage of \(\mathcal {A}\) against \({\mathsf {KEYREC}}^{\varvec{M},n}_{\mathcal {E}}\) is defined as
where the experiment \({\mathsf {KEYREC}}^{\varvec{M},n}_{\mathcal {E}}(\mathcal {A})\) is given in Fig. 5.
Of course, it might be the case that it is impossible to win the key recovery game with certainty, since there could be more than one key that ‘matches’ the messages, nonces and ciphertexts. For our tightness results, we need to assume that there is some reasonably small l and some messages \(M_1, \dots , M_l\) such that the key recovery game corresponding to \(M_1, \dots , M_l\) can be won with certainty; we call this the key uniqueness property; its definition is below.
Definition 11
Let \(\mathcal {E}\) be an authenticated encryption scheme. Suppose there is some integer \(l \ge 1\) and certain messages \(M_1, \dots , M_l \in {\mathsf {M}}\) such that,for all keys \(K \in \mathsf {K}\) and all nonces \(N_1, \dots , N_l \in {\mathsf {N}}\),
Then we say \(\mathcal {E}\) is \(\varvec{M}\) -key-unique, where \(\varvec{M} = \left( M_1, \dots , M_l\right) \in {\mathsf {M}}^l\). This means that encryptions of \(M_1, \dots , M_l\) under the same key uniquely determine the key, regardless of the nonces used.
As mentioned above, \({\mathsf {KEYREC}}^{\varvec{M},n}_{\mathcal {E}}\) corresponds to a very weak notion of security. In the following Lemma, we prove that this weak notion of security is implied, with only a small loss, by many of the more reasonable n-key security notions given in Definition 7. For succinctness we present the reduction in a compact way, but split the analysis in different cases (depending on the adversary goal and on the requirements to respect uniqueness or not).
Lemma 12
Let \({\mathsf {GOAL}}\in \{{\mathsf {AE}}, {\mathsf {LRAE}}, \mathsf {IND}, {\mathsf {LRIND}}, {\mathsf {CTI}}\}\), \({\mathsf {POWER}}\in \{ {\mathsf {CCA}}, {\mathsf {CPA}}\}\) and suppose \(\mathcal {E}\) is \(\varvec{M}\)-key-unique. Then there exists an \((\mathbb {S},\mathbb {T})\) simple reduction from \({\mathsf {KEYREC}}_\mathcal {E}^{\varvec{M},n}\) to \({\mathsf {GOAL}}{-}{\mathsf {POWER}}_\mathcal {E}^{X,n}\) with \(\mathbb {T}(t_\mathcal {A})=t_\mathcal {A}+(l+m_{\mathsf {GOAL}})t_\mathcal {E}\) and \(\mathbb {S}(\epsilon _\mathcal {A})= \delta _X\cdot \delta _{\mathsf {GOAL}}\cdot \epsilon _\mathcal {A}\), where \(m_\mathsf {IND}= m \ge 1\), an arbitrary integer; \(m_{\mathsf {GOAL}}= 1\) if \({\mathsf {GOAL}}\ne \mathsf {IND}\); \(t_\mathcal {E}\) is a bound on the runtime of a single encryption with \(\mathcal {E}\);
and
Note that \(\delta _X\) and \(\delta _{\mathsf {GOAL}}\) are both close to 1: m can be set arbitrarily large and, for useful encryption schemes, the nonce space \({\mathsf {N}}\) is very large.
Remark 13
We are unable to show a corresponding result for \({\mathsf {POWER}}= \mathsf {CDA}\) or \({\mathsf {POWER}}= \mathsf {PAS}\). This is because we need the ‘always real’ encryption oracle \(\mathcal {E}\) to simulate the environment of \(\mathcal {A}\) in the key recovery game. As a consequence, looking forward, our lower bounds for tightness of simple reductions hold only for n-key games with such an oracle. Nevertheless, we feel it is natural to give the n-key adversary access to the \(\mathcal {E}\) oracle so that, for example, the adversary can use queries to this oracle to determine which keys to corrupt and which to challenge.
Proof
We construct \(\mathcal {R}_\mathcal {A}\) that runs the key recovery adversary \(\mathcal {A}\) to obtain the key used by the challenge oracle(s) and then uses it to guess the hidden bit \(b_1\). Therefore \(\mathcal {R}_\mathcal {A}\) will return \((1,b'_1)\) and wins if \(b'_1 = b_1\).
For each \(i \in [n]\) and \(j \in [l]\), \(\mathcal {R}_\mathcal {A}\) samples  and then queries the encryption oracle \(\mathcal {E}\) on input \(\left( i, M_j, N_{i,j}\right) \), receiving \(C_{i,j}\) (unless \(\mathcal {R}_\mathcal {A}\) has made this query before, since this is a pointless query, in which case it just sets \(C_{i,j}\) to be the response from the last time the query was made). Then \(\mathcal {R}_\mathcal {A}\) passes \(\left( C_{i,j}, N_{i,j}\right) _{i \in [n],j\in [l]}\) to the key recovery adversary \(\mathcal {A}\).
and then queries the encryption oracle \(\mathcal {E}\) on input \(\left( i, M_j, N_{i,j}\right) \), receiving \(C_{i,j}\) (unless \(\mathcal {R}_\mathcal {A}\) has made this query before, since this is a pointless query, in which case it just sets \(C_{i,j}\) to be the response from the last time the query was made). Then \(\mathcal {R}_\mathcal {A}\) passes \(\left( C_{i,j}, N_{i,j}\right) _{i \in [n],j\in [l]}\) to the key recovery adversary \(\mathcal {A}\).
When \(\mathcal {A}\) returns an index \(i^*\), \(\mathcal {R}_\mathcal {A}\) queries \(\mathrm {Cor}\) on each \(i \in [n \setminus i^*]\) and passes \(\left( K_i \right) _{i \in [n \setminus i^*]}\) to \(\mathcal {A}\).
When \(\mathcal {A}\) returns a key \(K^*\), \(\mathcal {R}_\mathcal {A}\) checks if \(\mathcal {E}_{K^*}^{N_{i^*,j}}(M_j) = C_{i^*,j}\) for each \(j \in [l]\). If not, then \(\mathcal {A}\) has been unsuccessful, so \(\mathcal {R}_\mathcal {A}\) samples a random bit  and returns \((1, b'_1)\). If the tests all succeed, then by \(\varvec{M}\)-key-uniqueness, \(K^* = K_{i^*}\). Then \(\mathcal {R}_\mathcal {A}\) does the following:
and returns \((1, b'_1)\). If the tests all succeed, then by \(\varvec{M}\)-key-uniqueness, \(K^* = K_{i^*}\). Then \(\mathcal {R}_\mathcal {A}\) does the following:
-
If \({\mathsf {GOAL}}= \mathsf {IND}\), for \(i=1,2,\ldots ,m\) (for some “large” m), \(\mathcal {R}_\mathcal {A}\) chooses random
 and
and  such that \(M_i^* \ne M_j\) for all \(j \in [l]\). Then \(\mathcal {R}_\mathcal {A}\) queries \(\mathrm {Enc}\) on input \(\left( i^*, 1, M_i^*, N_i^* \right) \), receiving \(C_i^*\). If for all \(i=1,2,\ldots ,m\) it holds that \(\mathcal {E}_{K^*}^{N_i^*}\left( M_i^*\right) = C^*\) then \(\mathcal {R}_\mathcal {A}\) returns \(\left( 1,0\right) \). Else, \(\mathcal {R}_\mathcal {A}\) returns \(\left( 1,1\right) \).
such that \(M_i^* \ne M_j\) for all \(j \in [l]\). Then \(\mathcal {R}_\mathcal {A}\) queries \(\mathrm {Enc}\) on input \(\left( i^*, 1, M_i^*, N_i^* \right) \), receiving \(C_i^*\). If for all \(i=1,2,\ldots ,m\) it holds that \(\mathcal {E}_{K^*}^{N_i^*}\left( M_i^*\right) = C^*\) then \(\mathcal {R}_\mathcal {A}\) returns \(\left( 1,0\right) \). Else, \(\mathcal {R}_\mathcal {A}\) returns \(\left( 1,1\right) \). -
If \({\mathsf {GOAL}}= {\mathsf {LRIND}}\), \(\mathcal {R}_\mathcal {A}\) chooses random
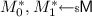 and
and 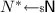 such that \(|M_0^*|=|M_1^*|\), \(M_0^* \ne M_j\) and \(M_1^* \ne M_j\) for all \(j \in [l]\). Then \(\mathcal {R}_\mathcal {A}\) queries \(\mathrm {LR}\) on input \(\left( i^*, 1, M_0^*, M_1^*, N^* \right) \), receiving \(C^*\). If \(\mathcal {E}_{K^*}^{N^*}\left( M_0^*\right) = C^*\), \(\mathcal {R}_\mathcal {A}\) returns \(\left( 1,0\right) \). Else, \(\mathcal {R}_\mathcal {A}\) returns \(\left( 1,1\right) \).
such that \(|M_0^*|=|M_1^*|\), \(M_0^* \ne M_j\) and \(M_1^* \ne M_j\) for all \(j \in [l]\). Then \(\mathcal {R}_\mathcal {A}\) queries \(\mathrm {LR}\) on input \(\left( i^*, 1, M_0^*, M_1^*, N^* \right) \), receiving \(C^*\). If \(\mathcal {E}_{K^*}^{N^*}\left( M_0^*\right) = C^*\), \(\mathcal {R}_\mathcal {A}\) returns \(\left( 1,0\right) \). Else, \(\mathcal {R}_\mathcal {A}\) returns \(\left( 1,1\right) \). -
If \({\mathsf {GOAL}}\in \{{\mathsf {AE}}, {\mathsf {LRAE}}, {\mathsf {CTI}}\}\), \(\mathcal {R}_\mathcal {A}\) chooses random
 and
and  such that \(M^* \ne M_j\) for all \(j \in [l]\). Then \(\mathcal {R}_\mathcal {A}\) computes \(C^* \leftarrow \mathcal {E}_{K^*}^{N^*}\left( M^*\right) \) and queries \(\mathrm {Dec}\) on input \(\left( i^*, 1, C^*, N^* \right) \), receiving M. If \(M \ne \bot \), \(\mathcal {R}_\mathcal {A}\) returns \(\left( 1,0\right) \). Else, \(\mathcal {R}_\mathcal {A}\) returns \(\left( 1,1\right) \).
such that \(M^* \ne M_j\) for all \(j \in [l]\). Then \(\mathcal {R}_\mathcal {A}\) computes \(C^* \leftarrow \mathcal {E}_{K^*}^{N^*}\left( M^*\right) \) and queries \(\mathrm {Dec}\) on input \(\left( i^*, 1, C^*, N^* \right) \), receiving M. If \(M \ne \bot \), \(\mathcal {R}_\mathcal {A}\) returns \(\left( 1,0\right) \). Else, \(\mathcal {R}_\mathcal {A}\) returns \(\left( 1,1\right) \).
For \({\mathsf {GOAL}}\in \{ {\mathsf {LRIND}},{\mathsf {AE}},{\mathsf {LRAE}},{\mathsf {CTI}}\}\), the adversary \(\mathcal {R}_\mathcal {A}\) returns (1, b) with \(b=b_1\) whenever the adversary \(\mathcal {A}\) against key recovery is successful.
For \({\mathsf {GOAL}}\in \{\mathsf {IND}\}\), the adversary \(\mathcal {R}_\mathcal {A}\) always returns the correct bit if \(b_1=1\). It also returns the correct bit \(b_1=0\), provided that the random ciphertexts \(\left( C_i^*\right) _{i \in [m]}\) that oracle \(\mathrm {Enc}\) returns do not all collide with the true ciphertexts \(\mathcal {E}_{K^*}^{N_i^*}(M_i^*)\). This collision event occurs with probability at most \(\frac{1}{2^m}\).
In other words, for \({\mathsf {GOAL}}\in \{\mathsf {IND}, {\mathsf {LRIND}},{\mathsf {AE}},{\mathsf {LRAE}},{\mathsf {CTI}}\}\), \(\mathcal {R}\) succeeds whenever \(\mathcal {A}\) succeds if \(b_1=0\), while, if \(b_1=1\), then \(\mathcal {R}\) succeeds with the same probability that \(\mathcal {A}\) succeds multiplied by \(\delta _{\mathsf {GOAL}}\), where \(\delta _{\mathsf {GOAL}}=1\) for \({\mathsf {GOAL}}\in \{{\mathsf {LRIND}},{\mathsf {AE}},{\mathsf {LRAE}},{\mathsf {CTI}}\}\) and \(\delta _{\mathsf {GOAL}}=\left( 1-\frac{1}{2^m}\right) \) for \({\mathsf {GOAL}}=\mathsf {IND}\).
Whenever \(\mathcal {A}\) does not recover \({\mathsf {K}}^*\), \(\mathcal {R}_\mathcal {A}\) guesses correctly with probability \(\frac{1}{2}\). Putting it all together we get the following:
from which we obtain
Ignoring the time taken for random sampling, the runtime of \(\mathcal {R}_\mathcal {A}\) is precisely the runtime of \(\mathcal {A}\), plus the time taken for additional encryptions using \(K^*\): if \({\mathsf {GOAL}}= \mathsf {IND}\), there are \(l+m\) additional encryptions and, if \({\mathsf {GOAL}}\ne \mathsf {IND}\), there are \(l+1\) additional encryptions. It follows that
where \(m_\mathsf {IND}= m\) and \(m_{\mathsf {GOAL}}= 1\) for \({\mathsf {GOAL}}\ne \mathsf {IND}\).
Moreover, \(\mathcal {R}_\mathcal {A}\), doesn’t compromise \(b_1\) and makes no pointless or prohibited queries: no queries are repeated, the messages used to generate the challenge queries do not appear in any of the previous encryption queries under key \(K_{i^*}\) and, in the \({\mathsf {LRIND}}\) case, the challenge messages are of equal length. It follows that \(\mathcal {R}_\mathcal {A}\) is a valid adversary against \({\mathsf {GOAL}}{-}{\mathsf {POWER}}^{X,n}_{\mathcal {E}}\) for \(X \in \{{\mathsf {IV}}, {\mathsf {MR}}\}\), since nonces are always chosen uniformly at random.
If \(X = {\mathsf {NR}}\), \(\mathcal {R}_\mathcal {A}\) might not be a valid adversary, since the randomly chosen nonces might accidentally collide. So we modify \(\mathcal {R}_\mathcal {A}\) to abort and output a random bit whenever there is a collision among the l randomly chosen nonces \(\left( N_{i,j} \right) _{j \in [l]}\) for each \(i \in [n \setminus i^*]\), or among the \(l+m_{\mathsf {GOAL}}\) randomly chosen nonces for encryptions under \(K_{i^*}\): the \(l\,+\,m\) nonces \(\left( N_{i^*,j} \right) _{j \in [l]}\) and \(\left( N^*_i\right) _{i \in [m]}\), if \({\mathsf {GOAL}}= \mathsf {IND}\), and the \(l+1\) nonces \(\left( N_{i^*,j} \right) _{j \in [l]}\) and \(N^*\), if \({\mathsf {GOAL}}\ne \mathsf {IND}\). Then \(\mathcal {R}_\mathcal {A}\) is a valid adversary and its advantage is \(\epsilon _\mathcal {A}\) multiplied by the probability that no such nonce collisions happen. By a simple union bound the probability of a collision among the l randomly chosen nonces \(\left( N_{i,j} \right) _{j \in [l]}\) is at most \(\frac{l(l-1)}{2|{\mathsf {N}}|}\) for each \(i \in [n \setminus i^*]\) and the probability of a collision among the \(l+m_{\mathsf {GOAL}}\) randomly chosen nonces for \(i^*\) is at most \(\frac{\left( l+m_{\mathsf {GOAL}}\right) \left( l+m_{\mathsf {GOAL}}-1\right) }{2|{\mathsf {N}}|}\). Thus the probability of a collision among the nonces for any of the n keys is at most
Thus the advantage of \(\mathcal {R}_\mathcal {A}\) is \(\epsilon _{\mathcal {R}_\mathcal {A}}\ge \delta _{{\mathsf {NR}}}\cdot \delta _{\mathsf {GOAL}}\cdot \epsilon _\mathcal {A}\), as desired. \(\square \)
Remark 14
In the proof, we assumed that the adversary is allowed to associate the bit \(b_1\) with any of the n keys \(K_1, \dots , K_n\). While this is permitted according to our definition of the \({\mathsf {GOAL}}{-}{\mathsf {POWER}}_\mathcal {E}^{n,X}\) game, in fact the result holds for more restrictive games: we only require that for all \(i \in [n]\) there exists some \(j \in [n]\) such that the adversary can associate the bit \(b_j\) with the key \(K_i\). In this case, \(\mathcal {R}_\mathcal {A}\) uses the recovered key \(K^*\) from \(\mathcal {A}\) to determine the value of any hidden bit \(b_j\) that can be associated with \(K_{i^*}\).
4 Multi-key to Single-Key Reductions Are Lossy
In this section we present our main results: any simple black-box reduction from multi-key security (in its many definitional variants) to single-key security loses a linear factor in the number of keys. Two remarks are in order. First, we show the lower bound for reductions from the security of an arbitrary construction of an (authenticated) encryption scheme \(C[\mathcal {E}]\) to that of \(\mathcal {E}\) (and in particular for the case where \(C[\mathcal {E}]=\mathcal {E}\)). This more general setting encompasses interesting cases, e.g. where \(C[\mathcal {E}]\) is double encryption with \(\mathcal {E}\), i.e.
which has been shown to have desirable multi-key properties [26]. Furthermore, showing the separation for \(C[\mathcal {E}]\) and \(\mathcal {E}\) also suggests how to circumvent the lower bound for the loss that we provide. Our lower bound requires that \(C[\mathcal {E}]\) satisfies key-uniqueness. It may therefore be possible to start from a secure single-key security that satisfies key-uniqueness, and show a tight reduction from multi-key security of a variant \(C[\mathcal {E}]\) of \(\mathcal {E}\), provided that \(C[\mathcal {E}]\) somehow avoids key uniqueness.
We consider separately reductions between different security flavours (authenticated encryption, privacy, integrity). For each case in turn, we proceed in two steps. First, we establish that if \(\mathcal {E}\) is a (single-key) secure encryption scheme and \(C[\mathcal {E}]\) is a key-unique encryption scheme, then all simple reductions from the multi-key key recovery game for \(C[\mathcal {E}]\) to the single-key security game for \(\mathcal {E}\) are lossy. Since by Lemma 12 there is a tight reduction from multi-key key recovery to multi-key security, it is an immediate corollary that there is no tight reduction from the multi-key security of \(C[\mathcal {E}]\) to the single-key security of \(\mathcal {E}\).
An interesting remark is that the bound on the inherent loss of simple reductions depends on the security of the scheme \(\mathcal {E}\): the more secure the scheme, the tighter the bound. While our bound is therefore not meaningful for insecure schemes, this case is of little interest in practice.
Authenticated Encryption. We give the formal results for the case of authenticated encryption below.
Theorem 15
Let \(\mathcal {E}\) and \(C[\mathcal {E}]\) be AE schemes such that \(C[\mathcal {E}]\) is \(\varvec{M}\)-key-unique for some \(\varvec{M} \in {\mathsf {M}}^l\). Then, for \(X \in \{ {\mathsf {IV}}, {\mathsf {NR}}, {\mathsf {MR}}\}\), any simple reduction \(\mathcal {R}\) from \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\) to \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\) loses at least \(\left( \frac{1}{n} + 2\epsilon \right) ^{-1}\), where \(\epsilon \) is the maximum advantage for a valid adversary against \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\) running in time at most \(nt_\mathcal {R}+ 2l(n-1)t_{C[\mathcal {E}]}\) (where \(t_{C[\mathcal {E}]}\) is an upper-bound on the runtime of a single encryption with \(C[\mathcal {E}]\)).
We sketch the proof before giving its details below. The crucial idea, following [3], is to construct a meta-reduction \(\mathcal {M}\) that rewinds the reduction \(\mathcal {R}\) in order to simulate its interaction with an ideal adversary \(\mathcal {A}\) against \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\). If the simulation works correctly, then the output of \(\mathcal {R}\) can be used by \(\mathcal {M}\) to win the \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\) game with probability \(\epsilon _\mathcal {R}\). Then the (single-key) security of \(\mathcal {E}\) yields an upper-bound on the success probability of \(\mathcal {M}\), i.e. an upper-bound on \(\epsilon _\mathcal {R}\).
We view \(\mathcal {R}\) as a collection of three algorithms, \(\mathcal {R}= \left( \mathcal {R}_1, \mathcal {R}_2, \mathcal {R}_3\right) \). The first, \(\mathcal {R}_1\), makes oracle queries in the \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\) game, then produces the ciphertexts and nonces that \(\mathcal {A}\) expects to receive in the \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\) game. The second, \(\mathcal {R}_2\), receives an index \(i^*\) from \(\mathcal {A}\) and the state \(st_1\) of the previous algorithm, \(\mathcal {R}_1\). Then \(\mathcal {R}_2\) makes oracle queries and eventually produces the vector of keys that \(\mathcal {A}\) expects to receive in the \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\) game. Finally, \(\mathcal {R}_3\) receives a guessed key \(K^*\) from \(\mathcal {A}\) and the state \(st_2\) of \(\mathcal {R}_2\). Then \(\mathcal {R}_3\) makes oracle queries and outputs a guessed bit \(b'\).
\(\mathcal {M}\) only rewinds \(\mathcal {R}_2\): \(\mathcal {M}\) executes \(\mathcal {R}_2\) on each of the n possible indices \(i^*\) that could be returned by \(\mathcal {A}\) and each \(\mathcal {R}_2\) then returns a set of keys. Then \(\mathcal {M}\) uses the keys returned by one execution of \(\mathcal {R}_2\) to construct the input to a different execution of \(\mathcal {R}_3\), i.e. \(st_2\) given to \(\mathcal {R}_3\) will not be from the same execution of \(\mathcal {R}_2\) used to construct the ‘guessed’ key \(K^*\).
The main obstacle in arguing that the above strategy works is that \(\mathcal {M}\) needs to break \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\), which is an interactive assumption. This is in contrast to the meta-reductions from [3], which are designed to violate a non-interactive complexity assumption. In our case, \(\mathcal {M}\) needs to simulate an appropriate environment towards multiple copies of \(\mathcal {R}\), each of which may make oracle queries, yet \(\mathcal {M}\) has access to a single set of oracles for the \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\) game. It is not obvious that \(\mathcal {M}\) can simply forward queries from all copies of \(\mathcal {R}\) to these oracles, since queries across different invocations of \(\mathcal {R}\) may interfere with one-another and render \(\mathcal {M}\) invalid. The key observation is that we can leverage the single-key security of \(\mathcal {E}\): instead of forwarding queries, \(\mathcal {M}\) simply simulates the \(\mathrm {Enc}\) and \(\mathrm {Dec}\) oracles by sampling random ciphertexts and returning \(\bot \), respectively. We argue, based on the security of \(\mathcal {E}\), that \(\mathcal {R}\) cannot distinguish this simulation from the real oracles in its game.
Proof
For ease of notation, let \(\mathsf {K}\), \({\mathsf {M}}\), \({\mathsf {N}}\) and \({\mathsf {C}}\) be the sets of keys, messages, nonces and ciphertexts, respectively, for the construction \(C[\mathcal {E}]\) (even though they may differ from the corresponding sets for \(\mathcal {E}\), but we shall not need to refer to those in the proof).
Consider the following (inefficient) adversary \(\mathcal {A}= \left( \mathcal {A}_1, \mathcal {A}_2 \right) \) in the game \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\). On input
\(\mathcal {A}_1\) first checks that each \(C_{i,j} \in {\mathsf {C}}\) and each \(N_{i,j} \in {\mathsf {N}}\). If this check fails, then \(\mathcal {A}_1\) aborts (by outputting a random index \(i^* \in [n]\) and recording an abort message in the state \(st_\mathcal {A}\) for \(\mathcal {A}_2\), triggering the latter to output \(\bot \)). If the check succeeds, then \(\mathcal {A}_1\) chooses \(i^* \in [n]\) uniformly at random, sets
and outputs \((i^*, st_\mathcal {A})\). On input \(\left( \left( K_i \right) _{i \in [n \setminus i^*]}, st_\mathcal {A}\right) \), \(\mathcal {A}_2\) checks that \(K_i\) is valid for each \(i \in [n \setminus i^*]\), that is:
-
1.
\(K_i \in \mathsf {K}\)
-
2.
For each \(j \in [l],\,C[\mathcal {E}]_{K_i}^{N_{i,j}} \left( M_j\right) = C_{i,j}\).
If this check fails, then \(\mathcal {A}_2\) outputs \(\bot \). If the check succeeds, then \(\mathcal {A}_2\) uses exhaustive search to find some \(K^* \in \mathsf {K}\) such that \(C[\mathcal {E}]_{K^*}^{N_{i^*,j}}\left( M_j\right) = C_{i^*,j}\) for each \(j \in [l]\). Since \(C[\mathcal {E}]\) is \(\varvec{M}\)-key-unique, either \(K^*\) exists and is unique, or the ciphertexts \(C_{i^*,j}\) were not all encryptions of the messages \(M_j\) with the nonces \(N_{i^*,j}\) under the same key. So if \(A_2\) does not find a \(K^*\) with this property, it outputs \(\bot \). Otherwise it outputs \(K^*\).
It is clear that the advantage of \(\mathcal {A}\) is \(\epsilon _\mathcal {A}= 1\) since, in the real \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\) game, all the checks performed by \(\mathcal {A}\) will succeed and \(K^*\) is uniquely defined.
We construct a meta-reduction \(\mathcal {M}\) that simulates the environment of \(\mathcal {R}\) in its interaction with this ideal adversary \(\mathcal {A}\). Then \(\mathcal {M}\) will use the output of \(\mathcal {R}\) to play the \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\) game. In what follows, we describe \(\mathcal {M}\) in detail. A diagram showing the overall structure of the interaction between \(\mathcal {M}\) and \(\mathcal {R}\) is given in Fig. 6.
An overview of the meta-reduction \(\mathcal {M}\), which rewinds a reduction \(\mathcal {R}= \left( \mathcal {R}_1, \mathcal {R}_2, \mathcal {R}_3\right) \). The inputs to each component of the reduction \(\mathcal {R}\) are shown in  , while the outputs are shown in
, while the outputs are shown in  . Some oracle queries from \(\mathcal {R}\) are
. Some oracle queries from \(\mathcal {R}\) are  to the oracles in the game played by \(\mathcal {M}\) and the responses sent back, while other oracle queries from \(\mathcal {R}\) are
to the oracles in the game played by \(\mathcal {M}\) and the responses sent back, while other oracle queries from \(\mathcal {R}\) are  by \(\mathcal {M}\). (Color figure online)
by \(\mathcal {M}\). (Color figure online)
First, \(K^*\) is initialised to \(\bot \). Then, \(\mathcal {M}\) uses its oracles to simulate the oracles used by \(\mathcal {R}_1\) by simply forwarding the queries from \(\mathcal {R}_1\) and the responses from the oracles, until \(\mathcal {R}_1\) returns
Then \(\mathcal {M}\) checks that each \(C_{i,j} \in {\mathsf {C}}\) and each \(N_{i,j} \in {\mathsf {N}}\). If this check fails, \(\mathcal {M}\) ‘aborts’ just as \(\mathcal {A}\) would. That is, \(\mathcal {M}\) runs \(\mathcal {R}_2\) on input \((i, st_1)\) for a random index \(i^* \in [n]\), forwarding oracle queries and responses, receives \(\left( \left( K_i\right) _{i \in \left[ n \setminus i^* \right] }, st_2\right) \) from \(\mathcal {R}_2\), runs \(\mathcal {R}_3\) on input \((\bot , st_2)\), receives a bit \(b'\) and outputs this in its game. If, on the other hand, the check succeeds, then \(\mathcal {M}\) chooses \(i^*\) uniformly at random from [n] and does the following for each \(i \in [n]\):
-
1.
\(\mathcal {M}\) runs \(\mathcal {R}_2\) on input \((i, st_1)\), which we call \(\mathcal {R}_2^i\) for ease of readability.
-
2.
When \(\mathcal {R}_2^i\) makes oracle queries:
-
(a)
If \(i = i^*\), \(\mathcal {M}\) uses its oracles to honestly answer all oracle queries; forwarding the queries to its oracles and then forwarding the replies to \(\mathcal {R}_2^{i^*}\).
-
(b)
If \(i \ne i^*\), \(\mathcal {M}\) simulates the ‘fake’ oracles, i.e. the oracles \(\mathrm {Enc}\) and \(\mathrm {Dec}\) in the case \(b=1\). Concretely, when \(\mathcal {R}_2^i\) makes an encryption query (M, N), \(\mathcal {M}\) samples
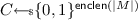 and returns this to \(\mathcal {R}_2^i\).Footnote 1 When \(\mathcal {R}_2^i\) makes a decryption query (C, N), \(\mathcal {M}\) returns \(\bot \) to \(\mathcal {R}_2^i\).
and returns this to \(\mathcal {R}_2^i\).Footnote 1 When \(\mathcal {R}_2^i\) makes a decryption query (C, N), \(\mathcal {M}\) returns \(\bot \) to \(\mathcal {R}_2^i\).
-
(a)
-
3.
When \(\mathcal {R}_2^i\) outputs \(\left( \left( K_r^i\right) _{r \in \left[ n \setminus i \right] }, st_2^i \right) \), if \(i \ne i^*\) then \(\mathcal {M}\) checks if \(K_{i^*}^i\) is valid, i.e.
-
(a)
\(K_{i^*}^i \in \mathsf {K}\),
-
(b)
For each \(j \in [l], C[\mathcal {E}]_{K_{i^*}^i}^{N_{i^*,j}} \left( M_j\right) = C_{i^*,j}\).
If \(K_{i^*}^i\) is valid, then \(K^* \leftarrow K_{i^*}^i\). By \(\varvec{M}\)-key-uniqueness, \(K_{i^*}^i\) is the only key with this property.
-
(a)
At the end of these runs of \(\mathcal {R}_2\), if \(\mathcal {R}_2^{i^*}\) did not provide a full set of valid keys, i.e. \(K_r^{i^*}\) is not valid for some \(r \in \left[ n \setminus i^*\right] \), then \(\mathcal {M}\) sets \(K^* \leftarrow \bot \) (mirroring the check performed by \(\mathcal {A}_2\)).
If \(\mathcal {R}_2^{i^*}\) did provide a full set of valid keys, but \(K^* = \bot \), (so none of the \(\mathcal {R}_2^i, i \ne i^*\) provided a valid key \(K_{i^*}^i\)), \(\mathcal {M}\) aborts the simulation and returns a random bit. We call this event \(\mathsf {BAD}\).
Otherwise, \(\mathcal {M}\) runs \(\mathcal {R}_3\) on input \(\left( K^*, st_2^{i^*}\right) \), forwarding oracle queries from \(\mathcal {R}_3\) to its oracles and sending back the responses.
When \(\mathcal {R}_3\) outputs a bit \(b'\), \(\mathcal {M}\) returns this bit in its game.
Now we consider the resources of \(\mathcal {M}\) and its advantage in the \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_\mathcal {E}\) game.
\(\mathcal {M}\) performs n runs of (part of) \(\mathcal {R}\) and carries out \(2(n-1)l\) encryptions with \(C[\mathcal {E}]\) (checking validity of \(K_{i^*}^i\) for each \(i \ne i^*\) and checking validity of \(K_r^{i^*}\) for each \(r \ne i^*\)), so if we ignore the time taken for random sampling and checking set membership, the runtime of \(\mathcal {M}\) is at most \(nt_\mathcal {R}+ 2l(n-1)t_{C[\mathcal {E}]}\). Moreover, \(\mathcal {M}\) makes at most \(q_\mathcal {R}\) oracle queries, since it only forwards the queries from \(\mathcal {R}_1\), \(\mathcal {R}_2^{i^*}\) and \(\mathcal {R}_3\).
Now consider the advantage \(\epsilon _\mathcal {M}\) of \(\mathcal {M}\) in \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\). From the definition of a simple reduction, \(\mathcal {R}\) must be a valid adversary in \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_\mathcal {E}\) whenever \(\mathcal {A}\) is a valid adversary in \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\). But all adversaries are automatically valid in \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\), so \(\mathcal {R}\) must always be a valid adversary against \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_\mathcal {E}\). Now the oracle queries \(\mathcal {M}\) makes are exactly the same queries as \(\left( \mathcal {R}_1, \mathcal {R}_2^{i^*}, \mathcal {R}_3\right) \) makes in the same game. Since \(\mathcal {R}\) is a valid adversary, this shows that \(\mathcal {M}\) does not make pointless or prohibited queries and uses nonces correctly with respect to X. Therefore \(\mathcal {M}\) is a valid adversary against \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_\mathcal {E}\) and so \(\epsilon _\mathcal {M}\le \epsilon \).
Note that for \(\mathcal {R}_1, \mathcal {R}_2^{i^*}\) and \(\mathcal {R}_3\), \(\mathcal {M}\) answers the oracle queries honestly with its own oracles. Therefore \(\mathcal {M}\) correctly simulates the view of \(\left( \mathcal {R}_1, \mathcal {R}_2^{i^*}, \mathcal {R}_3\right) \) in the game \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\). However, \(\mathcal {M}\) might not correctly simulate the responses from \(\mathcal {A}\). Indeed, to correctly simulate \(\mathcal {A}\), \(\mathcal {M}\) requires that some \(\mathcal {R}_2^i, i \ne i^*\) provides a valid key \(K_{i^*}^i\), but the oracle queries from \(\mathcal {R}_2^i, i \ne i^*\) are not handled honestly. The imperfect simulation of the view of \(\mathcal {R}_2^i\) might make it less likely to provide a valid key \(K_{i^*}^i\). We will therefore need to show that the change in behaviour of the \(\mathcal {R}_2^i\) due to the imperfect simulation is small. The intuition for this claim is that if \(\mathcal {R}_2^i\) could distinguish between the honest and the simulated oracles (having only received an index i from the key-recovery adversary \(\mathcal {A}\), not a key), then one can use \((\mathcal {R}_1, \mathcal {R}_2^i)\) directly, without \(\mathcal {A}\), to win the single-key game \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\).
Consider the three possible scenarios:
-
1.
\(\mathcal {R}_2^{i^*}\) did not provide a full set of valid keys.
-
2.
\(\mathcal {R}_2^{i^*}\) did provide a full set of valid keys and, for some \(i \ne i^*\), \(\mathcal {R}_2^i\) provided a valid key \(K_{i^*}^i\).
-
3.
\(\mathcal {R}_2^{i^*}\) did provide a full set of valid keys, but, for each \(i \ne i^*\), \(\mathcal {R}_2^i\) did not provide a valid key \(K_{i^*}^i\).
In the first case, both \(\mathcal {M}\) and \(\mathcal {A}\) submit \(\bot \) to \(\mathcal {R}_3\) as their ‘key’, so the simulation is correct. In the second case, both \(\mathcal {M}\) and \(\mathcal {A}\) submit a key \(K^*\) to \(\mathcal {R}_3\) that satisfies \(C[\mathcal {E}]_{K^*}^{N_{i^*,j}}(M_j) = C_{i^*,j}\) for all \(j \in [l]\), and \(K^*\) is the only key with this property by the \(\varvec{M}\)-key-uniqueness of \(C[\mathcal {E}]\). So the simulation is correct in this case too.
The third case is the event \(\mathsf {BAD}\) and is where the simulation fails. By construction \(\mathcal {M}\) aborts the simulation if \(\mathsf {BAD}\) occurs and outputs a random bit. Given that \(\mathsf {BAD}\) does not occur, the view of \(\left( \mathcal {R}_1, \mathcal {R}_2^{i^*}, \mathcal {R}_3\right) \) in its interaction with \(\mathcal {A}\) and the \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_\mathcal {E}\) oracles is identical to its view in its interaction with \(\mathcal {M}\) and \(\mathcal {M}\) returns the bit \(b'\) returned by \(\mathcal {R}_3\). This shows that
Write \(\mathsf {W}^X(\mathcal {M})\) (‘Win’) for the event \({\mathsf {AE}}{-}\mathsf {PAS}_\mathcal {E}^{X,1}(\mathcal {M})=1\). Then, as \(\mathcal {M}\) outputs a random bit if \(\mathsf {BAD}\) occurs, we have \(\mathrm {Pr}\left[ \mathsf {W}^{X}(\mathcal {M}) \mid \mathsf {BAD}\right] = \frac{1}{2}\) and it follows that:
Then,
It follows that:
To complete the proof we bound the probability of \(\mathsf {BAD}\) (see the next lemma) by \(\mathrm {Pr}\left[ \mathsf {BAD}\right] \le \frac{1}{n} + \epsilon \).
We therefore get that
So, \(\epsilon _\mathcal {R}\le (\frac{1}{n}+2\epsilon )\). Since \(\epsilon _\mathcal {A}=1\), we get that
as required to show that \(\mathcal {R}\) loses \(\left( \frac{1}{n} + 2\epsilon \right) ^{-1}\). \(\square \)
Lemma 16
Proof
Consider a meta-reduction \(\mathcal {M}'\) in the \({\mathsf {AE}}{-}\mathsf {PAS}_\mathcal {E}^{X,1}\) game that executes \(\mathcal {R}_1\) and each \(\mathcal {R}_2^i, i \in [n]\) exactly as \(\mathcal {M}\) does, but without treating \(\mathcal {R}_2^{i^*}\) differently. That is, encryption and decryption queries from \(\mathcal {R}_2^{i^*}\) are ‘faked’ in the same way as for the other \(\mathcal {R}_2^i, i \ne i^*\). Such an \(\mathcal {M}'\) could have chosen  after executing each \(\mathcal {R}_2^i\), simply by storing all the keys output by each \(\mathcal {R}_2^i\), and then, once \(i^*\) had been chosen, checking if \(\mathcal {R}_2^{i^*}\) returned a full set of valid keys and if each \(K_{i^*}^i\) was valid for \(i \ne i^*\).
after executing each \(\mathcal {R}_2^i\), simply by storing all the keys output by each \(\mathcal {R}_2^i\), and then, once \(i^*\) had been chosen, checking if \(\mathcal {R}_2^{i^*}\) returned a full set of valid keys and if each \(K_{i^*}^i\) was valid for \(i \ne i^*\).
Note that the probability of \(\mathsf {BAD}\) occuring for \(\mathcal {M}'\) does not depend on whether \(i^*\) was chosen at the start of executing the \(\mathcal {R}_2^i\), or at the end, since \(\mathcal {M}'\) runs each \(\mathcal {R}_2^i\) in the same way. Moreover, after executing each \(\mathcal {R}_2^i\), there can be at most one \(j \in [n]\) such that \(\mathcal {R}_2^j\) returned a full set of valid keys but for each \(i \ne j\), \(\mathcal {R}_2^i\) did not provide a full set of valid keys. Therefore there can be at most one \(j \in [n]\) such that \(\mathcal {R}_2^j\) returned a full set of valid keys but for each \(i \ne j\), \(\mathcal {R}_2^i\) did not provide a valid key \(K_{j}^i\). Since \(i^*\) was sampled uniformly from [n], the probability that \(i^*\) has the latter property, i.e. that \(\mathsf {BAD}\) occurs for \(\mathcal {M}'\), is at most \(\frac{1}{n}\).
Now we compare the probability that \(\mathsf {BAD}\) occurs for the two meta-reductions \(\mathcal {M}\) and \(\mathcal {M}'\). Let \(\mathsf {BAD}_\mathcal {M}= \mathsf {BAD}\) and let \(\mathsf {BAD}_{\mathcal {M}'}\) be the event that \(\mathsf {BAD}\) occurs in the game played by \(\mathcal {M}'\).
Consider the hidden bit b in the game played by \(\mathcal {M}\) and \(\mathcal {M}'\). If \(b=1\), then the views of \(\mathcal {R}_1\) and each \(\mathcal {R}_2^i\) are identically distributed in their interactions with \(\mathcal {M}\) and \(\mathcal {M}'\) (since \(\mathcal {R}_2^{i^*}\) receives ‘fake’ responses to its queries, regardless of whether the meta-reduction forwards them to its own oracles or simulates the responses.) It follows that \(\mathrm {Pr}\left[ \mathsf {BAD}_{\mathcal {M}'} \mid b=1 \right] = \mathrm {Pr}\left[ \mathsf {BAD}_{\mathcal {M}} \mid b=1 \right] .\)
Then
Now we construct an adversary \(\mathcal {B}\) that simulates the environment of \(\mathcal {R}_1\) and the \(\mathcal {R}_2^i\) in their interaction with either \(\mathcal {M}\) or \(\mathcal {M}'\), depending on the hidden bit \(b'\) in the game played by \(\mathcal {B}\). If \(\mathsf {BAD}\) occurs, \(\mathcal {B}\) will output 0. Otherwise \(\mathcal {B}\) will output 1.
Consider \(\mathcal {B}\) in the \({\mathsf {AE}}{-}{\mathsf {CCA}}_\mathcal {E}^{X,1}\) game. That is, \(\mathcal {B}\) has access to the usual challenge oracles \(\mathrm {Enc}\) and \(\mathrm {Dec}\), but can also query the ‘always real’ oracles \(\mathcal {E}\) and \(\mathcal {D}\) (provided it does not make pointless or prohibited queries). But if \(\mathcal {B}\) has significant advantage in this game, then there is another adversary, with the same resources as \(\mathcal {B}\), that has significant advantage against \({\mathsf {AE}}{-}\mathsf {PAS}_\mathcal {E}^{X,1}\):
Lemma 17
Suppose \(\mathcal {A}\) is a valid adversary against \({\mathsf {AE}}{-}{\mathsf {CCA}}_\mathcal {E}^{X,1}\), where \(X \in \{{\mathsf {IV}}, {\mathsf {NR}}, {\mathsf {MR}}\}\). Then
where \(\epsilon \) is the maximum advantage of a valid adversary against \({\mathsf {AE}}{-}\mathsf {PAS}_\mathcal {E}^{X,1}\) that runs in the same time as \(\mathcal {A}\) and makes the same number of oracle queries as \(\mathcal {A}\).
The proof of Lemma 17 is in the full version of the paper [31]. We remark that a similar statement can be easily derived by combining results from an existing work [5]. However, this approach only shows that the advantage in \({\mathsf {AE}}{-}{\mathsf {CCA}}_\mathcal {E}^{X,1}\) is at most four times the maximum advantage in \({\mathsf {AE}}{-}\mathsf {PAS}_\mathcal {E}^{X,1}\), whereas proving the statement directly gives a tighter bound.
Now we describe the adversary \(\mathcal {B}\) in the \({\mathsf {AE}}{-}{\mathsf {CCA}}_\mathcal {E}^{X,1}\) game. First, \(\mathcal {B}\) runs \(\mathcal {R}_1\), but all queries are forwarded to the genuine oracles \(\mathcal {E}\) and \(\mathcal {D}\). Then \(\mathcal {B}\) carries out the same checks as \(\mathcal {M}\) (or \(\mathcal {M}'\)) and, if the checks succeed, \(\mathcal {B}\) samples  and, for each \(i \in [n]\), \(\mathcal {B}\) runs \(\mathcal {R}_2\) on input \((i, st_1)\).
and, for each \(i \in [n]\), \(\mathcal {B}\) runs \(\mathcal {R}_2\) on input \((i, st_1)\).
When \(\mathcal {R}_2^i\) makes oracle queries:
-
1.
If \(i = i^*\), \(\mathcal {B}\) uses its challenge oracles \(\mathrm {Enc}\) and \(\mathrm {Dec}\) to honestly answer all oracle queries; forwarding the queries to its oracles and then forwarding the replies to \(\mathcal {R}_2^{i^*}\).
-
2.
If \(i \ne i^*\), \(\mathcal {B}\) simulates the ‘fake’ oracles, i.e. the oracles \(\mathrm {Enc}\) and \(\mathrm {Dec}\) with \(b=1\), just as \(\mathcal {M}\) (or \(\mathcal {M}'\)) does.
Finally, \(\mathcal {B}\) checks if \(\mathsf {BAD}\) has occured. If so \(\mathcal {B}\) outputs 0. Otherwise, \(\mathcal {B}\) outputs 1.
Let \(b'\) be the hidden bit in the game played by \(\mathcal {B}\). So the oracle queries from \(\mathcal {R}_1\) will always be ‘real’ (as they are for \(\mathcal {M}\) and \(\mathcal {M}'\), given that \(b=0\)), the oracle queries from \(\mathcal {R}_2^i\) for \(i \ne i^*\) will always be ‘fake’ (as they are for \(\mathcal {M}\) and \(\mathcal {M}'\)) and, depending on \(b'\), the oracle queries from \(\mathcal {R}_2^{i^*}\) will be real (like \(\mathcal {M}\), given that \(b=0\)), or fake (like \(\mathcal {M}'\)). It follows that \(\mathrm {Pr}\left[ 0 \leftarrow \mathcal {B}\mid b' = 0 \right] = \mathrm {Pr}\left[ \mathsf {BAD}_{\mathcal {M}} \mid b = 0 \right] \) and \(\mathrm {Pr}\left[ 0 \leftarrow \mathcal {B}\mid b' = 1 \right] = \mathrm {Pr}\left[ \mathsf {BAD}_{\mathcal {M}'} \mid b = 0 \right] \). Now,
and so
Like \(\mathcal {M}\) (or \(\mathcal {M}'\)), \(\mathcal {B}\) performs n runs of (part of) \(\mathcal {R}\) and carries out \(2(n-1)l\) encryptions to check if \(\mathsf {BAD}\) has occured. So the runtime of \(\mathcal {B}\) is at most \(nt_\mathcal {R}+ 2l(n-1)t_{C[\mathcal {E}]}\). Moreover \(\mathcal {B}\) makes at most \(q_\mathcal {R}\) oracle queries (only forwarding queries from \(\mathcal {R}_1\) and \(\mathcal {R}_2^{i^*}\)).
Consider \(\mathsf {Adv}_{\mathcal {E}}^{{\mathsf {AE}}{-}{\mathsf {CCA}},X,1}(\mathcal {B})\). Firstly, note that \(\mathcal {B}\) uses nonces correctly with respect to X, since any query to \(\mathrm {Enc}\) or \(\mathcal {E}\) is a query made to \(\mathrm {Enc}\) by \(\left( \mathcal {R}_1, \mathcal {R}_2^{i^*}, \mathcal {R}_3 \right) \) and \(\mathcal {R}\) is a valid adversary against \({\mathsf {AE}}{-}\mathsf {PAS}_\mathcal {E}^{X,1}\). Also, \(\mathcal {B}\) will not make pointless queries:
-
A repeated query to \(\mathcal {E}\) or \(\mathcal {D}\) by \(\mathcal {B}\) would be a repeated query to \(\mathrm {Enc}\) or \(\mathrm {Dec}\) from \(\mathcal {R}_1\), which is a pointless or prohibited query in the game played by \(\mathcal {R}\).
-
A repeated query to \(\mathrm {Dec}\) by \(\mathcal {B}\) would be a repeated query to \(\mathrm {Dec}\) from \(\mathcal {R}_2^{i^*}\), which is a pointless query in the game played by \(\mathcal {R}\).
-
A query \(\mathcal {D}(C,N)\) by \(\mathcal {B}\), where C was the response to a query \(\mathcal {E}(M,N)\), would be a query \(\mathrm {Dec}(C,N)\) from \(\mathcal {R}_1\), where C was the response to a query \(\mathrm {Enc}(M,N)\), which is a prohibited query in the game played by \(\mathcal {R}\).
-
A query \(\mathcal {E}(M,N)\) by \(\mathcal {B}\), where \(M \ne \bot \) was the response to a query \(\mathcal {D}(C,N)\), would be a query \(\mathrm {Enc}(M,N)\) from \(\mathcal {R}_1\), where \(M\ne \bot \) was the response to a query \(\mathrm {Dec}(C,N)\), which is a pointless query in the game played by \(\mathcal {R}\).
-
Finally, suppose \(\mathcal {B}\) makes a query \(\mathcal {E}(M,N)\) or \(\mathrm {Enc}(M,N)\), where \(M \ne \bot \) was the response to a query \(\mathrm {Dec}(C,N)\). The query \(\mathrm {Dec}(C,N)\) from \(\mathcal {B}\) would correspond to a query \(\mathrm {Dec}(C,N)\) from \(\mathcal {R}_2^{i^*}\) and so the subsequent encryption query would correspond to a query \(\mathrm {Enc}(M,N)\) from \(\mathcal {R}_2^{i^*}\). But as \(M \ne \bot \) this is a pointless query for \(\mathcal {R}\).
Moreover, \(\mathcal {B}\) will not make prohibited queries:
-
A repeated query to \(\mathrm {Enc}\) by \(\mathcal {B}\) would be a repeated query to \(\mathrm {Enc}\) from \(\mathcal {R}_2^{i^*}\), which is a prohibited query in the game played by \(\mathcal {R}\).
-
Suppose \(\mathcal {B}\) makes two queries of the form \(\mathrm {Enc}(M,N)\) and \(\mathcal {E}(M,N)\). Each of these queries would correspond to the same query \(\mathrm {Enc}(M,N)\) from \(\mathcal {R}\), which is prohibited in the game played by \(\mathcal {R}\).
-
A query \(\mathcal {D}(C,N)\) from \(\mathcal {B}\), where C was the response to a query \(\mathrm {Enc}(M,N)\), is impossible since \(\mathcal {B}\) only queries \(\mathrm {Enc}\) and \(\mathrm {Dec}\) after querying \(\mathcal {E}\) and \(\mathcal {D}\).
-
A query \(\mathrm {Dec}(C,N)\) from \(\mathcal {B}\), where C was the response to a query \(\mathcal {E}(M,N)\) or \(\mathrm {Enc}(M,N)\), would correspond to a query \(\mathrm {Dec}(C,N)\) from \(\mathcal {R}_2^{i^*}\), where C was the response to a query \(\mathrm {Enc}(M,N)\) from \(\mathcal {R}_1\) or \(\mathcal {R}_2^{i^*}\), which is a prohibited query in the game played by \(\mathcal {R}\).
-
A query \(\mathrm {Enc}(M,N)\) from \(\mathcal {B}\), where \(M\ne \bot \) was the response to a query \(\mathcal {D}(C,N)\), would correspond to a query \(\mathrm {Enc}(M,N)\) from \(\mathcal {R}_2^{i^*}\), where \(M\ne \bot \) was the response to a query \(\mathrm {Dec}(C,N)\) from \(\mathcal {R}_1\), which is a pointless query in the game played by \(\mathcal {R}\).
It follows that \(\mathcal {B}\) is a valid adversary against \(\mathsf {Adv}_{\mathcal {E}}^{{\mathsf {AE}}{-}{\mathsf {CCA}},X,1}(\mathcal {B})\). Then, by Lemma 17, we have
from which the result follows. \(\square \)
Theorem 15 establishes that reductions from \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\) to \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\) are lossy. By Lemma 12, there exists a tight reduction from \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\) to \({\mathsf {GOAL}}{-}{\mathsf {POWER}}_{C[\mathcal {E}]}^{X',n}\) (for \({\mathsf {POWER}}\in \{ {\mathsf {CCA}}, {\mathsf {CPA}}\}\)); it immediately follows that reductions from \({\mathsf {GOAL}}{-}{\mathsf {POWER}}_{C[\mathcal {E}]}^{X',n}\) to \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\) must be lossy (for \({\mathsf {POWER}}\in \{ {\mathsf {CCA}}, {\mathsf {CPA}}\}\)). We formalise this intuition in the following corollary:
Corollary 18
Let \(\mathcal {E}\) and \(C[\mathcal {E}]\) be AE schemes such that \(C[\mathcal {E}]\) is \(\varvec{M}\)-key-unique for some \(\varvec{M} \in {\mathsf {M}}^l\). Then for \({\mathsf {GOAL}}\in \{{\mathsf {AE}}, {\mathsf {LRAE}}, \mathsf {IND}, {\mathsf {LRIND}}, {\mathsf {CTI}}\}\), \({\mathsf {POWER}}\in \{ {\mathsf {CCA}}, {\mathsf {CPA}}\}\), \(X,X' \in \{{\mathsf {IV}},{\mathsf {NR}},{\mathsf {MR}}\}\) and \(n > 1\), all simple reductions from \({\mathsf {GOAL}}{-}{\mathsf {POWER}}_{C[\mathcal {E}]}^{X',n}\) to \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\) must lose
where \(\delta _{\mathsf {GOAL}}\) and \(\delta _{X'}\) are as in Lemma 12 and \(\epsilon \) is as given in Theorem 15.
We emphasise that the ‘nonce use’ parameters \(X',X \in \{{\mathsf {IV}}, {\mathsf {NR}}, {\mathsf {MR}}\}\) can differ between the n-key game and the single key game. While it is natural to consider \(X' = X\) we prefer to state the result in full generality and show that a very large class of reductions are necessarily lossy. Note that multi-key games for \({\mathsf {POWER}}\in \{ \mathsf {PAS}, \mathsf {CDA}\}\) are not known to be (tightly) equivalent to those where \({\mathsf {POWER}}\in \{ {\mathsf {CCA}}, {\mathsf {CPA}}\}\) (see the full version of the paper [31]). It therefore remains an open problem to obtain tightness lowerbounds for \({\mathsf {POWER}}\in \{ \mathsf {PAS}, \mathsf {CDA}\}\).
Proof
Recall from Lemma 12 the \((\mathbb {S},\mathbb {T})\)-simple reduction from \({\mathsf {KEYREC}}_\mathcal {E}^{\varvec{M},n}\) to \({\mathsf {GOAL}}{-}{\mathsf {POWER}}_\mathcal {E}^{X,n}\), where \(\mathbb {S}(\epsilon _\mathcal {A}) = \delta _X\cdot \delta _{\mathsf {GOAL}}\cdot \epsilon _\mathcal {A}\) and \(\mathbb {T}(t_\mathcal {A}) = t_\mathcal {A}+ (l+m_{\mathsf {GOAL}})t_\mathcal {E}\). Relabelling, we obtain a \((\mathbb {S}',\mathbb {T}')\)-simple reduction from \({\mathsf {KEYREC}}_{C[\mathcal {E}]}^{\varvec{M},n}\) to \({\mathsf {GOAL}}{-}{\mathsf {POWER}}_{C[\mathcal {E}]}^{X',n}\), where \(\mathbb {S}'(\epsilon _\mathcal {A}) = \delta _{X'}\cdot \delta _{\mathsf {GOAL}}\cdot \epsilon _\mathcal {A}\) and \(\mathbb {T}'(t_\mathcal {A}) = t_\mathcal {A}+ (l+m_{\mathsf {GOAL}})t_{C[\mathcal {E}]}\), which we call \(\mathcal {R}\).
We argue by contradiction. Suppose there is a simple reduction \(\mathcal {R}'\) from \({\mathsf {GOAL}}{-}{\mathsf {POWER}}_{C[\mathcal {E}]}^{X',n}\) to \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\) such that, for all valid adversaries \(\mathcal {B}\) against \({\mathsf {AE}}{-}\mathsf {PAS}^{X,n}_{\mathcal {E}}\), \(\epsilon _{\mathcal {R}'} > L^{-1} \epsilon _\mathcal {B}.\)
Then we can form a simple reduction \(\mathcal {R}''\) from \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\) to \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\): for any adversary \(\mathcal {A}\) against \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\), running \(\mathcal {R}\) with \(\mathcal {A}\) provides a valid adversary \(\mathcal {B}\) against \({\mathsf {GOAL}}{-}{\mathsf {POWER}}_{C[\mathcal {E}]}^{X',n}\) for \(\mathcal {R}'\) to turn into a valid adversary against \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\).
By construction, the advantage \(\epsilon _{\mathcal {R}''}\) of \(\mathcal {R}''\) is equal to the advantage of \(\mathcal {R}'\) with access to an adversary with advantage \(\epsilon _\mathcal {R}\), i.e. \(\epsilon _{\mathcal {R}''} > L^{-1} \epsilon _\mathcal {R}\). Since \(\epsilon _\mathcal {R}\ge \delta _{X'}\cdot \delta _{\mathsf {GOAL}}\cdot \epsilon _\mathcal {A}\) for all adversaries \(\mathcal {A}\) against \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\), we have
But this is a contradiction since, by Theorem 15, for any simple reduction \(\mathcal {R}''\) from \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\) to \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\), there exists an adversary \(\mathcal {A}\) against \({\mathsf {KEYREC}}^{\varvec{M},n}_{C[\mathcal {E}]}\) such that
Thus for any simple reduction \(\mathcal {R}'\) from \({\mathsf {GOAL}}{-}{\mathsf {POWER}}_{C[\mathcal {E}]}^{X',n}\) to \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\) there exists a valid adversary \(\mathcal {B}\) against \({\mathsf {GOAL}}{-}{\mathsf {POWER}}_{C[\mathcal {E}]}^{X',n}\) such that \(\epsilon _{\mathcal {R}'} \le L^{-1} \epsilon _\mathcal {B}\), i.e. \(\mathcal {R}'\) loses L. \(\square \)
Privacy and Integrity. The above results hold for notions of authenticated encryption schemes. It is natural to ask whether the loss for simple reductions from \({\mathsf {GOAL}}{-}{\mathsf {POWER}}^{X',n}_{C[\mathcal {E}]}\) to \({\mathsf {AE}}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\) is an artefact of considering the two orthogonal single-key security properties of secrecy and authenticity at the same time. Perhaps it is possible to circumvent the loss when looking at these properties separately, e.g. there could there be non-lossy simple reductions from \({\mathsf {GOAL}}{-}{\mathsf {POWER}}^{X',n}_{C[\mathcal {E}]}\) to \(\mathsf {IND}{-}\mathsf {PAS}^{X,1}_{\mathcal {E}}\) and from \({\mathsf {GOAL}}{-}{\mathsf {POWER}}^{X',n}_{C[\mathcal {E}]}\) to \({\mathsf {CTI}}{-}{\mathsf {CPA}}^{X,1}_{\mathcal {E}}\). We show that this is not the case.
We proceed as for the authenticated encryption case. For privacy and integrity, in turn, we show that reductions from multi-key recovery to single-key security are inherently lossy; the lower bound then follows by Lemma 12. We give the details in the full version of the paper [31].
Other Single-Key Security Notions. Given the results above concerning reductions from multi-key AE security notions to the single-key notions \({\mathsf {AE}}{-}\mathsf {PAS}\), \(\mathsf {IND}{-}\mathsf {PAS}\) and \({\mathsf {CTI}}{-}{\mathsf {CPA}}\), one can obtain analogous results for equivalent or weaker single key notions, such as where ciphertexts being indistinguishable from random strings (\(\mathsf {IND}\), \({\mathsf {AE}}\)) is replaced by (weaker) left-or-right indistinguishability (\({\mathsf {LRIND}}\), \({\mathsf {LRAE}}\)). The idea is that if there were a tight reduction from an n-key game to single-key \({\mathsf {LRAE}}{-}\mathsf {PAS}\), say, then this reduction could be combined with the tight reduction from \({\mathsf {LRAE}}{-}\mathsf {PAS}\) to \({\mathsf {AE}}{-}\mathsf {PAS}\) to obtain a tight reduction from the n-key game to \({\mathsf {AE}}{-}\mathsf {PAS}\) that contradicts Corollary 18. However, “tight” is defined here with respect to a number of parameters including, crucially, \(\epsilon \): the maximum advantage in the \({\mathsf {AE}}{-}\mathsf {PAS}\) game. If \(\epsilon \) is close to 1, then so is the “loss”. In other words, the tightness lowerbounds that one can prove using our existing results for strictly weaker single-key security notions are only meaningful for schemes that are secure according to the stronger notions. This leaves open the possibility that tight multi-key to single-key reductions exist for schemes that achieve the weaker single-key security notions, but not the stronger ones. Moreover, our meta-reduction techniques cannot be directly applied to left-or-right indistinguishability, since the meta-reduction cannot correctly simulate left-or-right encryption queries during the rewinding phase without making its own (possibly prohibited) oracle queries (unlike for \(\mathsf {IND}\) when the meta-reduction simply samples random strings of the appropriate length).
Public Key Encryption. It should be possible to adapt our existing techniques to the public key setting. Let \({\mathsf {LRIND}}{-}{\mathsf {CPA}}\) be the standard game in which the adversary is given the public key and can query a left-or-right encryption oracle. Note that the honest encryption oracle is omitted as it is rendered superfluous by the public key. Since public key encryption is typically randomised rather than nonce-based, repeated left-or-right encryption queries are not prohibited, so a meta-reduction \(\mathcal {M}\) can use its own left-or-right challenge oracle to correctly simulate left-or-right queries from the reduction \(\mathcal {R}\) during the rewinding phase, without \(\mathcal {M}\) becoming an invalid adversary. However, if \(\mathcal {R}\) can also make decryption queries, then simulating these queries during the rewinding phase might force \(\mathcal {M}\) to be invalid (such as if one instance of \(\mathcal {R}\) attempts to decrypt the output of the left-or-right encryption oracle sent to an earlier instance of \(\mathcal {R}\)). In summary, it should be possible to show reductions from multi-key games to single-key \({\mathsf {LRIND}}{-}{\mathsf {CPA}}\) are lossy for public key encryption schemes secure according to \({\mathsf {LRIND}}{-}{\mathsf {CPA}}\), but to show an analogous result for \({\mathsf {LRIND}}{-}{\mathsf {CCA}}\) one needs to additionally assume that ciphertexts are indistinguishable from random strings (which is a rather strong assumption in the public key setting). We leave formally proving these claims for future work.
5 Conclusion
We have presented a general family of multi-key security definitions for authenticated encryption, where the adversary can adaptively corrupt keys. We have shown, for a very large class of authenticated encryption schemes, for most members of our family of definitions and for widely-accepted single-key security definitions, that any black-box reduction from the n-key security of an encryption scheme to its single-key security will incur a loss close to n.
For practitioners who set security parameters based on provable guarantees, this shows that security reductions have an inherent shortcoming. Since keys are sampled independently, the corruption of one key should not affect the security of another, yet it is impossible in many cases to prove that security does not degrade from the single-key setting to the n-key setting. It appears that the loss of n is an unfortunate, unavoidable artefact of the proof.
We have shown that the loss of reductions is inevitable for multi-key definitions where the adversary has access to an honest encryption oracle. We therefore left open the possibility that for security notions without such an oracle, tight reductions may be found. Furthermore, our impossibility results apply to schemes where ciphertexts are indistinguishable from random strings. It may be possible that tight reductions exist for schemes that achieve weaker forms of confidentiality, such as left-or-right indistinguishability. Historically, the community has tended to opt for stronger and stronger security notions, but perhaps a slightly weaker single-key notion would be preferred if it tightly implied a meaningful multi-key notion. Finally, it was pointed out by an anonymous reviewer that, in practice, the number of keys an adversary can corrupt is likely to be much smaller than the number of keys in use; it might be possible to find tighter multi-key to single-key reductions for multi-key games where the adversary can corrupt at most \(q_c\) keys (with \(q_c \ll n\)). We leave these interesting open questions for future work.
Notes
- 1.
Of course, here \({\mathsf {enclen}}\) refers to the lengths of ciphertexts from \(\mathcal {E}\), not \(C[\mathcal {E}]\).
References
Abdalla, M., Fouque, P.-A., Lyubashevsky, V., Tibouchi, M.: Tightly-secure signatures from lossy identification schemes. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 572–590. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_34
Bader, C., Hofheinz, D., Jager, T., Kiltz, E., Li, Y.: Tightly-secure authenticated key exchange. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 629–658. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_26
Bader, C., Jager, T., Li, Y., Schäge, S.: On the impossibility of tight cryptographic reductions. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 273–304. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_10
Baecher, P., Brzuska, C., Fischlin, M.: Notions of black-box reductions, revisited. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 296–315. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_16
Barwell, G., Page, D., Stam, M.: Rogue decryption failures: reconciling AE robustness notions. In: Groth, J. (ed.) IMACC 2015. LNCS, vol. 9496, pp. 94–111. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-27239-9_6
Bellare, M., Boldyreva, A., Micali, S.: Public-key encryption in a multi-user setting: security proofs and improvements. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 259–274. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_18
Bellare, M., Hofheinz, D., Kiltz, E.: Subtleties in the definition of IND-CCA: When and how should challenge decryption be disallowed? J. Cryptol. 28(1), 29–48 (2015)
Bellare, M., Ristenpart, T., Tessaro, S.: Multi-instance security and its application to password-based cryptography. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 312–329. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_19
Bellare, M., Tackmann, B.: The multi-user security of authenticated encryption: AES-GCM in TLS 1.3. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 247–276. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_10
Biham, E.: How to decrypt or even substitute DES-encrypted messages in \(2^{28}\) steps. Inf. Process. Lett. 84(3), 117–124 (2002). https://doi.org/10.1016/S0020-0190(02)00269-7
Biryukov, A., Mukhopadhyay, S., Sarkar, P.: Improved time-memory trade-offs with multiple data. In: Preneel, B., Tavares, S. (eds.) SAC 2005. LNCS, vol. 3897, pp. 110–127. Springer, Heidelberg (2006). https://doi.org/10.1007/11693383_8
Blazy, O., Kakvi, S.A., Kiltz, E., Pan, J.: Tightly-secure signatures from chameleon hash functions. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 256–279. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_12
Blazy, O., Kiltz, E., Pan, J.: (Hierarchical) Identity-based encryption from affine message authentication. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 408–425. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_23
Boneh, D., Venkatesan, R.: Breaking RSA may not be equivalent to factoring. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 59–71. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054117
Chatterjee, S., Koblitz, N., Menezes, A., Sarkar, P.: Another look at tightness II: Practical issues in cryptography. Cryptology ePrint Archive, Report 2016/360 (2016). http://eprint.iacr.org/2016/360
Chatterjee, S., Menezes, A., Sarkar, P.: Another look at tightness. In: Miri, A., Vaudenay, S. (eds.) SAC 2011. LNCS, vol. 7118, pp. 293–319. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28496-0_18
Chen, J., Wee, H.: Fully, (Almost) tightly secure IBE and dual system groups. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 435–460. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_25
Coron, J.-S.: Security proof for partial-domain hash signature schemes. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 613–626. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_39
Fischlin, M., Fleischhacker, N.: Limitations of the meta-reduction technique: the case of schnorr signatures. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 444–460. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_27
Fischlin, M., Lehmann, A., Ristenpart, T., Shrimpton, T., Stam, M., Tessaro, S.: Random oracles with(out) programmability. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 303–320. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_18
Fleischhacker, N., Jager, T., Schröder, D.: On tight security proofs for schnorr signatures. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 512–531. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45611-8_27
Fouque, P.-A., Joux, A., Mavromati, C.: Multi-user collisions: applications to discrete logarithm, even-mansour and PRINCE. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 420–438. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45611-8_22
Garg, S., Bhaskar, R., Lokam, S.V.: Improved bounds on security reductions for discrete log based signatures. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 93–107. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_6
Gay, R., Hofheinz, D., Kiltz, E., Wee, H.: Tightly CCA-secure encryption without pairings. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 1–27. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_1
Hoang, V.T., Krovetz, T., Rogaway, P.: Robust authenticated-encryption AEZ and the problem that it solves. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 15–44. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_2
Hoang, V.T., Tessaro, S.: The multi-user security of double encryption. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 381–411. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_13
Hofheinz, D.: Algebraic partitioning: fully compact and (almost) tightly secure cryptography. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 251–281. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_11
Hofheinz, D., Jager, T.: Tightly secure signatures and public-key encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 590–607. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_35
Hofheinz, D., Jager, T., Knapp, E.: Waters signatures with optimal security reduction. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 66–83. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30057-8_5
Hsiao, C.-Y., Reyzin, L.: Finding collisions on a public road, or do secure hash functions need secret coins? In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 92–105. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_6
Jager, T., Stam, M., Stanley-Oakes, R., Warinschi, B.: Multi-key authenticated encryption with corruptions: Reductions are lossy. Cryptology ePrint Archive, Report 2017/495 (2017). http://eprint.iacr.org/2017/495
Kakvi, S.A., Kiltz, E.: Optimal security proofs for full domain hash, revisited. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 537–553. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_32
Katz, J., Wang, N.: Efficiency improvements for signature schemes with tight security reductions. In: Jajodia, S., Atluri, V., Jaeger, T. (eds.) ACM CCS 2003, pp. 155–164. ACM Press, October 2003
Mouha, N., Luykx, A.: Multi-key security: The Even-Mansour construction revisited. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 209–223. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_10
Namprempre, C., Rogaway, P., Shrimpton, T.: Reconsidering generic composition. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 257–274. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_15
Paillier, P., Vergnaud, D.: Discrete-log-based signatures may not be equivalent to discrete log. In: Roy, B. (ed.) ASIACRYPT 2005. LNCS, vol. 3788, pp. 1–20. Springer, Heidelberg (2005). https://doi.org/10.1007/11593447_1
Panjwani, S.: Tackling adaptive corruptions in multicast encryption protocols. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 21–40. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_2
Rogaway, P., Shrimpton, T.: A provable-security treatment of the key-wrap problem. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 373–390. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_23
Safavi-Naini, R., Canetti, R. (eds.): CRYPTO 2012. LNCS, vol. 7417. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5
Schäge, S.: Tight proofs for signature schemes without random oracles. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 189–206. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_12
Seurin, Y.: On the exact security of Schnorr-type signatures in the random oracle model. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 554–571. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_33
Tessaro, S.: Optimally secure block ciphers from ideal primitives. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9453, pp. 437–462. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48800-3_18
Acknowledgements
This work was supported by an EPSRC Industrial CASE award and DFG grant JA 2445/1-1. The authors would also like to thank the anonymous TCC reviewers for their constructive comments on our paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix
Valid Adversarial Behaviour for AE Games
Pointless and Prohibited Queries. Since encryption is deterministic, the response to certain oracle queries can be predicted in advance. Therefore the adversary learns nothing from these queries; we call them pointless. Without loss of generality we assume that valid adversaries do not make such queries. The following queries are pointless:
-
Repeat a query to any oracle other than \(\mathrm {Enc}\)(the \(\mathrm {Enc}\) oracle sometimes samples random ciphertexts, but all other oracles are deterministic).
-
Make a query \(\mathcal {D}(i,C,N)\), where C was the response to a query \(\mathcal {E}(i,M,N)\) (since the response will be M, by correctness).
-
Make a query \(\mathcal {E}(i,M,N)\), where \(M \ne \bot \) was the response to a query \(\mathcal {D}(i,C,N)\) (since the response will be C, by tidiness).
-
Make a query \(\mathcal {E}(i,M,N)\) or \(\mathrm {Enc}(i,j,M,N)\), where a query \(\mathrm {Dec}(i,j,C,N)\) was made with response \(M \ne \bot \) (since the response \(M \ne \bot \) reveals \(b_j = 0\) and \(\mathcal {E}_{K_i}^N(M) = C\) by tidiness).
Some other queries lead to hidden bits being trivial to recover (without having to corrupt a key); we call these queries prohibited, since valid adversaries are not permitted to make them. The following queries are prohibited:
-
Repeat a query \(\mathrm {Enc}(i,j,M,N)\) (if the response to both queries is the same, then with very high probability \(b_j = 0\) and otherwise \(b_j = 1\)).
-
Make a query of the form \(\mathrm {LR}(i,j,M_0,M_1,N)\) with \(|M_0| \ne |M_1|\) (since the length of the ciphertext reveals the length of the plaintext, trivially revealing which of \(M_0\) or \(M_1\) was encrypted).
-
Make two queries of the form \(\mathrm {LR}(i,j,M_0,M_1,N)\), \(\mathrm {LR}(i,j,M'_0,M'_1,N)\) such that \(M_b = M'_b\) and \(M_{1-b} \ne M'_{1-b}\) for some \(b \in \{0,1\}\) (if the response to both queries is the same, then \(b_j = b\) by correctness, and otherwise \(b_j = 1-b\)).
-
Make two queries of the form \(\mathrm {Enc}(i,j,M,N)\) and \(\mathcal {E}(i,M,N)\), in any order (which trivially reveals \(b_j\)).
-
Make two queries of the form \(\mathrm {LR}(i,j,M_0,M_1,N)\) and \(\mathcal {E}(i,M_b,N)\), in any order, for some \(b \in \{0,1\}\) (which trivially reveals \(b_j\)).
-
Make a query \(\mathcal {D}(i,C,N)\), where C was the response to a query \(\mathrm {Enc}(i,j,M,N)\) or \(\mathrm {LR}(i,j,M_0,M_1,N)\) (which trivially reveals \(b_j\), by correctness).
-
Make a query \(\mathrm {Dec}(i,j,C,N)\), where a query \(\mathcal {E}(i,M,N)\), \(\mathrm {Enc}(i,j,M,N)\) or \(\mathrm {LR}(i,j,M_0,M_1,N)\) was previously made with response C (which trivially reveals \(b_j\), by correctness).
-
Make a query \(\mathrm {Enc}(i,j,M,N)\), \(\mathrm {LR}(i,j,M,M_1,N)\) or \(\mathrm {LR}(i,j,M_0,M,N)\), where \(M\ne \bot \) was the response to a query \(\mathcal {D}(i,C,N)\) (which trivially reveals \(b_j\), by tidiness).
It is not necessary to prohibit queries being forwarded between the \(\mathrm {Enc}\) and \(\mathrm {LR}\) oracles, since we do not consider games where both these challenge oracles are present.
Correct Nonce Use. The parameter \(X \in \{{\mathsf {IV}}, {\mathsf {NR}}, {\mathsf {MR}}\}\) determines how the adversary may use nonces in encryption queries. We say \(\mathcal {A}\) uses nonces correctly with respect to X if the following statements hold:
-
If \(X = {\mathsf {IV}}\), then for each query of the form \(\mathcal {E}(-,-,N)\), \(\mathrm {Enc}(-,-,-,N)\), or \(\mathrm {LR}(-,-,-,-,N)\), N is sampled uniformly at random from \({\mathsf {N}}\).
-
If \(X = {\mathsf {NR}}\), then each nonce appears in at most one encryption query under the same key. That is, for each \(i \in [n]\), each nonce N appears in at most one query of the form \(\mathrm {Enc}(i,-,-,N)\), \(\mathrm {LR}(i,-,-,-,N)\) or \(\mathcal {E}(i,-,N)\).
-
If \(X = {\mathsf {MR}}\), then nonces may chosen be arbitrarily and repeated in different queries (modulo the pointless and prohibited queries specified above).
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Jager, T., Stam, M., Stanley-Oakes, R., Warinschi, B. (2017). Multi-key Authenticated Encryption with Corruptions: Reductions Are Lossy. In: Kalai, Y., Reyzin, L. (eds) Theory of Cryptography. TCC 2017. Lecture Notes in Computer Science(), vol 10677. Springer, Cham. https://doi.org/10.1007/978-3-319-70500-2_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-70500-2_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70499-9
Online ISBN: 978-3-319-70500-2
eBook Packages: Computer ScienceComputer Science (R0)







 and
and  such that
such that 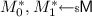 and
and 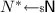 such that
such that  and
and  such that
such that 
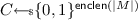 and returns this to
and returns this to 