Model Checking of Concurrent Software Systems via Heuristic-Guided SAT Solving

Abstract

An established approach to software verification is SAT-based bounded model checking where a state space model is encoded as a Boolean formula and the exploration is performed via SAT solving. Most existing approaches in SAT-based model checking rely on general-purpose solvers that do not exploit the structural features of the encoding. Aiming at a significantly better runtime performance in such settings, we show in this paper that SAT algorithms can be specifically tailored w.r.t. the structure of the Boolean encoding of the model checking problem to be solved. We define a state space encoding of concurrent software systems that preserves control flow information. This allows to modify the solver such that the number of SAT decision levels can be significantly reduced by assigning a set of atoms at each level. Such set assignment always characterises a location in the control flow of the encoded system. Moreover, we introduce heuristics that guide the SAT search into directions where a violation of the property of interest may be most likely detected. The heuristic approach enables to quickly discover errors while keeping the actually explored part of the state space small.

1 Introduction: Motivation and Related Work

In SAT-based bounded model checking (BMC) [1] the state space of a system to be verified is encoded as a propositional logic formula, and the state space exploration happens via satisfiability (SAT) solving. Thereby, each satisfying assignment of the formula characterises an error path, whereas an unsatisfiability result implies the correctness of the system under consideration. The advantage of BMC in comparison to explicit-state approaches is that the encoding yields a more compact symbolic state space representation, and that the capability of efficient solvers can be exploited to solve the encoded verification tasks. In BMC most existing approaches rely on general-purpose solvers that do not exploit the specific structure of the propositional logic encoding or any other available knowledge about the underlying verification task. In this paper we show that SAT algorithms can be specifically tailored towards solving encodings of verification tasks, which enables a significantly better solving performance. Here we focus on the verification of reachability properties (e.g. deadlocks, mutual exclusion violation) of concurrent software systems. We define a propositional logic state space encoding that can be directly constructed for a given input system. The encoding preserves control flow information that can be utilised to accelerate the SAT solving procedure. SAT solving algorithms are typically based on a systematic search for a satisfying assignment of the input formula by incrementally selecting an unassigned atom, assigning it by either 1 or 0, and propagating the resulting constraints to all clauses of the formula. In case the solver’s decisions lead to an unsatisfied sub formula, the solver tracks back to a previous decision level and continues its search from that point in a different branch of the search tree until a satisfying assignment is found or until the search tree is exhaustively explored [2]. We introduce an enhanced SAT algorithm that exploits the structure of our encodings in order to reduce the computational effort for solving the encoded verification task. In our approach the number of decision levels can be significantly narrowed down by instantiating a set of atoms at each level. Such a set instantiation always characterises a location in the control flow of the encoded system. Based on a simple query on whether such location is an admissible successor location of the current location, the number of branches that actually have to be explored can considerably reduced. Moreover, we show that the additional employment of heuristic guidance allows for a further enhancement of the solving performance. For this, we adapt the concept of directed model checking [5] which had been introduced for the exploration of explicit-state models, but was not yet considered for SAT-based model checking. We demonstrate that heuristics based on the property to be verified allow to guide the SAT search into directions where a property violation may be most likely detected. We prototypically implemented our encoding and our enhanced SAT approach with set assignments and heuristic guidance on top of the solver Sat4J [6]. Preliminary experiments show promising performance results.

Our technique is related to a number of existing approaches. In [8] we find an overview of principles of using SAT solvers as model checkers, including atom ordering strategies. It is assumed that the encoding is constructed based on an already given state space model – not based directly on the system to be verified. In [9] an algorithm is given to predict a beneficial ordering of the atoms before the SAT search descends into the tree. Performance improvement is achieved by knowing the unsatisfiable core of the $(b-1)$-bounded encoding which the solver explored in a previous iteration of incremental BMC [9]. A survey of directed model checking can be found in [5]. The focus in [5] is on the algorithmic techniques directed model checking approaches, including a classification of such techniques into categories like guided search, explicit-state directed model checking, and directed model checking based on binary decision diagrams. However, no approach for a directed search in SAT-based BMC is proposed. In [4] a heuristic-guided tool based on the model checker Spin is described. The used heuristics are tuned w.r.t specific characteristics of Spin’s input language Promela. Thus, the directed state space exploration algorithm assumes an explicit state space model rather than a symbolic encoding. SAT-based model checking of concurrent systems is also the topic of [10] which is based on the insight that concurrent executions cannot drive arbitrary values through the system, and thus it is not necessary to encode how the computation operates on all values, but rather just on the values that actually arise in such executions. On the basis of an event graph representation of the systems behaviour a SAT problem is constructed and solved in an iterative process of modelling, solving, and re-modelling. The idea of this approach is to use the solver to encode the execution, not the system. Conflict-directed clause learning (CDCL) is the topic of [11] which deals with the question of how to design a predictive measure of learnt clauses pertinence. The authors were able to show the relationship between the overall decreasing of decision levels and the performance of the solver. Thereby, a good learning schema should add explicit links between independent blocks of propagated literals, which should be beneficial for reducing the number of decision levels in the remaining computation. In our work we reduce the number of decision levels based on semantic dependencies of the literals (control flow information). In [13] a heuristic improvement of the Java PathFinder is described: To find errors faster, it is important to explore parts of the state space whose possibility of containing errors is higher than others, whereby heuristic techniques prioritise potential solution candidates according to particular efficiency considerations. The authors propose a depth-first search which can be applied to verification of LTL properties of Java bytecode. With regard to heuristic model checking, the authors of [12] evaluated the resulting search behaviour on a number of models from the BEEM database within the HSF-SPIN explicit-state model checker. The technique of [12] applies a distance function to estimate the distance from a given state to an error state, and explores states with the shortest estimated distance first. Guided by the distance function, error paths can often be found after exploring only a small part of the overall state space.

2 Concurrent Software Systems

We start with an introduction to the systems we consider. A concurrent software system Sys consists of a fixed number of possibly non-uniform processes $P_1\parallel \ldots \parallel P_{n}$, in parallel composition. Inter-process communication is assumed to happen via global variables in shared memory. In $Var = Var_s \cup \bigcup _{i=1}^{n} Var_i$ the set $Var_s$ contains the shared variables whereas $Var_1 \ldots Var_{n}$ are sets of local variables associated exclusively with the processes $P_1\ldots P_{n}$. Moreover, we assume that Boolean predicate abstraction [3] has been applied, which results in a system where all variables are Boolean variables, or more specifically, replaced by Boolean predicates over the original variables. Hence, in our approach variables and predicates are synonymous. Predicate abstraction is a well-established technique in software model checking to reduce the state space complexity of a verification task. In our approach we use the tool 3Spot [14] to transfer a concrete input system into an abstract system defined over predicates. 3Spot formally represents (abstracted) processes $P_i$ as control flow graphs (CFGs) $G_i = (Loc_i, \delta _i, \tau _i)$ where $Loc_i = \{0,\ldots , \vert Loc_i\vert \}$ is a finite set of control locations given as binary numbers, $\delta _i \subseteq Loc_i \times Loc_i$ is a location transition relation, and $\tau _i : Loc_i \times Loc_i \rightarrow Op$ is a function labelling location transitions with operations from a set Op. The set of operations Op on the variables form $Var = \{v_1, \ldots , v_{m}\}$ consists of all statements of the form $assume(e) \ : \ v_1 \! := \! e_1, \, \ldots , \, v_{m} \! := \! e_{m}$ in which $e, e_1, \ldots , e_{m}$ are Boolean expressions over Var. Thus every operation consists of a guard and a list of assignments. For convenience we sometimes just write e instead of assume(e). Moreover, we omit the guard if it is just true.

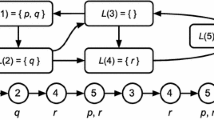
A concurrent software system given by n single control flow graphs $G_1, \ldots , G_n$ can be modelled by one compound control flow graph $G=(Loc, \delta ,\tau )$ where $Loc = Loc_1 \times \cdots \times Loc_n$, $\delta \subseteq Loc \times Loc$ and $\tau : Loc \times Loc \rightarrow Op$. G is the product graph of all single CFGs. We assume that initially all processes of a system at location 0. Moreover, we assume that a deterministic initialisation of the variables is given by an assertion over Var. Now, a computation of a concurrent system corresponds to a sequence where in each step one process is non-deterministically selected and the operation at its current location is attempted to be executed. In case the execution is not blocked by the guard, the variables are updated according to the assignment part, and the process advances to the consequent control location. Note that a CFG is a formal representation of a system but not a state space model. The state space over Var corresponds to the set $S_{ Var}$ of all type-correct valuations of the variables. Given a state $s \in S_{ Var}$ and an expression e over Var, then s(e) denotes the valuation of e in s. The overall state space S of a concurrent system corresponds to the set of states over Var combined with the possible locations, i.e.: $S = Loc \times S_{ Var}$. Thus each state in S is a tuple $\langle l,s \rangle$ with $l = (l_1,\ldots ,l_n) \in Loc$ and $s \in S_{ Var}$. An example for a system where each process is represented by a control flow graph is shown in Fig. 1. We represent the truth value t by 1, and f by 0. In the example we have two uniform processes operating on the shared Boolean variables p and q. The initial state of the system is $\langle (00,00), p=\mathbf 1 , q=\mathbf 1 \rangle$. The system implements a solution to the dining philosophers problem where each philosopher process continuously attempts to acquire the two exclusive resources p and q. Once a process has acquired both resources it releases them in a single step and attempts to acquire them again. The order in which the resources are requested is non-deterministically determined, which makes as deadlock possible: $G_1$ has acquired p and is waiting for q while $G_2$ has acquired q and is waiting for p.

CFGs allow us to model the control flow of a concurrent system. Checking properties of a system requires to explore a corresponding state space model. Typically, Kripke structures are used as state space models. A Kripke structure (KS) over a set of atomic predicates AP is a tuple $M = (S,s_0,R ,L)$ where

• S is a finite set of states and $s_0 \in S$ is the initial state,

• $R \subseteq S \times S$ is a state transition relation with $\forall s \in S : \exists s' \in S : R(s,s')$,

• is a labelling function that associates a truth value with each predicate in each state.

A path $\pi$ of a KS M is a sequence of states $s_0s_1s_2\ldots$ with $R(s_i, s_{i+1})$. $\pi _i$ denotes the i-th state of $\pi$, whereas $\pi ^i$ denotes the i-th suffix $\pi _i \pi _{i+1} \ldots$ of $\pi$. By $\Pi _M$ we denote the set of all paths of M starting in the initial state. All paths of a KS have to be explored in order to determine whether certain error states are reachable. Let $p \in AP$ be a predicate that characterises error states. Then an error state is reachable in M if and only if holds.

Fig. 1.

Concurrent system over the Boolean variables $Var=\{p,q\}$ given by the single control flow graphs $G_1$ and $G_2$, whereby initially $p=$ 1 and $q=$ 1.

Verifying such conditions for a given KS is known as model checking. As defined in [14] a concurrent system $Sys = \ \parallel _{i=1}^n P_i$ given by a set of CFGs $G_1$ to $G_n$ can be translated into a KS M over $AP = Var \cup \{(l_i = j) \ | \ i \in [1..n],\ j \in Loc_i\}$ where the predicate $(l_i = j)$ denotes that the process $P_i$ is currently at control location j. The number of states of a KS corresponding to a given system is exponential in the number of its locations and variables. For instance, a KS corresponding to our simple example system has already 64 states. State space explosion is the major challenge in model checking. Beside the aforementioned predicate abstraction, a common approach to cope with state space explosion is to use a symbolic and therefore more compact representation of the KS. In SAT-based bounded model checking [1] all possible path prefixes up to a bound $b \in \mathbb {N}$ are encoded in a propositional logic formula $Init_0 \wedge T_{0,1} \wedge \ldots \wedge T_{b-1,b}$. The formula is then conjuncted with an encoding $Error_b$ of the error property to be checked. In case the overall formula is satisfiable, the satisfying assignment characterises an error path of length b in the state space of the encoded system. Next, we define such a propositional logic encoding for concurrent systems given by abstract control flow graphs and for errors that can be expressed as reachability properties.

3 Propositional Logic Encoding

We now describe how a propositional logic encoding $Init_0 \wedge T_{0,1} \wedge \ldots \wedge T_{b-1,b} \wedge Error_b$ can be directly constructed for a concurrent system given by control flow graphs $G_i = (Loc_i,\delta _i,\tau _i)$, $1 \le i \le n$ and for a given error property with $b \in \mathrm{I\!N}$ being the bound of the encoding. This saves us the expensive construction of an explicit state space model. The encoding is defined over Boolean atoms. Since a state of a system is a tuple $\langle l,s\rangle$ where $l \in Loc$ is a compound location and s is a valuation of all Boolean variables in Var, we encode l and s separately.

A composite location $(l_1,\ldots ,l_n) \in Loc$ is a list of single locations $l_i \in Loc_i$ where $Loc_i = \{0,\ldots ,\left| Loc_i\right| \}$ and i is the identifier of the associated process $P_i$. Each $l_i$ is a binary number from $\{[0]_2,\ldots ,[\left| Loc_i\right| ]_2\}$. We assume that all these numbers have $d_i$ digits where $d_i$ is the number required to binary represent the max. value $\left| Loc_i\right|$. Then, for each $P_i$, we introduce $d_i$ Boolean atoms, each of which refers to a distinct digit along the binary representation of its locations: $LocAtoms := \{l_i[j] \ | \ i \in [1..n], \ j \in [1..d_i] \}$. Then $l_i$ can be encoded as:

where $l_i(j)$ is a function evaluating to 1 if the j-th digit of $l_i$ is 1, and to 0 otherwise. A composite location $l = (l_1,\ldots ,l_n)$ can subsequently be encoded as:

Because the function ${l_i}(j)$ evaluates to 1 or 0, a location encoding $enc(l_i)$ can be always simplified to a conjunction of literals over LocAtoms. In our example the initial location (00, 00) will be encoded to $\lnot l_1[1] \wedge \lnot l_1[2] \wedge \lnot l_2[1] \wedge \lnot l_2[2]$.

Next we encode the variable (resp. predicate) part of states. For $s \in S_{ Var}$, where $Var = \{v_1,\ldots , v_m\}$ is the set of Boolean variables over which the concurrent system is defined, we introduce $VarAtoms := \{v[j] \ | \ v_j \in Var\}$. Hence, each variable $v_i$ is encoded by an atom v[i], which allows a straightforward encoding of arbitrary logical expressions e over Var. For instance, $enc(v_1 \wedge \lnot v_2) := v[1] \wedge \lnot v[2]$. The initial state $\langle (00,00),p = \mathbf 1 , q = \mathbf 1 \rangle$ of our example system can now be encoded as $Init = \lnot l_1[1] \wedge \lnot l_1[2] \wedge \lnot l_2[1] \wedge \lnot l_2[2] \wedge p \wedge q$. Since in our simple example the variables p and q are not subscripted, we also omit the index values for the identically named atoms p and q.

For encoding the transition relation of a concurrent system we construct a formula $Init_0 \wedge T_{0,1} \wedge \ldots \wedge T_{b-1,b}$ that exactly characterises path prefixes of length $b \in \mathrm{I\!N}$ in the systems state space. Because we consider states as parts of such prefixes, we have to extend the encoding by index values $k \in \{0,\ldots ,b\}$ where k denotes the position along a path prefix. For this we introduce the notion of indexed encodings. Let F be a propositional logic formula over $Atoms = LocAtoms \cup PredAtoms$ and the constants 1 and 0. Then $F_k$ abbreviates the substitution $F[a/a_k \, | \, a \in Atoms]$. Our overall encoding will be thus defined over $Atoms_{[0,b]} = \{a_k \, | \, a \in Atoms, 0\le k\le b\}$. Since all execution paths start in the system’s initial state, we extend the initial state encoding by the index 0: $Init_0 = \lnot l_1[1]_0 \wedge \lnot l_1[2]_0 \wedge \lnot l_2[1]_0 \wedge \lnot l_2[2]_0 \wedge p_0 \wedge q_0$. The encoding of all possible state space transitions from position k to $k+1$ is defined as follows. Let $Sys = \ \parallel _{i=1}^n P_i$ over Var be a concurrent system given by the single control flow graphs $G_i = (Loc_i,\delta _i,\tau _i)$ with $1 \le i \le n$. Then all possible transitions for position k to $k+1$ can be encoded in propositional logic as follows:

$$\begin{aligned} \begin{array}{l} T_{k,k+1} := \\ \bigvee _{i=1}^n \bigvee _{(l_i,l'_i) \in \delta _i} \ (enc(l_i)_k \wedge enc(l'_i)_{k+1} \wedge \bigwedge _{i' \ne i} idle(i')_{k,k+1} \wedge enc(\tau _i(l_i,l'_i))_{k,k+1} ) \end{array} \end{aligned}$$

$\text {where } idle(i')_{k,k+1} \ := \ \bigwedge _{j =1}^{d_{i'}} \ (l_{i'}[j]_k \leftrightarrow l_{i'}[j]_{k+1})$

$\text {and } enc(\tau _i(l_i,l'_i))_{k,k+1} \ := \ enc(e)_k \wedge \bigwedge _{j=1}^{m} \big ( (enc(e_j)_k \leftrightarrow enc(v_j)_{k+1}\big )$

$\text {assuming that } \tau _i(l_i,l'_i) \ = \ assume(e) \, : \, v_1 \! := \! e_1, \, \ldots , \, v_{m} \! := \! e_m$.

Thus, we iterate over the system’s processes $P_i$ and over the processes’ control flow transitions $\delta _i(l_i,l'_i)$. Now we construct the k-indexed encoding of a source location $l_i$ and conjunct it with the $(k+1)$-indexed encoding of a destination location $l'_i$. This gets conjuncted with the sub formula $\bigwedge _{i' \ne i} idle(i')_{k,k+1}$ which encodes that all processes different to $P_i$ are idle, i.e. do not change their control flow location, while $P_i$ proceeds. The last part of the transition encoding concerns the operation associated with $\delta _i(l_i,l'_i)$: The sub formula $enc(\tau _i(l_i,l'_i))_{k,k+1}$ evaluates to 1 for assignments to the atoms in $Atoms_{[k,k+1]}$ that characterise pairs of states s and $s'$ over Var where the guard of the operation $\tau _i(l_i,l'_i)$ is 1 in s and the execution of the operation in s results in the state $s'$. Otherwise $enc(\tau _i(l_i,l'_i))_{k,k+1}$ evaluates to 0. Our transition encoding requires that an operation $\tau _i(l_i,l'_i)$ assigns to all Boolean variables. Thus, if a $v \in Var$ is not modified by the operation we implicitly assume that $v := v$ is part of the assignment list. The encoding of the control flow transition $\delta _1(00,01)$ of our example system with $\tau _1(00,01) \ = \ (assume(p) \, : \, p := \mathbf 0 )$ yields the following:

$$ \begin{array}{llll} enc(00)_k &{} = &{} \lnot l_1[1]_k \wedge \lnot l_1[2]_k \\ \wedge &{} &{} \wedge \\ enc(01)_{k+1} &{} = &{} \ l_1[1]_{k+1} \wedge l_1[2]_{k+1} \\ \wedge &{} &{} \wedge \\ idle(2)_{k,k+1} &{} = &{} (l_2[1]_k \leftrightarrow l_2[1]_{k+1}) \wedge (l_2[2]_k \leftrightarrow l_2[2]_{k+1}) \\ \wedge &{} &{} \wedge \\ enc(\tau _1(0,1))_{k,k+1} &{} = &{} \ p_k \wedge \big ((\mathbf 0 \leftrightarrow p_{k+1}) \wedge (q_k \leftrightarrow q_{k+1})\big ) \end{array} $$

The encoding of the operation only evaluates to 1 for assignments to the atoms in $Atoms_{[k,k+1]}$ that characterise the control flow transition $\delta _1(00,01)$ with idling $G_2$, the variable state s at position k with $s(p) =$ 1 and a state $s'$ at $k+1$ with $s'(p) =$ 0, and moreover, $s(q) = s'(q)$. All other assignments yield false indicating that corresponding pairs of states do not characterise valid transitions.

The previous definitions now allow us to construct a formula $Init_0 \wedge T_{0,1} \wedge \ldots \wedge T_{b-1,b}$ that characterises all possible path prefixes of length $b \in \mathrm{I\!N}$ in the state space of the encoded system. Each assignment that satisfies the formula characterises such a prefix. Next, we introduce the encoding of the property to be checked for the concurrent system. In general, want to verify whether a state is reachable that satisfies a particular predicate. Such a predicate can be an arbitrary Boolean expression over Loc and Var. For our example system, a deadlock circular-wait situation can be described by

$$ ((l_1 = 01) \wedge \lnot q \wedge (l_2 = 10) \wedge \lnot p) \vee ((l_1 = 10) \wedge \lnot p \wedge (l_2 = 01) \wedge \lnot q) \ $$

which can be straightforwardly encoded into a propositional logic formula

$$\begin{aligned} Error&:= (\lnot l_1[1] \wedge l_1[2] \wedge \lnot q \wedge l_2[1] \wedge \lnot l_2[2] \wedge \lnot p) \ \\&\vee \, (l_1[1] \wedge \lnot l_1[2] \wedge \lnot p \wedge \lnot l_2[1] \wedge l_2[2] \wedge \lnot q) \end{aligned}$$

over Boolean atoms. Finally we index such an Error formula with a search-bound $b \in \mathrm{I\!N}$ and conjunct it with our system’s state space encoding, yielding $F_{[0,b]} \ := \ Init_0 \wedge T_{0,1} \wedge \ldots \wedge T_{b-1,b} \wedge Error_b$, such that each assignment satisfying this formula witnesses a path prefix of length b ending in an error state in the state space of the encoded system. Hence the propositional logic encoding allows us to model check a system of interest via SAT solving, without the intermediate construction of an explicit Kripke structure. SAT-based BMC is typically performed incrementally by increasing the bound b until an error state or a threshold is reached. State-of-the-art SAT solvers e.g. [6] can be used for the satisfiability checks. In the remainder of this paper we introduce our enhanced SAT solving concepts that are tailored towards solving our propositional logic encodings of verification tasks for concurrent systems. For the sake of illustration, we present our approach based on a simple SAT solving algorithm that implements our enhanced concepts but not all features of modern solvers like conflict-driven clause learning [2], conflict clause minimisation [16] etc. Nevertheless, our concepts can be straightforwardly integrated into any state-of-the-art solver and combined with the advancements used in such solvers. For instance, our tool that we later present is implemented on top of the solver Sat4J [6].

4 Enhanced SAT Solving for Encoded Verification Tasks

Modern SAT solvers are based on a systematic search for a satisfying assignment of the input formula in conjunctive normal form (CNF) by incrementally selecting unassigned atoms, assigning them by either 1 or 0, and propagating the resulting constraints to the clauses of the formula. In case the solver decisions lead to an unsatisfied clause, the solver tracks back by revising a former assignment decision and continuing the search from this point until a satisfying assignment is found or the search space is entirely explored [2]. While general-purpose solvers do not make any assumption about the structure of the input formula, our enhanced SAT solving approach exploits the structure of our encoding $F_{[0,b]}$ and control flow information about the considered concurrent system. We will see that this enables us to reduce the number of recursive calls of the SAT algorithm. We reduce both the number of decision levels as well as the number of branches to be explored which enables to significantly improve the efficiency of SAT-based BMC in our chosen area of application. First, the structure of $F_{[0,b]}$ allows us to transform the conjuncted parts of the formula separately into CNF:

$$ cnf(Init_0) \wedge cnf(T_{0,1}) \wedge ... \wedge cnf(T_{b-1,b}) \wedge cnf(Error_b) $$

which can be done via the Tseytin transformation [15]. From now on we just write $F_{[0,b]}$ when we refer to the CNF-equivalent of the formula. The atoms of the encoding $F_{[0,b]}$ can be divided into disjoint sets: $Atoms(F_{[0,b]}) = \bigcup _{k=0}^b$ $LocAtoms_k \cup VarAtoms_k$ where $LocAtoms_k$ resp. $VarAtoms_k$ refers to the set of location resp. variable atoms with position index k. Our encoding has the useful property that the application of an assignment results in a formula $\alpha (F_{[0,b]})$ where all $a \in VarAtoms_k$ (i.e. all k-indexed variable atoms) occur in unit clauses. Hence, the subsequent application of unit propagation [17] will immediately assign truth values to all atoms in $VarAtoms_k$. This allows us to solely consider location atoms as branching atoms, since all variable atoms will be automatically assigned under unit propagation.¹

General-purpose SAT algorithms choose a single atom a as the branching atom at each decision level and then branch for $(a,\mathbf {0} )$ (a is assigned by 0) and $(a,\mathbf {1} )$ (a is assigned by 1). In our enhanced algorithm we choose the set $LocAtoms_{k+1}$ at each decision level k. (The use of unit propagation [17] will ensure that all atoms with index $k' \le k$ will be already assigned at level k.) Now instead of branching for each possible assignment to the atoms in $LocAtoms_{k+1}$, the structure of our encoding together with knowledge about the control flow allows us to reduce the number of assignments (i.e. branches) to admissible ones. Note that an assignment characterises a location $l' \in Loc$ in the overall control flow graph $G = (Loc,\delta ,\tau )$ representing the system under consideration. An assignment $\alpha$ is only admissible if it characterises a location $l'$ such that $\delta (l,l')$ holds, where l is the location characterised by the assignment decision at the previous decision level k. Hence, the consideration of the control flow of the encoded system allows us to narrow down the number of branches at each level. Moreover, the number of levels gets reduced to b – the bound of the encoding. Our new algorithm BMCSAT that implements such a decision level reduction and branch reduction is depicted below.

Beside the formula F and a decision level $k \in \mathbb {N}$ the recursive algorithm takes a location $l \in Loc$ of the encoded system as input. and eventually returns an assignment satisfying F or an unsatisfiability result. The assignment $\alpha$ is constructed incrementally. Hence, until the algorithm has terminated $\alpha$ may be a partial assignment for F, i.e. its domain may not necessarily contain all atoms of the input formula. The incremental construction of the overall assignment happens via the concatenation of partial assignments with disjoint domains: $\alpha \circ \alpha '$. We write $\alpha (F)$ to refer to the formula F under the assignment $\alpha$. For instance, the partial assignment $\alpha = \{(a_1,\mathbf 1 )\}$ for the formula $\lnot a_1 \vee a_2$ yields $\alpha (\lnot a_1 \vee a_2) = \mathbf 0 \vee a_2$, which gets simplified to $a_2$.

In Line 2 of the algorithm, unit propagation [17] is applied to the input formula: If a clause of F is a unit (single-literal) clause it can only be satisfied by assigning the underlying atom such that the literal is 1. This assignment will be then propagated to the remaining clauses, the formula will be simplified, and unit propagation will be repetitively applied as long as there exist further unit clauses with unassigned atoms. The application of unit propagation yields a (possibly partial) assignment $\alpha$. In case $\alpha$ already satisfies F, BMCSAT returns $\alpha$ as a satisfying assignment and terminates (Line 3). In case $\alpha$ makes the formula 0 the algorithm terminates with an unsatisfiability result (Line 4). In every other case, $LocAtoms_{k+1}$ is identified as the set of atoms that will be assigned at the next decision level (Line 8). Moreover, the set of possible assignments to $LocAtoms_{k+1}$ is computed and then restricted to admissible ones by the condition $\delta (l,\alpha ')$. Note that since such assignments $\alpha '$ always characterise control flow locations $l \in Loc$, we can also use them as arguments of the transition relation $\delta$ of the underlying control flow graph. In the Lines 9 to 13, BMCSAT is recursively called resulting in a branch for each admissible assignment. The result of the calls is then concatenated with the so far partial assignment. SAT solvers do not generally explore all possible branches. Commonly, one branch is explored at a time until a satisfiability result can be obtained or until the branch turns out to be inexpedient. In the latter case conflict-driven clause learning with non-chronological backtracking [2] is performed and an alternative branch is explored. An excerpt of the branching tree for BMCSAT $(F_{[0,2]},0,(00,00))$ where $F_{[0,2]}$ is the 2-bounded encoding of our example verification task is depicted below.

The sub formula $Init_0$ of $F_{[0,2]}$ is a conjunction of unit clauses over $LocAtoms_0$ and $VarAtoms_0$. Hence, the first application of unit propagation will yield an assignment that characterises the initial system state encoded in $Init_0$. The control flow location $l = (00,00)$ is part of this initial state. Subsequently, BMCSAT will identify $LocAtoms_1$ as the set of location atoms that are assigned next. Based on the transition relation $\delta$ of the control flow graph $G=(Loc,\delta ,\tau )$ the set of admissible assignments (i.e. direct successor locations of (00, 00) in G) is determined: $\{(00,01),(00,10),(01,00),(10,00)\}$. For each admissible assignment BMCSAT is recursively called. The branch corresponding to the assignment (00, 10) has three further branches at decision level 1. The corresponding assignments are (01, 10), (10, 10) and (00, 11). Choosing the assignment (01, 10) for $LocAtoms_2$ and the subsequent application of unit propagation immediately yields a satisfying assignment for $F_{[0,2]}$ and therefore proves that within two steps an error state is reachable in the encoded system. Thus, our BMCSAT only requires two decision levels in order to accomplish this SAT-based verification task, whereas a general-purpose SAT solving algorithm would require at least $\left| LocAtoms_1\right| + \left| LocAtoms_2\right|$ decision levels. The reduction of decision levels in our branching tree comes at the cost of an increase of branches at each level. However, our concept of admissible assignments (i.e. branches) allows us to reduce the number of branches that actually have to be explored – based on the exploitation of control flow information. In our example at decision level 0 the admissible assignment concept allows us to reduce the number of branches to be explored from 16 to only 4, and at level 1 each node of the search tree now only has 3 instead of 16 branches. The extent to which branch reduction is generally possible depends on the number of transitions in the CFG G. In case G is a complete digraph with $\left| Loc\right| ^2$ transitions (i.e. all pairs of locations are bi-directionally connected via direct transitions), then our branch reduction will not have any effect and at each decision level we have to consider $\left| Loc\right|$ branches. However, for most realistic software systems represented as CFGs the number of transitions is substantially smaller than $\left| Loc\right| ^2$. For the verification of such systems the application of branch reduction can enable computational savings of orders of magnitude, which we just exemplified based on our example. We implemented our enhanced concepts, that we illustrated here based on BMCSAT, on top of the solver Sat4j. Moreover, we integrated a concept for heuristic guided error detection into the solver which we introduce next.

5 Directed Model Checking via Heuristic SAT Solving

Directed model checking (DMC) [5] is a concept for guiding the state space exploration via heuristics in order to accelerate the detection of errors. Such heuristics are typically based on the structure of the system to be checked and the property of interest. While DMC has been successfully used to improve automata- and BDD-based model checking [5, 7], this concept has not been transferred yet to SAT-based bounded model checking. Here we show how the DMC concept can be integrated into our SAT-based bounded model checking approach such that the performance of SAT solving algorithm profits from heuristic guidance.

Heuristic model checking algorithms exploit useful information to guide the search. This information is given as an evaluation function $h : S \rightarrow \mathbb {N}_{\infty }$ that estimates the distance from the current state $\langle l,s \rangle \in S$ to an error state where S is the overall set of states. This is known as best-first search. The heuristic function h is precomputed before the search starts. In [4] a concept for computing such a h based on the system and the property to be checked is introduced and it is shown that based on h the exploration of an explicit state space model can be guided. Here we show that h can be also straightforwardly computed based on our verification tasks and then used in order to guide the SAT solver.

The evaluation function of [4] combines distances in the control flow and property-based heuristics. Our system under consideration is given as a composite CFG G composed of single CFGs $G_i=(Loc_i,\delta _i,\tau _i)$ for each process. Thus, we can easily compute a local distance function $d_i : Loc_i \times Loc_i \rightarrow \mathbb {N}_{\infty }$ for each process that returns the shortest directed path in $G_i$ for a pair of its control flow locations. Now the global distance function is defined as $d(l,l') := \sum _{i=1}^n d_i(l_i,l'_i)$ where $l,l' \in Loc$ and $l = (l_1,\ldots ,l_n)$. Remember that in our encoding-based approach each l can be expressed by an assignment . Hence, we can also use assignments $\alpha$ as arguments of the distance functions, as long as the assignments characterise actual locations. Since the control flow distance does not incorporate constraints induced by variable values, the function d gives us an under-approximation of the length of a shortest path in the actual state space. From [4] we also get a property-based evaluation function that extends the distance-based one. Our property is the characterisation of an error state given as an arbitrary propositional logic expression $Error_b$ over the b-indexed atoms. For the computation of the evaluation function it is sufficient to consider the non-indexed equivalent Error. In our running example we had $Error :=$

$$ (\lnot l_1[1] \wedge l_1[2] \wedge \lnot q \wedge l_2[1] \wedge \lnot l_2[2] \wedge \lnot p) \vee (l_1[1] \wedge \lnot l_1[2] \wedge \lnot p \wedge \lnot l_2[1] \wedge l_2[2] \wedge \lnot q) $$

We now can adapt the property-based evaluation function for our SAT-based approach as follows. Let Error over $Atoms = LocAtoms \cup VarAtoms$ be a formula characterising an error state. Let F and G be arbitrary sub formulae of Error and $a \in VarAtoms$. Let $enc(l_i)$ be a sub formula of Error characterising a location $l_i \in Loc_i$. Then $h_{Error} : \mathcal {A} \rightarrow \mathrm{N\!I}_{\infty }$ (where $\mathcal {A}$ is a set of assignments characterising states of the encoded system) is inductively defined as follows:

$$ \begin{array}{lll} h_{true}(\alpha ) &{} := &{} 0 \\ h_{false}(\alpha ) &{} := &{} \infty \\ h_{a}(\alpha ) &{} := &{} \hbox {if } \alpha (a)= \mathbf 0 \hbox { then } 1 \hbox { else } 0 \\ h_{\lnot a}(\alpha ) &{} := &{} \hbox {if } \alpha (a)= \mathbf 1 \hbox { then } 1 \hbox { else } 0 \\ h_{F\vee G}(\alpha ) &{} := &{} min\{h_{F}(\alpha ), h_{G}(\alpha )\} \\ h_{F\wedge G}(\alpha ) &{} := &{} h_{F}(\alpha ) + h_{G}(\alpha ) \\ h_{enc(l_i)}(\alpha ) &{} := &{} d_i(\alpha ,l_i) \\ \end{array} $$

With our running example we illustrate how h can guide the search of the SAT solving algorithm BMCSAT in the right direction: We assume that at decision level 0 the atoms of $LocAtoms_1$ have been assigned by (00, 10) and we are currently at decision level 1. Hence, the atoms of $LocAtoms_2$ will be assigned next. The execution of Line 8 of our algorithm will yield the set $\mathcal {A} = \{(01,10),(10,10),(00,11)\}$ of admissible assignments. For our heuristically enhanced approach, we replace Line 10 of BMCSAT by the following statement:

$$\begin{aligned} \alpha ' := select\hbox {-}min(\mathcal {A},h_{Error}) \end{aligned}$$

such that the branch resp. assignment $\alpha ' \in \mathcal {A}$ with the heuristically estimated shortest distance to an error state is selected for further expansion. For our three candidates from $\mathcal {A}$ we thus get:

$$ \begin{array}{lllll} h_{Error}((01,10)) &{} \ := &{} min\{0+0,3+3\} &{} \ = &{} \ 0 \ \\ h_{Error}((10,10)) &{} \ := &{} min\{3+0,0+3\} &{} \ = &{} \ 3 \ \\ h_{Error}((00,11)) &{} \ := &{} min\{1+2,1+2\} &{} \ = &{} \ 3 \ \\ \end{array} $$

Consequently (01, 10) is heuristically chosen as the assignment for $LocAtoms_2$. At the next level the application of unit propagation will immediately return a satisfying assignment for the encoding $F_{[0,2]}$ and thus prove that an error state is reachable within two steps. Our heuristic guidance has thus avoided the exploration of fruitless branches associated with the other admissible assignments. Thus we now have two new concepts for tuning SAT solving for model checking:

• the introduction of set assignments and admissible assignments in BMCSAT shrinks the total number of branches to be explored, and

• the heuristic function h additionally guides the search into fruitful branches

Our heuristic function does not yet incorporate the variable atoms, since all $\alpha ' \in \mathcal {A}$ only assign values to location atoms. For each $a \in VarAtoms$, $\alpha '(a)$ is undefined, and consequently $h_{a}(\alpha ')$ yields 0. Thus, in our current approach any costs associated with variable atoms are ignored. A straightforward way to incorporate those atoms would be to compute the assignment $\alpha _{ Var} := unit\hbox {-}propagate((\alpha \circ \alpha ')(T_{k,k+1}))$ for each $\alpha ' \in \mathcal {A}$, such that $\alpha _{ Var}$ would extend $\alpha '$ to all variable atoms with index $k+1$. In such a manner the costs associated with an $a \in VarAtoms$ would then be estimated by $h_{a}(\alpha '\circ \alpha _{ Var})$.

6 Implementation and Experiments

We have prototypically implemented our SAT-based bounded model checker with heuristic guidance on top of the solver Sat4j [6]. Our tool builds abstract CFGs for a given concurrent system Sys and a set of predicates Pred. It supports almost all control structures of the C language as well as int, bool, semaphore as data types. Based on the CFGs and an input Error property (e.g. mutual exclusion violation, deadlock) defined over locations and predicates, our tool automatically constructs an encoding F of the corresponding verification task. The checker now iterates over the bound b starting with b = 0, until a the reachability of an Error state can be proven or a predefined threshold for b is reached. In each iteration the encoding is processed by an solver instance of Sat4j. We have modified the solver such that it implements our proposed concepts of set assignments, admissible assignments and property-based heuristic guidance of the SAT search. For this, the heuristic function that estimates the distance from the current state to an Error state is precomputed based on the abstract CFGs and the Error property. In experiments we compared the performance of our heuristic-guided solver with the performance under the general-purpose solving of Sat4j. As input systems we used the concurrent Boolean program benchmark collection of the CProver project². The programs of the collection implement device drivers with multiple threads i.e. processes. We checked for the reachability of states with particular combinations of program locations which we henceforth denote as error states. The experimental results are summarised below.

Benchmark		General-purpose	Heuristic-guided
ib700wdt	Reachable	11.3 s	2.7 s
	Unreachable	27.6 s	39.2 s
sc1200wdt	Reachable	306 s	35.7 s
	Unreachable	124 s	143 s
i8xx_tco	Reachable	807 s	122 s
	Unreachable	201 s	163 s
Machzwd	reachable	97.0 s	31.6 s
	Unreachable	11.3 s	10.7 s

The experiments were conducted on a 2.6 GHz Intel Core i5 with 8 GB. All benchmark items consist of a set of concurrent programs. We checked all programs individually. For some programs of each item the outcome of verification was the reachability of the error state, whereas for other programs an unreachability result was obtained. In the table we consider verification tasks with a reachability result and those with an unreachability result separately. The displayed times denote the average runtime of all reachability resp. all unreachability cases of each benchmark item. Our experiments revealed that our heuristic approach significantly enhances the solving performance of verification tasks where the reachability of an error state can be finally proven, whereas verification tasks with an unreachability outcome can be typically solved equally efficient with the general-purpose and the heuristic approach. Hence, our new approach is particularly useful for detecting errors in concurrent systems, while it does not introduce any drawbacks in case no error can be detected. Our enhanced concepts allow us to guide the SAT search into directions where errors will be most likely detected.

7 Conclusion

We presented a new approach for accelerating SAT-based model checking. We defined a propositional logic state space encoding of concurrent systems that preserves control flow information. Moreover, we designed an enhanced SAT algorithm that exploits the structure of our encodings in order to reduce the computational effort for solving the encoded verification task. The concepts set assignments and admissible assignments allow to narrow down the number of decision levels and branches to be explored. Furthermore, we introduced a heuristic based on the property to be verified, which enables to guide the SAT search into directions where a property violation will be most likely detected. The heuristic approach facilitates further computational savings. We implemented our state space encoding and integrated our enhanced SAT concepts into the solver Sat4j. Our tool allows to perform guided SAT-based BMC with a considerably faster error detection compared to BMC via general-purpose SAT solving.