Keywords

1 Introduction

In the last decades many research institutes, companies and academic initiatives have focused their efforts in the research and production of humanoids robots. Some academic initiatives such as RoboCup [1] have set soccer robot as their main goal, but this objective is just one topic in the bigger scope covered by RoboCup. The three main robotics areas are education, search & rescue and soccer. The first one is focused on the research on improving search and rescue of victims in disaster zones using robots. The second area relates to education, where the main objective is to introduce high school students and children into the fascinating world of science and robotics [2]. Finally, the soccer is focused on the development of wheeled robots [3] with small size and middle size leagues and humanoid robots with kid, teen, and adult size leagues. The soccer initiative is approached by different research fields such as artificial intelligent [4], computer vision [5], and locomotion skills. Darpa [6] encourages the development of humanoid robots that collaborate in the rescue of human casualties in hazardous areas. The Darpa Humanoid Challenge proposes different tasks, which are focused on the design and improvement of humanoid robots with new skills and applications in the real world. To achieve a so-called humanoid-robot interaction in the real world, improving skills such as walking, running, jumping is a must. To improve these locomotion skills, it is necessary to keep the robot balanced while it performs different movements. With the purpose of keeping balance, Vukobratovic and Borovac introduced in [7] the use of Center of Mass (CoM) and Zero Moment Point (ZMP) as a reference points to perfom balance control. Aditionally, Kajita et al. [8] proposed the inverted pendulum model as a reduced dynamic model for humanoid robots, thus simplifying the design of balance control systems for these robots. However, sometimes the balance control fails and the robot falls. Then it is necessary to answer a new question: what does a robot have to do when falling is unavoidable? Some authors describe different kinds of a possible solution to this problem. The consensus is that the main goal is to prevent or diminish damage at the moment of hitting the ground.

Previous works try to reduce the impact force through the use of different aproaches such as: the design of movement sequences inspired by martial arts [9], falling simulation used by the animation industry [10], mechanical additions in the contact zones of the robot [11] and the use of variable stiffness in motors located in the arms [12]. The present paper proposes an idea similar to the latter approach, but it includes a new method to generate low stiffness in the arms motors. This method uses an optimal control approach to calculate the PID parameters. This paper is organized as follows: Sect. 2 presents related work; Sect. 3 presents the impact reduction strategy; Sect. 4 presents experiments and results; while Sect. 5 presents the final conclusions.

2 Related Work

Falling robots have become one of the most interesting research topics recently. It tries to minimize the damage in the robot joints and it even tries to protect the important parts such as chest and head where the processors, cameras and batteries are usually located. Some previous works propose different ways to reduce the impact force in falling robots, such as fall prediction, fall sequences generation, reducing the shock force exerted in the ground impact, mechanical improvements, and manipulation of joint stiffness. One of the most important steps in the study on the falling robot is to predict and detect when the robot is falling [14]. Karsen and Wirsen [15] predict fall events using principal component analysis. The most popular technique to reduce the damage on the robot at the moment of impact is to take inspiration from what the human reaction would be in different falling scenarios. Fujiwara et al. [9] take decisions based in martial arts or more specifically judo techniques, while also trying to reduce the angular momentum. Ruiz-del Solar [16] uses a similar approach based in Japanese martial arts skills, but he adds another concept based on the idea of keeping the Center of Mass (COM) as low as possible to reduce the impact force on the joints. Wilken et al. [11] propose an algorithm for a diving motion in a goalkeeper robot. This algorithm optimizes the falling time and defines the movement trajectory according to the direction and velocity of the ball. Ha et al. [10] is focused in another interesting approach of the falling motion field. It consists on the use of technics from animation to reduce impact forces in falling bodies. Hu and Liu [17] also show other kind of research to reduce the damage in humanoid falls. They propose an algorithm focused on the dissipation of the momentum in the initial phase of the fall. They do so by using multiple contact points with the ground, thus splitting the impact force through various contact points. They validated their algorithm using physics simulation software and a BioloidGp humanoid robot. Wilken et al. [11] study the case of a goalkeeper robot, they propose to add mechanical improvements to the more exposed parts, susceptible to damage due to falls, such as the hip and the upper limbs. The goal is to enlarge the lifespan of the joints. Thus they propose the use of springs to recover the target position of the joints, and the addition of something padded to dampen the shock as well. Pratt et al. [18] propose the idea that full stiffness is not always the best way to work. They make a mathematical study about the effect of low stiffness in a robotic joint and how to control it. Additionally, they list several cases in which low stiffness has a good performance, such as: stable force control, lowering reflecting inertia, less damages during unexpected contact and shock tolerance. Shock tolerance and unexpected contact are the two main arguments in favor of the use of variable stiffness in the present work.

Other works use low stiffness to save energy or reduce impact forces. Elibol et al. [19] make a study about the performance variation of the walking process of a humanoid robot using different joint stiffness values. Calderon et al. [20] propose a statistic algorithm to compute the low stiffness value required for the robot to perform a stand up movement correctly, while reducing energy consumption by lowering each joint’s stiffness value.

An earlier work related with this paper is presented by Calderon et al. [21]. They propose the variation of the ankle and knee stiffness value throughout the different stages of a jumping process for a humanoid robot. They indicate when it is necessary to decrease or increase the proportional gain, but they do not provide a method to estimate the P value in a control system. The present work uses a similar approach than that depicted by Calderon et al. in [22, 23] where they propose a complete control method to perform a vertical jump movements in a legged robot. Additionally, they depicted a fuzzy method to estimate the low stiffness required to reduce the impact force in the landing phase of the vertical jump. In a similar way the present work proposes a method to estimate the stiffness value when the robot is falling. A preliminary version of this work was presented at SoutheastCon (2016) in Cardona et al. [12]. They proposed a fuzzy logic method to calculate the low stiffness value with the aim to reduce the impact force when a humanoid robot is falling. This new version includes an improved method to calculate the desired low stiffness according with an estimation of the impact force and impact velocity. The low stiffness is reached through the calculation of the motor control gains using an optimal approach. Additionally the optimal gains are transformed to an optimal PID to allow the implementation in a PID controlled actuator robot, in this case a Darwin robot. The current work is the improvement proposed in the future work section in Cardona et al. [12].

3 Impact Reduction Strategy

The impact force reduction strategy is based on the use of low stiffness in the arm motors of the humanoid robot. The proposed strategy is inspired in real human behavior. When humans are falling, they try to protect their chest and head using their hands and arms. Consquently, the most common fracture in human fall accidents are the wrist, arm, or clavicule. According to Ruiz-del Solar [16] in human accidents is very common to break the bones, but in humanoid robots the links are particularly strong and the impact force affects the joints, breaking the motors. Using the last two ideas. Once the robot detects that it is falling, it moves its arms to the front position trying to protect the head and chest from the impact force. But, with this movement the robot is putting at risk the integrity of the arm motors. To protect the motors, the stiffness of every arm motor is decreased, affecting the gains of the motor control system. The control gains are calculated using an optimal (LQR) approach and these values are redesigned to implement in the PID control of the Darwin Robot motors. As mentioned in the last section, this work bases the impact reduction strategy in the motor stiffness variation using a LQR approach. Thus, this section is divided into three parts. The first one is the mathematical model of the electrical motor. The second one is the formulation of the optimal control system, and finally the calculation of PID constants from the LQR, according with the requirements of the robotic platform.

3.1 Electrical Motor Model

Since most actuators of actual robots are electric motors, the present work uses the mathematical model of a typical electric motor for the controller design. The characteristic equation of the electrical motor is presented in Eq. 1

$$\begin{aligned} \frac{\theta (s)}{V_{in}(s)}=\frac{K_t G_r}{s\Big ((Js+b)(Ls+R)+K_tK_b\Big )} \end{aligned}$$
(1)

where, \(V_{in}\) is the input voltage, \(\theta \) is angular position, L is the armature inductance, R is the armature resistance, b is the motor viscous friction constant, J is the moment of the inertia of the rotor, \(K_t\) is the motor torque constant, Gr is gear ratio, and \(K_b\) is the electromotive force constant.

3.2 Linear Quadratic Regulator

The Linear Quadratic Regulator (LQR) optimal control has been widely studied over decades with a broad range of applications. It minimizes the error in the state variable trajectories of a system while requiring the minimum control energy. The objective to use LQR is to generate a variable stiffness effect in the actuator (electric motor) as it will be explained ahead. LQR is based in the minimization of the performance index as shown by Eq. 2.

$$\begin{aligned} J=\int _{0}^{\infty }\Big [x^{T}(t)Qx(t)+u^{T}Ru(t)\Big ]dt \end{aligned}$$
(2)

where Q and R are the penalization matrices for state variables error and control signal, respectively. The relation between Q and R determines what is more important between the minimization of state error or the control energy. Thereby, the present work proposes to determine the stiffness of the motors using the Q matrix. When Q has large values, the motor position error is penalized. Then, the motor tries to keep the position against any disturbance (high stiffness). Otherwise, if Q has small values, a certain position error is allowed, generating low stiffness in the motor. The feedback control law is defined by 3.

$$\begin{aligned} u(t)=-R^{-1}B^{T}Px(t)=-Kx(t) \end{aligned}$$
(3)

where, K is known as the Kalman gain and it is defined as \(K=R^{-1}BP\) and P is a symmetric positive defined matrix and it is a solution of the Continuous Algebraic Riccatti Equation defined by 4.

$$\begin{aligned} A^{T}P+PA-PB R^{-1} P+Q=0 \end{aligned}$$
(4)

Here, A and B are the matrices of the state space description of the plant (motor), Q is symmetric positive semi-definite weighted matrix, and R is a constant matrix. Using the Riccati Equation, the feedback gains can be calculated and the design of the control system can be performed. However, the system performance depends of the adequate selection of the Q matrix. The next section explains how to calculate Q based on a desired model and how to tune a PID using the LQR approach.

3.3 Optimal PID

PID is a control system widely used around the world. For the current case, this paper tries to provide a method to vary the stiffness in a motor using PID, with an optimal approach. The variable stiffness is used to reduce the impact force in falling robots, as previously mentioned. The design of optimal PID is based in the works presented by [24, 25]. Where they first proposed a PID design using LQR approach, but the selection of the Q matrix was not defined. The second one designs the PID using LQR and provides a method to determine the Q values, based on the characteristic polynomial of the desired behavior. The current work assumes the designs of PID as a LQR optimal control design, where the error is the state variables and the optimal state-feedback gains are the PID parameters (\(K_p\), \(K_i\), and \(K_d\)). The Fig. 1 shows the typical PID configuration, where r(t) is the desired actuator position.

Fig. 1.
figure 1

PID controller for second order system

Full size image

The PID and the second order plant (motor) are defined by 5 and 6 respectively.

$$\begin{aligned} G(s)=\frac{c}{s^{2}+as+b}=\frac{y(s)}{u(s)} \end{aligned}$$
(5)
$$\begin{aligned} u(s)=e(s) \left( \frac{K_{i}}{s}+K_{p}+K_{d}s \right) \end{aligned}$$
(6)

Now, the state variables are defined as 7.

$$\begin{aligned} x_{1}=\int e(t)dt, x_{2}=e(t), x_{3}=\frac{de(t)}{dt} \end{aligned}$$
(7)

For the feedback design, the external desired set-point does not affect the controller design and it is possible to assume \(r(t)=0\), thus \(e(t)=-y(t)\). This is a common assumption in the standard regulator design. Assuming \(r(t)=0\) the transfer function can be expressed as 8.

$$\begin{aligned} \frac{Y(s)}{U(s)}=\frac{c}{s^{2}+as+b}=\frac{-E(s)}{U(s)} \end{aligned}$$
(8)

Now the relation between U(s) and E(s) is written in the time domain and shown in 9.

$$\begin{aligned} \ddot{e}(t)+ a\dot{e}(t)+be(t)=-cu(t) \end{aligned}$$
(9)

replacing 8 in 9 the relation between u(t) and y(t) is expressed in terms of the state variables as 10.

$$\begin{aligned} \dot{x_{3}}+ax_{3}+bx_{2}=-cu(t) \end{aligned}$$
(10)

finally, using 7 and 10 the state space formulation is depicted in 11.

$$\begin{aligned} \begin{bmatrix} \dot{x_{1}}\\ \dot{x_{2}}\\\dot{x_{3}}\\ \end{bmatrix}=\begin{bmatrix} 0&1&0 \\ 0&0&1\\ 0&-b&-a \end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ \end{bmatrix}+\begin{bmatrix} 0\\ 0\\ -c\\ \end{bmatrix}u(t); \quad A=\begin{bmatrix} 0&1&0\\ 0&0&1\\ 0&-b&-a \end{bmatrix}, B=\begin{bmatrix} 0\\ 0\\ -c\\ \end{bmatrix} \end{aligned}$$
(11)

Now it looks as a standard state-space representation \(\dot{x}=Ax(t)+Bu(t)\) where A and B are shown by 11. Then, using Eq. 4 the Riccatti Equation Solution can be applied using A and B from the 11 and P is defined as a 3\(\,\times \,\)3 symmetric matrix as depicted in 12.

$$\begin{aligned} P=\begin{bmatrix} P_{11}&P_{12}&P_{13}\\ P_{21}&P_{22}&P_{23}\\ P_{31}&P_{32}&P_{33} \end{bmatrix} \end{aligned}$$
(12)

Using the results of P matrix, the K gains are obtained using Eq. 3 where \(K_1=K_i\), \(K_2 =K_p\), and \(K_3=K_d\).

3.4 Variable Stiffness Design Using Optimal PID

In order to develop variable stiffness in a motor using an optimal PID design, it is necessary to establish a desired transfer function according with the desired performance. Usually the desired function is determined according with requirements of settling time, overshoot and rise time among others. However, for the present case those parameters can be defined according to the normal performance of the motor in common robot activities like walk.

The idea of this point is to set up a standard point where the motor stiffness will be defined as a normal stiffness. Starting from this point a low and high stiffness will be defined. Thus, the desired function is defined as a third order system, which characteristic polynomial has three roots defined by \((s+\alpha _{1})\), \((s+\alpha _{2})\), and \((s+\alpha _{3})\). The objective of this section is to design a PID controller, starting from the desired performance using optimal approach. The PID transfer function is defined as shown by 13

$$\begin{aligned} G_{PID}(s)=k_{p}+\frac{k_{i}}{s}+k_{d}s \end{aligned}$$
(13)

Following the method described by [25], Q and P matrices are defined as shown by 14 and 12 respectively.

$$\begin{aligned} Q=\begin{bmatrix} q_{1}&0&0\\ 0&q_{2}&0\\ 0&0&q_{3} \end{bmatrix} \end{aligned}$$
(14)

According with the optimal conditions, where P has to be a solution of the Riccati Eq. 4. The values of Q can be set in terms of motor transfer function coefficients and the roots of the desired polynomial characteristic equation. The Q values are depicted by 15-17.

$$\begin{aligned} q_{1}=\frac{R\alpha _{1}^{2}\alpha _{2}^{2}\alpha _{3}^{2}}{c^{2}} \end{aligned}$$
(15)
$$\begin{aligned} q_{2}=\frac{R\left( \alpha _{1}^{2}\alpha _{2}^{2}+\alpha _{1}^{2}\alpha _{3}^{2}+\alpha _{3}^{2}\alpha _{2}^{2}-b^{2} \right) }{c^{2}} \end{aligned}$$
(16)
$$\begin{aligned} q_{3}=\frac{R\left( \alpha _{1}^{2}+\alpha _{2}^{2}+\alpha _{3}^{2}-a^{2}+2b \right) }{c^{2}} \end{aligned}$$
(17)

Once Q has been defined, the Riccati equation is applied using 4 and the P matrix is obtained. The solution of the Riccati equation can be found using numerical methods or mathematical software as Matlab. Now, the optimal PID constants are computed using 18.

$$\begin{aligned} K_{i}=R^{-1}cP_{13};\quad \quad K_{p}=R^{-1}cP_{23};\quad \quad K_{d}=R^{-1}cP_{33} \end{aligned}$$
(18)

Because the optimal PID gains were calculated using a characteristic polynomial of the desired transfer function with the usual performance parameters, the stiffness in the motor is assumed as a usual stiffness. But, based on this design, it is possible to calculate a new set of optimal PID gains. These new gains can produce a high or low stiffness from the usual stiffness perspective. The low and high stiffness can be designed scaling the \(Q_{usual}\) matrix by a \(\rho \) factor as shown by 19.

$$\begin{aligned} Q_{new}=\rho Q_{usual} \end{aligned}$$
(19)

where \(\rho \) is a scalar parameter, for \(\rho >1\) a high stiffness is obtained and \(0<\rho <1\) the low stiffness will be reached by the motor. Finally with the \(Q_{new}\) defined, it is necessary to solve the Riccati equation for \(Q_{new}\) and get the P values to calculate the new PID control gains.

4 Experiment and Results

In order to perform experiments of the falling protection, a Darwin Op Humanoid Robot was chosen. This robot was used because it is one of the most popular humanoid robots in RoboCup and its actuators are used along the different leagues, such as Humanoid soccer, rescue, junior, and @home. The robot is 45.5 cm high, 3 kg weight, and it has 20 Degrees of Freedom (DoF). The motor actuators are Dynamixel MX-28, having an absolute encoder resolution of 4,096, stall torque of 31.6 kg-cm and programmable PID control. The last characteristic is the most important, because the present work proposes an optimal PID to generate variable stiffness. The proposed method depends of the transfer function of the motor to design the PID. Since there is not enough information about the motor model, a reduced model is proposed, as shown in Fig. 2. Where \(G_o\) is the internal model of the electrical motor. For the sake of simplicity, some variables were set to zero, such as target velocity (\(\dot{\theta }_d\)), \(K_i\) and \(K_d\). According with the manufacturer’s specifications if \(\dot{\theta }\) is zero, the feedback loop of velocity control is disabled. So that the internal model just depends of the proportional gain (\(K_p\)). The proposed model is a second order system as depicted by 1 and shown in Fig. 2. It was estimated using the “Ident Tool Box” from Matlab. The obtained constants are \(a=106.1\), \(b=3\), and \(c=1319\) with \(K_p=16\). This model is affected by the nonlinearity of the saturation function. This function is the operation voltage limit of the motor. This reduced model works with \(K_p\) values less than 64 and position error less than 1000, which is not a problem for the proposed method, as it is used in situation where the position error is close to zero and the system is trying to keep the set point.

Fig. 2.
figure 2

Reduced motor model

Full size image

The other important parameters of the proposed method are the roots of the characteristic equation of the desired behavior. In this case \(a_1\)=−238, \(a_2\)=−79, and \(a_3\)=−8.5. The method can now be applied using the transfer function and desired roots established.

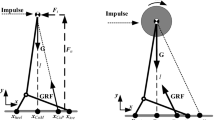
The experiment consists of running several trials of the falling robot with different values of \(\rho \). The robot is standing up and it is pushed from back to front, then it moves its arms to the safe position. The new values of PID according with \(\rho \) are programmed in the elbow and shoulder motors. Figure 3 shows a motion sequence of the experiment.

Fig. 3.
figure 3

Motion sequence of the experiment

Full size image

At the end of the motion sequence in Fig. 3, the reader can observe how the arms are displaced from the safe position and the impact between the robot body and the ground is reduced.

Figure 4 shows the position of the center of mass (CoM) of the robot in five different trials. Every trial has different values of \(\rho \), for these cases \(\rho \) = 0.05, 0.1, 0.3, 1, and 3.

Fig. 4.
figure 4

Center of mass position with different \(\rho \) values

Full size image

Other important parameter used to measure the ground impact force is the displacement (d) of the CoM in the impact moment. Figure 4 shows how d increases as \(\rho \) is reduced.

The average impact force can be estimated using 20, where d is inversely proportional to the impact force. \(V_l\) is the impact velocity and m is the robot mass.

$$\begin{aligned} F_{i-avg}=\frac{\frac{1}{2}mV_l^2}{d} \end{aligned}$$
(20)

The results of the Impact force, impact velocity, and CoM displacement are depicted in Table 1. Table 1 depicts the results of the five trials shown by Fig. 4.

Results show how the displacement (d) increases according to the decrements of \(\rho \). The impact force is reduced with smaller values of \(\rho \) and it rises with large values of \(\rho \). This highlights the importance of the stiffness variation to reduce the impact force. The low stiffness generates large values of displacement and a significant reduction of the impact force.

Table 1. Experiment results
Full size table

5 Conclusions

The reduction of the impact force in a falling robot was achieved using a variable stiffness approach. This work illustrates how the reduction of the stiffness in the motor can help to reduce the impact force. The stiffness variation is performed through the design of a PID controller. Additionally, the coefficients of the PID are calculated using a LQR design. The proposed design of the PID controller was tested using a Darwin OP humanoid robot, and several trials with different parameters were performed. The results were satisfactory showing a reduction of ground impact force of up to 86%. The stiffness variation was proposed in terms of the Q matrix variation using a modulating coefficient, \(\rho \). Low stiffness is reached with \(0<\rho <1\) and high stiffness is generated using \(\rho >1\). According with experiments low stiffness allows for the reduction of the impact force through the center of mass displacement. Nevertheless, it is necessary to take into account that as \(\rho \) gets close to 0, the stiffness is becomes too low. Then, the arms don’t stop the robot body and it crashes to the ground. The estimation of the motor parameters was performed using a reduced model of the Dynamixel MX-28. The proposed algorithm can be applied to full size robots, but it is necessary to take into consideration the robot weight, mathematical model of the arm motors, and the type of control system used in the motor. If the controller is not a PID, a different control model must be designed, based in calculated LQR values. In contrast to the traditional robot falling protection algorithms, the present work does not propose special trajectories inspired in martial arts or animation technologies. Alternately, the variable stiffness is proposed in terms of a LQR design. Future work includes the use of optimization theory to generate variable stiffness. Additionally, the proposed algorithm could be joined to trajectory generation algorithms to complement each other.