Abstract
Faceted search is the de facto approach for exploration of data in e-commerce: it allows users to construct queries in an intuitive way without a prior knowledge of formal query languages. This approach has been recently adapted to the context of RDF. Existing faceted search systems however do not allow users to construct queries with aggregation and recursion which poses limitations in practice. In this work we extend faceted search over RDF with these functionalities and study the corresponding query language. In particular, we investigate complexity of the query answering and query containment problems.
Work supported by the Royal Society under a University Research Fellowship and the EPSRC under an IAA award and the projects DBOnto, MaSI\(^3\), ED\(^3\), and VADA(EP/M025268/1).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Faceted search is a prominent search and data exploration paradigm in Web applications, where users can progressively narrow down the search results by applying filters, called facets [28]. Faceted search has also been proposed in the Semantic Web context as a suitable paradigm for exploring and querying RDF graphs, and a number of RDF-based faceted search systems have been developed in recent years [1, 4, 8, 12, 14,15,16,17, 20, 25].
The theoretical underpinnings of faceted search in the Semantic Web context were first studied in [10, 23, 30] and more recently in [1], where the authors identified a class of first-order faceted queries providing a balance between expressivity of the query language and complexity of query answering. On the one hand, faceted queries naturally capture the core functionality of faceted query interfaces as implemented in existing systems; on the other hand, in contrast to arbitrary first-order queries, their restrictions ensure that they can be answered in polynomial time in the combined size of the input RDF graph and query [1].
Faceted queries as defined in [1], however, do not capture some of the functionality needed for applications. We discuss this missing functionality on an example of a marketing company recording different kinds of information about products using an RDF graph. In enterprise data management such graphs are often the result of data integration, where data from disparate sources are exported into RDF for sharing and analysis purposes. An excerpt of our example graph is shown in Fig. 1. The graph describes mobile phones such as “Samsung S8” by providing information such as their price as advertised by different sellers, their parts (e.g., processors), or the country where phones and their parts were produced. The expert users working for the company would want to exploit faceted search to enable sophisticated searches such as the following ones:
-
(S1)
find smartphones with price between \( \pounds 500 \) and \(\pounds 900 \);
-
(S2)
find companies producing at least ten different models of smartphones; or
-
(S3)
find smartphones with processors produced by North American companies.
To capture search (S1), a faceted search system should support numeric value ranges; in particular, this requires the underpinning query language to allow for comparisons between variables and numbers. Search (S2) requires a form of aggregation since it involves counting the number of smartphone models produced by each company. Search (S3) is rather cumbersome to perform in a typical RDF faceted search system, where facets are generated by “following” the explicit links in the input graph. In particular, one would typically search for smartphones first, then select the relevant processor (note the direct link between phones and processors via the \(\mathsf {hasPart} \) relation), then select relevant cities and subsequently countries, until eventually reaching the selection for continents. Furthermore, by the time users are asked to select processors or even cities, they are unlikely to know whether these are related at all to North America. Thus, in many applications it is useful for faceted interfaces to provide “shortcuts” that would allow, for instance, a selection for continent without the need for first selecting processors, cities, or countries. Supporting such shortcuts requires a form of reachability (i.e., recursion) in the underpinning query language.
In this paper, we propose an extension of the faceted query language introduced in [1] with numeric comparisons, aggregation and recursion. Similarly to faceted queries, our extended query language strikes a nice balance between expressive power and computational properties. On the one hand, it is expressive enough to capture the typical searches that we have encountered in practical use cases provided by our industrial partners. On the other hand, we show that query answering remains tractable in the size of both the input graph and the query despite the additional expressivity. In addition to query answering, we also study the query containment and equivalence problems for (extended) faceted queries—the fundamental problems underpinning static analysis and query optimisation—which were not considered in prior work. We show that these problems are both \(\textsc {coNP} \)-complete for our extended language, where the \(\textsc {coNP} \) lower bound holds already for core faceted queries without comparisons, aggregation or reachability. This is in contrast to unrestricted positive existential queries in first-order logic for which the problems are known to be \(\varPi ^p_2\)-complete and thus in the second level of the polynomial hierarchy. Furthermore, we propose a practical fragment of our extended query language for which the problems become tractable. Finally, we have extended the faceted search system SemFacetFootnote 1 to support numeric value ranges and aggregation, and we are currently working on extending the system to further support the aforementioned reachability features.
2 Preliminaries
We assume a vocabulary consisting of pairwise disjoint countably infinite sets of individuals \({\mathbf {I}} \), numeric literals \(\mathbf {NL} \) (which we assume to correspond to the rational numbers), classes \(\mathbf {C} \)—that is, unary predicates that range over \({\mathbf {I}} \), object properties \(\mathbf {OP} \)—that is, binary predicates with both arguments ranging over \({\mathbf {I}} \), and datatype properties \(\mathbf {DP} \)—that is, binary predicates with the first argument ranging over \({\mathbf {I}} \) and the second over \(\mathbf {NL} \). We also consider a countably infinite set \(\mathbf {V} \) of variables, which is pairwise disjoint with all the aforementioned sets.
A fact is an expression of the form A(c) with \(A \in \mathbf {C} \) and \(c \in {\mathbf {I}} \), \(P(c_1, c_2)\) with \(P \in \mathbf {OP} \) and \(c_1, c_2 \in {\mathbf {I}} \), or D(c, n) with \(D \in \mathbf {DP} \), \(c \in {\mathbf {I}} \) and \(n \in \mathbf {NL} \). In the context of this paper, we define an RDF graph as a finite set of facts. The active domain \(\mathsf {ADom}(G)\) of an RDF graph G is the set of all its individuals and numeric literals. Note that our formalisation captures RDF datasets corresponding to sets of OWL 2 DL assertions—that is, the datasets that can be seamlessly used in conjunction with OWL 2 DL ontologies.
A relational atom is an expression of the form A(x) with \(A \in \mathbf {C} \) and \(x \in \mathbf {V} \) or \(R(x_1, x_2)\) with \(R \in \mathbf {OP} \cup \mathbf {DP} \) and \(x_1, x_2 \in \mathbf {V} \). An equality atom is an expression of the form \(x = a\), where \(x \in \mathbf {V} \) and \(a \in {\mathbf {I}} \cup \mathbf {NL} \).
A positive existential query \(Q(\bar{x})\) is a first-order logic formula with free variables \(\bar{x}\), denoted \(\mathrm{\mathsf {fvar}}(Q)\), built from relational and equality atoms using disjunction \(\vee \), conjunction \(\wedge \), and existential quantification \(\exists \). We assume all positive existential queries to be rectified—that is, without different quantifications of the same variable, and denote \(\mathsf {PEQ}\) the set of all such queries. A positive existential query is a conjunctive query if it is \(\vee \)-free. We denote \(\mathsf {CQ}\) the set of all conjunctive queries. A query Q is monadic if it has exactly one free variable.
We next define the semantics of \(\mathsf {PEQ}\). Let G be an RDF graph. A valuation over variables \(\bar{x}\) is a mapping \(\nu : \bar{x} \rightarrow \mathsf {ADom}(G)\). For \(\nu \) a valuation over \(\bar{x}\) and variables \(\bar{y} \subseteq \bar{x}\), we denote \(\nu \vert _{\bar{y}}\) the restriction of \(\nu \) to \(\bar{y}\). Let \(Q \in \mathsf {PEQ}\), and \(\nu \) be a valuation over \(\mathrm{\mathsf {fvar}}(Q)\). Then, G satisfies Q under \(\nu \), denoted \(G,\nu \,\models \,Q\), if
-
Q is an atom \(R(\bar{x})\) and \(R(\nu (\bar{x})) \in G\);
-
Q is an atom \(x = a\) and \(\nu (x) = a\);
-
\(Q = Q_1 \wedge Q_2\), \(G,\nu \vert _{\mathrm{\mathsf {fvar}}(Q_1)}\,\models \,Q_1\), and \(G,\nu \vert _{\mathrm{\mathsf {fvar}}(Q_2)}\,\models \,Q_2\);
-
\(Q = Q_1 \vee Q_2\) and either \(G,\nu \vert _{\mathrm{\mathsf {fvar}}(Q_1)}\,\models \,Q_1\) or \(G,\nu \vert _{\mathrm{\mathsf {fvar}}(Q_2)}\,\models \,Q_2\); or
-
\(Q = \exists y. \,Q'\) and \(G, \nu \cup \{y \mapsto c\}\,\models \,Q'\) for some \(c \in {\mathbf {I}} \cup \mathbf {NL} \).
The semantics \([Q]_{G}\) of a query \(Q(\bar{x})\) (in \(\mathsf {PEQ}\) or its extension) over an RDF graph G is the following set of tuples of elements in \({\mathbf {I}} \cup \mathbf {NL} \):
The query answering problem is to compute \([Q]_{G}\) given Q and G.
A query Q is contained in a query \(Q'\), written \(Q \subseteq Q'\) if \([Q]_{G} \subseteq [Q']_{G}\) holds for every RDF graph G. They are equivalent, written \(Q \equiv Q'\), if \([Q]_{G} = [Q']_{G}\) for every G. The query containment problem is to determine, given queries Q and \(Q'\) as input, whether \(Q \subseteq Q'\). The query equivalence problem is to determine whether \(Q \equiv Q'\). Note that these problems are easily reducible to each other for all query languages considered in this paper: \(Q \equiv Q'\) if and only if \(Q \subseteq Q'\) and \(Q' \subseteq Q\), while \(Q \subseteq Q'\) if and only if \(Q \wedge Q' \equiv Q\).
When talking about complexity of algorithms, we assume the usual binary representation of graphs and queries; in particular, rational numbers are represented by pairs of an integer and a positive integer in binary, one for the numerator and the other for the denominator. This representation size of a graph G should be distinguished from the number of facts in G, which is denoted as |G|.
3 Faceted Queries
In this section, we recapitulate the language of faceted queries as proposed in [1] and justify its main features using the example faceted interface on the left-hand-side of Fig. 2.Footnote 2 Our treatment is by no means comprehensive, and we refer the interested reader to the aforementioned papers for additional details.
The front-end of a typical RDF faceted search system provides (1) a search text box, where users can enter keywords; (2) a faceted interface, which contains facets and their possible values; and (3) a results pane, where the search results are provided. The keywords entered in the search box are used, on the one hand, to obtain an initial set of results (using standard information-retrieval techniques) and, on the other hand, to construct an initial faceted interface without selected values, which constitutes the starting point for faceted navigation. The set of values selected by users in the faceted interface are compiled into a query, which is then issued to a triple store holding the input RDF graph. The answers to the query are finally depicted in the results pane.
The basic element of a faceted interface is a facet, which consists of a facet name and a set of values (see Fig. 2). The special type facet is used to select the categories (classes) to which the results must belong. Facets can be conjunctive or disjunctive, depending on whether the selection of different values is interpreted disjunctively or conjunctively. For instance, the facet withHQ, which indicates the headquarters of companies, is disjunctive in the sense that selecting both Suwon and San Diego as values would result in a query asking for companies with headquarters in either of the aforementioned cities. In contrast to conventional faceted search systems, where the underpinning data has a simple “flat” structure, systems based on RDF must be able to search through complex graph data, and as a result facet nesting becomes an important feature. For instance, the producedBy facet in Fig. 2 (left) is nested under the hasPart facet, which indicates that the values of the facet refer to the companies that produce phone parts, rather than those producing phones themselves.
The queries obtained as a result of compiling user value selections in a faceted interface are referred to as faceted queries. We next discuss the intuition behind such compilation; a formal treatment can be found in [1].
Selections in the special facet type are interpreted as conjunctions (or disjunctions) of unary relational atoms over the same variable. Selections on any other facet yield either a binary relational atom whose second argument is existentially quantified (if the special value Any is selected), or in a conjunction (disjunction) of binary relational atoms having as second argument a constant or a variable belonging to a unary relational atom. Facet nesting involves a “shift” of variable from the parent facet to the nested facet as well as to the introduction of fresh existentially quantified variables. As a result, faceted queries can be seen as positive existential queries satisfying the following restrictions:
-
(R1)
they are monadic since query answers displayed in a system’s results pane are individual objects, rather than tuples of objects;
-
(R2)
they are tree-shaped since existentially quantified variables introduced by facet nesting are always fresh; and
-
(R3)
all disjuncts of a disjunctive (sub-)query are also monadic, with the same free variable shared across all their disjuncts.
For instance, the user selections on the left-hand side of Fig. 2 are compiled into the following faceted query \(Q^{\text {ex}}_1(x)\) asking for smartphones whose processor is produced by any company with headquarters in either Suwon or San Diego:
Note that query \(Q^{\text {ex}}_1\) has a single free variable x and hence satisfies restriction (R1). Furthermore, it has no cyclic dependencies between its variables and hence satisfies restriction (R2). Finally, the disjuncts in the only disjunctive sub-query of \(Q^{\text {ex}}_1\) share their only free variable y, and hence the query satisfies (R3). Restrictions (R1)–(R3) are formalised in the following definitions.
Definition 1
The graph of \(Q \in \mathsf {PEQ}\) is the directed labeled graph such that
-
its nodes are the variables mentioned in Q;
-
its edges are the pairs \((x_1, x_2)\) with relational atoms \(P(x_1, x_2)\) in Q; and
-
the label of \((x_1, x_2)\) is the set of all properties P with \(P(x_1, x_2)\) in Q.
A monadic query \(Q(x) \in \mathsf {PEQ}\) is tree-shaped if its graph is a directed tree rooted at x and the label of each edge is a singleton.
Definition 2
A (core) faceted query Q is a monadic, tree-shaped query in \(\mathsf {PEQ}\) satisfying the following additional property: if \(Q_1 \vee Q_2\) is a sub-query of Q, then \(\mathrm{\mathsf {fvar}}(Q_1) = \mathrm{\mathsf {fvar}}(Q_2) = \{x\}\) for some variable x. We denote with \(\mathsf {FQ}\) and \(\mathsf {CFQ}\) the classes of all faceted queries and all conjunctive faceted queries, respectively.
The restrictions in this definition are sufficient for an existence of a polynomial-time query answering algorithm [1].
4 Extended Faceted Queries
In this section, we present our extension of core faceted queries. We consider as a running example the faceted interface depicted on the right-hand-side of Fig. 2. Intuitively, the user selections in the figure represent a search for all smartphones with maximum price amongst all sellers comprised between \(\pounds 500\) and \(\pounds 900\), and whose processor has been manufactured by a North American company. The interface on the right-hand side of the figure extends that on the left-hand side with two additional elements:
-
an aggregate facet consisting of a selection for an aggregate and a numeric range slider, and which establishes the relevant restriction on the maximum smartphone price;
-
a special facet with a search box which allows users to search for “reachable” facets, thus providing a shortcut for the relevant continent selection.
To capture such new elements, we extend the query language in Sect. 4 with three new types of atoms, namely (i) comparison atoms, extending equality atoms and capture numeric comparisons between a variable and a numeric literal; (ii) aggregate atoms, capturing aggregation; and (iii) reachability atoms, representing a limited form of recursion sufficient to capture the shortcuts.
We start by defining comparison atoms and their semantics.
Definition 3
A comparison atom is an expression of the form \(x \, \mathbin {\mathtt {op}}\, a\), where \(x \in \mathbf {V} \), \(\mathbin {\mathtt {op}}\in \{=, \le , \ge , <, >\}\), and \(a \in {\mathbf {I}} \cup \mathbf {NL} \) if \(\mathbin {\mathtt {op}}\) is \(=\) and \(a \in \mathbf {NL} \) otherwise. An RDF graph G satisfies a comparison atom \(x \mathbin {\mathtt {op}}a\) under a valuation \(\nu \) over x, written \(G, \nu \,\models \,x \,\mathbin {\mathtt {op}}\, a\), if and only if \(\nu (x)\mathbin {\mathtt {op}}a\) holds under the conventional built-in meaning of comparison predicates (assuming that \(\nu (x)\mathbin {\mathtt {op}}a\) is false if \(\nu (x) \notin \mathbf {NL} \) and \(\mathbin {\mathtt {op}}\) is not \(=\)).
Note that each equality atom is a comparison atom by definition.
For instance, the following query uses comparison atoms to ask for all smartphones with price range between \(\pounds 500 \) and \(\pounds 900\):
Aggregate atoms in our language provide a restricted form of aggregation over what is available in standard query languages such as SPARQL 1.1 [13, 18]. An important restriction is that the value computed by the corresponding aggregate function is immediately compared to a constant and thus the atom is evaluated to either true or false in any given graph and valuation. This is in contrast to SPARQL 1.1, where the value computed by an aggregate function can be assigned to a variable which can then occur in other parts of the query. Another restriction is that grouping is always performed over the first argument of an object or datatype property and, as a result, the collection of values over which the aggregate function is evaluated cannot contain duplicates and thus can be seen as a set rather than a multiset.
Definition 4
An aggregate function is a function  , where \(\mathtt {undef}\) is a special symbol. We concentrate on several specific aggregate functions, defined as follows, for \(S \subseteq {\mathbf {I}} \cup \mathbf {NL} \):
, where \(\mathtt {undef}\) is a special symbol. We concentrate on several specific aggregate functions, defined as follows, for \(S \subseteq {\mathbf {I}} \cup \mathbf {NL} \):
-
\(\mathsf {count} (S)\) is the cardinality of S;
-
\(\mathsf {min} (S)\) is the minimum in S if \(S \subseteq \mathbf {NL} \) and \(S \ne \emptyset \), and it is \(\mathtt {undef}\) otherwise;
-
\(\mathsf {max} (S)\) is the maximum in S if \(S \subseteq \mathbf {NL} \) and \(S \ne \emptyset \), and \(\mathtt {undef}\) otherwise;
-
\(\mathsf {sum} (S)\) is the sum of literals in S if \(S \subseteq \mathbf {NL} \), and it is \(\mathtt {undef}\) otherwise;
-
\(\mathsf {avg} (S)\) is \(\mathsf {sum} (S) / \mathsf {count} (S)\) if \(\mathsf {sum} (S) \ne \mathtt {undef}\) and \(\mathsf {count} (S) \notin \{0, \mathtt {undef}\}\), and it is \(\mathtt {undef}\) otherwise.
An aggregate atom is an expression of the form \(\mathtt {Agg}(x,R,\mathsf {f}) \mathbin {\mathtt {op}}n\), where \(\mathsf {f} \) is one of the aforementioned aggregate functions, R is a property that is datatype if \(\mathsf {f} \ne \mathsf {count} \), x is a variable, \(\mathbin {\mathtt {op}}\in \{=, \le , \ge , <, >\}\), and \(n \in \mathbf {NL} \). An RDF graph G satisfies an aggregate atom \(\mathtt {Agg}(x,R,\mathsf {f}) \mathbin {\mathtt {op}}n\) under a valuation \(\nu \) over x, written \(G, \nu \,\models \,\mathtt {Agg}(x,R,\mathsf {f}) \mathbin {\mathtt {op}}n\), if and only if \(\mathsf {f} (\{ a \mid R(\nu (x),a) \in G\}) \mathbin {\mathtt {op}}n\) (assuming that all comparison operators return false if the first argument is \(\mathtt {undef}\)).
For instance, the following query relies on aggregate atoms to ask for smartphones with average price across all sellers greater than \(\pounds 500\):
We next define reachability atoms, capturing the shortcuts in navigation.
Definition 5
A reachability atom is an expression of the form  or
or  with \(x_1, x_2 \in \mathbf {V} \). An RDF graph G satisfies a reachability atom \(\alpha \) under a valuation \(\nu \), denoted \(G, \nu \,\models \,\alpha \), if
with \(x_1, x_2 \in \mathbf {V} \). An RDF graph G satisfies a reachability atom \(\alpha \) under a valuation \(\nu \), denoted \(G, \nu \,\models \,\alpha \), if
-
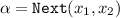 and there is a property R such that \(G,\nu \,\models \,R(x_1,x_2)\); or
and there is a property R such that \(G,\nu \,\models \,R(x_1,x_2)\); or -
 and there exist \(a^1, \ldots , a^n\), \(n \ge 1\), in \({\mathbf {I}} \cup \mathbf {NL} \) such that \(\nu (x_1) = a^1\), \(\nu (x_2) = a^n\), and, for each \(i = 1, \ldots , n-1\), there is a property \(R_i\) such that \(R_i(a^i, a^{i+1}) \in G\).
and there exist \(a^1, \ldots , a^n\), \(n \ge 1\), in \({\mathbf {I}} \cup \mathbf {NL} \) such that \(\nu (x_1) = a^1\), \(\nu (x_2) = a^n\), and, for each \(i = 1, \ldots , n-1\), there is a property \(R_i\) such that \(R_i(a^i, a^{i+1}) \in G\).
Our example search on the right-hand side of Fig. 2 can be captured by the following faceted query \(Q^{\text {ex}}_4 (x)\), involving aggregate and reachability atoms:

The languages of positive existential queries and faceted queries are extended in the obvious way by allowing for the new types of atoms (i.e., comparison, aggregate and reachability) in addition to relational atoms.
Definition 6
Extended positive existential queries are defined in the same way as positive existential queries, except that they allow for not only relational and equality, but also (arbitrary) comparison, aggregate, and reachability atoms as building blocks. Extended faceted queries are also defined in the same way as core faceted queries; in this case, the graph of the query takes into account binary relational atoms and reachability atoms (but not comparison or aggregate ones). We denote with \(\mathcal L[\mathcal O]\), for \(\mathcal L \in \{\mathsf {PEQ}, \mathsf {CQ}, \mathsf {FQ}, \mathsf {CFQ}\}\) and \(\mathcal O \subseteq \{Comp, Agg, Next, Next^+\}\) the language obtained by extending \(\mathcal L\) with atoms specified in \(\mathcal O\) as follows: comparison if \(Comp \in \mathcal O\), aggregate if \(Agg \in \mathcal O\),  if \(Next \in \mathcal O\), and
if \(Next \in \mathcal O\), and  .
.
It is known that core faceted queries are expressible in the standard RDF query language SPARQL [1]. Similarly, extended faceted queries allow for a direct translation to the current version of this language, SPARQL 1.1 [13, 18]. In particular, it has aggregation functionality, which captures aggregate atoms in faceted queries, and property paths, which capture reachability atoms.
5 Answering Extended Faceted Queries
In [1] it was shown that core faceted queries (i.e., faceted queries without comparison, aggregate, and reachability atoms) can be answered in polynomial time. This is in contrast to unrestricted positive existential (or even conjunctive) queries, where evaluation problem is well-known to be \(\textsc {NP} \)-complete.
Tractability of core faceted query answering relies on two key observations [1]. First, answering monadic tree-shaped conjunctive queries is a well-known tractable problem; thus, the only possible source of intractability is the presence of disjunction. Second, disjunctive subqueries in a faceted query can be answered in a bottom-up fashion: to compute the answers to \( Q_1(x) \vee Q_2(x)\) it suffices to answer \(Q_1(x)\) and \(Q_2(x)\) independently and “store” the answers as new unary relational facts in the input RDF graph using a fresh class \(C_{Q_1 \vee Q_2}\) uniquely associated to \( Q_1(x) \vee Q_2(x)\). The polynomial time algorithm in [1] stems from a direct application of these observations, and relies on an oracle for answering monadic tree-shaped conjunctive queries.
In this section, we study the problem of answering extended faceted queries over RDF graphs. Specifically, we propose a polynomial time query answering algorithm that generalises that in [1] to account for the additional features of the query language. We proceed in the following two steps.
-
1.
In the first step we show that comparison and aggregate atoms can be encoded away by a polynomial time rewriting of the input query and RDF graph; the correctness of this rewriting is independent from the special properties of faceted queries, and thus it equivalently transforms any query in \(\mathsf {PEQ}[Comp, Agg, Next, Next^+]\) into \(\mathsf {PEQ}[Next, Next^+]\).
-
2.
In the second step we show that, analogously to core faceted queries, any query in \(\mathsf {FQ}[Next, Next^+]\) can be efficiently answered in a bottom-up fashion while “storing” the results of disjunctive subqueries in the RDF graph. In contrast to the algorithm in [1], which relies on an oracle for answering monadic tree-shaped conjunctive queries, our extended algorithm relies on the existence of a polynomial time procedure for answering a special type of conjunctive regular path queries (CRPQs) [2].
In the intermediate steps of the algorithms in this and the following sections we operate with graphs and queries that allow for generalised predicates: a heterogeneous class is a unary predicate that ranges over \({\mathbf {I}} \cup \mathbf {NL} \), and a heterogeneous property is a binary predicate with the first argument ranging over \({\mathbf {I}} \) and the second over \({\mathbf {I}} \cup \mathbf {NL} \). For brevity, we assume that such graphs are RDF graphs and such queries belong to the corresponding languages (e.g., \(\mathsf {FQ}\)).
For the first step, consider a query Q(x) in \(\mathsf {PEQ}[Comp, Agg, Next, Next^+]\) and an RDF graph G. For every comparison or aggregate atom \(\alpha \) in Q, we introduce a fresh heterogeneous class \(C_{\alpha }\). Let \(\tilde{Q}\) be the query in \(\mathsf {PEQ}[Next, Next^+]\) obtained from Q by replacing each comparison or aggregate atom \(\alpha \) with the free variable x by \(C_{\alpha }(x)\). Note that if Q is in \(\mathsf {FQ}[Comp, Agg, Next, Next^+]\), then \(\tilde{Q}\) is in \(\mathsf {FQ}[Next, Next^+]\). Let also \(\tilde{G}\) be the union of G and the following graphs:
The following lemma establishes the correctness of the transformation.
Lemma 1
Given a query Q in \(\mathsf {PEQ}[Comp, Agg, Next, Next^+]\) and an RDF graph G, query \(\tilde{Q}\) and RDF graph \(\tilde{G}\) can be computed in polynomial time in the sizes of binary representations of Q and G. Moreover, \([Q]_{G} = [{\tilde{Q}}]_{{\tilde{G}}}\).
Note that, in particular, the number N of atoms in \(\tilde{Q}\) is the same as in Q, and \(|\tilde{G}| \le |G| + N \cdot |\mathsf {ADom}(G)|\).
Having Lemma 1 at hand, it is enough to define a polynomial-time procedure for answering queries in \(\mathsf {FQ}[Next, Next^+]\), which we do in the second step. To this end, we first note that tree-shaped queries in \(\mathsf {CQ}[Next, Next^+]\) can be directly translated into strongly acyclic CRPQs, which can be answered in linear time both in the size of the query and the RDF graph [2].
Lemma 2
Computing \([Q]_{G}\) for a monadic tree-shaped query Q in the class \(\mathsf {CQ}[Next, Next^+]\) and a generalised RDF graph G can be done in \(O(n \cdot m)\), where n and m are the sizes of binary representations of Q and G, respectively.
We next present Algorithm 1, which computes \([Q]_{G}\) for a query \(Q(x) \in \mathsf {FQ}[Comp, Agg, Next, Next^+]\) and an RDF graph G. First, the algorithm eliminates comparison and aggregation atoms on the basis of Lemma 1. Then, analogously to the algorithm in [1], it iterates, in a bottom-up manner, over all disjunctive subqueries of Q: each disjunctive-free subquery is dealt with using the procedure Answer-saCRPQ for answering strongly acyclic CRPQs on the basis of Lemma 2, while the disjunctive subquery is replaced with the atom \(C_{Q_1 \vee Q_2}(x)\) in Q (for \(C_{Q_1 \vee Q_2}\) a fresh heterogeneous class), and the graph is extended by atoms \(C_{Q_1 \vee Q_2}(a)\) for all a returned by the call to Answer-saCRPQ. The correctness of Algorithm 1 leads to our main result in this section.

Theorem 1
Query answering in \(\mathsf {FQ}[Comp, Agg, Next, Next^+]\) can be solved in polynomial time.
6 Query Containment and Equivalence
In this section we consider the containment and equivalence problems for faceted queries. These are fundamental problems for static analysis and query optimisation and, to the best of our knowledge, have not been considered in prior work on faceted search in the Semantic Web context.
We concentrate on containment: as argued in Sect. 2, containment and equivalence are polynomially inter-reducible. We start by showing that containment is coNP-complete for \(\mathsf {FQ}[Comp, Agg, Next, Next^+]\), and the hardness holds even for \(\mathsf {FQ}\) and for \(\mathsf {CFQ}[Next, Next^+]\). Then, we establish tractability of containment for practically important subclasses of faceted queries, namely \(\mathsf {CFQ}[Comp, Agg, Next]\) and \(\mathsf {CFQ}[Comp, Agg, Next^+]\). Finally, we show that the requirement on disjunction in the definition of faceted queries has a significant impact on complexity: containment of monadic tree-shaped \(\mathsf {PEQ}\) (without any additional restriction on disjunctive subformulas) is \(\varPi ^p_2\)-complete, and hence as hard as containment for unrestricted \(\mathsf {PEQ}\).
First we show a coNP upper bound for \(\mathsf {FQ}[Comp, Agg, Next, Next^+]\). We start with several definitions.
Let Q and \(Q'\) be \(\mathsf {FQ}[Comp, Agg, Next, Next^+]\) queries, and let N and \(N^+\) be fresh heterogeneous properties. We first show how to eliminate reachability atoms and fractional numbers from Q and \(Q'\). Consider all the numeric literals \(a_1, \ldots , a_n\) in the comparison and aggregate atoms of Q and \(Q'\) except aggregate atoms over \(\mathsf {count} \), as well as integers \(b_1, \ldots , b_n\) that are numerators of rational numbers obtained from \(a_1, \ldots , a_n\) by bringing them to the smallest common denominator. Denote \(\tilde{Q}\) and \(\tilde{Q}'\) the queries in \(\mathsf {FQ}[Comp, Agg]\) obtained from Q and \(Q'\), respectively, by replacing
-
1.
each \(a_i\) in comparison and non-\(\mathsf {count} \) aggregate atoms by \(b_i\); and
-
2.
each atom
 by \(N(x_1, x_2)\) and each
by \(N(x_1, x_2)\) and each  .
.
The size of binary representation of \(\tilde{Q}\) and \(\tilde{Q}'\) is polynomial in the size of Q and \(Q'\), and \(\tilde{Q}\) and \(\tilde{Q}'\) can be constructed efficiently, in polynomial time. As we will see later, containment of Q in \(Q'\) can be reduced to containment of \(\tilde{Q}\) in \(\tilde{Q}'\).
A generalised RDF graph G is a set of facts enriched, for each constant \(c \in {\mathbf {I}} \),
-
by a non-negative integer \(\textit{Val}(c,R,\mathsf {count}) \) for each \(R \in \mathbf {OP} \cup \mathbf {DP} \), and
-
by rational numbers \(\textit{Val}(c,D,\mathsf {f}) \) for all \(\mathsf {f} \in \{\mathsf {min}, \mathsf {max}, \mathsf {sum} \}\) and all \(D \in \mathbf {DP} \).
Graph G is realisable if there is an RDF graph \(G'\) such that all facts of G are also in \(G'\), and \(\mathsf {f} (\{a \mid R(c, a) \in G'\}) = \textit{Val}(c,R,\mathsf {f}) \) for all \(\textit{Val}(c,R,\mathsf {f}) \) in G.
The semantics \([Q]_{G}\) of a query \(Q(\bar{x})\) over a generalised RDF graph G is defined in the same way as over a usual one, except that, when evaluating aggregate atoms, aggregation values are not computed on the facts, but taken from the corresponding \(\textit{Val}(c,R,\mathsf {f}) \) (assuming \(\textit{Val}(c,R,\mathsf {avg}) = \textit{Val}(c,R,\mathsf {sum}) / \textit{Val}(c,R,\mathsf {count}) \) for uniformity).
Intuitively, the generalised RDF graph G represents (a part of) the usual RDF graph \(G'\) witnessing its realisability: numbers \(\textit{Val}(c,R,\mathsf {f}) \) describe the values of aggregates \(\mathsf {f} \) for c and R in \(G'\) in a concise way. Note, however, that the size of a binary representation of G may be exponentially smaller than that of \(G'\), because for some constants c and properties R graph G may store only the number of R-successors of c in binary instead of listing them one by one (of course, some parts of \(G'\) may also be not represented in G at all). If fact, as we will see soon, in search for a witness for non-containment, we can restrict ourselves to generalised graphs with polynomially-sized binary representation, while the corresponding witnessing usual graph may be necessarily exponential. But before formalising this, we show how to modify the graph to deal correctly with reachability.
A generalised RDF graph G is reachability-closed if
-
\(N(a_1, a_2) \in G\) if and only if \(R(a_1, a_2) \in G\) for some \(R \not \in \{N, N^+\}\); and
-
\(N^+(a_1, a_2) \in G\) if and only if there is a directed path from \(a_1\) to \(a_2\) in G via properties different from N and \(N^+\).
Lemma 3
Given queries Q and \(Q'\) in \(\mathsf {FQ}[Comp, Agg, Next, Next^+]\), \(Q \not \subseteq Q'\) if and only if there exists a realisable generalised reachability-closed RDF graph \(G'\) with binary representation of polynomial size in the sizes of representations of Q and \(Q'\) such that \([\tilde{Q}]_{G'} \not \subseteq [\tilde{Q}']_{G'}\).
The final key observation is that Theorem 1, which ensures that the query evaluation is feasible, applies to generalised graphs with minor modifications of justifying Algorithm 1, while realisability can also be easily checked.
Lemma 4
Containment is in coNP for \(\mathsf {FQ}[Comp, Agg, Next, Next^+]\).
We now move on to the \(\textsc {coNP} \) lower bound which, as we show next, holds already for rather restricted languages.
Lemma 5
Containment is coNP-hard for both \(\mathsf {FQ}\) and \(\mathsf {CFQ}[Next, Next^+]\).
Proof
(Sketch). We start with a reduction of 3SAT to the complement of the containment for \(\mathsf {FQ}\). Let \(\varphi \) be a propositional formula in 3CNF over m variables \(u_i\), \(i = 1, \ldots , m\), with n clauses \(\gamma _j = \ell ^1_j \vee \ell ^2_j \vee \ell ^3_j\), \(j = 1, \ldots , n\). For each \(i = 1, \ldots , m\), let \(T_i\) and \(F_i\) be classes, and, for each \(j = 1, \ldots , n\), let \(Q_j(x) = V^1_j(x) \vee V^2_j(x) \vee V^3_j(x)\), where \(V^k_j\), for \(k = 1, 2, 3\), is \(T_i\) if \(\ell ^k_j = u_i\) and \(F_i\) if \(\ell ^k_j = \lnot u_i\).
Consider the following queries in \(\mathsf {FQ}\):
Intuitively, Q encodes the fact that for every \(i = 1, \ldots , m\) either \(u_i\) or \(\lnot u_i\) must be true and that every clause \(\gamma _j\), \(1\le j\le n\), must be true as well. Negation of \(Q'\) encodes the fact that \(u_i\) and \(\lnot u_i\) cannot be true at the same time. We claim that \(\varphi \) is satisfiable if and only if \(Q \not \subseteq Q'\).
The \(\textsc {coNP} \)-hardness for \(\mathsf {CFQ}[Next, Next^+]\) can be proved in a similar way as the hardness of containment of tree patterns over trees in [22]. \(\square \)
Lemmas 4 and 5 give us the following theorem.
Theorem 2
Containment is coNP-complete for any query language between \(\mathsf {FQ}\) and \(\mathsf {FQ}[Comp, Agg, Next, Next^+]\) as well as for any query language between \(\mathsf {CFQ}[Next, Next^+]\) and \(\mathsf {FQ}[Comp, Agg, Next, Next^+]\).
This theorem leaves open the question what faceted queries have tractable containment. Next we show that it is true for conjunctive faceted queries that use either only  or only
or only  . We start with some definitions.
. We start with some definitions.
Consider a query Q in \(\mathsf {CFQ}[Comp, Agg, Next]\) or in \(\mathsf {CFQ}[Comp, Agg, Next^+]\). A variable x in Q is domain-inconsistent if Q has an atom of the form C(x) with \(C \in \mathbf {C} \), R(x, y) with  , \(P(x',x)\) with \(P \in \mathbf {OP} \), \(x \, \mathbin {\mathtt {op}}\, a\) with \(a \in {\mathbf {I}} \), or \(\mathtt {Agg}(x,R,\mathsf {f}) \mathbin {\mathtt {op}}n\), as well as an atom of the form \(D(x',x)\) with \(D \in \mathbf {DP} \) or \(x \, \mathbin {\mathtt {op}}\, n\) with \(n \in \mathbf {NL} \). Intuitively, domain-consistency ensures that no variable is required to match both a constant and a numeric literal.
, \(P(x',x)\) with \(P \in \mathbf {OP} \), \(x \, \mathbin {\mathtt {op}}\, a\) with \(a \in {\mathbf {I}} \), or \(\mathtt {Agg}(x,R,\mathsf {f}) \mathbin {\mathtt {op}}n\), as well as an atom of the form \(D(x',x)\) with \(D \in \mathbf {DP} \) or \(x \, \mathbin {\mathtt {op}}\, n\) with \(n \in \mathbf {NL} \). Intuitively, domain-consistency ensures that no variable is required to match both a constant and a numeric literal.
For each variable x in Q, let \(\varSigma _{Comp}(x, Q)\) be the set of all comparison atoms in Q where x appears. Then, for any variables x and y, denote \(x \sim _Q y\) the fact that \(\varSigma _{Comp}(x, Q)\) and \(\varSigma _{Comp}(y, Q)\) imply \(x = y\). Finally, for each x and property R, let \(\varSigma _{Agg}(x, R, Q)\) be the set of constraints
where, for each aggregate function \(\mathsf {f} \), \(x_{\mathsf {f}}\) is a fresh variable. Query Q is consistent if \(\varSigma _{Comp}(x, Q)\) has a solution for any x in Q, \(\varSigma _{Agg}(x, R, Q)\) has a solution for any x and any \(R\in \mathbf {OP} \cup \mathbf {DP} \), and Q has no domain-inconsistent variable.
Given queries Q(x) and \(Q'(x)\) both either in \(\mathsf {CFQ}[Comp, Agg, Next]\) or in \(\mathsf {CFQ}[Comp, Agg, Next^+]\), a homomorphism from \(Q'\) to Q is a mapping h from variables of \(Q'\) to variables of Q such that \(h(x) = x\) and, for every relational atom \(R(x'_1, \ldots , x'_n) \in Q'\), there exists \(R(x_1, \ldots , x_n) \in Q\) with \(h(x'_i) \sim _Q x_i\) for every i. Homomorphism h is comparison-preserving if \(\varSigma _{Comp}(h(x'), Q)\) implies \(\varSigma _{Comp}(x', Q')\) for any variable \(x'\) of \(Q'\). It is aggregation-preserving if \(\varSigma _{Agg}(h(x'), R, Q)\) implies \(\varSigma _{Agg}(x', R, Q')\) for any variable \(x'\) of \(Q'\) and any R. It is Next-preserving if, for every atom  in \(Q'\), there is \(R(x_1, x_2) \in Q\) with
in \(Q'\), there is \(R(x_1, x_2) \in Q\) with  , \(h(x'_1) \sim _Q x_1\), and \(h(x'_2) \sim _Q x_2\). It is \(Next^+\)-preserving if for every
, \(h(x'_1) \sim _Q x_1\), and \(h(x'_2) \sim _Q x_2\). It is \(Next^+\)-preserving if for every  in \(Q'\) there are \(R_1(y_1, z_1), \ldots , R_{n}(y_n, z_n)\), \(n \ge 1\), in Q with all
in \(Q'\) there are \(R_1(y_1, z_1), \ldots , R_{n}(y_n, z_n)\), \(n \ge 1\), in Q with all  , such that \(h(x'_1) \sim _Q y_1\), \(h(x'_2) \sim _Q z_n\), and \(z_i \sim _Q y_{i+1}\) for each \(i = 1, \ldots , n-1\).
, such that \(h(x'_1) \sim _Q y_1\), \(h(x'_2) \sim _Q z_n\), and \(z_i \sim _Q y_{i+1}\) for each \(i = 1, \ldots , n-1\).
Proposition 1
Let Q and \(Q'\) be queries in \(\mathsf {CFQ}[Comp, Agg, \mathcal N]\), where \(\mathcal N \in \{Next, Next^+\}\). Then, \(Q \subseteq Q'\) if and only if either Q is not consistent or there is a comparison-, aggregation- and \(\mathcal N\)-preserving homomorphism from \(Q'\) to Q.
Checking for existence of a comparison-, aggregation- and \(\mathcal N\)-preserving homomorphism for tree-shaped queries can be done in polynomial time using standard techniques for tree homomorphisms (see, e.g., [22]), while checking for consistency is straightforward. So, we have the following theorem.
Theorem 3
The containment problem both for \(\mathsf {CFQ}[Comp, Agg, Next]\) and for \(\mathsf {CFQ}[Comp, Agg, Next^+]\) is in \(\textsc {PTime} \).
We conclude by showing that the requirement on disjunction in the definition of faceted queries makes a difference, and containment for monadic tree-shaped \(\mathsf {PEQ}\) is \(\varPi ^p_2\)-complete. The following theorem can be proved by a reduction of \(\forall \exists \)3SAT; the matching upper complexity bound is inherited from arbitrary \(\mathsf {PEQ}\).
Theorem 4
Containment is \(\varPi ^p_2\)-hard for monadic tree-shaped \(\mathsf {PEQ}\).
7 Related Work
To the best of our knowledge, there is no theoretical study on extensions of faceted search with numeric value ranges, aggregation, and reachability. On the system side, we are not aware of any RDF-based faceted search system that currently supports aggregation (see [29] for a comprehensive survey). Aggregation in faceted search has so far been considered only in the context of conventional data models [3, 7], which are not graph-based; in that setting, the focus was on improved indexing schemes to optimise interface computation and update. A limited form of recursion is supported by the /facet system [15], where the transitive closure of transitive properties is precomputed and explicitly stored in the RDF graph. Finally, numeric value ranges have been implemented in several systems [12, 27] and their implementation is similar to ours in SemFacet.
Query containment is a classical problem in database theory. Containment of acyclic conjunctive queries is tractable [11, 31] which implies tractability of core conjunctive faceted queries that are tree-shaped and thus acyclic. Containment for (unions of) conjunctive queries is NP-complete [5]. It is also known that containment is \(\varPi ^p_2\)-complete for \(\mathsf {PEQ}\) [24], while our results show that hardness already holds for tree-shaped \(\mathsf {PEQ}\).
For \(\mathsf {CQ}\) it is known that adding comparison atoms changes complexity of containment from \(\textsc {NP} \)-complete to \(\varPi ^p_2\)-complete [9, 19, 21] and the known proofs of the lower bound either rely on ternary relations, or they exploit atoms that compare two variables. Our results show that adding comparison atoms of the form \(x~\mathtt {op}~a\) (for a a constant) does not increase the complexity of containment, which remains in \(\textsc {coNP} \). Moreover, containment for tree-shaped conjunctive queries with comparison atoms of the form \(x~\mathtt {op}~a\) is tractable [26], and thus the containment is also tractable for core conjunctive faceted queries with comparisons.
When aggregates are added to \(\mathsf {CQ}\) or \(\mathsf {PEQ}\), the complexity of containment becomes dependent on the supported aggregate functions [6]. Notably, most complexity upper bounds in the literature are formulated for queries containing a specific aggregate function only. In contrast, in this paper we allow for arbitrary combinations of aggregate functions in queries, while at the same time restricting other aspects of aggregation as discussed in Sect. 4.
A number of languages with recursive navigational features have been considered in the context of graph databases, including regular path queries (RPQs) and conjunctive regular path queries (CRPQs). These languages are very expressive and, as a result, containment becomes computationally expensive: it is \(\textsc {ExpSpace} \)-complete for CRPQs, where the lower bound already holds for acyclic CRPQs [2]. In contrast, the form of recursion provided by our query language is rather limited, and does not result in a complexity jump when added to faceted queries. Conjunctive faceted queries also resemble XML tree patterns, where the descendant axis in tree patterns is akin to our reachability atoms interpreted over XML trees. Containment of tree patterns is \(\textsc {coNP} \)-complete [22], and we used a similar idea to establish a \(\textsc {coNP} \) lower bound for conjunctive faceted queries with reachability atoms.
8 Conclusion and Future Work
In this paper we have extended existing faceted query languages with new features important in applications. We have shown that, despite the additional expressivity, query answering remains tractable in the combined size of the input query and RDF graph. We have also studied the query containment problem and established complexity bounds for a number of practically relevant fragments of our query language. From a practical point of view, we have extended the faceted search system SemFacet to support numeric value ranges and aggregation, and are currently working on extending it to also support reachability.
We see many directions for future work. From a theoretical perspective, we are planning to study extensions of faceted queries with additional features suggested by practical use cases, and in particular with a form of negation. Furthermore, we are also planning to study the computational properties of extended faceted queries in the presence of an ontology. From a practical perspective, we are working closely with our collaborators at EDF Energy on the development of a Semantic Search tool combining SemFacet and their in-house visualisation tool SemVue. The initial results of this collaboration have been very encouraging.
Notes
- 1.
- 2.
The figure is based on the front-end of the SemFacet system.
References
Arenas, M., Cuenca Grau, B., Kharlamov, E., Marciuška, Š., Zheleznyakov, D.: Faceted search over RDF-based knowledge graphs. J. Web Semant. 37, 55–74 (2016)
Barceló, P.: Querying graph databases. In: Proceedings of PODS (2013)
Ben-Yitzhak, O., Golbandi, N., Har’El, N., Lempel, R., Neumann, A., Ofek-Koifman, S., Sheinwald, D., Shekita, E., Sznajder, B., Yogev, S.: Beyond basic faceted search. In: Proceedings of WSDM (2008)
Berners-Lee, T., Hollenbach, J., Lu, K., Presbrey, J., Prudhommeaux, E., Schraefel, M.C.: Tabulator redux: browsing and writing linked data. In: LDOW (2008)
Chekuri, C., Rajaraman, A.: Conjunctive query containment revisited. Theor. Comput. Sci. 239(2), 211–229 (2000)
Cohen, S.: Containment of aggregate queries. SIGMOD Rec. 34(1), 77–85 (2005)
Dash, D., Rao, J., Megiddo, N., Ailamaki, A., Lohman, G.: Dynamic faceted search for discovery-driven analysis. In: Proceedings of CIKM (2008)
Fafalios, P., Tzitzikas, Y.: X-ENS: semantic enrichment of Web search results at real-time. In: Proceedings of SIGIR (2013)
Farré, C., Nutt, W., Teniente, E., Urpí, T.: Containment of conjunctive queries over databases with null values. In: Proceedings of ICDT (2007)
Ferré, S., Hermann, A.: Semantic search: reconciling expressive querying and exploratory search. In: Aroyo, L., Welty, C., Alani, H., Taylor, J., Bernstein, A., Kagal, L., Noy, N., Blomqvist, E. (eds.) ISWC 2011. LNCS, vol. 7031, pp. 177–192. Springer, Heidelberg (2011). doi:10.1007/978-3-642-25073-6_12
Gottlob, G., Leone, N., Scarcello, F.: The complexity of acyclic conjunctive queries. J. ACM 48(3), 431–498 (2001)
Hahn, R., Bizer, C., Sahnwaldt, C., Herta, C., Robinson, S., Bürgle, M., Düwiger, H., Scheel, U.: Faceted Wikipedia search. In: Proceedings of BIS (2010)
Harris, S., Seaborne, A.: SPARQL 1.1 query language. W3C recommendation, W3C, March 2013
Heim, P., Ziegler, J., Lohmann, S.: gFacet: a browser for the Web of Data. In: Proceedings of IMC-SSW (2008)
Hildebrand, M., van Ossenbruggen, J., Hardman, L.: /facet: a browser for heterogeneous semantic web repositories. In: Cruz, I., Decker, S., Allemang, D., Preist, C., Schwabe, D., Mika, P., Uschold, M., Aroyo, L.M. (eds.) ISWC 2006. LNCS, vol. 4273, pp. 272–285. Springer, Heidelberg (2006). doi:10.1007/11926078_20
Huynh, D., Mazzocchi, S., Karger, D.R.: Piggy bank: experience the semantic web inside your web browser. J. Web Sem. 5(1), 16–27 (2007)
Huynh, D.F., Karger, D.R.: Parallax and companion: set-based browsing for the Data Web (2013). www.davidhuynh.net
Kaminski, M., Kostylev, E.V., Cuenca Grau, B.: Semantics and expressive power of subqueries and aggregates in SPARQL 1.1. In: Proceedings of WWW (2016)
Klug, A.C.: On conjunctive queries containing inequalities. J. ACM 35(1), 146–160 (1988)
Kobilarov, G., Dickinson, I.: Humboldt: exploring linked data. In: LDOW (2008)
van der Meyden, R.: The complexity of querying indefinite data about linearly ordered domains. J. Comput. Syst. Sci. 54(1), 113–135 (1997)
Miklau, G., Suciu, D.: Containment and equivalence for a fragment of XPath. J. of the ACM 51(1), 2–45 (2004)
Oren, E., Delbru, R., Decker, S.: Extending faceted navigation for RDF data. In: Cruz, I., Decker, S., Allemang, D., Preist, C., Schwabe, D., Mika, P., Uschold, M., Aroyo, L.M. (eds.) ISWC 2006. LNCS, vol. 4273, pp. 559–572. Springer, Heidelberg (2006). doi:10.1007/11926078_40
Sagiv, Y., Yannakakis, M.: Equivalences among relational expressions with the union and difference operators. J. ACM 27(4), 633–655 (1980)
Schraefel, M.C., Smith, D.A., Owens, A., Russell, A., Harris, C., Wilson, M.L.: The evolving mSpace platform: leveraging the Semantic Web on the trail of the Memex. In: Proceedings of Hypertext (2005)
Sherkhonov, E., Marx, M.: Containment of acyclic conjunctive queries with negated atoms or arithmetic comparisons. Inf. Process. Lett. 120, 30–39 (2017)
Soylu, A., Giese, M., Schlatte, R., Jiménez-Ruiz, E., Kharlamov, E., Özçep, Ö.L., Neuenstadt, C., Brandt, S.: Querying industrial stream-temporal data: an ontology-based visual approach. J. AISE 9(1), 77–95 (2017)
Tunkelang, D.: Faceted Search. Synthesis Lectures on Information Concepts, Retrieval, and Services. Morgan & Claypool Publishers, Burlington (2009)
Tzitzikas, Y., Manolis, N., Papadakos, P.: Faceted exploration of RDF/S datasets: a survey. J. Intell. Inf. Syst. 48, 329–364 (2017)
Wagner, A., Ladwig, G., Tran, T.: Browsing-oriented semantic faceted search. In: Proceedings of DEXA (2011)
Yannakakis, M.: Algorithms for acyclic database schemes. In: Proceedings of VLDB (1981)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Sherkhonov, E., Cuenca Grau, B., Kharlamov, E., Kostylev, E.V. (2017). Semantic Faceted Search with Aggregation and Recursion. In: d'Amato, C., et al. The Semantic Web – ISWC 2017. ISWC 2017. Lecture Notes in Computer Science(), vol 10587. Springer, Cham. https://doi.org/10.1007/978-3-319-68288-4_35
Download citation
DOI: https://doi.org/10.1007/978-3-319-68288-4_35
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-68287-7
Online ISBN: 978-3-319-68288-4
eBook Packages: Computer ScienceComputer Science (R0)







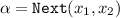 and there is a property R such that
and there is a property R such that  and there exist
and there exist  by
by  .
.