Keywords

1 Introduction

Statistics is a subject aiming to model the world by rather collecting and analyzing data than to inference and prove precisely. Lots of natural data have been fitted into statistical distributions with significant performances. And with these statistical distributions scientists can utilize their off-the-shelf distribution properties. While unfortunately the diversity of our world is far more complex than the level those statistical distributions can totally model. Alternatively, polynomial regression is also an approach to automatically find empirical laws from data [1]. It is proposed to fit various patterns of data, and has already shown its powerful fitting ability. Researchers who use polynomial regression are conveniently not required to preliminarily estimate data distribution [2]. Regrettably, by implementing polynomial regression we eventually get a polynomial expression with less prior properties than traditional statistical distributions have.

Given that features of natural scientific data are relatively fixed, and they will still be studied in the future, it is significant to determine the best fitting method for certain scientific data feature. And we creatively name it fitting label. As a solution to the dilemma, we propose a discriminative fitting model to help scientists automatically fitting scientific data into the optimal expression. Once scientists get the fitting label of a certain feature of natural scientific data, those later scientists are able to directly update the fitting expression parameters on new data’s arrival. We operated experiments on an astronomical data set, ANTF Pulsar Catalogue [3]. Besides, given the reliability of P value is still controversial [4], and mean squared error and KL divergence are trustworthy measures for both fields of statistics and machine learning, we complementally took them in consideration.

The structure of this paper is shown as follows: the comprehensive fitting model is proposed in Sect. 2; and with it its corresponding experiments are showed and discussed in Sects. 3 and 4; the section of conclusion comes as the end.

2 Methodology

2.1 Comprehensive Fitting Model

As is shown in Algorithm 1, the selection model consists of mainly 3 steps. Step 1 is to determine whether the data is subject to a certain natural distribution or not through significance testing. Step 2, fitting data into significant distributions and operating regression, then calculating their respective similarities. Step 3 is to classify the data’s fitting label with distance-based classifier according to the similarities. Consequently, scientists are able to learn as more properties as possible of the data.

figure a

2.2 Statistical Significance Testing

As is shown in Algorithm 2, firstly we need human experts, astronomers for example, to give us candidate statistical distribution families for each feature. These distribution families with empirical parameters are then be tested one by one for statistical significance under selected statistical significance measures, usually P value. Concretely with specified natural science feature data, we perform statistical significance test to screen out distribution families that have statistically large significance levels for the feature. Candidate statistical families and selected significance measures are given into the testing process, If the output P value reaches the threshold, a significance level of 0.05 by convention, the distribution will be recorded as a significant distribution.

figure b
figure c

2.3 Similarity Evaluation

For this step, we use similarity measures to detect how well the expression fits with the data, which is shown in Algorithm 3. Significant statistical distributions obtained from last step are introduced here, and with it selected similarity measures. We perform t times k-fold cross-validation test to acquire the average similarity between the distribution and scientific data.

2.4 Distance-Based Classification

It is the final outcome, the fitting label for the feature data, producing step. We can take those similarity measures as distances, and run a distance-based classifier to eventually select the expression with minimal distance as the optimal fitting label. Here we bring a classic classifier k-Nearest Neighbours (abbreviated as kNN) with its parameter k chosen 1.

3 Experiments

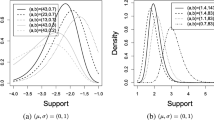
A logical starting point is to test a distribution’s normality for its popularity in natural world [5]. While for features whose scatter diagram is shown in Fig. 1, they seem obviously subject to lognormal distribution [6, 7]. We took the logarithm of that data first, then tested the resulting data’s normality, which is shown in Fig. 2. As we know, logarithm of scale parameter and shape parameter of lognormal distribution are respectively expectation and standard deviation of normal distribution.

Fig. 1.
figure 1

Original plot

Full size image
Fig. 2.
figure 2

Logarithm plot

Full size image
Table 1. Significance testing of P0
Full size table

Significance results are shown in Table 1. For those classic statistical testing methods, the values recorded are their P values. Results shows that lognormal has the highest significance among expert-selecting distributions.

Similarity evaluation results are shown in Table 2. The polynomial order is empirically chosen 2. Thus lognormal distribution has the lowest relative entropy and mean squared error. So it is the optimal fitting label for pulsar period feature. The temporary parameters of its corresponding normal distribution are mean \(-0.53455956344351729\) and standard deviation 0.99686283436845236.

Table 2. Similarity Evaluation of P0
Full size table

4 Discussions

As we know, the insight is a thought on inductive bias of Occam’s razor and the principle of maximum entropy. Occam’s razor has been the default heuristic technique in natural science for hundreds of years. It can be interpreted as stating that the one among competing hypotheses with the fewest assumptions should be selected [8, 9]. The preference for simplicity also comes to machine learning’s avoiding overfitting, a low-order fitting curve is almost always better than a high-order one. On the contrary, the second law of thermodynamics states that the total entropy of an isolated system can only increase over time. It is seen as an axiom of statistical thermodynamics. Here comes the principle of maximum entropy which states that the probability distribution that best represents the current state of knowledge is the one with largest entropy. And it also emphasizes a natural correspondence between statistical mechanics and information theory [10]. Numbers of statistical distributions widely used by natural scientists to model scientific data can be derived under the principle of maximum entropy. For any certain mean \(\mu \) and variance \(\sigma ^2\), the maximum entropy distribution \(p\left( x|\mu ,\sigma ^2\right) \) is normal distribution \(N\left( \mu ,\sigma ^2\right) \) [11].

5 Conclusions

For scientists we propose a discriminative fitting model through which diverse scientific data will be fitted into the optimal expression. And with our model as much as possible sample information can be used in future study. For data that is subject to a common statistical distribution, they then will be fitted into that distribution with parameters tuned by numerical optimization methods; comparatively for those who are not we model them by polynomial regression. Among main fields of natural science are still features whose fitting label remains unfixed, so it will be a great work to build a fitting label database with our model for scientists.