Abstract
An n-complete test suite for automata guarantees to detect all faulty implementations with a bounded number of states. This principle is well-known when testing FSMs for equivalence, but the problem becomes harder for ioco conformance on labeled transitions systems. Existing methods restrict the structure of specifications and implementations. We eliminate those restrictions, using only the number of implementation states, and fairness in test execution. We provide a formalization, a construction and a correctness proof for n-complete test suites for ioco.
P. van den Bos and R. Janssen—Supported by NWO project 13859 (SUMBAT).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The holy grail of model-based testing is a complete test suite: a test suite that can detect any possible faulty implementation. For black-box testing, this is impossible: a tester can only make a finite number of observations, but for an implementation of unknown size, it is unclear when to stop. Often, a so called n-complete test suite is used to tackle this problem, meaning it is complete for all implementations with at most n states.
For specifications modeled as finite state machines (FSMs) (also called Mealy machines), this has already been investigated extensively. In this paper we will explore how an n-complete test suite can be constructed for suspension automata. We use the ioco relation [11] instead of equivalence of FSMs.
An n-complete test suite for FSM equivalence usually provides some way to reach all states and transitions of the implementation. After reaching some state, it is tested whether this is the correct state, by observing behavior which is unique for that state, and hence distinguishing it from all other states.
Unlike FSM equivalence, ioco is not an equivalence relation, meaning that different implementations may conform to the same specification and, conversely, an implementation may conform to different specifications. In this paper, we focus on the problem of distinguishing states. For ioco, this cannot be done with simple identification. If an implementation state conforms to multiple specifications states, those states are defined to be compatible. Incompatible states can be handled in ways comparable to FSM-methods, but distinguishing compatible states requires more effort.
In this paper, we give a structured approach for distinguishing incompatible states. We also propose a strategy to handle compatible states. Obviously, they cannot be distinguished in the sense of incompatible states. We thus change the aim of distinguishing: instead of forcing a non-conformance to either specification state, we may also prove conformance to both. As our only tool in proving this is by further testing, this is a recursive problem: during complete testing, we are required to prove conformance to multiple states by testing. We thus introduce a recursively defined test suite. We give examples where this still gives a finite test suite, together with a completeness proof for this approach. To show an upper bound for the required size of a test suite, we also show that an n-complete test suite with finite size can always be constructed, albeit an inefficient one.
Related Work. Testing methods for Finite State Machines (FSMs) have been analyzed thoroughly, and n-complete test suites are already known for quite a while. A survey is given in [3]. Progress has been made on generalizing these testing methods to nondeterministic FSMs, for example in [6, 9]. FSM-based work that more closely resembles ioco is reduction of non-deterministic FSMs [4].
Complete testing in ioco received less attention than in FSM theory on this subject. The original test generation method [11] is an approach in which test cases are generated randomly. The method is complete in the sense that any fault can be found, but there is no upper bound to the required number and length of test cases.
In [8], complete test suites are constructed for Mealy-IOTSes. Mealy-IOTSes are a subclass of suspension automata, but are similar to Mealy machines as (sequences of) outputs are coupled to inputs. This makes the transition from FSM testing more straightforward.
The work most similar to ours [10] works on deterministic labeled transition systems, adding quiescence afterwards, as usual for ioco. Non-deterministic models are thus not considered, and cannot be handled implicitly through determinization, as determinization can only be done after adding quiescence. Some further restrictions are made on the specification domains. In particular, all specification states should be reachable without depending on choices for output transitions of the implementation. Furthermore, all states should be mutually incompatible. In this sense, our test suite construction can be applied to a broader set of systems, but will potentially be much less efficient. Thus, we prioritize exploring the bounds of n-complete test suites for ioco, whereas [10] aims at efficient test suites, by restricting the models which can be handled.
2 Preliminaries
The original ioco theory is defined for labeled transition systems, which may contain internal transitions, be nondeterministic, and may have states without outputs [11]. To every state without outputs, a self-loop with quiescence is added as an artificial output. The resulting labeled transition system is then determinized to create a suspension automaton, which is equivalent to the initial labeled transition system with respect to ioco [13]. In this paper, we will consider a slight generalization of suspension automata, such that our results hold for ioco in general: quiescent transitions usually have some restrictions, but we do not require them and we will treat quiescence as any other output. We will define them in terms of general automata with inputs and outputs.
Definition 1
An I/O-automaton is a tuple \((Q, L_I,L_O, T, q_0)\) where
-
Q is a finite set of states
-
\(L_I\) is a finite set of input labels
-
\(L_O\) is a finite set of output labels
-
\(T : Q \times (L_I \cup L_O) \rightharpoonup Q\) is the (partial) transition function
-
\(q_0 \in Q\) is the initial state
We denote the domain of I/O-automata for \(L_I\) and \(L_O\) with \(\mathcal {A}(L_I,L_O)\).
For the remainder of this paper we fix \(L_I\) and \(L_O\) as disjoint sets of input and output labels respectively, with \(L = L_I \cup L_O\), and omit them if clear from the context. Furthermore, we use a, b as input symbols and x, y, z as output symbols.
Definition 2
Let \(S = (Q,L_I,L_O,T,q_0)\in \mathcal {A}\), \(q \in Q\), \(B \subseteq Q\), \(\mu \in L\) and \(\sigma \in L^*\). Then we define:

We interchange singleton sets with its element, e.g. we write out(q) instead of out \((\{q\})\). Definitions on states will sometimes be used for automata as well, acting on their initial states. Similarly, definitions on automata will be used for states, acting on the automaton with that state as its initial state. For example, for \(S = (Q,L_I,L_O,T,q_0) \in \mathcal {A}\) and \(q \in Q\), we may write \(S\) after \(\mu \) instead of \(q_0\) after \(\mu \), and we may write that q is input-enabled if S is input-enabled.
In this paper, specifications are suspension automata in \(\mathcal {SA}\), and implementations are input-enabled suspension automata in \(\mathcal {SA}_{IE}\). The ioco relation formalizes when implementations conform to specifications. We give a definition relating suspension automata, following [11], and the coinductive definition [7] relating states. Both definitions have been proven to coincide.
Definition 3
Let \(S \in \mathcal {SA}\), and \(I \in \mathcal {SA}_{IE}\). Then we say that I ioco S if \( \forall \sigma \in Straces(S):\;\) out \((I\) after \(\sigma ) \subseteq \) out \((S\) after \(\sigma )\).
Definition 4
Let \(S = (Q_s,L_I,L_O,T_s,q_0^s) \in \mathcal {SA}\), and \(I = (Q_i,L_I,L_O,T_i,q_0^i) \in \mathcal {SA}_{IE}\). Then for \(q_i \in Q_i\), \(q_s \in Q_s\), we say that \(q_i\) ioco \(q_s\) if there exists a coinductive ioco relation \(R \subseteq Q_i \times Q_s\) such that \((q_i, q_s) \in R\), and \(\forall (q,p) \in R\):
-
\(\forall a \in \textit{in}(p): (q\text { }{} \textit{after}\text { }a,p\text { }{} \textit{after}\text { }a) \in R\)
-
\(\forall x \in \textit{out}(q): x \in \textit{out}(p) \wedge (q\text { }{} \textit{after}\text { }x,p\text { }{} \textit{after}\text { }x) \in R\)
In order to define complete test suites, we require execution of tests to be fair: if a trace \(\sigma \) is performed often enough, then every output x appearing in the implementation after \(\sigma \) will eventually be observed. Furthermore, the implementation may give an output after \(\sigma \) before the tester can supply an input. We then assume that the tester will eventually succeed in performing this input after \(\sigma \). This fairness assumption is unavoidable for any notion of completeness in testing suspension automata: a fault can never be detected if an implementation always chooses paths that avoid this fault.
3 Distinguishing Experiments
An important part of n-complete test suites for FSM equivalence is the distinguishing sequence, used to identify an implementation state. As ioco is not an equivalence relation, there does not have to be a one-to-one correspondence between specification and implementation states.
3.1 Equivalence and Compatibility
We first describe equivalence and compatibility relations between states, in order to define distinguishing experiments. We consider two specifications to be equivalent, denoted \(S_1 \approx S_2\), if they have the same implementations conforming to them. Then, for all implementations I, we have \(I \text { ioco } S_1 \text { iff } I \text { ioco }S_2\). For two inequivalent specifications, there is thus an implementation which conforms to one, but not the other.
Intuitively, equivalence relates states with the same traces. However, implicit underspecification by absent inputs should be handled equivalently to explicit underspecification with chaos. This is done by using chaotic completion [11]. This definition of equivalence is inspired by the relation wioco [12], which relates specifications based on their sets of traces.
Definition 5
Let \((Q,L_I,L_O,T,q_0) \in \mathcal {SA}\). Define chaos, a specification to which every implementation conforms, as \(X = (\{\chi \},L_I,L_O,\{(\chi ,x,\chi ) \mid x \in L\}, \chi )\). Let \(Q_X = Q \cup \{\chi \}\). The relation \({\approx } \subseteq Q_X \times Q_X\) relates all equivalent states. It is the largest relation for which it holds that \(q \approx q'\) if:
For two inequivalent specifications, there may still exist an implementation that conforms to the two. In that case, we define the specifications to be compatible, following the terminology introduced in [9, 10]. We introduce an explicit relation for compatibility.
Definition 6
Let \((Q,L_I,L_O,T,q_0) \in \mathcal {SA}\). The relation \({\mathrel {\Diamond }} \subseteq Q \times Q\) relates all compatible states. It is the largest relation for which it holds that \(q \mathrel {\Diamond }q'\) if:
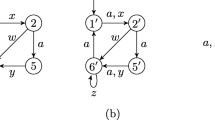
Compatibility is symmetric and reflexive, but not transitive. Conversely, two specifications are incompatible if there exists no implementation conforming to both. When \(q_1 \mathrel {\Diamond }q_2\), we can indeed easily make an implementation which conforms to both \(q_1\) and \(q_2\): the set of outputs of the implementation state can simply be out \((q_{1})\) \(\cap \) out \((q_{2})\), which is non-empty by definition of \(\mathrel {\Diamond }\). Upon such an output transition or any input transition, the two successor states are again compatible, thus the implementation can keep picking transitions in this manner. For example, in Fig. 1, compatible states 2 and 3 of the specification are both implemented by state 2 of the implementation.
Beneš et al. [1] describe the construction of merging specifications. For specification states \(q_s\) and \(q_s'\), their merge is denoted \(q_s \wedge q_s'\). For any implementation state \(q_i\), it holds that \(q_i \text { ioco } q_s \wedge q_i \text { ioco } q_s' \iff q_i \text { ioco } (q_s \wedge q_s')\). Intuitively, a merge of two states thus only allows behavior allowed by both states. Figure 1c shows the merge of specification states 2 and 3. The merge of \(q_s\) and \(q_s'\) can be implemented if and only if \(q_s \mathrel {\Diamond }q_s'\): indeed, for incompatible states, the merge has states without any output transitions, which is denoted invalid in [1].
3.2 Distinguishing Trees
When an implementation is in state \(q_i\), two incompatible specification states \(q_s\) and \(q_s'\) are distinguished by showing to which of the two \(q_i\) conforms, assuming that it conforms to one. Conversely, we can say that we have to show a non-conformance of \(q_i\) to \(q_s\) or \(q_s'\). Generally, a set of states D is distinguished by showing non-conformance to all its states, possibly except one. As a base case, if \(|D| \le 1\), then D is already distinguished. We will construct a distinguishing tree as an input-enabled automaton which distinguishes D after reaching pass.
Definition 7
Let \(\mu \) be a symbol and D a set of states. Then \( injective (\mu ,D)\) if \(\mu \in \bigcap \{\) in \((q) \mid q \in D\} \cup L_O \wedge \forall q,q' \in D: q \ne q' \wedge \mu \in \) init \((q) \cap \) init \((q') \implies q\) after \(\mu \ne q'\) after \(\mu \). This is extended to sets of symbols \(\varSigma \) as \( injective (\varSigma ,D)\) if \(\forall \mu \in \varSigma : injective (\mu ,D)\).
Definition 8
Let \((Q,L_I,L_O,T,q_0) \in \mathcal {SA}(L_I,L_O)\), and \(D \subseteq Q\) a set of mutually incompatible states. Then define \(\mathcal {DT}(L_I,L_O,D) \subseteq \mathcal {A}(L_O,L_I)\) inductively as the domain of input-enabled distinguishing trees for D, such that for every \(Y \in \mathcal {DT}(L_I,L_O,D)\) with initial state \(t_0\):
-
if \(|D| \le 1\), then \(t_0\) is the verdict state pass, and
-
if \(|D| > 1\), then \(t_0\) has either
-
a transition for a single input \(a \in L_I\) to a \(Y' \in \mathcal {DT}(L_I,L_O,D\) after \(a)\) such that \( injective (a,D)\), and transitions to a verdict state reset for all \(x \in L_O\), or
-
a transition for every output \(x \in L_O\) to a \(Y' \in \mathcal {DT}(L_I,L_O,D\) after \(x)\) such that \( injective (x,D)\).
Furthermore, pass or reset is always reached after a finite number of steps, and these states are sink states, i.e. contain transitions only to itself.
-
A distinguishing tree can synchronize with an implementation to reach a verdict state. As an implementation is output-enabled and the distinguishing tree is input-enabled, this never blocks. If the tree performs an input, the implementation may provide an output first, resulting in reset: another attempt is needed to perform the input. If no input is performed by the tree, it waits for any output, after which it can continue. In this way, the tester is guaranteed to steer the implementation to a pass, where the specification states disagree on the allowed outputs: the implementation has to choose an output, thus has to choose which specifications (not) to implement.
For a set D of mutually incompatible states, such a tree may not exist. For example, consider states 1, 3 and 5 in Fig. 2. States 1 and 3 both lead to the same state after a, and can therefore not be distinguished. Similarly, states 3 and 5 cannot be distinguished after b. Labels a and b are therefore not injective according to Definition 7 and should not be used. This concept is similar in FSM testing [5]. A distinguishing sequence always exists when \(|D| = 2\). When \(|D| > 2\), we can thus use multiple experiments to separate all states pairwise.
Lemma 9
Let \(S \in \mathcal {SA}\). Let q and \(q'\) be two states of S, such that  . Then there exists a distinguishing tree for q and \(q'\).
. Then there exists a distinguishing tree for q and \(q'\).
Proof
Since  , we know that:
, we know that:

So we have that some input or all outputs, enabled in both q and \(q'\), lead to incompatible states, for which this holds again. Hence, we can construct a tree with nodes that either have a child for an enabled input of both states, or children for all outputs enabled in the states (children for not enabled outputs are distinguishing trees for \(\emptyset \)), as in the second case of Definition 8. If this tree would be infinite, then this tree would describe infinite sequences of labels. Since S is finite, such a sequence would be a cycle in S. This would mean that \(q \mathrel {\Diamond }q'\), which is not the case. Hence we have that the tree is finite, as required by Definition 8. \(\square \)
3.3 Distinguishing Compatible States
Distinguishing techniques such as described in Sect. 3.2 rely on incompatibility of two specifications, by steering the implementation to a point where the specifications disagree on the allowed outputs. This technique fails for compatible specifications, as an implementation state may conform to both specifications. Thus, a tester then cannot steer the implementation to showing a non-conformance to either.
We thus extend the aim of a distinguishing experiment: instead of showing a non-conformance to any of two compatible states \(q_s\) and \(q_s'\), we may also prove conformance to both. This can be achieved with an n-complete test suite for \(q_s \wedge q_s'\); this will be explained in Sect. 4.1. Note that even for an implementation which does not conform to one of the specifications, n-complete testing is needed. Such an implementation may be distinguished, but it is unknown how, due to compatibility. See for example the specification and implementation of Fig. 1. State 2 of the implementation can only be distinguished from state 3 by observing ax, which is non-conforming behavior for state 2. Although y would also be non-conforming for state 2, this behavior is not observed.
In case that a non-conformance to the merged specification is found with an n-complete test suite, then the outcome is similar to that of a distinguishing tree for incompatible states: we have disproven conformance to one of the individual specifications (or to both).
4 Test Suite Definition
The number n of an n-complete test suite \(\mathbb {T}\) of a specification S tells how many states an implementation I is allowed to have to give the guarantee that I ioco S after passing \(\mathbb {T}\) (we will define passing a test suite later). To do this, we must only count the states relevant for conformance.
Definition 10
Let \(S=(Q_s,L_I,L_O,T,q_0^s) \in \mathcal {SA}\), and \(I=(Q_i,L_I,L_O,T_i,q_0^i) \in \mathcal {SA}_{IE}\). Then,
-
A state \(q_s \in Q_s\) is reachable if \(\exists \sigma \in L^*: S\) after \(\sigma = q_s\).
-
A state \(q_i \in Q_i\) is specified if \(\exists \sigma \in Straces(S): I\) after \(\sigma = q_i\). A transition \((q_i,\mu ,q_i') \in T_i\) is specified if \(q_i\) is specified, and if either \(\mu \in L_O\), or \(\mu \in L_I \wedge \exists \sigma \in L^*: I\) after \(\sigma = q_i \wedge \sigma \mu \in Straces(S)\).
-
We denote the number of reachable states of S with |S|, and the number of specified, reachable states of I with |I|.
Definition 11
Let \(S \in \mathcal {SA}\) be a specification. Then a test suite \(\mathbb {T}\) for S is n-complete if for each implementation I: \(I \text { passes } \mathbb {T} \implies (I \text { ioco } S \vee |I| > n)\).
In particular, |S|-complete means that if an implementation passes the test suite, then the implementation is correct (w.r.t. ioco) or it has strictly more states than the specification. Some authors use the convention that n denotes the number of extra states (so the above would be called 0-completeness).
To define a full complete test suite, we first define sets of distinguishing experiments.
Definition 12
Let \((Q,L_I,L_O,T,q_0) \in \mathcal {SA}\). For any state \(q \in Q\), we choose a set W(q) of distinguishing experiments, such that for all \(q' \in Q\) with \(q \ne q'\):
-
if
 , then W(q) contains a distinguishing tree for \(D \subseteq Q\), s.t. \(q,q' \in D\).
, then W(q) contains a distinguishing tree for \(D \subseteq Q\), s.t. \(q,q' \in D\). -
if \(q \mathrel {\Diamond }q'\), then W(q) contains a complete test suite for \(q \wedge q'\).
Moreover, we need sequences to access all specified, reachable implementation states. After such sequences distinguishing experiments can be executed. We will defer the explicit construction of the set of access sequences. For now we assume some set P of access sequences to exist.
Definition 13
Let \(S \in \mathcal {SA}\) and \(I \in \mathcal {SA}_{IE}\). Let P be a set of access sequences and let \(P^{+} = \{ \sigma \in P \cup P \cdot L \mid S\) after \(\sigma \ne \emptyset \}\). Then the distinguishing test suite is defined as \(\mathbb {T} = \{ \sigma \tau \mid \sigma \in P^{+}, \tau \in W(q_0\) after \(\sigma ) \}\). An element \(t \in \mathbb {T}\) is a test.
4.1 Distinguishing Experiments for Compatible States
The distinguishing test suite relies on executing distinguishing experiments. If a specification contains compatible states, the test suite contains distinguishing experiments which are themselves n-complete test suites. This is thus a recursive construction: we need to show that such a test suite is finite. For particular specifications, recursive repetition of the distinguishing test suite as described above is already finite. For example, specification S in Fig. 1 contains compatible states, but in the merge of every two compatible states, no further compatible states remain. A test suite for S needs to distinguish states 2 and 3. For this purpose, it uses an n-complete test suite for \(2 \wedge 3\), which contains no compatible states, and thus terminates by only containing distinguishing trees.
However, the merge of two compatible states may in general again contain compatible states. In these cases, recursive repetition of distinguishing test suites may not terminate. An alternative unconditional n-complete test suite may be constructed using state counting methods [4], as shown in the next section. Although inefficient, it shows the possibility of unconditional termination. The recursive strategy thus may serve as a starting point for other, efficient constructions for n-complete test suites.
Unconditional n -complete Test Suites. We introduce Lemma 16 to bound test suite execution. We first define some auxiliary definitions.
Definition 14
Let \(S \in \mathcal {SA}\), \(\sigma \in L^*\), and \(x \in L_O\). Then \(\sigma x\) is an ioco-counterexample if \(S\) after \(\sigma \ne \emptyset \), \(x \not \in \) out \((S\) after \(\sigma )\).
Naturally, I ioco S if and only if Straces(I) contains no ioco-counterexample.
Definition 15
Let \(S = (Q_s, L_I, L_O, T_s, q_s^0) \in \mathcal {SA}\) and \(I \in \mathcal {SA}_{IE}\). A trace \(\sigma \in Straces(S)\) is short if \(\forall q_s \in Q_s: |\{\rho \mid \rho \text { is a prefix of } \sigma \wedge q_s^0\) after \(\rho = q_s \}| \le |I|\).
Lemma 16
Let \(S \in \mathcal {SA}\) and \(I \in \mathcal {SA}_{IE}\). If I  S, then Straces(I) contains a short ioco-counterexample.
S, then Straces(I) contains a short ioco-counterexample.
Proof
If I  S, then Straces(I) must contain an ioco-counterexample \(\sigma \). If \(\sigma \) is short, the proof is trivial, so assume it is not. Hence, there exists a state \(q_s\), with at least \(|I|+1\) prefixes of \(\sigma \) leading to \(q_s\). At least two of those prefixes \(\rho \) and \(\rho '\) must lead to the same implementation state, i.e. it holds that \(q_i^0\) after \(\rho = q_i^0\) after \(\rho '\) and \(q_s^0\) after \(\rho = q_s^0\) after \(\rho '\). Assuming \(|\rho | < |\rho '|\) without loss of generality, we can thus create an ioco-counterexample \(\sigma '\) shorter than \(\sigma \) by replacing \(\rho '\) by \(\rho \). If \(\sigma '\) is still not short, we can repeat this process until it is. \(\square \)
S, then Straces(I) must contain an ioco-counterexample \(\sigma \). If \(\sigma \) is short, the proof is trivial, so assume it is not. Hence, there exists a state \(q_s\), with at least \(|I|+1\) prefixes of \(\sigma \) leading to \(q_s\). At least two of those prefixes \(\rho \) and \(\rho '\) must lead to the same implementation state, i.e. it holds that \(q_i^0\) after \(\rho = q_i^0\) after \(\rho '\) and \(q_s^0\) after \(\rho = q_s^0\) after \(\rho '\). Assuming \(|\rho | < |\rho '|\) without loss of generality, we can thus create an ioco-counterexample \(\sigma '\) shorter than \(\sigma \) by replacing \(\rho '\) by \(\rho \). If \(\sigma '\) is still not short, we can repeat this process until it is. \(\square \)
We can use Lemma 16 to bound exhaustive testing to obtain n-completeness. When any specification state is visited \(|I|+1\) times with any trace, then any extensions of this trace will not be short, and we do not need to test them. Fairness allows us to test all short traces which are present in the implementation.
Corollary 17
Given a specification S the set of all traces of length at most \(|S|*n\) is an n-complete test suite.
Example 18
Figure 3 shows an example of a non-conforming implementation with a counterexample yyxyyxyyxyyx, of maximal length \(4\cdot 3=12\).
4.2 Execution of Test Suites
A test \(\sigma \tau \) is executed by following \(\sigma \), and then executing the distinguishing experiment \(\tau \). If the implementation chooses any output deviating from \(\sigma \), then the test gives a reset and should be reattempted. Finishing \(\tau \) may take several executions: a distinguishing tree may give a reset, and an n-complete test suite to distinguish compatible states may contain multiple tests. Therefore \(\sigma \) needs to be run multiple times, in order to allow full execution of the distinguishing experiment. By assuming fairness, every distinguishing experiment is guaranteed to termininate, and thus also every test.
The verdict of a test suite \(\mathbb {T}\) for specification S is concluded simply by checking for observed ioco-counterexamples to S during execution. When executing a distinguishing experiment w as part of \(\mathbb {T}\), the verdict of w is ignored when concluding a verdict for \(\mathbb {T}\): we only require w to be fully executed, i.e. be reattempted if it gives a reset, until it gives a pass or fail. For example, if \(\sigma \) leads to specification state q, and q needs to be distinguished from compatible state \(q'\), a test suite \(\mathbb {T}'\) for \(q \wedge q'\) is needed to distinguished q and \(q'\). If \(\mathbb {T}'\) finds a non-conformance to either q or \(q'\), it yields fail. Only in the former case, \(\mathbb {T}\) will also yield fail, and in the latter case, \(\mathbb {T}\) will continue with other tests: q and \(q'\) have been successfully distinguished, but no non-conformance to q has been found. If all tests have been executed in this manner, \(\mathbb {T}\) will conclude pass.
4.3 Access Sequences
In FSM-based testing, the set P for reaching all implementation states is taken care of rather efficiently. The set P is constructed by choosing a word \(\sigma \) for each specification state, such that \(\sigma \) leads to that state (note the FSMs are fully deterministic). By passing the tests \(P \cdot W\), where W is a set of distinguishing experiment for every reached state, we know the implementation has at least some number of states (by observing that many different behaviors). By passing tests \(P\cdot L\cdot W\) we also verify that every transition has the correct destination state. By extending these tests to \(P \cdot L^{\le k+1} \cdot W\) (where \(L^{\le k+1} = \bigcup _{m \in \{0,\cdots , k+1\}} L^m\)), we can reach all implementation states if the implementation has at most k more states than the specification. For suspension automata, however, things are more difficult for two reasons: (1) A specification state may be reachable only if an implementation chooses to implement a particular, optional output transition (in which case this state is not certainly reachable [10]), and (2) if the specification has compatible states, the implementation may implement two specification states with a single implementation state.
Consider Fig. 4 for an example. An implementation can omit state 2 of the specification, as shown in Fig. 4b. Now Fig. 4c shows a fault not found by a test suite \(P\cdot L^{\le 1}\cdot W\): if we take \(y \in P\), \(z \in L\), and observe \(z \in W(3)\), we do not reach the faulty y transition in the implementation. So by leaving out states, we introduce an opportunity to make a fault without needing more states than the specification. This means that we may need to increase the size of the test suite in order to obtain the desired completeness. In this example, however, a test suite \(P\cdot L^{\le 2}\cdot W\) is enough, as the test suite will contain a test with \(yzz \in P\cdot L^2\) after which the faulty output \(y \not \in W(3)\) will be observed.
Clearly, we reach all states in a n-state implementation for any specification S, by taking P to be all traces in Straces(S) of at most length n. This set P can be constructed by simple enumeration. We then have that the traces in the set P will reach all specified, reachable states in all implementations I such that \(|I|~\le ~n\). In particular this will mean that \(P^{+}\) reaches all specified transitions. Although this generates exponentially many sequences, the length is substantially shorter than the sequences obtained by the unconditional n-complete test suite. We conjecture that a much more efficient construction is possible with a careful analysis of compatible states and the not certainly reachable states.
4.4 Completeness Proof for Distinguishing Test Suites
We let \(\mathbb {T}\) be the distinguishing test suite as defined in Definition 13. As discussed before, if q and \(q'\) are compatible, the set W(q) can be defined using another complete test suite. If the test suite is again a distinguishing test suite, completeness of it is an induction hypothesis. If, on the other hand, the unconditional n-complete test suite is used, completeness is already guaranteed (Corollary 17).
Theorem 19
Let \(S = (Q_s,L_I,L_O,T_s,q_0^s) \in \mathcal {SA}\) be a specification. Let \(\mathbb {T}\) be a distinguishing test suite for S. Then \(\mathbb {T}\) is n-complete.
Proof
We will show that for any implementation of the correct size and which passes the test suite we can build a coinductive ioco relation which contain the initial states. As a basis for that relation we take the states which are reached by the set P. This may not be an ioco relation, but by extending it (in two steps) we obtain a full ioco relation. Extending the relation is an instance of a so-called up-to technique, we will use terminology from [2].
More precisely, Let \(I = (Q_i,L_I,L_O,T_i,q_0^i) \in \mathcal {SA}_{IE}\) be an implementation with \(|I| \le n\) which passes \(\mathbb {T}\). By construction of P, all reachable specified implementation states are reached by P and so all specified transitions are reached by \(P^{+}\).
The set P defines a subset of \(Q_i \times Q_s\), namely \( R = \{ (q_0^i\) after \(\sigma , q_0^s\) after \(\sigma ) \mid \sigma \in P \} \). We add relations for all equivalent states: \(R' = \{(i,s) \mid (i,s') \in R, s \in Q_s, s \approx s' \}\). Furthermore, let \(\mathcal {J} = \{ (i,s,s') \mid i \in Q_i, s,s' \in Q_s \text { such that } i \text { ioco }s \wedge i \text { ioco }s' \}\) and \(R_{i,s,s'}\) be the ioco relation for \(i \text { ioco }s \wedge i \text { ioco }s'\), now define \(\overline{R} = R' \cup \bigcup _{(i,s,s') \in \mathcal {J}} R_{i,s,s'}\). We want to show that \(\overline{R}\) defines a coinductive ioco relation. We do this by showing that R progresses to \(\overline{R}\).
Let \((i, s) \in R\). We assume that we have seen all of out(i) and that out \((i)\) \(\,\subseteq \) out(s) (this is taken care of by the test suite and the fairness assumption). Then, because we use \(P^{+}\), we also reach the transitions after i. We need to show that the input and output successors are again related.
-
Let \(a \in L_I\). Since I is input-enabled we have a transition for a with \(i\) after \(a = i_2\). Suppose there is a transition for a from s: \(s\) after \(a = s_2\) (if not, then we’re done). We have to show that \((i_2, s_2) \in \overline{R}\).
-
Let \(x \in L_O\). Suppose there is a transition for x: \(i\) after \(x = i_2\) Then (since out \((i)\) \(\subseteq \) out(s)) there is a transition for x from s: \(s\) after \(x = s_2\). We have to show that \((i_2, s_2) \in \overline{R}\).
In both cases we have a successor \((i_2, s_2)\) which we have to prove to be in \(\overline{R}\). Now since P reaches all states of I, we know that \((i_2, s_2') \in R\) for some \(s_2'\). If \(s_2 \approx s_2'\) then \((i_2, s_2) \in R' \subseteq \overline{R}\) holds trivially, so suppose that \(s_2 \not \approx s_2'\). Then there exists a distinguishing experiment \(w \in W(s_2) \cap W(s_2')\) which has been executed in \(i_2\), namely in two tests: a test \(\sigma w\) for some \(\sigma \in P^+\) with \(S\) after \(\sigma = s_2\), and a test \(\sigma ' w\) for some \(\sigma ' \in P\) with \(S\) after \(\sigma '\). Then there are two cases:
-
If
 then w is a distinguishing tree separating \(s_2\) and \(s_2'\). Then there is a sequence \(\rho \) taken in w of the test \(\sigma w\), i.e. \(w\) after \(\rho \) reaches a pass state of w, and similarly there is a sequence \(\rho '\) that is taken in w of the test \(\sigma ' w\). By construction of distinguishing trees, \(\rho \) must be an ioco-counterexample for either \(s_2\) or \(s_2'\), but because \(\mathbb {T}\) passed this must be \(s_2'\). Similarly, \(\rho '\) disproves \(s_2\). One implementation state can implement at most one of \(\{\rho , \rho '\}\). This contradicts that the two tests passed, so this case cannot happen.
then w is a distinguishing tree separating \(s_2\) and \(s_2'\). Then there is a sequence \(\rho \) taken in w of the test \(\sigma w\), i.e. \(w\) after \(\rho \) reaches a pass state of w, and similarly there is a sequence \(\rho '\) that is taken in w of the test \(\sigma ' w\). By construction of distinguishing trees, \(\rho \) must be an ioco-counterexample for either \(s_2\) or \(s_2'\), but because \(\mathbb {T}\) passed this must be \(s_2'\). Similarly, \(\rho '\) disproves \(s_2\). One implementation state can implement at most one of \(\{\rho , \rho '\}\). This contradicts that the two tests passed, so this case cannot happen. -
If \(s_2 \mathrel {\Diamond }s_2'\) (but \(s_2 \not \approx s_2'\) as assumed above), then w is a test suite itself for \(s_2 \wedge s_2'\). If w passed in both tests then \(i_2 \text { ioco }s_2\) and \(i_2 \text { ioco }s'_2\), and hence \((i_2, s_2) \in R_{i,s'_2,s_2} \subseteq \overline{R}\). If w failed in one of the tests \(\sigma w\) or \(\sigma ' w\), then \(i_2\) does not conform to both \(s_2'\) and \(s_2\), and hence w also fails in the other test. So again, there is a counterexample \(\rho \) for \(s_2'\) and \(\rho '\) for \(s_2\). One implementation state can implement at most one of \(\{\rho , \rho '\}\). This contradicts that the two tests passed, so this case cannot happen.
We have now seen that R progresses to \(\overline{R}\). It is clear that \(R'\) progresses to \(\overline{R}\) too. Then, since each \(R_{i,s,s'}\) is an ioco relation, they progress to \(R_{i,s,s'} \subseteq \overline{R}\). And so the union, \(\overline{R}\), progresses to \(\overline{R}\), meaning that \(\overline{R}\) is a coinductive ioco relation. Furthermore, we have \((i_0, s_0) \in \overline{R}\) (because \(\epsilon \in P\)), concluding the proof. \(\square \)
We remark that if the specification does not contain any compatible states, that the proof can be simplified a lot. In particular, we do not need n-complete test suites for merges of states, and we can use the relation \(R'\) instead of \(\overline{R}\).
5 Constructing Distinguishing Trees
Lee and Yannakakis proposed an algorithm for constructing adaptive distinguishing sequences for FSMs [5]. With a partition refinement algorithm, a splitting tree is build, from which the actual distinguishing sequence is extracted.
A splitting tree is a tree of which each node is identified with a subset of the states of the specification. The set of states of a child node is a (strict) subset of the states of its parent node. In contrast to splitting trees for FSMs, siblings may overlap: the tree does not describe a partition refinement. We define \(\textit{leaves}(Y)\) as the set of leaves of a tree Y. The algorithm will split the leaf nodes, i.e. assign children to every leaf node. If all leaves are identified with a singleton set of states, we can distinguish all states of the root node.
Additionally, every non-leaf node is associated with a set of labels from L. We denote the labels of node D with \(\textit{labels}(D)\). The distinguishing tree that is going to be constructed from the splitting tree is built up from these labels. As argued in Sect. 3.2, we require injective distinguishing trees, thus our splitting trees only contain injective labels, i.e. \( injective (\textit{labels}(D),D)\) for all non-leaf nodes D.
Below we list three conditions that describe when it is possible to split the states of a leaf D, i.e. by taking some transition, we are able to distinguish some states from the other states of D. We will see later how a split is done. If the first condition is true, at least one state is immediately distinguished from all other states. The other two conditions describe that a leaf D can be split if after an input or all outputs some node \(D'\) is reached that already is split, i.e. \(D'\) is a non-leaf node. Consequently, a split for condition 1 should be done whenever possible, and otherwise a split for condition 2 or 3 can be done. Depending on the implementation one is testing, one may prefer splitting with either condition 2 or 3, when both conditions are true.
We present each condition by first giving an intuitive description in words, and then a more formal definition. With \(\varPi (A)\) we denote the set of all non-trivial partitions of a set of states A.
Definition 20
A leaf D of tree Y can be split if one of the following conditions hold:
-
1.
All outputs are enabled in some but not in all states.
$$\begin{aligned} \forall x \in \textit{out}(D): injective (x,D) \wedge \exists d \in D: d\text { }{} \textit{after}\text { }x=\emptyset \end{aligned}$$ -
2.
Some states reach different leaves than other states for all outputs.
$$\begin{aligned}&\forall x \in \textit{out}(D): injective (x,D) \wedge \exists P \in \varPi (D), \forall d,d' \in P:\\&\quad (d \ne d' \implies \forall l \in \textit{leaves}(Y): l \cap d\text { }{} \textit{after}\text { }x = \emptyset \vee l \cap d'\text { }{} \textit{after}\text { }x = \emptyset ) \end{aligned}$$ -
3.
Some states reach different leaves than other states for some input.
$$\begin{aligned}&\exists a \in \textit{in}(D): injective (a,D) \wedge \exists P \in \varPi (D), \forall d,d' \in P:\\&\quad (d \ne d' \implies \forall l \in \textit{leaves}(Y): l \cap d\text { }{} \textit{after}\text { }a = \emptyset \vee l \cap d'\text { }{} \textit{after}\text { }a = \emptyset ) \end{aligned}$$
Algorithm 1 shows how to split a single leaf of the splitting tree (we chose arbitrarily to give condition 2 a preference over condition 3). A splitting tree is constructed in the following manner. Initially, a splitting tree is a leaf node of the state set from the specification. Then, the full splitting tree is constructed by splitting leaf nodes with Algorithm 1 until no further splits can be made. If all leaves in the resulting splitting tree are singletons, the splitting tree is complete and a distinguishing tree can be constructed (described in the next section). Otherwise, no distinguishing tree exists. Note that the order of the splits is left unspecified.

Distinguishing tree of Fig. 5a. The states are named by the sets of states which they distinguish. Singleton and empty sets are the pass states. Self-loops in verdict states have been omitted, for brevity.
Example 21
Let us apply Algorithm 1 on the suspension automaton in Fig. 5a. Figure 5b shows the resulting splitting tree. We initialize the root node to \(\{1,2,3,4,5\}\). Condition 1 applies, since states 1 and 5 only have output y enabled, while states 2, 3 and 4 only have outputs x and z enabled. Thus, we add leaves \(\{1,5\}\) and \(\{2,3,4\}\).
We can split \(\{1,5\}\) by taking an output transition for y according to condition 2, as \(1\) after \(y = 4 \in \{2,3,4\}\), while \(5\) after \(y = 1 \in \{1,5\}\), i.e. 1 and 5 reach different leaves. Condition 2 also applies for \(\{2,3,4\}\). We have that \(\{2,3\}\) after \(x = \{2,4\} \subseteq \{2,3,4\} \) while \(4\) after \(x = 5 \in \{5\}\). Hence we obtain children \(\{4\}\) and \(\{2,3\}\) for output x. For z we have that \(2\) after \(z = 1 \in \{1\}\) while \(\{3,4\}\) after \(z = \{3,4\} \subseteq \{2,3,4\}\), so we obtain children \(\{2\}\) and \(\{3,4\}\) for z.
We can split {2,3} by taking input transition a according to condition 3, since \(2\) after \(a = 4\) and \(3\) after \(a = 2\), and no leaf of the splitting tree contains both state 2 and state 4. Note that we could also have split on output transitions x and z. Node \(\{3,4\}\) cannot be split for output transition z, since \(\{3,4\}\) after \(z = \{3,4\}\) which is a leaf, and hence condition 2 does not hold. However node \(\{3,4\}\) can be split for input transition a, as \(3\) after \(a = 2\) and \(4\) after \(a = 4\). Now all leaves are singleton, so we can distinguish all states with this tree.
A distinguishing tree \(Y \in \mathcal {DT}(L_I,L_O,D)\) for D can be constructed from a splitting tree with singleton leaf nodes. This follows the structure in Definition 8, and we only need to choose whether to provide an input, or whether to observe outputs. We look at the lowest node \(D'\) in the split tree such that \(D \subseteq D'\). If \(\textit{labels}(D')\) has an input, then Y has a transition for this input, and a transition to reset for all outputs. If \(\textit{labels}(D')\) contains outputs, then Y has a transition for all outputs. In this manner, we recursively construct states of the distinguishing tree until \(|D| \le 1\), in which case we have reached a pass state. Figure 6 shows the distinguishing tree obtained from the splitting tree in Fig. 5b.
6 Conclusions
We firmly embedded theory on n-complete test suites into ioco theory, without making any restricting assumptions. We have identified several problems where classical FSM techniques fail for suspension automata, in particular for compatible states. An extension of the concept of distinguishing states has been introduced such that compatible states can be handled, by testing the merge of such states. This requires that the merge itself does not contain compatible states. Furthermore, upper bounds for several parts of a test suite have been given, such as reaching all states in the implementation.
These upper bounds are exponential in the number of states, and may limit practical applicability. Further investigation is needed to efficiently tackle these parts of the test suite. Alternatively, looser notions for completeness may circumvent these problems. Furthermore, experiments are needed to compare our testing method and random testing as in [11] quantitatively, in terms of efficiency of computation and execution time, and the ability to find bugs, preferably on a real world case study.
References
Beneš, N., Daca, P., Henzinger, T.A., Křetínskỳ, J., Ničković, D.: Complete composition operators for IOCO-testing theory. In: Proceedings of the 18th International ACM SIGSOFT Symposium on Component-Based Software Engineering, pp. 101–110. ACM (2015)
Bonchi, F., Pous, D.: Hacking nondeterminism with induction and coinduction. Commun. ACM 58(2), 87–95 (2015)
Dorofeeva, R., El-Fakih, K., Maag, S., Cavalli, A.R., Yevtushenko, N.: FSM-based conformance testing methods: a survey annotated with experimental evaluation. Inf. Softw. Technol. 52(12), 1286–1297 (2010)
Hierons, R.M.: Testing from a nondeterministic finite state machine using adaptive state counting. IEEE Trans. Comput. 53(10), 1330–1342 (2004)
Lee, D., Yannakakis, M.: Testing finite-state machines: state identification and verification. IEEE Trans. Comput. 43(3), 306–320 (1994)
Luo, G., von Bochmann, G., Petrenko, A.: Test selection based on communicating nondeterministic finite-state machines using a generalized Wp-method. IEEE Trans. Software Eng. 20(2), 149–162 (1994)
Noroozi, N.: Improving input-output conformance testing theories. PhD thesis, Technische Universiteit Eindhoven (2014)
Paiva, S.C., Simao, A.: Generation of complete test suites from mealy input/output transition systems. Form. Asp. Comput. 28(1), 65–78 (2016)
Petrenko, A., Yevtushenko, N.: Adaptive testing of deterministic implementations specified by nondeterministic FSMs. In: Wolff, B., Zaïdi, F. (eds.) ICTSS 2011. LNCS, vol. 7019, pp. 162–178. Springer, Heidelberg (2011). doi:10.1007/978-3-642-24580-0_12
Simao, A., Petrenko, A.: Generating complete and finite test suite for ioco: is it possible? In: Proceedings Ninth Workshop on Model-Based Testing, MBT 2014, Grenoble, France, pp. 56–70 (2014)
Tretmans, J.: Model based testing with labelled transition systems. In: Hierons, R.M., Bowen, J.P., Harman, M. (eds.) Formal Methods and Testing. LNCS, vol. 4949, pp. 1–38. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78917-8_1
Volpato, M., Tretmans, J.: Towards quality of model-based testing in the ioco framework. In: Proceedings of the 2013 International Workshop on Joining AcadeMiA and Industry Contributions to Testing Automation, pp. 41–46. ACM (2013)
Willemse, T.A.C.: Heuristics for ioco-based test-based modelling. In: Brim, L., Haverkort, B., Leucker, M., van de Pol, J. (eds.) FMICS 2006. LNCS, vol. 4346, pp. 132–147. Springer, Heidelberg (2007). doi:10.1007/978-3-540-70952-7_9
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 IFIP International Federation for Information Processing
About this paper
Cite this paper
van den Bos, P., Janssen, R., Moerman, J. (2017). n-Complete Test Suites for IOCO. In: Yevtushenko, N., Cavalli, A., Yenigün, H. (eds) Testing Software and Systems. ICTSS 2017. Lecture Notes in Computer Science(), vol 10533. Springer, Cham. https://doi.org/10.1007/978-3-319-67549-7_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-67549-7_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-67548-0
Online ISBN: 978-3-319-67549-7
eBook Packages: Computer ScienceComputer Science (R0)






 , then W(q) contains a distinguishing tree for
, then W(q) contains a distinguishing tree for 

 then w is a distinguishing tree separating
then w is a distinguishing tree separating 

