Abstract
SMT solvers have become de rigueur in deductive verification to automatically prove the validity of verification conditions. While these solvers provide an effective support for theories—such as arithmetic—that feature strongly in program verification, they tend to be more limited in dealing with first-order quantification, for which they have to rely on special annotations—known as triggers—to guide the instantiation of quantifiers. Writing effective triggers is necessary to achieve satisfactory performance with SMT solvers, but remains a tricky endeavor—beyond the purview of non-highly trained experts.
In this paper, we experiment with the idea of using first-order provers instead of SMT solvers to prove the validity of verification conditions. First-order provers offer a native support for unrestricted quantification, but have been traditionally limited in theory reasoning. By leveraging some recent extensions to narrow this gap in the Vampire first-order prover, we describe a first-order encoding of verification conditions of programs written in the Boogie intermediate verification language. Experiments with a prototype implementation on a variety of Boogie programs suggest that first-order provers can help achieve more flexible and robust performance in program verification, while avoiding the pitfalls of having to manually guide instantiations by means of triggers.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Section 5 outlines the relatively few works that deal with trigger selection explicitly.
- 2.
- 3.
The typechecker establishes the correctness of a procedure’s
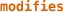 clause, so that the prover can just rely on it. This is possible because Boogie’s variables cannot be aliased.
clause, so that the prover can just rely on it. This is possible because Boogie’s variables cannot be aliased. - 4.
Since \(\tau \) is applied recursively as usual, consecutive assignments to the same variable translate to nested let-ins (see sequential composition and assignments rules).
- 5.
- 6.
The size of the SMT-LIB encoding gives an idea of the size of the generated VCs, but in the experiments we used Boogie in its default mode where it feeds VCs directly through Z3’s API.
- 7.
Remember that blt always ignores triggers and other prover annotations in the Boogie input.
- 8.
While the total number of VCs verified by Boogie in group T (137) is the same with (\(\checkmark _t\)) and without (\(\checkmark _0\)) prover-specific annotations, the two sets are different: 13 VCs verify without annotations but do not verify with annotations because they correspond to tests that should fail with the annotations; another 13 VCs verify with annotations but not without them.
References
Ameri, M., Furia, C.A.: Why just Boogie? Translating between intermediate verification. In: Ábrahám, E., Huisman, M. (eds.) IFM 2016. LNCS, vol. 9681, pp. 79–95. Springer, Cham (2016). doi:10.1007/978-3-319-33693-0_6
Amin, N., Leino, K.R.M., Rompf, T.: Computing with an SMT solver. In: Seidl, M., Tillmann, N. (eds.) TAP 2014. LNCS, vol. 8570, pp. 20–35. Springer, Cham (2014). doi:10.1007/978-3-319-09099-3_2
Barrett, C., Conway, C.L., Deters, M., Hadarean, L., Jovanović, D., King, T., Reynolds, A., Tinelli, C.: CVC4. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 171–177. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22110-1_14
Böhme, S., Leino, K.R.M., Wolff, B.: HOL-Boogie — an interactive prover for the boogie program-verifier. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) TPHOLs 2008. LNCS, vol. 5170, pp. 150–166. Springer, Heidelberg (2008). doi:10.1007/978-3-540-71067-7_15
Böhme, S., Moskal, M.: Heaps and data structures: a challenge for automated provers. In: Bjørner, N., Sofronie-Stokkermans, V. (eds.) CADE 2011. LNCS (LNAI), vol. 6803, pp. 177–191. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22438-6_15
Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78800-3_24
Detlefs, D., Nelson, G., Saxe, J.B.: Simplify: a theorem prover for program checking. J. ACM 52, 365–473 (2005)
Dross, C., Conchon, S., Kanig, J., Paskevich, A.: Reasoning with triggers. In: SMT. EPiC Series, pp. 22–31. EasyChair (2012)
Flanagan, C., Saxe, J.B.: Avoiding exponential explosion: generating compact verification conditions. In: POPL, pp. 193–205. ACM (2001)
Furia, C.A., Meyer, B., Velder, S.: Loop invariants: analysis, classification, and examples. ACM Comp. Sur. 46(3) (2014)
Gries, D.: The Science of Programming. Springer, New York (1981)
Kaliszyk, C., Sutcliffe, G., Rabe, F.: TH1: the TPTP typed higher-order form with rank-1 polymorphism. In: PAAR at IJCAR. CEUR Workshop Proceedings, vol. 1635, pp. 41–55. CEUR-WS.org (2016)
Kotelnikov, E., Kovács, L., Reger, G., Voronkov, A.: The Vampire and the FOOL. In: SIGPLAN CPP, pp. 37–48. ACM (2016)
Kotelnikov, E., Kovács, L., Suda, M., Voronkov, A.: A clausal normal form translation for FOOL. In: GCAI. EPiC, vol. 41, pp. 53–71. EasyChair (2016)
Kovács, L., Voronkov, A.: First-order theorem proving and Vampire. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 1–35. Springer, Heidelberg (2013). doi:10.1007/978-3-642-39799-8_1
Leino, K.R.M.: Efficient weakest preconditions. Inf. Process. Lett. 93(6), 281–288 (2005)
Leino, K.R.M., Monahan, R.: Reasoning about comprehensions with first-order SMT solvers. In: SAC, pp. 615–622. ACM (2009)
Leino, K.R.M., Pit-Claudel, C.: Trigger selection strategies to stabilize program verifiers. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016. LNCS, vol. 9779, pp. 361–381. Springer, Cham (2016). doi:10.1007/978-3-319-41528-4_20
Liew, D., Cadar, C., Donaldson, A.F.: Symbooglix: a symbolic execution engine for Boogie programs. In: ICST, pp. 45–56. IEEE Computer Society (2016)
Nelson, C.G.: Techniques for program verification. Ph.D. thesis, Xerox PARC (1981). CSL-81-10
Polikarpova, N., Furia, C.A., West, S.: To run what no one has run before: executing an intermediate verification language. In: Legay, A., Bensalem, S. (eds.) RV 2013. LNCS, vol. 8174, pp. 251–268. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40787-1_15
Rümmer, P.: E-matching with free variables. In: Bjørner, N., Voronkov, A. (eds.) LPAR 2012. LNCS, vol. 7180, pp. 359–374. Springer, Heidelberg (2012). doi:10.1007/978-3-642-28717-6_28
Sutcliffe, G.: The TPTP problem library and associated infrastructure. J. Autom. Reason. 43(4), 337–362 (2009)
Acknowledgments
We thank Evgenii Kotelnikov for helping us understand the latest features of Vampire’s support for FOOL.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Chen, Y., Furia, C.A. (2017). Triggerless Happy. In: Polikarpova, N., Schneider, S. (eds) Integrated Formal Methods. IFM 2017. Lecture Notes in Computer Science(), vol 10510. Springer, Cham. https://doi.org/10.1007/978-3-319-66845-1_19
Download citation
DOI: https://doi.org/10.1007/978-3-319-66845-1_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-66844-4
Online ISBN: 978-3-319-66845-1
eBook Packages: Computer ScienceComputer Science (R0)


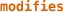 clause, so that the prover can just rely on it. This is possible because Boogie’s variables cannot be aliased.
clause, so that the prover can just rely on it. This is possible because Boogie’s variables cannot be aliased.