Abstract
We aim to give a pedagogic and essentially self-contained presentation of the construction of various stochastic objects appearing in the dynamical \(\varPhi ^4_3\) model. The construction presented here is based on the use of paraproducts. The emphasis is on describing the stochastic objects themselves rather than introducing a solution theory for the equation.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Here and below we write \(A \lesssim B\) to mean that there exists a constant C, which is independent of the quantities of interest, such that \(A \le CB\).
- 2.
One may estimate the error in (19) and show that it is negligible for our purpose, but the simplest way around this technical point is probably to interpret each periodic function on \(\mathbb {T}^d\) as a periodic function on \(\mathbb {R}^d\), and then use \(L^p(\mathbb {R}^d)\) norms and the continuous Fourier transform throughout, so that (19) becomes exact. The continuous Fourier transform of any Schwartz distribution is well-defined, by duality. For a periodic \(f \in L^1_\mathrm {loc}(\mathbb {R}^d)\), the Fourier transform is a sum of Dirac masses at every \(\omega \in \mathbb {Z}^d\), each carrying a mass \(\widehat{f}(\omega )\) as defined in (14).
- 3.
Actually, for finite n the heat kernels connecting to the leaves, i.e. \(P_{u_5-u_1}\), \(P_{u_5 - u_2}\), \(P_{t-u_3}\) and \(P_{t-u_4}\) (but not \(P_{t-u_5}\)) should be replaced by the regularised heat kernel \((t,x) \mapsto \sum _{|\omega | \le n} \widehat{P}_t(\omega ) e^{i 2 \pi \omega \cdot x}\). Similarly, in (59) and after we will leave implicit the constraint \(|\omega _1|, \ldots , |\omega _4| \le n\). Here and below we drop the regularisations for convenience.
- 4.
In fact, the sum represented by the diagram (62) does not coincide exactly with the constant \(\mathbf {c}_n'\) as defined in (8) because the latter is defined as the expectation of the resonant product
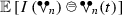 while the former coincides with
while the former coincides with 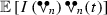 . However, as the reader can check, the difference between these constants remains bounded as n tends to infinity.
. However, as the reader can check, the difference between these constants remains bounded as n tends to infinity. - 5.
This is slightly formal - here \(\mathbf {c}'\) should denote the limit of \(\mathbf {c}_n'\) as \(n \rightarrow \infty \), which is infinite as discussed before. We are implicitly assuming that a regularisation is present, although we do not capture it in the notation.
References
Bahouri, H., Chemin, J.-Y., Danchin, R.: Fourier Analysis and Nonlinear Partial Differential Equations. Grundlehren der Mathematischen Wissenschaften, vol. 343. Springer, Heidelberg (2011)
Bertini, L., Presutti, E., Rüdiger, B., Saada, E.: Dynamical fluctuations at the critical point: convergence to a nonlinear stochastic PDE. Teor. Veroyatnost. i Primenen. 38(4), 689–741 (1993)
Biskup, M.: Reflection positivity and phase transitions in lattice spin models. In: Methods of Contemporary Mathematical Statistical Physics. Lecture Notes in Mathematics, vol. 1970, pp. 1–86. Springer, Berlin (2009)
Bogachev, V.: Gaussian Measures. Mathematical Surveys and Monographs, vol. 62, 1st edn. American Mathematical Society, Providence (1998)
Catellier, R., Chouk, K.: Paracontrolled distributions and the 3-dimensional stochastic quantization equation (2013). arXiv:1310.6869
Chandra, A., Weber, H.: Stochastic PDEs, Regularity Structures, and Interacting Particle Systems (2015). arXiv:1508.03616
Chandra, A., Hairer, M.: An analytic BPHZ Theorem for Regularity Structures (2016). arXiv:1612.08138
Da Prato, G., Debussche, A.: Strong solutions to the stochastic quantization equations. Ann. Probab. 31(4), 1900–1916 (2003)
Jentzen, W.E.A., Shen, H.: Renormalized powers of Ornstein–Uhlenbeck processes and well-posedness of stochastic Ginzburg–Landau equations. Nonlinear Anal. 142, 152–193 (2016)
Fritz, J., Rüdiger, B.: Time dependent critical fluctuations of a one-dimensional local mean field model. Probab. Theory Relat. Fields 103(3), 381–407 (1995)
Friz, P.K., Hairer, M.: A Course on Rough Paths, with An Introduction to Regularity Structures. Universitext. Springer, Berlin (2014)
Glimm, J., Jaffe, A.: Quantum Physics, 2nd edn. Springer, New York (1987)
Gubinelli, M., Imkeller, P., Perkowski, N.: Paraproducts, Rough Paths and Controlled Distributions (2012). arXiv:1210.2684
Hairer, M.: Solving the KPZ equation. Ann. Math. 2(178), 559–664 (2013)
Hairer, M.: A theory of regularity structures. Invent. Math. 198(2), 269–504 (2014)
Hairer, M., Quastel, J.: A Class of Growth Models Rescaling to KPZ (2015). arXiv:1512.07845
Hairer, M., Ryser, M., Weber, H.: Triviality of the 2\(d\) stochastic Allen–Cahn equation. Electron. J. Probab. 17(39), 1–14 (2012)
Kuo, H.-H.: Introduction to Stochastic Integration. Universitext. Springer, New York (2006)
Kupiainen, A.: Renormalization Group and Stochastic PDE’s (2014). arXiv:1410.3094
Mourrat, J.-C., Weber, H.: Convergence of the two-dimensional dynamic Ising–Kac model to \(\varPhi ^4_2\). Commun. Pure Appl. Math. (in press). arXiv:1410.1179
Mourrat, J.-C., Weber, H.: Global Well-Posedness of the Dynamic \(\varPhi ^4\) Model in the Plane (2015). arXiv:1501.06191
Mourrat, J.-C., Weber, H.: Global Well-Posedness of the Dynamic \(\varPhi ^4_3\) Model on the Torus (2016). arXiv:1601.01234
Nualart, D.: The Malliavin Calculus and Related Topics. Probability and its Applications (New York), 2nd edn. Springer, Berlin (2006)
Osterwalder, K., Schrader, R.: Axioms for Euclidean Green’s functions. Commun. Math. Phys. 31, 83–112 (1973)
Osterwalder, K., Schrader, R.: Axioms for Euclidean Green’s functions. II. Commun. Math. Phys. 42, 281–305 (1975). With an appendix by Stephen Summers
Parisi, G., Wu, Y.S.: Perturbation theory without gauge fixing. Sci. Sinica 24(4), 483–496 (1981)
Polyak, M.: Feynman diagrams for pedestrians and mathematicians. In: Graphs and Patterns in Mathematics and Theoretical Physics. Proceedings of Symposia in Pure Mathematics, vol. 73, pp. 15–42. American Mathematical Society, Providence (2005)
Revuz, D., Yor, M.: Continuous Martingales and Brownian Motion. Grundlehren der Mathematischen Wissenschaften, vol. 293, 2nd edn. Springer, Berlin (1994)
Acknowledgements
We are grateful to the very careful referees for their detailed and constructive criticisms, which led to many improvements over the whole paper. We were particularly impressed that one of the referees’ reports turned out to be longer than our paper itself! JCM is partially supported by the ANR Grant LSD (ANR-15-CE40-0020-03). HW is supported by the Royal Society through the University Research Fellowship UF140187. WX is supported by the EPSRC through the fellowship EP/N021568/1.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
We now give a second proof of Proposition 4, based on the following logarithmic Sobolev inequality (see [4, Sect. 1.6] and [23, Sects. 1.1 and 1.5]).
Lemma 7
(log-Sobolev inequality) Let \(\mu \) be a Gaussian measure and \(X \in W^{1,2}(\mu )\). We have
where \(\mathbf {D}\) is the Malliavin derivative, and \(\mathbb {E}\) is the expectation taken with respect to \(\mu \).
Now, let \(T_{t}\) be the Ornstein-Uhlenbeck semigroup defined by
where \(X_{n}\) is the component of X in \(\mathcal H_{n}\). The Ornstein-Uhlenbeck semigroup is closely related to the Malliavin derivative, because it determines the quadratic form associated with the infinitesimal generator L of \(T_t\). More precisely, for sufficiently nice random variables X, Y, we have
See [23, Sect. 1.4] for a more detailed discussion of these objects. The main use of the logarithmic Sobolev inequality will be to show the following hypercontractivity estimate.
Proposition 6
(Hypercontractivity) Let \(T_{t}\) be the Ornstein-Uhlenbeck semigroup. We have
for all \(p \ge 2\) and \(q = 1 + (p-1) e^{2t}\).
Proof
(Second proof of Proposition 4) If \(X \in \mathcal H_{n}\), then \(T_{t} X = e^{-nt} X\), and we can see that Proposition 4 is an immediate consequence of Proposition 6. It then remains to prove Proposition 6. We can assume \(X \ge 0\) without loss of generality.
Fix \(p \ge 2\). Let \(q(t) = 1 + (p-1) e^{2t}\), and let
Our aim is to show that \(G'(t) \le 0\) for all \(t > 0\), and (92) will follow. In fact, we have
Since \(q'(t) \ge 0\), it suffices to show that
Noting that
we see that (93) is equivalent to
Applying the log-Sobolev inequality to the random variable \((T_{t}X)^{\frac{q(t)}{2}}\) and using the integration by parts formula (91) which in the current context becomes
we see that (94) follows immediately.
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Mourrat, JC., Weber, H., Xu, W. (2017). Construction of \(\varPhi ^4_3\) Diagrams for Pedestrians. In: Gonçalves, P., Soares, A. (eds) From Particle Systems to Partial Differential Equations. PSPDE 2015. Springer Proceedings in Mathematics & Statistics, vol 209. Springer, Cham. https://doi.org/10.1007/978-3-319-66839-0_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-66839-0_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-66838-3
Online ISBN: 978-3-319-66839-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


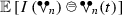 while the former coincides with
while the former coincides with 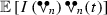 . However, as the reader can check, the difference between these constants remains bounded as n tends to infinity.
. However, as the reader can check, the difference between these constants remains bounded as n tends to infinity.