Practical Estimation of Mutual Information on Non-Euclidean Spaces

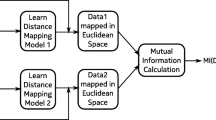
Abstract

We propose, in this paper, to address the issue of measuring the impact of privacy and anonymization techniques, by measuring the data loss between “before” and “after”. The proposed approach focuses therefore on data usability, more than in ensuring that the data is sufficiently anonymized. We use Mutual Information as the measure criterion for this approach, and detail how we propose to measure Mutual Information over non-Euclidean data, in practice, using two possible existing estimators. We test this approach using toy data to illustrate the effects of some well known anonymization techniques on the proposed measure.

1 Introduction

Legal and ethical data sharing and monetization is becoming a major topic and concern, for data holders. There is indeed a strong need to make use of all the Big Data accumulated by the hordes of devices that are becoming part of the Internet of Things (IoT) scene. One major difficulty holding back (some of) the parties in this data monetization and sharing scheme, is the ethical and legal problem related to the privacy of this collected data. Indeed, IoT devices are becoming more and more personal (even though smartphones are already holding on to very personal data), with wearables, medical-oriented devices, health and performance measuring devices...And while users often agree to the use of their collected data for further analysis by the service provider, data sharing to a third party is another type of problem. In this sense, data anonymisation in the broad sense is a rather hot topic, and of the utmost concern for such data sharing scenarios.

There exist many ways to obfuscate the data before data sharing, with the most extreme ones consisting in basically modifying the data so randomly and so much, that the end result becomes unusable. Encryption [9] (when properly carried out) would be one example of such data alteration. And while the promises of Homomorphic Encryption [7], for example, are appealing, the problem of the usability of the data by a third party remains the same: the data has already been so utterly modified by the encryption scheme, that the internal data structures are too altered to be used for even basic data mining.

Such approaches that obfuscate totally the data have several practical use cases; for example when storage is to be carried out by an untrusted third party. In this work, we focus on another type of use case: that of the need for usability of the data (in the eyes of a third party) while still carrying out some anonymization. The idea here, is to try and measure how much the data has been altered, in terms of its information content (and not in terms of the actual exact values contained in the data). We are thus looking for a measure that would allow for comparing usability to anonymization/privacy.

In this paper, we do not focus on the means of achieving privacy, or what tools can be used for anonymization, but on how to quantify objectively the information loss created by such techniques. Many techniques have already been proposed to alter the data so as to improve the anonymity levels in it: k-anonymity [8], l-diversity [4], differential privacy [2], as well as working towards ways to perform analysis on such modified or perturbed data [1, 5]...We give a brief overview of some of these approaches in the next Sect. 2. One of the issues that we attempt to address in this paper, is the fact that they lack an objective criterion to establish how much the data has actually changed, after using such anonymization techniques. In Sect. 3, we introduce some of the notations for the following Sect. 4 about mutual information as a possible criterion for measuring the data loss. In this section, we detail our approach to estimate mutual information over any data set (including those with non-Euclidean data), and the computational details of how we propose to do it. We present the results of this approach over toy data sets in Sect. 5.

2 A Short Primer on Anonymization Techniques

We first propose in this section to illustrate the effect of some of the most common anonymization techniques, on a limited, traditional data set, depicted in Table 1. The presented anonymization techniques in the following are by no means an exhaustive account of all the possibilities for data anonymization, but probably represent some of the most widely used techniques, in practice.

Table 1. Example of health data records from a medical institution.

The example data in Table 1 depicts some medical records for a set of patients, possibly from a health care provider. The classification of the data attributes in “Sensitive” and “Non-Sensitive” categories is somewhat arbitrary in this case. The records from Table 1 show no obvious easily identifiable information when considering single fields. Nevertheless, relationships between the non-sensitive fields in this data can probably make it relatively easy to identify some individuals: within a zip code, the nationality and the age allow someone to restrict the set of possible individuals dramatically. The last individual in the table is even more striking as her age, nationality and zip code surely make her stand out of the rest.

2.1 k-anonymity

The term k-anonymity designates in general both the set of properties a data set has to satisfy to be k-anonymous, and the various techniques that can be used to achieve this property. In practice, a data set is said to be k-anonymous if the information for each individual record in the data set cannot be distinguished from at least $k-1$ other records from the very same data set. Two examples of techniques used to achieve k-anonymity are Suppression and Generalisation, and are described in the next two subsections.

Suppression. Suppression is obviously the crudest of the possible data alterations, as the data gets simply removed, either for a specific set of records in the data, or for a whole field of data. In the following example Table 2, the whole field of the Age of the records has been removed. This approach can obviously lead to strong data alteration, and thus disturb whatever process using the data afterwards. A more subtle solution is provided by Generalization, as follows.

Table 2. Effect of suppression (k-anonymity).

Generalization. The idea behind generalisation is to abstract the values in a certain field to higher level (more general) categories. In the example of the data from Table 1, this could mean replacing the last two digits from the Zip Code by zeros, for example, or abstracting the Nationality to “Asian, Caucasian,...” instead of country level specifics. In the following example Table 3, we generalised the age of the records to 10 years age ranges.

Table 3. Effect of generalization (k-anonymity).

This approach asks the question of what is satisfying in terms of “granularity” of the abstraction? How much information is actually lost in generalising the data fields, and what is the best way to ensure k-anonymity: generalising several fields a little, or one field a lot?

2.2 Differential Privacy

Differential Privacy [2] aims at preserving higher level data statistical properties, typically by introducing controlled noise in the data fields. Without going into the details and the various versions of Differential Privacy [2], we focus in this work on the specific case of $\varepsilon$-differential privacy, in which the $\varepsilon$ parameter basically acts as a control parameter for the trade-off between privacy and usability. More specifically, in the rest of the paper (and for the experiments section), we will use Laplace noise added to the data fields, with the $\varepsilon$ parameter being the inverse of the Laplace distribution parameter $\lambda$.

In the following Sect. 3, we depart a little from the usual notations used in the data privacy literature, to present the mutual information estimators that we propose to use to measure the information loss created by the use of these anonymization techniques.

3 Notations

Let be a metric space on the set $\mathbb {X}_{i}$ with the distance function $d_{i}:\mathbb {X}_{i}\times \mathbb {X}_{i}\longrightarrow \mathbb {R}_{+}$. The need not be Euclidean spaces, and in the cases discussed in the following sections, are not.

Let us then define by $\mathbf {X}=\left[ \mathbf {x}^{1},\ldots ,\mathbf {x}^{n}\right]$ a $N\times n$ matrix, with each column vector $\mathbf {x}^{i}\in \mathbb {X}_{i}^{N\times 1}$. The $\mathbf {x}_{i}$ are thus discrete random variables representing a set of samples over the set of all the possible samples from the attribute represented here by $\mathbb {X}_{i}$. And $\mathbf {X}$ is a table over these attributes.

The fact that the are not necessarily Euclidean spaces in this work poses the problem of the definition of the distance function associated, $d_{i}$. Indeed, most data mining and machine learning tools rely on the Euclidean distance and its properties; and even if the learning of the model does not require the use of Euclidean distances directly, the evaluation criterion typically relies on it, for example as a Mean Square Error for regression problems.

Similarly, as described in Sect. 4, information theory metrics estimators such as mutual information estimators typically rely on the construction of the set of nearest neighbours, and therefore also typically (although not necessarily) on the Euclidean distance.

3.1 Distances over Non-Euclidean Spaces

The argument for considering the use of distances over non-Euclidean spaces in this work, is that it is possible to tweak and modify such non-Euclidean distances so that their distribution and properties will be “close enough” to that of the original Euclidean distance.

More formally, let us assume that we have two metric spaces and , with the canonical d-dimensional Euclidean space (i.e. $\mathbb {X}_{i}=\mathbb {R}^{d}$ and $d_{i}$ the Euclidean norm over it) and a non-Euclidean metric space endowed with a non-Euclidean metric. Drawing uniformly samples from the set $\mathbb {X}_{j}$, we form $\mathbf {X}_{j}=\left[ \mathbf {x}_{j}^{1},\dots ,\mathbf {x}_{j}^{n}\right]$, a set of random variables, with $\mathbf {x}_{j}^{l}$ having values over $\mathbb {X}_{j}$. Denoting then by $f_{d_{j}}$ the distribution of pairwise distances over all the samples in $\mathbf {X}_{j}$, we assume that it is possible to modify the non-Euclidean metric $d_{j}$ such that

$$\begin{aligned} \lim _{n\rightarrow \infty }f_{d_{j}}=f_{d_{i}}, \end{aligned}$$

(1)

where $f_{d_{i}}$ is the distribution of the Euclidean distances $d_{i}$ over the Euclidean space . The limit here is over n as the distribution $f_{d_{j}}$ is considered to be estimated using a limited number n of random variables, and we are interested in the limit case where we can “afford” to draw as many random variables as possible to be as close to the Euclidean metric as possible. That is, that we can make sure that the non-Euclidean metric behaves over its non-Euclidean space, as would a Euclidean metric over a Euclidean space.

This assumption is “theoretically reasonable”, as it comes down to being able to transform a distribution into another, given both. And while this may not be simple nor possible using linear transformation tools, most Machine Learning techniques are able to fit a continuous input to another different continuous output.

4 Mutual Information for Usability Quantification

4.1 Estimating Mutual Information

Using previous notations from Sect. 3, we use the definition of mutual information $I(\mathbf {x}_{i}, \mathbf {x}_{j})$ between two discrete random variables $\mathbf {x}_{i}, \mathbf {x}_{j}$ as

$$\begin{aligned} I(\mathbf {x}_{i}, \mathbf {x}_{j}) = \sum _{x_{i}\in \mathbf {x}_{i}}\sum _{x_{j}\in \mathbf {x}_{j}}p(x_{i},x_{j})\log \left( \frac{p(x_{i},x_{j})}{p(x_{i})p(x_{j})}\right) . \end{aligned}$$

(2)

In practice, the marginals $p(x_{i})$ and $p(x_{j})$ as well as the joint $p(x_{i},x_{j})$ are often unknown, and we can then use estimators of the mutual information.

Most of the mutual information estimators (and most famously Kraskov’s [3] and Pal’s [6]) use the canonical distance defined in the metric space in which lies the data. Typically, this is defined and computable for a Euclidean space, with the traditional Euclidean distance used as the distance function.

In the following, we detail shortly the two mutual information estimators that are (arguably) the most used in practice. The goal of this description being to illustrate their dependency on the metric space’s underlying distance functions. This is mainly to make the point that mutual information can thus be estimated using non-Euclidean distances over non-Euclidean spaces, given some precautions, as mentioned in the previous Sect. 3.1.

Kraskov’s Estimator. In [3], Kraskov et al. propose a mutual information estimator (more precisely, two of them) relying on counts of nearest neighbours, as follows. Kraskov’s First Estimator The initial mutual information estimator $I^{(1)}$ between two random variables $\mathbf {x}_{j}^{l}$ and $\mathbf {x}_{j}^{m}$ is defined as

$$\begin{aligned} I^{(1)}(\mathbf {x}_{j}^{l},\mathbf {x}_{j}^{m}) = \varPsi (k)-<\varPsi (\mathbf {n}_{\mathbf {x}_{j}^{l}}+1)+\varPsi (\mathbf {n}_{\mathbf {x}_{j}^{m}}+1)>+\varPsi (N), \end{aligned}$$

(3)

where $\varPsi$ is the digamma function, and the notation ${<}\cdot {>}$ denotes the average of the quantity between the brackets. In addition, the quantity $\mathbf {n}_{\mathbf {x}_{j}^{l}}$ (and defined in the same way, $\mathbf {n}_{\mathbf {x}_{j}^{m}}$) denotes the vector $\mathbf {n}_{\mathbf {x}_{j}^{l}}=\left[ n_{\mathbf {x}_{j}^{l}}(1),\ldots ,n_{\mathbf {x}_{j}^{l}}(N-1)\right]$ holding the counts of neighbours $n_{\mathbf {x}_{j}^{l}}(i)$ defined as

$$\begin{aligned} n_{\mathbf {x}_{j}^{l}}(i) = \text {Card}\left( \left\{ x_{i}\in \mathbf {x}_{j}^{l}:d_{j}(x_{j}-x_{i})\le \varepsilon (i)/2\right\} \right) \end{aligned}$$

(4)

where $\varepsilon (i)/2=||z_{i}-z_{k\text {NN}(i)}||_{\text {max}}$ is the distance between sample $z_{i}$ and its k-th nearest neighbour in the joint space $\mathbf {z}=(\mathbf {x}_{j}^{l},\mathbf {x}_{j}^{m})$, and the distance $||\cdot ||_{\text {max}}$ defined as $||z_{q}-z_{r}||_{\text {max}}=\max \left\{ ||x_{j}^{l}(q)-x_{j}^{l}(r)||,||x_{j}^{m}(q)-x_{j}^{m}(r)||\right\}$, where $x_{j}^{l}(q)$ clunkily denotes the q-th sample from the random variable $\mathbf {x}_{j}^{l}$.

Kraskov’s Second Estimator. The second mutual information estimator $I^{(2)}$ between two random variables $\mathbf {x}_{j}^{l}$ and $\mathbf {x}_{j}^{m}$ is defined as

$$\begin{aligned} I^{(2)}(\mathbf {x}_{j}^{l},\mathbf {x}_{j}^{m}) = \varPsi (k)-1/k-<\varPsi (\mathbf {n}_{\mathbf {x}_{j}^{l}})+\varPsi (\mathbf {n}_{\mathbf {x}_{j}^{m}})>+\varPsi (N), \end{aligned}$$

(5)

with $\varPsi$ the digamma function, k the number of neighbours to use (to be decided by the user), and this time, $\mathbf {n}_{\mathbf {x}_{j}^{l}}=\left[ n_{\mathbf {x}_{j}^{l}}(1),\ldots ,n_{\mathbf {x}_{j}^{l}}(N-1)\right]$ is the vector holding counts of neighbours $n_{\mathbf {x}_{j}^{l}}(i)$ defined as

$$\begin{aligned} n_{\mathbf {x}_{j}^{l}}(i) = \text {Card}\left( \left\{ x_{i}\in \mathbf {x}_{j}^{l}:d_{j}(x_{j}-x_{i})\le \varepsilon _{\mathbf {x}_{j}^{l}}(i)/2\right\} \right) \end{aligned}$$

(6)

where $\varepsilon _{\mathbf {x}_{j}^{l}}(i)/2$ is the distance between sample $z_{i}$ and its k-th nearest neighbour $z_{kNN(i)}$, both projected on the $\mathbf {x}_{j}^{l}$ space.

Basically, the calculation requires calculating the nearest neighbours of points in a joint space, and counting how many lie in a certain ball.

Note that while we have adapted the notations to our needs, here, the original article relies on the Euclidean distance, and not on arbitrary distances on non-Euclidean distances.

In the following, we illustrate the calculations of the mutual information by these two estimators, over simple non-Euclidean data, namely GPS traces of people.

5 Experimental Results

We take in the following experiments, a toy (synthetic) data set that has the same structure as internal data (which cannot be released), namely timestamped GPS locations. We generate five synthetic GPS traces for 5 individuals, as can be seen on Fig. 1. It is worth noting that some of the traces have similar routes, with identical start and end points, while others are totally different.

5.1 GPS Routes (Timestamped Data)

Assume we have a dataset $\varvec{X} = [\varvec{x_1},...,\varvec{x_N}]^{T}$ to depict the trajectory of one specific person, where the attributes of each record $\varvec{x_i}$ explain the location at the corresponding time $\varvec{t_i}$ for this specific person. The locations are represented in GPS coordinates ($\varvec{gps}$) with the form of latitudes ($\varvec{lat}$) and longitudes ($\varvec{lon}$). Each record $\varvec{x_i}$ can then be described by: $\varvec{x_i} = (\varvec{gps_i},\varvec{t_i}) = ((\varvec{lat_i},\varvec{lon_i}), \varvec{t_i}$). Hence, the mutual information of the dataset $\varvec{I}(\varvec{X})$ is in a $d \times d$ matrix (in this case $d=2$: the number of attributes) with the elements holding the mutual information values of the pairwise attributes, illustrated by:

$$\begin{aligned} \begin{aligned} \varvec{I}(\varvec{X})&= \{ I(\varvec{x}^i,\varvec{x}^j) \}_{1 \le i,j \le d} \\&= \left[ \begin{array}{llll} I(\varvec{gps},\varvec{gps}) &{} I(\varvec{gps},\varvec{t}) \\ I(\varvec{t},\varvec{gps}) &{} I(\varvec{t},\varvec{t}) \end{array}\right] , \end{aligned} \end{aligned}$$

(7)

Note that the metric space of the GPS coordinates is a non-Euclidean space, because the distance of two GPS coordinates $(\varvec{lat},\varvec{lon})$ is the shortest route between the two points on the Earth’s surface, namely, a segment of a great circle. It is obviously not a Euclidean distance. Meanwhile, the metric space of time is a Euclidean space with a typical Euclidean distance function.

Fig. 1.

Five trajectories from the five experimental datasets, respectively.

Table 4. Mutual information (MI) matrices of the five experimental datasets. $I^{(1)}$ and $I^{(2)}$ represent the MI calculated by the first and second Kraskov estimators.

We illustrate the mutual information matrices by introducing five experimental datasets, with each dataset recording the trajectory for one person. For each person, 100 timestamps and the corresponding $\varvec{gps}$ locations are recorded, where the locations are measured at uniform sampling intervals. The trajectories in the datasets are shown in Fig. 1.

Table 4 shows the mutual information (MI) matrices of the five experimental ids, respectively. Here we use $I^{(1)}$ and $I^{(2)}$ to represent the values of MI calculated from the first and second Kraskov estimators, respectively. We can see that the MI element value of two identical attributes stays constant, regardless of the variables of the attribute itself: $I^{(1)}(\varvec{gps},\varvec{gps}) = I^{(1)}(\varvec{t},\varvec{t})=5.18$, and $I^{(2)}(\varvec{gps},\varvec{gps}) = I^{(2)}(\varvec{t},\varvec{t})= 4.18$. Meanwhile, the MI matrices are symmetric with $I(\varvec{gps},\varvec{t}) = I(\varvec{t},\varvec{gps})$ for both estimators, of course. The MI values of non-identical pairwise attributes (e.g., $I(\varvec{gps},\varvec{t})$) are found to be relatively smaller than those values of two identical attributes (e.g., $I(\varvec{gps},\varvec{gps})$), with the obvious reason that the two identical sets of variables are more mutually dependent than two different variables sets.

The values of $I(\varvec{gps},\varvec{t})$ are calculated to be in the ranges of $3.65-3.69$ and $2.60-3.20$ for $I^{(1)}$ and $I^{(2)}$, respectively, compared with the $I(\varvec{gps},\varvec{gps})$ values of 5.18 and 4.18 for the two estimators. We can see that $I^{(2)}$ is more sensitive than $I^{(1)}$ for ids with different trajectories, by giving disparate $I^{(2)}(\varvec{gps},\varvec{t})$ values. For example, the $I^{(2)}(\varvec{gps},\varvec{t})$ of $id_1$ with the value of 3.20 is larger than those for $id_2$, $id_3$, and $id_4$, with values around 2.7. This is mainly due to the relatively more peculiar trajectory of $id_1$.

Fig. 2.

Mutual information (MI) dependence on the number of samples in the dataset.

5.2 Convergence of the MI Estimators

It is obvious that all the MI values calculated from $I^{(1)}$ are relatively larger than those from $I^{(2)}$. In principle, both estimators should give very similar results. The difference here is because the number of records with $N=100$ in each dataset is so small that in the estimators $n_x(i)$ and $n_y(i)$ tend to be also very small with considerably large relative fluctuations. This will cause large statistical errors. We discuss here about the MI convergence with increasing numbers of records.

We take the trajectory of $id_4$ for example to explain the MI convergence. In the original dataset, there are 100 uniform timestamps and the corresponding 100 uniform locations. We increase the number of records N to 200, 300, 400, ..., 2000, by interpolating uniformly denser timestamps and locations into the trajectory. $I^{(1)}(\varvec{gps},\varvec{t})$ and $I^{(2)}(\varvec{gps},\varvec{t})$ is then calculated with the ratio of k / N kept to be 0.01 in the estimators.

The dependence of $I(\varvec{gps},\varvec{t})$ values over number of record N is illustrated in Fig. 2. It can be seen that the discrepancy of $I^{(1)}$ and $I^{(2)}$ values is getting smaller with increasing N. When N is larger than 800, $I^{(1)}$ and $I^{(2)}$ converge to the values around 4.6.

5.3 k-anonymity Effects on the Trajectory Datasets

We have here used the Generalization approach from k-anonymity to modify the data set, and explore the influence of such changes on the mutual information values.

In the following Table 5, k-anonymity applied to the GPS field means that we have in practice rounded the GPS coordinates (lat and lon) by 2 digits, compared to the original precision; when applied to the time field, we have also rounded the time to 10 min intervals (instead of second precision).

Table 5. Effects of k-anonymity on mutual information (MI) matrices for the five experimental datasets.

It should be noted that we only report the values for the first estimator, here. In practice, the changes in mutual information incurred by the chosen k-anonymity values on the GPS are relatively minimal, as can be seen in Table 5. It is interesting to note that the changes on the time cause much more distortion in the data (in terms of the mutual information), possibly because the granularity of the generalization is higher for the time, given the “rounding” chosen. The most interesting feature is that by altering both GPS and time at the same time, the mutual information is higher than when time alone is affected. We explain this by the fact that when these two fields are changed in the same fashion at the same time, the disturbance to the relationship between them is less than when only changing the time. This change to both fields “preserves” some of the relationship better, it seems.

5.4 Differential Privacy Effects on the Trajectory Datasets

We have used $\varepsilon$-differential privacy to obfuscate the trajectory datasets by the Laplace mechanism. We define the privacy function to be a family set of $h=\{h^{(\varvec{gps})},h^{(\varvec{t})}\}$, where $h^{(\varvec{gps})}$, $h^{(\varvec{t})}$ are the obfuscating functions to perturb the GPS field and time field, respectively.

Differential privacy was applied by adding controllable noise to the corresponding attribute in the dataset, which satisfies the Laplace distribution with mean $\mu$ and standard deviation b: $h^{(i)}=\mathtt {diff}^{(i)}(\mu ,b)$. Let $\varepsilon$ be the differential privacy parameter, the standard deviation b of the Laplace noise can be then obtained by:

$$\begin{aligned} b=\frac{\varDelta f}{\varepsilon }, \end{aligned}$$

(8)

where $\varDelta f$ is the sensitivity of the attribute field.

In the following discussion, we used three family sets of privacy functions, which are:

$$\begin{aligned} \begin{aligned}&h_1=\{ \mathtt {diff}^{(\varvec{gps})}(\mu ,b), \quad \emptyset ^{(\varvec{t})}\}; \\&h_2=\{ \emptyset ^{(\varvec{gps})}, \qquad \qquad \quad \! \mathtt {diff}^{(\varvec{t})}(\mu ,b) \}; \\&h_3=\{ \mathtt {diff}^{(\varvec{gps})}(\mu ,b), \quad \mathtt {diff}^{(\varvec{t})}(\mu ,b) \}, \end{aligned} \end{aligned}$$

(9)

where $\emptyset ^{(\varvec{i})}$ stands for taking no action to the attribute $\varvec{i}$. For example, $h_1$ means adding Laplace noise only to the GPS attribute, while the timestamps stay the same; $h_2$ means adding Laplace noise only to the timestamps attribute; $h_3$ means adding Laplace noises to both GPS and timestamps attributes.

Fig. 3.

Mutual information (MI) values of $\varvec{I}(h^{(\varvec{gps})},h^{(\varvec{t})})$, with the GPS field and time field obfuscated by differential privacy technique with the privacy functions of $h^{(\varvec{gps})}$ and $h^{(\varvec{t})}$, respectively. The MI values are obtained by taking the average of $\varvec{I}(h^{(\varvec{gps})},h^{(\varvec{t})})$ values from the 5 trajectories. The discrete markers are the obtained averaged MI values, while the corresponding solid lines are the fitted functions with machine learning technique. (a) and (b) are the MI values calculated by the first and second Kraskov estimators, respectively.

Figure 3 shows the obtained pairwise MI values of $\varvec{I}(h^{(\varvec{gps})},h^{(\varvec{t})})$, where the privacy function sets are applied to the GPS field and time fields with various privacy parameters $\varepsilon$ from 0 to 20. We can see that $\varvec{I}(h^{(\varvec{gps})},h^{(\varvec{t})})$ is monotonically decreasing when the privacy parameter $\varepsilon$ decreases. When $\varepsilon$ turns to close enough, but not equal, to 0, the MI values collapse at 0, where the fluctuations are the statistic errors caused by small number of sample N in the datasets. It can be well explained by the fact that with smaller values of $\varepsilon$, the amplitudes of the Laplace noise (calculated by Eq. 8) become larger, which distort the metric space or topology of the original datasets more extensively to higher levels with increasing privacy. In another word, we can say that small $\varepsilon$ in differential privacy creates greatly anonymised datasets, and effectively alters the metric space with big distortion in terms of the mutual information between the data fields (GPS, time), while the information contents extracted from the anonymised datasets will reduce as a trade-off of increasing privacy. The linkability between the attributes is thus weakened to prevent re-identification of the individuals. Hence the pairwise MI values are decreased.

The efficiencies of altering the MI values by the privacy functions $h_1$, $h_2$, and $h_3$ can be compared in Fig. 3. Both estimators indicate that when applying differential privacy technique on GPS field ($h_1$) and time field ($h_2$) separately at the same privacy parameters $\varepsilon$, the time field is more sensitive to reduce the MI values, compared to the GPS field. Moreover, differential privacy applied on both GPS and time ($h_3$) fields at the same time is the most efficient data anonymization function (in terms of affecting the data relationships regarding mutual information).

As we have discussed before, small MI values stand for high distorsions of the data anonymization, at the possible cost of unusable data, while large MI values imply small alteration of the dataset topology, with a potentially high re-identifiability risk. Therefore, we want to find an acceptable range of MI values, where the dataset is sufficiently anonymized to ensure as low as possible risk of re-identification, while the amount of information in the distorted data is still sufficiently usable for future data analysis (in terms of relationships between data fields). Our goal is to control and quantify this distortion, by restricting the privacy parameters in the anonymization functions to specific, acceptable ranges, or by conveying restrictions over the obfuscation functions, also in a controllable manner.

6 Conclusion

In this paper, we have proposed an applied information theoretic approach to measure the impact of privacy techniques such as k-anonymity and differential privacy, for example. We examine, by this approach, the disturbances in the relationships between the different columns (“fields”) of the data, thus focusing on a data usability aspect, rather than actually measuring privacy. We propose to do this on any data that can be taken over a metric space, i.e. for which a distance between elements is the sole practical need. We develop an approach to estimate mutual information between such data types, using two well known estimators, and demonstrate their behaviour over simple experimental tests. We finally investigate the effects of k-anonymity (specifically, generalisation) and differential privacy over timestamped GPS traces, and illustrate the effects of these widely used privacy techniques over the information content and the relationships contained in the data. In effect, the results obtained are as expected, except possibly for the case where the generalisation in k-anonymity is performed over both fields at the same time, and leads to some preservation of the data structure and relationships. Future work will include other data types and other mutual information estimators to verify the results observed in this work.