Decentralized Computation of Homology in Wireless Sensor Networks Using Spanning Trees

Abstract

When deploying a wireless sensor network over an area of interest, the information on signal coverage is critical. It has been shown that even when geometric position and orientation of individual nodes is not known, useful information on coverage can still be deduced based on connectivity data. In recent years, homological criteria have been introduced to verify complete signal coverage, given only the network communication graph. However, their algorithmic implementation has been limited due to high computational complexity of centralized algorithms, and high demand for communication in decentralized solutions, where a network employs the processing power of its nodes to check the coverage autonomously. To mitigate these problems, known approaches impose certain limitations on network topologies. In this paper, we propose a novel distributed algorithm which uses spanning trees to verify homology-based network coverage criteria, and works for arbitrary network topologies. We demonstrate that its communication demands are suitable even for low-bandwidth wireless sensor networks.

1 Introduction

Wireless sensor networks (WSN) have in recent years become well-established ad-hoc networks with numerous applications in environmental and health care monitoring. Distributed nature of WSNs, random node deployment and frequent topology changes challenge the researchers to design special data mining techniques, suitable for WSNs [1]. Small sensing nodes, scattered over an area of interest, typically sample the domain in a point cloud fashion, making possible the use of computational geometry and algebraic topology to extract knowledge from the collected data [2]. An active field of research in WSN has been the problem of coverage [3], which is usually interpreted as how well a WSN monitors its area of interest. Substantial research has been done on how to assure coverage in WSN by manually deploying nodes [4,5,6]. In many cases, manual positioning is highly impractical or not possible at all, therefore a number of coverage verification methods had been introduced. Some of them employ geometric constructs based on Voronoi diagrams or Delaunay triangulation, and so rely on the geometric location of nodes [7,8,9,10,11]. Detecting geometric position is a difficult problem, requiring additional hardware such as GPS, which might not always be feasible (e.g. GPS does not work indoors). Other methods tend to verify coverage using relative node positions or angles between them [12,13,14]. These techniques rely on strengths of received signals and timing differentials.

Simple network devices mostly lack the ability to obtain their geometric layout. To provide a coverage verification feature for such low-cost networks, connectivity based solutions are required. We base our work on the work of Ghrist et al. [15,16,17,18], who introduced an innovative approach based on algebraic topology. They showed that under certain conditions regarding the ratio between the sensing range and the communication range of nodes in a WSN, a connection-based combinatorial construction called the Rips complex (also known as the Vietoris-Rips complex), captures certain information on sensing coverage. More precisely, the criterion derived from homological properties of the Rips complex states that a hole-free Rips complex over a WSN assures complete sensing coverage. Soon, decentralized implementations were proposed [19, 20] which rely on distributed processing and storage of large matrices. Such algorithms impose a heavy communication load on the network to the extent, that their use for practical purposes is questionable. To mitigate this problem, partitioning of large networks using divide-and-conquer method has been proposed [21,22,23,24]. This led to more pragmatic approaches of coverage verification where holes in the Rips complex are detected by local message flooding or systematic network reduction [25, 26]. To the best of our knowledge, all known algorithms assume certain topological limitations, most notably the demand for a circular fence made of specially designated and configured nodes.

In this paper, we propose a novel distributed algorithm for homological coverage verification that imposes no limitations on network topology and demands no special nodes to be designated and configured further, they are based on a common network structure, namely the spanning tree. We simulate the algorithm on networks of different sizes and demonstrate a low demand for data exchange, which should easily be handled even by low-bandwidth networks. The rest of the paper is organized as follows: in Sect. 2 we cover the basics of homological coverage verification in wireless sensor networks. In Sect. 3 we give a detailed description our algorithm. We then present the results of simulations in Sect. 4, and give our our final conclusions in Sect. 5.

2 Homological Coverage Criteria

We model a wireless sensor network as a collection of nodes scattered over a plane, each performing environmental measurements within the sensing radius $r_s$, and communicating with other nodes within the the communication radius $r_c$. We define wireless sensor network as a triple $N = (V, r_s, r_c)$, where $V = \{ v_1, \ldots , v_k \}, k \ge 2$, is a set of planar points representing nodes. We adopt the following WSN properties from [18]:

• P1. Nodes V lie in a compact connected domain $\mathcal {D} \subset \mathbb {R}^2$.

• P2. Every node has its unique ID number which can be broadcast to all nodes within its communication radius $r_c$.

• P3. The sensing and communication radii satisfy the condition $r_s \ge r_c / \sqrt{3}$.

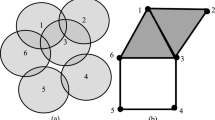
To optimize the performance, the power of transmission should be adjusted close to $r_c = \sqrt{3} \cdot r_s$. Two nodes within the range $r_c$ can communicate to each other, forming a link within the communication graph $\mathcal {G}_{N} = (V, E), E = \{ (u, v) \in V \times V | u \ne v, \text {d}(u, v) \le r_c \}$. The domain of interest is defined implicitly as the area spanned by connectivity graph $\mathcal {G}_{N}$ (see Fig. 1). The connectivity graph may assume arbitrary topology. In the case a network splits into disconnected sub-networks, the algorithm computes the coverage of each network independently.

Definition 1

(network domain). Domain $\mathcal {D} \subset \mathbb {R}^2$ of network $N = (V, r_s, r_c)$ is the smallest contractible set which contains all line segments $\overline{u v}$, where $u, v \in V$, and $d(u, v) \le r_c$.

Fig. 1.

Domain $\mathcal {D}$ assumes arbitrary topology. The failing of a node may split the coverage verification process into two independent tasks.

Each node covers a disk-shaped part of the domain within its sensing range $r_s$. We want to verify whether every point of domain $\mathcal {D}$ is within the sensing reach of at least one node.

Definition 2

(domain coverage). Let $\mathcal {D}$ be the domain of network $N = (V, r_s, r_c)$. Domain $\mathcal {D}$ is covered if $\mathcal {D} \subseteq \mathop \bigcup \limits _{v \in V} D_v$, where

$$\begin{aligned} D_v = \{ t \in \mathbb {R}^2 | \text {d}(v, t) \le r_s \}. \end{aligned}$$

(1)

Given a finite set of nodes V, a subset $\sigma = \{ v_0, v_1, \ldots , v_k \} \subseteq V$ is called a simplex. Every subset $\tau \subset \sigma$ is also a simplex, called face of $\sigma$. A simplicial complex over V is a collection K of simplices with vertices in V, such that the faces of every $\sigma \in K$ are also contained in K (see [27, 28]). We consider two types of simplicial complexes over V. One is the Čech complex $\check{\mathcal {C}}{(V)} = \{ \sigma \subseteq V | \mathop \bigcap \limits _{v \in \sigma } D_v \ne \emptyset \}$, where $D_v$ is as in (1). It has been shown that the Čech complex fully captures the homology of its underlying geometric shape [29]. This means that every hole in the coverage of network domain corresponds to a hole in $\check{\mathcal {C}}{(V)}$. Unfortunately, the Čech complex is not computable by our WSN since geometric information is needed, as evident from (1). The second simplicial complex we consider is the Rips complex $\mathcal {R}(\mathcal {G}_{N}) = \{ \sigma \subseteq V | \forall \{ u, v \} \subseteq \sigma : (u, v) \in \mathcal {G}_{N} \}$, which is built on connectivity information. As shown in [26], under assumption P3, there are no holes in $\check{\mathcal {C}}{(V)}$ if there are no holes in $\mathcal {R}(\mathcal {G}_{N})$. The absence of holes in the Rips complex therefore guarantees the coverage of domain $\mathcal {D}$.

Simplicial homology provides a convenient way to describe holes of a simplicial complex K. Take a sequence of links in K, such that they form a cycle c. If a set of triangles can be found in K, such that the border of their union is exactly the cycle c, then c does not encircle a hole. On the other hand, if such a set of triangles does not exist, c can be taken as a representative of the hole (or the sum of holes) around which it is wrapped. Cycles representing the same set of holes are called homologous cycles, and are considered homologically identical. These cycles form the first homology group of K, denoted $H_1(K)$. The rank of $H_1(K)$ is called first Betti number, denoted $\beta _1(K) = \text {rank}(H_1(K))$, and represents the number of holes in K. Domain $\mathcal {D}$ is covered if $\beta _1(\mathcal {R}(\mathcal {G}_{N})) = 0$.

3 Decentralized Computation of Homology

In this section, we propose a novel approach to computing the first Betti number of the network’s Rips complex. We construct the Rips complex distributively by merging smaller network segments into larger ones, until the complete Rips complex is obtained. This way, the parallel processing power of WSN can be exploited, requiring only local communication between nodes. We begin with the smallest segments which are hole-free, and if by merging two segments a hole is constructed, it is detected and considered only once. The process takes place in the direction of a precomputed spanning tree, from the leaves to the root. The final result is stored distributively, with each node holding the number of holes it discovered, and the global Betti number is obtained by simple summation of the local values up the tree.

The initial set of network segments is the set of all closed stars of nodes in $\mathcal {R}(\mathcal {G}_{N})$. The star of node v, denoted $St (v)$, is the set of all simplices that contain v, and is generally not a simplicial complex. The closure $\overline{S}$ of a set of simplices S is the smallest simplicial subcomplex of $\mathcal {R}(\mathcal {G}_{N})$ that contains all simplices from S. The closure $\overline{ St }(v)$, called the closed star of v, is therefore the set of all simplices that contain v, together with all their faces, that is $\overline{ St }(v) = \{ \tau \le \sigma | v \in \sigma , \sigma \in \mathcal {R}(\mathcal {G}_{N}) \}$. Initially, every node constructs its own closed star by examining its local 2-hop neighborhood. This is done in two steps. First, every node broadcasts its ID to all its immediate neighbors. After nodes collect their list of neighbors, lists are then broadcast in the second step. The precomputed spanning tree needs not be minimal for the algorithm to work correctly, but a minimal spanning tree improves performance. Distributed algorithms for constructing a minimal spanning tree are well-established (e.g. [30]).

3.1 Network Segmentation and Merging

At any time during the execution of our algorithm, the network is partitioned into segments, which merge into larger segments, until finally, all parts of the network are merged into the complete Rips complex. Two segments can be merged only if their intersection is non-empty, assuring that every segment is connected.

Definition 3

(network segment). Let $N = (V, r_s, r_c)$ be a wireless sensor network and $U \subseteq V$ such a subset of its nodes, that the simplicial complex $S = \mathop \bigcup \limits _{u_i \in U} \overline{ St }(u_i) \subseteq \mathcal {R}(\mathcal {G}_{N})$ is connected. We call the complex S, a segment of network N.

The process of merging begins with the set of closed stars as the smallest simplicial complexes, which are small enough to not allow any holes. Each node merges its star with the segments received from their children within the spanning tree. To describe the process of merging, we arbitrarily assign indices to segments that are being merged within a single node v. We shall call such ordered set of segments a sequence of segments and write $\{S_1, S_2, \ldots , S_n\}$.

Definition 4

(segment merging). A sequence of segments $z=\{S_1, S_2, \ldots , S_n\}$ is mergeable if for every $1 \ge k < n$ holds $(S_1 \cup \cdots \cup S_k) \cap S_{k+1} \ne \emptyset$. Segment merging is the operation that maps a mergeable sequence $\{ S_1, S_2, \ldots , S_n \}$ to simplicial complex $S = S_1 \cup S_2 \cup \cdots \cup S_n$.

In a spanning tree, the distance between a node v and its children is one hop, therefore all segments received by v have a non-empty intersection with $\overline{ St }(v)$. The order of merging can therefore be arbitrary if it begins with $\overline{ St }(v)$.

3.2 Computing Betti Numbers

Each node captures the number of holes generated by merging smaller segments into larger ones. The information on holes is then discarded and the merged segment forwarded to the parent node as a hole-free segment. This assures that the holes discovered by one node are not discovered again later in the process. We say that a node computes the local first Betti number, so that the summation of all local Betti numbers gives $\beta _1(\mathcal {R}(\mathcal {G}_{N}))$. In this section, we propose an algorithm to capture the number of locally generated holes. We begin with the following proposition which we prove with the help of the Mayer-Vietoris sequence (see [27,28,29]).

Proposition 1

Let A and B be network segments with nonempty intersection and trivial first homology group, that is $\tilde{H}_1(A) \cong \tilde{H}_1(B) = 0$, where $\tilde{H}$ denotes the reduced homology. Then there exists isomorphism

$$\begin{aligned} \tilde{H}_1(A \cup B) \cong \tilde{H}_0(A \cap B). \end{aligned}$$

(2)

Proof

Since A and B are network segments, they are by definition connected simplicial complexes, thus $\tilde{H}_0(A) \cong \tilde{H}_0(B) \cong 0$. The right tail of the reduced Mayer-Vietoris sequence of the triple $(A\cup B,A,B)$ is:

$$\begin{aligned} \underbrace{\tilde{H}_1(A) \oplus \tilde{H}_1(B)}_{\cong 0} \mathop {\longrightarrow }\limits ^{\phi } \tilde{H}_1(A \cup B) \mathop {\longrightarrow }\limits ^{\partial } \tilde{H}_0(A \cap B) \mathop {\longrightarrow }\limits ^{\psi } \underbrace{\tilde{H}_0(A) \oplus \tilde{H}_0(B)}_{\cong 0}. \end{aligned}$$

Obviously, $im \;\phi = 0$ and $\ker {\psi } = \tilde{H}_0(A \cap B)$. Exactness of the sequence implies $\ker {\partial } = 0$ and $im \;\partial = \tilde{H}_0(A \cap B)$, and hence $\partial$ is an isomorphism.   $\square$

In other words, if we merge two segments which are free of holes, there is a correspondence between the holes in the union and the number of disjoint components in their intersection. This yields the following corollary.

Corollary 1

Let A and B be network segments with nonempty intersection and $\beta _1(A) = \beta _1(B) = 0$. If $\#$ denotes the number of disjoint components of the simplicial complex, that is $\#K = \beta _0(K)=\tilde{\beta }_0(K)+1$, then:

$$\begin{aligned} \beta _1(A \cup B) = \#(A \cap B) - 1. \end{aligned}$$

(3)

Fig. 2.

Holes are formed by merging two segments.

Fig. 3.

A false hole can be formed by segments A and C.

When merging two segments, the above rule is used to count the number of holes in their union, as demonstrated in Fig. 2: The intersection of segments A and B consists of three components, namely $K_0$, $K_1$ and $K_2$, and their union contains two holes. Usually, more than two segments are being merged within a single node, therefore in the remainder of this section we consider extending this rule to an arbitrary mergeable sequence of segments. We address the following three problems:

• 1. When a hole is formed by merging two segments, the produced union is not a hole-free segment. In Sect. 3.3 we show that if such a segment is merged again higher in the spanning tree, the rule from Corollary 1 on counting the holes still applies.

• 2. The order in which segments are merged can produce fake holes, which are filled later in the process by succeeding segments (see Fig. 3). In Sect. 3.4 we show how such fake holes can be detected and excluded from computation of local Betti numbers.

• 3. Branches of the spanning tree may intersect, therefore a node is not guaranteed to receive the full information on segments local to its branch. In Sect. 3.5, we show that a node can detect the lack of such information. In such cases merging is done only partially, and instead of a single segment, a set of unmerged segments is forwarded to the parent node. Segments are then merged at the higher level, where the missing information becomes available. Our simulations show that in practice such scenarios occur infrequently.

3.3 Merging Within a Spanning Tree

We divide every network segment into two regions - the core and the frame. The core can be seen as the internal part of the segment where holes, if they exist, reside. The frame can be seen as the outer layer, where segments intersect when merged up the spanning tree.

Definition 5

(core and frame). Let $S = \mathop \cup \limits _{v \in M} \overline{ St }(v)$ be a network segment. We call the smallest simplicial complex that contains all nodes $v \in M$, the core of segment S, and denote $\mathcal {C}(S)$. We call the closure of its complement $\overline{S \backslash \mathcal {C}(S)}$, the frame of segment S, and denote $\mathcal {F}(S)$.

Recall that the closure $\overline{S}$ of a collection of simplices S is defined as the smallest simplicial complex that contains all simplices from S. The smallest segment core is the singleton $\{ v \}$ within a closed star $\overline{ St }(v)$. As two stars, $\overline{ St }(v)$ and $\overline{ St }(u)$, are being merged, new segment $\overline{ St }(v) \cup \overline{ St }(u)$ is formed, its core now containing u and v, while both stars cease to exist as separate network segments. Proceeding with the process up the spanning tree, each produced network segment is the union of closed stars that belong to a certain tree branch, and its core comprised of the nodes within that branch. At any time, each node belongs to the core of exactly one recorded network segment. This guarantees $\mathcal {C}(A) \cap \mathcal {C}(B) = \emptyset$ for any two segments A and B.

Proposition 2

Let A and B be mergeable network segments, such that $\mathcal {C}(A) \cap \mathcal {C}(B) = \emptyset$. Then

$$\begin{aligned} A \cap B = \mathcal {F}(A) \cap \mathcal {F}(B). \end{aligned}$$

(4)

Proof

First, let us show that $\mathcal {F}(A) \cap \mathcal {C}(B) \subseteq \mathcal {F}(A) \cap \mathcal {F}(B)$. We will do this by proving (i) $\mathcal {F}(A) \cap \mathcal {C}(B) \subseteq \mathcal {F}(A)$, and (ii) $\mathcal {F}(A) \cap \mathcal {C}(B) \subseteq \mathcal {F}(B)$. Statement (i) is obvious. To prove (ii) suppose there exists a $v \in \mathcal {F}(A) \cap \mathcal {C}(B)$, such that $v \notin \mathcal {F}(B)$. Since v is not in $\mathcal {F}(B)$, all its neighbors must also be in $\mathcal {C}(B)$. Recall that segments are composed of closed stars of their core nodes. Since $v \in A$, at least one of its neighbors has to be in $\mathcal {C}(A)$. This contradicts $\mathcal {C}(A) \cap \mathcal {C}(B) = \emptyset$, therefore $v \in \mathcal {F}(B)$. So we have proven (ii). In the same way we show that $\mathcal {F}(B) \cap \mathcal {C}(A) \subseteq \mathcal {F}(B) \cap \mathcal {F}(A)$. Finally, we deduce:

$$\begin{aligned} A \cap B&= (\mathcal {C}(A) \cup \mathcal {F}(A)) \cap (\mathcal {C}(B) \cup \mathcal {F}(B)) \\&= \underbrace{(\mathcal {C}(A) \cap \mathcal {C}(B))}_{= \emptyset } \cup \underbrace{(\mathcal {F}(A) \cap \mathcal {C}(B))}_{\subseteq \mathcal {F}(A) \cap \mathcal {F}(B)} \cup \underbrace{(\mathcal {C}(A) \cap \mathcal {F}(B))}_{\subseteq \mathcal {F}(A) \cap \mathcal {F}(B)} \cup (\mathcal {F}(A) \cap \mathcal {F}(B))\\&= \mathcal {F}(A) \cap \mathcal {F}(B) \end{aligned}$$

   $\square$

To obtain the intersection of two segments, only the intersection of their frames is required. This significantly lowers the amount of data needed to represent a segment within the network, since only their frames need to be forwarded from children to parent nodes. Intersected components are used as the basis to compute the local Betti number (3), after which they are discarded, as they join the core of the produced segment. Information on the discovered hole is lost, so the same hole cannot be discovered again higher in the tree.

3.4 Merging Multiple Segments

Consider a sequence of mergeable segments $z: \{ S_1, S_2, \ldots , S_n \}$ being merged at some node in the spanning tree. As seen from example in Fig. 3, temporary holes can be produced by an unfortunate ordering of segments. We propose the following equation to compute the local first Betti number when merging multiple segments:

$$\begin{aligned} \beta _1(z) = \mathop \sum \limits _{k=1}^{n-1} \left( b_1^k(z) - \delta _1^k(z) \right) . \end{aligned}$$

(5)

where

$$\begin{aligned} b_1^k(z) = \# \left( \mathop \bigcup \limits _{i=1}^k S_i \right) \bigcap S_{k+1} - 1, \end{aligned}$$

(6)

and $\delta _1^k(z)$ is the function that returns the number of false holes produced by $b_1^k(z)$. Note that (6) is the rule from Corollary 1, applied at the k-th step of merging the sequence z. Here we discuss how to implement function $\delta _1$ algorithmically.

Consider the operation of merging two segments A and B, as shown in Fig. 2. Each hole can be represented as a pair of distinct components $\{K_i, K_j\} \in \mathcal {K}$, for instance, one hole can be represented by $\{ K_0, K_1 \}$ and the other by $\{ K_1, K_2 \}$. These two pairs represent a possible choice of generators for group $H_1(\mathcal {R}(\mathcal {G}_{N}))$. When such a pair represents a false hole, it must be removed from the set of possible generators. This is done by connecting both components, which results in lowering the rank of the group $H_1(\mathcal {R}(\mathcal {G}_{N}))$ by 1. Say we detect $\{ K_0, K_1 \}$ as a false hole. We connect $K_{01} = K_0 + K_1$ and end up with only one choice of group generators, which is $\{ K_{01}, K_2 \}$.

Suppose a node merges a sequence of segments and computes $\beta _1(z)$ by (5). Denote by A, B, and C three segments to be merged in that particular order. Suppose segments A and B form two holes, one of which is being covered by C, as shown in Fig. 4. To check the hole represented by $\{ K_0, K_1 \}$, we consider the following four sets:

$$\begin{aligned} {\begin{matrix} M_a = A \cap C, \qquad M_b = B \cap C,\\ k_0 = K_0 \cap C, \qquad k_1 = K_1 \cap C. \end{matrix}} \end{aligned}$$

(7)

Recall that all segments intersect at their frames, therefore the information needed to compute the above intersections is available at the node. We are interested whether C spans over the hole g. This is true if and only if a path from $k_0$ to $k_1$ exists through $M_a$ and separately through $M_b$. Both paths are verified by the standard flooding algorithm. If both paths exist, hole g is a false hole. Note that we are not interested, neither possess the information on possible holes within C, for they have been treated and recorded elsewhere.

Fig. 4.

The false hole of $A \cup B$ is covered by segment C.

Now consider the case of four or more segments, for instance a sequence $z: \{ A, B, C, D \}$, where A and B are being merged, and the discovered hole g needs to be checked with C and D. This differs from the scenario of three segments in the fact, that we have to account for possible holes constructed by the union of C and D. The algorithm is the following:

• 1. Use the previous algorithm to check g with C and D separately. Continue only if g was not eliminated.

• 2. Construct the union $S = C \cup D$ and check g with S. If S contains holes, continue.

• 3. Let h be a hole in S, represented by disjoint components $\{ L_0, L_1 \}$ as shown in Fig. 5. Determine the scenario (a) or (b). Cycle c was constructed in the previous step. If scenario (a), g is a fake hole. If scenario (b), continue.

• 4. Elements g and h are homologous. Hole g is false if and only if hole h is false. If more than four segments, test hole h recursively with the remaining segments, e.g. $E, F, G, \ldots$

The problem is now reduced by one element. We repeat the process on sequence $z_1 : \{ (A \cup B), C, D, \ldots \}$ until all segments are merged.

Fig. 5.

Testing hole g against union $C \cup D$.

In step 3 of the above algorithm, scenario (a) or (b) from Fig. 5 must be determined. We do this in the following way. Pick a node inside $L_0$ and travel from there around the cycle c once, observing the transitions between regions $A, B, L_0$ and $L_2$. There are eight possible transitions: $L_0 \leftrightarrow A$, $L_0 \leftrightarrow B$, $L_1 \leftrightarrow A$, $L_1 \leftrightarrow B$. Define four counters, one for each pair. When crossing from left to right, increase the corresponding counter by 1, when crossing from right to left, decrease it by 1. If and only if the sum of all counters at the end is nonzero, the hole h lies inside the cycle c.

3.5 Partial Merging

In the preceding section we assumed that the sequence $z: \{ A, B, C, D, \ldots \}$ contained all segments which are needed to verify hole g. This assumption held in the vast majority of our simulations. However, there were some cases where crucial information was sent to a different branch of the tree. A node must be able to detect such a case and postpone a critical merging, until the missing segment is received higher in the tree. It can, nevertheless, still merge non-critical segments. It comes down to the question whether a hole that appears to be true according to the locally available information, is actually a hole in $\mathcal {R}(\mathcal {G}_{N})$. The following proposition states the criteria by which the lack of information can be verified.

Proposition 3

Let $\{ S_1, \ldots , S_n \}$ be a mergeable sequence of locally available network segments. Denote $S = S_1 \cup \cdots \cup S_n$. If for every mergeable pair $\{ S_i, S_j \}$ holds:

$$\begin{aligned} \forall \{ v \} \in S_i \cap S_j: \{ v \} \in \mathcal {C}(S), \end{aligned}$$

(8)

then every cycle $c \in H_1(S)$ which is not a border is also not a border in $H_1(\mathcal {R}(\mathcal {G}_{N}))$. Or in other words, every true hole in S is also a hole in $\mathcal {R}(\mathcal {G}_{N})$.

Proof

We prove the proposition by contradiction. Suppose a cycle c is nontrivial in $H_1(S)$ and trivial in $H_1(\mathcal {R}(\mathcal {G}_{N}))$, and (8) holds. Without loss of generality suppose the hole, represented by c, was constructed by merging segments $S_i$ and $S_j$, as depicted in Fig. 6. Because c is trivial in $H_1(\mathcal {R}(\mathcal {G}_{N}))$, a disk $D \subset H_1(\mathcal {R}(\mathcal {G}_{N}))$ exists, such that $\partial D \cong c$. Consider now all nodes $v_i \in c$ and their closed stars $\overline{ St }(v_i)$. Obviously, every such star contains at least one node in D and is therefore not fully contained in S. Nodes $v_i$ are therefore not contained in the core $\mathcal {C}(S)$. Circle c is contained in $S_i$ and $S_j$, so a node $v_0$ on c exists which is also in the intersection $S_i \cap S_j$. We have thus proven the existence of $\{ v_0 \} \in S_i \cap S_j$, $\{ v_0 \} \notin \mathcal {C}(S)$, which contradicts (8).   $\square$

Fig. 6.

The structure of $\mathcal {C}(S)$ carries information about the missing D.

Suppose a node v receives segments $S_1 \cup \cdots \cup S_n$ from its subtree. To use the above property, the core of segment $S = S_1 \cup \cdots \cup S_n$ needs to be known, or more precisely, its nodes. Withing a spanning tree, the set of core nodes at v is exactly the set of all descendants of v, which can easily be obtained by child – parent communication. Recall that each hole g which appears by merging $S = S_i \cup S_j$ is represented by a pair $\{ K_i, K_j \}$ of disjoint components $K_i, K_j \subset S_i \cap S_j$. If all nodes of $K_i$ and $K_j$ belong to $\mathcal {C}(S)$, node v possesses enough information to verify it. Otherwise $S_i$ and $S_j$ are forwarded to the parent node unmerged.

4 Results

We tested the algorithm in a simulated environment using a single processor system. To simulate the parallel computing feature of wireless sensor network, we ran each node in a separate thread, and used inter-thread communication to simulate wireless communication channels. The goals of simulations were the following:

• 1. To asses computational complexity on a parallel system.

• 2. To estimate the communication burden of algorithm on a WSN.

• 3. To measure the computational and communicational burden distribution between the nodes.

• 4. To measure the frequency of partial merging.

We ran the algorithm on 1000 randomly generated networks, grouped in 10 classes by size. The i-th class contained 100 networks of size $100 \cdot i$ nodes. We kept the density of nodes constant for all classes at an average of 8.9 neighbors per node with standard deviation of 0.3. Holes were formed by restricting node deployment at random parts of the domain. To verify the correctness of the algorithm, we compared the output of each simulation with the actual number of holes in the coverage. We kept the ratio $r_c / r_s = \sqrt{3}$ so that the holes in the coverage exactly matched the holes in the Rips complex. It turned out that in all 1000 cases the algorithm computed the number of holes correctly.

One of our simulated scenarios with a 1000-node network is shown In Fig. 7. Arrows depict the spanning tree. A large segment at the first level of the tree can be seen (root resides at level 0), with the frame and the core visibly distinct. The hole within the core has already been discovered within this tree branch. The three holes at the frame are discovered by the parent.

Fig. 7.

Simulation with a 1000-node network.

To asses computational time complexity on a distributed system, we identified the longest sequential computational path for each network. That is the branch within the spanning tree which performs the maximum number of operations and therefore takes the longest to finish. We chose functions of union and intersection of simplicial complexes on the level of nodes as basic operations. A number of n operations means that n nodes are input to the union or intersection function. Both these functions can be implemented in linear time [31], if the elements are kept sorted.

Our results are shown in Table 1. Column OP shows the average number of operations, i.e. the number of nodes participating in each operation of union or intersection. Column C is the normalization of OP by the size of the network. The trend shows a near linear correlation between the size of the network and the computational demand, which is heavily influenced by the number of partial mergings. The latter is a matter of the established topology and especially the shape of the constructed spanning tree. The average number of actual holes per simulation is displayed in column HOLES. All the holes were correctly detected by our algorithm, forming very few fake ones in the process, of which all we correctly classified as false. As seen from the column FALSE in the table, the algorithm in general is not prone to forming false holes. Column PART shows how often per simulation only partial merging had to be performed due to missing data. In the last column, we can see the average amount of data transmitted per node, for the purpose of our algorithm. Each data unit is a number, representing a node ID. A single number is needed to represent a node and a pair of numbers to represent a link. If we suppose 32-bit IDs, 1024 units implies 4 KB of transmitted data per node. The increase is obviously logarithmic with respect to the network size, since the size of the segments increase with the depth of the spanning tree.

Fig. 8.

Distribution of computational and communicational burden in a 1000 node network.

Computational and communicational burdens are not distributed equally between the nodes. We expect the nodes with larger subtrees to generally receive a larger amount of data and consequently be forced to carry out more processing task. Figure 8 shows distribution of computational and communicational share between nodes in relation to their level in the spanning tree, in a typical 1000-node network. Each vertical bar represents the load of a single node. A steady climb towards the root can be seen in the case of data exchange (Fig. 8b), with many shorter branches joining in throughout the whole path. The amount of transmitted data never exceeded 10, 000 units per node, which in the case of 32-bit IDs, means the maximum demand was 40 KB per node. In the case of computational distribution (Fig. 8a), a severe load increase is usually observed at the root node. This is due to the fact, that at the root level, the complete information is available and therefore many partially merged sequences finished there.

Table 1. Simulation results: averages of 100 simulations.

5 Conclusions

In this paper we presented a novel algorithm for coverage verification in wireless sensor networks using homological criteria. The algorithm exploits distributed computational power of WSN to compute the first Betti number of the underlying Rips complex, which encodes information on domain coverage. We introduced the concept of network segments as the basic building blocks of the Rips complex and showed that by systematically merging them up the spanning tree, its homology can correctly be computed. Our simulations confirm the correctness the algorithm and show its computational time on a distributed system to be linear with the size of the network, but under significant influence of established network topology. There is still, however, room for improvement on the parallelization of tasks. Each node could begin its task as soon as some data becomes available, rather than wait until all the data is received. The costly hole verification process could at least partially be distributed down the spanning tree to the child nodes which have already finished their tasks. The high computational burden at the root node could be lowered by constraining the upper part of the spanning tree to a lower branching factor. As far as the communicational load is concerned, we believe our solution is efficient enough to run even in networks with low data bandwidth.