Abstract
Although lattice-based cryptography has proven to be a particularly efficient approach to post-quantum cryptography, its security against side-channel attacks is still a very open topic. There already exist some first works that use masking to achieve DPA security. However, for public-key primitives SPA attacks that use just a single trace are also highly relevant. For lattice-based cryptography this implementation-security aspect is still unexplored.
In this work, we present the first single-trace attack on lattice-based encryption. As only a single side-channel observation is needed for full key recovery, it can also be used to attack masked implementations. We use leakage coming from the Number Theoretic Transform, which is at the heart of almost all efficient lattice-based implementations. This means that our attack can be adapted to a large range of other lattice-based constructions and their respective implementations.
Our attack consists of 3 main steps. First, we perform a template matching on all modular operations in the decryption process. Second, we efficiently combine all this side-channel information using belief propagation. And third, we perform a lattice-decoding to recover the private key. We show that the attack allows full key recovery not only in a generic noisy Hamming-weight setting, but also based on real traces measured on an ARM Cortex-M4F microcontroller.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
The current public-key infrastructure is threatened by progress towards large-scale quantum computing. Constructions based on RSA, DLP, or ECC, will succumb to Shor’s algorithm [32], which is able to defeat these systems in polynomial time. While estimates on the availability of powerful enough quantum computers vary greatly–they range from 15 years [18] to never [31]–the threat is still taken very seriously. This is demonstrated by, e.g., NIST’s current call for post-quantum secure proposals [19] and official recommendations regarding post-quantum security from the NSA [20].
When it comes to possible post-quantum secure algorithms, lattice-based cryptography appears to be a promising option and has garnered a lot of attention over the past decade. It proved to be versatile and efficient, as there already exist practical lattice-based constructions offering basic services such as public-key encryption, digital signatures, and key exchange. Furthermore, lattices also serve as the basis for new primitives such as homomorphic encryption.
A very popular building block for lattice-based constructions is the ring-variant of the Learning with Errors problem, RLWE [16]. Recent implementations of RLWE-based public-key encryption, e.g., [7, 24, 29], have shown that its performance can compete with (or even exceed) that of RSA and ECC-based systems on a large set of platforms.
While these results demonstrate practicality, the implementation-security aspect of lattice-based cryptography is still a vastly unexplored and open topic. Just like any other cryptographic algorithm, an unprotected implementation of RLWE-based encryption will succumb to side-channel attacks such as Kocher’s Differential Power Analysis (DPA) [14]. Due to the large number of linear operations in the en- and decryption process, masking [5] appears to be a natural fit for protecting lattice-based cryptosystems against DPA. In fact, there already exist masked implementations of lattice-based encryption [21, 26,27,28]. They also show that this countermeasure can be implemented with (relatively) little resource overhead.
However, especially for public-key primitives the Simple Power Analysis (SPA) security aspect is also of high importance. This is demonstrated by, e.g., the large number of single-trace attacks targeting implementations of RSA and ECC. Yet, for lattice-based cryptography this aspect has never been analyzed thus far. As implementation techniques for RLWE-based schemes differ drastically from those of established public-key constructions, there are new potential venues for such single-trace attacks.
Our Contribution. In this work, we are first to show that single-trace attacks are indeed a threat to implementations of lattice-based cryptography. We present a new side-channel attack on lattice-based encryption that can, given sufficient leakage, recover the private key using just the side-channel observation of a single decryption. Hence, it can also be applied to masked implementations to recover each individual share, recombine them, and still perform full decryption-key recovery.
Our attack targets the computation of the Number Theoretic Transform (NTT), which is an essential building block for almost all efficient implementations of lattice-based cryptography. Thus, the attack can be ported to not only different implementations of encryption, but also to implementations of other lattice-based constructions. Furthermore, the NTT is not the first target for a DPA attack and was thus less protected in earlier works [21].
Our attack is comprised of 3 main steps. First, we perform a side-channel template matching [6] on each modular operation performed during the inverse NTT in the decryption process. In the second step, we combine the information (probabilities of intermediates) of every operation in the entire NTT. We do so by representing the FFT-like structure of the NTT as a graph and then applying the belief propagation algorithm (BP). While the use of BP in context of side-channel attacks is not new [12, 13, 36], it hasn’t been used in the context of public-key encryption yet. In our setting, a simple implementation of BP would require an impractical amount of time. Thus, we designed several optimizations that are targeted specifically at the NTT analysis. In our third and final step, we combine the knowledge of some secret intermediate values with the public key in order to reveal the private key. Concretely, we recover the full decryption key by first reducing the size of the public key and then performing a lattice decoding.
We evaluate our single-trace key-recovery attack in two different settings. First, we determine the success rate in a generic Hamming-weight leakage model. There, our attack has a high success rate, i.e., \(>0.9\), with noise parameters of up to \(\sigma _l=0.4\). Second, to verify our findings in practice we use real traces from EM measurements of an ARM Cortex-M4F software implementation. In this latter scenario, we were always able to recover the decryption key. Finally, we also show that our attack performs similarly well even if masking is used.
Outline. In Sect. 2, we recall lattice-based encryption, efficient implementations, as well as proposed side-channel protection mechanisms. Then, in Sect. 3 we recall soft-analytical side-channel attacks and belief propagation as its main tool. The three steps of the attack are then described in the following sections. The first step, a side-channel analysis of the NTT, is given in Sect. 4. Then, in Sect. 5 we efficiently combine all information using belief propagation. The third and final step, i.e., lattice decoding, is given in Sect. 6. We present and discuss the outcome and performance of our attack in Sect. 7.
2 Lattice-Based Encryption and Implementation
In this section, we recall lattice-based encryption, efficient implementation techniques, and previous works on side-channel countermeasures.
2.1 Lattice-Based Public-Key Encryption
In this work, we use the RLWE-based public-key encryption scheme proposed by Lyubashevsky, Peikert, and Regev [16]. It operates with polynomials over the ring \(\mathcal {R}_q = \mathbb {Z}_q[x] / \langle x^n + 1\rangle \) and is parameterized by the tuple \((n, q, \sigma )\). n denotes the dimension of the polynomials, q is the modulus for the base field \(\mathbb {Z}_q\), and \(\sigma \) is the standard deviation for a discrete Gaussian distribution \(D_{\sigma }\). We use boldface lowercase letters to interchangeably denote polynomials in \(\mathcal {R}_q\) as well as their respective coefficient vectors. We now recall the basic encryption scheme.
-
Key generation. For key-pair generation, two polynomials \(\mathbf r _1\) and \(\mathbf r _2\) are sampled from the discrete Gaussian distribution \(D_{\sigma }\). Next, the public key p is computed as p = \(\mathbf r _1 - \mathbf a \mathbf r _2\). The uniformly-random polynomial a is either a global domain parameter or is also included in the public key. \(\mathbf r _2\) is the private key, \(\mathbf r _1\) is simply discarded.
-
Encryption. First, the plaintext m is encoded as
 . In a simple variant of encoding, the bits of m are simply multiplied by q / 2. Then, three error polynomials
. In a simple variant of encoding, the bits of m are simply multiplied by q / 2. Then, three error polynomials 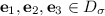 are sampled. The ciphertext is a pair of polynomials (\(\mathbf c _1, \mathbf c _2\)) with \(\mathbf c _1 = \mathbf a \mathbf e _1 + \mathbf e _2\) and
are sampled. The ciphertext is a pair of polynomials (\(\mathbf c _1, \mathbf c _2\)) with \(\mathbf c _1 = \mathbf a \mathbf e _1 + \mathbf e _2\) and  .
. -
Decryption. The private key \(\mathbf r _2\) is used to compute \(\mathbf m ^\star = \mathbf c _1 \mathbf r _2\, + \,\mathbf c _2\). The original message m is then retrieved by feeding \(\mathbf m ^\star \) to a decoder. There, one computes the distance of each coefficient in \(\mathbf m ^\star \) to q / 2. If this distance is \(< q/4\), then the decoder outputs 1, otherwise 0.
The above scheme only offers CPA security [8]. Recently, Oder et al. [21] presented an extension that also offers protection against adaptive chosen-ciphertext attacks (CCA2). However, the core encryption and decryption algorithms are identical, which is why we do not further discuss their CCA2 transformation here.
2.2 Efficient Implementation
There already exists a somewhat large body of work targeting efficient implementation of the above encryption scheme. They range from FPGAs to low-resource microcontrollers and desktop CPUs (e.g., [7, 11, 15, 23, 24, 29]).
In our work we use the parameter set \((n=256, q=7681, \sigma = 4.51)\), which was introduced by Göttert et al. [11] and is used by all of the above implementations. The concrete security level provided by this instance is still under debate and estimates vary (see, e.g., [2, 10, 21]). However, all our later analysis can be extended to other parameters.
Number Theoretic Transform (NTT). If q is prime, n a power of two, and \(q \equiv 1 \text { mod } 2n\) (which is the case for virtually all previously proposed parameter sets), then there exist primitive n-th roots of unity \(\omega _n\) in \(\mathbb {Z}_q\). This fact allows to efficiently compute polynomial multiplication in \(\mathcal {R}_q\) by means of the Number Theoretic Transform (NTT).
The NTT is essentially a Discrete Fourier Transform (DFT) in a prime field \(\mathbb {Z}_q\) instead of over the complex numbers \(\mathbb {C}\). Thus, this transformation is efficiently computed using the same optimizations found in, e.g., the Cooley-Tukey FFT, and runs in time \(\mathcal {O}(n \log n)\). The basic building block is a butterfly, which is comprised of a modular multiplication with a certain power of the chosen primitive root, a modular addition, and a modular subtraction. A total of \(n \log _2 (n)/2\) butterflies are computed during the NTT, as shown in Fig. 1 with the example of a 4-coefficient NTT. The required powers of the primitive root, i.e., \(\omega _n^0 \ldots \omega _n^{n/2}\), are typically called twiddle factors. The inverse transformation (INTT) is computed by simply invoking the NTT with \(\omega _n^{-1} \text { mod } q\). We denote \(\widetilde{\mathbf{a }}\) as the NTT transformed of a.
Multiplication of two polynomials a, b can now be implemented as \(\mathbf c = \text {INTT}(\text {NTT}(\mathbf a ) *\text {NTT}(\mathbf b ))\), where \(*\) denotes a point-wise multiplicationFootnote 1. Thus, a product can be computed in time complexity \(\mathcal {O}(n \log n)\) (compared to \(\mathcal {O}(n^2)\) for non-ring-based LWE constructions). This is one of the main arguments behind the choice of the particular ringFootnote 2 \(\mathcal {R}_q = \mathbb {Z}_q[x] / \langle x^n + 1\rangle \).
As proposed by Roy et al. [29], the encryption scheme described in Sect. 2.1 can be optimized by keeping the ciphertext in the NTT domain, i.e., transmitting (\(\widetilde{\mathbf{c }}_1, \widetilde{\mathbf{c }}_2\)). This requires that the same primitive root \(\omega _n\) is used for both encryption and decryption. Thus, it must be agreed upon and is public.
2.3 Side-Channel Protection of RLWE Encryption
Implementation security of lattice-based primitives is still a very new and open topic. Yet, there already exists some previous work that studies potential protection mechanisms. We now discuss these proposals.
Masking. Due to the linearity of the main operations, i.e., polynomial addition and multiplication, the masking countermeasure [5] is a natural fit for lattice-based public-key encryption. As proposed by Reparaz et al. [27, 28] and shown in Fig. 2, the private key \(\mathbf r _2\) can be split into two shares \(\mathbf r _2', \mathbf r _2''\) such that \(\mathbf r _2 = \mathbf r _2'\, + \, \mathbf r _2''\) mod q. Then, polynomial multiplications, additions, and the inverse NTT can be computed on each share individually.
The final decoding step, i.e., recovering m from \(\mathbf m ^\star \), is nonlinear and requires more care. Reparaz et al. designed a masked decoder which outputs two binary shares of the message, i.e., \(\mathbf m = \mathbf m '\,\oplus \mathbf m ''\), which can then be used as a shared key in a protected implementation of, e.g., the AES.
Shuffling and Blinding. In addition to masking, Oder et al. [21] propose to use further countermeasures. First, they suggest to use shuffling to protect the point-wise operations, i.e., point-wise addition and multiplication. They state that these operations are the most likely target for a DPA attack. Hence, the NTT is still computed in an unshuffled manner.
And second, they also use a randomization technique previously proposed by Saarinen [30]. They pick random values \(a, b \in [1, q-1]\) and then multiply the coefficients \(a\,\,\cdot \,\, \widetilde{\mathbf{c }}_1, b\,\,\cdot \,\, \widetilde{\mathbf{r }}_2\) and \(ab\,\,\cdot \,\, \widetilde{\mathbf{c }}_2 \text { mod } q\). Due to the linearity of the NTT, the mask can be removed by multiplying the output of the INTT with \((ab)^{-1} \text { mod } q\).
Additively Homomorphic Masking. In a later work, Reparaz et al. [26] present a different masking approach which exploits the additively homomorphic property of LWE. This, however, has some caveats. First, Reparaz et al. do not claim theoretical first-order security. And second, decoding errors are more likely. This makes their method incompatible with the CCA2-transformation presented by Oder et al. [21]. Due to these reasons, we do not further analyze the susceptibility of this approach to our attack.
3 Soft-Analytical Side-Channel Attacks
In this section, we describe Soft-Analytical Side-Channel Attacks (SASCA), which were proposed by Veyrat-Charvillon et al. [36] and are one of our main attack tools. The main goal of SASCA is to bridge the gap between divide-and-conquer approaches such as Kocher’s Differential Power Analysis (DPA) [14] and algebraic/analytical side-channel attacks [25]. DPA offers low time and memory complexity as well as high noise tolerance, but is suboptimal in terms of data complexity (number of observed traces). Algebraic attacks are better in this second regard, but are very sensitive to errors and often require exact information.
Veyrat-Charvillon et al. first perform a side-channel template matching [6] on all intermediates computed during an AES encryption. For each intermediate T, the template matching returns a vector of conditional probabilities \(\text {Pr} (T = t | \ell )\), where \(\ell \) denotes the observed side-channel leakage and t runs through all realizations of the random variable T. Then, they construct a factor graph of the AES and its specific implementation. This graph models the relationship between all intermediates. Finally, they use the belief propagation algorithm (BP) on this graph and the corresponding conditional probabilities to efficiently combine the information of all leakage points. We now give a brief description of this BP algorithm.
3.1 Belief Propagation
The belief propagation algorithm, originally proposed by Pearl et al. [22], allows to efficiently compute the marginalization of a function given its factorization. Our description and notation is largely based on that of MacKay [17, Chap. 26]. Given a function \(P^*\) of a set of N variables \(\mathbf x \equiv \left\{ x_n\right\} _{n=1}^N\) which is the product of M factors:

where each of the factors \(f_m\) (\(\mathbf x _m\)) is a function of a subset \(\mathbf x _m\) of x and the \(x_n\) are defined over a domain \(\mathcal {D}\), the problem of marginalization is defined as computing the marginal function \(Z_n\) of any variable \(x_n\):

or its normalized marginal \(P_n(x_n) = Z_n(x_n)/Z \) with the normalization constant  . The computational cost of marginalization is believed to grow exponentially with the number of variables N. The BP algorithm aims at reducing it by exploiting the factorization of the given function. BP is based on the message-passing principle. It requires a representation of the given function as a bipartite factor graph consisting of variable nodes and factor nodes. A variable node represents one of the variables \(x_i \in \mathbf x \), whereas a factor node corresponds to one of the factors \(f_{\mathrm {m}}\). Edges are drawn between \(x_i\) and \(f_{\mathrm {m}}\) iff the factor \(f_{\mathrm {m}}\) depends on the variable \(x_i\). The number of variables \(f_{\mathrm {m}}\) depends on is the factors degree \(\deg (f_{\mathrm {m}})\). The BP algorithm can be used to determine the marginal functions by iteratively executing the following two steps:
. The computational cost of marginalization is believed to grow exponentially with the number of variables N. The BP algorithm aims at reducing it by exploiting the factorization of the given function. BP is based on the message-passing principle. It requires a representation of the given function as a bipartite factor graph consisting of variable nodes and factor nodes. A variable node represents one of the variables \(x_i \in \mathbf x \), whereas a factor node corresponds to one of the factors \(f_{\mathrm {m}}\). Edges are drawn between \(x_i\) and \(f_{\mathrm {m}}\) iff the factor \(f_{\mathrm {m}}\) depends on the variable \(x_i\). The number of variables \(f_{\mathrm {m}}\) depends on is the factors degree \(\deg (f_{\mathrm {m}})\). The BP algorithm can be used to determine the marginal functions by iteratively executing the following two steps:
From variable to factor:

where \(\mathcal {M}(n)\) denotes the set of factors in which n participates.
From factor to variable:

where \(\mathcal {N}(m)\) denotes the indices of the variables that the m-th factor depends on and \(\mathbf x _{m \backslash n}\) denotes the set of variables in \(\mathbf x _m\) without \(x_n\).
After convergence, the marginal function \(Z_n(x_n)\) can be computed as:
and the normalized marginals can be obtained from: \( P_n(x_n) = Z_n(x_n)/Z, \) where the normalizing constant Z is given by: \( Z = \sum _{x_n} Z_n(x_n) \)
If the factor graph is tree-like (acyclic), then the above algorithm returns the exact marginals. Unfortunately, in many real life applications the factor graphs contains cycles. To overcome this problem, the so called loopy BP algorithm has been proposed. It uses the same update rules and also iterates until convergence is reached, but uses a slightly different initialization. While it is not guaranteed that the loopy BP algorithm will return correct values or even converge, it usually gives sufficiently precise approximations of the marginals in many real-world applications. The exact conditions under which the loopy BP algorithm converges are still unknown. However, some sufficient conditions that ensure BP convergence have been stated by, e.g., Su et al. [35].
4 Attack Step 1: Side-Channels in an NTT Butterfly
After having covered all required preliminaries, we now start the description of our attack. As the first step of the attack, we exploit side-channel leakage during the computation of the inverse NTT in the decryption algorithm. Concretely, we first perform a profiling and then, for the actual attack, we match the recorded templates at each modular operation. As outcome, we obtain information in form of a probability vector for each such operation.
In order to understand how much information a side-channel adversary can realistically expect in this first step, and to also allow attack evaluation in a realistic scenario, we performed a side-channel analysis of the NTT on a real device. We now discuss our targeted implementation and platform, the measurement setup, and some results of this analysis. We additionally introduce a generic and simpler Hamming-weight leakage model, which will later be used in addition to real traces. First, however, we explain the choice of the NTT as the primary target for our attack.
4.1 The NTT as Side-Channel Target
The Number Theoretic Transform (NTT) is a main building block of virtually all efficient instantiations and implementations of lattice-based cryptography. Yet, thus far it has not been target of any side-channel analysis.
One potential reason is that the point-wise operations, i.e., multiplications and additions while computing \(\widetilde{\mathbf{c }}_1\,*\, \widetilde{\mathbf{r }}_2\,\, +\,\, \widetilde{\mathbf{c }}_2\), are the prime target for DPA attacks as they allow easy coefficient-wise prediction of intermediates [21]. However, this makes it tempting to use less protection in other parts, i.e., the NTT.
Also, the NTT is an interesting target for algebraic side-channel attacks. As seen in Fig. 1, it is comprised of many potentially leaking modular operations which are additionally connected by relatively simple algebraic rules. This makes it possible to combine the information of all leaking computations.
4.2 Measurement Setup and Implementation
We performed side-channel measurements on a Texas Instruments MSP432 (ARM Cortex-M4F) microcontroller on a MSP432P401R LaunchPad development board. A Cortex-M4F was also used by many other (protected) implementations of RLWE encryption [7, 21, 27].
We exploit the EM side channel. As shown in Fig. 3, we placed a Langer RF-B 3-2 near-field probe in proximity to the external core-voltage regulation circuitry. This setup does not require any on-chip spatial profiling. Also, we expect similar outcomes for a power analysis. Our microcontroller was clocked at its maximum possible frequency of 48 MHz.
We base our analysis on the implementation techniques used in the open-sourced Cortex-M4F implementation of de Clercq et al. [7], which is also the basis of the masked software implementation of Reparaz et al. [27]. They implemented modular multiplication with division, i.e., \(a \text { mod } q = a - q \lfloor a/q\rfloor \), and use the integrated hardware multiplier and divider. On our platform, the multiplication runs in constant time, but the DIV instruction does not. Reduction after addition and subtraction is implemented using ARM conditional statements (IT instruction), which run in constant time.
4.3 Real-Device Side-Channel Analysis
The NTT is comprised of repeated applications of a butterfly. It is a reasonable assumption that all invocations utilize the same hardware, e.g., on-chip multiplier and divider, which results in loop-invariant leakage. To simplify our later analysis and attack evaluation, we thus opt for the following approach. We analyzed the butterfly operations, i.e., modular multiplication and addition/subtraction, independently. For the analysis, the operands were preloaded into registers and no leakage of loading and storing in memory was used. We prerecorded a set number of traces for each possible operand combination. For attack evaluation, we pick a random key, perform encryption/decryption, and for each of the \(n \log _2(n)/2 = 1024\) butterflies invoked during decryption randomly pick one of the prerecorded traces that corresponds to the processed intermediate. We now describe our results for each operation in the butterfly.
Modular Addition and Subtraction. de Clercq et al. implement modular addition and subtraction with conditional ARM statements. While these run in constant time, they still leak their state through other side-channels. With a template matching, we were able to correctly classify virtually all, i.e., \(> 0.99\), of the taken branches. In the following, we simply assume that an attacker can correctly detect whether a reduction happened or not. Alternatively, one could also include the probability that a reduction happened in the later analysis.
Modular Multiplication. In a butterfly, one of the inputs is multiplied by a known twiddle factor \(\omega \). There are \(qn/2= 983\,168\) possible operand/twiddle factor combinations, for each of them we prerecorded 100 traces. Thus, we use roughly 100 million traces for evaluation. For the attack, for each multiplication we randomly pick one out of the 100 traces corresponding to the processed value.
In the analysis, we use two steps to recover information on the unknown input. First, we exploit that the runtime of division is data dependent. We found that it depends on the bit size of the dividend, i.e., the value that is reduced (the divisor is the constant q). By measuring this time, which we do with a simple thresholding in the side-channel trace, we can immediately assign the intermediate to one out of several disjoint sets.
In the second step, we perform a side-channel template matching [6] to further narrow down the operand. For each multiplication, we use 99 (remaining) traces to build templates for each currently possible operand. The points-of-interest used for template building were determined with a t-test [9]. We then match all templates with the previously picked trace and compute the probability vector required for the next step of our attack.
In order to give a sense on the informativeness of our traces we use the metric proposed in [34], i.e., give the average entropy left in the probability vectors conditioned on the leakage \(\text {Pr} (T = t | \ell )\). Without leakage, we have an entropy of \(\log _2(q) \approx 12.9\) bit. After performing the template matching, the average entropy decreases to roughly 7 bit. However, we observed that the outcome somewhat correlates with the value of the used twiddle factor. With \(\omega _n^0 = 1\) we have a remaining entropy of about 10 bits. With larger values, we generally achieve better results.
4.4 A Simplified Model
In order to allow reproducibility, we additionally analyze the performance of our attack with a more generic and simpler model, namely the common noisy Hamming weight leakage model. That is, apart from knowing if a reduction happened after addition/subtraction, for each modular multiplication an attacker gets two samples of the form:
a is the unknown input and \(\omega _n^i\) the used twiddle factor. HW denotes the Hamming weight function and \(\mathcal {N}\) the Gaussian distribution with standard deviation \(\sigma _l\). For the experiments, we perform a 2-variate template matching on these simulated traces.
5 Attack Step 2: Belief Propagation in the NTT
In the above template matching, the adversary obtains side-channel information on each computed butterfly. In the second step of the attack, we now combine all this information over the entire (I)NTT. We efficiently do so by using belief propagation. We construct a factor-graph representation of the NTT, include the side-channel information in this graph, and then run BP until convergence is reached. With the constructed factor graph the runtime of a straight-forward BP implementation is impractical. Thus, we present optimizations designed specifically for the NTT factor-graph, which decrease the runtime drastically.
5.1 Factor-Graph Construction
A factor graph is a bipartite graph containing variable nodes and factor nodes. For modeling the NTT, we add one variable node x for each input/output of a butterfly. With \(n=256\), we thus have \(n(\log _2(n) + 1) = 2\,304\) variable nodes.
We then add three types of factor nodes: \(f_{\mathrm {ADD}}\), \(f_{\mathrm {SUB}}\), and \(f_{\mathrm {MUL}}\). As seen in Fig. 4, each type of factor occurs once per butterfly. Thus, there are a total of \(3 n\log _2(n)/2 = 3072\) factor nodes in the NTT model. Evidently, there are cycles in the graph shown in Fig. 4, so the loopy BP algorithm is needed.
\(f_{\mathrm {MUL}}\) is only connected to \(x_2\) and thus has degree 1. Its purpose is to add the side-channel information gathered from the modular multiplication of \(x_2\) with the known twiddle factor \(\omega \). We performed a template matching in Step 1 and therefore are given vector of probabilities conditioned on the leakage l. Thus we have:
The factors \(f_{\mathrm {ADD}}\) and \(f_{\mathrm {SUB}}\) represent the modular addition and subtraction, respectively. They are connected to both butterfly-input nodes \(x_1\) and \(x_2\), and one of the two output nodes \(x_3\) or \(x_4\). Thus, their degree is 3. These factors model how variable nodes inside a butterfly are related, e.g., that \(x_3 = x_1\,\, +\,\, x_2 \omega \text { mod } q\). Furthermore, we use these factors to include whether a reduction happened after addition or subtraction, respectively. For addition with subsequent reduction step, we have:
If no reduction happened, then the second clause \(x_{i_1} + (x_{i_2}\omega \text{ mod } q) > q\) is simply negated. For subtraction with subsequent reduction, we have:
Other Leakage Points. The factor-graph representation of the NTT is flexible, thus it can be modified to accommodate other leaking operations. One could, e.g., additionally include side-channel information of loading and storing in memory or leakage on operands of modular addition and subtraction.
5.2 BP Runtime Estimation Without Optimization
As it turns out, the runtime of a straight-forward implementation of BP on our constructed factor graph is impractically high. It depends on the number of iterations, the number of variable nodes and the size of their domain \(\mathcal {D}\), as well as the number of factor nodes and their degree.
Each iteration of BP involves the invocation of the update rules \(\mathfrak {q}\) (variable to factor, Eq. 1) and \(\mathfrak {r}\) (factor to variable, Eq. 2) for all variable nodes and factor nodes, respectively. In our case the number of required iterations is small, e.g., \(\le 25\), and therefore does not have a significant impact on the asymptotic runtime. The runtime of \(\mathfrak {q}\) is also fairly low.
However, the same cannot be said for \(\mathfrak {r}\). For a factor f with degree \(\deg (f)\) and its inputs \(x_1,\dots ,x_{\deg (f)}\) with domain \(\mathcal {D}\), one can compute the update rule given in Eq. 2 by simply looping over all \(|\mathcal {D}|^{\deg (f)}\) possible input combinations of f. In our scenario, we have factors \(f_{\mathrm {ADD}}\), \(f_{\mathrm {SUB}}\) with \(\deg (f)=3\) and variable nodes with domain size \(|\mathcal {D}| = q = 7681\). When additionally multiplying with the number of \(f_{\mathrm {ADD}}\) and \(f_{\mathrm {SUB}}\) in our factor graph, then we reach a runtime of \(\approx 2^{49}\) for a single iteration. Reducing from cubic to quadratic runtime can be done by only considering triplets where \(f_{\mathrm {ADD}}\), \(f_{\mathrm {SUB}}\) can be 1, but this still amounts to \(\approx 2^{37}\) operations. Obviously, both numbers are not very practical and optimizations are needed.
5.3 Runtime Optimizations
In Algorithm 1, we show an optimization that can decrease the runtime of \(\mathfrak {r}\) for all factor nodes of degree 3 in the factor graph, i.e. \(f_{\mathrm {ADD}}\) and \(f_{\mathrm {SUB}}\), drastically. We show it on the example of a factor node of type \(f_{\mathrm {ADD}}\). A slight variation of the presented algorithm can be used to optimize \(f_{\mathrm {SUB}}\).

Our optimization uses the fact that update rules for input/output distributions of modular additions/subtractions can be efficiently expressed in matrix-vector notation. Consider the addition \(a\,\, +\,\, b = c \text { mod } q\), with  the incoming messages from the corresponding variable nodes. Each such message is a q-dimensional vector assigning a probability to each value in \(\mathcal {D}\), we say that
the incoming messages from the corresponding variable nodes. Each such message is a q-dimensional vector assigning a probability to each value in \(\mathcal {D}\), we say that  . The output
. The output  depends on
depends on  and an entry
and an entry  can be computed as the sum over all \(a_i b_j\) with \(i+j \equiv k \text { mod } q\). The whole update can be written in matrix-vector notation:
can be computed as the sum over all \(a_i b_j\) with \(i+j \equiv k \text { mod } q\). The whole update can be written in matrix-vector notation:

where the columns of the left matrix are circular shifts of  . The above equation can be rewritten as a circular convolution
. The above equation can be rewritten as a circular convolution  , which can be efficiently computed using the FFT and the circular convolution theorem. Thus, we have :
, which can be efficiently computed using the FFT and the circular convolution theorem. Thus, we have :

The update rules for  and
and  can be obtained similarly by additionally using complex conjugations CONJ, as shown in Algorithm 1. Recall that we also include whether a reduction happened during modular addition and subtraction. This can be efficiently done by replacing the q-coefficient FFT with a 2q-coefficient FFT and by using only either the upper or lower half of the IFFT output.
can be obtained similarly by additionally using complex conjugations CONJ, as shown in Algorithm 1. Recall that we also include whether a reduction happened during modular addition and subtraction. This can be efficiently done by replacing the q-coefficient FFT with a 2q-coefficient FFT and by using only either the upper or lower half of the IFFT output.
The runtime of computing  for the degree-3 factor nodes is now reduced to \(\mathcal {O}(q\log {q})\), since the only runtime relevant operations are FFTs. This allows us to perform one iteration of the BP algorithm for our whole factor graph in about one minute using a single core of an Intel Core i7-5600U CPU.
for the degree-3 factor nodes is now reduced to \(\mathcal {O}(q\log {q})\), since the only runtime relevant operations are FFTs. This allows us to perform one iteration of the BP algorithm for our whole factor graph in about one minute using a single core of an Intel Core i7-5600U CPU.
5.4 BP on Subgraphs
In our experiments, we found that applying BP to the whole NTT factor graph does not yield satisfactory results. While we can narrow down values, the outcome was not sufficient for key recovery. Yet, we were able to identify two problems and show how to circumvent them by applying BP only to subgraphs.
-
Uneven availability of side-channel information. The template attack on multiplication is a primary source of information. Yet, multiplications are not spread evenly across the NTT, as illustrated in Fig. 5a (also compare to Fig. 1). Each cell of this figure corresponds to one variable node. White variables are multiplied with a twiddle factor, black ones are not. Due to the lack of multiplications and its side-channel information in the top-right corner, the BP algorithm cannot recover these variable with high-enough certainty.
-
Varying outcome of the template attack. As already pointed out in Sect. 4.3, the performance of the template attack depends on the used twiddle factor. In the first NTT layer, one always multiplies with \(\omega _n^0 = 1\). Even if this multiplication is not optimized out, the fact that no reduction is performed leads to little leakage.
We circumvent these two problems by applying BP not on the whole NTT graph, but instead only on disjoint subgraphs. As depicted in Fig. 5b, we have subgraphs FG 1, FG 2, and FG 3. These do not include the first layer and have a higher ratio of observed to unobserved variables (compared to the full graph). Thus, applying BP to these subgraphs gives significantly better results.
After convergence is reached on all 3 graphs, we perform a classification, i.e., pick the most likely value, on certain variable nodes. Concretely, we use variables from layer 6 (output of layer 5 and input of layer 6). This is the last layer of FG 1 and variables in later layers are usually recovered with higher confidence. As shown in Fig. 5c, we use the 192 variables with indices 32...128 and 160...255.
If masking is used, then we have to perform BP twice to get the intermediates in both invocations of the INTT. The unmasked intermediates can be computed by simply adding the recovered values of both INTTs.
6 Attack Step 3: Lattice Decoding
Due to applying BP only on subgraphs, we cannot recover the full INTT input \(\widetilde{\mathbf{c }}_1\,*\widetilde{\mathbf{r }}_2 + \widetilde{\mathbf{c }}_2\). Hence, the decryption key \(\widetilde{\mathbf{r }}_2\) (or equivalently \(\mathbf r _2\)) cannot be determined with simple linear algebra and another step is needed. In this third and final attack step, we combine the recovered intermediates with the public key. First, we create linear equations in the intermediates and \(\mathbf r _2\) and use them to decrease the rank of the lattice spanned by the public key (a, p). Then, we use lattice-basis reduction and decoding to find \(\mathbf r _2\) in the reduced-rank lattice.
6.1 Generating Linear Equations in the Key
We use the recovered intermediates to construct linear equations in the private key \(\mathbf r _2\). Polynomial multiplication in \(\mathcal {R}_q\) can be written as a matrix-vector product. We write the INTT output as \(\mathbf m ^\star = \mathbf c _1 \mathbf r _2 + \mathbf c _2 = \mathbf C _1 \mathbf r _2 + \mathbf c _2\), where the columns of matrix \(\mathbf C _1\) are nega-cyclic rotations of \(\mathbf c _1\). All operations inside the (I)NTT are linear, thus this system can be transformed to describe any of its intermediates. Concretely, we transform it such that it describes the recovered values of the sixth INTT layer.
We transform the system by performing a partial reversal of the INTT. We revert 3 butterfly stages by computing \(x_1 = (x_3 + x_4)/2 \text { mod } q\) and \(x_2 = (x_3 - x_4)/(2\omega )\) (cf. Fig. 4). We end up with a system of form  , with x being the 192 recovered intermediates and
, with x being the 192 recovered intermediates and  the transformed coefficients.
the transformed coefficients.
6.2 Key Recovery Using Lattice Reduction
The decryption key \(\mathbf r _2\) is finally recovered by combining the above system with the information embedded in the public key (a, p). Recall that  . As \(\mathbf r _1\) is small (it is sampled from a discrete Gaussian distribution with small \(\sigma \)), we have that
. As \(\mathbf r _1\) is small (it is sampled from a discrete Gaussian distribution with small \(\sigma \)), we have that  . Thats is, p is close to the vector
. Thats is, p is close to the vector  which is part of the q-ary lattice spanned by the columns of A (the matrix consisting of nega-cyclic rotations of a). Hence, the recovery of \(\mathbf r _2\) can be seen as a bounded-distance decoding problem. The chosen system-parameters \((n, q, \sigma )\) ensure that solving this decoding problem is not feasible without further information.
which is part of the q-ary lattice spanned by the columns of A (the matrix consisting of nega-cyclic rotations of a). Hence, the recovery of \(\mathbf r _2\) can be seen as a bounded-distance decoding problem. The chosen system-parameters \((n, q, \sigma )\) ensure that solving this decoding problem is not feasible without further information.
However, by incorporating the linear equations from above the problem can be reduced to a size that is solvable. We substitute the 192 equations  into
into  to get some
to get some  . The number of columns of A’, and hence the rank of the spanned lattice, is now reduced to \(256-192= 64\).
. The number of columns of A’, and hence the rank of the spanned lattice, is now reduced to \(256-192= 64\).
We then search for the closest vector to  by solving a shortest-vector problem. Concretely, we search for the error term
by solving a shortest-vector problem. Concretely, we search for the error term  ) as an unusually short vector in the lattice generated by
) as an unusually short vector in the lattice generated by  . This approach of solving the lattice decoding problem is described by, e.g., Albrecht et al. [1]. The short vector is recovered using the BKZ lattice basis reduction algorithm, we use the implementation provided by Shoup’s NTL [33]. We invoke BKZ with a blocksize of 25, but abort reduction as soon as a candidate for \(\mathbf r _1\), i.e., a vector with a small enough norm, is found.
. This approach of solving the lattice decoding problem is described by, e.g., Albrecht et al. [1]. The short vector is recovered using the BKZ lattice basis reduction algorithm, we use the implementation provided by Shoup’s NTL [33]. We invoke BKZ with a blocksize of 25, but abort reduction as soon as a candidate for \(\mathbf r _1\), i.e., a vector with a small enough norm, is found.
After that, one can compute the private key \(\mathbf r _2\) by solving the linear system  for both recovered \(\mathbf r _1\) and
for both recovered \(\mathbf r _1\) and  . The correct \(\mathbf r _2\) is the one that follows the distribution used for key generation. That is, we pick the smaller out of the two solutions.
. The correct \(\mathbf r _2\) is the one that follows the distribution used for key generation. That is, we pick the smaller out of the two solutions.
Performance of Decoding. We tested the correctness and performance of this key-recovery approach by performing well over 1 000 experiments. In each of them we use the correct intermediates (cf. Fig. 5c) and only perform the decoding step. All our experiments were successful. The average runtime on a single core of a Xeon E5-2699v4 CPU is approximately 45 s.
This decoding approach is not limited to using exactly 192 recovered intermediates, it can be invoked with any number of coefficients. However, the runtime of decoding will increase if fewer values are available. For instance, with 160 recovered intermediates the average runtime is 5 min and thus still well within practicality. Below that, however, it increases drastically. With 150 values, it reaches multiple hours. Experiments with 146 or fewer coefficients were not successful after 1 full day of computation.
7 Attack Results and Conclusion
Our attack consists of subsequent execution of the three attack steps described in the previous sections. We now present the outcome. First, we evaluate the attack using real traces. We illustrate an exemplary outcome and give a success rate. Then, we give the success rate for the Hamming-weight model with varying noise-parameter \(\sigma _l\), both with and without masking applied.
7.1 Real Device
With real traces obtained from the setup described in Sect. 4, we have the following results. Figure 6 illustrates an exemplary outcome of template-matching and the subsequent belief propagation on the subgraph FG 3 (cf. Sect. 5.4). For each variable node, we color-code the entropy of the probability vector. For black nodes, the probability distribution is close to uniform, whereas for white nodes one value has reached probability close to 1. After 1 iteration (Fig. 6a), the probability distributions essentially correspond to the direct output of the template matching. After 20 iterations of BP (Fig. 6c), the network has converged and almost all intermediates are determined with very high probability.
Lattice decoding is successful if all of the 192 intermediates used for key-recovery are correct. After observing Fig. 6, it should not come as a surprise that all our key-recovery experiments in the real-trace setting were successful. The success rate, i.e., the probability that all used coefficients are correct, is 1.
7.2 Hamming-Weight Model
In order to get a broader and more generic analysis of our attack, we also tested it with a noisy Hamming-weight model (cf. Sect. 4.4). We rerun all tests with varying noise parameter \(\sigma _l\). The outcome is illustrated in Fig. 7, where we show the success rate and the average entropy (after template matching) for each tested value of \(\sigma _l\). We give the entropy to allow at least a rough comparison to the real-trace setting.
In the non-masked case, we have a high single-trace success rate up to \(\sigma _l=0.4\) or 0.5, then it drops drastically. Note, however, that an attacker that can observe multiple decryptions can decrease the observed \(\sigma _l\) by averaging the traces. In the masked setting, key-recovery is successful if the correct intermediates are recovered in both invocations of the inverse NTT (see Fig. 2). Only then their sum is equal to the unmasked value. Thus, the expected success rate is squared, which is confirmed by our results. Obviously, averaging cannot be done if masking is used.
7.3 Conclusion
Our attack clearly shows that SPA security of lattice-based schemes cannot be neglected and that relying on masking alone is not sufficient. Implementation techniques that are vastly different to established constructions such as RSA and ECC open up new venues in this regard. In fact, the regular structure of the NTT allows to efficiently combine leakage of the entire decryption process. Furthermore, each recovered intermediate can be used to decrease the difficulty of key-recovery with the public key. And while this work focuses on lattice-based encryption, our attack can be adapted to any other implementation of lattice-based cryptography which employs the NTT.
When it comes to potential countermeasures, masking appears to be effective against DPA, yet it does not prevent our attack. Thus, additional countermeasures should be implemented and will now be discussed.
Possible Countermeasures. One of the first measures to strengthen an implementation against SPA attacks is to ensure a constant runtime and control flow. In our side-channel analysis of a real device, we exploit timing differences stemming from the DIV operation invoked during modular reduction. There do exist constant-time alternatives, as already shown by Oder et al. [21].
Like many other algebraic attacks, our key recovery can be thwarted by employing shuffling. Concretely, the operations inside the NTT, e.g., the order in which the butterflies are processed within one NTT layer, need to be shuffled. Shuffling only point-wise operations, as proposed by Oder et al., clearly does not hamper our attack. Other hiding countermeasures, such as the random insertion of dummy operations inside the NTT, can also make our attack harder.
Oder et al. also propose to use a blinding countermeasure (cf. Sect. 2.3). Our attack still applies, but needs an additional step and potentially a different selection of recovered intermediates. Concretely, it requires that a sufficient amount of the INTT output coefficients are recoverable or can be computed from the recovered intermediates. Then, one can test if the distribution of the unblinded INTT output, i.e., after multiplication with \(ab^{-1} \bmod q\), corresponds to that of a valid  (centered around 0 and q / 2). For a non-masked implementation, or if the same blinding values a, b are reused for both shares, then one can run through all \(q-1\) possibilities of \(ab \text{ mod } q\). If different a, b are used for both shares, then one needs to try all \((q-1)^2\) combinations. With our parameters, this can be easily done within a minute. When using 64 output coefficients, this always returned the correct blinding values in our tests. Hence, this countermeasure does not significantly increase single-trace security. It, however, prevents averaging in the non-masked scenario.
(centered around 0 and q / 2). For a non-masked implementation, or if the same blinding values a, b are reused for both shares, then one can run through all \(q-1\) possibilities of \(ab \text{ mod } q\). If different a, b are used for both shares, then one needs to try all \((q-1)^2\) combinations. With our parameters, this can be easily done within a minute. When using 64 output coefficients, this always returned the correct blinding values in our tests. Hence, this countermeasure does not significantly increase single-trace security. It, however, prevents averaging in the non-masked scenario.
Notes
- 1.
This explanation is slightly simplified and omits, e.g., the scaling required for the negative-wrapped convolution. For a more thorough explanation, we refer to [29].
- 2.
References
Albrecht, M.R., Fitzpatrick, R., Göpfert, F.: On the efficacy of solving LWE by reduction to unique-SVP. In: Lee, H.-S., Han, D.-G. (eds.) ICISC 2013. LNCS, vol. 8565, pp. 293–310. Springer, Cham (2014). doi:10.1007/978-3-319-12160-4_18
Albrecht, M.R., Player, R., Scott, S.: On the concrete hardness of learning with errors. J. Math. Cryptol. 9(3), 169–203 (2015)
Bernstein, D.J., Chuengsatiansup, C., Lange, T., van Vredendaal, C.: NTRU prime. IACR Cryptology ePrint Archive 2016, 461 (2016)
Bos, J.W., Costello, C., Ducas, L., Mironov, I., Naehrig, M., Nikolaenko, V., Raghunathan, A., Stebila, D.: Frodo: take off the ring! practical, quantum-secure key exchange from LWE. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S. (eds.) CCS 2016, pp. 1006–1018. ACM (2016)
Chari, S., Jutla, C.S., Rao, J.R., Rohatgi, P.: Towards sound approaches to counteract power-analysis attacks. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 398–412. Springer, Heidelberg (1999). doi:10.1007/3-540-48405-1_26
Chari, S., Rao, J.R., Rohatgi, P.: Template attacks. In: Kaliski, B.S., Koç, K., Paar, C. (eds.) CHES 2002. LNCS, vol. 2523, pp. 13–28. Springer, Heidelberg (2003). doi:10.1007/3-540-36400-5_3
de Clercq, R., Roy, S.S., Vercauteren, F., Verbauwhede, I.: Efficient software implementation of ring-lwe encryption. In: Nebel, W., Atienza, D. (eds.) DATE 2015, pp. 339–344. ACM (2015)
Fluhrer, S.R.: Cryptanalysis of ring-lwe based key exchange with key share reuse. IACR Cryptology ePrint Archive 2016, 85 (2016)
Gierlichs, B., Lemke-Rust, K., Paar, C.: Templates vs. stochastic methods. In: Goubin, L., Matsui, M. (eds.) CHES 2006. LNCS, vol. 4249, pp. 15–29. Springer, Heidelberg (2006). doi:10.1007/11894063_2
Göpfert, F., van Vredendaal, C., Wunderer, T.: A quantum attack on lwe with arbitrary error distribution. Cryptology ePrint Archive, Report 2017/221 (2017)
Göttert, N., Feller, T., Schneider, M., Buchmann, J., Huss, S.: On the design of hardware building blocks for modern lattice-based encryption schemes. In: Prouff, E., Schaumont, P. (eds.) CHES 2012. LNCS, vol. 7428, pp. 512–529. Springer, Heidelberg (2012). doi:10.1007/978-3-642-33027-8_30
Grosso, V., Standaert, F.-X.: ASCA, SASCA and DPA with enumeration: which one beats the other and when? In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9453, pp. 291–312. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48800-3_12
Grosso, V., Standaert, F.: Masking proofs are tight (and how to exploit it in security evaluations). IACR Cryptology ePrint Archive 2017, 116 (2017)
Kocher, P., Jaffe, J., Jun, B.: Differential power analysis. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 388–397. Springer, Heidelberg (1999). doi:10.1007/3-540-48405-1_25
Liu, Z., Seo, H., Sinha Roy, S., Großschädl, J., Kim, H., Verbauwhede, I.: Efficient ring-LWE encryption on 8-bit AVR processors. In: Güneysu, T., Handschuh, H. (eds.) CHES 2015. LNCS, vol. 9293, pp. 663–682. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48324-4_33
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 1–23. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_1
MacKay, D.J.C.: Information Theory, Inference, and Learning Algorithms. Cambridge University Press, New York (2003)
Mariantoni, M.: Building a superconducting quantum computer. Invited Talk at PQCrypto 2014, October 2014. https://www.youtube.com/watch?v=wWHAs-HA1c
NIST. Post-Quantum crypto standardization, December 2016. http://csrc.nist.gov/groups/ST/post-quantum-crypto/call-for-proposals-2016.html
NSA/IAD. CNSA Suite and Quantum Computing FAQ, January 2016. https://www.iad.gov/iad/library/ia-guidance/ia-solutions-for-classified/algorithm-guidance/cnsa-suite-and-quantum-computing-faq.cfm
Oder, T., Schneider, T., Pöppelmann, T., Güneysu, T.: Practical cca2-secure and masked ring-lwe implementation. IACR Cryptology ePrint Archive 2016, 1109 (2016)
Pearl, J.: Reverend bayes on inference engines: a distributed hierarchical approach. In: Proceedings of the Second AAAI Conference on Artificial Intelligence, AAAI 1982, pp. 133–136. AAAI Press (1982)
Pöppelmann, T., Güneysu, T.: Towards practical lattice-based public-key encryption on reconfigurable hardware. In: Lange, T., Lauter, K., Lisoněk, P. (eds.) SAC 2013. LNCS, vol. 8282, pp. 68–85. Springer, Heidelberg (2014). doi:10.1007/978-3-662-43414-7_4
Pöppelmann, T., Oder, T., Güneysu, T.: High-performance ideal lattice-based cryptography on 8-bit atxmega microcontrollers. In: Lauter, K., Rodríguez-Henríquez, F. (eds.) LATINCRYPT 2015. LNCS, vol. 9230, pp. 346–365. Springer, Cham (2015). doi:10.1007/978-3-319-22174-8_19
Renauld, M., Standaert, F.-X.: Algebraic side-channel attacks. In: Bao, F., Yung, M., Lin, D., Jing, J. (eds.) Inscrypt 2009. LNCS, vol. 6151, pp. 393–410. Springer, Heidelberg (2010). doi:10.1007/978-3-642-16342-5_29
Reparaz, O., Clercq, R., Roy, S.S., Vercauteren, F., Verbauwhede, I.: Additively homomorphic ring-LWE masking. In: Takagi, T. (ed.) PQCrypto 2016. LNCS, vol. 9606, pp. 233–244. Springer, Cham (2016). doi:10.1007/978-3-319-29360-8_15
Reparaz, O., Roy, S.S., de Clercq, R., Vercauteren, F., Verbauwhede, I.: Masking ring-lwe. J. Cryptogr. Eng. 6(2), 139–153 (2016). Extended journal version of [28]
Reparaz, O., Roy, S.S., Vercauteren, F., Verbauwhede, I.: A masked ring-LWE implementation. In: Güneysu, T., Handschuh, H. (eds.) CHES 2015. LNCS, vol. 9293, pp. 683–702. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48324-4_34
Roy, S.S., Vercauteren, F., Mentens, N., Chen, D.D., Verbauwhede, I.: Compact ring-LWE cryptoprocessor. In: Batina, L., Robshaw, M. (eds.) CHES 2014. LNCS, vol. 8731, pp. 371–391. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44709-3_21
Saarinen, M.-J.O.: Arithmetic coding and blinding countermeasures for lattice signatures. J. Cryptogr. Eng. 1–14 (2017)
Shamir, A.: Financial cryptography: past, present, and future. Invited Talk at Financial Cryptography 2016, February 2016. https://www.lightbluetouchpaper.org/2016/02/22/financial-cryptography-2016/#comment-1456744
Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 41(2), 303–332 (1999)
Shoup, V.: NTL: a library for doing number theory. http://www.shoup.net/ntl/
Standaert, F.-X., Malkin, T.G., Yung, M.: A unified framework for the analysis of side-channel key recovery attacks. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 443–461. Springer, Heidelberg (2009). doi:10.1007/978-3-642-01001-9_26
Su, Q., Wu, Y.C.: On convergence conditions of gaussian belief propagation. IEEE Trans. Signal Process. 63(5), 1144–1155 (2015)
Veyrat-Charvillon, N., Gérard, B., Standaert, F.-X.: Soft analytical side-channel attacks. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 282–296. Springer, Heidelberg (2014). doi:10.1007/978-3-662-45611-8_15
Acknowledgements
This work has been supported by the Austrian Research Promotion Agency (FFG) under project SCALAS (grant number 845589) and under the COMET K-Project DeSSnet (grant number 862235).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Primas, R., Pessl, P., Mangard, S. (2017). Single-Trace Side-Channel Attacks on Masked Lattice-Based Encryption. In: Fischer, W., Homma, N. (eds) Cryptographic Hardware and Embedded Systems – CHES 2017. CHES 2017. Lecture Notes in Computer Science(), vol 10529. Springer, Cham. https://doi.org/10.1007/978-3-319-66787-4_25
Download citation
DOI: https://doi.org/10.1007/978-3-319-66787-4_25
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-66786-7
Online ISBN: 978-3-319-66787-4
eBook Packages: Computer ScienceComputer Science (R0)


 . In a simple variant of encoding, the bits of m are simply multiplied by q / 2. Then, three error polynomials
. In a simple variant of encoding, the bits of m are simply multiplied by q / 2. Then, three error polynomials 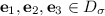 are sampled. The ciphertext is a pair of polynomials (
are sampled. The ciphertext is a pair of polynomials ( .
.






