Network Intrusion Detection Based on Semi-supervised Variational Auto-Encoder

Abstract

Network intrusion detection systems (NIDSs) based on machine learning have been attracting much attention for its potential ability to detect unknown attacks that are hard for signature-based NIDSs to detect. However, acquisition of a large amount of labeled data that general supervised learning methods need is prohibitively expensive, and this results in making it hard for learning-based NIDS to become widespread in practical use.

In this paper, we tackle this issue by introducing semi-supervised learning, and propose a novel detection method that is realized by means of classification with the latent variable, which represents the causes underlying the traffic we observe. Our proposed model is based on Variational Auto-Encoder, unsupervised deep neural network, and its strength is a scalability to the amount of training data. We demonstrate that our proposed method can make the detection accuracy of attack dramatically improve by simply increasing the amount of unlabeled data, and, in terms of the false negative rate, it outperforms the previous work based on semi-supervised learning method, Laplacian regularized least squares which has cubic complexity in the number of training data records and is too inefficient to leverage a huge amount of unlabeled data.

1 Introduction

Applying machine learning techniques to network intrusion detection systems (NIDSs) has been attracting much attention recently, as it has a potential to detect unknown attacks, which is hard for signature-based ones to capture. Along with the popularization of IoT devices and big data analysis, we can expect that acquisition of data for model training will get easier and that its volume will be much bigger, and hence it is predictable that machine learning will exert stronger presence furthermore in network security research and practice.

However, the need for acquiring labeled data, which is required in general supervised learning, such as classification, exists as a barrier against its widespread adoption. Attacks in the wild are rarely captured, and even then, labeling process to determine whether it is normal or adversarial on every traffic record requires expertise and obviously takes vast times, which ends up with prohibitively high cost. To make matters even more troublesome, the characteristics of traffic data vary from environment to environment. Considering the fact that most machine learning methodologies assume that training data and test data should be sampled from independent and identically distributed (i.i.d.) random variables, ideally, it is desirable that data is collected in the actual network environments where the defense system will be deployed, rather than using data that is sampled from other environments. Furthermore, as the trend of network traffic changes day by day even in one environment, it is required to keep the defense systems up-to-date through updating themselves continuously [5]. This necessity means that labeling work is required many times.

We will tackle this issue by introducing semi-supervised learning so that the amount of such labeling operations decreases. Our primal contributions are as follows:

• 1. We propose a network intrusion detection method based on semi-supervised learning that can reduce the number of labeling operations drastically without sacrificing detection performance. Our proposed method outperforms the previous work of [13] in terms of the false negative rate which is a crucial index for NIDSs: our method gave 4.67$\%$, compared with 10.86$\%$ in [13].

• 2. Our proposed method has the capability to improve its performance dramatically by simply increasing the amount of unlabeled data, which would be easily available. While [13] has proposed NIDSs based on semi-supervised learning, their method, Laplacian regularized least squares, cannot leverage large scale data for training because it has cubic complexity in the number of labeled and unlabeled examples [2]. On the other hand, since our proposed method would be trained by mini-batch gradient descent optimization, it is not restricted in terms of the amount of training data, which is an important aspect to create a synergetic effect with semi-supervised learning. This property also allows us to use the whole training data without the need to extract part of training data. Taking into account the fact that the trend of network traffic changes over a some period as mentioned above, which part of data we extract from the whole data for training can have a great influence on the detection performance. Thus if we are required to extract part of data for training, it means that we need to establish an appropriate extraction method, but such an extraction method would be no longer necessary if there is no limit on the number of processable training data records.

• 3. In order to realize the above 1 and 2, we propose Forked Variational Auto-Encoder (Forked VAE) as an extension of Variational Auto-Encoder (VAE) [6, 11], unsupervised deep neural network. Although there are Deep Generative Model (DGM) [7] and Auxiliary Deep Generative Model [9] as extended the VAE for semi-supervised learning, their objectives are to reconstruct input data, especially images, and they utilized label information for that aim. On the other hand, our objective is to perform classification with the latent variable which is represented with lower dimension and a simpler distribution than the original input data, and for that purpose our Forked VAE utilizes label information.

In this paper, we describe the aforementioned learning model and show experimental results that were done to evaluate its performance as an NIDS using Kyoto2006+ and NSL-KDD datasets.

2 Our Approach

In this section, while we clarify our problem, we describe our detection approach and intention for introducing semi-supervised learning.

2.1 Direction of Attack Detection

Outlier Detection vs. Classification. There are mainly two types of machine learning techniques useful for network intrusion detection systems, namely, outlier detection and classification. As the term of outlier detection is often used interchangeably with anomaly detection, what outlier methods do is to detect a deviation from normal behavior. However, attackers often mimic normal traffic, and in an environment where the users are not imposed a special restriction on their use of network, we can expect that it is very often the case that previously unseen but normal behaviors are observed. We can argue that the aim of outlier detection techniques is just to find unknown behaviors and that distinguishing attacks from benign traffic is out of their scope. In light of this, we choose an approach of classification to judge whether the traffic is normal or not, rather than detecting the outlier.

Unfortunately, classification methods need labeled data to train a model in general. The downside of using labels is the cost of obtaining them as argued before, so outlier detection methods that can be trained in an unsupervised manner without using labels are attractive. However, the upside of using labels is the ability to steer a model in a desired direction, which can only be done by supervised learning methods [15]. The contribution of this paper is mainly to mitigate the above downside of supervised learning classification methods by introducing semi-supervised learning.

Classification with Latent Variable. As mentioned in the above section attackers often mimic benign traffic, so that the observed data can become hard to distinguish from benign traffic. The intent behind the generation of those traffic, however, should clearly be different from that behind benign traffic. Therefore, we work on detecting the presence of malice underneath the generated traffic rather than classifying the raw observed data. To realize this, we bring in the latent variable model, which is a statistical model used in machine learning as a powerful tool. As a latent variable model, let us consider that a single observed traffic data x is generated by a corresponding unobserved continuous random variable z, the latent variable, through some random process. We assume that z is the cause of why traffic x is generated and that each x has corresponding z. If z can be represented in the latent space such that it highlights the presence or absence of malice and with a lower dimension than x in the observation space, we can expect that attack detection can be performed in the latent space more efficiently than in the observation space. Together with the discussion so far, what we need to do is to do classification with the latent variable, for which two things are needed:

• To know how to map the observed data x into the corresponding latent variable z. This can be viewed as a matter of posterior distribution inference, and we try to solve this with the technique called approximate inference. As we will describe in detail in Sect. 3.1, we use the VAE as a building block for that.

• To make the representation of latent variables z focus on the presence or absence of malice. For this purpose, we introduce the essence of supervised learning and incorporate it into the VAE, which leads to our new technique, Forked VAE in Sect. 3.2.

Fig. 1.

The whole picture of labeling operation. Black and orange arrows indicate labeling flow and input to model training respectively. (Color figure online)

2.2 Data Label

Before entering the section for semi-supervised learning, with consideration of actual use, we describe the labels that we assume to put on each traffic record. Figure 1 is the whole picture of labeling operations, from the observed data (i.e., raw data) to the labeled data for model training. First, we define three levels of labels based on the granularity and these levels change through phases of analysis. Level 0 means that no labeling has been done yet, i.e., the observed data has no label. Level 2 indicates either “normal” or the name of attack types, and it would be given through the expert analysis, which corresponds to Analysis 2 of Fig. 1. Here, we assume that a Level 1 label would be attached to the data tentatively before Analysis 2 is finished. An analysis for unknown attacks can often take much time, and until it gets finished, the labeled data for that kind of new attack would be unavailable, which means that the defense system would be left vulnerable during that time. However, even if the expert analysis has not fully figured out the tactics of attackers yet, if the traffic is enough suspicious for us to decide that it is a symptom of attack, immunization of the defense system against those kind of attacks should be started in parallel with Analysis 2. Hence, for the Level 1 label, a bit that indicates whether the traffic is a symptom of attack or not is sufficient, and in order to handle this labeling process automatically in a short time, we assume that a signature based or anomaly detection based NIDS is used in Analysis 1. Due to the use of NIDS, mis-labeling could happen in Analysis 1. We therefore arrange Analysis 2 at the end of the system in Fig. 1 so that every traffic can be re-labeled correctly through that. However, here we focus on using only Level 0 and 1 labeled data for the model training in this paper because these labels are easily obtained timely, and a Level 2 label is out of the scope of this paper.

It is not hard to imagine that once the system gets prepared, it would become possible to collect a massive amount of Level 0 data. Hence, it is desirable that the model has no restriction on the amount of training data so as to fully utilize a vast amount of unlabeled data. In addition, to achieve the property of supervised learning from Level 1 labeled data, we introduce semi-supervised learning.

2.3 Advantage of Semi-supervised Learning

The roles of supervised learning that uses labeled data and unsupervised learning that uses unlabeled one are basically different. The main purpose of supervised learning is clear enough: figuring out how relevant data should be extracted from input data to perform a task at hand (e.g., classification). On the other hand, unsupervised leaning tries to keep as much information about the original data as possible [15]. Semi-supervised learning is known as combination of these two to complement each other.

The detection of unknown attacks is obviously a crucial task for NIDSs, but at the same time it also must be guaranteed that previously unseen normal traffic can pass through the NIDS without being blocked. This can be viewed as a problem of over-fitting, i.e., how well the learned model can handle correctly the data record that was not contained in the training dataset, and we consider this challenge as one of the most important missions for NIDSs. A more in-depth argument about unsupervised learning and over-fitting can be found in other literature, and we just briefly introduce the result of [3], which showed that unsupervised learning outperformed supervised learning in the experiment to verify whether a model can recognize the cluster that did not exist in the training dataset.

The reason why we bring semi-supervised is to take full advantage of the property of unlabeled data, and this leads to the reduction of labeling cost, fast updating of the defense system and the tolerance to over-fitting inherent in unsupervised learning.

3 Proposed Model

On the basis of the discussion so far, our machine learning model needs to have the following functionalities:

• Semi-supervised learning to leverage unlabeled data.

• Scalability to be able to deal with a huge amount of data for training.

• Latent variable modeling by which unobserved latent variables are represented in such a way that the presence or absence of malice underlying the observed traffic data is highlighted.

• Classification with latent variables.

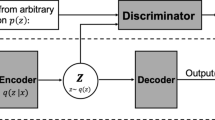
To build our model, we choose the Variational Auto-Encoder (VAE) [6, 11] as a building block. In this section, we first describe the VAE and then explain our proposed model named Forked Variational Auto-Encoder (Forked VAE) while comparing it with the Deep Generative Model (DGM) [7], which is previously proposed as a semi-supervised learning version of the VAE.

3.1 Variational Auto-Encoder

Variational Inference. Before going into the description of the VAE, we introduce a general approximating technique called Variational Inference, also known as Variational Bayesian methods. As in Sect. 2.1, we consider a model in which observed data x is considered to be generated from the latent variable z. We assume that the input data and the latent variable consist of some feature variables, and from now on we denote them as ${\varvec{x}}$ and ${\varvec{z}}$ respectively. In the context of the NIDS, for example, ${\varvec{x}}$ corresponds to a single line of network traffic log, and ${\varvec{z}}$ corresponds to the intention with which ${\varvec{x}}$ is generated. Our objective is to predict whether ${\varvec{x}}$ is normal or adversarial. As mentioned in Sect. 2.1, we would like to perform classification with the latent variable, rather than the observed data, and to do so what we have to know is $p({\varvec{z}} |{\varvec{x}})$, which means posterior probability. Suppose $p({\varvec{z}}|{\varvec{x}})$ is parametrized by $\theta$, what we want to do is to optimize the model via tuning $\theta$. Now, rather than trying to obtain $p({\varvec{z}}|{\varvec{x}})$ directly, we introduce an arbitrary simple distribution $q({\varvec{z}}|{\varvec{x}})$, such as Gaussian, and consider approximating $p({\varvec{z}}|{\varvec{x}})$ by using $q({\varvec{z}}|{\varvec{x}})$. Let’s suppose that $q({\varvec{z}}|{\varvec{x}})$ is parametrized by $\phi$ where $\phi$ is a parameter like the mean and covariance in case $q({\varvec{z}}|{\varvec{x}})$ is Gaussian. Here, logarithm marginal likelihood which we want to maximize can be represented with q as follows:

$$\begin{aligned} \begin{aligned} \text {log} \ p({\varvec{x}})&= \int { q({\varvec{z}}|{\varvec{x}}) \ \text {log} \ p({\varvec{x}}) \ d{\varvec{z}}} \\&= \int { q({\varvec{z}}|{\varvec{x}}) \ \text {log} \ \frac{ p({\varvec{x}},{\varvec{z}}) q({\varvec{z}}|{\varvec{x}})}{ p({\varvec{z}}|{\varvec{x}}) q({\varvec{z}}|{\varvec{x}})} \ d{\varvec{z}}} \\&= L + D_{KL}(q({\varvec{z}}|{\varvec{x}}) \Vert p({\varvec{z}}|{\varvec{x}})) \\&\ge L \end{aligned} \end{aligned}$$

(1)

$$\begin{aligned} L= & {} \int { q({\varvec{z}}|{\varvec{x}}) \ \text {log} \ \frac{ p({\varvec{x}},{\varvec{z}}) }{ q({\varvec{z}}|{\varvec{x}}) } \ d{\varvec{z}} } \end{aligned}$$

(2)

$$\begin{aligned} D_{KL}(q({\varvec{z}}|{\varvec{x}}) \Vert p({\varvec{z}}|{\varvec{x}}))= & {} \int { q({\varvec{z}}|{\varvec{x}}) \ \text {log} \ \frac{ q({\varvec{z}}|{\varvec{x}}) }{ p({\varvec{z}}|{\varvec{x}}) } \ d{\varvec{z}} } \end{aligned}$$

(3)

where the first line of Eq. (1) can be obtained just by insertion of weighted sum by $q({\varvec{z}}|{\varvec{x}})$ that is independent of $p({\varvec{x}})$ and whose summation is one. Applying Bayes rule leads to the second line and it can be transformed into the third line by multiplying both the numerator and the denominator inside the logarithm by $q({\varvec{z}}|{\varvec{x}})$. There are two goals in this scenario. One is to make marginal likelihood log $p({\varvec{x}})$ as large as possible, which is equivalent to optimizing the model with regard to $\theta$. The other is to make the shape of approximate distribution $q({\varvec{z}}|{\varvec{x}})$ closer to true distribution $p({\varvec{z}}|{\varvec{x}})$ by tuning $\phi$, which is equivalent to making Eq. (3) closer to 0. With the fact that the KL divergence, Eq. (3), is nonnegative, $\log p(x)$ is larger than L called variational lower bound, and these two goals can be viewed as a single task, maximization of L. The VAE uses the gradient descent method for this optimization problem in the line of neural networks.

Variational Auto-Encoder. In order to maximize the variational lower bound L of Eq. (2) with regard to both the parameter $\theta$ and $\phi$, the VAE uses the gradient descent method called Stochastic Gradient Variational Bayes [6] or Stochastic Back-propagation [11]. To derive the object function of VAE, we will do two-step conversion to the variational lower bound L, Monte Calro estimation and a technique called re-parameterization trick. First, we introduce the Monte Carlo sampling, by which the integral at ${\varvec{z}}$ in Eq. (6) is approximated by taking the average of samples from $q({\varvec{z}}|{\varvec{x}})$:

$$\begin{aligned} \int {q({\varvec{z}}|{\varvec{x}}) \ f({\varvec{z}}) \ d{\varvec{z}}} = \mathbb {E}_{{\varvec{z}} \sim q({\varvec{z}}|{\varvec{x}})} \left[ f({\varvec{z}}) \right] \simeq \frac{ 1 }{ M } \sum _{m=1}^M f({\varvec{z}}^{(m)}) \end{aligned}$$

(4)

where ${\varvec{z}} \sim q({\varvec{z}}|{\varvec{x}})$ means that the distribution of the random variable ${\varvec{z}}$ is consistent with the probabilistic distribution $q({\varvec{z}}|{\varvec{x}})$, ${\varvec{z}}^{(m)}$ indicates the m-th sample from $q({\varvec{z}}|{\varvec{x}})$, M is the number of the Monte Carlo sampling runs and $\mathbb {E}_{{\varvec{z}} \sim q({\varvec{z}}|{\varvec{x}})}$ means the expected value over empirical samples from the distribution of $q({\varvec{z}}|{\varvec{x}})$. Then applying re-parameterization trick, we express the random variable ${\varvec{z}}$ as a deterministic variable $z = g_{ \phi } ({\varvec{x}}, \varvec{\epsilon } )$, where $\varvec{\epsilon }$ is an auxiliary noise variable and $\varvec{\epsilon } ^{(m)} \sim p(\varvec{\epsilon })$. If we let the variational approximate posterior be a univariate Gaussian, $q({\varvec{z}}|{\varvec{x}}) = \mathcal {N} ({\varvec{z}}|\varvec{\mu }, \varvec{\sigma }^2 )$, the latent variable ${\varvec{z}}$ can be expressed as ${\varvec{z}}^{(m)} = \varvec{\mu } + \varvec{\sigma } \varvec{\epsilon }^{(m)}$, where multiplication of $\varvec{\sigma }$ and $\varvec{\epsilon }^{(m)}$ is done as element-wise. Equation (4) then can be written as:

$$\begin{aligned} \mathbb {E}_{{\varvec{z}} \sim q({\varvec{z}}|{\varvec{x}})} \left[ f({\varvec{z}}) \right] = \mathbb {E}_{\varvec{\epsilon } \sim p(\varvec{\epsilon })} \left[ f(\varvec{\mu } + \varvec{\sigma } \varvec{\epsilon }) \right] \simeq \frac{ 1 }{ M } \sum _{m=1}^M f(\varvec{\mu } + \varvec{\sigma } \varvec{\epsilon }^{(m)}) \end{aligned}$$

(5)

To make the sampling variance smaller, using the Bayes rule again ($p({\varvec{x}},{\varvec{z}}) = p({\varvec{x}}|{\varvec{z}})p({\varvec{z}})$), we convert Eq. (2) as follows:

$$\begin{aligned} L = \int {q({\varvec{z}}|{\varvec{x}}) \ \text {log} \ p({\varvec{x}}|{\varvec{z}}) \ d{\varvec{z}}} - D_{KL}(q({\varvec{z}}|{\varvec{x}}) \Vert p({\varvec{z}})) \end{aligned}$$

(6)

Note that the KL-divergence between two Gaussians can be integrated analytically. Let $P({\varvec{z}}) = \mathcal {N} (\varvec{\mu }_1, \varvec{\sigma }_1 )$, $Q({\varvec{z}}) = \mathcal {N} (\varvec{\mu }_2, \varvec{\sigma }_2 )$ and D be the dimensionality of ${\varvec{z}}$, then:

$$\begin{aligned} \begin{aligned} D_{KL}(P_{1}({\varvec{z}}) \Vert P_{2}({\varvec{z}}))&= \frac{1}{2} ( \log \frac{|\varvec{\sigma }_2|}{|\varvec{\sigma }_1|} + \mathrm {tr}\left\{ \varvec{\sigma }_2^{-1}\varvec{\sigma }_1\right\} ) \\&\quad + \frac{1}{2}\ ( \varvec{\mu }_1 - \varvec{\mu }_2)^\mathrm {T} \varvec{\sigma }_2^{-1} (\varvec{\mu }_1 - \varvec{\mu }_2) - \frac{D}{2} \end{aligned} \end{aligned}$$

(7)

In our case, $P_{1}({\varvec{z}})$ is the posterior approximation $q({\varvec{z}}|{\varvec{x}}) = \mathcal {N} (\varvec{\mu }, \varvec{\sigma })$ and $P_{2}({\varvec{z}})$ is $\mathcal {N} (0, I)$ if we set the prior $p({\varvec{z}})$ as a standard normal distribution. Then putting them altogether, the objective function of the VAE for a single data point ${\varvec{x}}$ ends up as follows:

$$\begin{aligned} L = \frac{ 1 }{ M } \sum _{m=1}^M \ \text {log} \ p({\varvec{x}}|{\varvec{z}}^{(m)}) - \frac{1}{2} \sum _{d=1}^{D} \left[ 1 + \log (\sigma _{d})^2 - (\mu _{d})^2 - ( \sigma _{d})^2 \right] \end{aligned}$$

(8)

where ${\varvec{z}}^{(m)} = \varvec{\mu } + \varvec{\sigma } \varvec{\epsilon }^{(m)}$, $\varvec{\epsilon }^{(m)} \sim \mathcal {N} (0, \mathbf I )$ and $\mu _{d}$ and $\sigma _{d}$ denote the d-th element of each vector. If the mean and variance of the approximate posterior, $\varvec{\mu }$ and $\varvec{\sigma }^2$, are outputs of a fead-forward network $q({\varvec{z}}|{\varvec{x}})$ parameterized by $\phi$ which takes ${\varvec{x}}$ as input, and so is $p({\varvec{x}}|{\varvec{z}})$ by $\theta$, we can optimize both of them simultaneously as a single neural network whose objective function is L of Eq. (8). It then can be viewed as a kind of Auto-Encoder that consists of the encoder $q({\varvec{z}}|{\varvec{x}})$ and the decoder $p({\varvec{x}}|{\varvec{z}})$. In Eq. (8), while the first term corresponds to the reconstruction error similar to typical Auto-Encoders, the second term is the advantage of the VAE. The second term of Eq. (8) works as regularization that makes the shape of the posterior approximation distribution $q({\varvec{z}}|{\varvec{x}})$ of the latent space close to the one of the prior distribution $p({\varvec{z}})$, which means that in the test time the model would be able to predict a reasonable ${\varvec{z}}$ to some extent, even for the traffic ${\varvec{x}}$ that was not contained in the training dataset. Note that, ${\varvec{z}}$ in the VAE is represented as a continuous variable and the number of its dimensionality can be specified arbitrarily, just in the same way as a usual hidden layer.

3.2 Extension to Semi-supervised Learning

The VAE now enables us to predict a latent representation ${\varvec{z}}$ for a certain observed traffic ${\varvec{x}}$. Additionally, its optimization is done by a mini-batch gradient descent method similarly to usual feedforward neural net models, and the amount of training data that the VAE can handle is unlimited in principle. The other thing we have to do is to add the functionalities of semi-supervised learning and classification using the latent variable to the VAE. Here, we first explain the architecture of the deep generative model (DGM) [7], which is previously proposed as an extension of the VAE to make it possible to generate data conditionally using labels, and then describe our proposed model, Forked VAE.

Deep Generative Model. The deep generative model (DGM) [7], also known as the conditional VAE (CVAE), has been proposed aiming to control the shape of the data that would be generated. Let y be a scalar indicating a label of input data ${\varvec{x}}$, and in the context of the NIDS with a Level 1 label in Sect. 2.2, y is a bit indicating whether a certain observed connection ${\varvec{x}}$ shows a symptom of attack or not. As the graphical model shown in Fig. 2a, the DGM represents the inference model as $q({\varvec{x}},y,{\varvec{z}}) = q({\varvec{z}} |{\varvec{x}},y)q(y|{\varvec{x}})q({\varvec{x}})$ (the left-hand of Fig. 2a) and the generative model as $p({\varvec{x}},y,{\varvec{z}}) = p({\varvec{z}} |{\varvec{x}},y)p(y)p({\varvec{z}})$ (the right-hand of Fig. 2a) respectively¹. When ${\varvec{x}}$ with label y is existent, by doing the expression expansion similar to Eq. (1), the variational bound $L_\ell$ for a single data point $({\varvec{x}}, y)$ can be shown as follows:

$$\begin{aligned} \begin{aligned} \text {log} \ p({\varvec{x}},y)&= \int { q({\varvec{z}}|{\varvec{x}}) \ \text {log} \ \frac{p({\varvec{x}},y,{\varvec{z}})}{p({\varvec{z}} |{\varvec{x}},y)} \frac{q({\varvec{z}} |{\varvec{x}},y)}{q({\varvec{z}} |{\varvec{x}},y)}} d{\varvec{z}} \\&= \mathbb {E}_{{\varvec{z}} \sim q({\varvec{z}}|{\varvec{x}},y)} \left[ \text {log} \ \frac{p({\varvec{x}},y,{\varvec{z}})}{q({\varvec{z}} |{\varvec{x}},y)} \right] - D_{KL}(q({\varvec{z}}|{\varvec{x}},y) \Vert p({\varvec{z}}|{\varvec{x}},y)) \\&\ge \mathbb {E}_{{\varvec{z}} \sim q({\varvec{z}}|{\varvec{x}},y)} \left[ \text {log} \ \frac{p({\varvec{x}},y,{\varvec{z}})}{q({\varvec{z}} |{\varvec{x}},y)} \right] \\&= L_\ell \end{aligned} \end{aligned}$$

(9)

For the case where the label is missing, the variational bound $L_u$ for a single data point ${\varvec{x}}$ with unobserved label y is:

$$\begin{aligned} \begin{aligned} \text {log} \ p({\varvec{x}})&= \sum _{y}q({\varvec{z}}|{\varvec{x}}) \int { q({\varvec{z}}|{\varvec{x}}) \text {log} \ \frac{p({\varvec{x}},y,{\varvec{z}})q(y,{\varvec{z}} |{\varvec{x}})}{p(y,{\varvec{z}} |{\varvec{x}})q(y,{\varvec{z}} |{\varvec{x}}) }} d{\varvec{z}} \\&= \sum _{y}q({\varvec{z}}|{\varvec{x}}) \ \mathbb {E}_{{\varvec{z}} \sim q({\varvec{z}} |{\varvec{x}})} \left[ \text {log} \ \frac{p({\varvec{x}},y,{\varvec{z}})}{q(y,{\varvec{z}} |{\varvec{x}}) } \right] - D_{KL}(q(y,{\varvec{z}}|{\varvec{x}}) \Vert p(y,{\varvec{z}}|{\varvec{x}})) \\&\ge \sum _{y}q({\varvec{z}}|{\varvec{x}}) \ \mathbb {E}_{{\varvec{z}} \sim q({\varvec{z}} |{\varvec{x}})} \left[ \text {log} \ \frac{p({\varvec{x}},y,{\varvec{z}})}{q(y,{\varvec{z}} |{\varvec{x}}) } \right] \\&= L_u \end{aligned} \end{aligned}$$

(10)

Introducing an explicit classification loss $\text {log} \ q(y|{\varvec{x}})$ multiplied by coefficient $\alpha$ so as to improve classification accuracy, the resultant objective function of DGM to be maximized is as follows:

$$\begin{aligned} L = \sum _{({\varvec{x}}_{\ell }, y_{\ell })} L_\ell + \sum _{{\varvec{x}}_u} L_u - \alpha \ \sum _{({\varvec{x}}_{\ell }, y_{\ell })} \left[ - \text {log} \ q(y|{\varvec{x}})\right] \end{aligned}$$

(11)

where $({\varvec{x}}_{\ell }, y_{\ell })$ indicates a data point ${\varvec{x}}_{\ell }$ with corresponding label $y_{\ell }$ and ${\varvec{x}}_{u}$ denotes an unlabeled one.

Fig. 2.

Graphical models of DGM and Forked VAE. Each left one represents inference model $q({\varvec{x}},y,{\varvec{z}})$ and right one does generative model $p({\varvec{x}},y,{\varvec{z}})$ respectively.

Proposed Model. While the DGM is a semi-supervised learning model, it does not satisfy our requirements. In the left-hand inference model of Fig. 2a, we can see that a label y would be used as additional information to help infer a latent variable ${\varvec{z}}$ from ${\varvec{x}}$, as $q({\varvec{z}}|{\varvec{x}},y)$, while what we want is exactly the opposite of that, i.e., predicting y given ${\varvec{z}}$, as $p(y|{\varvec{z}})$². In addition, in a generative model of Fig. 2a, while the DGM is modeled so that the reconstructed data ${\varvec{x}}$ would be conditioned by a label y as well as a latent variable ${\varvec{z}}$, that is, $p({\varvec{x}}|y, {\varvec{z}})$, we consider that such structure is not appropriate for our task. As explained in Sect. 2.2, since the labels we are going to use for NIDSs will be coarse and simply indicate whether an observed data ${\varvec{x}}$ is benign or not, we consider that it is not natural that such rough labels can decide the actual form of traffic data ${\varvec{x}}$. The reason why such a difference exists between our expectation and the structure of a DGM is simply that the purpose of a DGM is not a classification task but data generation as well as the VAE, and we can see such a similar structure also in the Auxiliary Deep Generative Model (ADGM) [9], which is an extended model of the DGM.

We therefore propose a model in which labels would not be used for data generation, but only for training of classification. Our model is different from the DGM in the following points:

• Replace $q({\varvec{z}}|y)$ with $p(y|{\varvec{z}})$ so that the classifier for ${\varvec{z}}$ is trained.

• Use $q({\varvec{z}}|{\varvec{x}})$ instead of $q({\varvec{z}}|{\varvec{x}},y) q(y|{\varvec{x}})$ and prohibit y from engaging in producing ${\varvec{x}}$ via ${\varvec{z}}$.

• Use $p({\varvec{x}}|{\varvec{z}})$ instead of $p({\varvec{x}}|y,{\varvec{z}})$ and prohibit y from causing ${\varvec{x}}$.

Fig. 3.

The graphical model of Forked VAE. Circles are stochastic variables and diamonds are deterministic variables.

Figure 2b represents a graphical model of our proposed model in a form in comparison with one of the DGM, where the inference model is $q({\varvec{x}},y,{\varvec{z}}) = q({\varvec{x}},{\varvec{z}}) = q({\varvec{z}}|{\varvec{x}})q({\varvec{x}})$ and the generative model is $p({\varvec{x}}, y, {\varvec{z}}) = p({\varvec{x}}|{\varvec{z}})p(y|{\varvec{z}})p({\varvec{z}})$. We will also give an intuitive explanation with the whole picture with a single hidden layer h in Fig. 3. We refer to this model as Forked VAE because its graphical model has a form where a generative flow branches from the point of ${\varvec{z}}$ to two directions, towards $p(y|{\varvec{z}})$ and towards $p({\varvec{x}}|{\varvec{z}})$. The difference compared with the typical VAE is just the presence of the classifier, the functionality to predict the label y of inputs ${\varvec{x}}$. Our basic idea is to make the latent variable z subject to the presence or absence of malice by leveraging labeled data ${\varvec{x}}_{\ell }$. To do so, the model learns to predict the label y of ${\varvec{x}}_{\ell }$, taking the mean of ${\varvec{z}}$, $\varvec{\mu }$, as inputs, and the classification error is propagated from y to the leftmost ${\varvec{x}}$ through $\varvec{\mu }$, as a supervised leaning signal. Additionally, for both the labeled data ${\varvec{x}}_{\ell }$ and the unlabeled data ${\varvec{x}}_{u}$, the model learns to reconstruct each of them, and its unsupervised learning signal is back propagated from the rightmost ${\varvec{x}}$ to the leftmost ${\varvec{x}}$. Note that both unsupervised and supervised learning are performed for a labeled data ${\varvec{x}}_{\ell }$. The variational lower bound of the marginal likelihood for a single labeled data point is:

$$\begin{aligned} \begin{aligned} \text {log} \ p({\varvec{x}},y)&= \int { q({\varvec{z}}|{\varvec{x}}) \text {log} \ \frac{p({\varvec{x}},y,{\varvec{z}})q({\varvec{z}}|{\varvec{x}})}{p({\varvec{z}}|{\varvec{x}}) q({\varvec{z}}|{\varvec{x}})}} \\&= \mathbb {E}_{{\varvec{z}} \sim q({\varvec{z}} |{\varvec{x}})} \left[ \text {log} \ \frac{p({\varvec{x}},y,{\varvec{z}})}{q({\varvec{z}}|{\varvec{x}})} \right] - D_{KL}(q({\varvec{z}}|{\varvec{x}}) \Vert p({\varvec{z}}|{\varvec{x}})) \\&\ge \mathbb {E}_{{\varvec{z}} \sim q({\varvec{z}} |{\varvec{x}})} \left[ \text {log} \ \frac{p({\varvec{x}},y,{\varvec{z}})}{q({\varvec{z}}|{\varvec{x}})} \right] \\&= \mathbb {E}_{{\varvec{z}} \sim q({\varvec{z}} |{\varvec{x}})} \left[ \text {log} \ p({\varvec{x}}|{\varvec{z}}) \right] + \mathbb {E}_{{\varvec{z}} \sim q({\varvec{z}} |{\varvec{x}})} \left[ \text {log} \ p(y|{\varvec{z}}) \right] - D_{KL}(q({\varvec{z}}|{\varvec{x}}) \Vert p({\varvec{z}})) \\&= L_{\ell }^{(\mathrm {forked})} \end{aligned} \end{aligned}$$

(12)

where the way of changing mathematical expressions is similar to Eqs. (1) and (9) again, and Bayes rule of $p({\varvec{x}},y) = p({\varvec{x}},y,{\varvec{z}})/p({\varvec{z}}|{\varvec{x}},y) = p({\varvec{x}},y,{\varvec{z}})/p({\varvec{z}}|{\varvec{x}})$ based on the independence of y on ${\varvec{z}}$ (as the left side of Fig. 2b) is applied in the first line. For a single unlabeled data point, it is simply equal to the variational lower bound of typical VAE, Eq. (2), and we denote that as $L_{u}^{(\mathrm {forked})}$ here. Adding the classification loss term like the DGM and the ADGM, our objective function to be maximized is as follows:

$$\begin{aligned} \begin{aligned} L^{(\mathrm {forked})} =&\sum _{({\varvec{x}}_{\ell }, y_{\ell })} L_{\ell }^{(\mathrm {forked})} + \sum _{{\varvec{x}}_u}L_{u}^{(\mathrm {forked})} - \alpha \sum _{({\varvec{x}}_{\ell }, y_{\ell })} \mathbb {E}_{{\varvec{z}} \sim q({\varvec{z}} |{\varvec{x}}_{\ell })} \left[ - \text {log} \ p(y|{\varvec{z}})\right] \end{aligned} \end{aligned}$$

(13)

where $\alpha$ is a trade-off hyper-parameter, and since it includes the expected value over samples $\mathbb {E}_{{\varvec{z}} \sim q({\varvec{z}} |{\varvec{x}})}$, the number of sampling times M has to be given.

Finally, we present an implementation of multi-layered perceptrons (MLPs) of Fig. 3 as a concrete example. Although this example is relatively simple, there are many possible choices of encoders and decoders. Since ${\varvec{x}}$ is traffic data in our case and consists of mixed data type, such as a real-valued number for the connection duration and a categorical for the state of the connection, we handle ${\varvec{x}}$ as real-valued vector, and hence we select a multivariate Gaussian with a diagonal covariance structure for a decoder of our MLP.

$$\begin{aligned} \begin{aligned} h&= \text {tanh}(\mathbf {W_{1}}x+{\varvec{b}}_{1}) \\ \varvec{\mu }&= \mathbf {W_{2}}{\varvec{h}}+{\varvec{b}}_{2} \\ \text {log} \ \varvec{\sigma }^2&= \mathbf {W_{3}}{\varvec{h}}+{\varvec{b}}_{3} \\ {\varvec{z}}^{(m)}&= \varvec{\mu } + \varvec{\sigma } \varvec{\epsilon }^{(m)}, \ \varvec{\epsilon }^{(m)} \sim \mathcal {N} (0, \mathbf I )\\ \hat{{\varvec{h}}}&= \mathbf {W}_{4}{\varvec{z}}^{(m)}+{\varvec{b}}_{24} \\ \hat{\varvec{\mu }}&= \text {tanh}(\mathbf {W}_{5} \hat{{\varvec{h}}}+{\varvec{b}}_{5}) \\ \text {log} \ \hat{\varvec{\sigma }}^2&= \text {tanh}(\mathbf {W}_{6} \hat{{\varvec{h}}}+{\varvec{b}}_{6}) \\ \hat{x}&\sim \mathcal {N} (\hat{\varvec{\mu }},\hat{\varvec{\sigma }}^2 \mathbf I ) \\ y&= \mathop {\text {arg max}}\limits _{i} (\mathop {\text {softmax}}\limits _{i} (\mathbf {W}_{7_{i}} {\varvec{z}}^{(m)} +{\varvec{b}}_{7} )) \end{aligned} \end{aligned}$$

(14)

where a tanh and multiplication of $\varvec{\sigma }$ and $\varvec{\epsilon }^{(m)}$ are performed as element-wise, and the variances $\varvec{\sigma }^2$ and $\hat{\varvec{\sigma }}^2$ are outputs as a logarithm so that it is guaranteed to be a positive value. The value i in the last line indicates a class label, that is normal or attack traffic, and $\mathbf {W_{7_{i}}}$ is the i-th row of a weight matrix $\mathbf {W_{7}}$. The values $\{ \mathbf {W_{1}}, {\varvec{b}}_{1}, \mathbf {W_{2}}, {\varvec{b}}_{2}, \mathbf {W_{3}}, {\varvec{b}}_{3} \}$ are the weights and biases of the MLP and corresponding to variational parameters $\phi$ that composes an encoder $q({\varvec{z}}|{\varvec{x}})$, and $\{ \mathbf {W_{4}},{\varvec{b}}_{4}, \mathbf {W_{5}},{\varvec{b}}_{5}, \mathbf {W_{6}},{\varvec{b}}_{6}, \mathbf {W_{7}},{\varvec{b}}_{7} \}$ are parameters $\theta$ of a decoder $p({\varvec{x}}|{\varvec{z}})$. Then we obtain the likelihoods used in the objective function Eq. (13) as follows:

$$\begin{aligned} \text {log} \ p({\varvec{x}}|{\varvec{z}})= & {} \ \text {log} \ \mathcal {N} (\hat{\varvec{\mu }},\hat{\varvec{\sigma }}^2 \mathbf I ) \\ \text {log} \ p(y|{\varvec{z}})= & {} y_{\ell } \ \text {log} \ y + (1 - y_{\ell }) \ \text {log} \ (1 - y) \end{aligned}$$

(15)

As mentioned in the explanation of Eq. (8), $\text {log} \ p({\varvec{x}}|{\varvec{z}})$ can be seen as a reconstruction error since it contains the term of squared error. The value $\text {log} \ p(y|{\varvec{z}})$ is simply classification error as cross-entropy loss.

4 Experiments

We evaluate the detection performance of our proposed method using Kyoto2006+ [12] and NSL-KDD [14] datasets, and test it in two settings: one setting is in the semi-supervised learning model where a large amount of unlabeled data and very few labeled data are used, and the other setting is in the unsupervised learning model using only unlabeled data. The detail of the experimental conditions will be described in Sect. 4.2.

Our experimental procedure is simple. We first selected training data and testing data respectively from each dataset, and then put them into the model implemented based on the settings described in Sect. 4.1. Model training and detection test were also performed with the parameters described in Sect. 4.1.

4.1 Preparation

Datasets. Kyoto2006+ dataset covers nearly three years of real network traffic through the end of 2008 over a collection of both honeypots and regular servers that are operationally deployed at Kyoto University, while NSL-KDD is dataset artificially generated over the virtual network nearly two decades ago. Labels provided with Kyoto2006+ just indicates whether each traffic is malicious or non-malicious, whereas labels with NSL-KDD consist of five categories, normal traffic and four types of attack, such as DoS, probing, unauthorized access to local super user (root) privileges and unauthorized access from a remote machine. In this experiment, we deal with the label of NSL-KDD as binary, that is, the presence or absence of malice, similar to Kyoto2006+, with the intent of realization of Level 1 labeling in Sect. 2.2.

For Kyoto2006+, in order to compare the performance with previous works, the condition on how to select the data used for training and for testing was made consistent with [5, 13]. Specifically, for Kyoto2006+, we used the traffic data of the day of Jan 1, 2008 for training, which amounts to 111,589 examples and the traffic of 12 days, 10th and 25th of each month from July to December, for testing, which amounts to 1,261,616 examples in total. Note that the data of 10th and 23rd were chosen for testing only in September because the honey pot system was shut down on 25th due to scheduled power outage. For NSL-KDD we used both training data and testing data as they were provided, and the amounts of traffic are 125,973 and 22,543 respectively. More detailed information on datasets can be found in relevant literature.

Parameters. Here, we present the parameters of the model we used in our experiment. Both the inferring and generative models are provided with a hidden layer between an input data layer and a latent variables layer, h in Fig. 3, and the number of units they have is 200 for both. The number of the latent space dimension is 30. As we set the prior distribution $p({\varvec{z}})$ as a standard normal distribution $\mathcal {N} ({\varvec{z}}|0, \mathbf I )$, for the sake of the second term of Eq. (6), as the training progresses $q({\varvec{z}}|{\varvec{x}})$ becomes gradually close to a spherical distribution and each element of z gets independent of each other. However, at the same time we anticipate that at least two clusters corresponding to the attack and the benign would emerge. Therefore, we relieved such regularizing effect stemming from KL divergence a bit by multiplying the second term of Eq. (6) by 0.01. In addition, we let $\alpha$ in Eq. (13) be 100 and let the frequency of Monte Carlo sampling for ${\varvec{x}}$, M be 1, and AdaGrad was used as optimization and its learning rate was set to 0.001.

The values for those parameters were chosen heuristically through our experiments. From the difference in the size of the dimension of the input data, the number of units of hidden layers and the size of latent variables are a bit smaller respectively compared with the previous VAE based works, but the remaining parameters ended up with the same as the previous works. For the parameter of Random Forest, we used the default values defined by sickit-learn’s API as it is.

Environments. The program for our experiments was implemented using Theano 0.7.0 [17], and the specification of the machine used for the experiment is iMac, Intel Core i5 2.7 GHz processor and 12 GB RAM. Although the program runs only on CPU without using GPU, the computational time for the model training was so short that millions of iterations of training for a single mini-batch, that consists of 100 data records, got finished in a couple of hours.

Table 1. Summary of experimental conditions.

4.2 Experimental Conditions

For comparison, we evaluated our models under three different conditions in terms of the amounts of the training data. Table 1 shows the summary, and the actual number of labeled and unlabeled data records for each condition is shown in Tables 2 and 3, along with their corresponding results.

Condition 1 corresponding to No. 1 in Table 2 and No. 7 in Table 3, is set to aim to evaluate the proposed model as unsupervised learning. The purpose of the experiment of Condition 1 is to qualitatively evaluate the effectiveness of the proposed model in terms of the ability to make the latent representation, i.e., as a feature extractor, for network traffic data. In this evaluation, the latent space is visualized where the raw traffic data is mapped in the unsupervised learning way by using the training dataset without label information. In addition, we also perform a detection experiment that is to classify the latent features extracted by VAE, by using another machine learning classification method. As our proposed model of Condition 1 is equivalent to the normal VAE and does not have a classification function in itself, we chose Random Forest as our classifier, due to its processing speed, the ability to use large amounts of data for training and testing, and ease of implementation³. Note that the classification results of Nos. 1 and 7 are done by supervised learning with Random Forest.

Conditions 2 and 3 were set to evaluate our model as semi-supervised learning, which corresponds to Nos. 3, 5, 8 and 9 in Tables 2 and 3. In both conditions the number of labeled data records was only 100 that were selected from the beginning of each training data file, whereas in Condition 2 unlabeled data consists of all but the 100 data records, and in Condition 3 unlabeled data consists of 3,000 records chosen from 101st to 3,100th lines of training file of each datasets. Condition 3 was created to adapt our evaluation to the experimental condition of [13] where Kyoto2006+ was used in the same way. Indeed, considering that the training data consists of only 3,100 records in total and this number is very small compared with the test data of 1,261,616 records, performance of the trained model is heavily dependent on which records are used for training. Therefore, we tried to match our condition exactly with [13], however unfortunately that could not be realized because in [13] the data had been selected randomly. For NSL-KDD, unlabeled data records for Conditions 2 and 3 were selected in the same way, namely, 3,000 records extracted from 100 line from the beginning of the training data file and all the remaining records except for first 100 lines of that file, which are corresponding to Nos. 8 and 9 in Table 3 respectively.

Fig. 4.

Visualization of the latent space. Plots on each figure correspond to first 2,000 traffic records of Jul 15, 2008 of Kyoto2006+. According to corresponding labels in the data file, each traffic is plotted as a red point if it is normall or as blue if adversarial. (Left) The model trained in unsupervised learning under Condition 1 (corresponding to No. 1 in Table 2). (Right) The model trained in semi-supervised learning under Condition 2 (corresponding to No. 5 in Table 2). To visualize, the dimensionality is converted from 30 to 2 by using t-SNE. (Color figure online)

4.3 Results

Figure 4 shows that how the trained model recognizes the observed traffic data in the latent space ${\varvec{z}}$, where each blue plot corresponds to a normal connection and each red does to an attack. Note that all records in the training data have corresponding labels, and hence in the evaluation as the unsupervised model, after we mapped data into the latent space (Fig. 4 left) or performed classification with Random Forest (No. 1 in Table 2 and No. 7 in Table 3), we could distinguish normal from adversarial by using those label information as the ground truth. In the left side of Fig. 4, the plots form concentric circles with different radius between normal traffic and adversarial ones, which can be naturally considered as the manifestation of the effect of the second term of Eq. (6), and although the model has been trained in an unsupervised manner as typical VAE, we can see that it succeeded in isolating adversarial traffic from normal traffic fairly well. The right side of Fig. 4, which is the projection through our Forked VAE, forms no longer a concentric circles nor two clusters. Although the detection accuracy ended up being good as discussed later, there is probably room for the model parameter tuning, especially $\alpha$ in Eq. (13).

Table 2. Classification performance on the Kyoto2006+ dataset.

Table 3. Classification performance on the NSL-KDD dataset.

Tables 2 and 3 show the classification results respectively. In both datasets, the relative superiority of Conditions 1, 2 and 3 was as expected. Focusing on Area Under the Curve (AUC), we can see that [13] (No. 4) has still outperformed our result despite the fact that [13] used only 3,000 unlabeled data. However, the results of Conditions 2 and 3 show that the performance of our model was drastically improved with the increase of unlabeled data records. In particular, the recall of our proposed semi-supervised model (No. 5) ends up being remarkably higher than that of [13] (No. 4), and that means our model outperforms [13] in terms of the false negative rate which is a crucial index for NIDSs: our model gave 4.67%, compared with 10.86% in [13]⁴. As argued in Sect. 2, our ultimate goal is to construct a defense systems that can fully leverage unlabeled data, which would be available with very low cost, and this results can be regarded as taking the first step towards the realization of that.

5 Related Work

There have been many works related to network intrusion detection system using machine learning techniques. The works [4, 8, 10] proposed anomaly detection methods that measure changes of traffic volume on the basis of entropy. Establishing a way to collect normal data that defines the baseline is a challenge for their methodology, and [10] worked on that issue with the algorithm that makes it possible to sample packets efficiently. While the direction of the detection method of [10] is different from ours, their method can be considered to be related to our objective in terms of data sampling. Once we succeed in reducing the amount of labeling by introducing semi-supervised learning, what would become as the next primary problem is possibly how to select a small amount of data to be labeled efficiently and effectively.

The work [1] proposed an anomaly detection method using the VAE, in which the model was trained only with benign traffic data, and whether observed data is normal or adversarial would be judged based on the likelihood of reconstruction $p({\varvec{x}}|{\varvec{z}})$. However, acquiring traffic data exclusive of adversarial traffic requires the task that is equivalent to labeling, and hence the need for preparing pure benign traffic data may become problematic when it is put into practical use.

The works [5, 13] dealt with network intrusion detection as a classification task, and especially [13] had much in common with us including the reason why they did not use outlier detection methods. The work [13] is also a pioneering work introducing semi-supervised learning and their method is based on Laplacian regularized least squares. Compared with [13] in terms of the semi-supervised learning based technique, the strength of our proposed Forked VAE is being a more scalable model. As mentioned in Sect. 1, the computation complexity of [13] is a cubic of the number of labeled and unlabeled training data records [2], whereas our model is not much affected by the data volume because, as mentioned in Sect. 3.1, its learning process would be done by gradient descent just as in the other neural network model, which leads to the synergy with semi-supervised learning through making full use of a huge amount of unlabeled data.

6 Summary

In this paper, we have proposed the novel NIDS based on the Forked VAE, a semi-supervised learning model extending the VAE. The strength of our proposed method is the scalability of the model, which makes it possible to train the model with a huge amount of unlabeled data, and in the experiment using Kyoto2006+ dataset, we demonstrated that the false negative rate gets improved from 37.99$\%$ to 4.67$\%$ by simply increasing the number of unlabeled data records from 3,000 to 111,489 with only 100 labeled data records.