Abstract
The action of a translation on a continuous object before its digitization generates several digitizations. The dual, introduced by the authors in a previous paper, stands for these digitizations in function of the translation parameters. This paper focuses on the combinatorics of the dual by making a link between the digitization number and the boundary curve, especially through its dual representation. The convex case is then studied and a few significant examples are exhibited.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
For a given grid step and a given digitization method, a planar object produces several digitizations in function of its position on the grid. The object digital properties and digitally estimated characteristics depend on the obtained digitization. Thereby, this study of the digitization variability is an important issue in image analysis.
This field has been explored for some geometrical primitives. For instance, the set of straight segment digitizations in function of the segment slope and offset is known as the segment preimage and is used for digital straight segment recognition [3]. Several papers are also dedicated to the study of the generation and combinatorics of the disc digitization set in function of its radius and center position [4, 6,7,8,9,10, 12,13,14] and the combinatorics of the strictly convex sets [5]. In the general case, the digitization set can be seen as the consequence of a group action on the object. A function, so-called dual, linking the group action and the produced digitization is used by the authors to study the digitization set up to a translation, for function graphs in [1] and for planar object in [11]. In the latter case, the dual has been proved to be piecewise constant in function of the translation. This paper focuses on the dual combinatorics.
Two upper bounds are given for the number of digitizations of a planar object whose boundary is a Jordan curve. The first one is expressed in terms of the number of grid cells crossed by the boundary and the second one in terms of the intersection number when plotting the boundary on the torus  . The latter bound is proved to be quadratic in the convex case. Some examples are provided in order to compare the two upper bounds both in the convex and the non-convex cases. A conclusion and some perspectives end the paper.
. The latter bound is proved to be quadratic in the convex case. Some examples are provided in order to compare the two upper bounds both in the convex and the non-convex cases. A conclusion and some perspectives end the paper.
2 Background
Let us consider a connected compact set S in  hose boundary is a simple closed (Jordan) curve \(\varGamma \). Thanks to the Jordan curve theorem, we may assume a continuous map
hose boundary is a simple closed (Jordan) curve \(\varGamma \). Thanks to the Jordan curve theorem, we may assume a continuous map  such that \(\varGamma \) and S are implicitly defined by
such that \(\varGamma \) and S are implicitly defined by

We are interested in the variability of the Gauss digitization when the group of the translations acts on S, that is on the sets  ,
,  . In this paper, we focus on the combinatorial aspects of this variance. Of course, the variance has to be understood “up to integer translations”. This is the reason why we defined in a previous paper [11] the dual by translation
Footnote 1 of the digitizations of S as a set-valued function \(\varphi _S\) defined on the torus
. In this paper, we focus on the combinatorial aspects of this variance. Of course, the variance has to be understood “up to integer translations”. This is the reason why we defined in a previous paper [11] the dual by translation
Footnote 1 of the digitizations of S as a set-valued function \(\varphi _S\) defined on the torus  which maps each point \( t\in \mathbb T\) to the digitization, up to integer translations, of \(u+S\) where the vector u is any representative of t in
which maps each point \( t\in \mathbb T\) to the digitization, up to integer translations, of \(u+S\) where the vector u is any representative of t in  . Let us pick a representative in each class of \(\mathbb T\) so as to form a connected set M called the structuring element. We note C the symmetric of M with respect to the origin: \(C=-M\). The family of sets \(p+C\),
. Let us pick a representative in each class of \(\mathbb T\) so as to form a connected set M called the structuring element. We note C the symmetric of M with respect to the origin: \(C=-M\). The family of sets \(p+C\),  , is a tiling of
, is a tiling of  . For instance, we can take \(M=[0,1)^2\), \(C=(-1,0]^2\). From now on, to simplify the notations, we identify \(t\in T\) with its representative in M and the subsets of
. For instance, we can take \(M=[0,1)^2\), \(C=(-1,0]^2\). From now on, to simplify the notations, we identify \(t\in T\) with its representative in M and the subsets of  with their orbits for the action of the integer translations so we can write
with their orbits for the action of the integer translations so we can write  . For any point or set X in
. For any point or set X in  , we denote by \({\text {proj}}(X)\) its projection on the quotient space \(\mathbb T\). We proved in [11] that the plot of the curve \(\varGamma \) on the torus \(\mathbb T\), \({\text {proj}}(\varGamma )\), delineates regions on which the dual function \(\varphi _S\) is constant.
, we denote by \({\text {proj}}(X)\) its projection on the quotient space \(\mathbb T\). We proved in [11] that the plot of the curve \(\varGamma \) on the torus \(\mathbb T\), \({\text {proj}}(\varGamma )\), delineates regions on which the dual function \(\varphi _S\) is constant.
We define the grid boundary \(\mathcal B\) as the set of grid points that lie in the (morphological) dilation of the boundary \(\varGamma \) of S by the structuring element M:

where \(\oplus \) denotes the Minkowski sum. The set \(\mathcal B\) contains all the points of  whose membership to the digitization may change when the set S is shifted by a vector \(u\in M\). Nevertheless, since
whose membership to the digitization may change when the set S is shifted by a vector \(u\in M\). Nevertheless, since  is connected, M is not open so there may exist some points in \(\mathcal B\cap S\) not liable to change, namely those points p in \(\mathcal B\) for which \(p+C\subseteq S\) (see Fig. 1). That is why we have in fact to consider the toggling boundary \(\mathfrak {B}\) as the set of grid points whose membership effectively toggle for some translation by a vector \(u\in M\):
is connected, M is not open so there may exist some points in \(\mathcal B\cap S\) not liable to change, namely those points p in \(\mathcal B\) for which \(p+C\subseteq S\) (see Fig. 1). That is why we have in fact to consider the toggling boundary \(\mathfrak {B}\) as the set of grid points whose membership effectively toggle for some translation by a vector \(u\in M\):

The set  of the grid points that are in any digitization of \(u+S\), \(u\in M\), is called the digitization core.
of the grid points that are in any digitization of \(u+S\), \(u\in M\), is called the digitization core.
(a) A Jordan curve \(\varGamma \) and a set of tiles \(z+C\),  and \(C=(-1,0]^2\). The point p is in \(\mathfrak {B}\) for the square \(p+C\) intersects both \(\varGamma \) and
and \(C=(-1,0]^2\). The point p is in \(\mathfrak {B}\) for the square \(p+C\) intersects both \(\varGamma \) and  ; the point q is in \(\mathcal B\setminus \mathfrak {B}\) for the square \(q+C\) intersects the boundary \(\varGamma \) but is included in S; the point r is in the digitization core for the square \(r+C\) is included in S and does not intersect \(\varGamma \) (b) Black: a Jordan curve, medium red discs: the toggling boundary, big blue discs: two points that lie in the grid boundary but that cannot change their membership, small green discs: the digitization core. (Color figure online)
; the point q is in \(\mathcal B\setminus \mathfrak {B}\) for the square \(q+C\) intersects the boundary \(\varGamma \) but is included in S; the point r is in the digitization core for the square \(r+C\) is included in S and does not intersect \(\varGamma \) (b) Black: a Jordan curve, medium red discs: the toggling boundary, big blue discs: two points that lie in the grid boundary but that cannot change their membership, small green discs: the digitization core. (Color figure online)
Finally, for any  , we set
, we set
so \(\varGamma _p=\emptyset \) if \(p\notin \mathcal B\), and we denote by  the indicator function of the set \(\varGamma _p\), so
the indicator function of the set \(\varGamma _p\), so  is not constant iff \(p\in \mathfrak {B}\). Then,
is not constant iff \(p\in \mathfrak {B}\). Then,

In the rest of the article, we use the notation \(\left| E\right| \) for the cardinal of a set E ( ), \({\text {CC}}(A)\) for the family of the connected components of a subset A of
), \({\text {CC}}(A)\) for the family of the connected components of a subset A of  and \(I\sqcup J\) for the disjoint union of the sets I and J.
and \(I\sqcup J\) for the disjoint union of the sets I and J.
In the following section, upper bounds are given for the number of digitizations up to a translation. The first upper bound is naive. For the second one, the idea is to link the digitization number to the number of the intersection of the translated curves \(\varGamma _p\). Indeed, the dual induces a partition of the torus whose cells frontiers are arcs of the curve \({\text {proj}}(\varGamma )\). Then, we bound from above the partition size by counting the number of curve intersections in \({\text {proj}}(\varGamma )\).
3 Contribution
3.1 Bounding up by Counting the Crossed Tiles
Since the grid boundary \(\mathcal B\) contains any integer point whose value may change when shifting the set S, we have a first, obvious, upper bound on the number of Gauss digitizations given by \(2^{\left| \mathcal B\right| }\). As \(\left| \mathcal B\right| \) is also the number of tiles \(p+C\),  , crossed by the frontier of S, we can state the following proposition.
, crossed by the frontier of S, we can state the following proposition.
Proposition 1
The number of Gauss digitizations, up to integer translations, is upper bounded by \(2^{\,\mathrm {a}(\varGamma )}\) where \({\mathrm {a(\varGamma )}}\) is the number of tiles crossed by \(\varGamma \).
Generally, the digitization enumeration provided by Proposition 1 includes false positives and multiple counts. For instance, the grid boundary of a circle with diameter 1.7 involves 4 to 8 pixels, depending on the grid position, which gives an upper bound according to Proposition 1 equals to 16, while there exists only 8 digitizations (see Fig. 2). Nevertheless, from any set, it is possible to build a new set that avoids false positives by replacing the initial boundary by a family of Hilbert curves and it is possible to extend the set to prevent multiple counts so that the theoretical upper bound \(2^\mathfrak {B}\) is obtained (see Appendix B).
(a) A circle with diameter 1.7 and the four pixels in the toggling boundary (which is equal to the grid boundary): a, b, c, d. (b) The (flatten) dual of the closed disc bounded by the circle. Among the \(16=2^4\) potential digitizations provided by the 4-pixels a, b, c, d, three of them does not actually appear (\(\emptyset \), ac and bd) and some others appear multiple times (the four singular digitizations, which are obviously congruent, and the vertical and horizontal pairs which each appear twice. Eventually, there are only 8 digitizations (and actually the (sewed) dual is divided into 8 regions).
3.2 Bounding up by Counting the Intersections
In Sect. 3.2, we assume a parametrization of \(\varGamma \). It induces an order on the points of the curve \(\varGamma \) (for \(\varGamma \) is simple) that is used in the proof of the following proposition.
The dual \(\varphi _S\) can be regarded as the projection, on the torus \(\mathbb T\) of a finite labeled partition of the tile C (whose cells need not be connected). For the order by refinement on the partitions, this partition is lower bounded by the infimum of the binary partitions \(\mathcal {P}_p\) associated to the indicator functions  , \(p\in \mathfrak {B}\) (actually,
, \(p\in \mathfrak {B}\) (actually,  , \(p\in \mathfrak {B}\)). Indeed some cells of \(\bigwedge _{p\in \mathfrak {B}} \mathcal {P}_p\) need to be merged whenever the corresponding digitizations are equivalent up to an integer translation. Then, the next proposition proposes an upper bound on the size of the partition \(\bigwedge _{p\in \mathfrak {B}} \mathcal {P}_p\)—and thereby an upper bound to the number of digitizations—by inductively counting the intersections between the curves \(\varGamma _p\), \(p\in \mathfrak {B}\). The idea is to count the partition cells created when adding a curve \(\varGamma _p\). To do this we count the intersection of \(\varGamma _p\) with the already added curves. Nevertheless, such an intersection can be with one or more curves and can be a singleton, a set of several points or an arc. Then, let us specify how we handle intersections in this context (the definition is illustrated in Fig. 3).
, \(p\in \mathfrak {B}\)). Indeed some cells of \(\bigwedge _{p\in \mathfrak {B}} \mathcal {P}_p\) need to be merged whenever the corresponding digitizations are equivalent up to an integer translation. Then, the next proposition proposes an upper bound on the size of the partition \(\bigwedge _{p\in \mathfrak {B}} \mathcal {P}_p\)—and thereby an upper bound to the number of digitizations—by inductively counting the intersections between the curves \(\varGamma _p\), \(p\in \mathfrak {B}\). The idea is to count the partition cells created when adding a curve \(\varGamma _p\). To do this we count the intersection of \(\varGamma _p\) with the already added curves. Nevertheless, such an intersection can be with one or more curves and can be a singleton, a set of several points or an arc. Then, let us specify how we handle intersections in this context (the definition is illustrated in Fig. 3).
Definition 1
Let \(\mathfrak {B}=\{b_1, \cdots , b_i, \cdots ,b_n\}\), \(n\ge 1\). Let \(m\in [2,n]\). Then,

Note that the components of all the \({\text {inter}}_{\gamma ,I}\) are two by two disjoint and that \(\#{\text {inter}}_m\) may be infinite.
The set \({\text {inter}}_{\gamma ,I}\) stands for the intersection of the curve \(\gamma \) with the curves whose indexes are in a subset I, excluding any other curve \(\varGamma _{b_i}\) whose index is not in I. The necessity to have all the index subsets comes from the fact that intersections between multiple curves can occur.
(a) Blue: \(\varGamma _{b_1}\). (b) Green: \(\varGamma _{b_2}\); \(\#{\text {inter}}_2=\left| {\text {inter}}_{\varGamma _{b_2},\{1\}}\right| =4\). (c) Brown: \(\varGamma _{b_3}\); \(\#{\text {inter}}_3=\left| {\text {inter}}_{\varGamma _{b_3},\{1\}}\right| +\left| {\text {inter}}_{\varGamma _{b_3},\{2\}}\right| +2\left| {\text {inter}}_{\varGamma _{b_3},\{1,2\}}\right| =0+0+2=2\). (d) Red: \(\varGamma _{b_4}\); \(\#{\text {inter}}_4=\left| {\text {inter}}_{\varGamma _{b_4},\{1\}}\right| +2\left| {\text {inter}}_{\varGamma _{b_4},\{1,2,3\}}\right| =2+2=4\). (Color figure online)
We are now able to state the proposition that relates the number of digitizations and the number of intersections \(\#{\text {inter}}_m\).
Proposition 2
The size of the partition \(\bigwedge _{p\in \mathcal B} \mathcal {P}_p\) is upper bounded by
Proof
The proposition is proved by induction. For \(m=1\), the result is obvious since, for any \(p\in \mathfrak {B}\), \(\mathcal {P}_p\) is a binary partition. Let \(m>1\). We assume that the number of cells of the partition \(\bigwedge _{ i=1}^{m-1} \mathcal {P}_{b_i}\) is upper bounded by \(2+\sum _{k=2}^{m-1} \#{\text {inter}}_k+\left| {\text {CC}}(\varGamma _{b_k})\right| \). The cells of \(\bigwedge _{i=1}^{m-1} \mathcal {P}_{b_i}\) which are included in one of the two cells of \(\mathcal {P}_{b_m}\), namely the sets \((\) and  , stay unchanged in the partition \(\bigwedge _{i=1}^{m} \mathcal {P}_{b_i}\). Conversely, the cells of \(\bigwedge _{i=1}^{m-1} \mathcal {P}_{b_i}\) that are intersected by both
, stay unchanged in the partition \(\bigwedge _{i=1}^{m} \mathcal {P}_{b_i}\). Conversely, the cells of \(\bigwedge _{i=1}^{m-1} \mathcal {P}_{b_i}\) that are intersected by both  and
and  , which obviously are cells intersected by \(\varGamma _{b_m}\), are each divided in two new cells. Thereby, the number \(N_m\) of new cells is upper bounded by \(N_m^\prime \), the number of cells in \(\bigwedge _{i=1}^{m-1} \mathcal {P}_{b_i}\) intersected by \(\varGamma _{b_m}\). Besides, the partition \(\bigwedge _{i=1}^{m-1} \mathcal {P}_{b_i}\) of the tile C induces a partition \(\mathcal {Q}\) of \(\varGamma _{b_m}\), as a subset of C, with \(N_m^\prime \) cells (these cells of \(\varGamma _{b_m}\) need not be connected). Then, the idea of the proof is to map each cell of \(\mathcal {Q}\) to its supremum, for the order induced by the parametrization of \(\varGamma \)—namely to the intersection, as defined in Definition 1—its supremum belongs to, or to the empty set when no such intersection exists. Then, though this mapping is not one-to-one, a careful examination of the different cases will permit to conclude that \(N_m^\prime \) is upper bounded by \(\#{\text {inter}}_m + \left| {\text {CC}}(\varGamma _{b_m})\right| \).
, which obviously are cells intersected by \(\varGamma _{b_m}\), are each divided in two new cells. Thereby, the number \(N_m\) of new cells is upper bounded by \(N_m^\prime \), the number of cells in \(\bigwedge _{i=1}^{m-1} \mathcal {P}_{b_i}\) intersected by \(\varGamma _{b_m}\). Besides, the partition \(\bigwedge _{i=1}^{m-1} \mathcal {P}_{b_i}\) of the tile C induces a partition \(\mathcal {Q}\) of \(\varGamma _{b_m}\), as a subset of C, with \(N_m^\prime \) cells (these cells of \(\varGamma _{b_m}\) need not be connected). Then, the idea of the proof is to map each cell of \(\mathcal {Q}\) to its supremum, for the order induced by the parametrization of \(\varGamma \)—namely to the intersection, as defined in Definition 1—its supremum belongs to, or to the empty set when no such intersection exists. Then, though this mapping is not one-to-one, a careful examination of the different cases will permit to conclude that \(N_m^\prime \) is upper bounded by \(\#{\text {inter}}_m + \left| {\text {CC}}(\varGamma _{b_m})\right| \).
Let \(\gamma \) be a connected component of \(\varGamma _{b_m}\) and \(s_\infty \) be the supremum of \(\gamma \) for the order induced by the parametrization of \(\varGamma \). Let \(\mathcal {Q}_\gamma \) be the restriction of \(\mathcal {Q}\) to \(\gamma \). We set \({\text {inter}}_\gamma =\bigcup _{\emptyset \subset I\subseteq [1,m-1]}{\text {inter}}_{\gamma ,I}\), and we assume the following facts that will be prove further:
-
(a)
each component in \({\text {inter}}_{\gamma }\) is included in a cell of \(\mathcal {Q}_\gamma \);
-
(b)
if a cell of \(\mathcal {Q}_\gamma \) has a supremum s distinct from \(s_\infty \), then s belongs to some component of \({\text {inter}}_{\gamma }\);
-
(c)
if two cells of \(\mathcal {Q}_\gamma \) have their supremums in the same component K of \({\text {inter}}_\gamma \), then these supremums are equal to the infimum of K.
-
(d)
if three cells of \(\mathcal {Q}_\gamma \) have the same supremum s, then \({\text {inter}}_\gamma \) has infinitely many components;
-
(e)
if two cells of \(\mathcal {Q}_\gamma \) have the same supremum s and \({\text {inter}}_m\) is finite then either \(s= s_\infty \) and \(s_\infty \) belongs to some component of \({\text {inter}}_\gamma \), or s belongs to at least two curves \(\varGamma _{b_i}\) and \(\varGamma _{b_j}\) where \(i, j <m\).
Then, with these five assumptions, we deduce the desired upper bound as follows. We map each cell of \(\mathcal {Q}_\gamma \) to the component of \({\text {inter}}_\gamma \) its supremum belongs to, if any. The other cells are map on the empty set. We denote by \(\psi \) this mapping. Hence, from Fact b,the supremum of the preimages by \(\psi \) of \(\emptyset \), if any, is \(s_\infty \) and so, \(s_\infty \notin {\text {inter}}_\gamma \) if such preimages exist. If a component K of \({\text {inter}}_\gamma \) has exactly two preimages \(K_1\) and \(K_2\) by the mapping \(\psi \), then from Fact c, we derive that the two cells share the same supremum and from Fact e, and the very definition of \(\#{\text {inter}}_m\), we see that the weight of K in \(\#{\text {inter}}_m\) is 2, which corresponds to the number of its preimages, or \(s=s_\infty \) and the empty set has no preimage. If the empty set has two or more preimages by \(\psi \), then \(\#{\text {inter}}_m=\infty \) (Fact e). If a component K of \({\text {inter}}_\gamma \) has three or more preimages by \(\psi \), these preimages share the same supremum (Fact c) and from Fact d we derive that \(\#{\text {inter}}_m=\infty \). We readily conclude that the number of cells of \(\mathcal {Q}_\gamma \) is upper bounded by \(1+\sum _{\emptyset \subset I\subseteq [1,m-1]}w_I\left| {\text {inter}}_{\gamma ,I}\right| \) where \(w_I=\min (2,\left| I\right| )\). By summing on all the connected components of \(\varGamma _{b_m}\), we derive that \(N_m^\prime \), the number of cells of \(\mathcal {Q}\), is upper bounded by \(\#{\text {inter}}_m+\left| {\text {CC}}(\varGamma _{b_m})\right| \) which achieves the proof.
Let us now prove the five facts stated above.
-
(a)
We demonstrate Fact a by contradiction. Suppose it exists K in \({\text {inter}}_{\gamma ,I}\), \(I\subseteq [1,m-1] \), and two distinct cells \(K_1\), \(K_2\) of \(\bigwedge _{i=1}^{m-1}\mathcal {P}_{b_{i}}\) such that \(K\cap K_1\ne \emptyset \) and \(K\cap K_2\ne \emptyset \). Let \(c_1\in K\cap K_1\) and \(c_2\in K\cap K_2\). Since \(K_1\ne K_2\), there exists \(i\in [1,m-1]\) such that
 . Then, the segment \([c_1,c_2]\) in \(\gamma \) contains a point \(c_3\in \varGamma _{b_i}\) which also belongs to K for K is connected. Then, on the one hand \(i\in I\) for \(c_3\in \varGamma _{b_i}\cap K\) and, on the other hand, \(c_1\), or \(c_2\), is in
. Then, the segment \([c_1,c_2]\) in \(\gamma \) contains a point \(c_3\in \varGamma _{b_i}\) which also belongs to K for K is connected. Then, on the one hand \(i\in I\) for \(c_3\in \varGamma _{b_i}\cap K\) and, on the other hand, \(c_1\), or \(c_2\), is in  , that is \(i\notin I\). Contradiction.
, that is \(i\notin I\). Contradiction. -
(b)
Suppose that the supremum s of the cell K of \(\mathcal {Q}_\gamma \) is not in any component of \({\text {inter}}_m\). Then, for any \(i\in [1,m-1]\), \(s\notin \varGamma _{b_i}\). In other words, for any \(i\in [1,m-1]\), s is in the open set
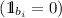 or in the interior of
or in the interior of  . Thus, there exists an open neighborhood U of s in the tile C which does not intersect any curve \(\varGamma _{b_i}\), \(1\le i < m\). Thereby, U is included in a cell of the partition \(\bigwedge _{i=1}^{m-1}\mathcal {P}_{b_i}\). Since \(s=\sup (K)\), there is no point t in \(\gamma \cap U\) such that \(t>s\). Thus, \(s=s_\infty \).
. Thus, there exists an open neighborhood U of s in the tile C which does not intersect any curve \(\varGamma _{b_i}\), \(1\le i < m\). Thereby, U is included in a cell of the partition \(\bigwedge _{i=1}^{m-1}\mathcal {P}_{b_i}\). Since \(s=\sup (K)\), there is no point t in \(\gamma \cap U\) such that \(t>s\). Thus, \(s=s_\infty \). -
(c)
Let \(K_1\), \(K_2\) be two cells of \(\mathcal {Q}_\gamma \) whose supremums are in \(K\in {\text {inter}}_\gamma \). Let \(K_3\) be the cell of \(\mathcal {Q}_\gamma \) which includes this component (Fact a). If s is not the infimum of K then there exists an interval [u, s], with \(u<s\), in \(K\subseteq K_3\) (for K is connected) and s is not the supremum of both \(K_1\) and \(K_2\). Contradiction.
-
(d)
Let \(K_1\), \(K_2\), \(K_3\) be three cells of \(\mathcal {Q}_\gamma \) that share the same supremum s. Since s belongs to at most one of these three cells, it is a limit point for the two others. For instance, assume that s is a limit point for \(K_1\) and \(K_2\). Let \(k\in [1,m-1]\) such that
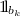 takes two distinct values on \(K_1\) and \(K_2\). For instance,
takes two distinct values on \(K_1\) and \(K_2\). For instance,  and
and  . Then, we can inductively build an infinite sequence \(c_1<c_2<\cdots<c_i<\cdots <s\) such that \(c_{2 i-1}\in K_1\) and \(K_{2 i}\in K_2\) for any \(i\ge 1\). In particular, we have
. Then, we can inductively build an infinite sequence \(c_1<c_2<\cdots<c_i<\cdots <s\) such that \(c_{2 i-1}\in K_1\) and \(K_{2 i}\in K_2\) for any \(i\ge 1\). In particular, we have 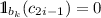 and
and  for any \(i\ge 1\). Then, \(c_{2 i-1}\notin \varGamma _{b_k}\) and \([c_{2 i-1}, c_{2*i}]\) intersects \(\varGamma _{b_k}\). Therefore, \({\text {inter}}_\gamma \) contains infinitely may components between \(c_1\) and s.
for any \(i\ge 1\). Then, \(c_{2 i-1}\notin \varGamma _{b_k}\) and \([c_{2 i-1}, c_{2*i}]\) intersects \(\varGamma _{b_k}\). Therefore, \({\text {inter}}_\gamma \) contains infinitely may components between \(c_1\) and s. -
(e)
We assume \(\#{\text {inter}}_m<\infty \). Let \(K_1\), \(K_2\) be two cells of \(\mathcal {Q}_\gamma \) that share the same supremum s. This supremum cannot be a limit point both in \(K_1\) and \(K_2\) otherwise we could make the same reasoning as in the previous item and concludes that \(\#{\text {inter}}_m=\infty \) which contradicts our assumption. So, s is an isolated point in one of the two cells, for instance \(K_1\) (therefore, \(s\in K_1\), \(s\notin K_2\) and s is a limit point in \(K_2\)). From Fact b, there exist a subset I of \([1,m-1]\) and a component K in \({\text {inter}}_{\gamma ,I}\) such that \(s\in K\). As in the proof of Fact b, we derive that there exists an open neighborhood U of s in C which does not intersect any curve \(\varGamma _{b_i}\), \(i\notin I\). Suppose that I is a singleton, say \(I=\{b_1\}\). Then, taking a point in \(K_2\cap U\) (recall that s is a limit point of \(K_2\)), we found that necessarily
 on \(K_2\), while
on \(K_2\), while  on \(K_1\), and
on \(K_1\), and  , \(i\ne 1\), coincides on \(K_1\) and \(K_2\). If \(s\ne s_\infty \), there exists a point u in \(\gamma \cap U\) greater than s. This point is not in \(K_1\) nor in \(K_2\) for \(s=\sup (K_1)=\sup (K_2)\). Thereby,
, \(i\ne 1\), coincides on \(K_1\) and \(K_2\). If \(s\ne s_\infty \), there exists a point u in \(\gamma \cap U\) greater than s. This point is not in \(K_1\) nor in \(K_2\) for \(s=\sup (K_1)=\sup (K_2)\). Thereby,  and
and  which is absurd. Thus, either \(s_\infty =s\in K_1\) or I is not a singleton. \(\square \)
which is absurd. Thus, either \(s_\infty =s\in K_1\) or I is not a singleton. \(\square \)
In the simplest case where the curve segments \(\varGamma _{b_m}\) all have one connected component and where the intersections are sets of points belonging to at most two curves, Formula 1 reduces to \(1+\left| \mathfrak {B}\right| +{I}\) where I is the number of intersection points between the curve segments \(\varGamma _{b_m}\). Furthermore, when projecting the partition \(\bigwedge _{i=1}^n\mathcal {P}_{b_i}\) on the torus \(\mathbb T\), the cells that touch the boundary of C are identified two by two, which decreases the number of cells in the partition. Unfortunately, it is difficult to count these cells in the general case.
3.3 The Convex Case
It seems plain that the structure of the dual should be simpler when the set S is convex compared to a set with a winding boundary. We could even hope that the digitizations coincide with the cells of the partition \(\bigwedge _{p\in \mathfrak {B}}\varGamma _p\), after sewing the boundary of the tile C, and with the connected regions of the torus \(\mathbb T\) delineated by the curve \(\varGamma \). Figure 4 annihilates this hope by exhibiting a convex object and one of its digitizations whose inverse image by the dual is not connected.
(a) A triangle and its toggling boundary. (b) The dual of the (filled) triangle. The four colored regions correspond to the same digitization: the horizontal pair. Red region: cell bc of the partition \(\bigwedge _{p\in \mathfrak {B}}\varGamma _p\). The red region is disconnected by the unique point of the cell abcd. Orange region: cell cd. Pink region: cell ae. (c) The configurations of the shifted triangle in the two red components. Since they are disconnected, it is not possible to continuously move to one configuration to the other without hurting a black toggling point. Note that the triangle could be slightly inflated so as to provide a strictly convex counterexample. (Color figure online)
Nevertheless, in this section we show that the structure of the sets \({\text {inter}}_{\gamma ,I}\) is simple when the set S is strictly convex and permits to obtain a quadratic bound for the complexity of the dual in terms of the grid boundary size (to be compare to the exponential bound of Proposition 1).
Proposition 3
We assume a convex quadrilateral structuring element M. Let \(n=\left| \mathfrak {B}\right| \). The number of Gauss digitizations of a strictly convex planar object up to a translation is upper bounded by
Proof
The proof invokes Lemma 3 which is stated and proved in the appendix. Let N be the digitization number. Thanks to Proposition 2, we have
From Lemma 3, we derive that, for any \(m\in [1,n]\), \(\gamma \in {\text {CC}}(\varGamma _{b_m})\), \(i\in [1,m-1]\),
Then,
Eventually, Eq. (2) turns into
It can easily be seen (from Lemma 2 for instance) that, for any convex curve \(\varGamma \) and any convex polygon P with c edges, the number of connected arcs in the intersection \({\varGamma \cap P}\) is upper bounded by c. Then, if we assume that the tile C is a convex quadrilateral, we straightforwardly obtain the desired bound. \(\square \)
The term \(4n^2\) in Proposition 3 comes down to \(n^2\) for sufficiently high resolutions because each curve \(\varGamma _{b_i}\) then have just one connected component instead of possibly 4 in the general case. Then, when S a disc of radius r, the result of Proposition 3 is close to the one in [7] which states that the number of digitizations of the disc is asymptotically \(4\pi r^2+O(r)\). As the ratio between the radius r and the size of the grid boundary is \(\pi /4\) for the disc, our upper bound in function of the radius r of the disc is asymptotically equivalent to \((16/\pi ^2)r^2\).
4 Conclusion
We present in this paper two upper bounds on the number of digitizations obtained from all the translated of a continuous object. The first one is exponential in the number of toggling object-boundary pixels and a generic example reaching this bound is given. The second one is based on the passage from the dual connected-component count to the curve intersection count which, if the curve is parameterized, comes down to count some equation solutions. In the convex case, the latter upper bound is shown to yield a quadratic digitization number in term of the grid boundary size. An example of a convex object is given where the set of translation parameter classes corresponding to a given digitization is not connected.
The perspectives of this work are first to explicit the second upper bound under assumptions less restrictive that the convexity, e.g. bounded curvature; then to study the combinatorics of the digitization under the rigid transformations and to propose an algorithm for the digitization generation.
Notes
- 1.
The “dual” term is an analogy with the algebraic dual because our construction transforms a set of binary images on a discrete set (
 ) in a labeled image on a set of transformations (the translations).
) in a labeled image on a set of transformations (the translations).
References
Baudrier, É., Mazo, L.: Curve digitization variability. In: Normand, N., Guédon, J., Autrusseau, F. (eds.) DGCI 2016. LNCS, vol. 9647, pp. 59–70. Springer, Cham (2016). doi:10.1007/978-3-319-32360-2_5
Berger, M.: Geometry, vol. 1 (1987)
Dorst, L., Smeulders, A.W.M.: Discrete Representation of Straight Lines. IEEE Trans. Pattern Anal. Mach. Intell. 6(4), 450–463 (1984). http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=4767550
Heath-Brown, D.: Lattice points in the sphere. Number Theory Prog. 2, 883–892 (1997)
Huxley, M.N.: The number of configurations in lattice point counting I. Forum Mathematicum 22(1), 127–152 (2010)
Huxley, M.N., Žunić, J.: On the number of digitizations of a disc depending on its position. In: Klette, R., Žunić, J. (eds.) IWCIA 2004. LNCS, vol. 3322, pp. 219–231. Springer, Heidelberg (2004). doi:10.1007/978-3-540-30503-3_17
Huxley, M.N., Žunić, J.D.: Different digitisations of displaced discs. Found Comput. Math. 6(2), 255–268 (2006). doi:10.1007/s10208-005-0177-y
Huxley, M.N., Zunić, J.D.: The number of \(N\)-point digital discs. IEEE Trans. Pattern Anal. Mach. Intell. 29(1), 159–161 (2007). doi:10.1109/TPAMI.2007.250606
Huxley, M.N., Zunić, J.D.: The number of different digital \(N\)-discs. J. Math. Imaging Vis. 56(3), 403–408 (2016). doi:10.1007/s10851-016-0643-y
Mazo, J.E., Odlyzko, A.M.: Lattice points in high-dimensional spheres. Monatshefte für Mathematik 110(1), 47–61 (1990)
Mazo, L., Baudrier, É.: Object digitization up to a translation, September 2016. preprint https://hal.archives-ouvertes.fr/hal-01384377
Nagy, B.: An algorithm to find the number of the digitizations of discs with a fixed radius. Electron. Notes Discr. Math. 20, 607–622 (2005). doi:10.1016/j.endm.2005.04.006
Žunić, J.D.: On the number of digital discs. J. Math. Imaging Vis. 21(3), 199–204 (2004). doi:10.1023/B:JMIV.0000043736.15525.ed
Žunić, J.D.: On the number of ways to occupy \(n\) lattice points by balls in \(d\)-dimensional space. J. Number Theor. 110(2), 396–402 (2004)
Acknowledgements
We thank Renan Lauretti for his idea to link the dual regions to the dual region border crossings in his study of the function graph dual.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix
A Convex Sets
The proof of Lemma 3 relies on the two following lemmas about convex sets that seem obvious at the first glance. Nevertheless, since we did not find any result related to these lemmas in the literature, we provide our own justifications of the two statements.
Lemma 1
(Chords of convex sets). Let [a, b] be a chord of the boundary \(\varGamma \) of a closed convex set S. If \([a,b]\nsubseteq \varGamma \), then \((ab)\cap S=[a,b]\) and \((ab)\cap \varGamma =\{a,b\}\).
Proof
Since \([a,b]\nsubseteq \varGamma \), the line (ab) does not support S at any point (the notion of supporting line of a convex set is exposed for instance in [2]). So, there exists two supporting lines of S at a and b that cross the line (ab). Then, \((ab)\cap S\) is included in [a, b]. Let \(c\in [a,b]\cap \varGamma \), \(c\ne a\). Applying the first part of the proof to the chord [a, c], we derive that \((ac)\cap S\subseteq [a,c]\) and, since \(b\in (ac)\cap S\), we conclude that \(b=c\). \(\square \)
Lemma 2
(Cuts of convex sets). Let a, b be two points of the boundary \(\varGamma \) of a closed convex set S. If \([a,b]\nsubseteq \varGamma \), then the open curve segments of \(\varGamma \), \(\sigma _1\), \(\sigma _2\), whose extremities are a and b are included in distinct open half-planes bounded by the line (ab).
Proof
Let \(H^-\) and \(H^+\) be the two open half-planes bounded by (ab). Since \([a,b]\nsubseteq \varGamma \), from Lemma 1, \((ab)\cap \varGamma =\{a,b\}\). Thereby, by connectivity, either \(\sigma _1\subset H^-\) or \(\sigma _1\subset H^+\) and \(\sigma _2\subset H^-\) or \(\sigma _2\subset H^+\). Suppose for instance that \(\sigma _1\subset H^-\) and \(\sigma _2\subset H^-\). Then, S, which is the connected subset of  bounded by \(\sigma _1\cup \sigma _2\cup \{a,b\}\) is included in \(H^-\cup (ab)\) and, since \((ab)\cap S=[a,b]\) from Lemma 1, \([a,b]\subset \varGamma \): contradiction. \(\square \)
bounded by \(\sigma _1\cup \sigma _2\cup \{a,b\}\) is included in \(H^-\cup (ab)\) and, since \((ab)\cap S=[a,b]\) from Lemma 1, \([a,b]\subset \varGamma \): contradiction. \(\square \)
Lemma 3
(Intersection of two segments of a convex curve). Let \(\varGamma \) be a Jordan curve whose interior is convex. Let \(\varGamma _1\) and \(\varGamma _2\) two disjoint closed segments of the curve \(\varGamma \) and \(\tau \) a vector of  . Then the intersection of \(\varGamma _1 \) and \(\tau +\varGamma _2\) is composed of none, one, two points or a line segment.
. Then the intersection of \(\varGamma _1 \) and \(\tau +\varGamma _2\) is composed of none, one, two points or a line segment.
Proof
Let p, q be two distinct points in \(\varGamma _1 \cap (\tau +\varGamma _2)\) if such a pair exists. We denote by \( \varSigma _1 \) the open segment of \( \varGamma _1 \) between p and q. Alike, \( \varSigma _2 \) is the open segment of \( \varGamma _2 \) between \(-\tau + p \) and \(-\tau + q \). We set \(\overline{\varSigma }_1=\varSigma _1\cup \{p,q\}\) and \(\overline{\varSigma }_2=\varSigma _2\cup \{p,q\}\). Firstly, we prove that \(\varSigma _1\cup (\tau +\varSigma _2)\) is a straight line segment whenever it contains more than two points. First case: \(\varSigma _1\cup (\tau +\varSigma _2)\subseteq (pq)\). Then, since \(\overline{\varSigma }_1\) and \(\overline{\varSigma }_2\) are connected and \(\varGamma \) is simple, \(\overline{\varSigma }_1=\overline{\varSigma }_2=[p,q]\). Second case: \(\exists x\in \big (\varSigma _1\cup (\tau +\varSigma _2)\big )\setminus (pq)\). For instance, we assume \(x\in \varSigma _1\setminus (pq)\). By Lemma 2, \(\varSigma _1=\varGamma \cap H_1\), where \(H_1\) is the open half-plane bounded by the line (pq) and containing x, and \(-\tau +p\) is in  . Then, it can easily be seen that \(-\tau +H_1\) is the open half-plane bounded by the line joining \(-\tau +p\) and \(-\tau +q\) and including p. Thanks to Lemma 2, we derive that \(\varSigma _2\) does not intersect \(-\tau +H_1\). Thus, \(\tau +\varSigma _2\) does not intersect \(H_1\). In particular, \((\tau +\varSigma _2)\cap \varSigma _1=\emptyset \). This achieves the first part of the proof. Now, let r be a point in \(\varGamma _1 \cap (\tau +\varGamma _2)\) which is not in \(\varSigma _1\) (if such a point exists). For instance, p belongs to the segment of \(\varGamma _1\) between q and r. Then, the first part of the proof, applied to the points q and r, implies that \(\varGamma _1 \cap (\tau +\varGamma _2)\) includes the segments [q, r]. We straightforwardly concludes that either the intersection of \(\varGamma _1 \) and \(\tau +\varGamma _2\) is composed of at most two points or it is a line segment. \(\square \)
. Then, it can easily be seen that \(-\tau +H_1\) is the open half-plane bounded by the line joining \(-\tau +p\) and \(-\tau +q\) and including p. Thanks to Lemma 2, we derive that \(\varSigma _2\) does not intersect \(-\tau +H_1\). Thus, \(\tau +\varSigma _2\) does not intersect \(H_1\). In particular, \((\tau +\varSigma _2)\cap \varSigma _1=\emptyset \). This achieves the first part of the proof. Now, let r be a point in \(\varGamma _1 \cap (\tau +\varGamma _2)\) which is not in \(\varSigma _1\) (if such a point exists). For instance, p belongs to the segment of \(\varGamma _1\) between q and r. Then, the first part of the proof, applied to the points q and r, implies that \(\varGamma _1 \cap (\tau +\varGamma _2)\) includes the segments [q, r]. We straightforwardly concludes that either the intersection of \(\varGamma _1 \) and \(\tau +\varGamma _2\) is composed of at most two points or it is a line segment. \(\square \)
B Examples and Counterexamples
1.1 B.1 Building Examples Without Proper Congruent Digitizations in the Image of the Dual
Let u and v be two vectors in \([0,1)^2\) such that the sets \(u+S\) and \(v+S\) have distinct but congruent digitizations. Then, there exists an integer vector w, \(w\ne 0\), such that  . Let p be a point in the digitization core. Then,
. Let p be a point in the digitization core. Then,  and
and  . Therefore,
. Therefore,  and
and  , which can be rewritten as
, which can be rewritten as  and
and  . Then, at least one of the vectors \(w+v\) or \(-w+u\) has one of its coordinates which is negative. We derive that if there exists a point in the digitization core which is maximal in S for both coordinates then there is no proper congruent digitizations in the dual.
. Then, at least one of the vectors \(w+v\) or \(-w+u\) has one of its coordinates which is negative. We derive that if there exists a point in the digitization core which is maximal in S for both coordinates then there is no proper congruent digitizations in the dual.
1.2 B.2 Building Toric Partitions in One-to-one Correspondence with the Power Set of the Toggling Boundary
In this section, we exhibit a way to modify the boundary of the set S in order to ensure that any subset of the toggling boundary is represented in the dual. To do so, we move along \(\mathcal B\), ordered in the same way as in Definition 1. Then, a new boundary is built thanks to the approximations of the Hilbert filling curve: the segment of \(\varGamma \) intersecting the n-th cell of \(\mathcal B\) is replaced by a n-th approximation of the Hilbert filling curve \(H_n\) (extended at its extremities to ensure the continuity of the boundary). We consider the family of binary partitions \(\mathcal {P}_n\) of the unit square that comes with the curves \(H_n\). We claim that each curve \(H_{n+1}\) crosses each cell of the partition \(\bigwedge _{i=1}^n\mathcal P_i\) so that the size of the final torus partition is \(2^N\) where N is the cardinal of the toggling boundary. To justify our claim, we divide the unit square in a family of \(2^n\times 2^n\) small squares \((K_{i,j}^n)_{1\le i,j\le 2^n}\) (\(n\ge 0\)) whose sizes are \(\frac{1}{2^n}\times \frac{1}{2^n}\). It can be seen that on the one hand, the Hilbert curve \(H_n\) passes through the center of each of the squares \(K_{i,j}^n\) and, on the other hand, does not intersect any of the interior of the squares \(K_{i,j}^{n+1}\) (\(H_0\) is just the center of the unit square). Thereby, the partition \(\bigwedge _{i=1}^n\mathcal {P}_i\) is coarser than the partition \(\{K_{i,j}^{n+1}\mid {1\le i,j<n}\}\) (the boundaries of the squares \(K_{i,j}^k\) are assigned to the cells so as to coincide with \(\mathcal {P}_n\)). Since \(H_{n+1}\) passes through the center of each of the squares \(K_{i,j}^{n+1}\), it passes in each cell of \(\bigwedge _{i=1}^n\mathcal {P}_i\) which gives the claim.
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Mazo, L., Baudrier, É. (2017). Study on the Digitization Dual Combinatorics and Convex Case. In: Kropatsch, W., Artner, N., Janusch, I. (eds) Discrete Geometry for Computer Imagery. DGCI 2017. Lecture Notes in Computer Science(), vol 10502. Springer, Cham. https://doi.org/10.1007/978-3-319-66272-5_29
Download citation
DOI: https://doi.org/10.1007/978-3-319-66272-5_29
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-66271-8
Online ISBN: 978-3-319-66272-5
eBook Packages: Computer ScienceComputer Science (R0)





 . Then, the segment
. Then, the segment  , that is
, that is 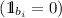 or in the interior of
or in the interior of  . Thus, there exists an open neighborhood U of s in the tile C which does not intersect any curve
. Thus, there exists an open neighborhood U of s in the tile C which does not intersect any curve 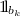 takes two distinct values on
takes two distinct values on  and
and  . Then, we can inductively build an infinite sequence
. Then, we can inductively build an infinite sequence 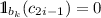 and
and  for any
for any  on
on  on
on  ,
,  and
and  which is absurd. Thus, either
which is absurd. Thus, either 
 ) in a labeled image on a set of transformations (the translations).
) in a labeled image on a set of transformations (the translations).