Recognition of Digital Polyhedra with a Fixed Number of Faces Is Decidable in Dimension 3

Abstract

We consider a conjecture on lattice polytopes $Q\subset \mathbb {R}^d$ (the vertices are integer points) or equivalently on finite subsets $S\subset \mathbb {Z}^d$, Q and S being related by $Q\cap \mathbb {Z}^d = S$ or $Q=\mathrm {conv (S)}$: given the vertices of Q or the list of points of S and an integer n, the problem to determine whether there exists a (rational) polyhedron $P\subset \mathbb {R}^d$ with at most n faces and verifying $P \cap \mathbb {Z}^d= S$ is decidable.

In terms of computational geometry, it’s a problem of polyhedral separability of S and $\mathbb {Z}^d \setminus S$ but the infinite number of points of $\mathbb {Z}^d \setminus S$ makes it intractable for classical algorithms. This problem of digital geometry is however very natural since it is a kind of converse of Integer Linear Programming.

The conjecture is proved in dimension $d=2$ and in arbitrary dimension for non hollow lattice polytopes Q [6]. The purpose of the paper is to extend the result to hollow polytopes in dimension $d=3$. An important part of the work is already done in [5] but it remains three special cases for which the set of outliers can not be reduced to a finite set: planar sets, pyramids and marquees. Each case is solved with a particular method which proves the conjecture in dimension $d=3$.

1 Introduction

The recognition of digital primitives is a classical task of pattern recognition and digital geometry. It is usually question of recognizing digital primitives such as digital straight segments, conics or more generally some families of shapes in several dimensions. These problems can be stated in the following terms:

Problem 1

(Recognition $(d,\mathscr {F},S)$ ). Input: Let $\mathscr {F}$ be a family of subsets F of $\mathbb {R}^d$ and S be a subset of $\mathbb {Z}^d$.

Output: Does there exists a set F of $\mathscr {F}$ verifying $F\cap \mathbb {Z}^d = S$?

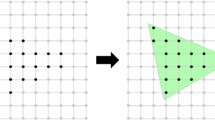
We focus in this paper on the problem [Recognition$(d,\mathscr {F},S)$] where the family $\mathscr {F}$ is a set of polyhedra with a prescribed number of faces. By denoting $\mathscr {P}_n$ the set of polyhedra of $\mathbb {R}^d$ defined as intersections of at most n linear half-spaces (by convention, a polyhedron of $\mathscr {P}_n$ is in $\mathscr {P}_{n+1}$), we investigate [Recognition$(d,\mathscr {P}_n,S)$] (Fig. 1).

Fig. 1.

An instance of [Recognition$(d,\mathscr {P}_n,S)$] is the given of dimension d (here $d=2$), a number of faces n (here $n=4$) and a finite set of integer points. The problem is to find a polyhedron $P\subset \mathscr {P}_n$ with the prescribed number of faces containing S but no other integer point: $P\cap \mathbb {Z}^d=S$. The problem can be restated as a problem of polyhedral separability [PolyhedralSeparability$(d,n,S,\mathbb {Z}^d \setminus S)$] of S and its complementary $\mathbb {Z}^d \setminus S$ by a polyhedron of $\mathscr {P}_n$.

This problem [Recognition$(d,\mathscr {P}_n,S)$] is mentioned in the review of open questions in digital geometry [1]. Until 2015, it has been only investigated in dimension 2 with specific polyhedra such as squares and rectangles [4, 7, 10]. The difficulty of [Recognition$(d,\mathscr {P}_n,S)$] is that even its decidability is not straightforward. By definition, [Recognition$(d,\mathscr {P}_n,S)$] enters in the class of problems of polyhedral separability investigated in Computational Geometry:

Problem 2

(PolyhedralSeparability(d, n, S, T)).

Input: A dimension d, an integer n, a set $S\subset \mathbb {R}^d$ of inliers and a set $T\subset \mathbb {R}^d$ of outliers.

Output: Find a polyhedron $P\subset \mathscr {P}_n$ such that all the points of S and none point of T are in P: $S\subset P \subset \mathbb {R}^d \setminus T$.

The problem [Recognition$(d,\mathscr {P}_n,S)$] can be stated as [PolyhedralSeparability$(d,n,S,\mathbb {Z}^d \setminus S)$] where the set of outliers T is the complementary of S in $\mathbb {Z}^d$. For finite sets S and T, polyhedral separability can be solved in linear time if $n=1$ [8] or in $O((|S|+|T|) \ log (|S|+|T|))$ if $d=2$ for any n [3]. It becomes NP-complete in arbitrary dimension even with $n=2$ [9]. With any finite sets S and T, the decidability of [PolyhedralSeparability(d, n, S, T)] is completely straightforward but it is no more the case with the infinite set of outliers $T= \mathbb {Z}^d \setminus S$ considered for [Recognition$(d,\mathscr {P}_n,S)$]. The problem is intractable for classical algorithms of polyhedral separability.

This problem is however interesting because it is a kind of converse problem of Integer Linear Programming [11]. In ILP, the input is a set of n linear inequalities and the purpose is to provide the integer points which satisfy them. In [Recognition$(d,\mathscr {P}_n,S)$], we have the set of integer points and we want to recover a prescribed number of inequalities which characterize it. Although the geometry of numbers provides a powerful framework to work on lattice polytopes, the classical algorithms of this field do not allow to solve directly [Recognition$(d,\mathscr {P}_n,S)$].

We can however imagine a direct strategy by reducing the infinite set of outliers $T= \mathbb {Z}^d \setminus S$ to the subset of its minimal elements according to a partial order relation “is in the shadow of” [5, 6]. The minimal elements of $\mathbb {Z}^d \setminus S$ are called the lattice jewels of S while the non minimal elements do not need to be taken into account. This approach allows to prove the decidability of the problem if the number of lattice jewels is finite. It holds in dimension $d=2$ or in arbitrary dimension, if the polytope $Q=\mathrm {conv}(S)$ is not hollow (its interior contains at least an integer point) [6]. In dimension $d=3$, the hollow 3-polytopes with a finite number of lattice jewels are characterized in [5]. For them, [Recognition$(3,\mathscr {P}_n,S)$] is also decidable. In this dimension, it just remains the cases of the hollow 3-polytopes with an infinite number of lattice jewels (Fig. 2), namely if

• S is coplanar,

• or S is a pyramid of lattice height 1, namely the lattice width of S is 1 and one of the two consecutive planar sections of S is reduced to a point,

• or S is a marquee: the lattice width of S is 1 and one of the two consecutive planar sections of S in the thin direction is reduced to a segment.

Fig. 2.

The three types of 3-polytopes S with infinitely many lattice jewels (thus the decidability of [Recognition$(3,\mathscr {P}_n,S)$] in dimensions $d=3$ is an open question). On the left, S is planar. In the middle, S is a pyramid of lattice height 1. On the right, the lattice width of S is again 1 but one of its consecutive planar sections in the thin direction is reduced to a segment. We refer to this case as a (circus) marquee.

In both cases, we provide an algorithm to decide [Recognition$(3,\mathscr {P}_n,S)$] in a finite time. It solves the last cases allowing to prove the following theorem:

Theorem 1

The problem [Recognition$(3,\mathscr {P}_n,S)$] is decidable.

Section 2 is devoted to the easiest cases of planar sets and pyramids while marquees are investigated in Sect. 3.

2 Decidability for Planar Sets and Pyramids

For planar set S of $\mathbb {Z}^3$, the strategy to solve [Recognition$(3,\mathscr {P}_n,S)$] is to consider the problem [Recognition$(2,\mathscr {P}_n,S)$] in the sublattice of $\mathbb {Z}^3$ containing S. If [Recognition$(2,\mathscr {P}_n,S)$] admits no solution, neither [Recognition$(3,\mathscr {P}_n,S)$]. If [Recognition$(2,\mathscr {P}_n,S)$] has a solution P, then we have to expand P in a 3-polytope without adding any integer point and by preserving the number of faces.

2.1 Polytope’s Expansion in Higher Dimensions

The following lemma is not easy to find in the state of the art may be while its dual is trivial.

Lemma 1

Any polytope P of $\mathbb {R}^d$ with $n\ge d+2$ faces is the planar section of a polytope of $\mathbb {R}^{d+1}$ with the same number n of faces (Fig. 3).

Fig. 3.

According to Theorem 1, any polytope of $\mathbb {R}^d$ with at least $d+2$ faces is the planar section of a polytope of $\mathbb {R}^{d+1}$with the same number of faces.

Proof

Although its dual formulation is not far to be trivial, this sketch of proof (Fig. 4) is necessary to follow the proof of Lemma 2.

We assume that P is of full dimension in $\mathbb {R}^d$. Otherwise, we proceed by induction. Since P has n faces, the polar polytope $P^*$ of P is the convex hull of a finite set $A\subset \mathbb {R}^d$ of n points (we consider as origin O or pole an interior point of P) [12]. We can elevate the points of A in a set $A'$ of full dimension in $\mathbb {R}^{d+1}$. The intersection of the convex hull of $A'$ with the vertical line passing through the origin is not reduced to a point (since the interior of the projection of the convex hull of A contains the origin). It’s a segment. If it does not contain the origin, we can translate $A'$ to obtain this property. It provides a polytope $(P^{+})^*$. Its polar $P^+$ is a polytope with n faces and P as planar section (Fig. 4).    $\square$

Fig. 4.

In (a), we consider a d-polytope with n faces and $n\ge d+2$. In (b), we introduce its polar polytope $P^*$ for instance with respect to the barycenter of P. In (c), we introduce the elevation lines where we can move the vertices of $P^*$. In (d), we provide a vertical expansion of $P^*$ but the origin is not in the $d+1$-polytope. In (e), we translate it vertically so that the origin enters in its interior. In (f), we obtain a $d+1$-polytope $(P^+)^*$ whose polar polytope has n faces and P as planar section.

There is n degrees of freedom which allow to build an expanded polyhedron with complementary constraints. We express it in the following lemma which holds in general dimension but is given here for $d=2$.

Lemma 2

Given a polytope $P\subset \mathbb {R}^2$ with n non parallel faces ($n\ge 4$), embedded in the plane $z=0$ and a point X with $z_X\not = 0$, there exists a pyramid $P^X$ with n faces, X as apex, a basis as close as we want from P and P as planar section of height $z=0$.

Proof

The construction follows from the proof of Lemma 1. The property that P has no parallel faces means that there are no collinear vertices in its polar polytope. We denote A the set of the vertices of $P^*$. According to Carathéodory Theorem, we can remove a vertex of A (it remains at least 3 vertices) and provide a reduced set of vertice $A'$ with the origin in its convex hull. The condition of non collinearity of the points of A guarantees that the origin is in the interior of the convex hull of $A'$. Then we elevate the points of $A'$ at level $+1$ and send the point of $A\setminus A'$ with a negative height h. This elevation puts the points in the position of the vertices of a pyramid $P^{*h} \subset \mathbb {R}^3$. There is a limit value $h_0$ for which the origin enters in the pyramid $P^{*h}$. Its polar polyhedron with $h<h_0$ is a pyramid $P^h$ with the prescribed horizontal section. We can change the apex of $P^h$ with linear transformations preserving the horizontal plane and send it to X. And as h is tending to $-\infty$, the lower face of the solution $P^h$ -its basis- is becoming closer and closer and as close as we want from P.   $\square$

2.2 Proof of Decidability for Planar Sets

We prove the decidability of [Recognition$(3,\mathscr {P}_n,S)$] for planar subsets of $\mathbb {Z}^3$:

Lemma 3

If S is a finite planar set of $\mathbb {Z}^3$ and $n\ge 4$, [Recognition$(3,\mathscr {P}_n,S)$] is decidable.

Notice that polyhedra with only $n=2$ faces and a finite intersection with the lattice $\mathbb {Z}^3$ exist but they are a bit pathological (they are planes with irrational normal directions and an intersection with the lattice reduced to a point).

Proof

If S is reduced to a point or to a segment, the answer is positive for $n\ge 4$. Then we assume that the dimension of S is 2. We consider the sublattice of a support plane $H_S$ of S. According to [5], [Recognition$(d,\mathscr {P}_n,S)$] is decidable in dimension $d=2$. It allows to determine whether there exists a two dimensional polyhedron $P\subset H_S$ with n faces separating S from the other integer points. If there is no polyhedron of $\mathbb {R}^2$ solution in the sublattice, there exists no solution in $\mathbb {R}^3$. If there is a polyhedron solution P, as S is finite, P is a polytope (the only unbounded polyhedra of $\mathbb {R}^2$ having a finite intersection with $\mathbb {Z}^2$ have necessarily a recession cone reduced to an irrational direction. It’s only possible if S is a singleton). Then Lemma 1 allows to expand it in dimension 3. It provides a solution of [Recognition$(3,\mathscr {P}_n,S)$].    $\square$

2.3 Proof of Decidability for Pyramids

We prove the decidability of [Recognition$(3,\mathscr {P}_n,S)$] for pyramids of $\mathbb {Z}^3$ of lattice height 1:

Lemma 4

If S is an pyramid of $\mathbb {Z}^3$ of lattice height 1, [Recognition$(3,\mathscr {P}_n,S)$] is decidable (we assume $n\ge 4$).

Proof

Up to an unimodular affine isomorphism preserving $\mathbb {Z}^3$, we can assume that S is the union of a basis B in the horizontal plane $z=0$ and the point (0, 0, 1). We decompose the pyramid in its basis that we denote B and its vertex y. The basis B is a planar set embedded in a plane $H_B$. As for Lemma 3, we consider the problem [Recognition$(2,\mathscr {P}_n,B)$] in the sublattice of the plane $z=0$. If [Recognition$(2,\mathscr {P}_n,B)$] is not feasible, neither [Recognition$(3,\mathscr {P}_n,S)$]. Conversely if [Recognition$(2,\mathscr {P}_n,B)$] has a solution P, we have to consider the parallelism of the faces of P in order to provide a three dimensional solution.

Fig. 5.

In (a), we consider a pyramid as instance of [Recognition$(3,\mathscr {P}_4,S)$] of basis B. In (b), we provide a two-dimensional solution P of [Recognition$(2,\mathscr {P}_4,B)$] but its faces are parallel, which does not allow to use Lemma 2. In (c), we can pertub P in $P'$ in order to break the faces parallelism by remaining between P and $(1+\epsilon )P$. Then Lemma 2 allows to expand $P'$. The only new integer point in the expanded polyhedron is the apex of the pyramid.

If P has no parallel faces, then Lemma 2 allows to expand with a finite number of computations P in a pyramid having (0, 0, 1) as apex and a basis as close as we want from the plane $z=0$. It allows to provide solutions whose only integer points are (0, 0, 1) and the ones of B. In other words, the expansion does not introduce any new integer point in the polytope. It proves that [Recognition$(3,\mathscr {P}_n,S)$] is feasible.

If P has parallel faces, we can perturb it to avoid the difficulty that it occurs. By definition, a solution P of [Recognition$(2,\mathscr {P}_n,B)$] contains all the points of B and none point of $\mathbb {Z}^2 \setminus B$. As it is compact, its minimal distance to $\mathbb {Z}^2 \setminus B$ is strictly positive. It means that there exists an $\epsilon >0$ for which P and $(1+\epsilon )P$ are both solutions of [Recognition$(2,\mathscr {P}_n,B)$]. The space between P and $(1+\epsilon )P$ allows to move vertices and break the parallelism of the faces (Fig. 5).

With a finite number of computations, we have reduced [Recognition$(3,\mathscr {P}_n,S)$] to [Recognition$(2,\mathscr {P}_n,B)$] which is a decidable problem [6].    $\square$

3 Decidability for Marquees

The approach to prove the decidability of [Recognition$(3,\mathscr {P}_n,S)$] for marquees can not be done just by considering its basis. Up to an affine isomorphism of $\mathbb {Z}^d$ sending S in a reference position, we can assume that the set S is covered by the two consecutive planes $z=0$ and $z=1$ and that the section $S_1$ of S is a segment containing at least two integer points on the line passing through (0, 0, 1) in the direction x. The section of S in the lower plane $z=0$ is denoted $S_0$. We are interested in the width $\mathrm {width}_y(S_0)$ of $S_0$ in the y direction. We decompose the proof of the decidability of [Recognition$(3,\mathscr {P}_n,S)$] for marquees according to the value of the width $\mathrm {width}_y(S_0)$:

• if $\mathrm {width}_y(S_0)=0$, the marquee S is a planar set (previously solved).

• if $\mathrm {width}_y(S_0)=1$, the basis of the marquee is reduced to two consecutive segments in the x direction. It is a particular case to which we refer as a prism (Fig. 6).

• if $\mathrm {width}_y(S_0)\ge 2$, we have a general case which requires some specific work.

Fig. 6.

In (a), we consider a prism S contained by three lines in the x direction and passing through the points (0, 0, 0) (red), (0, 1, 0) (blue) and (0, 1, 0) (green). In (b) we introduce a vertex Q (red) on a line in the x direction passing through the interior of the prism. We build a tetrahedron $T_Q$ containing S. In (c), we notice that by construction, the spike (the right part of the tetrahedron in red) can not contain any integer point. By choosing Q far enough, we can guarantee that the tetrahedron does not contain other integer points than the ones of the prism. (Color figure online)

3.1 Decidability for Prisms

The problem for prisms is particular because there are three lines of lattice jewels (the three lines in the x direction passing through the points $(0,-1,1)$, $(0,1,-1)$ and (0, 1, 1)) but it is easy to solve. They are intersections of a tetrahedron with the lattice:

Lemma 5

If $S\subset \mathbb {Z}^3$ is a prism namely a finite set unimodularly equivalent to the union of three segments in the x direction passing through the three points (0, 0, 0), (0, 1, 0) and (0, 0, 1), then [Recognition$(3,\mathscr {P}_n,S)$] is feasible for any $n\ge 4$.

Proof

Notice that the notion of prism has here a very precise meaning. We introduce a vertex Q on a line in the x direction crossing the interior of the prism. Then we consider the tetrahedron containing S, with Q as apex and the plane of the opposite face of Q in the prism as basis (Fig. 6). We choose a first position of $Q_0$. The corresponding tetrahedron $T_{Q_0}$ might contain a finite number of unwanted integer points (the important point is here that it is finite). Then we push Q far enough to remove these integer points from the tetrahedron $T_Q$. The key-point is that by driving away the point Q in the x direction, the spike is increasing but by construction, it does not contain any integer point. The rear part of the tetrahedron is decreasing. It means that by choosing Q far enough, we can exclude all the unwanted integer points from $T_Q$.

3.2 Strategy for General Marquees

It remains to establish the decidability of [Recognition$(3,\mathscr {P}_n,S)$] for the general marquees.

Lemma 6

If $S\subset \mathbb {Z}^3$ is a marquee and not a prism, then [Recognition$(3,\mathscr {P}_n,S)$] is decidable.

Before sketching a proof of Lemma 6, let us consider the particular case where the basis $S_0$ is of dimension 1. The marquee is made of two segments whose convex hull is a tetrahedron. In this case, the convex hull of S is a solution of [Recognition$(3,\mathscr {P}_n,S)$] for any $n\ge 4$. In the remaining case, a first result provides a localization of an infinite set of the lattice jewels of S (Fig. 7).

Lemma 7

For a finite marquee $S\subset \mathbb {Z}^3$ which is not a prism, with a non degenerated basis and placed in the reference position, we denote $T^-=\{ (k,-1,1) | k\in \mathbb {Z}\}$ and $T^+=\{ (k,1,1) | k\in \mathbb {Z}\}$ (Fig. 7). We have two properties:

• For any $k\in K$, the points (k, 1, 1) and $(k,-1,1)$ are lattice jewels of S.

• The set of the other jewels $T^0=\mathrm {jewels}(S) \setminus (T^- \cup T^+ )$ is finite.

Fig. 7.

On the left a marquee which is not a prism and on the right, the sets of points $T^-$ and $T^+$ are the two main sets of lattice jewels (with a finite number of other integer points not colored here).

The proof of Lemma 7 is based on the same arguments of compacity than the ones used in [5] but due to the lack of space, it is absent from the paper.

Let us prove now Lemma 6 in the case of a basis $S_0$ of dimension 2:

Proof

The approach provided in [5, 6] allows to reduce [Recognition$(3,\mathscr {P}_n,S)$] to [PolyhedralSeparability$(3,n,S,\mathrm {jewels(S)})$]. With Lemma 7, we rewrite it [Poly hedralSeparability(3, n, S,  $T^0 \cup T^-\cup T^+)$]. Then the strategy is to process differently with the constraints coming from S and $T^0$ than for the ones excluding the points of $T^-$ and $T^+$.

As $T^0$ is finite, the problem [PolyhedralSeparability$(3,n,S,T^0)$] is decidable. The first key point is to decompose [PolyhedralSeparability$(3,n,S,T^0)$] in n instances [PolyhedralSeparability$(3,n,S,T_i)$] with an index i going from 1 to n where the sets $T_i$ define a partition of T. We notice that any solution P of [PolyhedralSeparability$(3,n,S,T^0)$] is the intersection of n half-planes $H_i$ respectively solutions of some instances [PolyhedralSeparability$(3,n,S,T_i)$] where the sets $T_i$ define a partition of T. Conversely, since any solution can be decomposed in this way, our strategy is to consider all the partitions of $T^0$ in sets $T_i$. Given such a partition, each one of the n half-space $H_i$ has to be chosen in a set of half-spaces $K_i$ defined by the linear constraints expressing [PolyhedralSeparability$(3,n,S,T_i)$]. By denoting $a_ix +b_i y + c_i z\le h_i$ an equation of the half-space $H_i$, the set $K_i$ is a convex cone defined by the linear inequalities $a_iu +b_i v + c_i w\le h_i$ where (u, v, w) is in S and $a_iu' +b_i v' + c_i w'> h_i$ where $(u',v',w')$ is in $T_i$. Choosing the n half-spaces $H_i$ in $K_i$ guarantees that their intersection contains S and no point of $T^0$. The separation from S and $T^0$ being already taken into account, it remains to add the constraints of exclusion of the points of $T^-$ and $T^+$.

The restriction of $H_i$ to the lines $z=1$ and $y=\delta$ with $\delta =\pm 1$ (these two lines contain respectively $T^-$ and $T^+$) is given by the linear inequalities $H_i: a_i x +b_i \delta + c_i\le h_i$. Our task is to determine coefficients $a_i$, $b_i$, $c_i$ and $h_i$ in each $K_i$ so that no integer $x\in \mathbb {Z}$ with $\delta =+1$ or $-1$ satisfies the n conditions.

The sets $K_i$ are polyhedral cones in the space of dimension 4 of coordinates $(a_i, b_i, c_i, h_i)$. They can be described by their three sections by the hyperplanes $a_i=1$, $a_i=0$ or $a_i=-1$. The section of $K_i$ with the hyperplane $a_i=\alpha$ is denoted $K_i ^\alpha$ with $\alpha =-1$ or 0 or $+1$.

For $a_i=1$, the linear inequality becomes $H_i: x \le h_i -b_i \delta - c_i$ with linear constraints on the coefficients $h_i$, $b_i$ and $c_i$. For $a_i=0$, we have $H_i: 0 \le h_i -b_i \delta - c_i$ and for $a_i=-1$, $x\ge b_i \delta + c_i - h_i$. Our problem is to decide if we can choose the coefficients $a_i$ equal to $-1$, 0 or 1 and the coefficients $h_i$, $b_i$ and $c_i$ so that we can exclude all the points of $T^-$ and $T^+$ namely all the integers x with $\delta \in \{ -1 , 1\}$. We can decompose again the problem in the following questions:

• 1. given $K_i$, does there exist an half-space in $K_i ^0$ excluding all the points of $T^+$? of $T^-$? of both?

• 2. given $K_i ^\alpha$ and $K_{j} ^{-\alpha }$ with $i\not = j$, does there exist a pair of half-spaces in $K_i ^\alpha \times K_{j} ^{-\alpha }$excluding all the points of $T^+$? of $T^-$? of both? ($\alpha$ and $-\alpha$ because their orientation in the direction x should not be the same)?

• 3. given $K_i ^\alpha$, $K_{j} ^{-\alpha }$ and $K_{j'} ^{-\alpha }$ with different indices, does there exist a triplet of half-spaces excluding $T^-$ and $T^+$?

• 4. same questions with a pair excluding $T^+$ and a pair excluding $T^-$, but it can be reduced to the second question.

There is no reason to increase the size of the tuple considered in these questions, because if three intervals of the form $]\infty , \beta ]$ and $[\gamma , +\infty [$ and $[\gamma ' , +\infty [$ are excluding the integers, one of them is redundant. Then if we cannot exclude $T^+$ (or $T^-$) with two half-spaces, we cannot exclude them at all.

The case 1 is solved by comparing $h_i -b_i \delta - c_i$ to 0 with $\delta =+1$ for $T^+$ and $\delta =-1$ for $T^-$.

Let us focus now on the case 2. The equation of $H_i$ can be rewriten $x\le -b_i \delta + d_i$ with $d_i=h_i-c_i$ for $H_i \in K_i ^{+1}$ and $x\ge b_{j} \delta - d_{j}$ for $H_ {j}\in K_{j} ^{-1}$ with $d_{j}=h_{j}-c_{j}$. By replacing the coordinates c and h by the coordinate $d=h-c$, we proceed to a projection of the convex sets $K_{i} ^{\alpha }$. Its image by this projection in the space of parameters (b, d) is denoted $K _{i} ^{\prime \alpha }$. It is a two-dimensional convex set described by a finite number of inequalities which can be obtained from the inequalities characterizing $K_{i} ^{\alpha }$ by Fourier-Motzkin elimination.

We notice now that two constraints issued from $K_{i} ^{+1}$ and $K_{j} ^{-1}$ exclude $T^+$ if and only if there is no integer x verifying $b_{j} \delta - d_{j} \le x \le -b_i \delta + d_i$ for $\delta =+1$. We can determine the existence of such pair of points $(b_i,d_i)\in K _{i} ^{\prime +1}$ and $(b_j,d_j)\in K _{j} ^{\prime -1}$ by computing the maximum $\mathrm {max _+} ^{+1}_i$ and $\mathrm {max_+} ^{-1}_j$ of $b-d$ for $(b_i,d_i)\in K _{i} ^{\prime +1}$ and $(b_j,d_j)\in K _{j} ^{\prime -1}$. It follows that $T^+$ can be excluded by a pair of constraints coming from $K_{i} ^{+1}$ and $K_{j} ^{-1}$ if and only if the interval $[ \mathrm {max_+} ^{+}_j, -\mathrm {max_+} ^{+} _i ]$ does not contain any integer. This last question can be solved by Linear Programming (a similar approach holds for $T^-$ with $-b-d$ instead of $b-d$) (Fig.  8).

Fig. 8.

In the cases (2) and (2’), excluding all the outliers of $T^+$ with two half-spaces in $K_i ^{+1}$ and $K_{j} ^{ -1}$ is equivalent with finding a pair of points $(b_i, d_i)\in -K_i ^{\prime +1}$ and $(b_j,d_j)\in K_{j} ^{\prime -1}$ with no integer x verifying $b_{j} - d_{j} \le x \le -b_i + d_i$. It’s not possible in (2) because there is a diagonal line $b-d=x \in \mathbb {Z}$ with $K_{j} ^{\prime -1}$ above and $- K_{i} ^{\prime +1}$ below. It is possible in (2). This possibility is determined by the extreme points in the diagonal direction namely the result of the comparison of $\lceil \mathrm {max_+} ^{+}_j \rceil$ and $-\mathrm {max_+} ^{+} _i$. In the cases (3) and (3’), we deal with the possibility to exclude all the outliers of $T^-$ and $T^+$ with only three constraints coming from the sets $K_i ^{+1}$, $K_j ^{-1}$ and $K_{j'}^{-1}$. We can compute a quadrant Q determined by the extreme points of $K_j ^{\prime -1}$ and $K_{j'}^{\prime -1}$ and determine its intersection with $K_i ^{\prime +1}$. The outliers of $T^- \cup T^+$ can all be excluded in this manner iff the intersection is non empty (as in (3) and not in (3’)).

We end the proof with the case 3. In order to determine whether three constraints coming from $K _i ^{\prime +1}$, $K _{j} ^{\prime -1}$ and $K _{j'} ^{\prime -1}$ can exclude $T^-$ and $T^+$, we use Linear Programming in the same manner. We compute again the maximum $\mathrm {max _+} ^{-1}_j$ of $b-d$ for $(b_j,d_j)\in K _{j} ^{\prime -1}$ and the maximum $\mathrm {max _-} ^{-1}_{j'}$ of $-b-d$ for $(b_j,d_j)\in K _{j} ^{\prime -1}$. Then, we determine whether the set $-K _i ^{\prime +1}$ has a non empty intersection with the quadrant $Q=\{ (b_i,d_i) \in \mathbb {R}^2 | -b_i+d_i< \lceil \mathrm {max _+} ^{-1}_j \rceil \ \mathrm {and} \ b_i+d_i < \lceil \mathrm {max _+} ^{-1}_j \rceil \}$. It can be done with a linear program.    $\square$

3.3 Perspectives

We have proved the decidability of the recognition of digital polyhedra [Recognition$(3,\mathscr {P}_n,S)$] in dimension 3. This result is weak and the three cases considered in the paper can be considered as marginal. They are not because they require to deal with an infinite number of irreducible constraints but we have proved that by using their geometry, it is possible to decide in a finite time.

The reader can however believe that this standalone approach is not appropriate and that some known results coming from the lattice polytope’s theory allow to prove stronger results with less work. The problem [Recognition$(d,\mathscr {P}_n,S)$] is a kind of converse of Integer Linear Programming but the idea that some kinds of ILP approaches could avoid the difficulty requires more than an intuition. One of the most interesting results related with the conjecture could be the existence of the finiteness threshold width [2]: for larger width than the threshold denoted $w^\infty (d)$ (we have for instance $w ^\infty (3)=1$), there exists only a finite number of lattice polytopes (up to lattice preserving affine isomorphisms) containing a prescribed number of integer points. Such a deep result could be used to prove that for lattice polytopes Q verifying $\mathrm {width}(Q)> w^\infty (d)$, the number of lattice jewels is finite which makes the problem decidable. It remains the mystery of what happens below the threshold namely exactly where infiniteness occures. We can at last notice that as for the conjecture of decidability of [Recognition$(d,\mathscr {P}_n,S)$] which is unsolved in dimension $d\ge 4$ for hollow polytopes, the infiniteness threshold width is also related with hollow polytopes... It can explain that for this specific class of objects, the decidability of [Recognition$(d,\mathscr {P}_n,S)$] which seems to be a so weak question remains challenging.