A New Shape Descriptor Based on a Q-convexity Measure

Abstract

In this paper we define a new measure for shape descriptor. The measure is based on the concept of convexity by quadrant, called Q-convexity. Mostly studied in Discrete Tomography, this convexity generalizes hv-convexity to any two or more directions, and presents interesting connections with “total” convexity. The new measure generalizes that proposed by Balázs and Brunetti (A measure of Q-convexity, LNCS 9647 (2016) 219–230), and therefore it has the same desirable features: (1) its values range intrinsically from 0 to 1; (2) its values equal 1 if and only if the binary image is Q-convex; (3) its efficient computation can be easily implemented; (4) it is invariant under translation, reflection, and rotation by $90^\circ$. We test the new measure for assessing sensitivity using a set of synthetic polygons with rotation and translation of intrusions/protrusions and global skew, and for a ranking task using a variety of shapes. Based on the geometrical properties of Q-convexity, we also provide a characterization of any binary image by the matrix of its “generalized salient points”, and we design a linear-time algorithm for the construction of the binary image from its associated matrix.

1 Introduction

Shape descriptors are widely used in image processing and computer vision for object detection, classification, and recognition [8, 12]. One class of descriptors captures single geometrical or topological characteristics of shapes, like moments [7], orientation and elongation [15], circularity [10], just to mention a few. Among them, probably the most often studied descriptor is the measure of convexity. Depending on whether the interior or the boundary of the shape is investigated in order to determine the degree of convexity, these measures can be grouped into area-based [2, 12, 13] and boundary-based [14] categories.

In [1] we proposed a convexity measure which uses both boundary and area information, thus falls between the two above mentioned classes. It is based on the concept of Q-convexity [4, 5], mostly studied in Discrete Tomography [9] for its good properties (it generalizes so-called hv-convexity to any two or more directions, and has interesting connections with “total” convexity). The notion of salient points of a Q-convex image has been introduced in [6] as the analogue of extremal points of a convex set. They have similar features, and in particular a Q-convex image is characterized by its salient points. Salient points can be generalized for any binary image, and they have been studied to model the “complexity” of a binary image which led to the convexity measure of [1, 3].

The novel idea of this paper is to consider generalized salient points to have different weights – depending on “how” far they are from the boundary – when calculating the convexity measure. In this way we provide a flexible extension of the measure of [1]. For this purpose we introduce the matrix of generalized salient points of a binary image (shortly, GS matrix) and study its properties. We provide a linear-time algorithm for the construction of the binary image from its GS matrix and also describe how the measure can also be computed in linear time.

The structure of the paper is the following. In Sect. 2 we present the basic concepts and give the definition of the new measure of Q-convexity. In Sect. 3 we introduce the matrix of generalized salient points (GS matrix, for short) and describe its properties. We also design a linear-time algorithm for the construction of the binary image from its GS matrix. The aim of Sect. 4 is to briefly show how the introduced measure can be efficiently computed, in linear time in the size of the image. In Sect. 5 we present experimental results. Finally, Sect. 6 is for the conclusion.

2 New Q-convexity Measure

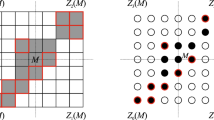
Any binary image $\mathcal {F}$ is a $m\times n$ binary matrix, and it can be represented by a set of black, foreground pixels denoted by F, and white, background pixels (unit squares) (see Fig. 1 left). Equivalently, foreground pixels can be regarded as points of $\mathbb {Z}^2$ contained in a lattice grid $\mathcal {G}$ (rectangle of size $m\times n$) up to a translation so that any binary image can be viewed as a subset of $\mathcal {G}$, also called lattice set (see Fig. 1 right). Throughout the paper, we will consider images different from the emptyset and use both representations as interchangeable, since notation for the latter one is more suitable to describe geometrical properties (even if the order of the points in the lattice and the order of the items in a matrix are different). For our convenience when not confusing, we use $\mathcal {F}$ for both the image and its representations, and we denote by $\mathcal {F}^c$ the complement of $\mathcal {F}$, i.e., the image obtained as the complement of its pixel values reversing foreground and background pixels. In the lattice representation, $\mathcal {F}^c$ corresponds to $\mathcal {G}{\setminus } {F}$.

Fig. 1.

A binary image represented as black and white pixels (left), and by a lattice set (right).

2.1 Background

Let us introduce the main definitions concerning Q-convexity [4, 6]. In order to simplify our explanation, let us consider the horizontal and vertical directions, and denote the coordinate of any point M of the grid $\mathcal {G}$ by $(x_M,y_M)$. Then, M and the directions determine the following four quadrants:

$$\begin{aligned}\begin{gathered} Z_0(M)=\{ N\in \mathcal {G}:\; 0\le x_N\le x_M, \; 0\le y_N\le y_M\}\\ Z_1(M)=\{ N\in \mathcal {G}:\; x_M\le x_N< m, \; 0\le y_N\le y_M\}\\ Z_2(M)=\{ N\in \mathcal {G}:\; x_M\le x_N< m, \; y_M\le y_N< n\}\\ Z_3(M)=\{ N\in \mathcal {G}:\; 0\le x_N\le x_M, \; y_M\le y_N< n\}.\\ \end{gathered}\end{aligned}$$

Definition 1

A lattice set F is Q-convex if $Z_p(M)\cap {F}\ne \emptyset$ for all $p=0,\ldots ,3$ implies $M\in F$.

If $Z_p(M)\cap {F}= \emptyset$, we say that $Z_p(M)$ is a background quadrant. Thus, in other words, a binary image is Q-convex if there exists at least a background quadrant $Z_p(M)$ for every pixel M in the background of $\mathcal {F}$. Figure 2 illustrates the above concepts.

Fig. 2.

Illustration of the concept of Q-convexity. A Q-convex (left) and a non-Q-convex (right) lattice set. Note that the image on the left is the Q-convex hull of the image on the right.

The Q-convex hull of $\mathcal {F}$ can be defined as follows:

Definition 2

The Q-convex hull $\mathcal {Q}({F})$ of a lattice set F is the set of points $M\in \mathcal {G}$ such that $Z_p(M)\cap {F}\ne \emptyset$ for all $p=0,\ldots ,3$.

By Definitions 1 and 2, if F is Q-convex then ${F}=\mathcal {Q}({F})$. Differently, if F is not Q-convex, then $\mathcal {Q}({F}){\setminus } {F}\ne \emptyset$ (see Fig. 2, again, where for the lattice set F on the right, $\mathcal {Q}({F}){\setminus } {F}=\{M\}$).

Fig. 3.

Generalized salient points are in black. Leftmost: $\mathcal {F}_1$. Centre-left: $\mathcal {F}_2$. Centre-right: $\mathcal {F}_3$. Rightmost: $\mathcal {F}_4$.

We define a new measure in between region- and boundary-based measures exploiting some geometrical properties of the “shape”.

Definition 3

Let F be a lattice set. A point $M\in {F}$ is a salient point of F if $M \notin \mathcal {Q}({F} {\setminus } \{M\})$.

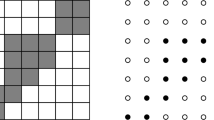
Denote the set of salient points of $\mathcal {F}$ by $\mathcal {S}({F})$. Of course $\mathcal {S}({F})=\emptyset$ if and only if ${F}=\emptyset$. In particular, Daurat proved in [6] that the salient points of $\mathcal {F}$ are the salient points of the Q-convex hull $\mathcal {Q}({F})$ of F, i.e. $\mathcal {S}({F})=\mathcal {S}(\mathcal {Q}({F}))$. This means that if F is Q-convex, its salient points completely characterize F. If it is not, there are other points belonging to the Q-convex hull of F but not in F that “track" the non-Q-convexity of F. These points are called generalized salient points (abbreviated by g.s.p.). The set of generalized salient points $\mathcal {S}_g({F})$ of F is obtained by iterating the definition of salient points on the sets obtained each time by discarding the points of the set from its Q-convex hull, i.e., using the set notation:

Definition 4

If F is a lattice set, then the set of its generalized salient points (g.s.p.) $\mathcal {S}_g({F})$ is defined by $\mathcal {S}_g({F})=\bigcup _i \mathcal {S}({{F}}_i)$, where ${{F}}_1={F}$, ${{F}}_{i}=\mathcal {Q}({{F}}_{i-1}){\setminus } {{F}}_{i-1}$.

With the obvious meaning we may denote the binary images related to $\mathcal {Q}(F)$, $\mathcal {S}(F)$, and $F_i$ by $\mathcal {Q}(\mathcal {F})$, $\mathcal {S}(\mathcal {F})$, and $\mathcal {F}_i$, respectively. Figure 3 illustrates the definition in the lattice representation. We notice that ${\mathcal {F}}_{i}$ is contained in ${\mathcal {F}}_{i-1}^c$ (more precisely, in $\mathcal {Q}({{F}}_{i-1}){\setminus } {{F}}_{i-1}$), and if i is even, ${\mathcal {F}}_{i}$ is contained in ${\mathcal {F}}_{1}^c$, else if i is odd ${\mathcal {F}}_{i}$ is contained in ${\mathcal {F}}_{1}$. In the pixel-representation, this corresponds to say that foreground and background pixels in $\mathcal {F}_i$ correspond to white and black pixels for i even, and to black and white pixels for i odd, respectively. In this view, the Q-convex hull of the foreground pixels of $\mathcal {F}_{i-1}$ contains the Q-convex hull of the foreground pixels of $\mathcal {F}_{i}$. Moreover if $\mathcal {F}$ and $\mathcal {F}'$ are two binary images, then $\mathcal {S}_g(\mathcal {F})$ is different from $\mathcal {S}_g(\mathcal {F}')$ (see Theorem 9 of [6]).

Let k be the index such that ${F}_{k+1}=\emptyset$. By definition, $\mathcal {S}(\mathcal {F})=\mathcal {S}(\mathcal {F}_1)\subseteq \mathcal {S}_g(\mathcal {F})=\mathcal {S}(\mathcal {F}_1)\cup \mathcal {S}(\mathcal {F}_2)\cup \ldots \cup \mathcal {S}(\mathcal {F}_k)$ and the equality holds when $\mathcal {F}$ is Q-convex. Moreover, the points of $\mathcal {S}_g(\mathcal {F})$ are chosen among the points of subsets of $\mathcal {Q}(\mathcal {F})$, thus $\mathcal {S}_g(\mathcal {F})\subseteq \mathcal {Q}(\mathcal {F})$.

2.2 The Generalized Shape Descriptor

In [1], we defined a shape measure in terms of proportion between salient points and generalized salient points. Denoting the cardinality of an arbitrary set $\mathcal {P}$ of points by $|{\mathcal {P}}|$, here we generalize the measure as follows:

Definition 5

For a given binary image $\mathcal {F}$, its Q-convexity measure $\varPsi _{(c_i)}(\mathcal {F})$ is defined by

$$\varPsi _{(c_i)}(\mathcal {F})= \frac{|{\mathcal {S}(\mathcal {F})}|}{\sum _i c_i |{\mathcal {S}(\mathcal {F}_i)}|},$$

where $\mathcal {S}(\mathcal {F})$ and $\mathcal {S}(\mathcal {F}_i)$ are as in Definition 4, $c_1=1$, and each $c_i$ is a non-negative real number.

Notice that $c_1=1$ must hold in order to get value 1 for Q-convex sets. Note also that the measure is purely qualitative because is independent from the size of the image. It coincides with the measure in [1] if $c_i=1$, for all i, and, more generally, if the g.s.p. are many with respect to salient points, then $\mathcal {F}$ is far to be Q-convex. Besides, the dependence on successive $|{\mathcal {S}(\mathcal {F}_i)}|$ depends on the choice of $c_i$: if $c_i$ is a decreasing function, then the measure scores heavily g.s.p. in the boundary with respect to the g.s.p. in the interior, and vice-versa in case of an increasing function. This approach provides, in fact, a family of shape descriptors (by setting the weights differently). Each member of the family could complement other ones, thus, giving a finely tuneable tool for solving pattern recognition issues, as different weightings can capture different aspects of the shapes (see the ranking examples in Sect. 5).

Since $\mathcal {S}(\mathcal {F})\subseteq \mathcal {S}_g(\mathcal {F}) \subseteq \mathcal {Q}(\mathcal {F})$, the Q-convexity measure satisfies the following properties:

• the Q-convexity measure ranges from 0 to 1;

• the Q-convexity measure equals 1 if and only if $\mathcal {F}$ is Q-convex.

In particular, $\mathcal {S}(\mathcal {F})=\mathcal {S}_g(\mathcal {F})$, and hence $\varPsi _{(c_i)}(\mathcal {F})=1$, (for instance when $\mathcal {F}$ is a full rectangle as the rightmost image in Fig. 6) if and only if $\mathcal {F}$ is Q-convex. If $\mathcal {S}_g(\mathcal {F})=\mathcal {Q}(\mathcal {F})$ (for instance if $\mathcal {F}$ is a chessboard), $\varPsi _{(c_i)}(\mathcal {F})$ decreases with the inverse of the size of $\mathcal {Q}(\mathcal {F})$ in the case where $c_i=1$ for all i. So, if we consider the sequence of images starting from the full rectangle and ending with the chessboard, and having intermediate images obtained by deleting each time one suitable pixel iteratively row by row, they have measure values decreasing from 1 to $\frac{4}{mn}$ (circa $6\cdot 10^{-5}$ for $m=n=256$).

Moreover, since ${\mathcal {S}(\mathcal {F})},\;{\mathcal {S}(\mathcal {F}_i)}$ and ${\mathcal {Q}(\mathcal {F})}$ are invariant under translation, reflection, and rotation by $90^\circ$ for the horizontal and vertical directions, the measure is also invariant.

3 The GS Matrix

Let $\mathcal {F}$ be a $m\times n$ binary image, and $\mathcal {S}_g(\mathcal {F})=\mathcal {S}(\mathcal {F}_1)\cup \mathcal {S}(\mathcal {F}_2)\cup \ldots \cup \mathcal {S}(\mathcal {F}_k)$. Consider the matrix representation of $\mathcal {F}=(f_{ij})$. We may associate $\mathcal {F}$ to the $m\times n$ integer matrix B of its generalized salient points defined as follows: $b_{ij}=h$, if and only if $f_{ij}$ is a g.s.p. of $\mathcal {F}_h$; $b_{ij}=0$ otherwise. Informally, items $0<h(\le k)$ of the integer matrix B correspond to g.s.p in $\mathcal {S}(\mathcal {F}_h)$; items 0 do not correspond to any g.s.p. of $\mathcal {F}$. For example, the rightmost matrix in Fig. 4 is the GS matrix associated to the leftmost binary matrix (which corresponds to $\mathcal {F}$ in Fig. 3). We call B, the GS matrix associated to $\mathcal {F}$, where GS stands for “generalized salient”. The GS matrix is well-defined since by Definition 4, we have that $\cap _i \mathcal {S}(\mathcal {F}_i)=\emptyset$.

Theorem 1

Any two binary images are equal if and only if their GS matrices are equal.

Proof

The following construction permits to determine the binary image by its GS matrix: For all item i in the GS matrix considered in decreasing order (of i), compute the Q-convex hull of the pixels corresponding to the items i and fill the corresponding pixels not already considered with the foreground w.r.t. i.

It is easy to see that the construction is correct. Let k be the maximum value in the GS matrix; then, ${F}_{k+1}=\emptyset$, and $\mathcal {F}_k$ is Q-convex. Therefore, the Q-convex hull of its g.s.p. is $\mathcal {F}_k$, and so the first step $i=k$ of the construction determines $\mathcal {F}_k=Q(\mathcal {S}(\mathcal {F}_k))$. In the second step $i=k-1$, the construction determines $\mathcal {F}_{k-1}$: it computes the Q-convex hull of the pixels corresponding to the items $k-1$ in the GS matrix, i.e. $Q(\mathcal {S}(\mathcal {F}_{k-1}))=Q(\mathcal {F}_{k-1})$, and fills the corresponding pixels not already considered with the foreground w.r.t. $k-1$, i.e. $Q({F}_{k-1}){\setminus } {F}_k$. By definition, $\mathcal {F}_k=Q({F}_{k-1}){\setminus } {F}_{k-1}$, and since $Q(\mathcal {F}_{k-1})={F}_{k-1}\cup {F}_{k}$ and ${F}_{k-1}\cap {F}_{k}=\emptyset$, we have $\mathcal {F}_{k-1}=Q(\mathcal {F}_{k-1}){\setminus } {F}_k$. By proceeding in this way, in the last step $i=1$, the construction determines $\mathcal {F}=\mathcal {F}_1$ since $F_1=Q({F}_{1}){\setminus } {F}_2$. Finally, since two different binary images have different GS matrices, there is a one-to-one correspondence between images and matrices.    $\square$

In order to design an efficient algorithm based on the constructive proof of the theorem, we extend the definition of Q-convex hull as follows: The Q-convex hull $\mathcal {Q}({F}_i)$ of the lattice set ${F}_i$ is the set of points $M\in \mathcal {G}$ such that $Z_p(M)\cap {F}_i\ne \emptyset$ for all $p=0,\ldots ,3$.

Therefore, pixel M belongs to the Q-convex hull of ${F}_i$ if there is an item i in the GS matrix associated to $\mathcal {F}_i$ in each zone of M. Since the Q-convex hull of the foreground pixels of $\mathcal {F}_i$ contains the Q-convex hull of the foreground pixels of $\mathcal {F}_{i+1}$, pixel M belongs to $Q({F}_i){\setminus } Q({F}_{i+1})$, if i is the minimum among the maximum items in the GS matrix in each zone in M. This ensures that every item is considered once. Let $Z_t=(z^t_{ij})$ such that $z^t_{ij}=h$ iff h is the maximum item in the submatrix $Z_t(b_{ij})$, for $t=0,1,2,3.$

Starting from the GS matrix B in input, Algorithm 1 constructs $\mathcal {F}$ by using $Z_0,Z_1,Z_2$ and $Z_3$. For example:

$$ {\scriptscriptstyle B= \begin{bmatrix} 0&1&2&2&1&0\\ 0&0&3&3&0&0\\ 1&0&0&0&0&1\\ 0&0&0&0&3&2\\ 2&3&0&4&0&1\\ 1&0&0&0&0&0\\ 0&0&0&4&0&0\\ 0&0&0&3&0&0\\ 0&6&1&2&1&0 \end{bmatrix},\ Z^0= \begin{bmatrix} 2&0&0&0&2&4\\ 2&3&0&0&4&4\\ 0&2&3&4&4&0\\ 2&3&3&4&0&0\\ 0&0&3&0&4&0\\ 0&1&1&4&4&4\\ 0&0&1&0&4&0\\ 0&0&1&0&3&0\\ 0&0&0&0&0&0 \end{bmatrix}, \ Z^1= \begin{bmatrix} 4&0&0&0&0&2\\ 4&4&0&0&4&4\\ 0&4&4&4&3&0\\ 4&4&4&4&0&0\\ 0&0&4&0&1&0\\ 0&4&4&4&1&0\\ 0&0&4&0&1&0\\ 0&0&3&0&1&0\\ 0&0&0&0&0&0 \end{bmatrix}, \ Z^2= \begin{bmatrix} 2&0&0&0&0&0\\ 3&3&0&0&1&0\\ 0&3&3&3&1&0\\ 3&3&3&3&0&0\\ 0&0&4&0&3&0\\ 0&4&4&4&3&2\\ 0&0&4&0&3&0\\ 0&0&4&0&3&0\\ 0&0&0&0&0&0 \end{bmatrix}, \ Z^3= \begin{bmatrix} 0&0&0&0&0&2\\ 0&1&0&0&3&3\\ 0&1&3&3&3&0\\ 1&1&3&3&0&0\\ 0&0&3&0&4&0\\ 0&3&3&4&4&4\\ 0&0&3&0&4&0\\ 0&0&3&0&4&0\\ 0&0&0&0&0&0 \end{bmatrix}\ .}$$

If we consider for instance $b_{22}=0$, since $\min \{z_{22}^0=3,z_{22}^1=4,z_{22}^2=3,z_{22}^3=3\}=3$, then $f_{22}$ is in $\mathcal {Q}(\mathcal {F}_3)$ and so $f_{22}=1$. Note that Algorithm 1 reconstructs $\mathcal {F}$ of Fig. 4. The correctedness of the algorithm derives by previous discussion.

Theorem 2

Algorithm 1 computes the binary image from its GS matrix in linear time.

Proof

Let $B=(b_{ij})$ be the GS matrix in input, and $\mathcal {F}=(f_{ij})$ be the binary matrix representation of the image associated to B. Initially, $f_{ij}=0$, for all i, j. The computation of the maximum in any zone for each item $b_{ij}=0$ (statements 2–4) can be done in linear time in the size of the image. Indeed consider zone $Z_0$: for $b_{ij}$, by definition, $Z_0(b_{ij})=Z_0(b_{i-1 j})\cup Z_0(b_{i j-1})$. Therefore the maximum in $Z_0(b_{ij})$ can be computed by previous computations for $Z_0(b_{i-1 j})$ and $Z_0(b_{i j-1})$, and stored in a matrix $Z^0$. (Analogous, relations hold for $Z_1,\,Z_2,\,Z_3$.) For any item $b_{ij}$, the minimum among four corresponding values stored in the four matrices $Z^0,Z^1,Z^2,Z^3$ (statement 15), and the determination of the parity of the minimum cost O(1) (statements 16–18, 21–23). Hence, the complexity of the algorithm is linear in the size of matrix B.    $\square$

4 Computation of $\varPsi$

The GS matrix and the shape measure $\varPsi _{(c_1,\ldots ,c_k)}$ can be computed in linear time in the size of the binary image by the algorithm designed in [3] for the determination of generalized salient pixels.

Here we briefly describe the algorithm. The basic idea is that salient points and generalized salient points of a binary image $\mathcal {F}$ can be determined by implicit computation of the $Q(\mathcal {F})$. Indeed, the authors in [3] proved that $Q(\mathcal {F})$ is the complement of the union of maximal background quadrants. At each step i, the algorithm finds the foreground (generalized) salient pixels of $\mathcal {F}_i$ by computing the maximal background quadrants of $\mathcal {F}_i$. Pixels in the background quadrants are discarded and the remaining complemented image is considered in the next step being the Q-convex hull of $\mathcal {F}_i$ (recall that $\mathcal {F}_{i+1}=Q(\mathcal {F}_{i}){\setminus } \mathcal {F}_i$). During the computation of generalized salient points, the algorithm constructs the GS matrix $B=(b_{ij})$. Indeed, $b_{ij}=h$, if $f_{ij}$ is a g.s.p. in $\mathcal {F}_h$ and the algorithm finds it at step h (and $b_{ij}=0$ for any item which is not a g.s.p.). Therefore, B is the matrix of the steps at which every g.s.p. is found. Figure 4 shows an example of the execution of the algorithm and the corresponding GS matrix.

Fig. 4.

Illustrative example of the algorithm for finding g.s.p. of image $\mathcal {F}$ (first matrix). In each step (first four matrices, from left to right) the identified g.s.p. are drawn bold and pixels of the background quadrants are grey. The positions inside the polygon constitute the Q-convex hull of the g.s.p. $\mathcal {Q}(\mathcal {S}(\mathcal {F}_i)){\setminus } \mathcal {S}(\mathcal {F}_i)$ and will be investigated in the successive step. The rightmost matrix is the GS matrix of $\mathcal {F}$.

5 Experiments

Depending on the choice of $c_i$ we obtain shape measures that score differently pixels closer to the boundary and those internal. In [3] we considered the case where $c_i=1$ for all i, thus weighting all the g.s.p. in the same way. Here we investigate two pairs of opposite choices:

• $c_i=i$, and $c_i=i^2$ for $i=1,\ldots ,k$

• $c_i=1/i$, and $c_i=(1/i)^2$ for $i=1,\ldots ,k$.

In the first experiment, we used the set of synthetic polygons in [11] to study the behavior of the measures in case of rotation, translation of intrusions/protrusions and global skew. In Fig. 5 are illustrated the results. We observe that $\varPsi _{(c_i=i)}$ and $\varPsi _{(c_i=i^2)}$ assign values lower than those assigned by $\varPsi _{(c_i=1)}$, whereas $\varPsi _{(c_i=1/i)}$ and $\varPsi _{(c_i=1/i^2)}$ assign values greater than those assigned by $\varPsi _{(c_i=1)}$. In this experiment, all the measures rank the images in the same order except $\varPsi _{c_i=i^2}$ (which exchanges first with second image). Let us notice that measures are invariant under translation of intrusions and protrusions (see fourth and fifth shapes, for example), but are sensitive to rotations of angles different from $90^\circ$ (see second shape).

Fig. 5.

Synthetic shapes ranked into ascending order by shape measures. Values are rounded to four digits.

In the second experiment, we considered a variety of shapes, and we ranked them by each measure. In Fig. 6 the ranking in ascending order and the values for measure $\varPsi _{(c_i=1)}$ are illustrated, whereas in Fig. 7 we report on the results for $\varPsi _{(c_i=i)}$, $\varPsi _{(c_i=i^2)}$, $\varPsi _{(c_i=1/i)}$, and $\varPsi _{(c_i=1/i^2)}$. Note that all the measures correctly assign value 1 to the “L” and rectangular shapes. Moreover, by definition, $\varPsi _{(c_i=i)}$ and $\varPsi _{(c_i=i^2)}$ assign lower values to shapes with the majority of g.s.p in the interior (thus, to images with many narrows but deep intrusions) than to shapes with the majority of g.s.p in the boundary, whereas $\varPsi _{(c_i=1/i)}$ and $\varPsi _{(c_i=1/i^2)}$ behave on the contrary. This is shown for example by the eagle and spiral images (fourth and eighth in Fig. 6, respectively). Indeed the spiral shape has most of its g.s.p. in the boundary so that it is in position four and two in the ranking for $\varPsi _{(c_i=1/i)}$ and $\varPsi _{(c_i=1/i^2)}$, respectively, whereas it is in position nine in the ranking for $\varPsi _{(c_i=i)}$ and $\varPsi _{(c_i=i^2)}$ in Fig. 7. The contrary happens for the eagle shape, where most of its g.s.p. are in the interior. This is in accordance of our expectations and shows that different weightings can be appropriate for different classification tasks.

Table 1. Average difference of the convexity value of the original and rescaled images.

Fig. 6.

Shapes ranked into ascending order by $\varPsi _{(c_i=1)}$. Values are rounded to four digits.

In both experiments we used the images with original size (in both dimensions varying between 100 and 555 pixels), even if we illustrate them rescaled for better presentation quality. We also investigated scale invariance. This time we omitted the two fully convex images as their convexities are naturally scale-invariant. Taking the vectorized versions of the remaining 12 original images we digitized them on different scales ($32\times 32$, $64\times 64$, $128\times 128$, $256\times 256$, and $512\times 512$). Then, for each image we computed the convexity values and compared them to the convexity of the original sized image. Formally, we measured the normalized difference

$$\varDelta \varPsi =\frac{|\varPsi (F_o)-\varPsi (F_r)|}{\varPsi (F_o)},$$

where $\varPsi (F_o)$ and $\varPsi (F_r)$ is the convexity of the original sized and the rescaled image, respectively. Table 1 shows the average of the measured convexity differences over the 12 pair of images. Of course, in lower resolutions the small details of the shapes disappear, therefore the shown difference values are higher. As expected, $\varPsi _{(c_i=i)}$ and $\varPsi _{(c_i=i^2)}$ are fairly intolerant to rescaling which has a high impact on the narrow and deep intrusions. On the other hand, the values for $\varPsi _{(c_i=1/i)}$ and $\varPsi _{(c_i=1/i^2)}$ in Table 1 are small (less than 0.1), from which we can deduce a reasonable scale-invariance of these convexity measures.

Fig. 7.

Shapes ranked into ascending order by $\varPsi _{(c_i=i)}$, $\varPsi _{(c_i=i^2)}$, $\varPsi _{(c_i=1/i)}$, and $\varPsi _{(c_i=1/i^2)}$ measures, from top to bottom, respectively. Values are rounded to four digits.

6 Further Work

In this paper we presented a flexible extended version of the measure of Q-convexity defined in [1]. By introducing the matrix of generalized salient points we can give different weights for different groups of g.s.p. when calculating the degree of convexity.

Choosing the proper weightings depends, of course, always on the classification/recognition/image precessing problem and whether we are more interested in differentiating the images based on their boundaries or on their interiors. To find the proper weights, either trial-and-fail or more sophisticated methods, such as stochastic search or machine learning constructions can be used. This issue can be investigated in more detail in a further paper as well as the performance of the measures in real-life pattern recognition applications.