1 Introduction

Topographic regularity is a fundamental property in the wiring of mammalian brains [1,2,3,4], but has received relatively little attention in connectome research with MRI data, which typically focuses on macro-scale brain connections. For specific sensory systems in human brain, task fMRI has been successfully applied to extract the topography of cortical areas such as the primary visual cortex [5], but such task fMRI tools have limitations for patients and are hard to generalize to other brain regions. There have thus been increasing interests recently in extracting brain topography using resting-state fMRI (rfMRI) [6,7,8]. If successful, this will be widely applicable for studying the perturbation of the functional topography in various brain disorders.

Functional topography has been observed and reported previously on rfMRI using Linear regression [6] and correlation-based functional connectivity [7, 8]. However, the reliance of these methods on seed regions makes them sensitive to seeds selection and difficult to use in large-scale analysis of general brain regions. More importantly, rfMRI signals are not mere reflection of the co-activation between brain regions with topographic correspondences because they are affected by spontaneous neuronal activity from various brain processes even after removing physiological noise.

To overcome these difficulties, our idea is to directly decompose the rfMRI signal and extract those components that follow topographic regularity via a novel semi-blind independent component analysis (ICA) method [9,10,11]. The components from conventional ICA are valuable in revealing the co-activation of different brain regions in the presence of complex neuron activities [11], albeit with limited link to functional topography. In our work, we build upon the recent developments in computing the topographically regular fiber tractography [12, 13] with cutting-edge diffusion MRI data from the Human Connectome Project (HCP) [14]. Using these structural topography, we construct a kernel matrix to augment the ICA methods and compute functional topography from resting fMRI signals. Our method is group-based and generally applicable to different brain regions as long as a set of topographically regular fiber tracts can be computed. In our experiments, we demonstrate our method on studying the functional topography of the motor cortex between two hemispheres, which have well-known topographic correspondences from post-mortem studies [7]. On a dataset from 35 right handed HCP subjects, we show that our kernel regularized ICA extracts functional topography agreeable to previously reported results and it also extracts topographically organized functional co-activations between the motor cortices.

2 Methods

2.1 Modeling Topographic Regularity in Structural Connectivity

Novel algorithms have been developed recently for modeling structural topography with tractography. In [12], Aydogan and Shi observed that fiber tracts within topographically regular fiber bundles are often locally parallel and they showed that by enforcing fiber tracts to form as parallel as possible fiber bundles, the optical radiation in visual pathway agrees significantly better with the retinotopic maps established from task fMRI studies than the standard tractography. In a more recent work [13], topographic regularity of structural connectivity has been modeled using spectral graph theory. They also applied the topographic regularity model to fiber filtering and they showed that the filtered bundles agree better with known topography in neuroanatomy. An example of the regular fiber tracts connecting the motor cortices of an HCP subject is shown in Fig. 1.

Fig. 1.
figure 1

Axial view of the fiber bundles connecting the motor cortices generated by the topographic tract filtering method in [13].

Full size image

We adopt the mean strength weighted structural connectome [15] to represent the prior belief on the functionally connectedness of two locations. The conventional structural connectome is usually defined for ROIs. Since we are interested in voxel-wise connectivity, we slightly customize the mean strength of structural connectivity as a kernel weighted mean strength. Suppose we have a topographically regular tractogram, or fiber bundle, generated by the tract filtering method in [13], denoted as \(\mathcal {T}=\{t_1,t_2,...,t_M\}\), and a pair of voxels \(p_i\) and \(p_{i'}\). We can compute the distance from the two voxels to each of the fiber tracts, and the distances can be denoted as \(\{d(p_i,t_1),d(p_i,t_2),\ldots ,\) \(d(p_i,t_M)\}\) and \(\{d(p_{i'},t_1),d(p_{i'},t_2),...,d(p_{i'},t_M)\}\). The mean strength of the structural connectivity for this pair of voxels is defined as follows:

$$\begin{aligned} K^W(i,{i'})={1\over M}\sum _{j=1}^M e^{-{d^2(p_{i},t_j)\over \sigma ^2}}e^{-{d^2(p_{i'},t_j)\over \sigma ^2}} \end{aligned}$$
(1)

where d() is point-to-set Euclidean distance and \(\sigma \) is a scale parameter which models the relative strength of connection from a fiber tract to a voxel. A small sigma would eliminate the effect of fibers relatively far from the voxel. In this work, we tend to favor a relatively small sigma to eliminate false connectivity as much as possible at the cost of missing certain true connections. Compared to the ROI based mean strength weighted structural connectome [16], this formulation relaxes the 0–1 valued connectivity into a continues-valued kernel combination.

2.2 Incorporating Structural Topography into ICA

Suppose we have a set of pre-whitened fMRI signals \(\mathbf {X}=\{\mathbf {x}_i|i=1,2,...\}\), we can rewrite the signals are modeled as linear combinations of a set of mutually independent spatial maps.

$$\begin{aligned} \mathbf {x}_i(t)=\sum _{j}{a}_{j}(t){s}_{ij} \end{aligned}$$
(2)

where \(\{\mathbf {s}_j=[s_{1j},s_{2j},...,s_{Nj}]^T|j=1,2,...\}\) are the independent spatial maps and N is the total number of voxels in the cortical region(s) of interest. This formulation has been successfully applied to group study of functional connectivity [11]. Especially, it has been shown that the temporal catenation with spatial ICA is capable of identifying activations similar to task stimulated activations in resting state fMRI scans and it can also identify default mode networks formed by multiple spontaneously activated anatomically defined brain regions.

We propose to impose the topographically regular structural connectivity as our prior in modeling the temporally catenated group ICA spatial maps. Our prior term is defined as follows:

$$\begin{aligned} \mathcal {R}(\mathbf {S}) = {1\over 2} \sum _j|\mathbf {s}_{j}^T\mathbf {K}^W\mathbf {s}_{j}|^2 \end{aligned}$$
(3)

where \(\mathbf {K}^W\) is the \(N\times N\) topographic structural connectivity matrix defined in Eq. (2). In our group analysis setting, \(\mathbf {K}^W\) is the group averaged connectivity matrix. Note that \( \mathbf {s}_{j}^T\mathbf {K}^W\mathbf {s}_{j}=\sum _{i=1}^N\sum _{i'=1}^N K^W(i,i')s_{ij} s_{i'j} \) and \(K^W(i,i')\ge 0\). Hence, by maximizing \(\mathcal {R}(\mathbf {S})\) we encourage large \(s_{ij}\) and \(s_{i'j}\) magnitudes at voxel pairs with strong topographic structural connection. This formulation also permits the spatial maps at two topographically connected sites to have different signs.

In most of the ICA formulations, we usually optimize over the de-mixing matrices \(\mathbf {W}\). Therefore, we can rewrite the regularization term as follows:

$$\begin{aligned} \mathcal {R}(\mathbf {W}) = {1\over 2} \sum _j \left| \mathbf {w}_{j}\mathbf {X}\mathbf {K}^W\mathbf {X}^T\mathbf {w}_{j}^T\right| ^2. \end{aligned}$$
(4)

By maximizing this term in addition to the non-gaussianity in the ICA formulation, we expect to find the independent components that are mainly co-activated at the topographic voxel pairs in different brain regions. The overall objective function for our topographic regularity regularized ICA can be written as follows

$$\begin{aligned} \mathbf {W}^*=\mathop {\mathrm {argmax}}E(\phi (\mathbf {W}^T\mathbf {X}))+\lambda \mathcal {R}(\mathbf {W}),\hbox { s.t.: }\forall j,~\Vert \mathbf {w}_j\Vert ^2=1 \end{aligned}$$
(5)

where \(E(\cdot )\) is the expectation operator, \(\phi (\cdot )\) is the non-Gaussianity measure, the first term is called negentropy, and \(\lambda \) is a positive penalty parameter. We chose \(\phi (u)=-e^{-u^2/2}\) for robustness [17]. Both the negentropy and our topographic regularity measure \(\mathcal {R}(\cdot )\) may be non-concave for the maximization problem, and the solution to such optimization would still rely on gradient ascent:

(6)

where \(\varDelta _t\) is a time step in gradient ascent and

$$\begin{aligned} {\begin{matrix} &{}\frac{D [E+\lambda \mathcal {R}]}{D\mathbf {W}}=E(\phi '(\mathbf {W^T\mathbf {X}})\mathbf {X}^T)^T+\lambda \mathbf{diag }(\mathbf {W}\mathbf {C}\mathbf {W}^T)(\mathbf {C}+\mathbf {C}^T)\mathbf {W}^T\\ \end{matrix}} \end{aligned}$$
(7)

where \(\mathbf {C}=\mathbf {X}\mathbf {K}^W\mathbf {X}^T\) and \(\phi '\) is the first-order derivative of \(\phi \). Each row of \(\mathbf {W}\) may is normalized at each iteration and we also further perform the symmetric de-correlation [17] to avoid multiple identical solutions by using \(\mathbf {W}=\mathbf {U}\mathbf {D}^{-{1\over 2}}\mathbf {U}^T\mathbf {W}\), where \(\mathbf {W}^T\mathbf {W}=\mathbf {U}\mathbf {D}\mathbf {V}^T\) is the SVD of \(\mathbf {W}^T\mathbf {W}\). Although this solution converges slower than the fixed point FastICA algorithm, its convergence is stable with a small \(\varDelta _t\).

3 Experimental Results

3.1 Data Preparation and Experiment Configuration

In this paper, we mainly experiment on the motor cortex of both hemispheres to evaluate our method for extracting somatotopic functional connectivity. We used the rfMRI scans of 35 unrelated right-handed subjects from Human Connectome Project (HCP). We extracted the motor cortex from the outputs of the HCP structural preprocessing pipeline [18]. The HCP structural preprocessing pipeline aligns the cortical meshes in T1 native space to the standard 32K Conte69 mesh and the CIFTI file contains time series corresponding to each vertex in the 32K Conte69 mesh. This allows us to perform time catenation for group ICA and group average in group correlation analysis on motor cortices.

The structural connectivity matrices were computed by applying the topographic tract filtering algorithm [13] to the corpus callosum fiber bundle generated by the iFOD1 tractography algorithm of MRtrix3 [19]. The fiber orientation distributions (FODs) used in the tractography were generated by the algorithm in [20]. We empirically chose \(\lambda =0.01\) in Eq. (5) and \(\sigma =1\) in Eq. (2). For both conventional group ICA and our kernel-regularized ICA, we mainly show results with 20 components in Sect. 3.2. The impact of number of components will be evaluated in the reproducibility experiments in Sect. 3.3.

3.2 Somatotopic Organization in Functional Connectivity

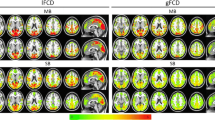
Topographic regularity in motor cortex is called somatotopic organization. Strong somatotopy has been shown via seeded correlation [7]. Specifically, the vertices on the motor cortex of one hemisphere is first treated as seed points to be correlated with all the vertices on motor cortex of the other hemisphere. Afterwards, the maximally correlated vertex pairs are picked out to form a functional connectivity map (fcMap). This process applies to both sides of motor cortex. In our experiment, we compute the fcMap by casting it as a bipartite graph matching problem with the matching cost defined as \(1-|R(x_i,x_{i'})|\), where \(R(\cdot , \cdot )\) is the correlation coefficient of corresponding components from ICA. A global optimal solution for this problem is then computed with the Hungarian algorithm. Due to the bipartite graph matching formulation, we call the Hungarian algorithm based fcMap bilateral fcMap. Using group ICA computed from conventional methods and our kernel-regularized ICA, we have computed the bilateral fcMap for the HCP data set and the results are visualized in Fig. 2(a) and (b), respectively. We can clearly see that fcMap obtained from novel ICA method demonstrate much more regular functional topography that agrees with previous findings [4, 7].

Fig. 2.
figure 2

A comparison of group bilateral fcMaps computed with (a) conventional group ICA and (b) our kernel-regularized group ICA.

Full size image
Fig. 3.
figure 3

Representative spatial maps from the conventional group ICA (top row) and our method (bottom row).

Full size image

In Fig. 3, we also compare the extracted spatial maps from conventional group ICA and our method. Due to space limitation, we only present some representative components here. We can see that the spatial maps produced by our method successfully captures the functional topography between the left and right motor cortex. These spatial maps are thus not only useful for computing the fcMap shown in Fig. 2, but also hold great potential for detecting detailed and topographically organized co-activation between different brain regions.

3.3 Reproducibility

We further evaluate the reproducibility of our method. We rerun the conventional group ICA and our method 20 times for different number of components. We used 5, 10, 20, 30, and 40 components in the experiments. We adopt three measures for reproducibility: the Coefficient of Variation (CoV), Structural Connectivity (SC) fidelity and FC fidelity. The CoV is a common intra-class reproducibility measure for connectome [16]. It is defined as the average ratio of the standard deviation of each edge weight in the FC matrices against the mean of each edge weight over all runs of experiments for fixed parameters. The SC fidelity is defined as the correlation between the ICA based group connectivity matrices and the SC matrix calculated using Eq. (2). The FC fidelity is defined as the correlation between the ICA based group FC matrices and the FC matrix calculated from Pearson correlation. These two measures quantify the fidelity of the connectivity matrices in terms of FC and SC respectively. The results are shown in Fig. 4. We can observe that our method gives more valid and reproducible FC matrix, compared to the conventional ICA. Interestingly, we find that our method can produce a connectivity matrix that well approximates both the FC and SC matrices. Besides, the number of components reaches overall best performance is around 25. The relatively large CoV is perhaps due to the local algorithms we chose for optimization. This problem can be alleviated by using stochastic gradient ascent or other global optimization strategies.

Fig. 4.
figure 4

Reproducibility measures. The baselines in SC and FC fidelity plots are the correlation value between SC matrix and correlation based FC matrix. The spreads at each point in the fidelity plots denote the standard deviation of the value.

Full size image

4 Conclusion

In this work, we proposed a framework to extract functional topography by incorporating structural topographic regularity in ICA. This gives rises to a novel kernel regularized semi-blind ICA for extracting functional topography. The experimental results show that our method extracts functional connectopy agreeable with previous findings and it also extracts topographically organized spatial maps in the primary motor cortex. For future work, we will apply this method to general brain regions connected with topographically organized fiber bundles such as the visual cortex.