Deformable Registration of a Preoperative 3D Liver Volume to a Laparoscopy Image Using Contour and Shading Cues

Abstract

The deformable registration of a preoperative organ volume to an intraoperative laparoscopy image is required to achieve augmented reality in laparoscopy. This is an extremely challenging objective for the liver. This is because the preoperative volume is textureless, and the liver is deformed and only partially visible in the laparoscopy image. We solve this problem by modeling the preoperative volume as a Neo-Hookean elastic model, which we evolve under shading and contour cues. The contour cues combine the organ’s silhouette and a few curvilinear anatomical landmarks. The problem is difficult because the shading cue is highly nonconvex and the contour cues give curve-level (and not point-level) correspondences. We propose a convergent alternating projections algorithm, which achieves a $4\%$ registration error.

1 Introduction

Hepatic laparosurgery presents at least two main challenges for the surgeons. The first challenge is that they see locally, as the liver is large and the laparoscope is close to it. The second challenge is the absence of tactile feedback, as the liver can only be manipulated by tools. Consequently, the surgeons’ navigation on and through the liver may deviate from the resection path planned on the preoperative volumetric MRI or CT. Augmented Reality (AR) can ameliorate this problem by augmenting the laparoscopy image with the preoperative data. These contain the planned resection path and the subsurface tumours and vessels which are invisible to the laparoscope.

To apply AR, one must (i) register the preoperative volume to an initial laparoscopy image and (ii) track the organ in the live laparoscopy video. When (ii) fails, the algorithm branches back to (i). Recent works [1, 2] showed very convincing results regarding (ii). Note that (ii) is optional, as (i) on its own facilitates AR on a single image. However, (i) still forms an open problem for both monocular and stereo laparoscopy. We are interested in the monocular case which forms the current standard. Any monocular solution extends easily to stereo. The problem is unsolved for three main reasons. First, the soft organ’s state is different in the preoperative and intraoperative modalities (due to breathing, gas insufflation, gravitational forces and evolution of the disease). Second, the preoperative volume’s textureless surface cannot be directly matched to the laparoscopy image. Third, a monocular laparoscope does not perceive depth. For the liver, (i) turns out to be harder to solve because the liver is highly deformable and only partially visible in the laparoscopy image.

The state-of-the-art for step (i) in monocular laparoscopy is manual rigid registration [3]. However, there also exist advanced registration methods, but designed to work in different conditions. For instance, [4] requires a stereoscope for deformable registration using contours; [5] needs multiple intraoperative images of a fully visible and rigid organ for rigid registration using the silhouette; [6] necessitates an intraoperative scanner for rigid registration using shading; [7] requires rigid views to be able to build a silhouette visual hull for deformable registration. None of the existing methods thus solve registration in the de facto conditions of monocular laparoscopy.

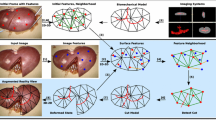
We propose a semi-automatic deformable registration framework for the liver in monocular laparoscopy. Our algorithm uses the Neo-Hookean elastic model for the liver’s preoperative volume as deformation law, and shading and contour as visual cues from the single laparoscopy image. We use two types of contour cues: the silhouette and curvilinear anatomical landmarks. Both types of contour are challenging to use because they do not directly give point correspondences. We solve this by embedding an ICP (Iterative Closest Point) mechanism in our algorithm. More specifically, the silhouette changes and slides as the model is evolved. Therefore, even though it is a necessary constraint, it is weak, as a large set of different deformations will satisfy it. The anatomical landmarks form stronger constraints by being stationary on the model. However they may also often be occluded. The anatomical landmarks we propose are the ridge contours (formed due to the negative imprints of the surrounding organs) and the falciform ligament separating the left and right lobes. We require the user to mark the liver’s visible contour segments in the image. The user may also mark a few corresponding points on the anatomical landmarks, if available. Our algorithm then cycles through the constraints given by the deformation law and the visual cues and solves them by optimal projections, including the contours’ ICP. We model shading using the Lambertian model with light fall-off following the inverse-square distance law. We propose a new projection operator for the shading constraint, which is challenging to handle because of its nonconvexity. Our algorithm is the first one to combine a deformable model with the contour and shading cues to achieve registration on a single laparoscopy image.

2 Proposed Problem Formulation

2.1 Preliminaries

Metric spaces. Let $x\in \mathbb {R}^{k}$ be a point with $k\in \{1,2,3\}$ and $\mathcal {X}\in \mathcal {S}$ be a shape (a point set) with $\mathcal {S}=\cup _{n>0}~\mathbb {R}^{k\times n}$ the set of non-empty shapes of any size n. We define the distance metric $\rho :\mathbb {R}^{k}\times \mathbb {R}^{k}\rightarrow \mathbb {R}^{+}$ as $\rho (x,\,y) \,=\, \Vert \, x \,-\, y \,\Vert \,$ for all $x,\,y\,\in \mathbb {R}^{k}$ with $\Vert \, \cdot \,\Vert$ the Euclidean norm. We define the distance of a point $x\in \mathbb {R}^{k}$ to a shape $\mathcal {Y}\in \mathcal {S}$ as $\mathtt {dist}(x,\,\mathcal {Y}) \,=\, \mathtt {min}\, \{\,\rho (x,\,y)\,|\,y\in \mathcal {Y}\,\}$. We use the modified Hausdorff distance [9] of a shape $\mathcal {X}\in \mathcal {S}$ to a shape $\mathcal {Y}\in \mathcal {S}$:

(1)

Constraints. Each registration constraint has a function $\phi :\mathcal {S}\rightarrow \mathbb {R}$ defining its solution set $\varOmega ~=~\{\,\mathcal {X}~|~\phi (\mathcal {X})~=~0,\,\mathcal {X}\in \mathcal {S}\,\}$ and a projection map $\varPi :\mathcal {S}\rightarrow \varOmega$.

Laparoscope. A laparoscope is composed of a camera and a light source. We use the pinhole model for the camera’s geometry and denote its known projection function as $\pi :\mathbb {R}^{3}\rightarrow \mathbb {R}^{2}$. $\pi$ is written from the intrinsics of the camera, computed using images of a checkerboard and Agisoft’s Lens software. We use a linear model with saturation for the camera’s photometry. We denote as $\tau \in \mathbb {R}^{+}$ this linear model’s unknown coefficient. We express everything in the camera frame. The point light source model is used for the light and collocated with the camera. We denote as $i_{s}\in \mathbb {R}^{+}$ its unknown intensity ($W/m^{2}$).

2.2 Organ Model and Deformation Law

Organ model. The organ model is a volumetric shape with tetrahedral topology. The topology is fixed and initialised from the organ’s preoperative radiological data segmented using MITK [8]. We denote as $\mathcal {M}_{\text {0}}\subset \mathbb {R}^{3}$ the liver’s preoperative volumetric model and as $\mathcal {M}^{*}\subset \mathbb {R}^{3}$ the liver’s unknown ground-truth intraoperative volume seen in the laparoscopy image. We later propose an algorithm $\mathtt {Register}(\mathcal {M}_{\text {0}})\rightarrow \mathcal {M}$ with $\mathcal {M}$ the evolved model.

Deformation law. We deform the liver’s volumetric model $\mathcal {M}$ tetrahedron-wise using the isotropic Neo-Hookean elastic model [10]. We thus have a deformation function $\phi _{\text {deformation}}$ per tetrahedron. We use generic values for the human liver’s mechanical parameters. We set Young’s modulus to $E=60,000\,Pa$ [11] and, assuming that the liver is almost incompressible, Poisson’s ratio to $v=0.49$. We use the Neo-Hookean elastic model because of its simplicity and robustness to extreme deformations.

2.3 Visual Cues

Contour. The deformable model $\mathcal {M}$ allows us to predict image contours such as $\mathcal {C}\subset \mathbb {R}^{2}$. These contours must resemble the observed image contours, here $\mathcal {C}^{*}\subset \mathbb {R}^{2}$. A generic contour constraint is thus $\phi _{\text {contour}}(\mathcal {M}) \,=\, \mathtt {dist}(\mathcal {C},\,\mathcal {C}^{*})$. We use two types of contour on the liver’s preoperative model. The first type is the silhouette $\mathcal {C}_{\text {silhouette}}\subset \pi (\mathcal {M})$. The second type is an anatomical curvilinear landmark. The falciform ligament’s contour $\mathcal {C}_{\text {ligament}}$ is available directly from the preoperative radiological data. A ridge contour $\mathcal {C}_{\text {ridge}}\subset \pi (\kappa (\mathcal {M}))$ is computed automatically using a thresholded Gaussian curvature operator $\kappa$. Usually ridge contours $\kappa (\mathcal {M})$ have very distinctive profiles. If such a distinctive contour segment is visible in the image, the user also marks its model counterpart segment by clicking the two end points on $\kappa (\mathcal {M})$. This also allows us to exploit these two end points in registration. Consequently, we use multiple contour segment correspondences and, if any, a few point correspondences. The end point constraint function is $\phi _{\text {point}}(\mathcal {M}) \,=\, \mathtt {dist}(x,\,\varvec{\ell }^{*})$. Here $x\in \mathcal {M}$ is an end point of a contour segment $\mathcal {C}$ and $\varvec{\ell }^{*}$ is the sight-line passing through this point’s image position on $\mathcal {C}^{*}_{\text {ridge-segment}}$. The end points form globally attractive convex constraints.

Shading. We use the Lambertian model without the ambient term. This is because no other light source than the laparoscope exists in the abdominal cavity. We assume that the unknown albedo $a\in \mathbb {R}^{+}$ (surface reflection coefficient) of the visible liver surface is constant. We remove specular pixels with a simple saturation test. We want that the liver model $\mathcal {M}$ shades as in the laparoscopy image $\mathcal {I}$. The visible surface emerges as a triangular mesh in the tessellated $\mathcal {M}$. We thus apply the shading constraint triangle-wise. We have a shading function $\phi _{\text {shading}}$ for each visible triangle $\triangle \subset \mathcal {M}$, which we write as $\phi _{\text {shading}}(\mathcal {M})~=~\rho (\eta ,\,\eta ^{*})$. Here $\eta ^{*}\in \mathbb {R}^{+}$ is the median of the pixels’ measured intensities (gray level) inside the projected triangle $\pi (\triangle )$ in the laparoscopy image $\mathcal {I}$ and $\eta \in \mathbb {R}^{+}$ is the computed Lambertian intensity for the corresponding model triangle $\triangle$:

$$\begin{aligned} \eta \,=\, -\,\frac{\gamma }{\ \Vert \mathbf {Q}\Vert ^{2}}\,\,\mathbf {n}^{\top }\,\mathbf {\bar{q}} \end{aligned}$$

(2)

Here $\mathbf {Q}\in \mathbb {R}^{3}$ is the triangle’s center and $\mathbf {\bar{q}}=\mathbf {Q}/\Vert \mathbf {Q}\Vert$. The denominator models light fall-off with the inverse-square law. Because the laparoscope hovers at close range (5 cm to 15 cm) to the liver, light falls off strongly across the visible surface. Our shading model (2) combines all the photometric unknowns into a single parameter $\gamma =i_{s}\,\tau \,a$. It is estimated using least median regression between the observed and predicted shading images.

3 Proposed Optimisation Solution

We propose a convergent alternating projections algorithm. A sequence of projection mappings form a nonexpansive asymptotically regular mapping [12]. Our algorithm cycles through the constraints’ projection mappings and this generates a convergent sequence of shapes. Shading is a local constraint which can only be applied when close to the solution. We therefore introduce it after the convergence of a first round of optimisation using the contour constraints.

3.1 Refining Algorithm

Cost. We search the closest $\mathcal {M}$ to all constraints’ solution sets $\varOmega _{i}$, $i=1,\ldots \,\,m$:

$$\begin{aligned} \mathcal {M} \,\in \, \mathop {{{\mathrm{argmin}}}}\limits _{\mathcal {M}}\,\, \sum _{i=1}^{m} \,\, \mathtt {dist}(\,\mathcal {M},\,\varOmega _{i}\,) \end{aligned}$$

(3)

Algorithm. We solve (3) with the algorithm in Fig. 1. The algorithm has four stages: marking (line 00), rough automatic initialisation (line 01), contour-based refinement (lines 02–05) and contour-and-shading-based refinement (lines 06–10). First, the user marks visible contour segments on the image and a ridge contour segment on the liver model. Marking takes approximately 1 min. Second, the initialisation registers the liver’s rigid model to the input laparoscopy image by putting it in a canonical pose. In hepatic laparosurgery, the laparoscope is inserted in a port around the belly button and is directed to the liver. The canonical pose thus describes an approximate configuration of the liver relative to the belly button computed from the preoperative radiological data. Third, the contour-based refinement ($c\mathtt {-}refine$) registers the liver model close to a solution by iterating on the deformation and contour constraints’ projection mappings. Fourth, the contour-and-shading-based refinement ($cs\mathtt {-}refine$) improves the registration using the locally valid shading cue by iterating on the deformation, contour and shading constraints’ projection mappings. An iteration is very fast to compute because each projection is computed in closed-form and involves few parameters.

Fig. 1.

Registration algorithm. $\epsilon _{c}=10^{-3}$, $\epsilon _{cs}=10^{-3}$ and $\mathtt {maxiter}=10^{2}$ are respectively the thresholds in parameter space and the maximum number of iterations to stop refinements.

3.2 Constraint Mappings

Deformation. We solve a tetrahedron’s deformation using an approximated projection mapping $\varPi _{\text {deformation}}(\mathcal {M})\rightarrow \varOmega _{\text {deformation}}$. We write this approximated projection mapping by linearising the non-linear $\phi _{\text {deformation}}$ at current $\mathcal {M}$ and solving it [10]. This yields the exact deformation step along the gradient direction of $\phi _{\text {deformation}}$ to correct the model’s shape.

Contour. We minimise the distance between a contour pair with a mapping $\varPi _{\text {contour}}(\mathcal {M})\rightarrow \varOmega _{\text {contour}}$. This mapping uses an iteration of ICP. The mapping projects each 3D point related to $\mathcal {C}$ onto the sight-line drawn from $\mathcal {C}^{*}$ closest to the 3D point along its surface normal. We use a mapping $\varPi _{\text {point}}(\mathcal {M})~\rightarrow ~\varOmega _{\text {point}}$ to solve a contour segment’s given end point matches, if any. This mapping projects a 3D point onto its sight-line through the closest path.

Shading. It is possible to solve the shading constraint of a triangle by updating either its depth or orientation. Once the contours are aligned, we assume that the triangle’s orientation is reasonably close to its final value. Consequently, so is the term $\mathbf {n}^{\top }\,\mathbf {\bar{q}}$. We thus solve the shading constraint by updating the depth of the triangle’s centroid. $\varPi _{\text {shading}}(\mathcal {M})~\rightarrow \varOmega _{\text {shading}}$ is derived by substituting (2) into $\phi _{\text {shading}}$ under the previous assumption. This yields the depth correction $\delta$:

$$\begin{aligned} \delta \,=\, \root \of {\,-\,\frac{\gamma }{\eta ^{*}}\,\mathbf {n}^{\top }\,\mathbf {\bar{q}}\,} \,\,-\,\, \Vert \mathbf {Q}\Vert \end{aligned}$$

(4)

which we use to translate the triangle along the direction $\mathbf {\bar{q}}$.

Fig. 2.

Quantitative registration experiments with the preoperative liver model. White arrows show the laparoscope’s look at directions.

Fig. 3.

3D errors versus different initialisations (left) which also cover the range of the canonical pose. Manual rigid registration error for patient B’s deformed shape seen in Fig. 2 (right).

Fig. 4.

Qualitative in-vivo registration experiments. The augmented images show the registered tumours and veins seen through the translucent liver models. The second row is for our algorithm and the third row for the rigid manual registrations.

4 Experimental Results

We conducted quantitative simulations using two patients’ segmented liver models from their preoperative CT scans and qualitative in-vivo experiments with the laparosurgery images of a patient. Quantitative evaluation on in-vivo hepatic laparosurgery images is difficult and does not exist in the literature.

Quantitative results. Patients’ liver models are deformed to different shapes used as ground-truths and their synthetic images are rendered. Each column in Fig. 2 shows one registration obtained from the canonical pose. In Fig. 2, the first row shows the ground-truth images with marked contours (yellow for silhouette, red for ridges, blue for ligament) inside the field of view rectangle (cyan). The second and third rows show the colour mapped volumetric registration errors (mm) from a different viewpoint. We observe that the preoperative model’s inner structures are registered within 1 cm error. This corresponds to about $4\%$ registration error regarding the greatest transverse diameter of the liver. We tested our algorithm for different initial poses chosen with progressively increasing displacements from the ground-truth. A $1\%$ displacement in Fig. 3 corresponds to a 10 mm translation and 10 degrees of rotation about a random axis. Figure 3 also shows (right) colour mapped rigid registration error (mm) for patient B’s deformed shape seen in Fig. 2 which is worse than our algorithm’s registration.

Qualitative results. Figure 4 shows the in-vivo liver registration experiments. Each column shows a different registration. The second row shows the registered liver models (initialised from the canonical pose) on the input images. The third row shows the state-of-the-art manual rigid registration results. We observe that the manual rigid registration cannot align the models as good as our algorithm.

5 Conclusion

We proposed the first preoperative to intraoperative deformable registration algorithm from a single laparoscopy image by evolving a deformable model using the contour and shading cues. Our algorithm registers inner structures of the liver within 1 cm error. Registration takes 2 to 3 min including markings. As future work, we shall study on (i) automating markings, (ii) localising and using laparoscopic tooltips’ positions as new constraints and (iii) adapting the preoperative model to the topological changes occurring during the surgery.