1 Introduction

We view aging as the passage of time that is characterized by a multifaceted set of neurobiological cascades that occur at different rates in different people, together with complex and often interdependent effects on cognitive decline [1]. The distinction between disease-related processes and “normal” aging is important for etiology and diagnostics, however, the boundaries of aging and neurodegenerative diseases remain difficult to separate [7]. Some of the aging-related neurobiological changes may be the result of developing pathology, such as preclinical Alzheimer’s disease (AD) or incipient cerebrovascular disease. Other changes may have similarities to certain diseases, while arising from a different etiology than the pathological pathway linked to disease, such as dopamine loss in Parkinson’s disease. In this article, we investigate if it is possible to use magnetic resonance imaging to differentiate disease-related changes in brain morphology from those associated with normal aging in the same set of individuals.

Important for the distinction between what is normal and what may be an indicator of disease is to consider that brain structural changes are not uniform across the brain. Regions that accommodate neural systems with high susceptibility to deleterious factors are likely affected by disease as well as aging-related changes. At the same time, there are other structures, which are known to show effects of aging but are relatively spared in a neurodegenerative disease, e.g., the striatum in Alzheimer’s disease [7]. Capitalizing on the regional heterogeneity in aging and disease-related effects, joint modeling of changes across multiple structures rather than focusing on single structures in isolation is a promising avenue to identifying general patterns that are best at distinguishing aging from disease. We assume that there are a number of underlying processes that cause these changes, which we model as latent factors. It is further known that aging and disease can cause different changes in subregions of anatomical structures. For instance, recent analysis on high-field MRI suggests that hippocampal subfields subiculum and CA1 are associated with AD and CA3/DG with aging [7]. While volume measurements of the entire hippocampus do not permit to distinguish between such variations in subregions, they cause shape changes in the structure that can potentially be identified by shape descriptors.

To obtain a discriminative characterization of neuroanatomy, we work with BrainPrint [11]; a composition of spectral shape descriptors from the Laplace-Beltrami operator. The change in shape is studied in cross-sectional and longitudinal designs. We hypothesize that observed, high-dimensional shape changes are governed by a few underlying, latent processes. We identify neuroanatomical processes that are best associated to aging and disease by maximizing the covariance between morphology and response variables, yielding the projection of the data to latent structures. An alternative to the latent factor model would be to directly estimate changes in aging from clinically normal subjects, however, it is presumed that preclinical forms of disease are likely to be present in normals so that a pure aging process cannot be measured [7]. In this work, we focus on Alzheimer’s disease but the developed technology is of general nature.

Related Work: A model for healthy aging based on image voxels and relevance vector regression was used for the prediction of Alzheimer’s disease in [6]. The longitudinal progression of AD-like patterns in brain atrophy in normal aging subjects and, furthermore, an accelerated AD-like atrophy in subjects with mild cognitive impairment (MCI) was reported in [2]. A framework for the spatiotemporal statistical analysis of longitudinal shape data based on diffeomorphic deformation fields was presented in [4].

2 Method

We are given structural magnetic resonance (MR) images from N subjects, \(I_1, \ldots , I_N\), with corresponding response variables, \(R_1, \ldots , R_N\), including age and scores from neuropsychological tests. MR scans for each subject n are available for m time points, \(I_n^1, \ldots , I_n^m\). Our objective is to find patterns of neuroanatomical change associated to aging and dementia.

2.1 Longitudinal Change in Brain Morphology

We use BrainPrint [11] as representation of brain morphology based on the automated segmentation of anatomical brain structures with FreeSurfer [5]. BrainPrint uses the spectral shape descriptor shapeDNA [10] to capture shape information from cortical and subcortical structures. ShapeDNA is computed from the intrinsic geometry of an object by calculating the Laplace-Beltrami spectrum

$$\begin{aligned} \varDelta f = - \lambda f . \end{aligned}$$
(1)

The solution consists of eigenvalue \(\lambda _i \in \mathbb {R}\) and eigenfunction \(f_i\) pairs, sorted by eigenvalues, \(0 \le \lambda _1 \le \lambda _2 \le \ldots \) The first l non-zero eigenvalues, computed with the finite element method, form the ShapeDNA: \({\varvec{\lambda }}= (\lambda _1, \dots , \lambda _l)\). We normalize the eigenvalues to make the representation independent of the objects’ scale and therefore focus on the shape information, \(\lambda ' = \text {vol}^{\frac{2}{d}} \lambda \), where vol is the Riemannian volume of the d-dimensional manifold (i.e., the area for 2D surfaces) [10]. We further linearly re-weight the eigenvalues, \(\hat{\lambda }_i = \lambda _i' / i\), to balance the impact of higher eigenvalues that show higher variance [11]. The morphology of each scan I is described by the concatenation of the spectra of \(\eta \) brain structures \(\varLambda = ({\varvec{\lambda }}_1, \ldots , {\varvec{\lambda }}_{\eta })\), yielding a \(D = l \cdot \eta \) dimensional representation.

In addition to the cross-sectional BrainPrint \(\varLambda _n\) for subject n, we also compute the longitudinal change in morphology. Given the BrainPrints \(\varLambda ^1_n, \ldots , \varLambda ^m_n\) for m time points, we use linear least squares fitting to estimate the slope \(\mathbf{s}_n\). The slope has the same dimensionality D as the original shape characterization and captures longitudinal morphological change within a subject. We process follow-up scans with the longitudinal processing stream in FreeSurfer [9], which avoids processing bias in the surface reconstruction and segmentation by an unbiased, robust, within-subject template creation.

2.2 Latent Factor Model

We consider observed neuroanatomical changes as the result of a combination of a few underlying processes related to aging and disease that are shared across the population. The response variables are chronological age and performance of the mini-mental state examination (MMSE), a clinical screening instrument for loss of memory and intellectual abilities (from hereon simply referred to as age and dementia, respectively). Our objective is to extract latent factors that account for much of the manifest factor variation. Latent variable models such as factor analysis, principal component analysis (PCA), or independent component analysis are a natural choice for this task. However, these models only focus on describing the data matrix and do not take the response variables into account. The extracted components may therefore well explain the variation in the data but may not be associated to specific variations in aging or dementia. To address this issue, we use projections to latent structures (PLS) [12], also known as partial least squares, which combines information about the variation of both the predictors and the responses, and the correlations among them.

The rows of the data matrix \(X \in {\mathbb R}^{N \times D}\) are the baseline BrainPrint \(\varLambda _n\) or the slopes \(\mathbf{s}_n\), depending on a cross-sectional or longitudinal analysis. The matrix \(Y \in {\mathbb R}^{N \times M}\) gathers associated responses, with M the dimensionality of the responses. PLS regression searches for a set of components or latent vectors that performs a simultaneous decomposition of the data matrix X and the response matrix Y with the constraint that these components explain as much as possible of the covariance between X and Y. The underlying assumption of PLS is that the observed data is generated by a system or process, which is driven by a small number of latent variables. For K latent factors and mean centered matrices X and Y, the PLS equation model is

$$\begin{aligned} \mathbf{x}_n&= \sum _{k=1}^K t_{n,k} \mathbf{p}_k + \mathbf{e}_n&X&= T P^\top + E \end{aligned}$$
(2)
$$\begin{aligned} \mathbf{y}_n&= \sum _{k=1}^K u_{n,k} \mathbf{q}_k + \mathbf{f}_n&Y&= U Q^\top + F, \end{aligned}$$
(3)

where we show next to the matrix notation also the vector notation to highlight the notion of neuroanatomy \(\mathbf{x}_n\) being explained by a linear combination of a few processes \(\mathbf{p}_k\). The loadings matrix \(P \in {\mathbb R}^{D \times K}\) contains all the K processes. The scores matrix \(T \in {\mathbb R}^{N \times K}\) presents a lower, K-dimensional embedding of a subject. The matrices \(U \in {\mathbb R}^{N \times K}\) and \(Q \in {\mathbb R}^{M \times K}\) contain scores and loadings with respect to the response variable. E and F are matrices of residuals. The relation between the scores T and the original variables X is expressed as \(T = X W\) with the weight matrix W. The weights provide an interpretation of the scores and are essential for understanding which of the original variables are important.

The PLS method is an iterative procedure that finds, in a first step, the latent score vectors \(\mathbf{t}_1\) and \(\mathbf{u}_1\) by maximizing the sample covariance among predictors and responses

$$\begin{aligned}{}[\hat{\mathbf{r}}, \hat{\mathbf{s}}] = \mathop {\arg \,\mathrm{max}}\limits _{\Vert \mathbf{r}\Vert = \Vert \mathbf{s}\Vert = 1} [cov(X \mathbf{r}, Y \mathbf{s})]^2 = \mathop {\arg \,\mathrm{max}}\limits _{\Vert \mathbf{r}\Vert = \Vert \mathbf{s}\Vert = 1} [ \mathbf{r}^\top X^\top Y \mathbf{s}/ N]^2, \end{aligned}$$
(4)

where \(\mathbf{t}_1 = X \hat{\mathbf{r}}\) and \(\mathbf{u}_1 = Y \hat{\mathbf{s}}\). From Eq. (4), we see that \(\hat{\mathbf{r}}\) and \(\hat{\mathbf{s}}\) correspond to the first pair of left and right singular vectors, which permits an efficient computation. After the first score vectors were obtained, the matrices are deflated by subtracting their rank-one approximations based on \(\mathbf{t}_1\) and \(\mathbf{u}_1\). Several algorithms exist that vary in the details on the iterative scheme, where we use SIMPLS [3], which directly deflates the cross-product \(X^\top Y\) and therefore makes the factors easier to interpret as linear combinations of the original variables.

PLS is related to PCA, which maximizes, \(\max _{\Vert \mathbf{r}\Vert = 1} var(X \mathbf{r})\). PCA finds principal components that explain the data well, but does not account for corresponding response variables, which makes the association of components to specific processes difficult and limits the predictive power. Canonical correlation analysis (CCA) takes the response variable into account and maximizes the correlation, \(\max _{\Vert \mathbf{r}\Vert = \Vert \mathbf{s}\Vert = 1} cor(X \mathbf{r}, Y \mathbf{s})^2\). The maximization of the covariance in PLS and the correlation in CCA are similar, \(cov(X \mathbf{r}, Y \mathbf{s})^2 = var(X \mathbf{r}) cor(X \mathbf{r}, Y \mathbf{s})^2 var(Y \mathbf{s})\), where PLS also requires to explain the variances.

3 Results

We perform experiments on data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) [8]. We select all subjects from the ADNI1 dataset with baseline scans and follow-up scans after 6, 12, and 24 months, resulting in \(N=393\) subjects and 1,572 MRI scans. The average age is 75.4 years (SD = 6.31), with 221 male and 172 female subjects, and diagnosis HC = 133, MCI = 175, AD = 85. We use meshes from \(\eta =23\) brain structures in the multivariate analysis. Per mesh, we compute \(l=5\) eigenvalues. To a priori give equal importance to all variables in X, we center them and scale them to unit variance. We jointly model age and MMSE as response variables in Y. We set the number of PLS components \(K=4\) according to results from explained variance in X and Y, together with an evaluation of the model complexity by computing the mean squared error with 5-fold cross-validation and 20 Monte-Carlo repetitions.

Table 1. Pearson’s correlation of the four cross-sectional and longitudinal processes with MMSE and age. Significant correlations (\(p < 0.01\)) are in bold face.
Full size table

To understand the identified components, we investigate the scores in matrix T, which form a four-dimensional embedding of each subject. Table 1 reports the correlation of the low-dimensional embedding with respect to age and MMSE. The first cross-sectional process is significantly associated to MMSE and age. The correlations vary in the sign, which is explained by the general decrease in cognitive ability with increasing age. The second and fourth cross-sectional processes only show significant correlations with MMSE, while the third one shows a significant correlation with age. For the longitudinal processes, each one only shows significant correlations with one of the response variables, yielding two dementia (first and third) and two aging (second and fourth) processes. Overall, the correlation for MMSE is higher than for age.

Fig. 1.
figure 1

Lateral view on longitudinal processes on the left hemisphere. Colors are summed up weights across eigenvalues and signify importance.

Full size image
Fig. 2.
figure 2

Medial view on longitudinal processes on the left hemisphere. Colors are summed up weights across eigenvalues and signify importance.

Full size image

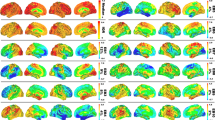
We will focus on the longitudinal progression in the following analysis because it more accurately reflects true aging-related brain changes, while cross-sectional estimates can be subject to selective drop out and biased sampling. To gain insights about the neuroanatomical change evoked by the latent factors, we study the weight matrix W, where numerically large weights indicate the importance of X variables [12]. Figures 1 and 2 illustrate a lateral and medial view of the four processes by coloring the brain structures according to their weights, summed up across eigenvalues. The first and third processes relate to progression of dementia (Table 1). The first process describes opposing effects on hippocampus and amygdala on the one hand, and the lateral and third ventricle on the other hand. This pattern likely reflects the typical brain changes associated with dementia: shrinkage of the hippocampus and amygdala together with an expansion of the ventricular spaces. When comparing the first and third process, we have to consider that one is positively and one is negatively correlated with MMSE, i.e., the colors are inverted. This suggests the existence of two separable dementia-related processes with inverse effects on the amygdala and accumbens. For the aging processes (second and fourth), the weights of the hippocampus and amygdala are notably lower in comparison to the dementia processes. Aging processes mainly evoke shape changes in the ventricular system, where process two exhibits higher weights for lateral ventricles and process four for the third ventricle.

Finally, we evaluate the predictive performance of the latent factor model with cross-validation and compare it to traditional multiple linear regression (MLR) on BrainPrint. We further compare to the prediction with volume measurements instead of shape in the PLS model. Figure 3 shows the mean absolute prediction error for age and MMSE on cross-sectional data. The prediction with PLS BrainPrint yields significant improvements over PLS volume and MLR BrainPrint, highlighting the advantages of neuroanatomical shape characterization and the latent factor model.

Fig. 3.
figure 3

Prediction results from cross-validation for MMSE (left) and age (right). Bars show mean absolute error and lines show standard error. * and *** indicate significance levels at 0.05 and 0.001.

Full size image

4 Conclusion

We presented a method for identifying latent processes that cause structural changes associated with aging and dementia in cross-sectional and longitudinal designs. Neuroanatomical changes were computed with the BrainPrint, and subsequently projected to latent structures by accounting for the response variables. Taken together, the results reveal the existence of four latent processes that separate the progression of dementia from normal aging and that can be clearly distinguished neuroanatomically. The large majority of previous work has used univariate analyses to relate morphology of individual structures or voxels to aging and dementia. Our work demonstrates the importance of multivariate analysis of multiple brain structures to accurately capture related, but spatially distributed, morphological changes of brain shapes. Finally, the latent factor model with BrainPrint yieldied significantly better prediction results. Future work may now investigate possible neuropathological correlates of the morphological processes identified in this paper (i.e., tau pathology versus accumulation of amyloid).