Kernel Generalized-Gaussian Mixture Model for Robust Abnormality Detection

Abstract

Typical methods for abnormality detection in medical images rely on principal component analysis (PCA), kernel PCA (KPCA), or their robust invariants. However, typical robust-KPCA methods use heuristics for model fitting and perform outlier detection ignoring the variances of the data within principal subspaces. In this paper, we propose a novel method for robust statistical learning by extending the multivariate generalized-Gaussian distribution to a reproducing kernel Hilbert space and employing it within a mixture model. We propose expectation maximization to fit our kernel generalized-Gaussian mixture model (KGGMM), using solely the Gram matrix and without the explicit lifting map. We exploit the KGGMM, including component means, principal directions, and variances, for abnormality detection in images. The results on 4 large publicly available datasets, involving retinopathy and cancer, show that our method outperforms the state of the art.

The authors are grateful for funding from Aditya Imaging Information Technologies. S.P. Awate thanks funding from IIT Bombay Seed Grant 14IRCCSG010.

1 Introduction and Related Work

Abnormality detection in medical images [3, 10] is a one-class classification problem [13], where training relies solely on data from the normal class. This is motivated by the difficulty of learning a model of abnormal image appearances because of their tremendous variability. Typical methods for abnormality detection rely on principal component analysis (PCA) or kernel PCA (KPCA) [4].

In clinical applications involving large training datasets intended to represent normal images, outliers naturally arise because of errors in specimen preparation (e.g., slicing or staining in microscopy), patient issues (e.g., motion), imaging artifacts, and manual mislabeling of abnormal images as normal. KPCA is very sensitive to outliers in the data, leading to unreliable inference. Some methods for abnormality detection [11] rely on PCA, assuming training sets to be outlier free. Typical robust KPCA (RKPCA) methods [3, 5, 7,8,9] are heuristic in their modeling and inference. For instance, [7,8,9] employ adhoc rules for explicitly detecting outliers in the training set. While [2, 5] describe RKPCA based on iterative data-weighting, using distance to the mean, the weighting functions seem adhoc. CHLOE [9] also uses rules involving free parameters to weight data based on kurtosis of individual features. One method [2] distorts data by projecting it onto a sphere (unit norm). In contrast, we propose a method using statistical (mixture) modeling to infer robust estimates of means and covariances. During estimation, our method implicitly, and optimally, reweights the data, to reduce the effect of outliers, based on the covariance structure of the data.

Typical abnormality detection methods [3, 5, 7, 8] compute robust means and modes of variation, but fail to compute and exploit variances along the modes. Thus, they perform poorly when the abnormal data lies within the subspace spanned by the normal data. In contrast, our method optimizes, in addition to means and modes, the associated variances to improve performance. Some methods [3, 6] for robust PCA model learning rely on $L_p$ norms ($p \ge 1$) in input space. In contrast, our method exploits $L_q$ quasi-norms ($q > 0$) coupled with Mahalanobis distances in a reproducing kernel Hilbert space (RKHS).

Some kernel methods for abnormality detection rely on the support vector machine (SVM), e.g., one-class SVM [13] and support vector data description (SVDD) [15]. Unlike KPCA, these SVM methods model only a spherical distribution or decision boundary in RKHS and, thus, are inferior to KPCA theoretically and empirically [4]. Also, the SVM methods lack robustness to outliers in the training data. In contrast, our method is robust to outliers and enables us to model arbitrarily curved distributions as well as decision boundaries in RKHS.

We propose a novel method for robust statistical learning by extending the multivariate generalized-Gaussian distribution to a RKHS for mixture modeling. We propose expectation maximization (EM) to fit our kernel generalized-Gaussian mixture model (KGGMM), using solely the Gram matrix, without the explicit lifting map. We model geometric and photometric properties of image texture via standard texton-label histograms [16]. We exploit the KGGMM, including component means, principal directions, and variances, for abnormality detection. The results on 4 large publicly available datasets, involving retinopathy and cancer, show that our method outperforms the state of the art.

2 Methods

In $\mathbb {R}^D$, the generalized Gaussian [12] is parametrized by the mean $\mu \in \mathbb {R}^D$, covariance matrix $C \in \mathbb {R}^{D \times D}$, and shape $\rho \in \mathbb {R}_{> 0}$; Gaussian ($\rho$ = 2), Laplacian ($\rho$ = 1), uniform ($\rho \rightarrow \infty$). We extend the generalized Gaussian to RKHS for mixture modeling. We exploit $\rho < 1$, when the distribution has increased concentration near the mean and heavier tails, for robust fitting amidst outliers.

2.1 Kernel Generalized Gaussian (KGG)

Consider a set of N data points $\{ x_n \in \mathbb {R}^D \}_{n=1}^N$ in input space. Consider a Mercer kernel $\kappa (\cdot ,\cdot )$ that implicitly maps the data to a RKHS $\mathcal {H}$ such that each datum $x_n$ gets mapped to $\phi (x_n)$. Consider 2 vectors in RKHS: $f := \sum _{i=1}^I \alpha _i \phi (x_i)$ and $f' := \sum _{j=1}^J \beta _j \phi (x_j)$. The inner product $\langle f, f' \rangle _{\mathcal {H}} := \sum _{i=1}^I \sum _{j=1}^J \alpha _i \beta _j \kappa (x_i, x_j)$. The norm $|| f ||_{\mathcal {H}} := \sqrt{ \langle f, f \rangle _{\mathcal {H}} }$. When $f,f' \in \mathcal {H} \backslash \{ 0 \}$, let $f \otimes f'$ be the rank-one operator defined as $f \otimes f' (g) := \langle f',g \rangle _{\mathcal {H}} f$. The generalized Gaussian extended to RKHS is parametrized by shape $\rho \in \mathbb {R}_{>0}$, mean $\mu \in \mathcal {H}$, and covariance operator $C = \sum _{q=1}^Q \lambda _q v_q \otimes v_q$, where $\lambda _q$ is the q-th largest eigenvalue of covariance C, $v_q$ is the corresponding eigenfunction, and $Q < N$ is a regularization parameter. We set Q to the number of principal eigenfunctions that capture $95\%$ of the eigenspectrum energy. For $f \in \mathcal {H}$, the squared Mahalanobis distance is $d_{\mathcal {M}}^2 (f; \mu , C) := \langle f - \mu , C^{-1} (f - \mu ) \rangle _{\mathcal {H}}$, where $C^{-1} = \sum _{q=1}^{Q} (1 / \lambda _q) v_q \otimes v_q$ is the sample inverse-covariance operator. Then, our generalized Gaussian in RKHS is

$$\begin{aligned} P_{\mathcal {G}} (f; \mu , C, \rho ) := \frac{\delta (\rho /2)}{2 |C|^{0.5}} \exp \left[ - \Big ( \eta (\rho /2) d_{\mathcal {M}}^2 (f; \mu , C) \Big )^{\rho /2} \right] , \text{ where } \end{aligned}$$

(1)

$\delta (r) := r \varGamma (2/r) / (\pi \varGamma (1/r)^2)$, $|C| := \prod _{q=1}^Q \lambda _q$, and $\eta (r) := \varGamma (2/r) / (2 \varGamma (1/r))$.

2.2 Kernel Generalized-Gaussian Mixture Model (KGGMM)

We propose to model the distribution of data $x := \{ x_n \in \mathbb {R}^D \}_{n=1}^N$ using a Mercer kernel to implicitly map the data to a RKHS, i.e., $\{ \phi (x_n) \in \mathcal {H} \}_{n=1}^N$, and then representing the distribution in RKHS using a mixture of KGG distributions. Consider a KGG mixture model with K components, where the k-th component is the KGG $P_{\mathcal {G}} (\cdot ; \mu _k, C_k, \rho )$ coupled with weight $\omega _k \in \mathbb {R}_{\ge 0}$, such that $\omega _k \le 1$ and $\sum _{k=1}^K \omega _k := 1$. For each datum $x_n$, let $Z_n$ be the hidden (label) random variable indicating the mixture component from which the datum was drawn.

Each mean $\mu _k$ must lie in the span of the mapped data $\{ \phi (x_i) \}_{i=1}^N$. Thus, we represent each mean, using coefficient vector $\beta _k \in \mathbb {R}^N$, as $\mu _k (\beta _k) := \sum _{i=1}^N \beta _{ki} \phi (x_i)$. Estimating $\mu _k$ is then equivalent to estimating $\beta _k$. We represent each covariance operator $C_k$ using its Q principal eigenvectors $\{ v_{kq} \in \mathcal {H} \}_{q=1}^Q$ and eigenvalues $\{ \lambda _{kq} \in \mathbb {R}_{>0} \}_{q=1}^Q$. Each eigenvector of $C_k$ must lie in the span of the mapped data. So, we represent the q-th eigenvector of $C_k$, using coefficient vector $\alpha _{kq} \in \mathbb {R}^N$, as $v_{kq} (\alpha _{kq}) := \sum _{j=1}^N \alpha _{kqj} \phi (x_j)$. Estimating $v_{kq}$ is equivalent to estimating $\alpha _{kq}$.

Model Fitting. We propose EM to fit the KGGMM to the mapped data to maximize the likelihood function. The prior label probability $P (z_n = k) := \omega _k$. The complete-data likelihood $P (z, x) := \prod _{n=1}^N P (z_n) P_{\mathcal {G}} (\phi (x_n); \mu _{z_n}, C_{z_n}, \rho )$. We show that EM does not need the map $\phi (\cdot )$, but only the Gram matrix G, where $G_{ij} := \langle \phi (x_i), \phi (x_j) \rangle _{\mathcal {H}} = \kappa (x_i, x_j)$. In our framework, $\rho$ is a free parameter (fixed before EM) that we tune using training data; $\rho < 1$ gives best results.

Initialization. We use kernel k-means to initialize the parameters. We initialize (i) mean $\mu _k$ to the k-th cluster center, (ii) weight $\omega _k$ to the fraction of data assigned to cluster k, and (iii) covariance $C_k$ using KPCA on cluster k.

E Step. At the t-th iteration, let the set of parameters be $\theta ^t := \{ \beta _k^t \in \mathbb {R}^N, \{ \alpha _{kq}^t \in \mathbb {R}^N \}_{q=1}^Q, \{ \lambda _{kq}^t \in \mathbb {R} \}_{q=1}^Q, \omega _k^t \in \mathbb {R} \}_{k=1}^K$. Let $\alpha _k$ denote a $N \times Q$ matrix, representing the Q eigenfunctions of $C_k$, such that its q-th column is $\alpha _{kq}$. Let $\lambda _k$ denote a $Q \times Q$ diagonal matrix, representing the Q eigenvalues of $C_k$, such that its q-th diagonal element is $\lambda _{kq}$. Given $\theta ^t$, the E step defines the function $Q (\theta ; \theta ^t) := E_{P (Z | x, \theta ^t)} \left[ \log P (Z, x; \theta ) \right]$ that can be simplified to

$$\begin{aligned} \sum _{n=1}^N \sum _{k=1}^K \gamma _{nk}^t \left[ \log \omega _k - \sum _{q=1}^Q \left[ \frac{ \log (\lambda _{kq}) }{ 2 } + \left( \eta \left( \frac{\rho }{2} \right) \frac{ \langle \phi (x_n) - \mu _k (\beta _k), v_{kq} (\alpha _{kq}) \rangle _{\mathcal {H}}^2 }{ \lambda _{kq} } \right) ^{\frac{\rho }{2}} \right] \right] \end{aligned}$$

excluding terms independent of $\theta$, and where the membership of datum $x_n$ to mixture component k, given the current parameter estimate $\theta ^t$, is the posterior $\gamma _{nk}^t := P (Z_n = k | x_n, \theta ^t) = \omega _k^t P_{\mathcal {G}} (\phi (x_n); \mu _k, C_k, \rho ) / P (x_n; \theta ^t)$ by Bayes rule.

M Step. The M step updates parameter estimates to $\theta ^{t+1} := \arg \max _{\theta } Q (\theta ; \theta ^t)$ subject to constraints on: (i) weights, such that $\omega _k \ge 0, \sum _k \omega _k = 1$, (ii) eigenvalues, such that $\lambda _{kq} > 0$, and (iii) coefficients, such that eigenvectors $v_{kq} (\alpha _{kq})$ are unit norm ($||v_{kq} ||_{\mathcal {H}} = 1$) and mutually orthogonal ($\langle v_{kq}, v_{kr} \rangle _{\mathcal {H}} = 0, \forall q \ne r$).

Estimating Weights. The optimal weights $\omega _k^{t+1}$ are given by the solution to $\arg \max _{\omega } \sum _{n=1}^N \sum _{k=1}^K \gamma _{nk}^t \log \omega _k$, subject to the positivity and sum-to-unity constraints. The method of Lagrange multipliers gives $\omega _k^{t+1} = \sum _{n=1}^{N} \gamma _{nk}^t / N$.

Estimating Means. Given weights $\omega _k^{t+1}$, the optimal mean $\mu _k^{t+1} (\beta _k^{t+1})$ is given by $\beta _k^{t+1} := \arg \min _{\beta _k} \sum _n \gamma _{nk}^t \sum _q \left( (G_n^\top \alpha _{kq} - \beta _k^\top G \alpha _{kq})^2 / \lambda _{kq} \right) ^{\rho /2}$, where $G_n$ is the n-th column of the Gram matrix G. We optimize via gradient descent with adaptive step size (adjusted at each update) to ensure that each update improves the objective function value. When $\rho = 2$, the mean estimate is the (weighted) sample mean that is affected by outliers. As $\rho$ reduces, the effect of the outliers decreases in the objective function; the gradient term for an outlier j is weighted down far more than for the inliers, leading to robust estimates.

Estimating Eigenvectors. Given weights $\omega _k^{t+1}$ and means $\mu _k^{t+1} (\beta _k^{t+1})$, the optimal set of eigenfunctions $v_k^{t+1} (\alpha _k^{t+1})$ is given by $\alpha _k^{t+1} := \arg \min _{\alpha _k}$ $\sum _n \gamma _{nk}^t \left[ (\alpha _k^\top G_n - \alpha _k^\top G \beta _k^{t+1})^\top \lambda _k^{-1} (\alpha _k^\top G_n - \alpha _k^\top G \beta _k^{t+1}) \right] ^{\rho /2}$, subject to orthonormality constraints on the set of eigenfunctions $\{ v_{kq} (\alpha _{kq}) \}_{q=1}^Q$. We optimize via projected gradient descent with adaptive step size, where each step (i) first uses a gradient-descent step to update matrix $\alpha _k$ to $\widetilde{\alpha }_k$, implicitly updating the eigenfunctions to $\{ \widetilde{v}_{kq} (\widetilde{\alpha }_{kq}) \}_{q=1}^Q$, and (ii) then updates $\widetilde{\alpha }_k$ to $\alpha _k^{t+1}$ by projecting the eigenfunction set $\{ \widetilde{v}_{kq} (\widetilde{\alpha }_{kq}) \}_{q=1}^Q$ onto the space of orthogonal eigenfunction bases. In Euclidean space, the projection of a set of Q vectors, represented as the columns of a matrix M, onto the space of Q orthogonal vectors is given by $L R^\top$ where matrices L and R comprise the left and right singular vectors in the singular value decomposition (SVD) of M. In Euclidean space, $L R^\top = M (M^\top M)^{-0.5}$. In a RKHS, we replace the SVD by the kernel SVD as follows.

Consider Q functions $F := \{ f_q \in \mathcal {H} \}_{q=1}^Q$ that are not orthogonal. Let the kernel SVD of F be the operator $\sum _{q=1}^Q s_q a_q \otimes b_q$, where the singular values are $s_q \in \mathbb {R}_{\ge 0}$, and the left and right singular vectors are the orthonormal sets $\{ a_q \in \mathcal {H} \}_{q=1}^Q$ and $\{ b_q \in \mathbb {R}^Q \}_{q=1}^Q$, respectively. Consider the $Q \times Q$ matrix Y where $Y_{ij} := \langle f_i, f_j \rangle _{\mathcal {H}}$. The matrix Y also equals $\sum _{q'=1}^Q s_{q'} b_{q'} \otimes a_{q'} (\sum _{q''=1}^Q s_{q''} a_{q''} \otimes b_{q''})$ that reduces to $\sum _{q=1}^Q s_q^2 b_q b_q^\top$ because of the orthogonality of the left singular vectors. Thus, an eigen decomposition of the matrix Y yields the eigenvalues as $s_q^2$ and the eigenvectors as $b_q$. Subsequently, we observe that the required projection of F onto the space of orthogonal functions in RKHS is given by $\sum _{q=1}^Q s_q a_q \otimes b_q (Y^{-0.5}) = \sum _{q=1}^Q s_q a_q \otimes b_q (\sum _{q'=1}^Q s_{q'}^{-1} b_{q'} b_{q'}^\top ) = \sum _{q=1}^Q a_q \otimes b_q$. In practice, when we represent the eigenvectors using the $N \times Q$ matrix $\widetilde{\alpha }_k$, the matrix $Y = \widetilde{\alpha }_k^\top G \widetilde{\alpha }_k$ and the projection gives us $\alpha _k^{t+1} = \widetilde{\alpha }_k (Y)^{-0.5}$.

Estimating Variances. Given weights $\omega _k^{t+1}$, means $\mu _k^{t+1} (\beta _k^{t+1})$, and eigenfunctions $v_k^{t+1} (\alpha _k^{t+1})$, each optimal eigenvalue is given by $\lambda _{kq}^{t+1} := \arg \min _{\lambda _{kq} > 0} \sum _{n=1}^N \gamma _{nk}^t [ 0.5 \log (\lambda _{kq}) + ( \eta (\rho / 2) a_{nkq}^2 / \lambda _{kq} )^{\rho /2} ]$, where $a_{nkq} := G_n^\top \alpha _{kq}^{t+1} - (\beta _k^{t+1})^\top G \alpha _{kq}^{t+1}$. We optimize via projected gradient descent.

KGGMM for Abnormality Detection. We use the KGGMM with a small number of mixture components K, such that each component k models a significant fraction of the data, i.e., $\omega _k$ are not close to zero and comparable for different components k. After KGGMM fitting, we define a decision boundary $\mathcal {B}$ enclosing the normal class by a threshold $\tau$ on the minimum Mahalanobis distance across all K mixture components, such that, for a chosen component k, 98.5% of the probability mass lies within $\mathcal {B}$. $\tau$ varies with $\rho$; for the univariate Gaussian ($\rho = 2$) and variance $\sigma ^2$, $\tau$ limits the distance to $2.5 \sigma$ from the component-k mean. For the univariate generalized Gaussian, $\tau$ can be computed via the inverse cumulative distribution function that is known analytically. Because $\tau$ relies on Mahalanobis distance that is independent of scale, $\tau$ naturally extends to the multivariate case. Thus, $\mathcal {B}$ is set automatically via $\rho$ and $\theta$.

3 Results and Discussion

We evaluate our method for abnormality detection on simulated data and 4 large publicly available medical image datasets. Indeed, the training, i.e., model learning, for abnormality detection methods relies solely on data from the normal class, which includes outliers and mislabeled data incorrectly labeled to the normal class. We compare our KGGMM method with 7 other methods: (i) KGG, which is a special case of KGGMM with $K = 1$, (ii) standard KPCA [14], which is a special case of KGG when $\rho = 2$, (iii) Huang et al.’s RKPCA [5], (iv) one-class regularized kernel SVM [13], (v) regularized kernel SVDD [15], (vi) 2-class regularized kernel SVM, and (vii) CHLOE: a software tuned for outlier detection in images [9]. We use cross validation to tune free parameters underlying all methods, i.e., concerning the kernel, $\rho$ (for KGGMM), and SVM regularization.

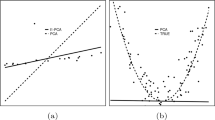
Results on Simulated Data. We simulate data in 2D Euclidean space to mimic what a real-world dataset would lead to in RKHS (after kernel-based mapping). We simulate data (Fig. 1) from a Gaussian mixture having $K = 2$ components (normal class): mean (0, 5) and (5, 0), modes of variation as the cardinal axes, and standard deviations along the modes of variation as (0.25, 1.4) and (1.4, 0.25). We then contaminate the data with outliers of 2 kinds: (i) spread uniformly over the domain; (ii) clustered at a location far away. For training, the normal-class sample size is 5000 contaminated with 1000 outliers. For testing, the normal-class sample size is 5000 and abnormal-class sample size is 3000. The kernel is the Euclidean inner-product. Our KGGMM learning (with $K = 2$, $\rho = 0.6$) is far more robust to outliers, with a classification accuracy of $93 \%$, outperforming (i) KGG ($K = 1$, $\rho = 0.6$; accuracy $77 \%$), (ii) KPCA (accuracy $54 \%$), (iii) SVDD (accuracy $70 \%$), and (iv) 2-class SVM (accuracy $38 \%$).

Fig. 1.

Results on simulated data. Data from a 2D Gaussian mixture model (2 components, shown in blue and black) contaminated with outliers (red and green).

Fig. 2.

Retinopathy data: Messidor. (a)–(b) Normal images. (c)–(d) Images labeled normal, but are outliers. (e)–(f) Abnormal images.

Results on Real-World Medical Image Data. We use 4 large publicly available image datasets. We use 2 retinopathy datasets: Messidor (www.adcis.net/en/Download-Third-Party/Messidor.html; Fig. 2) and Kaggle (www.kaggle.com/c/diabetic-retinopathy-detection; Fig. 3). We use 2 endoscopy datasets for cancer detection: chromoendoscopy in Gastric cancer (aidasub-chromogastro.grand-challenge.org; Fig. 5) and confocal laser endomicroscopy in Barrett’s esophagus (aidasub-clebarrett.grand-challenge.org; Fig. 6) comprising normal images including intestinal metaplasia and 2 kinds of abnormal images including dysplasia (potentially leading to cancer) and neoplastic mucosa (advanced stage cancer). The figures show that all 4 datasets, even though carefully constructed, already have outliers in the normal class. We use the texton-based histogram feature, using patches ($9 \times 9$) to compute textons, to classify regions ($50 \times 50$) as normal or abnormal. We use the intersection kernel [1]. From each dataset, we select training sets with 12000 normal image regions and, to mimic a clinical scenario, contaminate it by adding another 5–10% of abnormal image regions mislabeled as normal. The test set has 8000 normal and 5000 abnormal images. KGGMM performs best when $\rho < 1$ in retinopathy (Fig. 4(a)) and endoscopy datasets (Fig. 7(a)). The abnormality-detection accuracy of KGGMM is significantly more than all other methods for retinopathy (Fig. 4(b)–(c)) and endoscopy data (Fig. 7(b)–(c)). In almost all cases, KGGMM (we use $K = 2$ for model simplicity) performs better than KGG.

Fig. 3.

Retinopathy data: Kaggle. (a)–(b) Normal images. (c)–(d) Images labeled normal, but are outliers. (e)–(f) Abnormal images.

Fig. 4.

Results on retinopathy data. Classification accuracy after learning on training sets contaminated with outliers, for: (a) KGGMM, Messidor, varying $\rho$, ($\rho$ = 2 is Gaussian); (b) all methods, Messidor; (c) all methods, Kaggle. The box plots show variability in accuracy with resampling (uniform random) training data (20 repeats).

Fig. 5.

Chromoendoscopy data: gastric cancer. (a)–(b) Normal images. (c)–(d) Images labeled normal, but are outliers. (e)–(f) Abnormal images.

Fig. 6.

Confocal endoscopy data: barrett’s esophageal cancer. (a)–(b) Normal images. (c)–(d) Images labeled normal, but are outliers. (e)–(f) Abnormal images.

Fig. 7.

Results on endoscopy data. Classification accuracy after learning on training sets contaminated with outliers, for: (a) KGGMM, gastric cancer, varying $\rho$, ($\rho$ = 2 is Gaussian); (b) all methods, gastric cancer; (c) all methods, esophageal cancer. Box plots show accuracies with resampling (uniform random) training data (20 repeats).

Conclusion. We have proposed a novel method for robust kernel-based statistical learning that relies on the generalization of the multivariate generalized Gaussian to RKHS for mixture modeling. We fit our KGGMM using EM, using solely the Gram matrix. We exploit KGGMM, including covariance operators, for abnormality detection in medical applications where a (small) fraction of training data is inevitably contaminated because of outliers and mislabeling. The results on 4 large datasets, in retinopathy and cancer, shows that KGGMM outperforms one-class classification methods (KPCA, one-class kernel SVM, kernel SVDD), 2-class kernel SVM, and software tuned for outlier detection in images [9].