Sparse Multi-kernel Based Multi-task Learning for Joint Prediction of Clinical Scores and Biomarker Identification in Alzheimer’s Disease

Abstract

Machine learning methods have been used to predict the clinical scores and identify the image biomarkers from individual MRI scans. Recently, the multi-task learning (MTL) with sparsity-inducing norm have been widely studied to investigate the prediction power of neuroimaging measures by incorporating inherent correlations among multiple clinical cognitive measures. However, most of the existing MTL algorithms are formulated linear sparse models, in which the response (e.g., cognitive score) is a linear function of predictors (e.g., neuroimaging measures). To exploit the nonlinear relationship between the neuroimaging measures and cognitive measures, we consider that tasks to be learned share a common subset of features in the kernel space as well as the kernel functions. Specifically, we propose a multi-kernel based multi-task learning with a mixed sparsity-inducing norm to better capture the complex relationship between the cognitive scores and the neuroimaging measures. The formation can be efficiently solved by mirror-descent optimization. Experiments on the Alzheimers Disease Neuroimaging Initiative (ADNI) database showed that the proposed algorithm achieved better prediction performance than state-of-the-art linear based methods both on single MRI and multiple modalities.

1 Introduction

The Alzheimer’s disease (AD) status can be characterized by the progressive impairment of memory and other cognitive functions. Thus, it is an important topic to use neuroimaging measures to predict cognitive performance. Multivariate regression models have been studied in AD for revealing relationships between neuroimaging measures and cognitive scores to understand how structural changes in brain can influence cognitive status, and predict the cognitive performance with neuroimaging measures based on the estimated relationships. Many clinical/cognitive measures have been designed to evaluate the cognitive status of the patients and used as important criteria for clinical diagnosis of probable AD [5, 13, 15]. There exists a correlation among multiple cognitive tests, and many multi-task learning (MTL) seeks to improve the performance of a task by exploiting the intrinsic relationships among the related cognitive tasks.

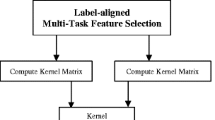
The assumption of the commonly used MTL methods is that all tasks share the same data representation with $\ell _{2,1}$-norm regularization, since a given imaging marker can affect multiple cognitive scores and only a subset of the imaging features (brain region) are relevant [13, 15]. However, they assumed linear relationship between the MRI features and the cognitive outcomes and the $\ell _{2,1}$-norm regularization only consider the shared representation from the features in the original space. Unfortunately, this assumption usually does not hold due to the inherently complex structure in the dataset [11]. Kernel methods have the ability to capture the nonlinear relationships by mapping data to higher dimensions where it exhibits linear patterns. However, the choice of the types and parameters of the kernels for a particular task is critical, which determines the mapping between the input space and the feature space. To address the above issues, we propose a sparse multi-kernel based multi-task Learning (SMKMTL) with a mixed sparsity-inducing norm to better capture the complex relationship between the cognitive scores and the neuroimaging measures. The multiple kernel learning (MKL) [4] not only learns a optimal combination of given base kernels, but also exploits the nonlinear relationship between MRI measures and cognitive performance. The assumption of SMKMTL is that the not only the kernel functions but also the features in the high dimensional space induced by the combination of only few kernels are shared for the multiple cognitive measure tasks. Specifically, SMKMTL explicitly incorporates the task correlation structure with $\ell _{2,1}$-norm regularization on the high dimensional features in the RKHS space, which builds the relationship between the MRI features and cognitive score prediction tasks in a nonlinear manner, and ensures that a small subset of features will be selected for the regression models of all the cognitive outcomes prediction tasks; and an $\ell _{q}$-norm on the kernel functions, which ensures various schemes of sparsely combining the base kernels by varying q. Moreover, MKL framework has advantage of fusing multiple modalities, we apply our SMKMTL on multi-modality data (MRI, PET and demographic information) in our study.

We presented mirror descent-type algorithm to efficiently solve the proposed optimization problems, and conducted extensive experiments using data from the Alzheimers Disease Neuroimaging Initiative (ADNI) to demonstrate our methods with respect to the prediction performance and multi-modality fusion.

2 Sparse Multi Kernel Multi-task Learning, SMKMTL

Consider a multi-task learning (MTL) setting with m tasks. Let p be the number of covariates, shared across all the tasks, n be the number of samples. Let $X \in \mathbb {R}^{n \times p}$ denote the matrix of covariates, $Y \in \mathbb {R}^{n \times m}$ be the matrix of responses with each row corresponding to a sample, and $\varTheta \in \mathbb {R}^{p \times m}$ denote the parameter matrix, with column $\theta _{.t} \in \mathbb {R}^p$ corresponding to task t, $t=1,\ldots ,m$, and row $\theta _{i.} \in \mathbb {R}^m$ corresponding to feature i, $i=1,\ldots ,p$.

$$\begin{aligned} \min _{\varTheta \in \mathbb {R}^{p \times t}} ~~ L(Y,X,\varTheta ) + \lambda R(\varTheta ), \end{aligned}$$

(1)

where $L(\cdot )$ denotes the loss function and $R(\cdot )$ is the regularizer.

The commonly used MTL is MT-GL model with $\ell _{2,1}$-norm regularization, which considers $R(\varTheta ) = \Vert \varTheta \Vert _{2,1} = \sum _{l=1}^p \Vert \theta _{l.} \Vert _2$ and is suitable for simultaneously enforcing sparsity over features for all tasks. Moreover, Argyriou proposed a Multi-Task Feature Learning (MTFL) with $\ell _{2,1}$-norm [1], the formulation of which is: $\Vert Y - \mathbf{U}^TX \varTheta \Vert _F^2+\Vert \varTheta \Vert _{2,1}$, where $\mathbf{U}$ is an orthogonal matrix which is to be learnt.

In these learning methods, each task is traditionally performed by formulating a linear regression problem, in which the cognitive score is a linear function of the neuroimaging measures. However, the assumption of these existing linear models usually does not hold due to the inherently complex patterns between brain images and the corresponding cognitive outcomes. Modeling cognitive scores as nonlinear functions of neuroimaging measures may provide enhanced flexibility and the potential to better capture the complex relationship between the two quantities. In this paper, we consider the case that the features are associated to a kernel and hence they are in general nonlinear functions of the features. With the advantage of MKL, we assume that $\varvec{x}_i$ can be mapped to k different Hilbert spaces, $\varvec{x}_i \rightarrow \phi _j(\varvec{x}_i), j = 1,\dots , k$, implicitly with k nonlinear mapping functions, and the objective of MKL is to seek the optimal kernel combination.

In order to capture the intrinsic relationships among multiple related tasks in the RKHS space, we proposed a multi-kernel based multi-task learning with mixed sparsity-inducing norm. With the $\varepsilon$-insensitive loss function, the formulation can be expressed as:

$$\begin{aligned} \begin{aligned} \min _{\varvec{\theta },\varvec{b},\xi ,\mathbf{U}}~&\frac{1}{2} \left( \sum \nolimits _{j=1}^k \left( \sum \nolimits _{l=1}^{\hat{p}_j} \Vert \theta _{.jl}\Vert _2 \right) ^q \right) ^{\frac{2}{q}} + C \sum \nolimits _{t=1}^m \sum \nolimits _{i=1}^{n_t} (\xi _{ti} + \xi _{ti}^* ) \\ \text {s.t.}&\qquad \left\{ \begin{aligned}&y_{ti} - \sum \nolimits _{j=1}^k \varvec{\theta }_{tj}^{\mathrm T} \mathbf{U}_j^{\mathrm T}\phi _j(x_{ti}) - b_t \le \varepsilon + \xi _{ti} \\&\sum \nolimits _{j=1}^k \varvec{\theta }_{tj}^{\mathrm T} \mathbf{U}_j^{\mathrm T}\phi _j(x_{ti}) + b_t - y_{ti} \le \varepsilon + \xi _{ti}^*, \qquad \forall t, i \\&\xi _{ti},\xi _{ti}^* \ge 0, \mathbf{U}_j \in O^{\hat{p}_j} \end{aligned} \right. \end{aligned} \end{aligned}$$

(2)

where $\varvec{\theta }_{j}$ is the weight matrix for the j-th kernel, $\theta _{tjl} (l=1,\ldots ,\hat{p}_j)$ is the entries of $\varvec{\theta }_{tj}$, $n_t$ is the number of samples in the t-th task, $\hat{p}_j$ is the dimensionality of the feature space induced by the j-th kernel, $\varepsilon$ is the parameter in the $\varepsilon$-insensitive loss, $\xi _{ti}$ and $\xi _{ti}^*$ are slack variables, and C is the regularization parameter.

In the formulation of Eq. (2), the use of $\ell _{2,1}$-norm for $\varvec{\theta }_{j}$, which forces the weights corresponding to the i-th feature across multiple tasks to be grouped together and tends to select features based on the k tasks jointly in the kernel space. Moreover, an $\ell _q$ norm ($q \in [1,2]$) over kernels is used over kernels instead of $\ell _1$ norm to obtain various schemes of sparsely combining the base kernels by varying q.

Lemma 1

Let $a_i \ge 0, i=1 \ldots d$ and $1< r < \infty$. Then,

$$\begin{aligned} \min _{\eta \in \varDelta _{d,r}} \sum _i \frac{a_i}{\eta _i} = \left( \sum _{i=1}^d a_i^{\frac{r}{r+1}}\right) ^{\frac{r+1}{r}} \end{aligned}$$

(3)

where $\varDelta _{d,r} = \left\{ \mathbf{z} \equiv [z_1 \ldots z_d]^{\mathrm {T}}~ |~ \sum \nolimits _{i=1}^d z_i^r \le 1, z_i \ge 0, i=1 \ldots d \right\}$. According to the Lemma 1 introduced in [8], we introduces new variables $\lambda = [\lambda _1 \ldots \lambda _k]^T$, and $\gamma _j = [\gamma _{j1} \ldots \gamma _{j\hat{p}_j}]^{\mathrm T}, j=1,\dots ,k$. Thus, the regularizer in (2) can be written as: $\min _{\lambda \in \varDelta _{k,\bar{q}}} \min _{\gamma _j \in \varDelta _{\hat{p}_j,1}} \sum _{t=1}^m \sum _{j=1}^k \sum _{l=1}^{\hat{p}_j} \frac{\theta _{tjl}^2}{\gamma _{jk} \lambda _j}$, where $\bar{q} = \frac{q}{2-q}$. Now we perform a change of variables: $\frac{\theta _{tjl}}{\sqrt{\gamma _{jk} \lambda _j}} = {\bar{\theta }}_{tjl}, l=1,\ldots ,\hat{p}_j$, and construct the Lagrangian for our optimization problem in (2) as:

$$\begin{aligned} \begin{aligned} \min _{\lambda ,\gamma _j,\mathbf{U}_j}~&\sum \nolimits _{t=1}^m \max \nolimits _{\varvec{\alpha }_t} \mathbf{y}^{\mathrm T} (\varvec{\alpha }_t - \varvec{\alpha }_t^*) - \frac{1}{2} (\varvec{\alpha }_t - \varvec{\alpha }_t^*)^{\mathrm T} \left( \sum \nolimits _{j=1}^k \varPhi _{tj}^{\mathrm T} \mathbf{U}_j^{\mathrm T} \varLambda _j \mathbf{U}_j \varPhi _{tj} \right) (\varvec{\alpha }_t - \varvec{\alpha }_t^*) \\ \text {s.t.}&\qquad \lambda \in \varDelta _{k,\bar{q}},\gamma _j \in \varDelta _{\hat{p}_j,1}{} \mathbf{U}_j \in O^{\hat{p}_j}, \varvec{\alpha }_t \in S_{n_t} (C) \end{aligned} \end{aligned}$$

(4)

where $\varLambda _j$ is a diagonal matrix with entries as $\lambda _j \gamma _{jl},l=1,\ldots ,\hat{p}_j$, $\lambda \in \varDelta _{k,\bar{q}},\gamma _j \in \varDelta _{\hat{p}_j,1}$, $\varPhi _{tj}$ is the data matrix with columns as $\phi _j (x_{ti}),i=1,\ldots ,n_t$, $\varvec{\alpha }_t,\varvec{\alpha }_t^*$ are vectors of Lagrange multipliers corresponding to the t-th task in the SMKMTL formulation, $S_{n_t}(C) \equiv \{\varvec{\alpha }_t~ |~ 0 \le \alpha _{ti},\alpha _{ti}^* \le C,~ i = 1,\ldots ,n_t, \sum \nolimits _{i=1}^{n_t} (\alpha _{ti}-\alpha _{ti}^*) = 0 \}$. Denoting $\mathbf{U}_j^{\mathrm T} \varLambda _j \mathbf{U}_j$ by ${\bar{\mathbf{Q}}}_j$ and eliminating variables $\lambda ,\gamma$,U leads to:

$$\begin{aligned} \begin{aligned} \min _{{\bar{\mathbf{Q}}}} \sum _{t=1}^m \max _{\varvec{\alpha }_t \in S_{n_t} (C)}&\quad \mathbf{y}^{\mathrm T} (\varvec{\alpha }_t - \varvec{\alpha }_t^*) - \frac{1}{2} (\varvec{\alpha }_t - \varvec{\alpha }_t^*)^{\mathrm T} \left( \sum \nolimits _{j=1}^k \varPhi _{tj}^{\mathrm T} {\bar{\mathbf{Q}}}_j \varPhi _{tj} \right) (\varvec{\alpha }_t - \varvec{\alpha }_t^*)\\ \text {s.t.}&\qquad {\bar{\mathbf{Q}}}_j \succeq 0, \sum \nolimits _{j=1}^k (\mathrm {Tr}({\bar{\mathbf{Q}}}_j))^{\bar{q}} \le 1 \end{aligned} \end{aligned}$$

(5)

Then, we use the method described in [6] to kernelize the formulation. Let $\varPhi _j \equiv [\varPhi _{1j} \ldots \varPhi _{Tj}]$ and the compact SVD of $\varPhi _j$ be $\mathbf{U}_j \Sigma _j \mathbf{V}_j^{\mathrm T}$. Now, introduce new variables $\mathbf{Q}_j$ such that ${\bar{\mathbf{Q}}}_j = \mathbf{U}_j \mathbf{Q}_j \mathbf{U}_j^{\mathrm T}$. Here, $\mathbf{Q}_j$ is a symmetric positive semidefinite matrix of size same as rank of $\varPhi _j$. Eliminating variables $\bar{\mathbf{Q}}_j$, we can re-write the above problem using $\mathbf{Q}_j$ as:

$$\begin{aligned} \begin{aligned} \min _{\mathbf{Q}} \sum _{t=1}^m \max _{\varvec{\alpha }_t \in S_{n_t} (C)}&\quad \mathbf{y}^{\mathrm T} (\varvec{\alpha }_t - \varvec{\alpha }_t^*) - \frac{1}{2} (\varvec{\alpha }_t - \varvec{\alpha }_t^*)^{\mathrm T} \left( \sum \nolimits _{j=1}^k \mathbf{M}_{tj}^{\mathrm T} \mathbf{Q}_j \mathbf{M}_{tj} \right) (\varvec{\alpha }_t - \varvec{\alpha }_t^*)\\ \text {s.t.}&\qquad \mathbf{Q}_j \succeq 0, \sum \nolimits _{j=1}^k (\mathrm {Tr}(\mathbf{Q}_j))^{\bar{q}} \le 1 \end{aligned} \end{aligned}$$

(6)

where $\mathbf{M}_{tj} = \Sigma _j^{-1} \mathbf{V}_j^{\mathrm T} \varPhi _j^{\mathrm T} \varPhi _{tj}$. Given $\mathbf{Q}_j$s, the problem is equivalent to solving m SVM problems individually. The $\mathbf{Q}_j$s are learnt using training examples of all the tasks and are shared across the tasks, and this formulation with trace norm as constraint can be solved by a mirror-descent based algorithm proposed in [2, 6].

3 Experimental Results

3.1 Data and Experimental Setting

In this work, only ADNI-1 subjects with no missing features or cognitive scores are included. This yields a total of $n = 816$ subjects, who are categorized into 3 baseline diagnostic groups: Cognitively Normal (CN, $n_1 = 228$), Mild Cognitive Impairment (MCI, $n_2 = 399$), and Alzheimer’s Disease (AD, $n_3 = 189$). The dataset has been processed by a team from UCSF (University of California at San Francisco), who performed cortical reconstruction and volumetric segmentations with the FreeSurfer image analysis suite. There were $p=319$ MRI features in total, including the cortical thickness average (TA), standard deviation of thickness (TS), surface area (SA), cortical volume (CV) and subcortical volume (SV) for a variety of ROIs. In order to sufficiently investigate the comparison, we further evaluate the performance on all the widely used cognitive assessments (e.g. ADAS, MMSE, RAVLT, FLU and TRAILS, totally $m=10$ tasks) [11, 12, 14]. We use 10-fold cross valuation to evaluate our model and conduct the comparison. In each of twenty trials, a 5-fold nested cross validation procedure for all the comparable methods in our experiments is employed to tune the regularization parameters. Data was z-scored before applying regression methods. The candidate kernels are: six different kernel bandwidths (${2^{-2},2^{-1},\ldots ,2^3}$), polynomial kernels of degree 1 to 3, and a linear kernel, which totally yields 10 kernels. The kernel matrices were pre-computed and normalized to have unit trace. To have a fair comparison, we validate the regularization parameters of all the methods in the same search space C (from $10^{-1}$ to $10^{3}$) and q (1,1.2,1.4,..,2) in our method on a subset of the training set, and use the optimal parameters to train the final models. Moreover, a warm-start technique is used for successive SVM retrainings.

In this section, we conduct empirical evaluation for the proposed methods by comparing with three single task learning methods: Lasso, ridge and simpleMKL, all of which are applied independently on each task. Moreover, we compare our method with two baseline multi-task learning methods: MTL with $\ell _{2,1}$-norm (MT-GL) and MTFL. We also compare our proposed method with several popular state-of-the-art related methods: Clustered Multi-Task Learning (CMTL) [16]: CMTL($\min _{\varTheta :F^TF=I_k}~L(X,Y,\varTheta ) + \lambda _1 (\text {tr}(\varTheta ^T\varTheta ) - \text {tr}(F^T\varTheta ^T\varTheta F)) + \lambda _2 \text {tr}(\varTheta ^T\varTheta )$, where $F \in \mathbb {R}^{m \times k}$ is an orthogonal cluster indicator matrix) incorporates a regularization term to induce clustering between tasks and then share information only to tasks belonging to the same cluster. In the CMTL, the number of clusters is set to 5 since the 7 tasks belong to 5 sets of cognitive functions. Trace-Norm Regularized Multi-Task Learning (Trace) [7]: The assumption that all models share a common low-dimensional subspace ($\min _{\varTheta }~L(X,Y,\varTheta ) + \lambda \Vert \varTheta \Vert _*$, where $\Vert \cdot \Vert _*$ denotes the trace norm defined as the sum of the singular values). Table 1 shows the results of the comparable MTL methods in term of root mean squared error (rMSE). Experimental results show that the proposed methods significantly outperform the most recent state-of-the-art algorithms proposed in terms of rMSE for most of the scores. Moreover, compared with the other multi-task learning with different assumption, MT-GL, MTFL and our proposed methods belonging to the multi-task feature learning methods with the idea of sparsity, have a advantage over the other comparative multi-task learning methods. Since not all the brain regions are associated with AD, many of the features are irrelevant and redundant. Sparse based MTL methods are appropriate for the task of prediction cognitive measures and better than the non sparse based MTL methods. Furthermore, CMTL and Trace are worse than the Ridge, which demonstrates that the model assumption in them may be incorrect for modeling the correlation among the cognitive tasks.

Table 1. Performance comparison of various methods in terms of rMSE.

3.2 Fusion of Multi-modality

To estimate the effect of combining multi-modality image data with our SMKMTL methods and provide a more comprehensive comparison of the result from the proposed model, we further perform some experiments, that are (1) using only MRI modality, (2) using only PET modality, (3) combining two modalities: PET and MRI (MP), and (4) combining three modalities: PET, MRI and demographic information including age, years of education and ApoE genotyping (MPD). Different the above experiments, the samples from ADNI-2 are used instead of ADNI-1, since the amount of the patients with PET is sufficient. From the ADNI-2, we obtained all the patients with both MRI and PET, totally 756 samples. The PET imaging data are from the ADNI database processed by the UC Berkeley team, who use a native-space MRI scan for each subject that is segmented and parcellated with Freesurfer to generate a summary cortical and subcortical ROI, and coregister each florbetapir scan to the corresponding MRI and calculate the mean florbetapir uptake within the cortical and reference regions. The procedure of image processing is described in http://adni.loni.usc.edu/updated-florbetapir-av-45-pet-analysis-results/. In our SMKMTL, ten different kennel function described in the first experiment are used for each modality. To show the advantage of SMKMTL, we compare our SMKMTL with MTFL, which concatenated the multiple modalities features into a long vector features. The prediction performance results are shown in Table 2. From the results, it is clear that the method with multi-modality outperforms the methods using one single modality of data. This validates our assumption that the complementary information among different modalities is helpful for cognitive function prediction. Regardless of two or three modalities, the proposed SMKMTL achieved better performances than the linear based multi-task learning for the most cases, same as for the single modality learning task above.

Table 2. Performance comparison with multi-modality data in terms of rMSE.

4 Conclusions

In this paper, we propose to multi-kernel based multi-task learning with $\ell _{2,1}$-norm on the correlation of tasks in the kernel space combined with $\ell _{q}$-norm on the kernels in a joint framework. Extensive experiments illustrate that the proposed method not only yields superior performance on cognitive outcomes prediction, but also is a powerful tool for fusing different modalities.