Abstract
This paper revisits the life of Adolf Lindenbaum in light of new research findings, then looks at two areas among many—metric spaces, and decompositions of point sets—where his work has been underappreciated.
Dedicated to Mariusz Pandura, in gratitude for his tireless research efforts.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
More precisely, it is from our translation of Tarski’s letter. The original letter was in Polish. McFarland–McFarland–Smith [2014] offer their own translation on pp. 377–379, very close to ours, but with two material differences: “efficiency” instead of “effective character”, and “two” instead of “
 ”. We make some changes to parts of their footnote 82 (ibid., page 378), while adopting other parts of it verbatim.
”. We make some changes to parts of their footnote 82 (ibid., page 378), while adopting other parts of it verbatim. - 2.
Some of this article draws on Marczewski–Mostowski [1971] and in several places is a straightforward translation of that dictionary entry—a debt which the present authors are keen to acknowledge up front. As well, some of this article overlaps with the paper Zygmunt–Purdy [2014], where readers will find a more detailed treatment of Lindenbaum’s university student years, professional life and participation in congresses. That said, much of the present material is new: some of it even overturns parts of Zygmunt–Purdy [2014].
- 3.
A private school for girls, at that time on the corner of Marszałkowska and Sienkiewicza (ul. Marszałkowska 122). In 1919 the school was nationalized and renamed Państwowe Gimnazjum Żeńskie im. Klementyny z Tańskich Hoffmanowej.
- 4.
At the present time this cannot be substantiated, as the Polish National Archives have “masked” the relevant records, and the U.K. National Archives have “closed” them for 100 years, on the grounds that they “contain sensitive personal information which would substantially distress or endanger a living person or his or her descendants”. The “slight evidence” consists of scanned pages from the registry of residents of the building at ulica Złota 45 inadvertently revealing some details that are less-than-perfectly masked, and U.K. naturalization records HO 405/33558 and HO 405/33790.
- 5.
Although purchasing power comparisons across 80 years are dicey, he is thought to have lost between 350,000 and half a million in 2009/2010 PLN zł.
- 6.
In the months before his disappearance Mowsza may even have feared for the safety of his wife and children. See our caption to Fig. 8 below.
- 7.
The courses “Teorja Promieniowania” and “Promieniowanie i Kwanty” were taught by Czesław Białobrzeski. Mathematical astronomy and astrometry were taught by Michał Kamieński.
- 8.
See [35], page 595.
- 9.
See Eilenberg [1993], page 1. Eilenberg writes:
In the academic year 1930–31 I was a first-year student at the University of Warsaw, while Karol Borsuk was an assistant conducting exercises in real analysis. I was a member of a class which was huge but he soon started to notice me and we got involved in several conversations. In the spring of 1931 he received his doctorate and I attended the ceremony. At the same time I attended a course on set theory given by Docent Bronisław Knaster. There were two other students in the course, however, I was the only one who did all the homework. I struck up a friendship with Knaster which lasted as long as he did. Set theory naturally led to Topology, which in Warsaw meant strictly Set-theoretical Topology.
I remember a curious incident. In the fall of 1931 I was browsing through the Mathematics Library and I came across a book entitled Topology by Solomon Lefschetz. I looked at the bibliography to see to what extent the “Polish School” was quoted. I found only one reference. It was a paper of Knaster, Kuratowski and Mazurkiewicz in volume 15 of Fundamenta Matematicae containing a combinatorial proof of the Brouwer Fixed Point Theorem. I was very surprised to find no other references and I conveyed my concern to Dr. Adolf Lindenbaum (an excellent logician) who was then the assistant in charge of the library. He told me that it was a terminological misunderstanding, that the book was not about Topology but about some sort of algebra.
- 10.
The petition was issued in the name of the editorial staff, co-workers and “friends” of Głos Współczesny <Contemporary Voice>, a left-leaning monthly newspaper with national circulation, and was splashed across the front page of the March 1936 issue. The signatures of editorial staff and co-workers were grouped separately from those of “friends”. Lindenbaum’s signature was included among editorial staff and co-workers.
- 11.
Published in Lewar, 15th May, 1936, no. 4, page 10. Lewar was a biweekly literary magazine sponsored and influenced by the Polish Communist Party from 1933 through 1936. Its name was a play on words, combining “leverage” and “leftist”.
- 12.
See Marianowicz [1995], pp. 230–231, or Marianowicz [1995] (1), pp. 192–193.
- 13.
Janina’s mother Zofja Hosiasson, née Feigenblatt, and Antoni’s mother Róż a Pańska, née Seidemann, were first cousins—(Antoni’s maternal grandfather Adolf Seidemann and Janina’s maternal grandmother Leona Feigenblatt, née Seidemann, were brother and sister).
- 14.
The biblical Hebrew origin of today’s expression (see: Deuteronomy 32:10, Psalms 17:8, Proverbs 7:2, Lamentations 2:18).
- 15.
German forces invaded Poland on September 1st and within days German artillery shells were raining down on Warsaw. Janina and Adolf fled their home under fire.
- 16.
Polish: Równe; Ukrainian: Рівне; Russian: Ровно; Hebrew:
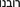 ; Yiddish:
; Yiddish: 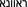 —a name that reverberates in Aliyah consciousness. According to Polish Wikipedia, in 1939 Rivne had a population of 41,500 persons, slightly more than half of whom (21,000) were Jews. See: https://pl.wikipedia.org/wiki/R%C3%B3wne.
—a name that reverberates in Aliyah consciousness. According to Polish Wikipedia, in 1939 Rivne had a population of 41,500 persons, slightly more than half of whom (21,000) were Jews. See: https://pl.wikipedia.org/wiki/R%C3%B3wne. - 17.
On September 17th Soviet forces entered Poland and on September 22nd Białystok came under Soviet occupation. We do not know if Lindenbaum was already in Białystok by then, or if he arrived after it was in Soviet hands. It would have been a difference of only a few days. In either case it would have suited him, as he was attracted by Soviet communism—or at least, by his imagined picture of it.
- 18.
On September 19th, 1939, Soviet forces wrested the city of Wilno from Poland and on October 28th re-attached it to its ancestral home of Lithuania, upon which they bestowed (notional) “independent statehood”, a dubious arrangement which lasted only until August 3rd, 1940.
- 19.
The Pedagogical Institute was a Soviet institution.
- 20.
In Zygmunt–Purdy [2014], §1, p. 299, we wrote that on June 22nd, 1941, Germany “declared war” on the Soviet Union. Germany of course did nothing of the sort. It simply invaded, without bothering to observe such niceties as telling anyone what it was doing. We thank Piotr Wojtylak for pointing this out.
- 21.
We have this on the authority of Professor Bogusław Wolniewicz, who cites testimony of Professor Maria Renata Mayenowa (born Rachela Gurewicz), from a conversation he held with her on 26 April 1986. See Wolniewicz [2015].
- 22.
Remarks attributed to Oskar Lange suggest that Janina and Antoni Pański were living in the same apartment in Vilnius at that time, which might explain why Adolf chose to live elsewhere.
- 23.
See Bender [1997] (1), pp. 87–90.
- 24.
According to the Dédicace, Fundamenta Mathematicae, vol. 33 (1945), p.V, Adolf Lindenbaum was shot in Naujoji Vilnia (Polish: Nowa Wilejka). This was where Soviet forces withdrew to on October 28th, 1939, after handing Vilnius over to a notionally independent Lithuania. Naujoji Vilnia is one train stop—4 km—east of Pavilnys/Kolonia Wileńska, and larger. However it must be underlined that by August, 1941, German forces were in control of both places. Stefanja and Adolf were not shot by the Soviets. They were shot either by Germans or by Lithuanian collaborators.
- 25.
Dadaczyński [2003].
- 26.
SUNY, University at Albany, Science Library 352, M.E. Grenander Department of Special Collections and Archives, German and Jewish Intellectual Émigré Collection (GER-017), Series 4: individual files from Else Staudinger, Director of the American Council for Émigrés in the Professions (ACEP), Box 3, folder 147.
- 27.
The Rockefeller Archive Center, the Rockefeller Foundation (RF) Archives collection, Record Group 2, RG2 1940, Series 200, Box 192, folders 1368 & 1369; and RG2 1941, Series 200, Box 212, folder 1487.
- 28.
Lord Russell, three of whose books Janina had translated, and himself an “economic immigrant” in the U.S. at that time, on a work visa, declined to support her, claiming that he did not recall her.
- 29.
Lithuanian: Lukiškių tardymo izoliatorius kalėjimas. Polish: więzienie na Łukiszkach, or simply Łukiszki. It was on the same street—Gedimino—as Janina’s apartment.
- 30.
The prison and its hospital were under German direction and control but staffed by Lithuanians.
- 31.
The Roman “I” in the title implies that a sequel was planned. In footnote 1, p. 214 (see also footnote 1, p. 218) Lindenbaum indicated what he intended the sequel to be about: it was going to be a study of the notion of the equivalence of point sets by decomposition, in the sense of Banach and Tarski (see also [26a], p. 327). In the event, no sequel was ever published. Nor was his doctoral dissertation ever published in its entirety, although both he and Sierpiński expected it to be: they each referred to it as “à paraître” (see [33a], p. 106, note 18; and Sierpiński [1936], p. 32). As there is no surviving copy in Warsaw University’s archives, or anywhere else we know of, we are unsure precisely how his dissertation related to his publications. Many authors, including Lindenbaum himself, credited his dissertation for results that were never set out in any of his (other) publications (see, e.g., Aronszajn [1932], p. 99, note 12′′; Kirszbraun [1934], p. 78, note 4, and p.102; Sierpiński [1936], p. 32; Lindenbaum [33a], p. 106, note 18).
- 32.
Lindenbaum and Tarski’s collaboration on decomposability and congruence of point sets in Euclidean and general metric spaces began as early as 1923, when Lindenbaum was a freshman/sophomore (see [26a], p. 327).
- 33.
In [26], p. 210, one reads, “Je termine cette préface par remercier MM. Kuratowski et Tarski, qui ont bien voulu prendre intérêt à ces recherches: j’en ai profité beaucoup.” Recognition of Kuratowski’s impact on [26] is also expressed on p. 216 in a parenthetical suffix to the statement of Théorème 7 (“C’est M. Kuratowski qui a su généraliser de cette manière intéressante une idée de ma démonstration primitive du th. 8”) and on p. 222, note 1 (“Le problème auquel le théorème (II) donne réponse m’a été posé par M. Kuratowski.”)
- 34.
See Hausdorff [1914].
- 35.
The terms themselves—l’espace métrique and metrischer Raum—were not new. L’espace métrique even predated Fréchet’s dissertation. See Couturat [1905], page 204; and Couturat [1905] (1), page 216. However, these earlier usages were not related to the theory of metric spaces discussed here.
- 36.
In the 1920s Stanisław Leśniewski and Jan Łukasiewicz, among others, advocated minimizing the number of axioms in formalized deductive systems. For more on this issue see, e.g., Sobociński [1955].
- 37.
He noted two other avantageuses modifications which could as well do the trick—“ρ(x, z) + ρ(y, z) ≥ ρ(x, y)” and “ρ(z, x) + ρ(y, z) ≥ ρ(x, y)”—the second of which he credited to Piotr Szymański. Garrett Birkhoff, citing Lindenbaum’s [26], gave yet another modification (see Birkhoff [1944], p. 466): “ρ(x, y) + ρ(y, z) ≥ ρ(z, x)”. Birkhoff thought this “circularity postulate,” as he called it, had “a clear intuitive content: if one journeys from p to q and then from q to r, the minimum energy required to get back to p is not more than that already expended.”
- 38.
A similar shorthand is frequently adopted in speaking of metric spaces of differing dimensions, where the space of lower dimension can be considered as embedded in the higher-dimensional space: in this case, too, their distance functions are often presented using the same symbol to designate both.
- 39.
This attitude toward the axiom of choice is stated explicitly in [26] on page 212, footnotes 1 and 3.
- 40.
Let a ∈ M and A ⊆ M. Recall that a is an accumulation point of A in the metric space <M, ρ> iff every open sphere with centre a contains at least one point of A which is distinct from a (and consequently an infinite number of points of A). It is easy to see that a’s being (or not being) an accumulation point of A does not depend on the whole space M, but only on the subspace A∪{a}.
- 41.
As a student of Sierpiński, Lindenbaum must certainly have known that the theorem “If A is closed (=\( \overline{A} \)), then A contains all its limit points” is provable without using the axiom of choice, whereas the proof of the converse implication needs AC. See Sierpiński [1918].
- 42.
To be more precise, Lindenbaum defined what it means for an arbitrary subset A ⊆ M to be compact in a metric space <M, ρ>. Then if A is closed and compact in <M, ρ>, then the subspace <A, ρ> is compact. In general the assumption of closedness cannot be omitted.
- 43.
One can prove without AC that if a metric space is compact by the first definition, using the Cantor condition, then it is also compact by the second definition. The proof of the converse implication requires AC. In general topology, a topological Hausdorff space (a T2 space) satisfying the Cantor condition, or equivalently the dual Borel condition for open sets, is called countably compact. In the class of metric spaces, compactness and countable compactness are equivalent.
- 44.
…though there are plenty of non-standard distance functions for which this is not true (readers of a certain age may recall slide rules). Subspaces of the real line with the standard distance function are called linear sets (not to be confused with linearly ordered sets).
- 45.
An equivalence relation is said to be more (/less) inclusive iff the corresponding partition has coarser (/finer) granularity.
- 46.
This readable formulation of Lindenbaum’s Théorème 7 (p.216) is due to Ryszard Engelking [1989], p. 278.
- 47.
In his words, “Le théorème 8, les corollaires 15 et 14, nous fourniront des conditions suffisantes, de plus en plus générales, pour qu’un ensemble compact soit monomorphe.”
- 48.
Theorem 4 was generalized by Tarski as theorem 17(T) in [26a], p. 329.
- 49.
In the Introduction to [26] Lindenbaum wrote, “Au §4 j’examine la propriété singulière d’un ensemble de points d’être superposable avec son vrai sous-ensemble . On peut indiquer des ensembles plans bornés jouissant de cette propriété paradoxale, bien qu’ils ne puissent être Fσet Gδà la fois, ni linéaires; donc, à plus forte raison, ils ne sauraient être fermés, ni ouverts, cependant il y en a qui sont Fσou Gδ. Voilà le sujet principal, mais, à ce propos, j’étudie encore de plus près la notion (bien élémentaire) de congruence (§3).” And in a footnote he explained, “Un ensemble est Fσ, s’il est une somme dénombrable d’ensembles fermés; s’il est complémentaire d’un Fσ(c.-à-d.: produit dénombrable d’ensembles ouverts)—il est Gδ.”
- 50.
By “Euclidean” is meant, that the distance function is the “natural” or “standard” distance function on ℝn—i.e., the square root of the sum of the squares: \( \sqrt{{\left({x}_2-{x}_1\right)}^2+{\left({y}_2-{y}_1\right)}^2+\dots} \).
- 51.
Theorem 5b for n = 2 was generalized by Tarski as theorem 18(T) in [26a], p. 330.
- 52.
See [26a], pp. 327–329.
- 53.
If <M, ρ> and <N, σ> are two metric spaces, then a mapping f:M → N fulfilling σ(f(x), f(y)) ≥ ρ(x, y) for all x, y ∈M is called expanding.
- 54.
For a given (fixed) distance function ρ, the diameter δ(X) of a set X is the farthest distance between any two points in X—i.e., δ(X) = sup {ρ(x, y): x, y ∈ X}. Since a distance function is by definition real valued, it is always possible to compare diameters of spaces of different dimension.
- 55.
See Freudenthal and Hurewicz [1936].
- 56.
See [33a], p. 102, footnote 10, and p. 104, footnote 13; and Sierpiński [1933], p. 107, footnote 2.
- 57.
We use the word “denumerable” in the sense of “at most denumerable”, i.e., either finite or at most countably infinite. We understand, for example, that a singleton is denumerable. So is the empty set.
- 58.
Sierpiński admitted (p. 107, footnote 2) that Lindenbaum had pointed out to him that this theorem was “implicitement contenu dans un théorème de M. Alexandroff (Math. Ann. 92, p. 299, Fundamentalsatz 2)”, but that Alexandrov’s proof was “plus compliquée que la nôtre”.
- 59.
Always bearing in mind, of course, that this definition of
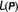 is relative to the given metric space <M, ρ>.
is relative to the given metric space <M, ρ>. - 60.
We allow ourselves to go off on a small sidetrack here. For readers who may be wondering if isolated and scattered are the same notion: no, they are not. Every isolated set is scattered, but in general, not all scattered sets are isolated.
- 61.
Again, using our own numbering scheme, not Lindenbaum’s original numbering.
- 62.
“…la condition Mt 1.2 n’étant point essentielle [Cf. ma Thèse (Varsovie, 1927; à paraître), §22].”
- 63.
Ryszard Engelking, in his treatise General Topology, makes extensive use of pseudometric spaces “as a convenient tool” for investigating a wide variety of topological spaces.
- 64.
On the most obvious level, of course, their result was another example of the paradox of infinity, namely, that the part could equal the whole—a family of paradoxes, actually, with an august lineage, from Zeno of Elea in the fifth century BC, through Galileo’s Two New Sciences of 1638, to Bolzano’s Paradoxes of the Infinite, published posthumously in 1851. But after Cantor’s work on cardinality, and certainly by 1914, mathematicians had gotten used to such paradoxes. The novelty of Mazurkiewicz and Sierpiński’s result lay not in showing that the part could equal the whole (which by then was old news), but in the partition and the transformations they devised, which were truly novel, prefiguring and in a sense anticipating the isometry group E(n) of Euclidean motions and the notion of E(n)-equidecomposability, and ultimately the definition of a paradoxical set. See also Hausdorff’s 1914 paradoxical decomposition of the sphere.
- 65.
Ruziewicz actually obtained this result some 2 years earlier, in the summer of 1919, and ran it past Sierpiński for publication in the first issue of Fundamenta Mathematicae, i.e., the 1920 issue (Sierpiński was its founding editor). Sierpiński suggested a simplification, which Ruziewicz incorporated. The existence of the set B could be proved directly from Zermelo’s axioms (including the axiom of choice), without any need of Zermelo’s theorem on well-ordering, or transfinite numbers. Sierpiński also urged Ruziewicz to consult Hugo Steinhaus, who allegedly had an example of a non-denumerable planar set congruent to its halves. As it turned out, Steinhaus did not have such an example. See the letters from Sierpiński to Ruziewicz dated: 01 April 1919, 17 August 1919, 20 August 1919, and 19 April 1920, in Więsław [2004], pp. 141–143.
- 66.
Sierpiński wrote: “La démonstration de A. Lindenbaum n’a pas été publiée et elle m’est inconnue.” (p. 9).
- 67.
See especially [26a], §2, “Propriétés des transformations univoques” <Properties of one-to-one functions>, pp. 316–318.
- 68.
See Arboleda [1981].
- 69.
See [26a], page 318.
- 70.
See pp. 302–303.
- 71.
Ibid, p. 303.
- 72.
See [26a], §5, “Théorie des ensembles de points,” p. 328.
- 73.
Erdős [1943].
- 74.
Ibid., page 644.
- 75.
See: Sierpiński [1947].
- 76.
See [31a], [34aa], [36a]; see also Sierpiński’s paper “Sur un problème concernant les types de dimensions” in Fundamenta Mathematicae, vol. 19 (1932), pp. 65–71, wherein Sierpiński on pages 67–68 quotes verbatim Lindenbaum’s two-page proof of a generalization—a strengthening—of one of Sierpiński’s own results.
- 77.
The symbol “σ” was chosen because of the first letter of the Polish word “stopień”, which means “degree”.
- 78.
Ibid., page 314.
- 79.
See Więsław [2004], page 158.
- 80.
Cited in Ruch Pedagogiczny, rok 27, nr 6–10 (1938).
- 81.
An advance notice was given in Głos Nauczycielski, nr 5, (25 September 1938), page 78. Some of the titles of individual lectures in the second series are rather philosophical in tone: Co to są nauki scisłe (matematyczno-przyrodnicze)? <What are exact sciences (mathematical-natural)?> Jakie nauki należą do tej grupy? <What sciences belong to this group?> Trudności podziału nauk: przedmiot a metoda. <Difficulties in the divisions of sciences: subject matter vs. method.> Metoda dedukcyjna. <The deductive method.> Czy matematyka posiada przedmiot i jaki? <Does mathematics have a subject, and if so, what?> Rachmistrz-technik a matematyk-badacz. <Number cruncher-technician versus mathematician-researcher.> Element twórczy i “artystyczny” w matematyce. <The creative and “artistic” element in mathematics.>
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Purdy, R., Zygmunt, J. (2018). Adolf Lindenbaum, Metric Spaces and Decompositions. In: Garrido, Á., Wybraniec-Skardowska, U. (eds) The Lvov-Warsaw School. Past and Present. Studies in Universal Logic. Birkhäuser, Cham. https://doi.org/10.1007/978-3-319-65430-0_36
Download citation
DOI: https://doi.org/10.1007/978-3-319-65430-0_36
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-319-65429-4
Online ISBN: 978-3-319-65430-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 ”. We make some changes to parts of their footnote 82 (ibid., page 378), while adopting other parts of it verbatim.
”. We make some changes to parts of their footnote 82 (ibid., page 378), while adopting other parts of it verbatim.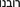 ; Yiddish:
; Yiddish: 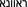 —a name that reverberates in Aliyah consciousness. According to Polish Wikipedia, in 1939 Rivne had a population of 41,500 persons, slightly more than half of whom (21,000) were Jews. See:
—a name that reverberates in Aliyah consciousness. According to Polish Wikipedia, in 1939 Rivne had a population of 41,500 persons, slightly more than half of whom (21,000) were Jews. See: 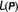 is relative to the given metric space <M, ρ>.
is relative to the given metric space <M, ρ>.