Abstract
In his work of 1918, Hermann Weyl extended the general theory of relativity, which Albert Einstein had set forth in the years 1915–1916, to unify the two field phenomena known at this time, namely those described by electromagnetic and gravitational fields. But more was at stake. At the beginning of the paper in which Weyl worked out the mathematical foundations of the theory, he observed.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
See Corry’s contribution in this volume.
- 2.
In the early twentieth century, Göttingen was the location of an exceptionally vibrant community within which a belief in the mathematical comprehensibility of nature was widespread and facilitated very free exchanges between mathematicians.
- 3.
This can also be seen as a most interesting attempt to understand the inner organic unity of the corpus of mathematical knowledge [66].
- 4.
For the relation between Hilbert and Einstein, see Stachel and Kouneiher’s contribution in this volume.
- 5.
For the history of the mathematization and geometrization of physics and the role of Euclid, Aristotle, Archimedes and the Greek philosophers, followed by Gallileo, Descartes, Newton, Leibniz, and, even later, Grassmann, Hamilton and Elie Cartan, see [73].
- 6.
For more details, see Masson et al’s contribution in this volume.
- 7.
Paul Dirac in 1931 discussed the possible existence of elementary magnetic charges-magnetic monopoles [41]. He showed that in quantum mechanics, such magnetic monopoles made sense if, and only if, the product of their charge, g, with the electric charge of the electron, e, was an integer multiple of Planck’s constant \(\hbar \), precisely: \(ge = n\hbar \). This was very exciting, since it meant that as long as there existed one magnetic monopole in the universe, all charges had to be quantized in units of \(\hbar /g\). In mathematical terms, Dirac had discovered an integer that characterized the topological classification of vector bundles, mathematical constructs that were being invented at about the same time by mathematicians. These concepts have come to play a role of increasing importance in modern gauge theories.
- 8.
Supersymmetry, the link between bosons and fermions, is a closely related concept from physics that has also influenced differential geometry. As first noted by Edward Witten, supersymmetry applied within quantum mechanics is an elegant way to derive the basic principles of Morse theory [125]. Another application is in the development of hyper-Kähler geometry - the curved manifestation of Hamilton’s quaternions. Although the definition has been in the differential-geometric literature since the 1950s, it was 30 years later, as a result of the infiltration of ideas from the supersymmetric sigma model, that a mechanism for constructing good examples was found.
- 9.
Henceforth in this section, we follow [8].
- 10.
Donaldson’s work involved a melting pot of ideas, not so much from physics, but from the mathematical areas of nonlinear analysis of partial differential equations, differential and algebraic geometry, and topology. Nevertheless, the whole idea of studying a moduli space in this context- a space of connections up to gauge equivalence - had its essential origin in physics. In fact, Donaldson found his invariants by studying special solutions of the Yang-Mills equations, which had already been introduced by physicists under the name of instantons’. These solutions have the property that they are essentially localized to a small region in space-time, thereby describing an approximately instantaneous process. Instantons had a family resemblance to the solitons’ or solitary waves first observed by John Scott Russell in the early nineteenth century.
- 11.
Remarkably, Donaldson theory is viewed as perturbative. The distinct, non-perturbative picture of the same theory yields Seiberg-Witten theory. The last one describes, in a different way, the same invariants as Donaldson did, they are two limiting forms of the same quantum field theory.
The point here is that the perturbative/non-perturbative physics view allowed for he resolution of some old problems. In another setting, that of Chern-Simons theory applied to the theory of knots and links, the perturbative view gives the Vassiliev invariants and the non-perturbative the Jones-Witten polynomial invariants.
- 12.
Seiberg and Witten were able to make this physical intuition precise for the class of twisted supersymmetric quantum field theories relevant for the Donaldson invariants [67, 112]. The resulting Seiberg-Witten invariants were based on a U(1) gauge field interacting nonlinearly with a spinor field [127].
These invariants again involved characters familiar to the mathematician, Dirac operators and Spin structures, and this area was the focus of intense research activity in the 1990s. It seemed as if results that were difficult to prove using Donaldson’s theory were easier here, and vice versa. The pay-off in mathematics from the appeal to the physicists”s intuition was clear: one had a new tool for studying four-dimensional manifolds.
On the other hand, to establish that really there was a link between the two theories in conventional terms proved to be an enormous task, one that was only recently accomplished.
- 13.
In the mid-nineteenth century Riemann introduced analytical methods into the algebraic geometry of curves. These were sometimes proved by appeal to physical principles such as the Dirichlet principle, a technique motivated by the physical tenet that nature works by minimizing actions and energy.
Yet the whole apparatus of differentials and theta functions enabled remarkable results to be proved or rendered obvious; special facts like the existence of precisely 28 bitangents to a quartic curve or 120 tritangent planes to a genus four curve are not so far removed in spirit from the remarkable count of rational curves on the quintic threefold by Candelas et al. [15], which is the most startling application of the string theorists’s mirror symmetry in algebraic geometry. If one looks at the journals of the time, one will also see a very rapid succession of applications of these methods before a settling down at the end of the century to a mixture of techniques.
- 14.
Just prior to Grothendieck’s entry into the subject, Weil had gotten important results in number theory through algebro-geometric arguments, and pointed the way to far more, but some of his methods went beyond existing rigorous foundations. He aimed to supply new foundations adequate to his ideas. Around the same time, Zariski and van der Waerden were also generalizing the foundations of algebraic geometry, and many others were introducing various innovations. In particular, the “Weil conjectures” suggested that topological methods of cohomology applied to algebraic geometry might have huge consequences for number theory – but neither Weil nor anyone else in, say, 1954 could see how to actually do that. Serre believed more strongly than Weil himself did that such a cohomology could actually be created.
- 15.
For more details, see Colin MacLarty’s contribution and [79].
- 16.
It is in an article of 1895 that Poincaré [97,98,99] defines, for the first time, differential manifolds and chains (or sub-varieties), which he qualifies as homologous (see [97]). Its definition was somewhat imprecise, but the notion he used matches up exactly with the current acceptance: two closed chains are homologous if their difference is a boundary. However, Poincaré’s text did not reveal the idea of Cohomology. The reason for this is that on a manifold, we can obtain completely cohomology from homology through Poincaré’s duality. Roughly, Poincaré’s duality connects the local statements of cohomology to the global statements of homology.
- 17.
Usually, the non-vanishing of a cohomology class in algebra, geometry, and topology, express some sort “failure”. Indeed, often in mathematics, you wish something were true, but in general, it is not. However, the quantification of how badly it fails help us in determining a more precise statement that holds generally. The size (or dimension) of the corresponding cohomology group is a measurement of how many ways things can go wrong. If it is nice or if you can understand it completely, then you may be able to analyze all the possible failure modes exhaustively, and use that to prove something interesting. This idea can be applied in an amazingly broad set of contexts. This somewhat explains the use of cohomology to describe quantization.
- 18.
In deciding to extend the concepts of homology and cohomology outside the ideal world of mathematics, we are led to accept the use of certain analogies. The homology appeared as a redoubling of abstraction; the homological forms have doubled the algebra of the geometric forms that they enveloped. We can quite clearly distinguish two movements: a birth of geometry or algebra followed by homological stabilization. From a logical point of view, a geometric object and homological object have the same nature.
- 19.
The cycles carried by a surface \(\Sigma \) are formal combinations of manifolds of dimension 3 bordered by \(\Sigma \); The partition function Z defines a form of intersection on cycles, and homology occurs when we quotient by the kernel of this form.
- 20.
See Witten’s contribution in this volume.
- 21.
As we said, string theory makes use of deep structures in differential geometry and algebraic geometry, and connects to the theory of modular functions and finite groups. It even appears to have a place for branches of mathematics as number theory and knot theory.
- 22.
From the point of view of perturbative String Theory, we usually consider the classical motion of a fundamental string, so that the action is given by \(S_{string} = - T_{string} V \), where \(T = \frac{1}{2\pi \alpha }\) is the tension of the string, \(\alpha \) is the Regge slope parameter and V is the area of the string world sheet. The action is called the Nambu-Goto action. Classically, the Nambu-Goto action is equivalent to the Polyakov action (the string sigma-model action):
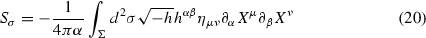
where \(\sigma \) and \(\tau \) are coordinates on the world sheet, and \(h_{\alpha \beta }(\sigma , \tau )\) is a world sheet metric, \(h = det h_{\alpha \beta }\), \(h^{\alpha \beta }\) is the inverse of \(h_{\alpha \beta }\). \(\Sigma \) denotes the world sheet, and \(d^2\sigma = d\sigma d\tau \). The functions \(X^{\mu }(\sigma , \tau )\) describe the space-time embedding of the string world sheet. Quantum mechanically, we use the path integral to deal with the local symmetries and gauge fixing. Unfortunately, in this case, we have to handle the problem of anomalies, more specifically a conformal anomaly, unless the space-time dimension is \(D = 26\). In superstrings (i.e. strings for which supersymmetry is added - either on the world sheet, as in the so-called RNS sector, or to the background space-time as in the GS sector), an analogous analysis gives a critical dimension \(D = 10\).
- 23.
For more details, see [40].
- 24.
See Butterfield and de Haro’s contribution in this volume.
- 25.
String theorists would freely admit that they don’t know what the theory is, but they are fairly sure that what they have is a genuine theory. What they observe is its implications at different limits of coupling constants, where it makes contact with other areas of mathematics. The fundamental concepts in the terra incognito at its centre are unknown, yet its deep consistency unearths structures across a wide range of mathematics. They also admit that is harder than they initially thought when the possibilities opened up in the mid-1980s, but by being harder, it has drawn them closer to mathematics, and they are quite happy to use the predictive power within that domain, given that the physical experiments are currently impractical.
- 26.
See Smolin’s contribution in this volume.
- 27.
There are now two different types of indices, “space” indices a, b, c that behave like regular indices in a curved space, and ‘internal” indices i, j, k that behave like indices of flat-space (the corresponding‘metric’ that raises and lowers internal indices is simply \(\delta _{ij}\)).
- 28.
Whereas in the connection representation, one works with functionals \(\Psi [A]\), which are supported ‘on all of \(\Sigma \)’.
- 29.
This is also the reason why the kinematical Hilbert space employed in loop quantum cosmology is already different from the standard one for a finite number of degrees of freedom [2]. When the number of degrees of freedom is infinite (as in quantum field theory), the Stone-von Neumann theorem does not apply anyhow.
- 30.
For more details, see Connes and Chamsddine’s contributions in this volume.
- 31.
Using spectral action (26) we can get the Einstein-Hilbert action, which, in turn, gives us the field equations of General Relativity, including a cosmologial constant!
- 32.
For more details, see Penrose’s contribution in this volume.
- 33.
Non-locality of the fields in a physical theory is achieved by encoding the field information at a point in space-time into holomorphic functions on the twistor space. By choosing an appropriate description, one can cause the field equations to vanish on twistor space, i.e., holomorphy of a function on the twistor space automatically guarantees that the corresponding field satisfies its field equations.
- 34.
The original setting of the Riemann-Hilbert correspondence concerned the Riemann sphere and the existence of regular differential equations with prescribed monodromy groups. However, a Riemann sphere can be replaced by an arbitrary Riemann surface, so in the case of higher dimensions, Riemann surfaces can be replaced by complex manifolds of dimension \(> 1\). In this case, we have a correspondence between certain systems of (linear) partial differential equations and possible monodromies of their solutions.
- 35.
This is an equivalence from the category of flat connections on algebraic vector bundles on X with regular singularities to the category of local systems of finite-dimensional complex vector spaces on X in the case of regular singular connections. For X connected, the category of local systems is also equivalent to the category of complex representations of the fundamental group of X.
- 36.
In physics, it is very crucial to characterize the systems in interaction and to distinguish between bare parameters (such as mass, electric charge, acceleration, etc.), which are the values they would take if the interaction were switched off, and the actually observed parameters. Renormalisation is a “procedure” that is able to transform the bare parameters into the actually observed ones, which are called renormalized (i.e., with interaction taken into account).
- 37.
Dimensional regularization is a popular one, because it preserves many of the symmetries of the QFT in question. It involves rewriting physically interesting integrals over space-time as formal, but conceptually meaningless, integrals, in which the dimension of space-time becomes a complex number D. The integrals can then be written in terms of a Laurent series in a complex parameter, \(z = D -d\), with a pole at \(z = 0\). The point \(z = 0\) corresponds to the original dimension of the problem, d. Finite values for divergent integrals are then extracted as residues taken around paths avoiding the singular points, by an application of Cauchy’s theorem. This process of extraction is called minimal subtraction.
- 38.
For more details, see [74].
- 39.
More complicated action functionals are required to account for the real world physics: Spinors \(\psi \) for fermionic particles and gauge connections A for their interactions, as is the case for QED and the Standard Model of elementary particles. Nevertheless, we restrict our attention in the sequel to the simplest example of a scalar field theory.
- 40.
A Feynman graph is a (non-planar) graph with a finite number of vertices and edges. An internal edge is an edge connected at both ends to a vertex (which can be the same in the case of a self-loop), an external edge is an edge with one open end, the other end being connected to a vertex. A Feynman graph is referred to by physicists as a vacuum graph, a tadpole graph, or a self-energy graph (respectively an interaction graph) if its number of external edges is \(0,1, 2, \,\,\,(respectively \,\,\, > 2)\). An edge can be of various types depending on which elementary particle it represents. A one-particle irreducible graph (in short, 1PI graph) is a connected graph that remains connected when we cut any internal edge. A disconnected graph is said to be locally 1PI if any of its connected components is 1PI.
- 41.
The mathematical description of the BPHZ method in renormalization is basically designed according to Atkinson’s theorem. It provides inductive formulae (i.e., integral renormalization theorems) for components of the Birkhoff factorization of characters on rooted trees such that at this level, one can find the notion of a decomposition of determined Lie algebras with the Connes-Kreimer theory.
- 42.
Not necessarily connected.
- 43.
Born around 460 BC in Abdera, Thrace, Greece.
- 44.
From this perspective particles are discrete, their energy is concentrated into what appears to be a finite space, which has definite boundaries and contents that we consider to be homogenous (the same at any point within the particle). Particles exist at a specific location. If they are shown on a 3D graph, they have x, y, and z coordinates. They can never exist in more than one place at once, and to travel to a different place in space, a particle must move there under the laws of kinematics, acceleration, velocity, and so forth.
Interactions between particles have been studied for many centuries, and a few simple laws underpin how particles behave in collisions and interactions. The most primary of these are the conservation of energy and momentum, which allow us to simplify calculations between particle interactions on scales of magnitude that vary between planets and quarks.
Waves, unlike particles, cannot be considered a finite entity. Their energy cannot be considered to exist in a single place, since a wave, by definition, varies in both displacement and time. For example, a sound wave is a deformation in air pressure, and water waves a deformation of the water’s surface.
In an area of space, unlike a particle, a wave can propagate until it exists in all locations and at all times; as a mathematical example we can use a pure sine wave, which has no beginning or end, but repeats every \(2\pi \). However, like particles, we can analyze a part or phase of the wave and obtain a value for its velocity within this area.
- 45.
Because then, charged electrons would have infinite energy.
- 46.
Kelvin suggested that molecules are knots in the aether. While we now know that there is no aether and that molecules are not the fundamental constituents of matter, the idea that matter has a topological origin remains beautiful and compelling.
- 47.
The Skyrme model is based on a group-valued field from \(\mathbb {R}^{3}\),

where the Lie group G is usually taken to be SU(2), and \(U({\varvec{x}}) \rightarrow 1\) as \(|{\varvec{x}}| \rightarrow \infty \). The degree of U as a map \(S^3 \rightarrow SU(2)\) is identified with a baryon number. The minima of the Skyrme energy, for each baryon number, are called Skyrmions.
Skyrmions are free to rotate, both in physical space and through conjugation by elements of SU(2). Quantising this motion gives the Skyrmions spin and electric charge. The proton and neutron, for example, are distinct quantum states of the essentially unique Skyrmion of degree 1. Therefore, the Skyrme model [9, 113] is a non-linear theory of pions whose topological soliton solutions are candidates for an effective description of nuclei, with an identification between soliton and baryon numbers. Indeed, in the Skyrme model, the basic idea is that a baryon number is identified with the degree of the map U in (2.1), or equivalently, with the instanton number (or second Chern class) of the SU(2) bundle over \(\mathbb {R}^4\).
- 48.
Recently, M. Atiyah et al., based on the skyrmion idea developed a geometrical model for matter [9].
- 49.
Physicists use quantum field theories to describe fundamental particles. These quantum field theories are derived by quantizing classical field theories. Whereas classical field theories describe the dynamics of continuum fields, quantum field theories can be interpreted as describing the interactions of individual particles. Unlike the particles introduced by the quantization procedure, solitons are germane to the classical, continuum, theory. They owe their particle-like properties, not to quantization, but to the topology of the field theory itself.
- 50.
The sine-Gordon model was invented by Tony Skyrme, the name is a joke because it sounds like Klein-Gordon.
- 51.
The basic properties of solitons, like propagation and interaction without change in their velocity and shape, make it possible to treat them as robust localized objects. Solitons show their duality, having properties of both particles and waves. A soliton has the wave’s nature and finite width, but it behaves like a particle when interacting with other solitons. That is why the solitons are often spoken of as quasiparticles.
- 52.
See Butterfield and de Haro’s contribution in this volume.
- 53.
A consequence of the supersymmetry involved is that the action has the form \({\mathcal A}[\phi ]:=\int _{\mathbb {R}\times \mathbb {R}}\left( {1\over 2c^2} \left| \phi _t\right| ^2 - {1\over 2}\left| \phi _x\right| ^2 - 2(W'(\phi ))^2 \right) dtdx\), where here, \(W(s)={1\over 2}\left( {1\over 3}s^3-s\right) \). It implies, in particular, that a function f of x is a solution to (51) if, and only if, it is a critical point of the functional \({\mathcal E}[f]:=\int _{\mathbb {R}}\left( (f')^2 + 4\beta ^2\left( W'(f)\right) ^2 \right) dx\). Now, we can write this functional as \({\mathcal E}[f]= \int _{\mathbb {R}}\left( \left( f'+ 2\beta W'(f)\right) ^2 - 4\beta f'W'(f)\right) dx = \int _{\mathbb {R}}\left( \left( f'+ 2\beta W'(f)\right) ^2 - 4{\beta d\over dx}\left( W(f)\right) \right) dx\). If we assume that \(\lim _{x\rightarrow \pm \infty }f(x)=f_{\pm }\), then the last term on the right hand side is just \(C:=4\left( W(f_-)-W(f_+)\right) \). So, \({\mathcal E}[f]-C\) is the integral of the square of \(f'+ 2\beta W'(f)\) and a trivial solution is to set \(f'+ 2\beta W'(f)=0\): this is exactly (52) (see [54]).
- 54.
In 1917, German mathematician Emilie Emmy Noether had shown that the mass, charge and other attributes of elementary particles are generally conserved because of symmetries. For instance, conservation of energy follows if one assumes that the laws of physics remain unchanged with time, or are symmetric as time passes. And conservation of electrical charge follows from a symmetry of a particle’s wave function. Sometimes, however, as in our case, attributes may be maintained because of deformations in fields. Such conservation laws are called topological, because topology is that branch of mathematics that concerns itself with the shape of things.
- 55.
\(\phi \) is also a Bogomol’nyi solution of the form \(\phi (t,x)=f(x-vt)\), where \(f'+2\beta W'(f)=0\) and \(W(s):= -{2\sqrt{\alpha }\over \lambda ^2}\cos {\lambda f\over 2}\).
- 56.
Skyrme’s explanation was that, in the full quantum theory, it is possible to construct a new quantum field whose fluctuations are the solitons. The new field operator is obtained through an exponential expression in the original field \(\phi \)

with two spin components (and a normal ordering understood).
The construction (56) is an example of the vertex operator construction that would later become important in string theory and in the representation theory of infinite dimensional algebras (resembling quantum field theories).
- 57.
Here, we should understand the word laws as a set of true principles that form a strong but simple and unified system that can be used to predict and explain. In other words, it’s a way to understand a great many complicated phenomena in a unified way, in terms of a few principles.
- 58.
The laws of nature are supposed to be objective, independent of any interest and belief.
- 59.
These models follow from symmetry assumptions that dramatically simplify the task of solving Einstein’s Fields Equations (EFE). They require that the space-time geometry is both homogeneous and isotropic. Roughly speaking, homogeneity requires that at a given moment of cosmic time, every spatial point looks the same, and isotropy holds if there are no geometrically preferred spatial directions. These requirements imply that the models are topologically \(\Sigma \times {\mathbb R}\), visualizable as a stack of three-dimensional spatial surfaces \(\Sigma (t)\) labeled by values of the cosmic time t. The worldlines of “fundamental observers”, taken to be at rest with respect to matter, are orthogonal to these surfaces, and the cosmic time corresponds to the proper time measured by the fundamental observers. The spatial geometry of \(\Sigma \) is such that there is an isometry carrying any point \(p \in \Sigma \) to any other point lying on the same surface (homogeneity), and at any point p, the three spatial directions are isometric (isotropy).
- 60.
The main results of the FLRW model were first derived by the Soviet mathematician Alexander Friedmann in 1922 and 1924, but his work remained relatively unnoticed by his contemporaries [52, 53]. Albert Einstein, who, on behalf of Zeitschrift fr Physik, acted as the scientific referee for Friedmann’s work, acknowledged the correctness of Friedmann’s calculations, but failed to appreciate the physical significance of their predictions.
Friedmann died in 1925. In 1927, Georges Lemaître, arrived independently at results similar to those that Friedmann had and published them in the Annals of the Scientific Society of Brussels [78]. In the face of the observational evidence for the expansion of the universe obtained by Edwin Hubble in the late 1920s. Howard P. Robertson from the US and Arthur Geoffrey Walker from the UK explored the problem further during the 1930s. In 1935, Robertson and Walker rigorously proved that the FLRW metric is the only one on a space-time that is spatially homogeneous and isotropic [52, 53, 78, 101, 123].
- 61.
For more details, see [77].
- 62.
Repeated indices in pairs with one contravariant and one covariant are summed over. Greek indices take values between 0 and 3.
- 63.
Hubble’s distance estimates have since been modified, leading to a drastic decrease in the estimate of the current rate of expansion (the Hubble parameter, \(H_0\)). However, the linear redshift-distance relation has withstood scrutiny, as the sample size has increased from 24 bright galaxies (in Hubble 1929) to hundreds of galaxies at distances 100 times greater than Hubble’s, and as astrophysicists have developed other observational methods for testing the relation (see [48, 91, 92]).
- 64.
Where r, \(\Psi \) and \(\theta \) are ‘comoving’ polar coordinates, which remain fixed for objects that have no other motion than the general expansion of the universe. The parameter k is the ‘scalar curvature’ of the 3-space and \(k=0\), \(k>0\) and \(k<0\) correspond to flat, closed and open universe, respectively (for more understanding of the Manifolds with scalar curvature see Gromov’s contribution in this volume).
- 65.
During one aeon: one cycle of universe.
- 66.
See Marcolli’s contribution about the interaction between mathematics and computational linguistics.
References
A. Ashtekar, New variables for classical and quantum gravity. Phys. Rev. Lett. 57, 2244 (1986)
A. Ashtekar, Gravity, Geometry and the Quantum, in Vers une nouvelle Philosophie de la nature, Joseph Kouneiher ed. Hermann, 2010
A. Ashtekar, J. Lewandowski, Quantum theory of geometry. I: area operators. Class. Quant. Grav.14 (1997) A55–A82. http://xxx.lanl.gov/abs/gr-qc/9602046
A. Ashtekar, J. Lewandowski, Quantum theory of geometry. II: volume operators. Adv. Theor. Math. Phys.1 (1998) 388. http://xxx.lanl.gov/abs/gr-qc/9711031
M.F. Atiyah, I.M. Singer, The index of elliptic operators on compact manifolds. Bull. Amer. Math. Soc. 69(3), 422–433 (1963)
M.F. Atiyah, I.M. Singer, The index of elliptic operators I. Ann. Math. 87(3), 484–530 (1968)
M.F. Atiyah, I.M. Singer, The index of elliptic operators V. Ann. Math. Second Ser. 93(1), 139–149 (1971)
M. Atiyah, R. Dijkgraaf, N.l Hitchin, Geometry and physics. Phil. Trans. R. Soc. A 368, 913–926 (2010)
M. Atiyah, N.S. Manton, B.J. Schroers, Geometric Models of Matter, arXiv:1108.5151
K.A. Brading, T.A. Ryckman, Hilbert’s foundations of physics’: gravitation and electromagnetism within the axiomatic method. Stud. Hist. Philos. Sci. B: Stud. Hist. Philos. Mod. Phys. 39(1), 102–153 (2008)
N.N. Bogoliubov, D.V. Shirkov, The Theory of Quantized Fields (Interscience, New York, 1959)
N.N. Bogoliubov, O. Parasiuk, On the multiplication of the causal function in the quantum theory of fields. Acta Math. 97, 227–266 (1957)
R. Bott, On Mathematics and Physics, Collected Works, vol. 4, p. 382
K. Brading, E. Castellani, Symmetries in Physics: Philosophical Reflections, 2003
P. Candelas, P. Green, L. Parke, X. de la Ossa, A pair of Calabi-Yau manifoldsas an exactly soluble superconformal eld theory. Nucl. Phys. B 359, 21–74 (1991) https://doi.org/10.1016/0550-3213(91)90292-6
A.H. Chamseddine, A. Connes, M. Marcolli, Gravity and the standard model with neutrino mixing. Adv. Theor. Math. Phys. 11, 991–1089 (2007)
S. Chern, J. Simons, Some cohomology classes in principal fiber bundles and their application to Riemannian geometry, Proc. Nat. Acad. Sci. USA 68, 791–794, Or, characteristic forms and geometrical invariants. Ann. Math. 99(48–69), 1974 (1971)
S. Chern, Vector bundles with a connection, Studies in Global Differential Geometry. Math. Asso. Amer. Studies No. 27, 1–26 (1989)
S. Chern, Complex Manifolds without Potential Theory, 2nd edn. (Springer, Berlin, 1979)
S.-S. Chern, What Is Geometry? The American Mathematical Monthly, vol. 97(8), Special Geometry Issue, pp. 679-686 (1990)
S. Coleman, Quantum sine-Gordon equation as the massive Thirring model. Phys. Rev. D 11, 2088 (1975)
A. Connes, M. Marcolli, Noncommutative Geom. (American Mathematical Society, Quantum Fields and Motives, 2007)
Alain Connes, Dirk Kreimer, Renormalization in quantum field theory and the Riemann-Hilbert problem II: the \(\beta \)-function, diffeomorphisms and renormalization group. Commun. Math. Phys. 216, 215–241 (2001). arXiv:hep-th/0003188v1
A. Connes, M. Marcolli, Renormalization, the Riemann-Hilbert correspondence and motivic Galois theory, Frontiers in number theory, physics and geometry, vol. II (Springer, Berlin, 2007). pp. 617–713
A. Connes, Noncommutative Geometry (Academic Press, Cambridge, 1994)
A. Connes, J. Lott, Particle models and noncommutative geometry. Nucl. Phys. Proc. Suppl. B18, 29 (1989)
A. Connes Geometry and Physics
A. Connes, D. Kreimer, Hopf algebras, renormalization and noncommutative geometry. Commun. Math. Phys. 199, 203 (1998). arXiv:hep-th/9808042
A. Connes, D. Kreimer, Renormalization in quantum field theory and the Riemann-Hilbert problem. I: the Hopf algebra structure of graphs and the main theorem. Commun. Math. Phys. 210, 249 (2000). arXiv:hep-th/9912092
A. Connes, D. Kreimer, Renormalization in quantum field theory and the Riemann-Hilbert problem. II: the beta-function, diffeomorphisms and the renormalization group. Commun. Math. Phys. 216, 215 (2001). arXiv:hep-th/0003188
A. Connes, M. Marcolli, Noncommutative Geometry, Quantum Fields and Motives. preliminary version available at http://www.alainconnes.org/en/downloads.php
A. Connes, D. Kreimer, Hopf algebras, renormalization and noncommutative geometry. Comm. Math. Phys. 199, 203–242 (1998)
A. Connes, D. Kreimer, Renormalization in quantum field theory and the Riemann-Hilbert problem. I. The Hopf algebra structure of graphs and the main theorem. Comm. Math. Phys. 210(1), 249–273 (2000)
A. Connes, D. Kreimer, Renormalization in quantum field theory and the Riemann-Hilbert problem. II. The \(\beta \)-function, diffeomorphisms and the renormalization group. Comm. Math. Phys. 216(1), 215–241 (2001)
A. Connes, M. Marcolli, From Physics to Number theory via Noncommutative Geometry, II: Renormalization, the Riemann-Hilbert correspondence, and motivic Galois theory, to appear in Frontiers in Number Theory, Physics, and Geometry, vol. II. Preprint hep-th/0411114
D. A. Cox, S. Katz, Mirror symmetry and algebraic geometry. Mathematical Surveys and Monographs no. 68. Providence, RI: American Mathematical Society. 1999
L. Corry, David Hilbert and the Axiomatization of Physics (1898-1918): From Grundlagen der Geometrie to Grundlagen der Physik (Kluwer Academic Publishers, Dordrecht, 2004). p. 429
B. Delamotte, A hint of renormalization. Am. J. Phys., 72(2) (2004)
P. Deligne, Quelques idées maîtresses de l’œuvre de A. Grothendieck, Matériaux pour l’histoire des mathématiques au XXe sicle, in Proceedings of the workshop on the honour of Jean Dieudonné (Nice 1996), France Mathematical society, pp. 11–19 (1998)
R. Dijkgraaf, The mathematics of strings theory, Séminaire Poincaré, 2004
P. A. M. Dirac, Quantised singularities in the electromagnetic field. Proc. Roy. Soc. A 133, 60
P.A.M. Dirac, The Relation between Mathematics and Physics. Proc. R. Soc. (Edinburgh) 59(Part II), 122–129 (1939)
S. Donaldson, P. Kronheimer, The Geometry of Four-Manifolds (Oxford, 1990)
S. Donaldson, J. Diff. Geom. 18, 269 (1983)
S. Donaldson, R. Friedman, Connected sums of self-dual manifolds and deformations of singular spaces. Nonlinearity 2, 197–239 (1989)
R. Durrer, R. Maartens, Dark energy and dark gravity, Gen. Rel. Grav. 40, 301–328 (2008) arXiv:0711.0077 (2007)
F.J. Dyson, The S-matrix in quantum electrodynamics. Phys. Rev. 75, 1736. https://doi.org/10.1103/PhysRev.75.1736 (1949)
G. Efstathiou, in The Physics of the Early Universe, ed. by J.A. Peacock, A.F. Heavens, A. Davies (Adam-Higler, Bristol, 1990)
A. Einstein, Philosopher-Scientist, in The Library of Living Philosophers, ed. by P.A. Schilpp (Evanston, 1949), pp. 2–95
A. Einstein, Ideas and opinions, quoted from Schweber, Einstein and Oppenheimer: the meaning of genius (1954)
A. Floer, Bull. Am. Math. Soc. 16, 279 (1987)
A. Friedman, Über die Krümmung des Raumes. Z. Phys. 10(1), 377–386 (1922)
A. Friedman, Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes. Z. Phys. 21(1), 326–332 (1924)
D.S. Freed, G.W. Moore, Twisted equivariant matter. Ann. Henri Poincare 14, 1927 (2013). arXiv:1208.5055 [hep-th]
F. Helein,Dualités, supersymétries et systèmes complètement intégrables, in Vers une nouvelle Philosophie de la nature, ed. by J. Kouneiher, Hermann edn. (2010)
F. Helein, J. Kouneiher, On the soliton-particle dualities, in Geometries of Nature, Living Systems and Human Cognition, ed. by L. Boi (World Scientific, 2005). pp. 93–128
K. Hepp, Proof of the Bogoliubov-Parasiuk theorem on renormalization. Commun. Math. Phys. 2, 301–326 (1966)
D. Hilbert, Uber die Grundlagen der Geometrie. Gottinger Nachrichten 233–241 (1902)
D. Hilbert, Lecture delivered before the International Congress of Mathematicians, Paris France (1900). English translation appeared in Bull. Am. Math. Soc. 8 (1902), 437–479. A reprint of appears in Mathematical Developments Arising from Hilbert Problems, ed. by F. Brouder, Am. Math. Soc. 1976. The original address “Mathematische Probleme” appeared in Göttinger Nachrichten, 1900, pp. 253–297, and in Archiv der Mathematik und Physik, 3(1), 44–63 and 213–237 (1901)
N. Hitchin, Interaction between mathematics and physics, ARBOR Ciencia, Pensamiento y Cultura, CLXXXIII 725, mayo-junio, pp. 427–432 (2007)
G. ’t Hooft, M. Veltman, Regularization and renormalization of gauge fields. Nucl. Phys. B 44, 189 (1972)
K. Hori, S. Katz, A. Klemm, R. Pandharipande, R. Thomas, C. Vafa, R. Vakil, E. Zaslow, Mirror symmetry. Clay Mathematics Monographs. Providence, RI: American Mathematical Society (2003)
E. Hubble, A relation between distance and Radial Velocity among Extra-Galactic Nebulae. Proc. Natl. Acad. Sci. 15, 168–173 (1929)
V.F.R. Jones, A polynomial invariant for knots via von Neumann algebras. Bull. Am. Math. Soc. 12, 103–111 (1985). https://doi.org/10.1090/S0273-0979-1985-15304-2
F. Klein, Vergleichende Betrachtungen über neuere geometrische Forschungen, in Gesammelte mathematische Abhandlungen, vol. i (1872) pp. 460–497
F. Klein, Vorlesungen über die Entwicklung der Mathematik im 19 (Wissenschaftliche Buchgesellschaft, Jahrhundert. Darmstadt, 1979)
M. Kontsevich, Y. Soibelman, Stability structures, motivic Donaldson-Thomas invariants and cluster transformations, arXiv:0811.2435 [math.AG]
Kontsevich, M. Homological algebra of mirror symmetry. In Proc. Int. Congress of Mathematicians, Zrich, vols. 1-2 (Birkhuser, Basel, Switzerland, 1995). pp. 120–139
M. Kontsevich, M. Yu, Gromov-Witten classes, quantum cohomology, and enumerativegeometry. Commun. Math. Phys. 164, 525–562 (1994). https://doi.org/10.1007/BF02101490
J. Kouneiher, in Leibniz and the Dialogue between Sciences, Philosophy and Engineering, 1646-2016. New Historical and Epistemological Insights, ed. by R. Pisano, M. Fichant, P. Bussotti, A.R.E. Oliveira (The College’s Publications, London, 2017)
J.Kouneiher, Conceptual Foundations of Soliton Versus Particle Dualities Toward a Topological Model for Matter. International Journal of Theoretical Physics, vol. 55(6), pp. 2949–2968. 20p (2016)
J. Kouneiher, C. Barbachoux, Cartan’s soldered spaces and conservation laws in physics. Int. J. Geom. Methods Mod. Phys. 12(9) (2015)
J. Kouneiher, Geometric Continuum and the Birth of the Mathematical-Physics, to appear in IJGMMP, 2018
T. Krajewski, P. Martinetti, Wilsonian renormalization, differential equations and Hopf algebras, Talk given by T. Krajewski at the conference “Combinatorics and Physics" Max Planck Institut Für Mathematik Bonn, March 2007
D. Kreimer, On the Hopf algebra structure of perturbative quantum field theories. Adv. Theor. Math. Phys. 2, 303 (1998). arXiv:q-alg/9707029
D. Kreimer, On the Hopf algebra structure of perturbative quantum field theories. Adv. Theor. Math. Phys. 2, 303–334 (1998)
G. Lazardies, Introduction to Cosmology, arXiv:hep-ph/9904502
G. Lemaitre, Ann. Soc. Sci. Brux. A53, 81 (1933)
Colin MacLarty, How Grothendieck simplified algebraic geometry. Not. AMS 63(3), 250 (2016)
N.S. Manton, Skyrme fields and instantons, in "Geometry of Lowdimensional Manifolds : 1", ed. by S.K. Donaldson, C.B. Thomas, Lond. Math. Soc. Lec. Notes Ser. 150 (Cambridge University Press, Cambridge, 1990)
S. Mandelstam, Soliton operators for the quantized sine-Gordon equation. Phys. Rev. D 11(10), 3026–30 (1975)
Y.I. Manin, M. Marcolli, Big Bang, blowup, and modular curves: algebraic geometry in cosmology. Symmetry Integrability Geom.: Methods Appl. SIGMA 10, 73 (2014)
J.C. Maxwell, Mathematical and Physical Science, Section A (Mathematical and Physical Sciences) of the British Association, Liverpool, 1870. Nature 2, 419–422 (1870)
T. Miwa, M. Jimbo, E. Date, Solitons, Cambridge Tracts in Math. 135 (Cambridge University Press, Cambridge, 2000)
C. Montonen, D. Olive, Magnetic monopoles as gauge particles, Phys. Lett. 72B(1) (1977)
G.W. Moore, Physical Mathematics and the Future, Preprint
J. von Neumann, Die Eindeutigkeit der Schrödingerschen Operatoren. Math. Ann. 104, 570 (1931)
E.T. Newman, A fundamental solution to the CCC equations, Gen. Relativ. Gravit. 46(5), 1717, 13p (2014). arXiv:1309.7271
H. Nicolai, K. Peeters, M. Zamaklar, Loop Quantum Gravity: An Outside View, 2014. arXiv:hep-th/0501114
D. Olive, E. Witten, Supersymmetry algebra that include topological charges, Phys. Lett. 78B(1) (1978)
P.J.E., Peebles, The Large-scale Structure of the Universe (Princeton University Press, Princeton, 1980)
P.J.E. Peebles, D.N. Schramm, E.L. Turner, R.G. Kron, Nature 352, 769 (1991)
Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe (A.A. Knopf, New York, 2005)
R. Penrose, Angular momentum: an approach to combinatorial space-time, in Quantum Theory And Beyond, ed. by T. Bastin (Cambridge University Press, Cambridge, 1971)
R. Penrose, W. Rindler, Spinors and space-time, in Two-Spinor Calculus and Relativitic Fields, vol. 1 (Cambridge University Press, Cambridge, 1984)
H. Poincaré, Sur les rapport de l’analyse pure et de la physique mathématique, Address to the 1897 ICM, Zurich
H. Poincaré, Analysis situs. J. Sec. Polyt. 1, 1–121 (1895)
H. Poincaré, Sur la connexion des surfaces algébriques. C. R. Acad. Sc. 133, 969–973 (1901)
H. Poincaré, Sur les cycles des surfaces algébriques; quatrième complement a l’Analysis situs. J. Math. Pures Appl. 8, 169–214 (1902)
A. Pressley, G.B. Segal, Loop Groups (Oxford University Press, Oxford, 1986)
H.P. Robertson, On the foundations of relativistic cosmology. Proc. Natl. Acad. Sci. 15(11), 822–829 (1929)
I. Robinson, Report to the Eddington Group, Cambridge, (1956)
I. Robinson, J. Math. Phys. 2, 290 (1961)
C. Rovelli, Quantum Gravity (Cambridge University Press, Cambridge, 2010)
C. Rovelli, L. Smolin, Loop space representation of quantum general relativity. Nucl. Phys. B 331, 80 (1990)
J. Rosenberg, A selective history of the Stone-von Neumann theorem’, in Operator Algebras, Quantization, and Noncommutative Geometry: A Centennial Celebration Honoring John von Neumann and Marshall H. Stone, ed. by R.S. Doran, R.V. Kadison, Contemporary Mathematics, vol. 365 (American Mathematical Society, 2004)
Y. Ruan, G. Tian, A mathematical theory of quantum cohomology. J. Differ. Geom. 42, 259–367 (1995). http://projecteuclid.org/euclid.jdg/1214457234
T. Sauer, The Relativity of Discovery: Hilbert’s First Note on the Foundations of Physics. arXiv:physics/9811050
U. Majer, T. Sauer, Hilbert’s World Equations and His Vision of a Unified Science. http://arxiv.org/abs/physics/0405110v1
S.S. Schweber, Qed and the Men Who Made It: Dyson (Schwinger, and Tomonaga, Princeton University Press, Feynman, 1994)
A. Sen, Dyon-monopole bound states, self-dual harmonic forms on the multi-monopole moduli space, and SL(2, Z ) invariance in string theory. Phys. Lett. B 329, 217–221 (1994)
N. Seiberg, E. Witten, Monopole condensation, and connement in N = 2 supersymmetricYang-Mills theory. Nucl. Phys. B 426, 19–52 (1994)
T.R.H. Skyrme, A Unified Theory for Mesons and Baryons. Nucl. Phys. 31, 556 (1962); Proc. Roy. Soc. A 247, 260 (1958)
T.R.H. Skyrme, Kinks and the Dirac equation. J. Math. Phys. 12, 1735–42 (1971)
T.H.R. Skyrme, A non-linear field theory. Proc. Roy. Soc. A260, 127–138 (1961)
C. Rovelli, L. Smolin, Spin networks and quantum gravity. Phys. Rev. D 52, 5743–5759 (1995)
H. Spiesberger, M. Spira, P.M. Zerwas. The Standard Model: Physical Basis and Scattering Experiments. Appears in: Scattering, ed. by R. Pike et al., vol. 2, (Academic Press, Cambridge, 2002). 1505–1533
M.H. Stone, Linear transformations in Hilbert space, III: operational methods and group theory. Proc. Nat. Acad. Sci. 16, 172–175 (1930)
J.J. Sylvester, A plea for the mathematician, II. Nature 1(10), 261–263 (1870)
W. Thirring, Ann. Phys. (N.Y.) 3, 91 (1958)
P. Tod, Penrose’s circles in the CMB and a test of inflation. Gen. Relativ. Gravitat. 44, 2933–2938 (2012). arXiv:1107.1421
R. Vakil, Foundations of Algebraic Geometry. http://math.stanford.edu/~vakil/216blog/index.html
A.G. Walker, On Milne’s theory of world-structure. Proc. Lond. Math. Soc., Ser. 2, 42(1), 90–127 (1937)
H. Weyl, Reine Infinitesimalgeometrie, in Weyl, Gesammelte Abhandlungen, 4 vols., vol. II (Springer, Berlin, 1968). pp. 1-28, on p. 2
E. Witten, Supersymmetry and Morse theory. J. Differ. Geom. 17, 661–692 (1982)
E. Witten, Quantum eld theory and the Jones polynomial. Commun. Math. Phys. 121, 351–399 (1989)
E. Witten, Monopoles and four manifolds. Math. Res. Lett. 1, 769–796 (1994)
E. Witten, Quantum field theory and the Jones polynomial, Braid Group, Knot Group, and Statistical Mechanics, ed. by C. N. Yang, M. L. Ke (World Scientific, 1989). pp. 239–329
E. Witten, Topological quantum field theory. Comm. Math. Phys. 117(3), 353–386 (1988)
K.G. Wilson, The renormalization group: critical phenomena and the Kondo problem. Rev. Mod. Phys. 47(4), 773 (1975)
C.N. Yang, Magnetic monopoles, fiber bundles, and gauge fields. Ann. NY Acad. Sci. 294, 86–97 (1977)
C.N. Yang, R.L. Mills, Conservation of isotopic spin and isotopic gauge invariance. Phys. Rev. 96, 191–195 (1954)
W. Zimmermann, Convergence of Bogoliubov’s method of renormalization in momentum space’. Commun. Math. Phys. 15, 208 (1968)
J. Zinn-Justin, Quantum Field Theory and Critical Phenomena (Oxford University Press, Oxford, 1999)
Acknowledgements
First of all, I apologize to those whose works I forgot to mention and which helped to improve the quality of the paper. Secondly, I would like to thank all my friends who have contributed to this volume, and all the colleagues who, through exchanges, suggestions or their own writings, have enriched the content of this paper. I am particularly grateful to Michael Atiyah, Alain Connes, Edward Witten, Roger Penrose, Misha Gromov, Ali Chamsddine, Lee Somlin, Jeremy Butterfield and John Stachel for exchanges and suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Kouneiher, J. (2018). Where We Stand Today. In: Kouneiher, J. (eds) Foundations of Mathematics and Physics One Century After Hilbert. Springer, Cham. https://doi.org/10.1007/978-3-319-64813-2_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-64813-2_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-64812-5
Online ISBN: 978-3-319-64813-2
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)