Reconfiguration of Control Allocation Module Based on Reliability Estimated by Stochastic Models

Abstract

The paper presents the results of the regulation strategy based on the reconfiguration of the control allocation module steering redundant actuators. As the reconfiguration criterion the required level of system reliability was assumed at the end of the operating time, estimated by the means of stochastic differential equations. In this case, two tasks become the key. The first concerns the choice of the method of determining the pseudo inverse matrix taking into account the constraints on the control signal. The second concerns the prioritization of the actuators. i.e. the distribution of the increased demand for the control signal so that, this increase, in minimum way, decreases the reliability.

1 Introduction

The main task of fault–tolerant control algorithms is to maintain the process capability for control procedures with certain system capabilities that can be used in fault conditions [1, 2]. In the most cases, fault tolerance is achieved by redundancy of the actuators relative to the required control efforts. Often, this redundancy is related not to one control signals [3]. It is possible to implement various complex control strategies that achieve the same control efforts by redundancy and integration the control effects of the various actuators [4, 5]. This leads to situation when the control signal isn’t uniquely determined. It can be redistributed between each actuators of the system according to the adopted criterion, e.g. minimizing the control energy, but also providing their prioritization [6, 7]. Any reconfiguration of the control allocation due to faults, needs to generate an increased control signal to fault compensation, and as consequence increase the load of the individual actuators. This, in turn, reduces their reliability and finely the reliability of the entire system [8]. It is important to redistribute the control signals in such a way, that realize increased control efforts, but at the same time ensure the longest use of the actuators and thus the highest total reliability at the end of the task [9, 10].

The procedure of estimating the life time of very reliable components is a very difficult issue. The extremely long nominal time to failure makes it impossible to determined the life time distribution in nominal conditions in experimental form. For this reason, accelerated aging tests have become a practical solution. However, in this type of tests, the testing procedure is also carried out until hard failure is observed, so for highly reliable components or devices this takes a very long time. Therefore, the so–called accelerated degradation tests, become increasingly popular [11]. In this type of tests, we don’t observe the time to hard failures but we analyse the degradation changes of the selected quantities that determine the reliability properties of the element. Based on this information we predict the time at which the considered quantities reach the threshold limit, what is treats as a failure. In this type of tests it is very important to properly determine the effect of accelerating quantities on degradation processes as well as the choice of the mathematical model describing the behavior of changes in observed parameters. Due to the influence of many elements on the degradation processes, the stochastic differential equations models in this paper are proposed [12]. For such models it is possible, at the same time, taking into account both the progressive trend and the random changes. In addition, it is possible to scale the process to take into account the load changing [13].

This paper is organized as follows. Section 2 describes the control allocation as one of the methods to increase the system reliability in case of actuators redundancy. Section 3 presents the possibility of using the stochastic differential equations to describe the accelerated degradation processes. Based on them the life time of the component in fault states was calculated. Section 4 presents the method of reconfiguration the control allocation module due to fault, taking into account the system reliability. Also the method of determining the priority matrix of the actuators is presented. In Sect. 5, a model of tested system have been presented and the results of the simulations are discussed. The article concludes with a brief summary containing information on other reconfiguration criteria and the continuation of the research work with the real system.

2 Control Allocation

According to the Fig. 1 the discrete LTI system can be defined as

$$\begin{aligned} \left\{ \begin{array}{rl} x(t+1) &{} = Ax(t)+Bu(t)\\ y(t) &{} = Cx(t), \end{array} \right. \end{aligned}$$

(1)

Fig. 1.

The structure of the control system

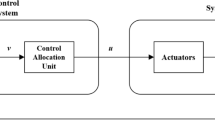
where $A\in \mathbbm {R}^{n\times n}$, $B\in \mathbbm {R}^{n\times m}$ and $C\in \mathbbm {R}^{p\times n}$ are the state, the control and the output matrices, respectively. $x\in \mathbbm {R}^n$ is the system state, $u\in \mathbbm {R}^m$ is the control input, and $y\in \mathbbm {R}^p$ is the system output. The control allocation task can be realized only in over–actuated systems, i.e. where the number of operable controls is greater than the controlled variables (Fig. 2). In such case, the block nominal controller defines a control signal v(t), which next is distributed in the allocation module into u(t) signal. Such solution allows us to introduce fault tolerance mechanisms by control allocation [10, 14]. For such systems, while $rank(B)=q<m$, a virtual control input $v(t)\in \mathbbm {R}^q$ can be introduced. Then (1) can be modified to

$$\begin{aligned} \left\{ \begin{array}{rl} x(t+1) &{} = Ax(t)+B_vv(t)\\ v(t) &{} = B_uu(t)\\ y(t) &{} = Cx(t), \end{array} \right. \end{aligned}$$

(2)

by considering the factorization

$$\begin{aligned} B=B_vB_u, \end{aligned}$$

(3)

where $B_v\in \mathbbm {R}^{n\times q}$ and $B_u\in \mathbbm {R}^{q\times m}$.

Fig. 2.

The structure of the control system with control allocation module

The control vector v(t) can be defined by solving the linear quadratic optimization problem in the form

$$\begin{aligned} v(t)\rightarrow \min _u \int _0^\infty {(x(t)^TQ x(t)+v(t)^TR v(t))\text {d}t}, \end{aligned}$$

(4)

where $Q\in \mathbbm {R}^{n\times n}$ and $R\in \mathbbm {R}^{q\times q}$. For simplicity, the requirement $p=q$, i.e. the number of virtual controls equals the number of variables to be controlled, is consider.

If the matrix B is not full rank, i.e. the $rank(B)=q<n$, it can be factorized as $B=B_vB_u$, where $B_v\in \mathbbm {R}^{n\times q}$, $B_u\in \mathbbm {R}^{q\times m}$ and $rank(B_u)=q$. The virtual control input v(t) can be derived as $v(t)=B_uu(t)$, where $B_u=(B_v^TB_v)^{-1}B_v^TB$ [10]. The control allocation problem can be expressed as

$$\begin{aligned} v(t)=B_uu(t), \end{aligned}$$

(5)

with constraints due to saturation of actuators, as

$$\begin{aligned} u_{min}\le u \le u_{max}. \end{aligned}$$

(6)

The optimal control input can be obtained by a two–step optimization, namely, sequential quadratic programming [4, 10]. The first is related to the determination of an acceptable set of controls, satisfying the condition

$$\begin{aligned} \mathcal {U}=\arg \min \limits _{u_{min}\le u\le u_{max}} \left\| B_uu-v\right\| _2, \end{aligned}$$

(7)

while the second concerns the choice of control from the allowed set $\mathcal {U}$, as

$$\begin{aligned} u=\arg \min \limits _{u\in \mathcal {U}} \left\| W_uu\right\| _2. \end{aligned}$$

(8)

The weighting matrix $W_u\in \mathbbm {R}^{m\times m} \succ 0$ is used to give the specific priority level of the actuators. In order to ensure the requisite level of reliability the specific procedures for the use of actuators is required. The right choice must therefore be based on the indicator associated with the reliability of each actuators. Therefore, the elements of the matrix $W_u$ may play the role of such indicators, and they can be used to manage the allocation of control signal between redundant actuators to prioritize it. This allows to preserve the system reliability and increase the life time of the actuators [10].

3 Stochastic Differential Equations

The general form of the stochastic process can be described as

$$\begin{aligned} \text {d}y_t=F(t,y_t)\text {d}t+G(t,y_t)\text {d}W_t, \end{aligned}$$

(9)

where the functions $F(t,y_t)$ and $G(t,y_t)$ are called drift and process variation, respectively. Their form may be a function of the time t and process state $y_t$, while the $\text {d}W_t$ is a Wiener process determined for $t\ge 0$. Taking the appropriate form of the function $F(t,y_t)$ and $G(t,y_t)$, Eq. (9) may modeling different degradation processes (Fig. 3) [15, 16]. Taking

$$\begin{aligned} F(t,y_t)=\alpha y_t\quad \text{ oraz }\quad G(t,y_t)=\beta y_t, \end{aligned}$$

(10)

Fig. 3.

Examples of degradation processes: linear (a), concave (b) and convex (c)

we obtained the process defined as

$$\begin{aligned} \text {d}y_t=\alpha y_t\text {d}t+\beta y_t \text {d}W_t. \end{aligned}$$

(11)

For initial condition $y(t_0)=y_0$ and applying the Itô integral, we obtained the solution of (11), in the form

$$\begin{aligned} y_t = y_0\text {exp}\left[ \left( \alpha -\frac{\beta ^2}{2}\right) t+\beta W_t\right] \end{aligned}$$

(12)

called geometric Brownian motion [15]. The model parameters can be determined by the series of differences calculated as

$$\begin{aligned} y_i=\text {ln}\frac{p_{i+1}}{p_i}, \end{aligned}$$

(13)

where $p_i$ are the measured values of the quantity describing the degradation process. Based on the degradation processes, the time of failure $\mu _{nomi}$ (curve (a) in Fig. 4) is treated as time when the degradation process reaches the threshold level defined as the maximum allowed level $d_{max}$. The time to reach the maximal limit is random and can be described by selected statistical distributions, e.g. normal distribution. In this case, the reliability function takes the form

$$\begin{aligned} R(t;\mu ,\sigma ) = 1-\frac{1}{2}\left[ 1+\text {erf}\left( \frac{(t-\mu )}{\sigma \sqrt{2}}\right) \right] , \end{aligned}$$

(14)

where the error function is defined as

$$\begin{aligned} \text {erf}(t) = \frac{1}{\sqrt{\pi }}\int _{-t}^{t}e^{-\tau ^2}\text {d}\tau . \end{aligned}$$

(15)

The advantage of using normal distribution is the ability to scale it [17]. This allows us to determine the parameters of the new distribution by taking into account the scaling factor k, as

$$\begin{aligned} Y\sim N(\mu ,\sigma ^2)\Rightarrow kY \sim N(k\mu ,|k|\sigma ^2). \end{aligned}$$

(16)

Increasing the load of the actuators, e.g. due to the failure, causes acceleration of the degradation process, which leads to a shortening of the time to reaches the threshold level to the value $\mu _{f}$ (curve (b) in Fig. 4) [18, 19]. This shortening can be defined by the acceleration aging factor AF, defined as

$$\begin{aligned} AF = \frac{\mu _{nomi}}{\mu _f}, \end{aligned}$$

(17)

Fig. 4.

Change of the degradation process due to increased load caused by e.g. a failure: degradation process under nominal load (a), new degradation process caused by failure (b); $\mu _{nomi}$ – mean time to failure under nominal conditions, $\mu _f$ – mean time to failure after load increase due to damage

corresponds to the scaling factor k in (16). The necessity of providing a high reliability is related to maintaining the longest possible values of time to faults $\mu _i$. Therefore, the control allocator should redistribute the control signal to minimize the reliability of each actuators as low as possible. This task can be achieved through a priority matrix $W_u$. Indeed, it is possible to select the least reliable element based on time to failures, and allocate the required control signal to load it the least. The $W_u$ matrix can be defined as

$$\begin{aligned} W_u^{nomi} = \begin{pmatrix} \frac{\mu _{min}^{nomi}}{\mu _1}&{} &{} &{}0 \\ &{}\frac{\mu _{min}^{nomi}}{\mu _2}&{} &{} \\ &{} &{}\ddots &{} \\ 0 &{} &{} &{}\frac{\mu _{mim}^{nomi}}{\mu _m} \end{pmatrix}, \end{aligned}$$

(18)

where $\mu _{min}^{nomi}=\text {min}(\mu _i^{nomi})$ for $i=1,2,\ldots m$, means the time to failure in nominal conditions of the least reliable element.

4 Reconfiguration of Control Allocation Based on Reliability Index

Due to damage, material wear, or malfunction of components, the system will be diagnosed as failure. In that case the model (2) will be replaced by

$$\begin{aligned} \left\{ \begin{array}{rl} x(t+1) &{} = Ax(t)+B_vv(t)\\ u(t) &{} = B_u^fu(t)\\ y(t) &{} = Cx(t), \end{array} \right. \end{aligned}$$

(19)

where the matrix $B_u^f$ will be determined relative to the nominal input matrix $B_u$ by the control effectiveness factor $\varGamma$. Then $B_u^f = B_u (I_m-\varGamma )$. The elements of a diagonal matrix $\varGamma = \text {diag}(\gamma _1, \gamma _2, \ldots \gamma _m)$ take the value from the compartment $\gamma _i\in \begin{bmatrix} 0&1 \end{bmatrix}$ for $i=1,2,\ldots m$. When $\gamma _i=0$, then the i-th actuator remains functional. In case of partial loss of efficiency, $0<\gamma _i<1$, and while $\gamma _i=1$, the i-th element is completely inoperable, and is not considered in the control [10]. In the faulty case or malfunction the control allocator must be reconfigured. The reconfiguration criterion must be such a change in the allocation rules to ensure the maximum system reliability. It is known that as the demand for the control signal increases, the load of the actuators increases, and this results in an increase in the rate of the degradation in such components. Therefore, defining new rules for control allocation we must take into account the ability of each actuator to accept a higher load. And at the same time we should ensure that the new redistribution algorithm of the control signal should keep the reliability of the system as high as possible. So just like in nominal condition, also after the failure is detected, the prioritisation of the actuators can be realized by the weighing matrix $W_u$. Thus, after the process of failure identification and determining the loss of effectiveness of the control consumption $\varGamma$, a new operating point of the actuators can be determined and an estimate of the new load increment of the individual actuators. This, in turn, leads them to shorten their life time. In order to maximally extend this time, it is possible to divide the control signal taking into account the least reliable elements. The priority matrix will then be formatted as

$$\begin{aligned} W_u^f = \begin{pmatrix} \frac{\mu _{min}^f}{\mu _1^f}&{} &{} &{}0 \\ &{}\frac{\mu _{min}^f}{\mu _2^f}&{} &{} \\ &{} &{}\ddots &{} \\ 0 &{} &{} &{}\frac{\mu _{min}^f}{\mu _m^f} \end{pmatrix}, \end{aligned}$$

(20)

where $\mu _{min}^f=\text {min}(\mu _i^f)$ for $i=1,2,\ldots m$ and means time to damage due to increased load by the least reliable element [10].

5 Simulation Model

The simulation were carried out in the system shown in Fig. 5. As a control object, a model of parallel connection of the resistor and capacitor, charged by three current sources was adopted (Fig. 6). These allows us to obtained the redundancy of the actuators relative to the controlled variable.

Fig. 5.

The structure of the considered system

Adopted redundancy makes that the distribution of performance of individual current sources is not uniquely determined. In addition, it can be approximated in the constrained quadratic optimization process, both in terms of maximum load and change rates, while minimizing performance and taking into account the prioritization as a method to limits the reliability decreasing as result of increased load for each sources. For redundant systems, the reliability at the end of the task, is defined as

$$\begin{aligned} R(t_m)=1-\prod _{i=1}^k(1-R_i(t_m)) \end{aligned}$$

(21)

where $t_m$ means the time of the end of the task. For simulation purposes, the nominal yields of individual sources were determined and their reliability parameters as the time to reach the maximum allowable level of degradation ($\mu _i$) and standard deviation ($\sigma _i$). In the Table 1 the simulation parameters assumed in the model were presented.

Table 1. The reliability parameters of current sources

Fig. 6.

The control system containing three current sources charged the capacitor

Fig. 7.

Realization of control process with failure compensation

The control signal u(t) defined intensity of individual current sources, calculated in the control allocation module, must minimize the condition (8) subject to (5) but for fault case $B_u^f$. If the control constraint, defined the saturation of the actuators (6) is not considered, the solution can be obtained by minimizing the square problem (7) and (8) in the form

$$\begin{aligned} \begin{array}{c} u=\min \limits _{u}J_u = \left\| W_uu\right\| _2\\ \text {s.t.}\quad B_u^fu(t)=v(t). \end{array} \end{aligned}$$

(22)

This leads to solve a weighted pseudoinvers form

$$\begin{aligned} u(t)=W_u^{-1}\left( B_u^fW_u^{-1}\right) ^+v(t). \end{aligned}$$

(23)

In practical applications, the control allocation methods allow us to calculate the control vector u(t) taking into account the constraints leading to the saturation of the actuators. The proposed methods of solution, differ mainly in the method of rejection saturated inputs, while determination of the pseudo-inverse matrix is realized using different decomposition methods such QR-decomposition, SVD or Moor-Penros. Some methods of control allocation may differ in the methods of estimation the quality of the solutions, the use of additional scaling factors, or in addition to the rate of change of the control signal (dynamic methods) [20]. Various numerical algorithms are implemented to solve the problem of control allocation. These include such solutions as least squares algorithms (minimum, sequential, weighted), internal point methods, cascading methods or point weights [4]. The results presented in this paper were obtained using the minimal square method with sequential least squares algorithm [14, 21].

The system response to the control signal changes is shown in Fig. 7. In Fig. 8 the load characteristics of individual current sources are presented in order to implement such control. At thirty seconds the system generated a damage reducing the performance of the source 3. Based on the model, the damage was identified, the efficiency matrix of the individual sources was determined and next the reconfiguration of control allocation was performed. In Fig. 8 the performances of individual current sources are presented, with and without consideration the reconfiguration process of the redistribution control system. The Fig. 9 shows the total system reliability changes, determined for time $t_m=2000$ s, (i.e. the required maximum usage time) at any time of system operation. It is clear that, in the case of reconfiguration of the control allocation by taking into account the modified prioritisation matrix of the actuators, the required level of system reliability (e.g. 95%) is maintained.

Fig. 8.

The comparison of control signals generated by the control allocation system with and without the reconfiguration mechanism

Fig. 9.

The online changes of reliability $R^{t_m}(t)$ for mission time $t_m$ with and without the reconfiguration mechanism of control allocation

In Fig. 10 the part of the reliability function for the time $t_m$ of the actuators as well as the whole system are presented. Each figure shows changes in the reliability function for: nominal operating conditions (Fig. 10(a)), in the fault state but without reconfiguration of the control allocation (Fig. 10(b)) and with reconfiguration of the reallocation module (Fig. 10(c)). It can be seen that in case of (c), the required level of reliability has been obtained.

Fig. 10.

The reliability R(t) calculated for fault free system (a), with fault and without reconfiguration mechanism (b), with fault and with reconfiguration of the control allocation module (c)

6 Conclusion

The paper presents the results of simulation research using the reconfiguration of the control allocation module to maximize system reliability in the event of fault or loss of performance. It was proposed to use the reliability reduction index as a result of increased load of the actuators to determine the method of performing the reconfiguration. Its value can be calculated by scaling factor shorting the life time of the actuators due to the increased load, estimated by the stochastic equations. The simulations confirmed the possibility of using such solutions. Additionally, the use of allocation methods allow us to realize the minimal energy control procedures which is of particular importance for the actuators and controls systems powered from portable sources. The research will be continued on the real systems. The author also conducts research on the implementation other algorithms to realize reconfiguration of allocation control systems subject to achieve the maximum reliability in the required operating time of the system. They are based on the optimization the actuators load to achieve the desired control while minimizing the total system reliability.