PASCAL: A Parallel Algorithmic SCALable Framework for N-body Problems

Abstract

We propose PASCAL, a parallel unified algorithmic framework for generalized N-body problems. PASCAL utilizes tree data structures and user-controlled pruning or approximations to reduce the asymptotic runtime complexity from being linear in the number of data points to be logarithmic. In PASCAL, the domain scientists express their N-body problem in terms of application-specific operations, and PASCAL generates the pruning and approximation conditions automatically from this high-level specification. In order to evaluate PASCAL, we generate solutions for six problems: k-nearest neighbors, range search, Euclidean minimum spanning tree, kernel density estimation, expectation maximization (EM), and Hausdorff distance chosen from various domains.

We show that applying domain-specific optimizations and parallelizations to the algorithms generated by PASCAL achieves $10\times$ to $230\times$ speedup compared to state-of-the-art libraries on a dual-socket Intel Xeon processor with 16 cores on real world datasets. We also obtain a novel out-of-the-box asymptotically optimal algorithm for Hausdorff distance calculation and an improved algorithm for EM. This shows the impact and potential of PASCAL in rapidly extending to a larger class of problems that are yet to be explored.

1 Introduction and Motivation

N-body problems are those in which an update to a single element in the system depends on every other element. The general form applies a set of operators $\{op_1, \, ... , \, op_m\}$ to m datasets using a kernel function, $\mathcal {K}$, as follows.

$$\begin{aligned} op_1, \, ... , \, op_m \, \text {Compute}\mathcal {K}(x_1, ..., x_m) \end{aligned}$$

(1)

where $x_1 \in \mathcal {D}_1$,..., $x_m \in \mathcal {D}_m$ and $\mathcal {D}_1 ... \,\mathcal {D}_m$ are the m datasets. The naive computation of these problems is asymptotically $O(N^m)$ which is expensive.

N-body problems are ubiquitous, with applications in various domains ranging from scientific computing simulations to machine learning [8, 9, 16]. N-body methods were identified as one of the original seven dwarfs or motifs [2] and are believed to be important in the next decade. In fact, the well-known Fast Multipole Method (FMM) made the list for the top 10 algorithms having the greatest influence on the development of science and engineering in the 20th century [7]. According to data mining researchers, EM is one of the top ten algorithms having the most impact on data mining research [17].

However, a big gap exists between the algorithm one designs on paper and the code that runs efficiently on a billion-core system. It is time-consuming to write fast, parallel, and scalable code for an N-body problem on any architecture. On the other hand, the sheer scale and growth of modern scientific datasets necessitate exploiting the power of both asymptotically fast parallel algorithms and approximation algorithms where we can potentially trade-off accuracy for performance [11]. The goal of PASCAL is to automate the generation of asymptotically optimal N-body algorithms using the definition of the problem provided by domain scientists. This is especially useful in rapidly growing fields such as machine learning and data mining where new models are created at a much faster rate than optimal algorithms and implementations for the models.

Contributions and Findings. First, this paper strives to combine two areas that traditionally have not combined forces, namely high-performance computing and machine learning. We apply the knowledge and expertise gained from optimizing and tuning scientific N-body computations to N-body problems from other domains. We make the following contributions.

• 1. We design an algorithmic framework for N-body problems called PASCAL to automatically generate prune and approximate conditions from a high-level user specification. PASCAL can generate $\mathcal {O}(N \log N)$ and $\mathcal {O}(N)$ algorithms if the operators, and kernel function in Eq. 1 satisfy the decomposability property over subsets, and monotonically decrease with distance respectively. PASCAL is also the first to generalize beyond two operators by the design of a Nested Prune generator (Sect. 4).

• 2. We apply domain-specific optimizations and parallelize the algorithms generated by PASCAL. An asymptotically optimal algorithm generated by PASCAL combined with optimizations and parallelization results in 10–230$\times$ speedup compared to state-of-the-art libraries and software such as Weka, Scikit-learn, MLPACK, and MATLAB (Sects. 5 and 7).

• 3. PASCAL is able to generate an approximation condition for the log-likelihood step of EM which results in an improved EM algorithm for Gaussian Mixture Models. This algorithm is 7–16$\times$ faster compared to the best competing implementation. PASCAL also generates a nested prune condition for Hausdorff distance resulting in a new $\mathcal {O}(N)$ algorithm. To the best of our knowledge, this is the first dual-tree algorithm for Hausdorff distance (Sect. 4).

As a result, this paper lays a solid foundation for future scalable implementations of N-body problems on emerging systems. PASCAL enables us to rapidly obtain both an optimal algorithm and its parallel implementation for new and existing N-body problems.

2 Related Work

N-body Algorithms in Physical Simulations. The most popular and widely used fast algorithms for classical N-body problems are the Barnes-Hut [3] and the Fast Multipole Method (FMM) [9]. They use trees to approximate distance computations and achieve sub $\mathcal {O} (N^2)$ asymptotic runtime. There has been significant work on parallelizing tree codes [12].

PASCAL differs from the preceding work in many ways. First, PASCAL supports algorithms and operations beyond what is usually considered in classical physics. This makes PASCAL more general. Second, we consider high-dimensional trees (e.g. kd-trees, ball-trees, cover trees) which are required to handle high-dimensional datasets. Third, our approach is more portable and easily extensible compared to previous approaches which focus on optimizing a specific algorithm for a specific architecture.

N-body Algorithms in Machine Learning. While parallel N-body algorithms in physics have received significant attention, the same is not true for machine learning (ML). There are a number of freely accessible ML libraries, however, each of them lacks in one or both of the two ways, (a) efficient optimal algorithms and (b) parallelism and scalability on modern machines. For instance, MLPACK [6] which is a state-of-the-art C++ ML library offers a limited set of fast algorithms but is not parallel, or distributed. Other popular libraries emphasize ease of use but scale poorly such as Weka toolkit [10]. Even others implement fast algorithms but in languages such as Python resulting in poor performance such as Scitkit-learn [15].

Luckily, there is a theory on generalized N-body algorithms [5, 8] which is similar in spirit to long studied physics algorithms such as FMM that run in linear time. This theory is a stepping stone to our work but it is limited in two ways – (a) the pruning and approximation conditions are designed manually for every problem, and (b) the theory is limited to problems with only 2 operators. Although this is a useful first step, this approach is not scalable. In this paper, we address the above limitations by proposing an algorithm to automate the design of pruning and approximation conditions for two or more operators.

3 N-body Problems

This section provides an overview of N-body problems, and their main structure. Later, in Sect. 4, we will see how they fit in the PASCAL framework.

Given a system of N reference points ($N_r$) and N query points ($N_q$), an update to a single element depends on every other element in the system. The most familiar example arises in physical simulations and has the following form.

$$\begin{aligned} \forall _q, \, \sum _r K(x_q, x_r)\cdot s(x_r) \, , \end{aligned}$$

(2)

where $s(x_r)$ is the density of the reference point and $K(x_q, x_r)$ is an interaction kernel that specifies the physics of the problem. For instance, Laplace kernel is defined as, $K(x_q,x_r) = \frac{1}{||x_q - x_r||}$ which models gravitational interactions.

This style of N-body problem arises in other significant domains and the common theme that brings these problems under a single umbrella is the insight that their inner-loop computations are analogous and naively require $\mathcal {O}\left( {N^2}\right)$ operations for the all-pairs computation. Below, we present six examples.

(a) k - Nearest Neighbor ( k -NN) Search. One of the most ubiquitous N-body problems in ML is k-NN search which is defined as, $\forall q, \, \arg \text {min}_{r}^{k} ||x_q - x_r||$ where, for each query point $x_q$ we want to find its k nearest neighbors, i.e. the k reference points $x_r$ whose distance to $x_q$ is minimal. Comparing this to our familiar physical summation (Eq. 2), we see that the kernel function in this case is the Euclidean distance function and the operator sum has been replaced by another operator, arg min. The inputs for PASCAL in this case are the operators set, {$\forall$, arg min} and the kernel function, $||x_q- x_r||$.

(b) Range Search (RS). A related problem is range search, where the kernel function is a delta function. We want to find all the reference points that fall within a range $\left( h_{\text {min}}, h_{\text {max}}\right)$ of a query point, $x_q$ defined as $\forall q, \, \bigcup \arg _r I(h_{\text {min}} \le ||x_q - x_r|| \le h_{\text {max}})$ where $I(h_{min} \le ||x_q - x_r|| \le h_{max})$ is a delta function.

(c) Kernel Density Estimation (KDE). Another example of sum-based accumulations from statistics is KDE, which is a widely used method for non-parametric density estimation. The goal is to estimate the probability density at each $x_q$, using a kernel function $K_\sigma$. It is defined as $\forall q, \, \frac{1}{|N_r|} \sum _{r} K_{\sigma }\left( \frac{||x_q - x_r||}{\sigma }\right)$ where $K_\sigma$ is a zero-centered probability density function (e.g. Gaussian) and $\sigma$ is the bandwidth of the kernel. When the distance between two points $||x_q - x_r||$ is very large, the contribution of the kernel function to the probability density at $x_q$ is small. Therefore, we can approximate the kernel sum at the expense of reduced precision to achieve a faster algorithm similar to Barnes-Hut and FMM.

(d) Minimum Spanning Tree (MST). This is one of the oldest problems in computational geometry. Given a set of points $S \in \mathbb {R}^{d}$, the goal is to find the lowest weight spanning tree in the complete graph G, where the edge weights are given by the Euclidean distance between two points. We consider the iterative Boruvka’s algorithm for MST [14]. Borukva’s MST is an iterative algorithm that connects each component to its nearest vertex until only one component, the MST, remains. The computational bottleneck in MST is finding the nearest neighbor component which is identical to example (a). Computing all neighbor pairs efficiently will result in an efficient Boruvka’s algorithm.

(e) Expectation Maximization (EM). EM is a popular algorithm used in mixture models. Here, we consider problems where EM is used to learn the parameters of a multivariate Gaussian Mixture Model (GMM). Consider a dataset $D = \{x_1, x_2, .. ,x_N\}$, where $x_i \in \mathbb {R}^d$ generated independently from an underlying distribution p(x). If p(x) is a Gaussian distribution, we can define a GMM as,

$$\begin{aligned} p(x|\theta ) = \sum _{k=1}^{K} \pi _k f(x|\mu _k, \varSigma _k) , \quad f(x_{i}|\theta _k) = \frac{1}{\sqrt{2\pi |\varSigma _k|}} e^{-\frac{1}{2}(x_{i}-\mu _{k})^{T}\varSigma _k^{-1}(x_{i}-\mu _{k})} \end{aligned}$$

where K is the number of Gaussian mixture components, and $\theta _k= \{ \mu _k, \varSigma _k\}$ are the parameters of Gaussian component, k, with mean vector $\mu _k$ and covariance matrix $\varSigma _k$. $\pi _k$ are the mixing weights ($\sum _{k=1}^{K}\pi _k = 1$). EM starts with an initial estimate of $\theta$ (generated randomly, or using k-means), and iteratively updates $\theta$ until convergence (i.e. log-likelihood change is less than a threshold) as follows.

• 1. E-step: Compute the responsibility, $r_{nk} = \frac{\pi _k f(x_n|\mu _k, \varSigma _k)}{\sum _{j=1}^{K}\pi _j f(x_n|\mu _j, \varSigma _j)}$ (weight factor of data point n for cluster k).

• 2. M-step: Re-estimate $\theta$ using the responsibilities measured in the E-step.

• 3. Compute the log-likelihood, $l(\theta ) = \sum _{n=1}^{N} \log \sum _{k=1}^{K} \pi _k f(x_n|\mu _k, \varSigma _k)$ for convergence check.

E-step and log-likelihood computation are the two N-body problems in EM.

(f) Hausdorff Distance. The last example is Hausdorff distance calculation which has applications in computer vision. The Hausdorff distance between two subsets is computed as, $\text {max}_q, \, \text {min}_r ||x_q - x_r||$ where $||x_q - x_r||$ is the Euclidean distance which is the kernel function and the set of operators is {max, min}.

Fig. 1.

Block diagram outlining the overall approach. The dotted box represents the PASCAL framework and the blue shaded boxes are the contributions. (Color figure online)

4 PASCAL Framework

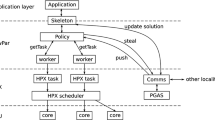
Leveraging the commonalities between N-body problems gives rise to the PASCAL framework shown in Fig. 1, which consists of space partitioning trees, a prune/approximate condition generator, and a tree-traversal scheme. We then apply domain specific transformations and parallelize the algorithms generated by PASCAL to produce an efficient code for comparison against other state-of-the-art libraries and software. The blue shaded boxes in the figure represent the contributions which we will discuss in detail in the rest of this paper.

Space-Partitioning Trees. A powerful class of space-partitioning tree-based algorithms exist that can reduce the complexity of N-body problems from $\mathcal {O}\left( {N^2}\right)$ to $\mathcal {O}\left( {N \log N}\right)$ or even $\mathcal {O}\left( {N}\right)$ [3, 9]. These algorithms use techniques such as approximation and pruning to estimate or discard regions of the space.

An example we consider is kd-trees which are used in data analytics and mining [4]. These are high-dimensional binary trees which maintain a bounding box for all the points in each node. Children are formed by recursively sub-dividing the parent’s bounding box along the median of its largest dimension. We stop partitioning when each node contains no more than $l$ points ($l> 0$). The bounding box information allows us to efficiently compute the minimum and maximum node-to-point or node-to-node distances during evaluation without accessing the actual points in each node, which is critical for performance.

Tree Traversals. Algorithm 1 describes multi-tree traversal given two inputs, a set of nodes and a rule set. The rule set consists of the following 3 functions.

BaseCase implements the direct point-to-point computation. For instance, for k-NN, this is equivalent to computing the distance between all the points in the reference node to every point in the query node.

Prune or Approximate checks to see if the computation for that set of nodes can be approximated or pruned based on the condition generated by Algorithm 2. In some cases, the algorithm prunes entire sub-trees, so the nodes and their descendants will not be visited.

ComputeApprox replaces the computation with the center contribution of each node multiplied by the density of that node which is equivalent to the number of data points in that node. This is only for approximation problems.

While the operations above are not completely orthogonal, they are convenient and powerful to express the range of N-body algorithms. Not only does this representation abstract the actual computation from the traversal, it also abstracts the tree type which gives us the freedom to plug and play with different trees. Moreover, we are able to express both pruning and approximation algorithms in the same framework which enables us to translate our optimizations and parallelization to a much larger class of algorithms.

Prune/Approximate Condition Generator. In order to generate a prune or approximate condition, we first classify N-body problems into 3 categories namely, (a) approximation, (b) single pruning, and (c) nested pruning. Approximation problems are those in which the contribution by a subset of the data to the solution can be approximated by a smaller subset. Two examples are KDE and EM. Pruning problems are those in which a part of the data and associated computation are discarded. The main distinction between single and nested pruning is that former has only one pruning opportunity (e.g. k-NN) while the latter has more than one opportunity for pruning (e.g. Hausdorff distance).

Algorithm 2 generates one of three conditions and distinguishes the category of problems by maintaining a queue of possible prune opportunities called PrunePipeline (Line 1). We iterate through the operators’ set, OP and kernel function, $\mathcal {K}$ and check if there is any pruning opportunity. If so, we push the reverse of OP and/or $\mathcal {K}$ into the PrunePipeline (Lines 2–6). The reverse function is defined for operators and kernel function, and defines the reverse of their functionality. For example, the reverse of $||x_q - x_r|| < h$ is $||x_q - x_r|| > h$, and the reverse of min operator is the relational operator greater than (>).

The problem falls under approximation if the size of PrunePipeline is zero (Lines 8–13). For approximating the contribution of a node, we check if the minimum and maximum contribution of that node are very close (i.e.less than a threshold). If so, we know that all the data points in that node have a similar contribution and therefore, PASCAL uses the center to approximate the computation of that node. Note that $(\mathcal {N}^{c}_1, \mathcal {N}^{c}_2,..., \mathcal {N}^{c}_m)$ defined in line 11, represents the centers of nodes $\mathcal {N}_i \in (\mathcal {N}_1, \mathcal {N}_2,..., \mathcal {N}_m)$ and this is pre-computed as metadata information during tree construction.

The problem falls under the single prune category if the size of Prune Pipeline is one (Lines 15–19). First, we define a threshold for pruning. To do so, we randomly choose points in each set and compute a temporary value using the kernel function. We define $\mathcal {N}^{border}_r$ as the set of border data points which have either maximum or minimum values in each dimension. Line 18 pops the prune operator and Line 19 generates the prune condition by applying the operator on the tuple of points from the nodes in $\mathcal {N}_1,...,\mathcal {N}_{m_1}$, and border points of $\mathcal {N}_m$.

Note that in Algorithm 2, the notation $op_{\oplus }$ is similar to non-member function operators in C++ language. For instance, $op_{\le }(x_r, x_q)$ is equal to $x_r \le x_q$.

When the size of the PrunePipeline is greater than one, the problem belongs to the nested prune category and the nested prune Algorithm 3 is called in line 22. In Line 2, for each node, we calculate the border data points using the maximum and minimum values of data points in each dimension as defined in $\{b_{\min }, b_{\max }\}^d_{i=1}$. Line 3 pops the prune operator from the PrunePipeline. Initially, a temporary threshold $\tau$ is defined for each prune operator. Subsequently, $\tau$ is refined as the computation progresses. Line 5 returns the nested prune condition that we generate. For generating this condition, first, we apply the innermost operator to the border points in the innermost dataset. The result of this is used to call the next innermost operator, and so on. We will continue this process from the innermost operator to the outermost operator in the PrunePipeline and apply each operator on the corresponding node borders with the computed thresholds. Each prune operator corresponds to one level in the multi-tree. Note that single prune can be considered as a special case of nested prune with a nesting level of one.

Case Studies. In this section, we show how N-body algorithms are generated using PASCAL. Specifically, we consider the six N-body problems discussed in Sect. 3 as case studies. The choice of these six problems is because they cover (a) approximation, single pruning, and nested pruning problems, (b) both direct and iterative algorithms, and (c) problems from multiple domains.

In all the problems, the BaseCase is the direct point-to-point computation at the leaf nodes. So, we will focus specifically on how the prune/approximate condition is generated since this is the most challenging step.

(a) k -NN Search. k-NN has only one pruning opportunity, arg min, so it is classified as a single prune problem by PASCAL. PASCAL generates the prune condition using Algorithm 2. The prune operator that is pushed into PrunePipeline is arg min and the reverse is $\ge$. The reverse of arg min is similar to the reverse of min since they both compute the minimum. The difference is the return value, the latter returns the value of minimum while the former returns the argument of it. The threshold $\tau$ is initialized at the beginning with a temporary computation of the kernel (or a default value such as the maximum value of double precision) and is updated through the algorithm.

PASCAL evaluates $\mathcal {K}$ for each reference point in $\mathcal {N}_r^{\text {border}}$ with respect to the query point $x_q$. Then, it checks to see if it is greater than or equal to $\tau$. So, the prune condition is $op_{\oplus }(\tau , \mathcal {K}(x_q,x_r)) \implies \mathcal {K}(x_q,x_r) \ge \tau , \quad \forall x_r \in \mathcal {N}_r^{\text {border}}$.

(b) Range Search (RS). Range search has only one pruning opportunity via its kernel function, $I(h_{\text {min}} \le ||x_q - x_r|| \le h_{\text {max}})$. The reverse of this kernel function that is saved in PrunePipeline is $h_{\text {min}} > ||x_q - x_r||$ or $||x_q - x_r|| > h_{\text {max}})$ which is used as $op_{\oplus }$ to generate the prune condition ($op_{\oplus _1} \, \text {is} >, \, op_{\oplus _2} \, \text {is} <$). The two thresholds, $\tau _1$ and $\tau _2$ are defined by the kernel function as $h_{\text {max}}$ and $h_{\text {min}}$. We evaluate the kernel function on the points in $\mathcal {N}_r^{\text {border}}$ for each $x_q$ as $\delta$, $\mathcal {K}(x_q,x_r) = \delta$. Then, the prune condition is defined as follows.

$$\begin{aligned} op_{\oplus _1}(\tau _1 , \mathcal {K}(x_q,x_r)) \quad \text {or} \quad op_{\oplus _2}(\tau _2 , \mathcal {K}(x_q,x_r))\implies \delta > \tau _1 | \delta < \tau _2 , \forall x_r \in \mathcal {N}_r^{\text {border}} \end{aligned}$$

(c) Kernel Density Estimation (KDE). This is an approximation problem since there is no pruning opportunity by the definition of the problem, and the PrunePipeline queue is empty. ComputeApprox will return the probability density at the center of the node, $K_{\text {center}}$, multiplied by the number of data points in that node. In this problem, $\tau$ is a default constant that can be overridden by the user to adjust the overall accuracy. PASCAL uses Algorithm 2 to generate the approximation condition, $(K_{\text {max}} - K_{\text {min}}) < \tau \times K_{\text {center}}$.

(d) Minimum Spanning Tree (MST). MST is an iterative algorithm and in each iteration, it uses the same operations as k-NN search. So PASCAL generates exactly the same prune condition and rule set as k-NN.

(e) Expectation Maximization (EM). EM is an approximation problem. EM has three steps namely, E-step, M-step, and Log-likelihood where $99\%$ of the time is spent in E-step and Log-likelihood. Moore [13] proposed a powerful space-partitioning tree-based algorithm to reduce the complexity of E-step from $\mathcal {O}(KN)$ to $\mathcal {O}(K \log N)$, where N is the number of data points and K is the number of clusters. We extend Moore’s idea and propose a fast algorithm for estimating both the E-step and log-likelihood computation in $\mathcal {O}(K\log N)$.

The first N-body computation in EM is the E-step. In the E-step, if the difference between the maximum and the minimum responsibility of the points i from cluster j, $r_{ij}$, is less than a threshold, we can approximate the influence of these data points. This is because all the data points in that node will approximately have a similar responsibility to the cluster. PASCAL generates the approximation condition $(r_{ij}^{\max } - r_{ij}^{\min }) < \sigma \times \, r_{ij}^{\text {center}},~ i = 1,..,K$ where, $\sigma$ is the threshold parameter, ${r_{i}^{\text {center}}}$ is the responsibility of the center data points in the node from cluster i, $r_{i}^{\min }$ and $r_{i}^{\max }$ are the minimum and maximum responsibilities between all the data point from cluster i.

ComputeApprox will return the value of responsibility at the center of the node multiplied by the number of data points in that node. Note that in this algorithm, the distance we compute is the Mahalanobis distance which is defined as $(x-\mu )^{T}\varSigma ^{-1}(x-\mu )$ for a Gaussian with $\theta = (\mu , \varSigma )$.

The second N-body computation in EM is the log-likelihood computation. In order to calculate the log-likelihood, we traverse the same tree as in the E-step. The computation pattern is similar in style to E-step albeit with a different approximation condition generated by PASCAL presented below. To the best of our knowledge, this is the first $\mathcal {O}(K\log N)$ algorithm for computing log-likelihood.

$$\begin{aligned} \log \sum _{i=1}^{K}\pi _i f(x_{\max }|\theta _i) - \log \sum _{i=1}^{K} \pi _i f(x_{\min }|\theta _i) < \sigma |\log (\sum _{i=1}^{K}\pi _i f(x_{\text {center}}|\theta _i))| \end{aligned}$$

(f) Hausdorff Distance. One of the N-body problems with more than one pruning opportunity is Hausdorff distance. In this problem, the kernel function is the Euclidean distance with the operators set {max, min} both of which provide pruning opportunities. PASCAL generates the prune condition using the nested prune algorithm, Algorithm 3.

First, PASCAL constructs dual-trees and applies each of its operators on one of the levels of the tree. The PrunePipeline queue consists of the reverse of max and min which are $\le$ and $\ge$. Therefore, $op_{\oplus _1} \text {is} \le$ and $op_{\oplus _2} \text {is} \ge$. To form the prune condition, PASCAL creates two nested loops. The inner loop runs over the borders of the inner tree (for example, reference dataset) applying the inner operator which is $\ge$. The outer loop covers the borders of the second tree (for example, the query dataset), applying the $\le$ operator.

Note that by the definition of the N-body problem, each operator that is applied to a dataset is regarded as the operator that is applied to the tree built for that dataset. We define two thresholds, $\tau _1$ and $\tau _2$ and the nested prune condition generated is shown below.

$$\begin{aligned} \begin{aligned}&op_{\oplus _1}(\tau _1 , \mathcal {K}(x_q,x_r) | op_{\oplus _2}(\tau _2 , \mathcal {K}(x_q,x_r)))\implies \tau _1 \ge (\mathcal {K}(x_q, x_r) | \tau _2 \le \mathcal {K}(x_q, x_r)), \\&s.t. ~~~ {\forall x_q \in \mathcal {N}_q^{\text {border}}, \forall x_r \in \mathcal {N}_r^{\text {border}}} \end{aligned} \end{aligned}$$

5 Domain-Specific Optimizations and Parallelization

In order to achieve an optimized code, we first apply numerous optimizations to both the tree construction and the computational core of the evaluation. Then, we parallelize the tree traversal defined by Algorithm 1, and finally tune empirically for the associated tuning parameters (e.g. leaf size).

Incremental Bounding Box Calculation. During tree construction described in Sect. 4, we associate each node with its bounding box data. This is critical for efficient evaluation during traversal. For instance, during range search, we check if the reference node is within a specified range of the query node and if not, the entire node is pruned. This check requires computing the minimum and maximum node-to-point and node-to-node distances. Pre-computing the bounding box information significantly reduces the time to compute these distances since we do not have to access the actual data points each time.

For kd-trees, this is essentially computing the hyper-rectangle boundary information in each dimension. At the start of the computation, the root bounding box is computed from all the N points. During partitioning, we only incrementally update the bounding box of the dimension that is being split at each node based on the splitting value. This results in a complexity of $\mathcal {O}\left( {Nd}\right)$.

Optimal Metric Calculation. The evaluation can be performed using a variety of distance metrics. We consider Euclidean: $\sqrt{\sum _{i=1}^{d}(x_i - y_i)^2}$, Manhattan: $\sum _{i=1}^{d}|x_i - y_i|$, Chebyshev: $\max _{i=1}^{d}|x_i - y_i|$, and Mahalanobis: $(\overrightarrow{x}-\overrightarrow{\mu })^{T}\varSigma ^{-1}(\overrightarrow{x}-\overrightarrow{\mu })$ ($\mu$ and $\varSigma$ are distribution’s parameters) metrics for real-valued vector spaces.

Outlined below are two techniques to efficiently compute these metrics which are repeatedly used in all phases of the algorithm. Additionally, we ensure that the compiler generates vectorized code for the metric calculation.

• 1. Each metric defines both a distance and a reduced distance, which is often faster to compute and is used whenever possible. For example, in the case of Euclidean distance, the reduced distance is squared Euclidean distance. This eliminates the expensive sqrt instruction which has long latencies.

• 2. Partial distance between two d-dimensional points x and y is defined as the distance computed on a subset of the d dimensions. For example, when searching for k-nearest neighbors, we compute the distance between two points and insert the reference point into our neighbor list only if the computed distance is smaller than the $k^{th}$ largest distance in our sorted list. When d is large as in the case for some of our datasets, this optimization offers additional savings in processing time where we can terminate the computation earlier if the computed partial distance exceeds our threshold.

Incremental Distance Calculation. This idea was introduced by Arya and Mount [1] where the node-to-point distance at each node during single-tree traversal is incrementally computed from the parent’s distance in constant time independent of dimension. For datasets with large d, this has the potential for significant savings in computation at the cost of minimal additional storage of distance information. We support this optimization and note that it is possible to extend this idea for computing node-to-node distances as well in multi-trees.

Parallelization and Tuning. After applying serial optimizations, we parallelize the multi-tree traversal using Cilk. Since there are dependencies across the recursion, we exploit a combination of data and task parallelism. At first, we spawn Cilk tasks recursively until all the threads are saturated, at which point we switch to data parallelism. Since the tree traversal is abstracted from the actual computation, parallelizing the tree traversal leads to parallel implementations of all six algorithms. Moreover, for any new algorithm expressed in PASCAL, we can obtain parallel multi-tree implementations at no additional cost. This greatly accelerates the ability to scale new problems in rapidly growing domains.

Algorithmically, the tree is parameterized by the maximum number of points per leaf node, $l$. As $l$ increases, the cost of tree construction decreases at the expense of increased cost in performing the BaseCase. On the other hand, small $l$ results in a large number of nodes and an increase in the cost of tree traversal. We exhaustively tune $l$ for all implementations.

6 Experimental Setup

Libraries. We compare PASCAL’s performance against state-of-the-art software namely, WEKA [10], Scitkit-learn [15], MLPACK [6], and MATLAB.

Architecture and Compilers. We evaluate our implementations on a dual-socket Intel Xeon E5-2630 v3 processor (Haswell-EP). Each socket has 8 cores, for a total of 16 cores (32 threads with hyper-threading) and a theoretical double precision peak performance of 614.4 GFlop/s. We use Intel C++ compiler (icpc version 15.0.2) with C++11 feature support. We use Python v2.7.6 for scikit-learn and Java v1.8.0 for Weka.

Table 1. Description of the datasets. N: number of points, d: dimensionality.

Benchmarks. We present results on five real-world datasets characterized in Table 1. These include Yahoo! front page module user click log dataset, v1.0 (Yahoo!), Higgs boson’s signals and background process dataset (HIGGS), Individual Household Electric Power Consumption dataset (IHEPC), US Census data from 1990 (Census), and KDD Cup 1999 dataset (KDD) from the UCI ML repository.

7 Results and Discussion

The combined benefits of asymptotically optimal algorithms, optimizations, and parallelization are substantial. In this section, we first compare our performance against state-of-the-art ML libraries and software. Then, we break down the performance gain step by step and finally, evaluate the scalability of our algorithms.

Performance Summary. Figure 2 presents the performance of k-NN and EM. The choice of these two algorithms is because they are the only ones supported by all competing libraries and therefore make good candidates for a comprehensive comparison. Moreover, the choice of these two algorithms albeit space constraints is because k-NN is a direct pruning algorithm while EM is an iterative approximation algorithm that represents two ends of the spectrum.

Fig. 2.

Speedup summary of single-tree EM (top) and dual-tree k-NN for $k=3$ (bottom). The slowest library is used as the baseline for comparison.

Across the board, our implementation shows significantly better performance compared to Scikit-learn, MLPACK, MATLAB, and Weka.

Performance Breakdown. To gain a better understanding of the factors contributing to the performance improvement, we break down the speedups in Table 2. Specifically, it helps distinguish the improvements that are purely algorithmic (tree algorithm) from improvements via optimization and parallelization. For example, for the Yahoo! dataset, we observe a 3.1$\times$ speedup from an asymptotically faster algorithm, 12.1$\times$ due to optimizations on top of the tree algorithm, and 173.1$\times$ with parallelization for k-NN. The breakdown for EM are 1.6$\times$, 3.2$\times$, and 53.7$\times$ respectively for the same dataset.

Table 2. Speedup breakdown. Alg stands for algorithmic improvement, +Opt refers to optimization on top of Alg, and +Par is parallelization on top of Opt.

We observe that each dataset benefits differently from algorithmic changes, optimizations, and parallelization based on the number of data points, dimensionality, and distribution of the points.

Scalability. Figure 3 shows the scalability of the six algorithms namely, (i) k-NN with $k=3$, (ii) RS with range between 0 and 2, (iii) KDE for Gaussian kernel, K with bandwidth, $\sigma = 0.1$ and relative error tolerance set to 0.1, (iv) EM with error tolerance of 0.1, (v) MST, and (vi) Hausdorff distance.

We observe good scaling on all six algorithms. Note that 32 threads is with hyper-threading enabled where we assign 2 threads per core. In all cases, hyper-threading further improves the performance resulting in $14\times$, $16\times$, $13\times$, $14\times$, $10\times$, and $14\times$ speedup for Yahoo! over the serial optimized code for k-NN, EM, RS, MST, KDE, and Hausdorff distance respectively.

Fig. 3.

Multicore scalability using Cilk. X-axis is the number of threads.

Scalability Difference in Multi-trees. Tree algorithms are irregular. The dynamic nature of pruning/approximation of sub-trees during tree-traversal makes these problems challenging to parallelize. This load-balancing problem is further exacerbated in dual-tree traversal. As a result, we observe that EM which uses single-tree traversal with one tree (we use a single-tree over a dual-tree traversal for EM because of the small number of clusters) shows better scalability compared to the other five algorithms which use dual-tree traversals.

We currently defer to Cilk to manage scheduling of tasks using its work-stealing scheduler. In future work, we will explore a locality aware work-stealing scheduler for better load balance which is critical especially on NUMA machines.

In summary, these results show the potential of our approach to achieve orders of magnitude improvement in performance through the use of tree data structures, optimizations, and parallelization.

8 Conclusions

In this paper, we proposed PASCAL, a parallel unified algorithmic framework for N-body problems. PASCAL generates prune and approximation conditions automatically from the high-level specification of the problem, which is one the most challenging components in the design of these algorithms. We evaluated PASCAL with six N-body problems from different domains and observe 10–230$\times$ speedup compared to state-of-the-art libraries/software. The broader impact is to enable scientific discovery not only for N-body problems in scientific computing and machine learning but also to a number of related problems in other unexplored domains that can be expressed in the same style of execution to obtain an out-of-the-box parallel optimized implementation.