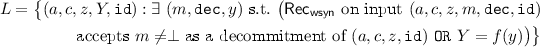Abstract
How many rounds and which assumptions are required for concurrent non-malleable commitments? The above question has puzzled researchers for several years. Pass in [TCC 2013] showed a lower bound of 3 rounds for the case of black-box reductions to falsifiable hardness assumptions with respect to polynomial-time adversaries. On the other side, Goyal [STOC 2011], Lin and Pass [STOC 2011] and Goyal et al. [FOCS 2012] showed that one-way functions (OWFs) are sufficient with a constant number of rounds. More recently Ciampi et al. [CRYPTO 2016] showed a 3-round construction based on subexponentially strong one-way permutations.
In this work we show as main result the first 4-round concurrent non-malleable commitment scheme assuming the existence of any one-way function.
Our approach builds on a new security notion for argument systems against man-in-the-middle attacks: Simulation-Witness-Independence. We show how to construct a 4-round one-many simulation-witnesses-independent argument system from one-way functions. We then combine this new tool in parallel with a weak form of non-malleable commitments constructed by Goyal et al. in [FOCS 2014] obtaining the main result of our work.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Commitment schemes are a fundamental primitive in Cryptography. Here we consider the intriguing question of constructing round-efficient schemes that remain secure even against man-in-the-middle (MiM) attacks: non-malleable (NM) commitments [12].
Non-malleable commitments. The round complexity of commitment schemes in the stand-alone setting is nowadays well understood. Non-interactive commitments can be constructed assuming the existence of 1-to-1 one-way functions (OWFs) [18]; 2-round commitments can be constructed assuming the existence of OWFs only. Moreover non-interactive commitments do not exist if one relies on the black-box use of OWFs only [33].
Instead, the round complexity of NM commitmentsFootnote 1 after 25 years of research remains a fascinating open question, in particular when taking into account the required computational assumptions. The original construction of [12] required a logarithmic number of rounds and the sole use of OWFs. Then, through a long sequence of very exciting positive results [1, 19, 22, 29,30,31, 41,42,43,44,45,46, 50], the above open question has been in part solved obtaining a constant-roundFootnote 2 (even concurrent) NM commitment scheme by using any OWF in a black-box fashion. On the negative side, Pass proved that NM commitments require at least 3 rounds [40]Footnote 3 when security is proved through a black-box reduction to polynomial-time hardness assumptions.
Breaking the multiple rewind-slot barrier. The above papers left open the question of achieving (concurrent) non-malleable commitments with optimal round complexity. A main common issue for round-efficient non-malleable commitments is that typically a security proof requires some simulation on the left and extraction on the right that should not interfere with each other. Indeed, a known paradigm introduced by Pass [39] proposes to have in a protocol multiple potential rewind slots so that extraction and simulation can both be run in 2 independent sequential steps. On the negative side, the use of multiple rewind slots increases the round complexity of the protocol (i.e., two rewind slots require at least 5 rounds).
More recently the multiple rewind-slot technique has been bypassed in [25] but only for the (simpler) one-one case (i.e., just one sender and one receiver). In particular, Goyal et al. [25] showed a one-one 4-round NM commitment scheme based on OWFs only. The more recent work of Goyal et al. [23, 24] exploited the use of the NM codes in the split-state model to show a 3-round one-one NM commitment scheme based on the black-box use of any 1-to-1 OWF that is secure against super-polynomial time adversariesFootnote 4. Ciampi et al. [6] obtained concurrent non-malleability in 3 rounds starting from any one-one non-malleable (and extractable) commitment scheme, but their security proof crucially relies on the existence of one-way permutations secure against subexponential-time adversaries. Assumptions against super-polynomial time adversaries allow to avoid multiple rewind slots even in presence of polynomially many sessions since the security proof can rely on straight-line simulation/extractionFootnote 5.
1.1 Our Results
In this paper we break the multiple-slot barrier for concurrent NM commitments by showing a 4-round scheme based on the sole existence of OWFs. While previous work relied on having either (1) stronger assumptions or (2) multiple rewind slots or (3) limited concurrency, in this work we introduce new techniques that allow to have just one rewind slot, minimal hardness assumptions and full concurrency.
More specifically we give the following four contributions.
-
Non-malleable commitments w.r.t. non-aborting adversaries. We prove that a subprotocol of [25] is a 4-round statistically binding concurrent NM commitment scheme from OWFs (resp. a 3-round perfectly binding concurrent NM commitment scheme from 1-to-1 OWFs), if the adversary is restricted to playing well-formed commitments in the right sessions when receiving well formed commitments from the left sessions. We refer to this weaker security notion as concurrent weak non-malleability (wNM).
-
Simulation-Witness-Independence. We define a new security notion for argument systems w.r.t. man-in-the-middle attacks that we refer to as simulation-witness-independence (SimWI). This security notion seemingly is not implied by previous notions as simulation-extractability/soundness and strong non-malleable witness indistinguishability.
-
4-Round One-Many SimWI from OWFs. We then construct a 4-round one-many SimWI argument of knowledge for some specific languages by relying on OWFs only. This construction circumvents the major problem caused by the need of rewinding on the left to simulate and on the right to extract when there is only one available rewind slot.
-
Concurrent wNM + One-Many SimWI \(\Rightarrow \) 4-Round Concurrent NM Commitments. We present our new paradigm consisting in combining the above two notions in a protocol that runs in parallel the concurrent wNM commitment scheme and the one-many SimWI argument of knowledge. Therefore as main result of this work we upgrade concurrent wNM to full-fledged concurrent non-malleability without any penalization in rounds and assumptions.
We now discuss in more details each of the above 4 contributions.
Weak Non-Malleable Commitments. We define commitment schemes enjoying a limited form of non-malleabilityFootnote 6.
Informally, we say that a commitment scheme is weak non-malleable (wNM) if it is non-malleable w.r.t. adversaries that never commit to \(\bot \) when receiving honestly computed commitments. This form of non-malleability is significantly weaker than full-fledged non-malleability. Indeed, a full-fledged MiM \(\mathcal {A}\) can for instance maul as follows: \(\mathcal {A}\) creates a commitment of \(m_0\) making use of messages computed by the sender in the left session so that if the sender commits to \(m_0\) then the commitment of \(\mathcal {A}\) is a well formed commitment of \(m_0\), while instead if the sender commits to \(m_1 \ne m_0\) then the commitment of \(\mathcal {A}\) is not well formed and therefore corresponds to \(\bot \). Such attacks can be explicitly instantiated as shown in [6] where a generalization of the above \(\mathcal {A}\) is used to prove that a preliminary version of the scheme of [24] is not concurrent non-malleable.
While by itself the wNM guarantee is certainly unsatisfying as protection against MiM attacks, the design of a wNM commitment scheme can be an easier task and schemes with such light non-malleability flavor might exist with improved round complexity, efficiency and complexity assumptions compared to schemes achieving full-fledged non-malleability.
We show that a protocol due to [25] is a 4-round statistically binding concurrent wNM commitment scheme requiring OWFs only (resp., a 3-round perfectly binding concurrent wNM commitment scheme requiring 1-to-1 OWFs only). Moreover their protocol can be instantiated to be public coin. The security proof consists of some pretty straightforward observations on top of various useful lemmas already proven in [25]. Our contribution on wNM commitments therefore consists in (1) introducing and formalizing this notion; (2) observing the existence of a secure construction in previous work; (3) using it as one of the two main building blocks of our paradigm allowing to obtain 4-round concurrent (full-fledged) NM commitments from OWFs. For lack of space we postpone further details on wNM commitments to the full version (see [5]) so that in this work we can give more details on the more interesting results of this work (i.e., the definition and construction of SimWI, and the new paradigm for concurrent NM commitments). A formal definition of weak NM commitments can be found in Sect. 2.3 (see Definition 5). The proof that a scheme proposed in [25] satisfies this notion can be found in the full version (see [5]).
Simulation-Witness-Independence. We introduce a new security notion against MiM attacks to argument systems. We call our security notion simulation-witness-independence (SimWI) since it has similarities both with simulation extractability/soundness (see [43, 48]) and with (strong) non-malleable witness indistinguishability [32, 36] (sNMWI, NMWI). For simplicity we will discuss now the case of one prover and one verifier only, however our formal definition, construction and application will focus on the one-many case (i.e., up to 1 prover and polynomially many verifiers).
The 1st security flavor that our notion tries to capture is the concept that the view of a MiM in the real game should be simulatable. Therefore we will have an experiment corresponding to the real game where the MiM plays with a honest prover and a honest verifier, and an experiment corresponding to the simulated game that simply consists of the output of a stand-alone simulator that emulates the prover and runs the code of honest verifiers when interacting internally with the MiMFootnote 7.
While the above 1st security flavor guarantees that the statements proven by the MiM in the real-world experiment and in the simulated experiment are indistinguishable, there still is no guarantee that the MiM is unable to prove in the two experiments statements that are associated to witnesses belonging to distinguishable distributions. In other words, as 2nd flavor we want to capture the independence of the witnesses associated to the statements proven by the MiM with respect to the fact that the actual witness in the left session is used (this is the case of the real game) or is not used (this is the case of the simulated game). In order to avoid any ambiguity on which witness is associated to a statement, we associate to an \(\mathcal {N}\mathcal {P}\) language a non-negative integer \(\gamma \). More precisely, for any \(\mathcal {N}\mathcal {P}\) language L we consider a non-negative integer \(\gamma \) such that for any \(x \in L\) all witnesses of x have the same first \(\gamma \) bitsFootnote 8. The reason why we assign such a value \(\gamma \) to every \(\mathcal {N}\mathcal {P}\) language is that it fixes in some non-ambiguous way the input for the distinguisher of SimWI (indeed the input will be the first \(\gamma \) bits of any witness) and at same time the prefix of all the witnesses of an instance can be recovered by extracting any witness.
The above 2nd flavor makes our security definition non-trivial. Indeed standard zero knowledge is clearly insufficient against MiM attacks and the definition has strong connections with the (hard to achieve) concept of committed message in NM commitmentsFootnote 9. One might think that some heavy machinery could already imply our new notion. However, by taking into account all subtleties of the definitions it turns out that SimWI is seemingly not implied by simulation extractability, simulation soundness and sNMWI/NMWI. We stress that our goal is to get a one-many 4-round construction under minimal assumptions.
Comparison with simulation extractability and simulation soundness. Simulation extractability requires the simulator to output a transcript and witnesses for the statements appearing in the right sessions of the transcript.
Simulation soundness requires the MiM to fail in proving false statements when receiving simulated proofs of false statements.
SimWI requires the simulator to output a transcript that includes statements proven in right sessions. The distribution of the instance/witness pairs associated to those statements is required to be indistinguishable from the distribution of the instance/witness pairs associated to the statements proved by the MiM in the real game. In simulation extractability there is no requirement on the witness given in output by the simulator beyond being valid witnesses. Simulation soundness does not have any requirement on the witnesses associated to the statements proven by the MiM.
Comparison with sNMWI/NMWI. sNMWI considers two indistinguishable distributions of instance/witnesses pairs. Very informally, the requirement of sNMWI/NMWI is that the instance/witness pairs associated to the arguments given by the MiM in the right sessions be independent of the distribution from which the instance/witness pair of the argument given to the MiM in the left session has been sampled.
SimWI requires the existence of a simulator while instead sNMWI/NMWI only considers experiments where the actual prover plays.
One-Many SimWI From OWFs in 4 Rounds (i.e., in Just One Rewind Slot!). As discussed above, SimWI is an interesting security notions w.r.t. MiM attacks and similarly to all previous non-malleability notions is certainly non-trivial to achieve, especially when considering (1) the one-many case (2) only four rounds (i.e., one rewind slot) and (3) minimal assumptions. In this work we show how to construct a 4-round one-many SimWI argument of knowledge (AoK) from OWFs, therefore avoiding multiple rewind slots.
A common approach to construct 4-round zero-knowledge arguments (even without non-malleability requirements) relies on the FLS/FS paradigm [14, 15]. First there is a subprotocol useful to extract a trapdoor from the adversarial verifier. Then there is a witness-indistinguishable proof of knowledge (WIPoK) where the prover proves knowledge of either a witness for the statement or of the trapdoor. In order to save rounds the two subprotocols are parallelized.
The above common approach fails in presence of MiM attacks. The reason is that the MiM adversary can attack the witness indistinguishability (WI) of the WIPoK received in the left session in order to prove his statements in the right sessions. Using such a MiM to contradict the WI of the WIPoK is problematic since one should extract some useful information from the right session but this would require also to rewind the challenger of the WI of the WIPoK on the left.
We bypass the above difficulty as follows. Instead of relying on the WI of the WIPoK that requires two messages played by the challenger, we propose a construction where we essentially break the interactive challenger of WI into two non-interactive challengers. We implement this idea by relying on: (1) instance-dependent trapdoor commitments (IDTCom) and (2) special honest-verifier zero knowledge (special HVZK). More in details, let \((\pi _1,\pi _2,\pi _3,\pi _4)\) be the transcript of a delayed-inputFootnote 10 4-round special HVZK adaptive-input proof of knowledge (PoK). We require the prover to send an IDTCom \({\mathtt {com}}\) of \(\pi _2\) that is opened, sending the opening \(\mathtt {dec}\), only in the last round, when \(\pi _4\) is sent. The actual transcript therefore becomes \((\pi _1,{\mathtt {com}},\pi _3,(\pi _2,\mathtt {dec},\pi _4))\).
Consider now an experiment where the trapdoor is known and \(\pi _2\) can be opened arbitrarily. If the output of the experiment deviates from the original one, we will have a reduction to the trapdoorness of the IDTCom. The reduction is not problematic since the challenger of the trapdoorness is non-interactive, sending a pair (commitment, decommitment) that is either computed using the regular procedure or through the use of the trapdoor. Next, in another experiment we can replace the prover of the PoK with the special HVZK simulator that will compute \(\pi _2\) and \(\pi _4\) after having as input \(\pi _1\) and \(\pi _3\). Again, the output of this experiment will not deviate from the previous one otherwise we can show an adversary for the special HVZK property. The reduction again is not problematic since the challenger of special HVZK is non-interactive.
We implement the trapdoor-extraction subprotocol through OWFs by using as trapdoor knowledge of two signatures under the same public key sent by the verifier in the 1st round. The verifier will send a signature of one message (chosen by the prover) in the 3rd round (with this approach we follow previous ideas of [3, 4, 11, 20]). We will use a delayed-input special HVZK adaptive-input PoK where the prover proves knowledge of either a witness for the statement or of signatures of messages. The IDTCom will have the public key of the signature scheme as instance, therefore the simulator after having extracted the signatures will be able to equivocate the commitments. The security proof presents one more caveat. Once the simulator rewinds on the left to obtain the trapdoor it is not clear how to argue that the extraction from the right is meaningful since the extractor might simply obtain the same trapdoor. More specifically, the adversary might be able to equivocate on the right, therefore the extractor of the PoK would fail, and the best we can get from such a binding violation is the trapdoor of the IDTCom played in the right session. This does not give any contradiction since the trapdoor of the right session had to be already known in order to answer twice (before and after the rewind) in the right session to the MiM. We resolve this problem by relying on a specific proof approach where while the initial transcript is generated by the simulator, when the extractions are played in the right sessions, the transcript of the left session is re-completed by running the prover of the special HVZK PoK. The reason why in this case the extraction on the right will succeed is that if we extract the trapdoor from the right session then this will also happen in the real game where the trapdoor is never used. In turn it would break the security of the signature scheme.
Caveat: adaptive-input selection. We will give a formal definition that allows the MiM to select the instance/witness pair for the left session only at the end, while the MiM must fix the statement for a right session already when playing his first round in that session. Our construction satisfies this notion and even a more important form of adaptiveness. We allow the MiM to specify the statement in the last round of a right session, as long as the witness is already fixed when playing his first round in that session. The reason why we prove such more sophisticated form of adaptive-input selection is that it is required in our application for concurrent NM commitments. Ideally one would like to satisfy the best possible adaptive-input selection, in order to make this new primitive useful in a broader range of applications. However we can not prove our construction secure with fully adaptive-input selection since we are not able to extract the witness from a MiM selecting a new statement (with possibly a new witness) in the last round of a right session. Indeed we would end up having a certain statement in the transcript of the simulator and then a witness for another statement obtained through rewinds. This would negatively affect our proof approach.
4-Round Concurrent NM Commitments from OWFs. We solve the problem left open by [25] by showing a 4-round concurrent NM commitment scheme relying on OWFs only. The new paradigm that we propose to obtain concurrent non-malleability consists in combining in parallel a 4-round public-coin concurrent wNM commitment scheme from OWFs \(\varPi _{0}\), and a one-many 4-round SimWI argument of knowledge from OWFs \(\varPi _{1}\).
The new paradigm. \(\varPi _0\) is run in order to commit to the message m. \(\varPi _1\) is instead used to prove knowledge of a valid message and randomness explaining the transcript of \(\varPi _0\). The power of the new approach consists in using the above two tools that are in perfect synergy to defeat a concurrent MiM attack. The idea of the security proof is now quite simple. Since any one-many NM commitment is also many-manyFootnote 11 NM, we focus the following discussion on the one-many case.
In the 1st experiment (the real game RG0) the sender commits to \(m_0\). Clearly there can not be a commitment to \(\bot \) on the right otherwise the soundness of \(\varPi _1\) is contradicted. Symmetrically there is an experiment RG1 where the sender commits to \(m_1\) and there is no commitment to \(\bot \) on the right. Then we consider an hybrid game H0 where the simulator of one-many SimWI of \(\varPi _1\) is used. Observe that if (by contradiction) the distribution of the messages committed on the right changes w.r.t. RG0 we have that also the distribution of the witnesses corresponding to the statements proved in \(\varPi _1\) on the right changes. However this clearly violates SimWI. Therefore it must still be the case that a commitment played on the right corresponds to \(\bot \) with negligible probability only. Symmetrically, there is an experiment H1 that is indistinguishable from RG1 and such that commitments played on the right are well formed (i.e., different from \(\bot \)). Therefore we can conclude that RG0 is indistinguishable from RG1 by noticing that H0 is indistinguishable from H1. Indeed, both H0 and H1 guarantee that the messages committed by the adversary on the right correspond to \(\bot \) with negligible probability only. Summing up, a detectable deviation from H0 to H1 implies a contradiction of the concurrent wNM of \(\varPi _0\) Footnote 12. This observation concludes the high-level overview of the security proof. However, some remarks are in order.
Remark 1: the required adaptive-input flavor. As specified in the previous section, our 4-round one-many SimWI AoK \(\varPi _1\) is fully adaptive on the left but instead on the right requires the witness to be fixed already in the first round of the MiM. The statements instead can be decided in the last round also in the right sessions. The flexibility with the statement is important since \(\varPi _0\) is completed only in the last round and the entire transcript of \(\varPi _0\) is part of the statement of \(\varPi _1\). The lack of flexibility on the witness in the right sessions forces us to add one more requirement to \(\varPi _0\). We need that message and randomness are already fixed in the 2nd round of \(\varPi _0\), since they will be the witness for \(\varPi _1\). This property is satisfied by the construction of [25] that we prove to be concurrent wNM in the full version (see [5]).
Remark 2: on the need of public coins in \(\varPi _{0}\) . In a reduction we will have to simulate the last round of the receiver of \(\varPi _{0}\) without knowing the randomness he used to compute the previous round. Obviously public coins are easy to simulate.
1.2 3-Round Concurrent Non-Malleable Commitments
The work of Ciampi et al. [6] relied on subexponentially strong one-way permutations and the existence of any 3-round one-one non-malleable commitment scheme \(\varPi \). In this work we propose a different approach for 3-round one-one non-malleable commitments that instead can start with a limited form of non-malleability enjoyed by both a subprotocol of [25] and a subprotocol of [24] (therefore we can instantiate our result in two completely different ways). The result of Ciampi et al. [6] can still be instantiated using our 3-round one-one non-malleable commitment scheme that we present in this work. Therefore our work combined with the one of [6] gives the first 3-round concurrent non-malleable commitment scheme from falsifiable assumptionsFootnote 13.
Our 3-round one-one non-malleable commitment scheme combines some ideas of [6] along with the concept of weak non-malleable commitment. In particular we start with a scheme that is one-one non-malleable only against synchronous adversaries that do not commit to \(\bot \). As we discuss in the paper, both a subprotocol of [25] and a subprotocol of [24] satisfy this security property. Considering this notion we construct a compiler that, on input a 3-round synchronous weak one-one NM commitment scheme, gives as output a 3-round extractable one-one NM commitment scheme assuming OWPs secure against subexponential-time adversaries. This can then be used inside [6] to get 3-round concurrent non-malleable commitments from subexponential one-way permutations.
1.3 The New State of the Art
In Table 1 we summarize the new state of the art.
2 Definitions and Tools
2.1 Preliminaries
We denote the security parameter by \(\lambda \) and use “|” as concatenation operator (i.e., if a and b are two strings then by a|b we denote the concatenation of a and b). For a finite set Q, \(x\leftarrow Q\) sampling of x from Q with uniform distribution. We use the abbreviation ppt that stays for probabilistic polynomial time. We use \(\mathsf{poly}(\cdot )\) to indicate a generic polynomial function and \(\mathbb {N}\) to denote the set of positive integer. We use the notation \(s^t\) to denote the first t-bits of a string s. A polynomial-time relation \({\mathsf {Rel}}\) (or polynomial relation, in short) is a subset of \(\{0, 1\}^*\times \{0,1\}^*\) such that membership of (x, w) in \({\mathsf {Rel}}\) can be decided in time polynomial in |x|. For \((x,w)\in {\mathsf {Rel}}\), we call x the instance and w a witness for x. For a polynomial-time relation \({\mathsf {Rel}}\), we define the \(\mathcal {N}\mathcal {P}\)-language \(L_{{\mathsf {Rel}}}\) as \(L_{{\mathsf {Rel}}}=\{x|\exists w: (x, w)\in {\mathsf {Rel}}\}\). Analogously, unless otherwise specified, for an \(\mathcal {N}\mathcal {P}\)-language L we denote by \({\mathsf {Rel}}_\mathsf {L}\) the corresponding polynomial-time relation (that is, \({\mathsf {Rel}}_\mathsf {L}\) is such that \(L=L_{{\mathsf {Rel}}_\mathsf {L}}\)). Let A and B be two interactive probabilistic algorithms. We denote by \(\langle A(\alpha ),B(\beta )\rangle (\gamma )\) the distribution of B’s output after running on private input \(\beta \) with A using private input \(\alpha \), both running on common input \(\gamma \). Typically, one of the two algorithms receives \(1^\lambda \) as input. A transcript of \(\langle A(\alpha ),B(\beta )\rangle (\gamma )\) consists of the messages exchanged during an execution where A receives a private input \(\alpha \), B receives a private input \(\beta \) and both A and B receive a common input \(\gamma \). Moreover, we will refer to the view of A (resp. B) as the messages it received during the execution of \(\langle A(\alpha ),B(\beta )\rangle (\gamma )\), along with its randomness and its input.
Definition 1
(Proof/argument system). A pair of ppt interactive algorithms \(\varPi =(\mathcal {P},\mathcal {V})\) constitutes a proof system (resp., an argument system) for an \(\mathcal {N}\mathcal {P}\)-language L, if the following conditions hold:
Completeness: For every \(x\in L\) and w such that \((x,w)\in {\mathsf {Rel}}_\mathsf {L}\), it holds that: \(\text {Prob}\left[ \;\langle \mathcal {P}(w), \mathcal {V}\rangle (x) =1\;\right] =1.\)
Soundness: For every interactive (resp., ppt interactive) algorithm \(\mathcal {P}^{\star }\), there exists a negligible function \(\nu \) such that for every \(x \notin L\) and every z:
\(\text {Prob}\left[ \;\langle \mathcal {P}^{\star }(z), \mathcal {V}\rangle (x) =1\;\right] < \nu (|x|). \)
A proof/argument system \(\varPi =(\mathcal {P},\mathcal {V})\) for an \(\mathcal {N}\mathcal {P}\)-language L, enjoys delayed-input completeness if \(\mathcal {P}\) needs x and w only to compute the last round and \(\mathcal {V}\) needs x only to compute the output. Before that, \(\mathcal {P}\) and \(\mathcal {V}\) run having as input only the size of x. The notion of delayed-input completeness was defined in [8]. An interactive protocol \(\varPi =(\mathcal {P},\mathcal {V})\) is public coin if, at every round, \(\mathcal {V}\) simply tosses a predetermined number of coins (random challenge) and sends the outcome to the prover. We say that the transcript \(\tau \) of an execution \(b=\langle \mathcal {P}(z), \mathcal {V}\rangle (x)\) is accepting if \(b=1\).
Definition 2
(Special Honest-Verifier Zero Knowledge (Special HVZK)). Consider a public-coin proof/argument system \(\varPi =(\mathcal {P}, \mathcal {V})\) for an \(\mathcal {N}\mathcal {P}\)-language L where the verifier sends m messages of length \(\ell _1,\ldots ,\ell _m\). We say that \(\varPi \) is Special HVZK if there exists a PPT simulator algorithm \(\mathcal {S}\) that on input any \(x\in L\), security parameter \(1^\lambda \) and any \(c_1\in \{0,1\}^{\ell _1},\ldots ,c_m\in \{0,1\}^{\ell _m}\), outputs a transcript for proving \(x\in L\) where \(c_1,\ldots ,c_m\) are the messages of the verifier, such that the distribution of the output of \(\mathcal {S}\) is computationally indistinguishable from the distribution of a transcript obtained when \(\mathcal {V}\) sends \(c_1,\ldots ,c_m\) as challenges and \(\mathcal {P}\) runs on common input x and any w such that \((x,w)\in \mathsf {Rel}_\mathsf {L}\).
In this paper we consider the notion of proof/argument of knowledge (PoK/AoK) defined in [29]. Furthermore we consider the adaptive-input PoK/AoK property for all the protocols that enjoy delayed-input completeness. Adaptive-input PoK/AoK ensures that the PoK/AoK property still holds when a malicious prover can choose the statement adaptively at the last round. We consider the 3-round public-coin Special HVZK PoK proposed by Lapidot and Shamir [28], that we denote by LS. LS enjoys delayed-input completeness since the inputs for both \(\mathcal {P}\) and \(\mathcal {V}\) are needed only to play the last round, and only the length of the instance is needed earlier. LS also enjoys adaptive-input PoK. In particular we use a 4-round delayed-input special HVZK adaptive-input AoK that is a variant of LS [13] that relies on OWFs only. The additional round is indeed needed to instantiate the commitment scheme used in LS under any OWF.
2.2 2-Round Instance-Dependent Trapdoor Commitments
Here we define a special commitment scheme based on an \(\mathcal {N}\mathcal {P}\)-language L where sender and receiver also receive as input an instance x. While correctness and computational hiding hold for any x, we require that statistical binding holds for \(x \not \in L\) and knowledge of a witness for \(x \in L\) allows to equivocate. Finally, we require that a commitment along with two different openings allows to compute the witness for \(x \in L\). We recall that \(\hat{L}\) denotes the language that includes L and all well formed instances that are not in L.
Definition 3
Let \(1^\lambda \) be the security parameter, L be an \(\mathcal {N}\mathcal {P}\)-language and \({\mathsf {Rel}}_\mathsf {L}\) be the corresponding \(\mathcal {N}\mathcal {P}\)-relation. A triple of ppt algorithms \(\mathsf {TC}=(\mathsf {Sen}, \mathsf {Rec}, \mathsf {TFake})\) is a 2-Round Instance-Dependent Trapdoor Commitment scheme if the following properties hold.
-
Correctness. In the 1st round, \(\mathsf {Rec}\) on input \(1^\lambda \) and \(x \in \hat{L}\) outputs \(\rho \). In the 2nd round \(\mathsf {Sen}\) on input the message m, \(1^\lambda \), \(\rho \) and \(x \in L\) outputs \(({\mathtt {com}},\mathtt {dec})\). We will refer to the pair \((\rho ,{\mathtt {com}})\) as the commitment of m. Moreover we will refer to the execution of the above two rounds including the exchange of the corresponding two messages as the commitment phase. Then \(\mathsf {Rec}\) on input m, x, \({\mathtt {com}}\), \(\mathtt {dec}\) and the private coins used to generate \(\rho \) in the commitment phase outputs 1. We will refer to the execution of this last round including the exchange of \(\mathtt {dec}\) as the decommitment phase. Notice that an adversarial sender \(\mathsf {Sen}^\star \) could deviate from the behavior of \(\mathsf {Sen}\) when computing and sending \({\mathtt {com}}\) and \(\mathtt {dec}\) for an instance \(x \in \hat{L}\). As a consequence \(\mathsf {Rec}\) could output 0 in the decommitment phase. We will say that \(\mathtt {dec}\) is a valid decommitment of \((\rho ,{\mathtt {com}})\) to m for an instance \(x \in \hat{L}\), if \(\mathsf {Rec}\) outputs 1.
-
Hiding. Given a ppt adversary \(\mathcal {A}\), consider the following hiding experiment \(\mathsf {ExpHiding}^b_{\mathcal {A},\mathsf {TC}}(\lambda ,x)\) for \(b=0,1\) and \(x\in \hat{L}_R\):
-
On input \(1^\lambda \) and x, \(\mathcal {A}\) outputs a message m, along with \(\rho \).
-
The challenger on input \(x, m, \rho , b\) works as follows: if \(b=0\) then it runs \(\mathsf {Sen}\) on input m, x and \(\rho \), obtaining a pair \(({\mathtt {com}},\mathtt {dec})\), otherwise it runs \(\mathsf {TFake}\) on input x and \(\rho \), obtaining a pair \(({\mathtt {com}},\mathtt {aux})\). The challenger outputs \({\mathtt {com}}\).
-
\(\mathcal {A}\) on input \({\mathtt {com}}\) outputs a bit \(b'\) and this is the output of the experiment.
We say that hiding holds if for any ppt adversary \(\mathcal {A}\) there exist a negligible function \(\nu \), s.t.:
$$\Big |\text {Prob}\left[ \;\mathsf {ExpHiding}^0_{\mathcal {A},\mathsf {TC}}(\lambda ,x)=1\;\right] -\text {Prob}\left[ \; \mathsf {ExpHiding}^1_{\mathcal {A},\mathsf {TC}}(\lambda ,x)=1\;\right] \Big | <\nu (\lambda ).$$ -
-
Special Binding. There exists a ppt algorithm that on input a commitment \((\rho ,{\mathtt {com}})\), the private coins used by \(\mathsf {Rec}\) to compute \(\rho \), and two valid decommitments \((\mathtt {dec},\mathtt {dec}')\) of \((\rho ,{\mathtt {com}})\) to two different messages m and \(m'\) w.r.t. an instance \(x \in L\), outputs w s.t. \((x,w)\in {\mathsf {Rel}}_\mathsf {L}\) with overwhelming probability.
-
Trapdoorness. For any ppt adversary \(\mathcal {A}\) there exist a negligible function \(\nu \), s.t. for all \(x \in L\) it holds that:
$$\Big |\text {Prob}\left[ \;\mathsf {ExpCom}_{\mathcal {A},\mathsf {TC}}(\lambda , x)=1\;\right] -\text {Prob}\left[ \;\mathsf {ExpTrapdoor}_{\mathcal {A},\mathsf {TC}}(\lambda ,x)=1\;\right] \Big | <\nu (\lambda )$$where \(\mathsf {ExpCom}_{\mathcal {A},\mathsf {TC}}(\lambda ,x)\) and \(\mathsf {ExpTrapdoor}_{\mathcal {A},\mathsf {TC}}(\lambda ,x)\) are defined belowFootnote 14.

2.3 Non-Malleable Commitments
Here we follow [31]. Let  be a statistically binding commitment scheme and let \(\lambda \) be the security parameter. Consider MiM adversaries that are participating in left and right sessions in which \(\mathsf{poly}(\lambda )\) commitments take place. We compare between a MiM and a simulated execution. In the MiM execution the adversary \(\mathcal {A}\), with auxiliary information z, is simultaneously participating in \(\mathsf{poly}(\lambda )\) left and right sessions. In the left sessions the MiM adversary \(\mathcal {A}\) interacts with \(\mathsf {Sen}_1, \dots , \mathsf {Sen}_{\mathsf{poly}(\lambda )}\) receiving commitments to values \(m_1,\dots ,m_{\mathsf{poly}(\lambda )}\) using identities \({{\mathtt {id}}}_1,\dots , {\mathtt {id}}_{\mathsf{poly}(\lambda )}\) of its choice. In the right session \(\mathcal {A}\) interacts with \(\mathsf {Rec}_1, \dots , \mathsf {Rec}_{\mathsf{poly}(\lambda )}\) attempting to commit to a sequence of related values \(\tilde{m}_1,\dots ,\tilde{m}_{\mathsf{poly}(\lambda )}\) again using identities of its choice \(\tilde{{\mathtt {id}}}_1,\dots , \tilde{{\mathtt {id}}}_{\mathsf{poly}(\lambda )}\). If any of the right commitments is invalid, or undefined, its value is set to \(\perp \). For any i such that \(\tilde{{\mathtt {id}}}_i = {\mathtt {id}}_j\) for some j, set \(\tilde{m}_i=\perp \) (i.e., any commitment where the adversary uses the same identity of one of the honest senders is considered invalid). Let
be a statistically binding commitment scheme and let \(\lambda \) be the security parameter. Consider MiM adversaries that are participating in left and right sessions in which \(\mathsf{poly}(\lambda )\) commitments take place. We compare between a MiM and a simulated execution. In the MiM execution the adversary \(\mathcal {A}\), with auxiliary information z, is simultaneously participating in \(\mathsf{poly}(\lambda )\) left and right sessions. In the left sessions the MiM adversary \(\mathcal {A}\) interacts with \(\mathsf {Sen}_1, \dots , \mathsf {Sen}_{\mathsf{poly}(\lambda )}\) receiving commitments to values \(m_1,\dots ,m_{\mathsf{poly}(\lambda )}\) using identities \({{\mathtt {id}}}_1,\dots , {\mathtt {id}}_{\mathsf{poly}(\lambda )}\) of its choice. In the right session \(\mathcal {A}\) interacts with \(\mathsf {Rec}_1, \dots , \mathsf {Rec}_{\mathsf{poly}(\lambda )}\) attempting to commit to a sequence of related values \(\tilde{m}_1,\dots ,\tilde{m}_{\mathsf{poly}(\lambda )}\) again using identities of its choice \(\tilde{{\mathtt {id}}}_1,\dots , \tilde{{\mathtt {id}}}_{\mathsf{poly}(\lambda )}\). If any of the right commitments is invalid, or undefined, its value is set to \(\perp \). For any i such that \(\tilde{{\mathtt {id}}}_i = {\mathtt {id}}_j\) for some j, set \(\tilde{m}_i=\perp \) (i.e., any commitment where the adversary uses the same identity of one of the honest senders is considered invalid). Let  denote a random variable that describes the values \(\tilde{m}_1,\dots ,\tilde{m}_{\mathsf{poly}(\lambda )}\) and the view of \(\mathcal {A}\), in the above experiment. In the simulated execution, an efficient simulator S directly interacts with \(\mathsf {Rec}_1, \dots , \mathsf {Rec}_{\mathsf{poly}(\lambda )}\). Let
denote a random variable that describes the values \(\tilde{m}_1,\dots ,\tilde{m}_{\mathsf{poly}(\lambda )}\) and the view of \(\mathcal {A}\), in the above experiment. In the simulated execution, an efficient simulator S directly interacts with \(\mathsf {Rec}_1, \dots , \mathsf {Rec}_{\mathsf{poly}(\lambda )}\). Let  denote the random variable describing the values \(\tilde{m}_1,\dots ,\tilde{m}_{\mathsf{poly}(\lambda )}\) committed by S, and the output view of S; whenever the view contains in the i-th right session the same identity of any of the identities of the left sessions, then \(m_i\) is set to \(\perp \).
denote the random variable describing the values \(\tilde{m}_1,\dots ,\tilde{m}_{\mathsf{poly}(\lambda )}\) committed by S, and the output view of S; whenever the view contains in the i-th right session the same identity of any of the identities of the left sessions, then \(m_i\) is set to \(\perp \).
In all the paper we denote by \(\tilde{\delta }\) a value associated with the right session (where the adversary \(\mathcal {A}\) plays with a receiver) where \(\delta \) is the corresponding value in the left session. For example, the sender commits to v in the left session while \(\mathcal {A}\) commits to \(\tilde{v}\) in the right session.
Definition 4
(Concurrent NM commitment scheme [31]). A commitment scheme is concurrent NM with respect to commitment (or a many-many NM commitment scheme) if, for every ppt concurrent MiM adversary \(\mathcal {A}\), there exists a ppt simulator S such that for all \(m_i\in \{0,1\}^{\mathsf{poly}(\lambda )}\) for \(i=1,\dots , \mathsf{poly}(\lambda )\) the following ensembles are computationally indistinguishable:

As in [31] we also consider relaxed notions of concurrent non-malleability: one-many and one-one NM commitment schemes. In a one-many NM commitment scheme, \(\mathcal {A}\) participates in one left and polynomially many right sessions. In a one-one (i.e., a stand-alone secure) NM commitment scheme, we consider only adversaries \(\mathcal {A}\) that participate in one left and one right session. We will make use of the following proposition of [31].
Proposition 1
Let \((\mathsf {Sen}, \mathsf {Rec})\) be a one-many NM commitment scheme. Then, \((\mathsf {Sen},\mathsf {Rec})\) is also a concurrent (i.e., many-many) NM commitment scheme.
We say that a commitment is valid or well formed if it can be decommitted to a message \(m\ne \bot \). Following [29] we say that a MiM is synchronous if it “aligns” the left and the right sessions; that is, whenever it receives message i on the left, it directly sends message i on the right, and vice versa.
2.4 New Definitions: Weak NM and SimWI
Definition 5
( \(weak\) NM commitment scheme). A commitment scheme is weak one-one (resp., one-many) non-malleable if it is a one-one (resp., one-many) NM commitment scheme with respect to MiM adversary that when receiving a well formed commitment in the left session, except with negligible probability computes well formed commitments (i.e., the computed commitments can be opened to messages \(\ne \bot \)) in the right sessions.
In the rest of the paper, following [25], we assume that identities are known before the protocol begins, though strictly speaking this is not necessary, as the identities do not appear in the protocol until after the first committer message. The MiM can choose his identity adversarially as long as it differs from the identities used by honest senders. As already observed in previous work, when the identity is selected by the sender the id-based definitions guarantee non-malleability as long as the MiM does not behave like a proxy (an unavoidable attack). Indeed the sender can pick as identity the public key of a signature scheme signing the transcript. The MiM will have to use a different identity or to break the signature scheme.
Simulation-witness-independence (SimWI) for \(L^\gamma \). We define SimWI for an \(\mathcal {N}\mathcal {P}\) language L associating to the language a non-negative integer \(\gamma \). Roughly speaking all witnesses of an instance have in common the first \(\gamma \) bits, and this property holds for all instances of L. More formally we will consider \(\gamma \) as a non-negative integer such that for any \(x \in L\) it holds that any witness w of x can be parsed as \(w=\alpha |\beta \), where \(|\alpha |=\gamma \), and \(\alpha \) is the same for all witnesses of x. In order to easy the notation, we will note denote by \(L^\gamma \) the \(\mathcal {N}\mathcal {P}\) language having the above prefix \(\gamma \). We will say that \(L^\gamma \) is a \(\gamma \)-prefix language meaning that for any instance x of \(L^\gamma \) all witnesses of x have the same first \(\gamma \) bits.
When defining SimWI we will consider the one-many case since this is what we will use in the next part of the paper. Adapting the definition to the one-one case and to the fully concurrent case is straightforward.
Discussion on adaptive-input selection and black-box simulation. Since our definition considers a real game where the MiM plays with at most one prover and polynomially many verifiers, and a simulated game that consists of an execution of a stand-alone simulator, a natural definition would require the indistinguishability of the two games for any \(x \in L^\gamma \), giving to the prover as input also a witness. This definition however would be difficult to use when the argument of knowledge is played as a subprotocol of a larger protocol, especially if it is played in parallel with other subprotocols and the adversary contributes in selecting the statement for the left session. More specifically applications require a security definition that features a delayed-input property so that players start the protocol with the common input that is still undefined, and that will be defined later potentially with the contribution of the adversary. Therefore in our definition we will allow the adversary to explicitly select the statement, and as such the adversary will provide also the witness for the prover. The simulated game however will filter out the witness so that the simulator will receive only the instance. This approach strictly follows the one of [49] where adaptive-input selection is explicitly allowed and managed in a similar way. As final remark, our definition will require the existence of a black-box simulator since a non-black-box simulator could retrieve from the code of the adversary the witness for the adaptively generated statement. The non-black-box simulator could then run the honest prover procedure, therefore canceling completely the security flavor of the simulation paradigm.
For simplicity we now give the formal definition with non-delayed inputs.
Definition. Let \(\varPi =(\mathcal {P}, \mathcal {V})\) be an argument system for a \(\gamma \)-prefix language \(L^\gamma \) and let \({\mathsf {Rel}}_\mathsf {L^\gamma }\) be the corresponding witness relation. Consider a ppt MiM adversary \(\mathcal {A}\) that is simultaneously participating in one left session and \(\mathsf{poly}(\lambda )\) right sessions. When the execution starts, all parties receive as a common input the security parameter \(1^\lambda \) then \(\mathcal {A}\) chooses the statement \(x \in L^\gamma \) and witness w s.t. \((x,w)\in {\mathsf {Rel}}_\mathsf {L^\gamma }\) and sends them to \(\mathcal {P}\), furthermore \(\mathcal {A}\) receives as auxiliary input \(z\in \{0,1\}^\star \).
In the left session an honest prover \(\mathcal {P}\) interacting with \(\mathcal {A}\) proves the membership of x in \(L^\gamma \). In the \(\mathsf{poly}(\lambda )\) right sessions, \(\mathcal {A}\) proves the membership in \(L^\gamma \) of instances \(\tilde{x}_1,\dots , \tilde{x}_{\mathsf{poly}(\lambda )}\) of his choice to the honest verifiers \(\mathcal {V}_1, \dots , \mathcal {V}_{\mathsf{poly}(\lambda )}\). For simplicity, in this definition we consider an adversary \(\mathcal {A}\) that chooses the statement to be proved in the 1st round that he plays in every right sessionsFootnote 15.
Let \(\{\mathsf {wimim}_\varPi (1^\lambda , z)\}_{\lambda \in \mathbb {N}, z\in \{0,1\}^\star }\) be a random variable that describes the following 3 values: (1) the view of \(\mathcal {A}\) in the above experiment, (2) the output of \(\mathcal {V}_i\) for \(i=1,\dots ,\mathsf{poly}(\lambda )\) and (3) the first \(\gamma \) bits \(\tilde{w}^\gamma _1,\dots ,\tilde{w}^\gamma _{\mathsf{poly}(\lambda )}\) of the corresponding witnesses \(\tilde{w}_1,\dots ,\tilde{w}_{\mathsf{poly}(\lambda )}\) w.r.t. the instances \(\tilde{x}_1,\dots ,\tilde{x}_{\mathsf{poly}(\lambda )}\) that are part of \(\mathcal {A}\)’s view except that \(\tilde{w}^\gamma _i=\bot \) if \(\mathcal {V}_i\) did not output 1, with \(i=1,\dots ,\mathsf{poly}(\lambda )\).
Let \(\{\mathsf {sim}^\mathcal {S}_\varPi (1^\lambda ,z)\}_{\lambda \in \mathbb {N},z\in \{0,1\}^\star }\) be a random variable that describes the following 3 values: (1) and (2) correspond to the output of \(\mathcal {S}\), (3) consists of the first \(\gamma \) bits \(\tilde{w}^\gamma _1,\dots ,\tilde{w}^\gamma _{\mathsf{poly}(\lambda )}\) of the corresponding witnesses \(\tilde{w}_1,\dots ,\tilde{w}_{\mathsf{poly}(\lambda )}\) w.r.t. the instances \(\tilde{x}_1,\dots ,\tilde{x}_{\mathsf{poly}(\lambda )}\) that appear in the MiM view of the output of \(\mathcal {S}\) except that \(w^\gamma _i=\bot \) if \(b_i=0\). The output of \(\mathcal {S}\) is composed by the following two values: (1) a MiM view and (2) bits \(b_1,\ldots ,b_{\mathsf{poly}(\lambda )}\).
\(\mathcal {S}\) has black-box access to \(\mathcal {A}\) and has the goal to emulate the prover without having a witness, while perfectly emulating the verifiers of the right sessions. Therefore \(\mathcal {S}\) rewinds only when playing as proverFootnote 16 and every instance/witness pair (x, w) given in output by \(\mathcal {A}\) is replaced by \((x,\bot )\) and then returned to \(\mathcal {S}\) (i.e., the simulator runs without the witness w for the instance x chosen by \(\mathcal {A}\)).
Definition 6
(SimWI). An argument system \(\varPi =(\mathcal {P}, \mathcal {V})\) for a \(\gamma \)-prefix language \(L^\gamma \) with witness relation \({\mathsf {Rel}}_\mathsf {L^\gamma }\) is SimWI if there exists an expected polynomial-time simulator \(\mathcal {S}\) such that for every MiM adversary \(\mathcal {A}\) that participates in one left session and \(\mathsf{poly}(\lambda )\) right sessions the ensembles
\(\{\mathsf {wimim}_\varPi (1^\lambda , z)\}_{\lambda \in \mathbb {N}, z\in \{0,1\}^\star }\) and \(\{\mathsf {sim}^\mathcal {S}_\varPi (1^\lambda ,z)\}_{\lambda \in \mathbb {N},z\in \{0,1\}^\star }\) are computationally indistinguishable over \(\lambda \).
3 4-Round One-Many SimWI from OWFs
We now show our construction of a 4-round argument of knowledge \(\mathsf {SWI}= (\mathcal {P}^\mathsf {swi},\mathcal {V}^\mathsf {swi})\) for the \(\gamma \)-prefix language \(L^\gamma \) that is one-many SimWI and can be instantiated using any OWF. We will need the following tools:
-
1.
a signature scheme \(\mathsf {\Sigma }=(\mathsf {Gen},\mathsf {Sign},\mathsf {Ver})\);
-
2.
a 2-round IDTC scheme \(\mathsf {TC_\Sigma }=(\mathsf {Sen}_\mathsf {\Sigma }, \mathsf {Rec}_\mathsf {\Sigma }, \mathsf {TFake_\Sigma })\) for the following \(\mathcal {N}\mathcal {P}\)-language
$$\begin{aligned}{\begin{matrix} L_\Sigma =\big \{\mathsf {vk}: \exists \ (\mathtt {msg}_1, \mathtt {msg}_2, \sigma _1,\sigma _2)\ \text {s.t.}\ \mathsf {Ver}(\mathsf {vk}, \mathtt {msg}_1,\sigma _1)=1\\ \ \mathtt {AND}\ \mathsf {Ver}(\mathsf {vk}, \mathtt {msg}_2,\sigma _2)=1 \ \mathtt {AND}\ \mathtt {msg}_1\ne \mathtt {msg}_2 \big \}; \end{matrix}}\end{aligned}$$ -
3.
a 4-round delayed-input public-coin Special HVZK (Definition 2) proof system \(\mathsf {LS} =(\mathcal {P},\mathcal {V})\) for the \(\gamma \)-prefix language \(L^\gamma \) that is adaptive-input PoK for the corresponding relation \({\mathsf {Rel}}_\mathsf {L^\gamma }\).
Let \(x \in L^\gamma \) be the statement that \(\mathcal {P}^\mathsf {swi}\) wants to prove, and w a witness s.t. \((x,w) \in {\mathsf {Rel}}_\mathsf {L^\gamma }\). The high-level idea of our protocol is depicted in Fig. 1. In the 1st round the verifier \(\mathcal {V}^\mathsf {swi}\) computes and sends the 1st round \(\mathsf {ls}^1\) of \(\mathsf {LS} \), computes a pair of signature and verification keys (\(\mathsf{sk}, \mathsf {vk}\)), sends the verification key \(\mathsf {vk}\) to \(\mathcal {P}^\mathsf {swi}\) and computes and sends the 1st round \(\rho \) of \(\mathsf {TC_\Sigma }\) by running \(\mathsf {Rec}_\mathsf {\Sigma }\) on input \(1^\lambda \) and the instance \(\mathsf {vk}\in L_\Sigma \). Then \(\mathcal {P}^\mathsf {swi}\) on input x, w and the received 1st round, computes the 2nd round \(\mathsf {ls}^2\) of \(\mathsf {LS} \) and runs \(\mathsf {Sen}_\mathsf {\Sigma }\) on input \(1^{\lambda }\), \(\mathsf {vk}\), \(\rho \) and message \(\mathsf {ls}^2\) thus obtaining a pair \(({\mathtt {com}},\mathtt {dec})\). \(\mathcal {P}^\mathsf {swi}\) sends \({\mathtt {com}}\) and a random message \(\mathtt {msg}\) to \(\mathcal {V}^\mathsf {swi}\). In the 3rd round \(\mathcal {V}^\mathsf {swi}\) sends the 3rd round \(\mathsf {ls}^3\) of \(\mathsf {LS} \) and a signature \(\sigma \) (computed using \(\mathsf{sk}\)) of the message \(\mathtt {msg}\). In the last round \(\mathcal {P}^\mathsf {swi}\) verifies whether or not \(\sigma \) is a valid signature for \(\mathtt {msg}\). If \(\sigma \) is a valid signature, then \(\mathcal {P}^\mathsf {swi}\), using x, w and \(\mathsf {ls}^3\), computes the 4th round \(\mathsf {ls}^4\) of \(\mathsf {LS} \) and sends \(\mathtt {dec}\), \(\mathsf {ls}^2\) and \(\mathsf {ls}^4\) to \(\mathcal {V}^\mathsf {swi}\). At this point \(\mathcal {V}^\mathsf {swi}\) outputs 1 iff \(\mathsf {Rec}_\mathsf {\Sigma }\) on input \(\mathsf {vk}, {\mathtt {com}}, \mathtt {dec},\mathsf {ls}^2\) accepts \((\mathsf {ls}^2, \mathtt {dec})\) as a decommitment of \({\mathtt {com}}\) and the transcript for \(\mathsf {LS} \) is accepting for \(\mathcal {V}\) with respect to the instance x. We remark that to execute \(\mathsf {LS} \) the instance is not needed until the last round but the instance length is required from the onset of the protocol.
Figure 2 describes in details our SimWI AoK \(\mathsf {SWI}\).
Theorem 1
Assuming OWFs, \(\mathsf {SWI}=(\mathcal {P}^\mathsf {swi},\mathcal {V}^\mathsf {swi})\) is a 4-round one-many SimWI AoK for \(\gamma \)-prefix languages.
We divide the security proof in three parts, proving that \(\mathsf {SWI}\) enjoys delayed-input completeness, adaptive-input AoK and SimWI. Before that, we recall that \(\mathsf {LS} \) can be constructed from OWFs (see Sect. 2.1) as well as \(\mathsf {\Sigma }\) using [47]. We also observe that if \(\mathsf {\Sigma }\) relies on OWFs, then also \(\mathsf {TC_\Sigma }\) can be constructed from OWFs (see the full version [5]).
Delayed-Input Completeness. The completeness follows directly from the completeness of \(\mathsf {LS} \), the correctness of \(\mathsf {TC_\Sigma }\) and the validity of \(\mathsf {\Sigma }\). We observe that, due to the delayed-input property of \(\mathsf {LS} \), the statement x (and the respective witness w) are used by \(\mathcal {P}^\mathsf {swi}\) only to compute the last round. Therefore \(\mathsf {SWI}\) enjoys delayed-input completeness.
Adaptive-Input Argument of Knowledge. In order to prove that \(\mathsf {SWI}\) enjoys adaptive-input AoK for \({\mathsf {Rel}}_\mathsf {L^\gamma }\), we need to show an efficient extractor \(\mathsf {E}\) that outputs the witnesses for the statements proved by an adversarial prover \({\mathcal {P}^\mathsf {swi}}^\star \). \(\mathsf {E}\) simply runs \(\mathsf {ExtLS}\), the adaptive-input PoK extractor of \(\mathsf {LS} \), in every right session, and outputs what \(\mathsf {ExtLS}\) outputs. More precisely \(\mathsf {E}\) internally runs and interacts with a \(\mathsf {SWI}\) prover \(\mathcal {P}^\mathsf {swi}\) as \(\mathcal {V}^\mathsf {swi}_i\) does, but acting as a proxy between \({\mathcal {P}^\mathsf {swi}}^\star \) and \(\mathsf {ExtLS}\) w.r.t. the messages of \(\mathsf {LS} \) (for \(i=1,\dots , \mathsf{poly}(\lambda )\)). The important observation is that \(\mathsf {E}\) could fail if the following event \(\mathsf {NoExt}\) happens with non-negligible probability: \({\mathcal {P}^\mathsf {swi}}^\star \) opens the commitment \((\rho ,{\mathtt {com}})\) to a different \(\mathsf {ls}^2\) during the rewinds. Indeed, in this case \(\mathsf {ExtLS}\) could fail in obtaining a witness. We prove the following claim.
Claim 1
There exists a negligible function \(\nu \) such that \(\text {Prob}\left[ \;\mathsf {NoExt}\;\right] <\nu (\lambda )\).
Proof
The proof is by contradiction, more specifically we now show an adversary \(\mathcal {A}^\mathsf {\Sigma }\) that extracts two signatures for two different messages in order to break the signature scheme \(\mathsf {\Sigma }\) when \(\text {Prob}\left[ \;\mathsf {NoExt}\;\right] \) is non-negligible in \(\lambda \).
If two decommitments of \(({\mathtt {com}},\rho )\) w.r.t. two different messages (\(\mathsf {ls}^{2'}\) and \({\mathsf {ls}^2})\) are shown by \({\mathcal {P}^\mathsf {swi}}^\star \) in the last round of \(\mathsf {SWI}\), \(\mathcal {A}^\mathsf {\Sigma }\) can extract two different signatures for two different messages by using the special binding of \(\mathsf {TC_\Sigma }\). More precisely, let \(\mathsf {vk}\) be the verification key given by the challenger of the signature scheme, then our adversary \(\mathcal {A}^\mathsf {\Sigma }\) works as follows.
For all \(i\in \{1,\dots ,\mathsf{poly}(\lambda )\}-\{j\}\), \(\mathcal {A}^\mathsf {\Sigma }\) interacts in the i-th session against \({\mathcal {P}^\mathsf {swi}}^\star \) as \(\mathcal {V}^\mathsf {swi}_i\) would do. Instead in the j-th session \(\mathcal {A}^\mathsf {\Sigma }\) runs as \(\mathsf {E}\) would do, using \(\mathsf {vk}\) to compute the first round, and the oracle \(\mathsf {Sign}(\mathsf{sk},\cdot )\) to compute a signature \(\sigma \) of a message m sent by \(\mathcal {A}^\mathsf {\Sigma }\) in the second round. Since we are assuming (by contradiction) that during the rewinds from the 4th round to the 3rd round the commitment \((\rho , {\mathtt {com}})\) (sent in the second round by \({\mathcal {P}^\mathsf {swi}}^\star \)) is opened in more than one way, then, by using the special binding of \(\mathsf {TC_\Sigma }\), \(\mathcal {A}^\mathsf {\Sigma }\) extracts and outputs two signatures for two different messages. We conclude this proof with the following two observations. First, the signature oracle \(\mathsf {Sign}(\mathsf{sk},\cdot )\) is called only once since, by construction of \(\mathsf {E}\), the second round is played by \({\mathcal {P}^\mathsf {swi}}^\star \) only once. Second, the extractor \(\mathsf {E}\) is an expected polynomial-time algorithm while \(\mathcal {A}^\mathsf {\Sigma }\) must be a strict polynomial-time algorithm. This mean that the execution \(\mathsf {E}\) has to be truncated. Obviously the running time of the extraction procedure can be truncated to a sufficiently long value so that with non-negligible probability the truncated extraction procedure will still yield the event \(\mathsf {NoExt}\) to happened and this is sufficient for \(\mathcal {A}^\mathsf {\Sigma }\) to break the signature schemeFootnote 17.
SimWI. In order to prove that \(\mathsf {SWI}\) is SimWI (Definition 6) for any \(\gamma \)-prefix language \(L^\gamma \) we prove the following lemma.
Lemma 1
\(\{\mathsf {wimim}_\mathsf {SWI}(1^\lambda , z)\}_{\lambda \in \mathbb {N}, z\in \{0,1\}^\star }\approx \{\mathsf {sim}^{\mathcal {S}^\mathsf {swi}}_\mathsf {SWI}(1^\lambda ,z)\}_{\lambda \in \mathbb {N},z\in \{0,1\}^\star }.\)
Proof
Here we actually prove something stronger. Indeed we prove the security of \(\mathsf {SWI}\) considering a MiM adversary \({\mathcal {A}^\mathsf {swi}}\) that has additional power both in the left and in the right sessions. More precisely in the left session \({\mathcal {A}^\mathsf {swi}}\) can choose the statement to be proved (and the related witness) in the third round. That is, in the last round that goes from \({\mathcal {A}^\mathsf {swi}}\) to \(\mathcal {P}^\mathsf {swi}\).
Also, in all right sessions \(\mathcal {A}\) fixes a family of statements in the second round, and then adaptively picks the statement to be proved from that family in the last round. In this way the MiM adversary has the power to adaptively choose the statement to be proved in the last round of every right session conditioned on belonging to the already fixed family, that has to be fixed in the second round. In the rest of the paper we will refer to a SimWI protocol that is secure also in this setting as adaptive-input SimWI.
We start by showing the simulator \({\mathcal {S}^\mathsf {swi}}\) and giving an overview of the entire proof. The simulator is described in Fig. 3. Roughly, \({\mathcal {S}^\mathsf {swi}}\) interacts against \({\mathcal {A}^\mathsf {swi}}\) in both the left and right sessions. In the left session \({\mathcal {S}^\mathsf {swi}}\) runs \(\mathsf {TFake_\Sigma }\) to compute and send a commitment \({\mathtt {com}}\). \({\mathcal {S}^\mathsf {swi}}\) then rewinds \({\mathcal {A}^\mathsf {swi}}\) from the 3rd to the 2nd round, in order to obtain two valid signatures \(\sigma _1, \sigma _2\) for two different messages \((\mathtt {msg}_1,\mathtt {msg}_2)\). This informations constitute the trapdoor \(\mathtt {tk}\) for \(\mathsf {TC_\Sigma }\). After that \(\mathtt {tk}\) is computed, \({\mathcal {S}^\mathsf {swi}}\) comes back to the main thread execution. Upon receiving \(\mathsf {ls}^3\) and x in the 3rd round from \({\mathcal {A}^\mathsf {swi}}\), \({\mathcal {S}^\mathsf {swi}}\) computes an accepting transcript for \(\mathsf {LS} \) \((\mathsf {ls}^1, \mathsf {ls}^2, \mathsf {ls}^3, \mathsf {ls}^4)\) running the Special HVZK simulator of \(\mathsf {LS} \) on input \(\mathsf {ls}^1\), received in the 1st round from \({\mathcal {A}^\mathsf {swi}}\), and \((x, \mathsf {ls}^3)\). In the last round computes, by using \(\mathtt {tk}\), the decommitment information \((\mathtt {dec},\mathsf {ls}^2)\) for \({\mathtt {com}}\), and sends \((\mathtt {dec},\mathsf {ls}^2, \mathsf {ls}^4)\) to \({\mathcal {A}^\mathsf {swi}}\). In the i-th right session, for \(i=1,\dots , \mathsf{poly}(\lambda )\), \({\mathcal {S}^\mathsf {swi}}\) acts as \(\mathcal {V}^\mathsf {swi}_i\) would do against \({\mathcal {A}^\mathsf {swi}}\). When the execution against \({\mathcal {A}^\mathsf {swi}}\) ends, \({\mathcal {S}^\mathsf {swi}}\) outputs the view of \({\mathcal {A}^\mathsf {swi}}\).
In the security proof we denote by \(\{\mathsf {wimim}_{\mathcal {H}_i}(1^\lambda , z)\}_{\lambda \in \mathbb {N}, z\in \{0,1\}^\star }\) the random variable describing (1) the view of \({\mathcal {A}^\mathsf {swi}}\), (2) the output of \(\mathcal {V}^\mathsf {swi}_i\) for \(i=1,\dots ,\mathsf{poly}(\lambda )\), (3) the first \(\gamma \)-bits \(\tilde{w}^\gamma _1,\dots ,\tilde{w}^\gamma _{\mathsf{poly}(\lambda )}\) of the corresponding witnesses \(\tilde{w}_1,\dots ,\tilde{w}_{\mathsf{poly}(\lambda )}\) w.r.t. the instances \(\tilde{x}_1,\dots ,\tilde{x}_{\mathsf{poly}(\lambda )}\) that appear in \({\mathcal {A}^\mathsf {swi}}\)’s view except that \(\tilde{w}^\gamma _i=\bot \) if \(\mathcal {V}^\mathsf {swi}_i\) rejected, with \(i=1,\dots ,\mathsf{poly}(\lambda )\) Footnote 18.
The proof makes use of the following main hybrid experiments.
-
The 1st hybrid experiment is \(\mathcal {H}_1(1^\lambda , z)\). In this hybrid in the left session \(\mathcal {P}^\mathsf {swi}\) interacts with \({\mathcal {A}^\mathsf {swi}}\) in order to prove the validity of the instance x using the witness w, while in the right sessions \(\mathcal {V}^\mathsf {swi}_i\) interacts with \({\mathcal {A}^\mathsf {swi}}\) for \(i=1, \dots , \mathsf{poly}(\lambda )\). We want to prove that in the i-th right session \({\mathcal {A}^\mathsf {swi}}\) does not prove any false instance \(\tilde{x}_i \) for any \(i=1, \dots , \mathsf{poly}(\lambda )\) Footnote 19. This property follows immediately from the adaptive-input AoK of \(\mathsf {SWI}\). We observe that in this case it is crucial that \(\mathsf {SWI}\) is adaptive-input AoK, because we are considering an adversary \({\mathcal {A}^\mathsf {swi}}\) that can choose the instance to be proved in the last round of every right session.
-
The 2nd hybrid experiment is \(\mathcal {H}_{2}(1^\lambda , z)\) and differs from \(\mathcal {H}_1(1^\lambda , z)\) in the way the commitment \({\mathtt {com}}\) and the decommitment information \(\mathtt {dec}\) are computed in the left session. More precisely, \(\mathcal {P}^\mathsf {swi}\) runs \(\mathsf {TFake_\Sigma }\) to compute a commitment \((\rho ,{\mathtt {com}})\), and subsequently to compute a decommitment of \((\rho , {\mathtt {com}})\) to the value \(\mathsf {ls}^2\) (we remark that no trapdoor is needed to run \(\mathsf {TFake_\Sigma }\) in order to compute \((\rho , {\mathtt {com}})\)). In more details, this experiment rewinds the adversary \( {\mathcal {A}^\mathsf {swi}}\) from the 3rd to the 2nd round of the left session to extract two signatures \(\sigma _1\), \(\sigma _2\) of two different messages \((\mathtt {msg}_1,\mathtt {msg}_2)\) and uses them as trapdoor to run \(\mathsf {TFake_\Sigma }\). The indistinguishability between \(\mathsf {wimim}_{\mathcal {H}_1}(1^\lambda , z)\) and \(\mathsf {wimim}_{\mathcal {H}_{2}}(1^\lambda ,z)\) comes from the hiding and the trapdoorness of \(\mathsf {TC_\Sigma }\).
-
The 3rd hybrid experiment is \(\mathcal {H}_{3}(1^\lambda , z)\) and differs from \(\mathcal {H}_{2}(1^\lambda , z)\) in the way the transcript for \(\mathsf {LS} \) is computed. In more details the Special HVZK simulator \(\mathcal {S}\) of \(\mathsf {LS} \) is used to compute the messages \(\mathsf {ls}^2\) and \(\mathsf {ls}^4\) instead of using the honest procedure \(\mathcal {P}^\mathsf {swi}\). The indistinguishability between \(\mathsf {wimim}_{\mathcal {H}_{2}}(1^\lambda ,z)\) and \(\mathsf {wimim}_{\mathcal {H}_3}(1^\lambda ,z)\) comes from the Special HVZK of \(\mathsf {LS} \). We observe that the security proof ends with this hybrid experiment because \(\mathsf {wimim}_{\mathcal {H}_3}(1^\lambda , z)\equiv \mathsf {sim}^{\mathcal {S}^\mathsf {swi}}_\mathsf {SWI}(1^\lambda ,z)\).
A formal proof is given in the full version (see [5]).
4 4-Round Concurrent NM Commitment Scheme
Our construction makes use of an adaptive-input SimWI AoK \(\mathsf {SWI}= (\mathcal {P}^\mathsf {swi},\mathcal {V}^\mathsf {swi})\) combined with a weak concurrent NM commitment scheme \(\varPi _\mathsf {wom}\). For our propose we consider a weak NM commitment scheme that with overwhelming probability any well-formed commitment can be opened to only one message. We recall that the weak concurrent NM commitment scheme of [25] enjoys this property when instantiated with Naor’s commitment scheme [35].
We now consider the following language L based on the weak NM commitment scheme \(\varPi _\mathsf {wom}=(\mathsf {Sen}_\mathsf {wom},\mathsf {Rec}_\mathsf {wom})\):
and the corresponding relation \({\mathsf {Rel}}_{L}\).
We now use \(\mathsf {SWI}= (\mathcal {P}^\mathsf {swi},\mathcal {V}^\mathsf {swi})\) to upgrade a 4-round public-coin concurrent weak NM commitment scheme \(\varPi _\mathsf {wom}\) with the property that after the second round there is at most one valid message, to a concurrent NM commitment scheme. We will be able to invoke the security of \(\mathsf {SWI}\), since the language L is a \(\gamma \)-prefix language with overwhelming probability with \(\gamma =|m|\). In fact, given an instance \((\tau , {\mathtt {id}})\) of L all the witnesses \(w_1, \dots , w_n\) of \((\tau , {\mathtt {id}})\) have the form \(m|\mathtt {dec}_i\) for \(i=1,\dots , n\) (i.e., all witnesses have the same prefix m). Consider a SimWI AoK for L. Let m be the message that \(\mathsf {NM4Sen}\) wants to commit and \({\mathtt {id}}\) be the id for this session. The high-level idea of our protocol is depicted in Fig. 4.
In the 1st round the receiver \(\mathsf {NM4Rec}\) computes and sends the 1st round \( \mathsf {swi}^1\) of \(\mathsf {SWI}\) and the 1st round \(\mathsf {wom}^1\) of \(\varPi _\mathsf {wom}\) using as input the \({\mathtt {id}}\). Then \(\mathsf {NM4Sen}\) on input \({\mathtt {id}}\), the message m and the received 1st round, computes the 2nd round \(\mathsf {wom}^2\) of \(\varPi _\mathsf {wom}\) in order to commit to the message m, using \({\mathtt {id}}\), furthermore he obtains \(\mathtt {dec}_\mathsf {wom}\) s.t. \((m,\mathtt {dec}_\mathsf {wom})\) constitutes the decommitment informationFootnote 20. Moreover \(\mathsf {NM4Sen}\) computes and sends the 2nd round \( \mathsf {swi}^2\) of \(\mathsf {SWI}\). In the 3rd round \(\mathsf {NM4Rec}\) sends the 3rd round \(\mathsf {wom}^3\) of \(\varPi _\mathsf {wom}\) and the 3rd round \( \mathsf {swi}^3\) of \(\mathsf {SWI}\). In the last round \(\mathsf {NM4Sen}\) computes the 4th round \(\mathsf {wom}^4\) of \(\varPi _\mathsf {wom}\). Furthermore, \(\mathsf {NM4Sen}\), using \((\mathsf {wom}^1, \mathsf {wom}^2, \mathsf {wom}^3, \mathsf {wom}^4, {\mathtt {id}})\) as instance and \((m, \mathtt {dec}_\mathsf {wom})\) as a witness, computes the 4th round \( \mathsf {swi}^4\) of \(\mathsf {SWI}\) and sends \(\mathsf {wom}^4, \mathsf {swi}^4\) to \(\mathsf {NM4Rec}\). At this point \(\mathsf {NM4Rec}\) accepts the commitment (i.e., the transcript of the protocol generated so far) iff the transcript for \(\mathsf {SWI}\) is accepting for \(\mathcal {V}^\mathsf {swi}\) with respect to the instance \((\mathsf {wom}^1, \mathsf {wom}^2, \mathsf {wom}^3, \mathsf {wom}^4, {\mathtt {id}})\). The decommitment phase of our scheme simply corresponds to the decommitment phase of \(\varPi _\mathsf {wom}\).
As described before, \(\mathsf {SWI}= (\mathcal {P}^\mathsf {swi},\mathcal {V}^\mathsf {swi})\) is used by \(\mathsf {NM4Sen}\) to prove knowledge of a message and randomness consistent with the transcript computed using \(\varPi _\mathsf {wom}\). To execute \(\mathsf {SWI}\) the instance is not needed until the last round.
Figure 5 describes in details our 4-round concurrent NM commitment scheme \({\varPi _\mathsf {NM4Com}}\).
Theorem 2
Assuming OWFs, \({\varPi _\mathsf {NM4Com}}=(\mathsf {NM4Sen},\mathsf {NM4Rec})\) is a 4-round concurrent NM commitment scheme.
The 4-round concurrent NM commitment scheme \({\varPi _\mathsf {NM4Com}}=(\mathsf {NM4Sen},\mathsf {NM4Rec})\) relies on OWFs, because the adaptive-input SimWI AoK \(\mathsf {SWI}\) can be constructed using OWFs only (see Theorem 1). Furthermore \(\varPi _\mathsf {wom}\) can be instantiated using the weak one-one non-malleable commitment scheme of [25] that is proved to be weak concurrent non-malleable in the full version of our work (see [5]). Note that this construction relies on OWFs and has also the additional property that we require (i.e. after the second round the only valid message and the corresponding decommitment informations are fixed). The security proof is divided in two parts. In the 1st part we prove that \({\varPi _\mathsf {NM4Com}}\) is indeed a commitment scheme. In the second part we prove that \({\varPi _\mathsf {NM4Com}}\) is a one-many NM commitment scheme, and then we go from one-many to concurrent non-malleability by using Proposition 1.
Lemma 2
\({\varPi _\mathsf {NM4Com}}=(\mathsf {NM4Sen},\mathsf {NM4Rec})\) is a statistically binding computationally hiding commitment scheme.
Proof
Correctness. The correctness follows directly from the delayed-input completeness of \(\mathsf {SWI}\) and the correctness of \(\varPi _\mathsf {wom}\).
Statistically Binding. Observe that the message given in output in the decommitment phase of \({\varPi _\mathsf {NM4Com}}\) is the message committed using \(\varPi _\mathsf {wom}\). Moreover the decommitment of \({\varPi _\mathsf {NM4Com}}\) coincides with the decommitment of \(\varPi _\mathsf {wom}\). Since \(\varPi _\mathsf {wom}\) is statistically binding then so is \({\varPi _\mathsf {NM4Com}}\).
Computationally Hiding. Computational hiding follows immediately from Lemma 3.
Lemma 3
For all \(m\in \{0,1\}^{\mathsf{poly}(\lambda )}\) 
We denote by  the random variable describing the view of the MiM \({\mathcal {A}^\mathsf {NM4Com}}\) combined with the values that it commits in the \(\mathsf{poly}(\lambda )\) right sessions in hybrid \(\mathcal {H}^m_i(z)\).
the random variable describing the view of the MiM \({\mathcal {A}^\mathsf {NM4Com}}\) combined with the values that it commits in the \(\mathsf{poly}(\lambda )\) right sessions in hybrid \(\mathcal {H}^m_i(z)\).
As required by the definition, we want to show that the distribution of the real game experiment (i.e., the view of the MiM \({\mathcal {A}^\mathsf {NM4Com}}\) when playing with \(\mathsf {NM4Sen}\) committing m along with the messages committed in the right sessions) and the one of the output of a simulator are computationally indistinguishable. We start by showing the simulator \(S^\mathsf {NM4Com}\) and giving an overview of the entire proof. The simulator is described in Fig. 6.
-
The 1st hybrid experiment is \(\mathcal {H}^m_1(z)\). In this hybrid in the left session \(\mathsf {NM4Sen}\) commits to m, while in the right sessions \(\mathsf {NM4Rec}_i\) interacts with \( {\mathcal {A}^\mathsf {NM4Com}}\) for \(i =1, \dots , \mathsf{poly}(\lambda )\). We prove that in the i-th right session \({\mathcal {A}^\mathsf {NM4Com}}\) does not commit to a message \(\tilde{m}_i=\perp \) for any \(i =1, \dots , \mathsf{poly}(\lambda )\). The proof follows immediately from the adaptive-input AoK of \(\mathsf {SWI}\). We observe that in this case it is crucial that \(\mathsf {SWI}\) is adaptive-input AoK, because the theorem proved by \({\mathcal {A}^\mathsf {NM4Com}}\) are fully specified only in the last round of every right session. Clearly we have that
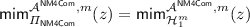 .
. -
The 2nd hybrid experiment is \(\mathcal {H}^m_2(z)\) and differs from \(\mathcal {H}^m_1(z)\) in the way the transcript of \(\mathsf {SWI}\) is computed. In this hybrid the simulator \({\mathcal {S}^\mathsf {swi}}\) of \(\mathsf {SWI}\) is used to compute the transcript of \(\mathsf {SWI}\). The indistinguishability between
 and
and  comes from the adaptive-input SimWI property of \(\mathsf {SWI}\). It is important to observe that we can properly rely on the adaptive-input SimWI property of \(\mathsf {SWI}\) since the committed message in \(\varPi _\mathsf {wom}\) is fixed in the second round. Therefore also the family of statement \(\mathcal {X}_w=\{x : (x,w)\in {\mathsf {Rel}}_\mathsf {L}\ \text {or}\ x \notin L\}\) proved using \(\mathsf {SWI}\) is implicitly fixed in the second round. Moreover we can rely on the security of \(\mathsf {SWI}\) because the language L is a \(\gamma \)-prefix language for \(\mathsf {prefix}=|m|\). Indeed, all witnesses of any instance of L have the same prefix (i.e., the committed message m). Therefore when using the simulator of \(\mathsf {SWI}\) we are guaranteed that the distribution of the first \(\gamma \) bits of the witnesses corresponding to the statements proven by the adversary in the right sessions of \(\mathsf {SWI}\) does not change. In turn, this implies that the distribution of the committed messages in the right sessions does not change since each message committed in a session is in the first \(\gamma \) bits of any witness corresponding to the statement proven in \(\mathsf {SWI}\) in that session.
comes from the adaptive-input SimWI property of \(\mathsf {SWI}\). It is important to observe that we can properly rely on the adaptive-input SimWI property of \(\mathsf {SWI}\) since the committed message in \(\varPi _\mathsf {wom}\) is fixed in the second round. Therefore also the family of statement \(\mathcal {X}_w=\{x : (x,w)\in {\mathsf {Rel}}_\mathsf {L}\ \text {or}\ x \notin L\}\) proved using \(\mathsf {SWI}\) is implicitly fixed in the second round. Moreover we can rely on the security of \(\mathsf {SWI}\) because the language L is a \(\gamma \)-prefix language for \(\mathsf {prefix}=|m|\). Indeed, all witnesses of any instance of L have the same prefix (i.e., the committed message m). Therefore when using the simulator of \(\mathsf {SWI}\) we are guaranteed that the distribution of the first \(\gamma \) bits of the witnesses corresponding to the statements proven by the adversary in the right sessions of \(\mathsf {SWI}\) does not change. In turn, this implies that the distribution of the committed messages in the right sessions does not change since each message committed in a session is in the first \(\gamma \) bits of any witness corresponding to the statement proven in \(\mathsf {SWI}\) in that session.
We also consider the hybrid experiments \(\mathcal {H}^0_1(z)\), \(\mathcal {H}^0_2(z)\), that are the same hybrid experiments described above with the difference that \(\varPi _\mathsf {wom}\) is used to commit to a message \(0^\lambda \) instead of m. From the same arguments described above we have that  and that in the i-th right session of \(\mathcal {H}^0_1(z)\) \({\mathcal {A}^\mathsf {NM4Com}}\) commits to a message \(\tilde{m}_i=\perp \) with negligible probability (for any \(i =1, \dots , \mathsf{poly}(\lambda )\)). We also observe that
and that in the i-th right session of \(\mathcal {H}^0_1(z)\) \({\mathcal {A}^\mathsf {NM4Com}}\) commits to a message \(\tilde{m}_i=\perp \) with negligible probability (for any \(i =1, \dots , \mathsf{poly}(\lambda )\)). We also observe that  .
.
The only thing that remains to argue to complete the proof is that the view of \({\mathcal {A}^\mathsf {NM4Com}}\), along with messages committed in the right sessions of the execution of \(\mathcal {H}^m_2(z)\), is indistinguishable from the view of \({\mathcal {A}^\mathsf {NM4Com}}\) along with the messages committed in the right sessions of \(\mathcal {H}^0_2(z)\). This is actually ensured by the weak concurrent non-malleability of \(\varPi _\mathsf {wom}\). Indeed, from the arguments given above, in both \(\mathcal {H}^m_2(z)\) and \(\mathcal {H}^0_2(z)\) the adversary \({\mathcal {A}^\mathsf {NM4Com}}\) commits to a message \(\tilde{m}_i=\bot \) with negligible probability for \(i=1,\dots , \mathsf{poly}(\lambda )\). Therefore we can use this \({\mathcal {A}^\mathsf {NM4Com}}\) to construct and adversary \(\mathcal {A}^\mathsf {wom}\) that breaks the weak concurrent non-malleability of \(\varPi _\mathsf {wom}\). Roughly speaking, let \(m, 0^\lambda \) be the challenge messages, then \(\mathcal {A}^\mathsf {wom}\) works as following against the challenger \(\mathcal {C}^\mathsf {wom}\). In the left session acts as a proxy for all the messages of \(\varPi _\mathsf {wom}\) between \(\mathcal {C}^\mathsf {wom}\) and \({\mathcal {A}^\mathsf {NM4Com}}\) and executes the simulator \({\mathcal {S}^\mathsf {swi}}\) of \(\mathsf {SWI}\) in parallel. In the i-th right session \(\mathcal {A}^\mathsf {wom}\) interacts as \({\mathsf {Rec}_\mathsf {wom}}_{,i}\) would do w.r.t. the messages of \(\varPi _\mathsf {wom}\) and as \(\mathcal {V}^\mathsf {swi}_i\) for the messages of \(\mathsf {SWI}\), for all \(i =1, \dots , \mathsf{poly}(\lambda )\). The distinguisher that break the concurrent weak non-malleability of \(\varPi _\mathsf {wom}\) runs \(\mathcal {D}^\mathsf {NM4Com}\) (that exists by contradiction) that distinguishes  from
from  , and outputs what \(\mathcal {D}^\mathsf {NM4Com}\) outputs.
, and outputs what \(\mathcal {D}^\mathsf {NM4Com}\) outputs.
A caveat that we have to address in this reduction is due to the rewinds made by \({\mathcal {S}^\mathsf {swi}}\) in the left session in order to compute the transcript of \(\mathsf {SWI}\). Indeed a rewind made in the left session could affect the reduction rewinding also the receivers of \(\varPi _\mathsf {wom}\) involved in the reduction. More precisely could happen that in a session \(j\in \{1,\dots ,\mathsf{poly}(\lambda )\}\) the third round of \(\varPi _\mathsf {wom}\) has to be played multiple times because of the multiple values  received in the j-th right session. We can avoid this problem by sending a random string as a third round of
received in the j-th right session. We can avoid this problem by sending a random string as a third round of  . In this way for the first value
. In this way for the first value  received from \({\mathcal {A}^\mathsf {NM4Com}}\) the reduction interacts with the receiver of
received from \({\mathcal {A}^\mathsf {NM4Com}}\) the reduction interacts with the receiver of  and for all the other values the reduction sends a random string. This is the reason why in our construction we require
and for all the other values the reduction sends a random string. This is the reason why in our construction we require  to be public coin. One additional issue is the following. The simulator of \(\mathsf {SWI}\) could rewind the entire left session during the reduction, therefore requiring to compute a new commitment of m for the protocol
to be public coin. One additional issue is the following. The simulator of \(\mathsf {SWI}\) could rewind the entire left session during the reduction, therefore requiring to compute a new commitment of m for the protocol  . Since we are assuming that
. Since we are assuming that  is weak concurrent non-malleable, the reduction can request to receive multiple commitments for the same message. A formal proof is given in the full version (see [5]).
is weak concurrent non-malleable, the reduction can request to receive multiple commitments for the same message. A formal proof is given in the full version (see [5]).
5 3-Round NM Commitments from Strong OWPs
In addition to the definition of NM commitments given in Sect. 2.3, in this section we consider also a synchronous NM commitment scheme secure against a sub-exponential time adversary. The definitions follow below.
5.1 Synchronous NM Commitment Scheme
Definition 7
( \(synchronous\) NM commitment scheme). A commitment scheme is synchronous one-one (resp., one-many) non-malleable if it is one-one (resp., one-many) NM with respect to synchronous MiM adversaries.
We also consider the definition of a NM commitment scheme secure against a MIM \(\mathcal {A}\) running in time bounded by \(T=2^{\lambda ^\alpha }\) for some positive constant \(\alpha <1\). In this case we will say that a commitment scheme is T-non-malleable. We will also say that an NM commitment scheme is \(\tilde{T}\)-breakable to specify that an algorithm which runs in time \(\tilde{T} = 2^{\lambda ^\beta }\), for some positive constant \(\beta < 1\), can maul the committed message.
5.2 3-Round NM Commitment Scheme: \(\varPi _{\mathsf {NMCom}}=(\mathsf {NMSen},\mathsf {NMRec})\)
Our construction is based on a compiler that takes as input a 3-round synchronous weak one-one NM commitment scheme \(\varPi _{\mathsf {wsyn}}=({\mathsf {Sen}_{{\mathsf {wsyn}}}}, {\mathsf {Rec}_{{\mathsf {wsyn}}}})\), a OWP f, a WI adaptive PoK for \(\mathcal {N}\mathcal {P}\) \({\mathsf {LS}}\), and outputs a 3-round extractable one-one NM commitment scheme \(\varPi _{\mathsf {NMCom}}=(\mathsf {NMSen},\mathsf {NMRec})\) Figs. 7 and 8.
In order to construct our compiler we consider the following tools:
-
1.
a OWP f that is secure against ppt adversaries and that is \(\tilde{T_f}\)-breakable;
-
2.
a 3-round one-one synchronous weak NM commitment scheme \(\varPi _{\mathsf {wsyn}}=({\mathsf {Sen}_{{\mathsf {wsyn}}}}, {\mathsf {Rec}_{{\mathsf {wsyn}}}})\) that is \(T_{{{\mathsf {wsyn}}}}\)-hiding/NM, and \(\tilde{T}_{{{\mathsf {wsyn}}}}\)-breakable;
-
3.
the LS PoK \({\mathsf {LS}}=(\mathcal {P},\mathcal {V})\) for the language
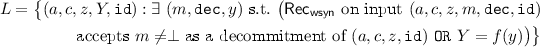
that is \({T_{{\mathsf {LS}}}}\)-WI for the corresponding relation \({\mathsf {Rel}}_{\mathsf {L}}\).
Let \(\lambda \) be the security parameter of our scheme. We use w.l.o.g. \(\lambda \) also as security parameter for the one-wayness of f with respect to polynomial-time adversaries. We consider the following hierarchy of security levels: \( \tilde{T_f}\ll T_{{{\mathsf {wsyn}}}}\ll \tilde{T}_{{\mathsf {wsyn}}}= \sqrt{{T_{{\mathsf {LS}}}}} \ll {T_{{\mathsf {LS}}}}\) where by “\(T \ll T'\)” we mean that “\(T\cdot \mathsf{poly}(\lambda ) < T'\)”.
Now, similarly to [6, 46], we define different security parameters, one for each tool involved in the security proof to be consistent with the hierarchy of security levels defined above. Given the security parameter \(\lambda \) of our scheme, we will make use of the following security parameters: (1) \(\lambda \) for the OWP f; (2) \(\lambda _{{\mathsf {wsyn}}}\) for the synchronous weak one-one NM commitment scheme; (3) \(\lambda _{\mathsf {LS}}\) for \({\mathsf {LS}}\). A formal proof of the following theorem is given in the full version (see [5]).
Theorem 3
Suppose there exists a synchronous weak one-one NM commitment scheme and OWPs, both secure against subexponential-time adversaries, then \(\varPi _{\mathsf {NMCom}}\) is an extractable one-one NM commitment scheme.
Notes
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
We remark that Goyal in [19] defined a weaker notion of non-malleable commitments (non-malleability w.r.t. replacement) that also had the goal to deal with commitments of \(\bot \). While the goal is similar to our definition, the actual formulation is quite different.
- 7.
There is nothing surprising so far, this is just the concept of zero knowledge naturally augmented by extending the simulator with the behavior of honest verifiers to feed the MiM with messages belonging to the right sessions too.
- 8.
Note that when \(\gamma =0\) the 2nd security flavor is cancelled and SimWI becomes equivalent to zero knowledge. Furthermore when \(\gamma \) is equal to the largest witness size then we are considering languages in \(\mathcal {U}\mathcal {P}\).
- 9.
We stress that the main goal of this work is to construct 4-round concurrent NM commitments from OWFs, and we will achieve it by making use of SimWI. As such, to avoid circularity, we can not use concurrent NM commitments to construct SimWI.
- 10.
- 11.
A many-many NM commitment scheme can be also indicate as a concurrent NM commitment scheme. In the rest of the paper we use the term concurrent.
- 12.
This reduction needs extra help, see Remark 2 below.
- 13.
We stress that after our results were publicly available, a construction for 3-round one-one non-malleable commitments with the black-box use of one-to-one one-way functions secure against quasi-polynomial-time adversaries was announced in [23]. Their work revisited the primitives that instantiated their prior construction [24] based on 1–1 OWFs that appeared before this work and before [6].
- 14.
We assume w.l.o.g. that \(\mathcal {A}\) is stateful.
- 15.
Our construction will satisfy a much stronger notion where in the left session \(\mathcal {A}\) can choose statement and witness in the last round, while in the right sessions \(\mathcal {A}\) can choose the statement in the very last round, as long as the witness is already fixed in the second round.
- 16.
The motivation behind this definitional choice is that \(\mathcal {S}\) is supposed to be an extended zero-knowledge simulator that takes care also of the honest behavior of the verifiers since \(\mathcal {A}\) expects to play with them. Instead allowing \(\mathcal {S}\) to have any behavior on the right would hurt the power of SimWI in composing in parallel with other protocols. Indeed if \(\mathcal {S}\) rewinds on the right as verifier, it would in turn rewind also the left player of the external protocol that is played in parallel. This would hurt the security of the overall scheme whenever the external protocol is not resettably secure. We will indeed compose a SimWI AoK with a weak NM commitment scheme that is not resettably secure.
- 17.
The same arguments are used in [17]. The same standard argument about truncating the execution of an expected polynomial-time algorithm is used in another proofs but for simplicity we will not repeat this discussion.
- 18.
To ease the notation sometimes we will refer to \(\{\mathsf {wimim}_{\mathcal {H}_i}(1^\lambda , z)\}_{\lambda \in \mathbb {N}, z\in \{0,1\}^\star }\) using just \(\mathsf {wimim}_{\mathcal {H}_i}(1^\lambda , z)\).
- 19.
When we refer to a proved instance \(\tilde{x}_i\) we implicitly assume that \(\mathcal {V}^\mathsf {swi}_i\) is accepting, with \(i=1,\dots ,\mathsf{poly}(\lambda )\).
- 20.
In order to match the adaptive-input selection satisfied by \(\mathsf {SWI}\), message and randomness explaining the entire transcript are already fixed in this round.
References
Barak, B.: Constant-round coin-tossing with a man in the middle or realizing the shared random string model. In: 43rd Symposium on Foundations of Computer Science (FOCS 2002), pp. 345–355 (2002)
Cao, Z., Visconti, I., Zhang, Z.: Constant-round concurrent non-malleable statistically binding commitments and decommitments. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 193–208. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13013-7_12
Chung, K.-M., Ostrovsky, R., Pass, R., Venkitasubramaniam, M., Visconti, I.: 4-round resettably-sound zero knowledge. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 192–216. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_9
Chung, K., Pass, R., Seth, K.: Non-black-box simulation from one-way functions and applications to resettable security. In: Symposium on Theory of Computing Conference, STOC 2013, pp. 231–240. ACM (2013)
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I.: 4-round concurrent non-malleable commitments from one-way functions. Cryptology ePrint Archive, Report 2016/621 (2016). http://eprint.iacr.org/2016/621
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I.: Concurrent non-malleable commitments (and more) in 3 rounds. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 270–299. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53015-3_10
Ciampi, M., Persiano, G., Scafuro, A., Siniscalchi, L., Visconti, I.: Improved OR-composition of sigma-protocols. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 112–141. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49099-0_5
Ciampi, M., Persiano, G., Scafuro, A., Siniscalchi, L., Visconti, I.: Online/offline OR composition of sigma protocols. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 63–92. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_3
Dachman-Soled, D., Malkin, T., Raykova, M., Venkitasubramaniam, M.: Adaptive and concurrent secure computation from new adaptive, non-malleable commitments. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 316–336. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42033-7_17
Damgård, I., Groth, J.: Non-interactive and reusable non-malleable commitment schemes. In: Proceedings of the 35th Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 9–11 June 2003, pp. 426–437 (2003)
Crescenzo, G., Persiano, G., Visconti, I.: Constant-round resettable zero knowledge with concurrent soundness in the bare public-key model. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 237–253. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28628-8_15
Dolev, D., Dwork, C., Naor, M.: Non-malleable cryptography (extended abstract). In: Proceedings of the 23rd Annual ACM Symposium on Theory of Computing, New Orleans, Louisiana, USA, 5–8 May 1991, pp. 542–552 (1991)
Feige, U.: Alternative models for zero knowledge interactive proofs. Master’s thesis, Weizmann Institute of Science, Rehovot, Israel. Ph.D. thesis (1990)
Feige, U., Lapidot, D., Shamir, A.: Multiple non-interactive zero knowledge proofs based on a single random string (extended abstract). In: 31st Annual Symposium on Foundations of Computer Science, St. Louis, Missouri, USA, 22–24 October 1990, vol. I, pp. 308–317. IEEE Computer Society (1990)
Feige, U., Shamir, A.: Witness indistinguishable and witness hiding protocols. In: Proceedings of the Twenty-second Annual ACM Symposium on Theory of Computing, STOC 1990, New York, NY, USA, pp. 416–426. ACM (1990)
Garg, S., Mukherjee, P., Pandey, O., Polychroniadou, A.: The exact round complexity of secure computation. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 448–476. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_16
Goldreich, O., Krawczyk, H.: On the composition of zero-knowledge proof systems. SIAM J. Comput. 25(1), 169–192 (1996)
Goldreich, O., Levin, L.A.: A hard-core predicate for all one-way functions. In: Proceedings of the 21st Annual ACM Symposium on Theory of Computing, Seattle, Washington, USA, 14–17 May 1989, pp. 25–32 (1989)
Goyal, V.: Constant round non-malleable protocols using one way functions. In: Proceedings of the 43rd ACM Symposium on Theory of Computing, STOC 2011, San Jose, CA, USA, 6–8 June 2011, pp. 695–704 (2011)
Goyal, V., Jain, A., Ostrovsky, R., Richelson, S., Visconti, I.: Constant-round concurrent zero knowledge in the bounded player model. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 21–40. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42033-7_2
Goyal, V., Khurana, D., Sahai, A.: Breaking the three round barrier for non-malleable commitments. In: 57th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2016. IEEE (2016)
Goyal, V., Lee, C., Ostrovsky, R., Visconti, I.: Constructing non-malleable commitments: a black-box approach. In: 53rd Annual IEEE Symposium on Foundations of Computer Science, FOCS 2012, pp. 51–60 (2012)
Goyal, V., Pandey, O., Richelson, S.: Textbook non-malleable commitments. Cryptology ePrint Archive, Report 2015/1178 (2015). http://eprint.iacr.org/2015/1178. Accessed 29 Dec 2016
Goyal, V., Pandey, O., Richelson, S.: Textbook non-malleable commitments. In: Proceedings of the 48th Annual ACM SIGACT Symposium on Theory of Computing, STOC 2016, pp. 1128–1141 (2016)
Goyal, V., Richelson, S., Rosen, A., Vald, M.: An algebraic approach to non-malleability. In: 55th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2014, pp. 41–50 (2014)
Hazay, C., Venkitasubramaniam, M.: On the power of secure two-party computation. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 397–429. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53008-5_14
Katz, J., Ostrovsky, R.: Round-optimal secure two-party computation. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 335–354. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28628-8_21
Lapidot, D., Shamir, A.: Publicly verifiable non-interactive zero-knowledge proofs. In: Menezes, A.J., Vanstone, S.A. (eds.) CRYPTO 1990. LNCS, vol. 537, pp. 353–365. Springer, Heidelberg (1991). doi:10.1007/3-540-38424-3_26
Lin, H., Pass, R.: Constant-round non-malleable commitments from any one-way function. In: Proceedings of the 43rd ACM Symposium on Theory of Computing, STOC 2011, pp. 705–714. ACM (2011)
Lin, H., Pass, R.: Constant-round nonmalleable commitments from any one-way function. J. ACM 62(1), 5:1–5:30 (2015)
Lin, H., Pass, R., Venkitasubramaniam, M.: Concurrent non-malleable commitments from any one-way function. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 571–588. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78524-8_31
Lin, H., Pass, R., Venkitasubramaniam, M.: A unified framework for concurrent security: universal composability from stand-alone non-malleability. In: Proceedings of the 41st Annual ACM Symposium on Theory of Computing, STOC 2009, Bethesda, MD, USA, 31 May – 2 June 2009, pp. 179–188 (2009)
Mahmoody, M., Pass, R.: The curious case of non-interactive commitments – on the power of black-box vs. non-black-box use of primitives. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 701–718. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_41
Mittelbach, A., Venturi, D.: Fiat–Shamir for highly sound protocols is instantiable. In: Zikas, V., Prisco, R. (eds.) SCN 2016. LNCS, vol. 9841, pp. 198–215. Springer, Cham (2016). doi:10.1007/978-3-319-44618-9_11
Naor, M.: Bit commitment using pseudorandomness. J. Cryptology 4(2), 151–158 (1991)
Ostrovsky, R., Persiano, G., Visconti, I.: Constant-round concurrent non-malleable zero knowledge in the bare public-key model. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008. LNCS, vol. 5126, pp. 548–559. Springer, Heidelberg (2008). doi:10.1007/978-3-540-70583-3_45
Ostrovsky, R., Persiano, G., Visconti, I.: Simulation-based concurrent non-malleable commitments and decommitments. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 91–108. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00457-5_7
Pandey, O., Pass, R., Vaikuntanathan, V.: Adaptive one-way functions and applications. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 57–74. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85174-5_4
Pass, R.: Bounded-concurrent secure multi-party computation with a dishonest majority. In: Proceedings of the 36th Annual ACM Symposium on Theory of Computing, Chicago, IL, USA, 13–16 June 2004, pp. 232–241. ACM (2004)
Pass, R.: Unprovable security of perfect NIZK and non-interactive Non-malleable Commitments. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 334–354. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36594-2_19
Pass, R., Rosen, A.: Bounded-concurrent secure two-party computation in a constant number of rounds. In: 44th Symposium on Foundations of Computer Science (FOCS 2003), Proceedings, pp. 404–413. IEEE Computer Society (2003)
Pass, R., Rosen, A.: Concurrent non-malleable commitments. In: Proceedings of the FOCS 2005, pp. 563–572 (2005)
Pass, R., Rosen, A.: New and improved constructions of non-malleable cryptographic protocols. In: Proceedings of the 37th Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 22–24 May 2005, pp. 533–542. ACM (2005)
Pass, R., Rosen, A.: Concurrent nonmalleable commitments. SIAM J. Comput. 37(6), 1891–1925 (2008)
Pass, R., Rosen, A.: New and improved constructions of nonmalleable cryptographic protocols. SIAM J. Comput. 38(2), 702–752 (2008)
Pass, R., Wee, H.: Constant-round non-malleable commitments from sub-exponential one-way functions. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 638–655. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_32
Rompel, J.: One-way functions are necessary and sufficient for secure signatures. In: Proceedings of the 22nd Annual ACM Symposium on Theory of Computing, pp. 387–394 (1990)
Sahai, A.: Non-malleable non-interactive zero knowledge and adaptive chosen-ciphertext security. In: Proceedings of the FOCS 1999, pp. 543–553. IEEE Computer Society (1999)
De Santis, A., Di Crescenzo, G., Ostrovsky, R., Persiano, G., Sahai, A.: Robust non-interactive zero knowledge. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 566–598. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_33
Wee, H.: Black-box, round-efficient secure computation via non-malleability amplification. In: 51st Annual IEEE Symposium on Foundations of Computer Science, FOCS 200, pp. 531–540. IEEE Computer Society (2010)
Yung, M., Zhao, Y.: Generic and practical resettable zero-knowledge in the bare public-key model. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 129–147. Springer, Heidelberg (2007). doi:10.1007/978-3-540-72540-4_8
Acknowledgments
We thank Vipul Goyal, and Silas Richelson for remarkable discussions on [24]. We thank Giuseppe Persiano and Alessandra Scafuro for several discussions on delayed-input protocols. We also thank to an anonymous reviewer of CRYPTO 2017 for suggesting prefix languages for SimWI. Research supported in part by “GNCS - INdAM”, EU COST Action IC1306, NSF grants 1065276, 1118126 and 1136174, US-Israel BSF grant 2008411, OKAWA Foundation Research Award, IBM Faculty Research Award, Xerox Faculty Research Award, B. John Garrick Foundation Award, Teradata Research Award, and Lockheed-Martin Corporation Research Award. This material is based upon work supported in part by DARPA Safeware program. The views expressed are those of the authors and do not reflect the official policy or position of the Department of Defense or the U.S. Government. The work of 1st, 3rd and 4th authors has been done in part while visiting UCLA.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I. (2017). Four-Round Concurrent Non-Malleable Commitments from One-Way Functions. In: Katz, J., Shacham, H. (eds) Advances in Cryptology – CRYPTO 2017. CRYPTO 2017. Lecture Notes in Computer Science(), vol 10402. Springer, Cham. https://doi.org/10.1007/978-3-319-63715-0_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-63715-0_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63714-3
Online ISBN: 978-3-319-63715-0
eBook Packages: Computer ScienceComputer Science (R0)











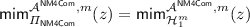 .
. and
and  comes from the adaptive-input SimWI property of
comes from the adaptive-input SimWI property of