Proving Resistance Against Invariant Attacks: How to Choose the Round Constants

Abstract

Many lightweight block ciphers apply a very simple key schedule in which the round keys only differ by addition of a round-specific constant. Generally, there is not much theory on how to choose appropriate constants. In fact, several of those schemes were recently broken using invariant attacks, i.e., invariant subspace or nonlinear invariant attacks. This work analyzes the resistance of such ciphers against invariant attacks and reveals the precise mathematical properties that render those attacks applicable. As a first practical consequence, we prove that some ciphers including Prince, Skinny-64 and $\textsf {Mantis}_{\mathsf {7}}$ are not vulnerable to invariant attacks. Also, we show that the invariant factors of the linear layer have a major impact on the resistance against those attacks. Most notably, if the number of invariant factors of the linear layer is small (e.g., if its minimal polynomial has a high degree), we can easily find round constants which guarantee the resistance to all types of invariant attacks, independently of the choice of the S-box layer. We also explain how to construct optimal round constants for a given, but arbitrary, linear layer.

1 Introduction

One of the main topics in symmetric cryptography in recent years is lightweight cryptography. Even though it is not really clearly defined what lightweight cryptography exactly is, the main idea can be embraced as designing cryptographic primitives that put an extreme focus on performance. This in turn resulted in many new, especially block cipher, designs which achieve better performance by essentially removing any operations that are not strictly necessary (or believed to be necessary) for the security of the scheme. One particular interesting case of reducing the complexity is the design of the key schedule and the choice of round constants. Both of these are arguably the parts that we understand least and only very basic design criteria are available on how to choose a good key schedule or how to choose good round constants. Consequently, many of the lightweight block ciphers remove the key schedule completely. Instead, identical keys are used in the rounds and (often very simple and sparse) round constants are added on top (e.g., see LED [10], Skinny [1], Prince [2], Mantis [1], to mention a few).

However, several of those schemes were recently broken using a structural attack called invariant subspace attack [14, 15], as well as the recently published generalization called nonlinear invariant attack [19]. Indeed, those attacks have been successfully applied to quite a number of recent designs including PRINTcipher [14], Midori-64 [9, 19], iSCREAM [15] and SCREAM [19], NORX v2.0 [4], Simpira v1 [17] and Haraka v.0 [12]. Both attacks, that we jointly call invariant attacks in this work, notably exploit the fact that these lightweight primitives have a very simple key schedule where the same round key (up to the addition of a round constant) is applied in several rounds.

It is therefore of major importance to determine whether a given primitive is vulnerable to invariant attacks. More generally, it would be interesting to exhibit some design criteria for the building blocks in a cipher which guarantee the resistance against these attacks. As mentioned above, this would shed light on the fundamental open question on how to select proper round constants.

Our Contribution. In this work, we analyze the resistance of several lightweight substitution-permutation ciphers against invariant attacks. Our framework both covers the invariant subspace attack, as well as the recently published nonlinear invariant attack. By exactly formalizing the requirements of those attacks, we are able to reveal the precise mathematical properties that render those attacks applicable. Indeed, as we will detail below, the rational canonical form of the linear layer will play a major role in our analysis. Our results show that the linear layer and the round constants have a major impact on the resistance against invariant attacks, while this type of attacks was previously believed to be mainly related to the behaviour of the S-box, see e.g., [9]. In particular, if the number of invariant factors of the linear layer is small (for instance, if its minimal polynomial has a high degree), we can easily find round constants which guarantee the resistance to all types of invariant attacks, independently of the choice of the S-box layer. In order to ease the application of our results in practice, we implemented all our findings in Sage [18] and added the source code in Appendix D.

In our framework, the resistance against invariant attacks is defined in the following sense: For each instantiation of the cipher with a fixed key, there is no function that is invariant for both the substitution layer and for the linear part of each round. This implies that any adversary who still wants to apply an invariant attack necessarily has to search for invariants over the whole round function, which appears to have a cost exponential in the block size in general. Indeed, all published invariant attacks we are aware of exploit weaknesses in the underlying building blocks of the round. Therefore, our notion of resistance guarantees complete security against the major class of invariant attacks, including all variants published so far.

This paper is split in two parts, a first part (Sect. 3) which can be seen as the attacker’s view on the problem and a second part (Sect. 4) which reflects more on the designer’s decision on how to avoid those attacks. More precisely, the first part of the paper details an algorithmic approach which enables an adversary to spot a possible weakness with respect to invariant attacks within a given cipher. For the lightweight block ciphers Skinny-64, Prince and $\textsf {Mantis}_{\mathsf {7}}$, the 7-round version of $\textsf {Mantis}_{\mathsf {,}}$ this algorithm is used to prove the resistance against invariant attacks.

These results come from the following observation, detailed in this first part: Let L denote the linear layer of the cipher in question and let $c_1,\dots ,c_t \in \mathbb {F}_2^n$ be the (XOR) differences between two round constants involved in rounds where the same round key is applied. Furthermore let $W_L(c_1,\dots ,c_t)$ denote the smallest L-invariant subspace of $\mathbb {F}_2^n$ that contains all $c_1,\dots ,c_t$. Then, one can guarantee resistance if $W_L(c_1,\dots ,c_t)$ covers the whole input space $\mathbb {F}_2^n$. As a direct result, we will see that in Skinny-64, there are enough differences between round constants to guarantee the full dimension of the corresponding L-invariant subspace. This directly implies the resistance of Skinny-64, and this result holds for any reasonable choice of the S-box layer.¹ In contrast, for Prince and $\textsf {Mantis}_{\mathsf {7}}$, there are not enough suitable $c_i$ to generate a subspace $W_L(c_1,\dots ,c_t)$ with full dimension. However, for both primitives, we are able to keep the security argument by also considering the S-box layer, using the fact that the dimension of $W_L(c_1,\dots ,c_t)$ is not too low in both cases.

In the second part of the paper, we provide an in-depth analysis of the impact of the round constants and of the linear layer on the resistance against invariant attacks. The first question we ask is the following:

Given the linear layer L of a cipher, what is the minimum number of round constants needed to guarantee resistance against the invariant attack, independently from the choice of the S-box?

Figure 1 shows the maximal dimension that can be reached by $W_L(c_1,\dots ,c_t)$ when $t$ values of $c_i$ are considered. It shows in particular that the whole input space can be covered with only $t=4$ values in the case of Skinny-64, while $8$ and $16$ values are needed for Prince and Mantis respectively. This explains why, even though Prince and Mantis apply very dense round constants, the dimension does not increase rapidly for higher values of t. The observations in Fig. 1 are deduced from the invariant factors (or the rational canonical form) of the linear layer, as shown in the following theorem.

Fig. 1.

For Skinny-64, Prince and Mantis, this figure shows the highest possible dimension of $W_L(c_1,\dots ,c_t)$ for $t$ values $c_1,\dots ,c_t$ (see Theorem 1).

Fig. 2.

For several lightweight ciphers, this figure shows the probability that $W_L(c_1,\dots ,c_t) = \mathbb {F}_2^n$ for uniformly random constants $c_i$ (see Theorem 2).

Theorem 1

Let $Q_1,\dots ,Q_r$ be the invariant factors of the linear layer L and let $t \le r$. Then

$$\begin{aligned} \max _{c_1,\dots ,c_t \in \mathbb {F}_2^n} \dim W_L(c_1, \ldots , c_t) = \sum _{i=1}^t \deg Q_i. \end{aligned}$$

For the special case of a single constant c, the maximal dimension of $W_L(c)$ is equal to the degree of the greatest invariant factor of L, i.e., the minimal polynomial of L. We will also explain how the particular round constants must be chosen in order to guarantee the best possible resistance.

As designers often choose random round constants to instantiate the primitive, we were also interested in the following question:

How many randomly chosen round constants are needed to guarantee the best possible resistance with a high probability?

We derive an exact formula for the probability that the linear subspace $W_L(c_1,\dots ,c_t)$ has full dimension for t uniformly random constants $c_i$. Figure 2 gives an overview of this probability for several lightweight designs.

Organization of the Paper. The principle of invariant attacks is first briefly recalled in Sect. 2. In Sect. 3, a new necessary condition is established on the functions which are both invariant for the S-box layer and for the linear parts (including the round key addition) of all rounds. This leads to a new security argument against invariant attacks. An algorithm to check whether the round constants avoid the existence of such invariants is then presented and applied to several lightweight ciphers, including $\textsf {Mantis}_{\mathsf {7}}$, Skinny-64 and Prince. Section 4 analyzes in more detail how the choice of the linear layer and of the round constants affects the resistance against invariant attacks. Some existing lightweight designs serve as examples to illustrate the arguments.

2 Preliminaries

By $\mathcal {B}_n$, we denote the set of all Boolean functions of n variables. The constant functions in $\mathbb {F}_2^n$ will be denoted by $\mathbf {0}$ and $\mathbf {1}$, respectively. The derivative of $f \in \mathcal {B}_n$ in direction $\alpha \in \mathbb {F}_2^n$ is the Boolean function defined as $\varDelta _{\alpha }f := x \mapsto f(x+\alpha ) + f(x)$. The following terminology will be extensively used in the paper. It refers to the constant derivatives which play a major role in our work.

Definition 1

[13] An element $\alpha \in \mathbb {F}_2^n$ is said to be a linear structure of $f \in \mathcal {B}_n$ if the corresponding derivative $\varDelta _{\alpha }f$ is constant. The set of all linear structures of a function $f$ is a linear subspace of $\mathbb {F}_2^n$ and is called the linear space of $f$:

$$\begin{aligned} \mathsf {LS}(f) := \{ \alpha \in \mathbb {F}_2^n \mid \varDelta _{\alpha }f = \varepsilon , \ \varepsilon \in \{ \mathbf {0},\mathbf {1}\} \}. \end{aligned}$$

The nonlinear invariant attack was described in [19] as a distinguishing attack on block ciphers. For a block cipher E operating on an n-bit block,

$$\begin{aligned} E: \mathbb {F}_2^n \times \mathbb {F}_2^{\kappa } \rightarrow \mathbb {F}_2^n, \quad (x,k) \mapsto E_k(x), \end{aligned}$$

the idea is to find a subset $\mathcal {S} \subset \mathbb {F}_2^n$ such that the partition of the input set into $\mathcal {S} \cup \left( \mathbb {F}_2^n \setminus \mathcal {S}\right)$ is preserved by the cipher for as many keys k as possible, i.e.,

$$\begin{aligned} E_k(\mathcal {S}) = \mathcal {S} \text { or } E_k(\mathcal {S}) = \mathbb {F}_2^n \setminus \mathcal {S}. \end{aligned}$$

The special case when $\mathcal {S}$ is a linear space corresponds to the so-called invariant subspace attacks [14].

An equivalent formulation is obtained by considering the $n$-variable Boolean function $g$ defined by $g(x)=1$ if and only if $x \in \mathcal {S}$. Then, finding an invariant consists in finding a function $g \in \mathcal {B}_n$ such that $g + g \circ E_k$ is constant. We call such a function g an invariant for $E_k$, and we obviously focus on non-trivial invariants, i.e., on $g \not \in \{ \mathbf {0}, \mathbf {1}\}$. In the following, for any permutation $F: \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$, we denote the set of all invariants for F by

$$\begin{aligned} \mathcal {U}(F) := \{ g \in \mathcal {B}_n \mid g + g \circ F \text { is constant}\}. \end{aligned}$$

As observed in [19], this set is a linear subspace of $\mathcal {B}_n$. An important remark, which will be used later, is that if $F$ has a cycle of odd length, then all $g \in \mathcal {U}(F)$ satisfy $g + g \circ F =\mathbf {0}$.

3 Proving the Absence of Invariants in Lightweight SPNs

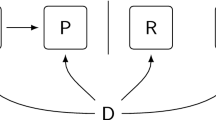
In the whole paper, we concentrate on block ciphers which follow the specific design of substitution-permutation networks (SPNs) as depicted in Fig. 3.

Usually, the technique applied for finding invariants for the cipher consists in exploiting its iterative structure and in searching for functions which are invariant for all constituent building blocks. Indeed computing invariants for the round function is in general infeasible for a proper block size, typically $n=64$ or $n=128$. Despite the fact that all published invariant attacks we are aware of exploit invariants for all the constituent building blocks, the algorithm described in [15] searches for invariant subspaces over the whole round function. However, it can only be applied in the special case for finding an invariant subspace, and not for detecting an arbitrary invariant set, and only detects spaces of large dimension efficiently.

Fig. 3.

SPN with S-box layer S and linear layer L. After the i-th round, one adds a round key $k_i$, where $(k_1,\dots ,k_t)$ is the expanded key resulting from the key schedule.

Therefore, we consider in the following only those invariants that are invariant under both the substitution layer S and the linear parts $\mathsf {Add_{k_i}} \circ L$ of all rounds. The linear spaces of these invariants have then a very specific structure as pointed out in the following proposition.

Proposition 1

Let $g \in \mathcal {B}_n$ be an invariant for both $\mathsf {Add}_{k_i} \circ L$ and $\mathsf {Add}_{k_j} \circ L$ for two round keys $k_i$ and $k_j$. Then $\mathsf {LS}(g)$ is a linear space invariant under L which contains $(k_i + k_j)$.

Proof

By definition of $g$, there exist $\varepsilon _i,\varepsilon _j \in \mathbb {F}_2$ such that, for all $x \in \mathbb {F}_2^n$,

$$\begin{aligned} g(x) = g(L(x) + k_i) + \varepsilon _i \text{ and } g(x) = g(L(x) + k_j) + \varepsilon _j. \end{aligned}$$

This implies that, for all $x \in \mathbb {F}_2^n$,

$$\begin{aligned} g(L(x) + k_i) + g(L(x) + k_j) = \varepsilon _i + \varepsilon _j, \end{aligned}$$

or equivalently, by replacing $(L(x)+k_j)$ by $y$:

$$\begin{aligned} g(y+k_i+k_j) + g(y) = \varepsilon _i + \varepsilon _j, \; \forall y \in \mathbb {F}_2^n \end{aligned}$$

and thus $(k_i+k_j) \in \mathsf {LS}(g)$. We then have to show that $\mathsf {LS}(g)$ is invariant under L. Let $s \in \mathsf {LS}(g)$. Then, there exists a constant $\varepsilon \in \mathbb {F}_2$ such that $g(x) = g(x + s) + \varepsilon$. Since $g$ is an invariant for $\mathsf {Add}_{k_i} \circ L$, we deduce

$$\begin{aligned} g(L(x) + k_i) + \varepsilon _i = g(x) = g(x+s) + \varepsilon = g(L(x) + L(s) + k_i) + (\varepsilon _i + \varepsilon ). \end{aligned}$$

Finally, we set $y \,:=\, L(x) + k_i$ and obtain

$$\begin{aligned} g(y) = g(y + L(s)) + \varepsilon \end{aligned}$$

(1)

which completes the proof.    $\square$

Therefore, the attack requires the existence of an invariant for the substitution layer whose linear space is invariant under $L$ and contains all differences between the round keys. The difference between two round keys, which should be contained in $\mathsf {LS}(g)$, is dependent on the initial key. However, if we consider only designs where some round keys are equal up to the addition of a round constant, we obtain that the differences between these round constants must belong to $\mathsf {LS}(g)$. Then, $\mathsf {LS}(g)$ is a linear space invariant under $L$ which contains the differences $(\mathsf {RC}_i+\mathsf {RC}_j)$ for any pair $(i,j)$ of rounds such that $k_i=k+\mathsf {RC}_i$ and $k_j=k+\mathsf {RC}_j$. The smallest such subspaces are spanned by the cycles of $L$ as shown by the following lemma. We use the angle bracket notation to denote the linear span.

Lemma 1

Let $L$ be a linear permutation of $\mathbb {F}_{2}^n$. For any $c \in \mathbb {F}_2^n$, the smallest L-invariant linear subspace of $\mathbb {F}_2^n$ which contains $c$, denoted by $W_L(c)$, is

$$\begin{aligned} \langle L^i (c), i \ge 0 \rangle . \end{aligned}$$

Proof

Obviously, $\langle L^i (c), i \ge 0 \rangle$ is included in $W_L(c)$, since $W_L(c)$ is a linear subspace of $\mathbb {F}_2^n$ and is invariant under $L$. Moreover, we observe that $\langle L^i (c), i \ge 0 \rangle$ is invariant under $L$. Indeed, for any $\lambda _1, \lambda _2 \in \mathbb {F}_2$ and any $(i,j)$,

$$\begin{aligned} L(\lambda _1 L^i(c) + \lambda _2 L^j(c)) = \lambda _1 L^{i+1}(c) + \lambda _2 L^{j+1}(c) \end{aligned}$$

and then belongs to $\langle L^i (c), i \ge 0 \rangle$. Then, this subspace is the smallest linear subspace of $\mathbb {F}_2^n$ invariant under $L$ which contains $c$.    $\square$

Let now $D$ be a set of known differences between round keys, i.e., a subset of all $k_i+k_j=(\mathsf {RC}_i + \mathsf {RC}_j)$. We define the subset

$$\begin{aligned} W_L(D) \,:=\, \sum _{c \in D} \langle L^i(c), \ i \ge 0 \rangle = \sum _{c \in D} W_L(c). \end{aligned}$$

We then deduce from the previous observations that the invariant attack applies only if there is a non-trivial invariant $g$ for the S-box layer such that $W_L(D) \subseteq \mathsf {LS}(g)$. A Sage code that computes the linear space $W_L(D)$ for a predefined list D is given in Appendix D (lines 31–38). It has been used for determining the dimension of $W_L(D)$ corresponding to the round constants in several lightweight ciphers.

Skinny-64. Considering the untweaked version Skinny-64-64, one observes that the round keys repeat every 16 rounds. We define

$$\begin{aligned} D \,:=\, \{ \mathsf {RC}_1 + \mathsf {RC}_{17}, \mathsf {RC}_2 + \mathsf {RC}_{18}, \mathsf {RC}_3 + \mathsf {RC}_{19}, \mathsf {RC}_4 + \mathsf {RC}_{20}, \mathsf {RC}_5 + \mathsf {RC}_{21} \} \end{aligned}$$

and obtain $\dim W_L(D) = 64$.

Skinny-128. In Skinny-128, The round constants are all of the following form:

$$\begin{aligned} \left[ \begin{array}{cccc} c_0 &{} 0 &{} 0 &{} 0 \\ c_1 &{} 0 &{} 0 &{} 0 \\ c_2 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \end{array}\right] \end{aligned}$$

with 8-bit values $c_0 \in \{ \mathtt {0x00},\dots ,\mathtt {0x0f} \}$, $c_1\in \{ \mathtt {0x00},\dots ,\mathtt {0x03} \}$ and $c_2=\texttt {0x02}$. Then, as the linear layer is defined by a binary matrix, we can see that the dimension of $W_L(D)$ is at most 64, because none of the four most significant bits will be activated with any round constant.

Prince. Prince uses ten round keys $k_i$, $1 \le i \le 10$, which are all of the form $k_i = k + \mathsf {RC}_i$. The so-called $\alpha$-reflection property implies that, for any $i$, $k_i + k_{11-i} = \alpha$ where $\alpha$ is a fixed constant. We can then consider the set of (independent) round constant differences

$$\begin{aligned} D = \{\alpha , \mathsf {RC}_1+\mathsf {RC}_2, \mathsf {RC}_1+\mathsf {RC}_3,\mathsf {RC}_1+\mathsf {RC}_4,\mathsf {RC}_1+\mathsf {RC}_5\}. \end{aligned}$$

We obtain that $\dim W_L(D) = 56$.

Mantis. As Prince, $\textsf {Mantis}_{\mathsf {7}}$ follows the $\alpha$-reflection construction. We therefore consider the following set of round constant differences:

$$\begin{aligned} D = \{ \alpha ,\mathsf {RC}_1+\mathsf {RC}_2, \mathsf {RC}_1+\mathsf {RC}_3,\mathsf {RC}_1+\mathsf {RC}_4,\mathsf {RC}_1+\mathsf {RC}_5, \mathsf {RC}_1+\mathsf {RC}_6, \mathsf {RC}_1 + \mathsf {RC}_7\} \end{aligned}$$

We obtain that $\dim W_L(D) = 42$.

Midori-64. In Midori-64, the round constants are only added to the least significant bit of each cell and the linear layer does not provide any mixing within the cells. Then $W_L(D) = \{ 0000, 0001\}^{16}$, and has dimension $16$ only.

As the invariant attack applies only if there is a non-trivial invariant $g$ for the S-box layer such that $W_L(D) \subseteq \mathsf {LS}(g)$, by intuition, the attack should be harder as the dimension of $W_L(D)$ increases. In the following, we analzye the impact of the dimension of $W_L(D)$ to the applicability of the attack in detail and present a method to prove the non-existence of invariants based on this dimension.

3.1 The Simple Case

We first consider a simple case, that is when the dimension of $W_L(D)$ is at least $n-1$.

Proposition 2

Suppose that the dimension of $W_L(D)$ is at least $n-1$. Then, any $g \in \mathcal {B}_n$ such that $W_L(D) \subseteq \mathsf {LS}(g)$ is linear or constant. As a consequence, there is no non-trivial invariant $g$ of the S-box layer such that $W_L(D) \subseteq \mathsf {LS}(g)$, unless the S-box layer has a component of degree $1$.

Proof

From [3, Proposition 14], it follows that

$$\begin{aligned} \dim \mathsf {LS}(g) \ge k \Leftrightarrow \deg (g) \le {\left\{ \begin{array}{ll} n-k &{}\text { if } k \ne n\\ 1 &{}\text { if } k = n \end{array}\right. }. \end{aligned}$$

This implies that g must be linear or constant. Linear invariants imply the existence of a linear approximation with probability 1, or equivalently that the S-box has a component (i.e., a linear combination of its coordinates) of degree $1$.    $\square$

In the rest of the paper, we will implicitly exclude the case when the S-box has a component of degree $1$, as the cipher would be already broken by linear cryptanalysis.

Skinny-64. As shown before, for the untweaked version Skinny-64-64 one obtains $\dim W_L(D) = 64$. This indicates that the round constants do not allow non-trivial invariants that are invariant for both the substitution and the linear parts of Skinny-64, and this result holds for any choice of the S-box layer.

Unfortunately, the dimension of $W_L(D)$ is not high enough for the other ciphers we considered. For those primitives, we therefore cannot prove the resistance against invariant attacks based on the linear layer only.

3.2 When the Dimension Is Smaller Than $(n-1)$

Not every cipher applies round constants such that the dimension of $W_L(D)$ is larger than or equal to $n-1$. Even for Prince and Mantis, which have very dense round constants, it is not the case and we cannot directly rely on this argument. However, if $n- \dim (W_L(D))$ is small, we can still prove that the invariant attack does not apply but only by exploiting some information on the S-box layer. This can be done by checking whether there exists a non-trivial invariant $g$ for the S-box layer which admits some given elements as $0$-linear structures, in the sense of the following definition.

Definition 2

A linear structure $\alpha$ of a Boolean function $f$ is called a 0-linear structure if the corresponding derivative equals the all-zero function. The set of all $0$-linear structures of $f$ is a linear subspace of $\mathsf {LS}(f)$ denoted by $\mathsf {LS}_0(f)$. Elements $\beta$ s.t. $\varDelta _{\beta }g = \mathbf {1}$ are called 1-linear structures of f.

Note that 0-linear structures are also called invariant linear structures. It is well-known that the dimension of $\mathsf {LS}_0(f)$ drops by at most 1 compared to $\mathsf {LS}(f)$ [5].

Checking that all invariants are constant based on 0-linear structures. In the following, we search for an invariant $g$ for the S-box layer S that is also invariant for the linear part of each round. Suppose now, in a first step, that we know a subspace Z of $\mathsf {LS}(g)$ which is composed of $0$-linear structures only. In other words, we now search for an invariant $g$ for $S$ such that $\mathsf {LS}_0(g) \supseteq Z$ for some fixed $Z$. If the dimension of this subspace $Z$ is close to $n$, we can try to prove that any such invariant is constant based on the following observation.

Proposition 3

Let $g$ be an invariant for an $n$-bit permutation $S$ such that $\mathsf {LS}_0(g) \supseteq Z$ for some given subspace $Z \subset \mathbb {F}_2^n$. Then

• $g$ is constant on each coset of $Z$;

• $g$ is constant on $S(Z)$.

Proof

Since $Z \subseteq \mathsf {LS}_0(g)$, for any $a \in \mathbb {F}_2^n$, we have that $g(a+z)=g(a)$ for all $z \in Z$, i.e., $g$ is constant on all $(a+Z)$. Now, we use that $g$ is an invariant for $S$, which means that there exists $\varepsilon \in \mathbb {F}_2$ such that $g(S(x)) = g(x) + \varepsilon$. Since $g$ is constant on $Z$, we deduce that $g$ is constant on $S(Z)$.    $\square$

To show that g must be trivial, the idea is to evaluate the S-box layer at some points in $Z$ and deduce that $g$ takes the same value on all corresponding cosets. The number of distinct cosets of $Z$ equals $2^{n-\dim Z}$, which is not too large when $\dim Z$ is close to $n$. Then, we hope that all cosets will be hit when evaluating $S$ at a few points in $Z$. In this situation, $g$ must be a constant function. In other words, we are able to conclude that there do not exist non-trivial invariants for both the substitution layer and the linear part.

In our experiments, we used the following very simple algorithm. If it terminates, all invariants must be constant. An efficient implementation in Sage of Algorithm 1 is given in Appendix D.

Determining a suitable Z from ${\varvec{W}}_{{\varvec{L}}}({\varvec{D}})$ . Up to now, we assumed the knowledge of a subspace Z of $W_L(D)$ for which $Z \subseteq \mathsf {LS}_0(g)$ for all invariants $g$ we are considering. But, the fact that some elements are $0$-linear structures depends on the actual invariant g and thus, each of the elements $d \in W_L(D)$ might or might not be a $0$-linear structure. However, some $0$-linear structures can be determined by using one of the two following approaches.

First approach. The first observation comes from (1) in the proof of Proposition 1.

Lemma 2

Let $g \in \mathcal {B}_n$ be an invariant for $\mathsf {Add}_{k_i} \circ L$ for some $k_i$ and let $V$ be a subspace of $\mathsf {LS}(g)$ which is invariant under L. Then, for any $v \in V$, $(v+L(v)) \in \mathsf {LS}_0(g)$.

Proof

Let $v \in V$. Similar as in the proof of Proposition 1, we use that g is an invariant for $\mathsf {Add}_{k_i} \circ L$ and see that there exists an $\varepsilon \in \mathbb {F}_2$ such that, for all $x \in \mathbb {F}_2^n$,

$$\begin{aligned} g(x) = g(x+v) + \varepsilon = g(x + L(v)) + \varepsilon . \end{aligned}$$

We finally set $y \,:=\, x+v$ and obtain

$$\begin{aligned} g(y) = g(y + v + L(v)), \end{aligned}$$

implying that $v + L(v)$ is a 0-linear structure for g.    $\square$

Following the previous lemma, one option is to just run Algorithm 1 on $Z = W_L(D')$ with $D' = \{ d+L(d), d \in D\}$. The disadvantage is that the dimension of Z might be too low and therefore the algorithm might be too inefficient. In this case, one can also consider a different approach and run the algorithm several times, by considering all possible choices for the $0$-linear structures among all elements in $D$. Suppose that, in the initial set of constants $D = \{d_1,d_2,\dots ,d_m,\dots ,d_{t}\}$, the elements $d_1,\dots ,d_m$ are all 1-linear structures for some invariant g with $\mathsf {LS}(g) \supseteq W_L(D)$. One can now consider

$$\begin{aligned} D' = \{d_1+L(d_1),d_2+L(d_2),\dots ,d_m +L(d_m),d_{m+1},\dots ,d_{t},d_1+d_2,\dots ,d_1+d_m \} \end{aligned}$$

which increases the dimension of $W_L(D')$ by adding the sums of the $1$-linear structures. We then have $W_L(D') \subseteq \mathsf {LS}_0(g)$ and we can apply Algorithm 1 on $Z=W_L(D')$. Since we cannot say in advance which of the constants are $1$-linear structures, there are $2^{t}$ possible choices of such a subspace $W_L(D')$ and we run Algorithm 1 on all of them. This approach still might be very inefficient due to the smaller dimension of $W_L(D')$ and since Algorithm 1 has to be run $2^{t}$ times.

Second approach. If the S-box layer S of the cipher has an odd-length cycle (i.e., if every S-box has an odd-length cycle), we can come up with the following.

Proposition 4

Let $g \in \mathcal {U}(S)$ where $S$ is an $n$-bit permutation with an odd cycle. Then, any linear structure of $g$ which belongs to the image set of $(S+\mathsf {Id}_n)$, i.e., $\{ S(x) + x \mid x \in \mathbb {F}_2^n\}$, is a $0$-linear structure of $g$.

Proof

If the S-box layer has an odd cycle, then any $g \in \mathcal {U}(S)$ necessarily fulfills $g(x) = g(S(x))$ for all $x \in \mathbb {F}_2^n$. Now let $g \in \mathcal {U}(S)$ and $c \in \mathsf {LS}(g)$. This linear structure belongs to $\mathsf {Im}(S+\mathsf {Id}_n)$ if there exists $x_0 \in \mathbb {F}_2^n$ such that $S(x_0) = x_0 + c$. We then deduce that

$$\begin{aligned} g(x_0) = g(S(x_0)) = g(x_0 + c), \end{aligned}$$

implying that c is a $0$-linear structure of g.    $\square$

Therefore, if we find enough of these $c \in W_L(D) \cap \mathsf {Im}(S+\mathsf {Id}_n)$, we can just apply Algorithm 1 on the resulting set. This approach will be used on $\textsf {Mantis}_{\mathsf {7}}$, as explained in the next section.

3.3 Results for Some Lightweight Ciphers

Prince. For Prince, we apply the first approach to $D' = \{d+L(d), \; d \in D\}$ where

$$\begin{aligned} D = \{\alpha , \mathsf {RC}_1+\mathsf {RC}_2, \mathsf {RC}_1+\mathsf {RC}_3,\mathsf {RC}_1+\mathsf {RC}_4,\mathsf {RC}_1+\mathsf {RC}_5\}. \end{aligned}$$

Then, $\dim W_L(D') = 51$. We run Algorithm 1 on $W_L(D')$ and the algorithm terminates within a few minutes on a standard PC. We now have proven that there are no non-trivial invariants that are invariant for both the substitution layer and the linear parts of all rounds in Prince.

Mantis. Since $\dim W_L(D) = 42$ for $\textsf {Mantis}_{\mathsf {7}}$, applying our algorithm $2^7$ times on a subspace of codimension 23 is a quite expensive task. We therefore exploit Proposition 4. Indeed, the S-box layer of Mantis is the parallel application of the following 4-bit S-box $\mathtt {Sb}$.

x	0	1	2	3	4	5	6	7	8	9	a	b	c	d	e	f
$\mathtt {Sb}(x)$	c	a	d	3	e	b	f	7	8	9	1	5	0	2	4	6
$x+\mathtt {Sb}(x)$	c	b	f	0	a	e	9	0	0	0	b	e	c	f	a	9

The S-box layer has an odd cycle because $\mathtt {Sb}$ has a fixed point. Moreover, the image set of $(\mathtt {Sb} +\mathsf {Id}_4)$ is composed of 7 values $\{ \mathtt {0},\mathtt {9},\mathtt {a},\mathtt {b},\mathtt {c},\mathtt {e},\mathtt {f}\}$. The $c \in W_L(D)$ for which each nibble is equal to a value in $\mathsf {Im}(\mathtt {Sb} +\mathsf {Id}_4)$ is a $0$-linear structure. For a random value $c \in \mathbb {F}_2^{64}$, we expect that every nibble belongs to $\mathsf {Im}(\mathtt {Sb} +\mathsf {Id}_4)$ with a probability of $\left( \frac{7}{16}\right) ^{16} \approx 2^{-19.082}$. In fact, one can find enough such $c \in W_L(D)$ in a reasonable time that generate the whole invariant space $W_L(D)$, implying that $W_L(D) \subseteq \mathsf {LS}_0(g)$ for all invariants $g \in \mathcal {U}(S)$. We then run Algorithm 1 on $Z = W_L(D)$. The algorithm terminates and we therefore deduce the non-existence of any non-trivial invariant which is invariant for S and the linear parts of all rounds in $\textsf {Mantis}_{\mathsf {7}}$.

Midori-64. For Midori-64, $W_L(D)=\{0000,0001\}^{16}$ and has dimension $16$ only. Then, there are $2^{48}$ different cosets of $W_L(D)$, implying that our algorithm is not efficient. Instead, we can theoretically describe the supports of all invariants of Midori-64. The proof of the following proposition is given in Appendix C.

Proposition 5

Let S be the substitution layer in Midori-64. Let further $W = \{0000,0001\}^{16}$. Let $g \in B_{64}$. Then, $g \in \mathcal {U}(S)$ and $W \subseteq \mathsf {LS}(g)$ if and only if the support of g is defined by

$$\begin{aligned} \mathsf {Supp}(g) = \bigcup _{b_0 \ldots b_{31} \in \mathsf {Supp}(h)} H_{b_0b_1} \times H_{b_2b_3} \times \ldots \times H_{b_{30}b_{31}} \end{aligned}$$

where $h$ is any Boolean function of $32$ variables such that $\{00, 10\}^{16} \subseteq \mathsf {LS}(h)$ and the sets $H_{ab}$ are defined by

$$\begin{aligned} H_{00} = \{8\}, H_{10}=\{9\}, H_{01}= \{0,3,5, 6, \mathtt {b}, \mathtt {c}, \mathtt {f}\} \text{ and } H_{11} = \{1,2,4,7, \mathtt {a} , \mathtt {d} , \mathtt {e}\}. \end{aligned}$$

The invariant $g_1$ exploited in the invariant subspace attack described in [9] is defined by ${{\mathrm{supp}}}(g_1) = \{8,9\}^{16}$. In our characterization, it corresponds to

$$\begin{aligned} h(b_0, \ldots , b_{31}) = \prod _{i=0}^{15} (1 + b_{2i+1}). \end{aligned}$$

In this case, all elements in $\{00,10\}^{16}$ are $0$-linear structures for $h$, implying that all elements in $W_L(D)$ are $0$-linear structures for $g_1$. If we denote the bits in the j-th cell of the Midori-64 state by $x_{j,3},x_{j,2},x_{j,1},x_{j,0}$ (the lsb corresponds to $x_{j,0}$), the algebraic normal form of $g_1$ is

$$\begin{aligned} g_1 (x) = \prod _{j=1}^{16} \left( x_{j,1} x_{j,2} x_{j,3} + x_{j,1} x_{j,3} + x_{j,2} x_{j,3} + x_{j,3}\right) , \end{aligned}$$

since $x_{1} x_{2} x_{3} + x_{1} x_{3} + x_{2} x_{3} + x_{3}$ is the ANF of the $4$-variable function with support $H_{00} \cup H_{10}$.

The quadratic nonlinear invariant described in [19] is given by

$$\begin{aligned} g_2(x) = \sum _{j=1}^{16} \left( x_{j,3} x_{j,2} + x_{j,2} + x_{j,1} + x_{j,0} \right) . \end{aligned}$$

It corresponds to $h(b_0, \ldots , b_{31}) = \sum _{i=0}^{15} b_{2i}.$ In this second case, only the words in $W_L(D)$ with an even number of non-zero nibbles are $0$-linear structures for $g_2$. It is worth noticing that the sum of these two invariants $(g_1+g_2)$ leads to a new invariant of degree 48 which has a linear space of dimension $32$. However, as this invariant does not admit any new weak keys, it does not lead to an improved attack on Midori-64.

4 Design Criteria on the Linear Layer and on the Round Constants

In this section, we study the properties of $W_L(D)$ in more detail and explain the different behaviors which have been previously observed. Most notably, we would like to determine whether the differences in the dimensions of $W_L(D)$ we noticed are due to a bad choice of the round constants or if they are inherent to the choice of the linear layer. At this aim, we analyze the possible values for the dimension of $W_L(D)$ from a more theoretical viewpoint. We first consider the L-invariant subspace $W_L(c)$ generated by a single element c. It is worth noticing that all results obtained in this section hold for any $\mathbb {F}_q$-linear layer operating on $\mathbb {F}_q^n$, where $q$ is any prime power. But, for the sake of simplicity, they are formulated for $q=2$ only, which is the case of all ciphers we are considering.

4.1 The Possible Dimensions of $W_L(c)$

We show that, for a single element c, the dimension of $W_L(c)$ is upper-bounded by the degree of the minimal polynomial of the linear layer, defined as follows.

Definition 3

(e.g., [7, p. 176]) Let $L$ be a linear permutation of $\mathbb {F}_{2}^n$. The minimal polynomial of $L$ is the monic polynomial $\mathsf {Min}_L(X)= \sum _{i=0}^d p_i X^i \in \mathbb {F}_2[x]$ of smallest degree such that

$$\begin{aligned} \mathsf {Min}_L(L) = \sum _{i=0}^d p_i L^i =0. \end{aligned}$$

Moreover, the minimal annihilating polynomial of an element $c \in \mathbb {F}_2^n$ (w.r.t $L$ ) (aka the order polynomial of $c$ or simply the minimal polynomial of $c$) is the monic polynomial $\mathsf {ord}_L(c)(X)= \sum _{i=0}^d \pi _i X^i \in \mathbb {F}_2[x]$ of smallest degree such that

$$\begin{aligned} \sum _{i=0}^d \pi _i (L^i(c)) =0. \end{aligned}$$

Proposition 6

Let $L$ be a linear permutation of $\mathbb {F}_{2}^n$. For any non-zero $c \in \mathbb {F}_2^n$, the dimension of $W_L(c)$ is the degree of the minimal polynomial of $c$.

Proof

We know from Lemma 1 that $W_L(c)$ is spanned by all $L^i(c), i \ge 0$. Let $d$ be the smallest integer such that $\{c, L(c), \ldots , L^{d-1}(c)\}$ are linearly independent. By definition, $d$ corresponds the degree of the minimal polynomial of $c$ since the fact that $L^d(c)$ belongs to $\langle L^i(c), 0 \le i <d\rangle$ is equivalent to the existence of $\pi _0, \ldots , \pi _{d-1}\in \mathbb {F}_2$ such that $L^d(c) = \sum _{i=0}^{d-1} \pi _i L^i(c)$, i.e., $P(L)(c)=0$ with $P(X)=X^d+ \sum _{i=0}^{d-1} \pi _i X^i$. It follows that $d \le \dim W_L(c)$.

We now need to prove that $d = \dim W_L(c)$, i.e., that all $L^{d+t}(c)$ for $t \ge 0$ belong to the linear subspace spanned by $\{c, L(c), \ldots , L^{d-1}(c)\}$. This can be proved by induction on $t$. The property holds for $t=0$ by definition of $d$. Suppose now that $L^{d+t}(c) \in \langle c, L(c), \ldots , L^{d-1}(c) \rangle$. Then,

$$\begin{aligned} L^{d+t+1}(c)= & {} L \left( L^{d+t}(c)\right) = L \left( \sum _{i=0}^{d-1} \lambda _i L^i(c)\right) = \sum _{i=0}^{d-1} \lambda _i L^{i+1}(c) \in \langle c, \ldots , L^{d-1}(c) \rangle . \end{aligned}$$

   $\square$

Obviously, the minimal polynomial of $c$ is a divisor of the minimal polynomial of $L$. The previous proposition then provides an upper bound on the dimension of any subspace $W_L(c)$, for $c \in \mathbb {F}_2^n \setminus \{0\}$.

Corollary 1

Let $L$ be a linear permutation of $\mathbb {F}_{2}^n$. For any $c \in \mathbb {F}_2^n$, the dimension of $W_L(c)$ is at most the degree of the minimal polynomial of $L$.

We can even get a more precise result and show that the possible values for the dimension of $W_L(c)$ correspond to the degrees of the divisors of $\mathsf {Min}_L$. Moreover, there are some elements $c$ which lead to any of these values. In particular, the degree of $\mathsf {Min}_L$ can always be achieved. This result can be proven in a constructive way by using the representation of the associated matrix as a block diagonal matrix whose diagonal consists of companion matrices.

Definition 4

Let $g(X) = X^d + \sum _{i=0}^{d-1} g_i X^i$ be a monic polynomial in $\mathbb {F}_2[X]$. Its companion matrix is the $d \times d$ matrix defined by

$$\begin{aligned} C(g)=\left( \begin{array}{ccccc} 0 &{} 1 &{} 0 &{} \ldots &{} 0 \\ 0 &{} 0 &{} 1 &{} \ldots &{} 0 \\ \vdots &{} &{} &{} &{} \\ 0 &{} 0 &{} 0 &{} \ldots &{} 1 \\ g_0 &{} g_1 &{} g_2 &{} \ldots &{} g_{d-1} \end{array}\right) \end{aligned}$$

Let us first focus on the special case when the minimal polynomial of $L$ has degree $n$. Then there is a basis such that the matrix of $L$ is the companion matrix of $\mathsf {Min}_L$ (e.g., [11, Lemma 6.7.1]). Using this property, we can prove the following proposition.

Proposition 7

Let $L$ be a linear permutation of $\mathbb {F}_{2}^n$ corresponding to the multiplication by some companion matrix $C(Q)$ with $Q \in \mathbb {F}_2[X]$ of degree $n$. For any non-constant divisor $P$ of $Q$ in $\mathbb {F}_2[X]$, there exists $c \in \mathbb {F}_2^n$ such that $\mathsf {ord}_L(c)=P$.

Proof

When the matrix of the linear permutation we consider is a companion matrix $C(Q)$, then the elements in the cycle of $c$, $\{c, L(c), L^2(c), \ldots \}$, can be seen as the successive internal states of the $n$-bit LFSR with characteristic polynomial $Q$ and initial state $c$. It follows that $\mathsf {ord}_L(c)$ corresponds to the minimal polynomial of the sequence produced by the LFSR with characteristic polynomial $Q$ and initial state $c$ (see [16, Theorem 8.51]). On the other hand, it is well-known that there is a one-to-one correspondence between the sequences $(s_t)_{t \ge 0}$ produced by the LFSR with characteristic polynomial $Q$ and the set of polynomials $C \in \mathbb {F}_2[X]$ with $\deg C < \deg Q$ [16, Theorem 8.40]. This comes from the fact that the generating function of any LFSR sequence can be written as

$$\begin{aligned} \sum _{t \ge 0}s_t X^t = \frac{C(X)}{Q^*(X)}, \end{aligned}$$

where $Q^*$ denotes the reciprocal of polynomial $Q$, i.e., $Q^*(X) = X^{\deg Q} Q(1/X)$, and $C$ is defined by the LFSR initial state.

Let now $P$ be any non-constant divisor of $Q$, i.e., $Q(X) = P(X) R(X)$ with $P \ne 1$. Then, the reciprocal polynomials satisfy $Q^*(X) = P^*(X) R^*(X)$. It follows that, for $C(X) = R^*(X)$,

$$\begin{aligned} \frac{C(X)}{Q^*(X)} = \frac{1}{P^*(X)}. \end{aligned}$$

Therefore, the sequence generated from the initial state defined by $C=R^*$ has minimal polynomial $P$. This is equivalent to the fact that the order polynomial of this initial state equals $P$.    $\square$

When the degree of the minimal polynomial of the linear layer is smaller than the block size, the previous result can be generalized by representing $L$ by a block diagonal matrix whose diagonal is composed of companion matrices. It leads to the following general result on the possible dimensions of $W_L(c)$.

Proposition 8

Let $L$ be a linear permutation of $\mathbb {F}_{2}^n$ and $\mathsf {Min}_L$ be its minimal polynomial. Then, for any divisor $P$ of $\mathsf {Min}_L$, there exists $c \in \mathbb {F}_2^n$ such that $\dim W_L(c) = \deg P$.

Most notably,

$$\begin{aligned} \max _{c \in \mathbb {F}_2^n} \dim W_L(c) = \deg \mathsf {Min}_L. \end{aligned}$$

Proof

If P equals the constant polynomial of degree zero, i.e., $P=1$, we choose $c=0$. Therefore, we assume in the following that P is of positive degree.

Let us factor the minimal polynomial of $L$ in

$$\begin{aligned} \mathsf {Min}_L(X) = M_1(X)^{e_1} M_2(X)^{e_2} \ldots M_k(X)^{e_k} \end{aligned}$$

where $M_1$, ..., $M_k$ are distinct irreducible polynomials over $\mathbb {F}_2$. From Theorem 6.7.1 and its corollary in [11], $\mathbb {F}_2^n$ can be decomposed into a direct sum of L-invariant subspaces

$$\begin{aligned} \mathbb {F}_2^n = \bigoplus _{i=1}^k \bigoplus _{j=1}^{r_i} V_{i,j} \end{aligned}$$

such that the matrix of the linear transformation induced by $L$ on $V_{i,j}$ is the companion matrix of $M_i^{\ell _{i,j}}$ where the $\ell _{i,j}$ are integers such that $\ell _{i,1}=e_i$ (the polynomials $M_i^{\ell _{i,j}}$ are called the elementary divisors of $L$). Let now $P$ be a non-constant divisor of $\mathsf {Min}_L$. Thus, we assume w.l.o.g that

$$\begin{aligned} P(X) = M_{1}(X)^{a_{1}} M_{2}(X)^{a_{2}} \ldots M_\kappa (X)^{a_\kappa } \text{ with } 1 \le a_i \le e_i. \end{aligned}$$

Since each $M_i^{a_i}$ is a non-constant divisor of $M_i^{e_i}$, we know from Proposition 7 that there exists $u_i \in V_{i,1}$ such that $\mathsf {ord}_{L_i}(u_i) = M_i^{a_i}$, where $L_i$ denotes the linear transformation induced by $L$ on $V_{i,1}$. Let us now consider the element $c \in \bigoplus _{i=1}^{\kappa } V_{i,1}$ defined by $c = \sum _{i=1}^\kappa u_i$. Let $\pi _0, \ldots \pi _{d-1} \in \mathbb {F}_2$ such that $R(X)\,:=\, X^d + \sum _{t=0}^{d-1} \pi _t X^t$ equals the order polynomial of c. In particular,

$$\begin{aligned} L^d(c) = \sum _{t=0}^{d-1} \pi _t L^t(c). \end{aligned}$$

Using that $L^t(c) = \sum _{i=1}^\kappa L^t(u_i)$ and the direct sum property, we deduce that, for any $1 \le i \le \kappa$,

$$\begin{aligned} L^d(u_i) = \sum _{t=0}^{d-1} \pi _t L^t(u_i). \end{aligned}$$

Then, $R$ is a multiple of the order polynomials of all $u_i$. It follows that $R$ must be a multiple of $\mathsf {lcm}(M_i^{a_i}) = P$. Since $P(L(c)) = 0$, we deduce that the order polynomial of $c$ is equal to $P$.    $\square$

LED. The minimal polynomial of the linear layer in LED is

$$\begin{aligned} \mathsf {Min}_L(X) = (X^8+X^7+X^5+X^3+1)^4(X^8+X^7+X^6+X^5+X^2+X+1)^4. \end{aligned}$$

Since its degree equals the block size, we deduce from the previous proposition that there exists an element $c \in \mathbb {F}_2^{64}$ such that $W_L(c)$ covers the whole space.

Skinny. The linear layer in Skinny with a $16 s$-bit state, $s \in \{4,8\}$, is an $\mathbb {F}_{2^s}$-linear permutation of $(\mathbb {F}_{2^s})^{16}$ defined by a $(16 \times 16)$ matrix $M$ with coefficients in $\mathbb {F}_2$. Moreover, the multiplicative order of this matrix in $\mathsf {GL}(16, \mathbb {F}_2)$ equals $16$, implying that the minimal polynomial of $L$ is a divisor of $X^{16}+1$. It can actually be checked that $(M+ \mathsf {Id}_{16})^e \ne 0$ for all $e < 16$, implying that

$$\begin{aligned} \mathsf {Min}_L(X) = X^{16} + 1 = (X+1)^{16}. \end{aligned}$$

It follows that there exist some elements $c \in (\mathbb {F}_{2^s})^{16}$ such that $\dim W_L(c) =d$ for any value of $d$ between $1$ and $16$. Elements $c$ which generate a subspace $W_L(c)$ of given dimension can be easily exhibited using the construction detailed in the proof of Proposition 7. Indeed, up to a change of basis, the matrix of $L$ in $\mathsf {GL}(16, \mathbb {F}_2)$ corresponds to the companion matrix of $(X^{16}+1)$, i.e., to a mere rotation of $16$-bit vectors. In other words, we can find a matrix $U \in GL(16, \mathbb {F}_2)$ such that $M=U\times C(X^{16}+1) \times U^{-1}$. Let us now consider elements $c \in (\mathbb {F}_{2^s})^{16}$ for which only the least significant bits of the cells can take non-zero values. Let $b$ be the $16$-bit vector corresponding to these least significant bits, then $\dim W_L(c)=d$ where $d$ is the length of the shortest LFSR generating $b'=U^{-1}b$. Table 1 provides some examples of such elements for various dimensions.

Table 1. Examples of $c \in (\mathbb {F}_{2^s})^{16}$ and the corresponding dimensions of $W_L(c)$.

Prince. The minimal polynomial of the linear layer in Prince is

$$\begin{aligned} \mathsf {Min}_L(X)= & {} X^{20}+X^{18}+X^{16}+X^{14}+X^{12}+X^8+X^6+X^4+X^2+1\\= & {} (X^4+X^3+X^2+X+1)^2 (X^2 + X + 1)^4 (X+1)^4. \end{aligned}$$

The maximal dimension of $W_L(c)$ is then $20$ and the factorization of $\mathsf {Min}_L$ shows that there exist elements which generate subspaces of much lower dimension.

Mantis and Midori-64. Mantis and Midori-64 share the same linear layer, which has minimal polynomial

$$\begin{aligned} \mathsf {Min}_L(X) = (X+1)^6. \end{aligned}$$

We deduce that $\dim W_{L}(c) \le 6$.

4.2 Considering More Round Constants

We can now consider more than one round constant and determine the maximum dimension of $W_L(c_1, \ldots , c_t)$ spanned by $t$ elements. This value is related to the so-called invariant factor form (aka rational canonical form) of the linear layer, as defined in the following proposition.

Proposition 9

(Invariant factors) [6, p. 476] Let $L$ be a linear permutation of $\mathbb {F}_{2}^n$. A basis of $\mathbb {F}_2^n$ can be found in which the matrix of L is of the form

$$\begin{aligned} \left( \begin{array}{cccc} C(Q_r) &{} &{} &{} \\ &{} C(Q_{r-1}) &{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} C(Q_1) \end{array}\right) \end{aligned}$$

for polynomials $Q_i$ such that $Q_r \mid Q_{r-1} \mid \dots \mid Q_1$. The polynomial $Q_1$ equals the minimal polynomial of L. In this decomposition, the $Q_i$ are called the invariant factors of L.

The invariant factors of the linear layer then define the maximal value of $W_L(c_1, \ldots , c_t)$, as stated in Theorem 1 which we restate below. A complete proof is given in Appendix A.

Theorem 1

Let $Q_1,\dots ,Q_r$ be the invariant factors of the linear layer L and let $t \le r$. Then

$$\begin{aligned} \max _{c_1,\dots ,c_t \in \mathbb {F}_2^n} \dim W_L(c_1, \ldots , c_t) = \sum _{i=1}^t \deg Q_i. \end{aligned}$$

Most notably, the minimal number of elements that must be considered in $D$ in order to generate a space $W_L(D)$ of full dimension is equal to the number of invariant factors of the linear layer.

Prince. The linear layer of Prince has $8$ invariant factors:

$$\begin{aligned} \begin{array}{lll} {Q_1(X)} &{} {=} &{} {Q_2(X)} = \mathsf {Min}_L(X) \\ &{} = &{} {X^{20}+X^{18}+X^{16}+X^{14}+X^{12}+X^8+X^6+X^4+X^2+1}\\ {Q_3(X)} &{} {=} &{} {Q_4(X) = X^8+X^6+X^2+1 = (X+1)^4 (X^2+X+1)^2} \\ {Q_5(X)}&{} {=} &{} {Q_6(X) = Q_7(X) = Q_8(X) = (X+1)^2} \end{array} \end{aligned}$$

Then, from any set $D$ with $5$ elements, the maximal dimension we can get for $W_L(D)$ is $20+20+8+8+2 = 58$, while we get $56$ for the particular $D$ derived from the effective round constants $D = \{\alpha , \mathsf {RC}_1+\mathsf {RC}_2, \mathsf {RC}_1+\mathsf {RC}_3,\mathsf {RC}_1+\mathsf {RC}_4,\mathsf {RC}_1+\mathsf {RC}_5\}$. We can then see that the round constants are not optimal, but that we can never achieve the full dimension with the number of rounds used in Prince.

Mantis and Midori-64. The linear layer of Mantis (resp. Midori-64) has $16$ invariant factors:

$$\begin{aligned} Q_1(X) = \ldots , Q_8(X)=(X+1)^6 \text{ and } Q_9(X) = \ldots , Q_{16}(X)=(X+1)^2. \end{aligned}$$

From the set $D$ of size $7$ (resp. $8$) obtained from the actual round constants of $\textsf {Mantis}_{\mathsf {7}}$ (resp. $\textsf {Mantis}_{\mathsf {8}}$), we generate a space $W_L(D)$ of dimension 42 (resp. 48) which is then optimal. We also see that one needs at least 16 round constant differences $c_1,\dots ,c_{16}$ to cover the whole input space. It is worth noticing that the round constants in Midori are only non-zero on the least significant bit in each cell, implying that $W_L(D)$ has dimension at most $16$. This is the main weakness of Midori-64 with respect to invariant attacks and this explains why the use of the same linear in Mantis does not lead to a similar attack.

The maximal dimension we can reach from a given number of round constants for the linear layers of Prince and of Mantis is then depicted in Fig. 1 in Sect. 1.

4.3 Choosing Random Round Constants

Often, the round constants of a cipher are chosen randomly. In this section, we want to compute the probability that a set of uniformly random chosen elements D generates a space $W_L(D)$ of maximal dimension. Again, we first consider the case of a single constant, i.e., $D = \{ c\}$.

Proposition 10

Let L be a linear permutation of $\mathbb {F}_2^n$. Assume that

$$\begin{aligned} \mathsf {Min}_L(X) = M_1(X)^{e_1} M_2(X)^{e_2} \ldots M_k(X)^{e_k} \end{aligned}$$

where $M_1$, ..., $M_k$ are distinct irreducible polynomials over $\mathbb {F}_2$. Then, the probability for a uniformly chosen $c \in \mathbb {F}_2^n$ to obtain $\dim W_L(c) = \deg \mathsf {Min}_L$ is

$$\begin{aligned} \mathrm {Pr}_{c \overset{\$}{\leftarrow } \mathbb {F}_2^n}[\dim W_L(c) = \deg \mathsf {Min}_L] = \prod _{i=1}^k \left( 1 - \frac{1}{2^{\mu _i \deg M_i}} \right) , \end{aligned}$$

where $\mu _i$ is the number of invariant factors of $L$ which are multiples of $M_i^{e_i}$.

Proof

We use the decomposition based on the elementary divisors, as in the proof of Proposition 8. From [11, p. 308], $\mathbb {F}_2^n$ can be decomposed into a direct sum

$$\begin{aligned} \mathbb {F}_2^n = \bigoplus _{i=1}^k \bigoplus _{j=1}^{r_i} V_{i,j} \end{aligned}$$

such that the matrix of the linear transformation induced by $L$ on $V_{i,j}$ is the companion matrix of $M_i(X)^{\ell _{i,j}}$ where, for each $i$, the $\ell _{i,j}$, $1 \le j \le r_i$, form a decreasing sequence of integers such that $\ell _{i,1}=e_i$. Then, the minimal polynomial of any element $u$ in $V_{i,j}$ is a divisor of $M_i(X)^{\ell _{i,j}}$. It follows that, if $c = \sum _{i=1}^k \sum _{j=1}^{r_i} u_{i,j} \in \bigoplus _{i=1}^k \bigoplus _{j=1}^{r_i} V_{i,j}$, $\mathsf {ord}_L(c) = \mathsf {Min}_L$ if and only if, for any $i$, there exists an index $j$ such that $\mathsf {ord}_L(u_{i,j}) = M_i^{e_i}$. Obviously, this situation can only occur if $\ell _{i,j}=e_i$. This last condition is equivalent to the fact that $j \le \mu _i$, where $\mu _i = \max \{j: \ell _{i,j}=e_i\}$. Using that the invariant factors of $L$ are related to the decomposition of $\mathsf {Min}_L$ by

$$\begin{aligned} Q_v = \prod _{i=1}^k M_i^{\ell _{i,v}} \end{aligned}$$

where $\ell _{i,v} =0$ if $v > r_i$, we deduce that $\mu _i$ is the number of invariant factors $Q_v$ which are multiples of $M_i^{e_i}$. Let us now define the event

$$\begin{aligned} E_{i,j}: \quad \mathsf {ord}_L(u_{i,j}) = M_i^{\ell _{i,j}}. \end{aligned}$$

Then, we have

$$\begin{aligned} \mathrm {Pr}_{c \overset{\$}{\leftarrow } \mathbb {F}_2^n}[\dim W_L(c) = \deg \mathsf {Min}_L] = \prod _{i=1}^k \mathrm {Pr}\left[ \bigcup _{j=1}^{\mu _i} E_{i,j}\right] . \end{aligned}$$

It is important to note that for a fixed i, the probability of the event $E_{i,j}$ is the same for all j. This probability corresponds to the proportion of polynomials of degree less than $\deg (M_i^{\ell _{i,j}})$ which are coprime to $M_i^{\ell _{i,j}}$. Indeed, as noticed in the proof of Proposition 7, there is a correspondence between the elements in $V_{i,j}$ and the initial states of the LFSR with characteristic polynomial $M_i^{\ell _{i,j}}$. Recall that the number of polynomials coprime to a given polynomial P is

$$\begin{aligned} \phi (P) \,:=\, | \{f \in \mathbb {F}_2[X] \mid \deg (f) < \deg (P),\ \gcd (f,P) = 1 \} |. \end{aligned}$$

If P is irreducible, then for any power of P we have $\phi (P^k) = 2^{(k-1)\deg P}$ $(2^{\deg P} - 1)$. We then deduce that

$$\begin{aligned} \mathrm {Pr}[E_{{i,j}}] = \frac{\phi (M_i^{\ell _{i,j}})}{2^{\ell _{i,j} \deg M_i}} = \frac{2^{(\ell _{i,j}-1)\deg M_i}(2^{\deg M_i} - 1)}{2^{\ell _{i,j} \cdot \deg M_i}} = 1 - \frac{1}{2^{\deg M_i}}. \end{aligned}$$

To compute $\mathrm {Pr}[\bigcup _{j=1}^{\mu _i} E_{i,j}]$, we use the inclusion-exclusion principle and obtain

$$\begin{aligned} \mathrm {Pr}\left[ \bigcup _{j=1}^{\mu _i} E_{i,j} \right] = \sum _{j=1}^{\mu _i} (-1)^{j-1} \left( {\begin{array}{c}\mu _i\\ j\end{array}}\right) \left( 1- \frac{1}{2^{\deg M_i}}\right) ^j = \left( 1- \frac{1}{2^{\mu _i \deg M_i}} \right) . \end{aligned}$$

   $\square$

LED. The minimal polynomial of the linear layer in LED is

$$\begin{aligned} \mathsf {Min}_L(X) = (X^8+X^7+X^5+X^3+1)^4(X^8+X^7+X^6+X^5+X^2+X+1)^4. \end{aligned}$$

A single constant c is sufficient to generate the whole space. Since $\mathsf {Min}_L$ has two irreducible factors, each of degree $8$, we get from the previous proposition that the probability that $W_{L}(c) = \mathbb {F}_2^{64}$ for a uniformly chosen constant c is

$$\begin{aligned} \mathrm {Pr}[W_{L}(c) = \mathbb {F}_2^{64}] = ( 1 - 2^{-8} )^2 \approx 0.9922. \end{aligned}$$

Probability to Generate the Whole Space with Several Random Constants. We now give a formula for the probability to get the maximal dimension with $t$ randomly chosen round elements, when $t$ varies. This probability highly depends on the degrees of the irreducible factors of the minimal polynomial of $L$. A full proof is given in Appendix B.

Theorem 2

Let $L$ be a linear permutation of $\mathbb {F}_{2}^n$. Assume that

$$\begin{aligned} \mathsf {Min}_L(X) = M_1(X)^{e_1} M_2(X)^{e_2} \ldots M_k(X)^{e_k} \end{aligned}$$

where $M_1$, ..., $M_k$ are distinct irreducible polynomials over $\mathbb {F}_2$. Then, the probability that $W_L(c_1,\cdots ,c_t)$ equals $\mathbb {F}_2^n$ is

$$\begin{aligned} \mathrm {Pr}_{c_1, \ldots , c_t \overset{\$}{\leftarrow } \mathbb {F}_2^n}[W_L(c_1,\cdots ,c_t)= \mathbb {F}_2^n] = \prod _{j=1}^k \prod _{i_j=0}^{r_j-1} \left( 1-\frac{1}{2^{(t-i_j)\deg (M_j)}}\right) , \end{aligned}$$

where $r_j$ is the number of invariant factors of $L$ which are multiples of $M_j$.

It is worth noticing that, when $t < r$ with $r$ the number of invariant factors, the product equals zero which corresponds to the fact that we need at least $r$ constants to generate the whole space.

Prince. Recall that the minimal polynomial of the linear layer in Prince is

$$\begin{aligned} \mathsf {Min}_L(X)= & {} X^{20}+X^{18}+X^{16}+X^{14}+X^{12}+X^8+X^6+X^4+X^2+1\\= & {} (X^4+X^3+X^2+X+1)^2 (X^2 + X + 1)^4 (X+1)^4. \end{aligned}$$

It then has three irreducible factors

$$\begin{aligned} M_1(X) = X^4+X^3+X^2+X+1, M_2(X)= X^2 + X + 1 \text{ and } M_3(X)=(X+1). \end{aligned}$$

Moreover, we know that the eight invariant factors of $L$ are

$$\begin{aligned} \begin{array}{lll} {Q_1(X)} &{} {=} &{} {Q_2(X)} = \mathsf {Min}_L(X), \\ {Q_3(X)} &{} {=} &{} {Q_4(X) = (X+1)^4 (X^2+X+1)^2}, \\ {Q_5(X)}&{} {=} &{} {Q_6(X) = Q_7(X) = Q_8(X) = (X+1)^2}. \end{array} \end{aligned}$$

We then deduce that $\mu _1 = 2$, $\mu _2=2$ and $\mu _3=4$. Proposition 10 then implies that $\dim W_{L}(c) \le 20$ and

$$\begin{aligned} \mathrm {Pr}[\dim W_{L}(c) = 20] = ( 1 - 2^{-8} )(1-2^{-4})^2 \approx 0.8755 \end{aligned}$$

for a uniformly chosen c. Since $L$ has $8$ invariant factors, at least $t=8$ elements $c_1,\dots ,c_{8}$ are needed to reach $W_{L}(c_1, \ldots , c_t) = \mathbb {F}_2^{64}$. The number of invariant factors in which each of the $M_i$ appears is given by $r_1=2$, $r_2=4$ and $r_3=8$. From Theorem 2, we get that the probability that $W_{L}(c_1, \ldots , c_8) = \mathbb {F}_2^{64}$ is

$$\begin{aligned} \prod _{i=0}^1 \left( 1-2^{-(8-i)\cdot 4}\right) \times \prod _{i=0}^3 \left( 1-2^{-(8-i)\cdot 2}\right) \prod _{i=0}^7 \left( 1-2^{-(8-i)}\right) \simeq 0.2895. \end{aligned}$$

Mantis and Midori-64. The minimal polynomial of the linear layer of Mantis and Midori-64 has a single irreducible factor, which is $(X+1)$. This linear layer has $16$ invariant factors. Since the first $8$ invariant factors equal the minimal polynomial, which has degree $6$, we derive from Proposition 10 that the probability that a uniformly chosen element generates a subspace of dimension $6$ is

$$\begin{aligned} \mathrm {Pr}[\dim W_{L}(c) = 6] = ( 1 - 2^{-8} ) \approx 0.9961. \end{aligned}$$

We need at least 16 elements $c_1,\dots ,c_{16}$ to cover the whole space and this occurs with probability

$$\begin{aligned} \prod _{j=1}^{16} \left( 1-\frac{1}{2^{j}}\right) \simeq 0.28879. \end{aligned}$$

It is worth noticing that when we increase the number of random round constants from $16$ to $20$, this probability increases to $0.93879$.

Figure 2 in Sect. 1 shows how the probability that the whole space is covered increases with the number of randomly chosen elements, for the linear layers of LED, Skinny-64, Prince and $\textsf {Mantis}_{\mathsf {.}}$ The fact that the curve corresponding to Skinny-64, Prince and Mantis have a similar shape comes from the fact that all three linear layers have a minimal polynomial divisible by $(X+1)$, and this factor appears in all invariant factors. Then, the term corresponding to the irreducible factor of degree $1$, namely

$$\begin{aligned} \prod _{j=t-r+1}^{t} \left( 1-\frac{1}{2^{j}}\right) \end{aligned}$$

is the dominant term in the formula in Theorem 2. Most notably, for $t=r$, the probability is close to $(1-2^{-1})(1-2^{-2})(1-2^{-3})(1-2^{-4})\simeq 0.3$.

5 Conclusion

For lightweight substitution-permutation ciphers with a simple key schedule, we provided a detailed analysis on the impact of the design of the linear layer and the particular choice of the round constants to the applicability of both the invariant subspace attack and the recently published nonlinear invariant attack. We did this analysis in a framework which unifies both of these attacks as so-called invariant attacks. With an algorithmic approach, a designer is now able to easily check the soundness of the chosen round constants, in combination with the choice of the linear layer, with regard to the resistance against invariant attacks and can thus easily avoid possible weaknesses by design. We stress that in many cases, this analysis can be done independently of the choice of the substitution layer. We directly applied our methods to several existing lightweight ciphers and showed in particular why Skinny-64-64, Prince, and $\textsf {Mantis}_{\mathsf {7}}$ are secure against invariant attacks; unless the adversary exploits weaknesses which are not based on weaknesses of the underlying building blocks, i.e., substitution layer and linear layer. In fact, we are not aware of any such strong attacks in the literature.

As future work, one can think about further generalizations of invariant attacks. As it was already mentioned in [19], it would be interesting to know if one can make use of statistical invariant attacks, i.e., invariant attacks that only work with a certain probability instead for all possible plaintexts. A further generalization could consider different invariants for the particular building blocks in each round of the analyzed primitive.

Appendices

A Proof of Theorem 1

In the whole section, we represent L in invariant factor form as in Proposition 9. We denote by $V_1,\dots ,V_r$ the invariant subspaces such that $\mathbb {F}_2^n = \bigoplus _{i=1}^r V_i$ and the linear transformation induced by L on $V_i$, denoted $L_{\mid V_i}$, is represented by the companion matrix $C(Q_i)$. We define $\mathbf {e_{V_i}}$ as the first unit vector in $V_i$, i.e., $V_i = \langle L^k(\mathbf {e_{V_i}}),\; 0 \le k < \deg Q_i\rangle$ and $\mathsf {ord}_{L_{\mid V_i}}(\mathbf {e_{V_i}})=Q_i$. Using Proposition 7, one can prove the following lemma.

Lemma 3

Let $t \le r$. Then

$$\begin{aligned} \max _{c_1,\dots ,c_t \in \mathbb {F}_q^n} \dim W_L(c_1,\ldots , c_t) \ge \sum _{i=1}^t \deg Q_i. \end{aligned}$$

Proof

We choose $c_1= \mathbf {e_{V_1}}$ and obtain $W_L(c_1) = W_{L_{\mid V_1}}(c_1) = V_1$. Then $\dim V_1$ equals $\deg Q_1$. We now continue with $L_{\mid V_2 \oplus \dots \oplus V_m}$ which has minimal polynomial $Q_2$ and choose $c_2$ accordingly. Iterating this until $c_t$, we construct $W_L(c_1,\ldots , c_t)$ as the direct sum $\bigoplus _{i=1}^t W_L(c_i)$ which has dimension $\sum _{i=1}^t \deg Q_i$.    $\square$

In order to prove equality, we need the following two lemmas.

Lemma 4

Let c in $\mathbb {F}_2^n= \bigoplus _{j=1}^r V_j$ be represented as $c = \sum _{j \in \mathcal {J}} u_j$ with $\mathcal {J} \subseteq \{1,\dots ,r \}$ and $u_j \in V_j \setminus \{0\}$. Then $W_L(c) \subseteq W_L(\bar{c})$ with $\bar{c} \,:=\, \sum _{j \in \mathcal {J}} \mathbf {e_{V_j}}$.

Proof

Let $v \in W_L(c)$. Then

$$\begin{aligned} v&= \sum _{i \in \mathbb {N}} \alpha _i L^i(c) = \sum _{i \in \mathbb {N}} \alpha _i L^i ( \sum _{j \in \mathcal {J}} u_j ) = \sum _{i \in \mathbb {N}} \sum _{j \in \mathcal {J}} \alpha _i L^i(u_j) \\&= \sum _{i \in \mathbb {N}} \sum _{j \in \mathcal {J}} \alpha _i L^i ( \sum _{k \in \mathbb {N}} \beta _k L^k(\mathbf {e_{V_j}} )) = \sum _{i \in \mathbb {N}} \sum _{j \in \mathcal {J}} \sum _{k \in \mathbb {N}} \alpha _i \beta _k L^{i+k}(\mathbf {e_{V_j}}) \\&= \sum _{i \in \mathbb {N}} \sum _{k \in \mathbb {N}} \alpha _i \beta _k L^{i+k}(\sum _{j \in \mathcal {J}} \mathbf {e_{V_j}}) = \sum _{i \in \mathbb {N}} \sum _{k \in \mathbb {N}} \alpha _i \beta _k L^{i+k}(\bar{c}) \in W_L(\bar{c}). \end{aligned}$$

   $\square$

This implies that for any $c_1,\dots ,c_t \in \mathbb {F}_2^n$, it is $W_L(c_1, \ldots , c_t) \subseteq W_L(\bar{c}_1, \ldots , \bar{c}_t)$. Thus, we can assume w.l.o.g. that all $c_i$ are of the form $\bar{c}_i =\sum _{j = 1}^r \gamma _{ij} \mathbf {e_{V_j}}$ with $\gamma _{ij} \in \mathbb {F}_2$. Then, to any t-tuple $(c_1,\dots ,c_t) \in (\mathbb {F}_2^n)^t$ where each $c_i$ is of the form described above, we associate a $t \times t$ matrix $\mathbf {M}_{(c_1,\dots ,c_t)} \,:=\, [\gamma _{ij}]_{i,j}$ over $\mathbb {F}_2^n$.

Lemma 5

Let $(c_1,\dots ,c_t) \in (\mathbb {F}_2^n)^t$ be such that $c_i = \sum _{j = 1}^r \gamma _{ij} \mathbf {e_{V_j}}$ and let $\mathbf {M}_{(c_1',\dots ,c_t')}$ be any matrix obtained from $\mathbf {M}_{(c_1,\dots ,c_t)}$ by elementary row operations. Then, for $(c_1',\dots ,c_t')$ corresponding to $\mathbf {M}_{(c_1',\dots ,c_t')}$, we have

$$\begin{aligned} W_L(c_1',\dots ,c_t') = W_L(c_1,\dots ,c_t). \end{aligned}$$

Proof

For a $t \times t$ matrix over $\mathbb {F}_2$, an elementary row operation is either

• (i) a swap of two different rows or

• (ii) an addition of one row to another.

Transforming a matrix $\mathbf {M}_{(c_1,\dots , c_r, \dots , c_s, \dots ,c_t)}$ by operation (i) results in the matrix $\mathbf {M}_{(c_1,\dots , c_s, \dots , c_r, \dots ,c_t)}$ and obviously $\sum _{i=1}^t W_L(c_i)$ is commutative.

We therefore only have to show that for two constants $c_r,c_s$ the equality $W_L(c_r) + W_L(c_s) = W_L(c_r + c_s) + W_L(c_s)$ holds. Let $v \in W_L(c_r) + W_L(c_s)$. Then,

$$\begin{aligned} u&= \sum _{i \in \mathbb {N}} ( \alpha _i L^i(c_r) + \beta _i L^i(c_s) ) = \sum _{i \in \mathbb {N}} (\alpha _i L^i(c_r) + \alpha _i L^i(c_s) + \alpha _i L^i(c_s) + \beta _i L^i(c_s) )\\&= \sum _{i \in \mathbb {N}} (\alpha _i L^i(c_r + c_s) + (\alpha _i + \beta _i) L^i(c_s) ) \in W_L(c_r + c_s) + W_L(c_s). \end{aligned}$$

The other inclusion $\supseteq$ follows accordingly.    $\square$

Now, we can prove the main theorem.

Proof

(of Theorem 1 ). The only thing left to show is $\le$. Given $c_1,\dots ,c_t \in \mathbb {F}_2^n$ with $t \le r$. By Lemma 4, $W_L(c_1, \ldots , c_t) \subseteq W_L(\bar{c}_1, \ldots , \bar{c}_t)$ for appropriate $\bar{c}_i = \sum _{j=1}^r \gamma _{ij} \mathbf {e_{V_j}}$ with $\gamma _{ij} \in \mathbb {F}_2$.

Consider the matrix $\mathbf {M}_{(\bar{c}_1,\dots ,\bar{c}_t)}$. Using elementary row operations, one can bring $\mathbf {M}_{(\bar{c}_1,\dots ,\bar{c}_t)}$ in reduced row-echelon form $\mathbf {M}_{(\tilde{c}_1,\dots ,\tilde{c}_t)}$. Now, by Lemma 5, the $\tilde{c}_i$ are such that $W_L(\bar{c}_1, \ldots \bar{c}_t) = W_L(\tilde{c}_1, \ldots , \tilde{c}_t)$ and, most importantly, $W_L(\tilde{c}_1, \ldots , \tilde{c}_t)= \sum _{i=1}^t W_{L_{\mid V_i \oplus \dots \oplus V_r}} (\tilde{c}_i)$. This is because $\tilde{c}_i = \sum _{j=1}^r \tilde{\gamma }_{ij} \mathbf {e_{V_j}}$ has $\tilde{\gamma }_{ij} = 0$ for all $j < i$.

Since the minimal polynomial of $L_{\mid V_i \oplus \dots \oplus V_r}$ equals $Q_i$, one finally obtains:

$$\begin{aligned} \dim W_L(c_1, \ldots , c_t) \le \dim W_L(\bar{c}_1, \ldots , \bar{c}_t) = \dim \sum _{i=1}^t W_{L_{\mid V_i \oplus \dots \oplus V_r}}(\tilde{c}_i)\le \sum _{i=1}^t \deg Q_i \end{aligned}$$

   $\square$

B Proof of Theorem 2

We now compute the probability to get the maximal dimension with $t$ randomly chosen elements, when $t$ varies. We need two preliminary results. The first one focuses on the case when $\mathsf {Min}_L$ is a power of an irreducible polynomial.

Proposition 11

Let $V$ be any vector space over $\mathbb {F}_2$. Let L be a linear application from V into V with exactly r invariant factors, such that the minimal polynomial of $L$ is of the form $P^e$ where P is an irreducible polynomial. Then, the probability that $W_L(c_1,\cdots ,c_t)$ equals V is

$$\begin{aligned} \mathrm {Pr}_{c_1, \ldots , c_t \overset{\$}{\leftarrow } V}[W_L(c_1,\cdots ,c_t)=V] = \prod _{i=0}^{r-1} \left( 1-\frac{1}{2^{(t-i)\deg (P)}}\right) \end{aligned}$$

Proof

Let $P^{e_1}$, ..., $P^{e_r}$ with $e=e_1 \ge e_2 \ldots \ge e_r$ be the invariant factors of $L$. Then, $V=V_1\oplus V_2\oplus \cdots \oplus V_r$ where $L_{\mid V_i}$ is represented by the companion matrix $C(P^{e_i})$. Therefore, for each $c_i \in V$, there exist $(u_{i,1},u_{i,2},\cdots ,u_{i,r}) \in V_1 \times V_2 \times \cdots \times V_r$ such that $c_i = u_{i,1} + u_{i,2} + \cdots + u_{i,r}.$

We first prove that if $W_L(c_1,\cdots ,c_t)=V$, there exists some constant $c_i$, $1 \le i \le t$, such that $W_L(u_{i,1})=V_1$. Obviously, the $u_{i,j}$ for $j\ge 2$ do not belong to the subspace $V_1$. Then, if $W_L(c_1,\cdots ,c_t)=V$, $W_L((u_{i,1})_{1\le i \le t})$ must cover the whole space $V_1$. Moreover, if $u_{i,1}$ and $u_{j,1}$ are such that $W_L(u_{i,1})\subsetneq V_1$ and $W_L(u_{j,1})\subsetneq V_1$, then $W_L(u_{i,1},u_{j,1})\subsetneq V_1$. Indeed, since $W_L(u_{i,1})\subsetneq V_1$, the order polynomial of $u_{i,1}$ with respect to $L$ equals $P^a$, for some $a < e_1$. Similarly, the order polynomial of $u_{j,1}$ equals $P^b$, for some $b < e_1$. Assume w.l.o.g that $a \le b$. It is well known that, for any linear application $M$ and any integer $\ell$, we have $\ker (M^\ell )\subseteq \ker (M^{\ell +1})$. Here, we apply this to the linear application $M=P(L)$: Using that $W_L(u_{i,1}) \subseteq \ker (P^a(L))$ and $W_L(u_{j,1}) \subseteq \ker (P^b(L))$, we deduce that

$$\begin{aligned} W_L(u_{i,1}) \subseteq \ker (P^a(L)) \subseteq \ker (P^b(L)) \subsetneq V_1 \end{aligned}$$

and thus

$$\begin{aligned} W_L(u_{i,1},u_{j,1}) \subseteq \ker (P^b(L)) \subsetneq V_1. \end{aligned}$$

This eventually implies that at least one of the $W_L(u_{i,1})$ must cover $V_1$.

We now prove the result by induction on r, the number of invariant factors.

• $\varvec{r=1}$. From the previous observation, $W_L(c_1,\cdots ,c_t)=V$ if and only if at least one of the $c_1, \ldots , c_t$ has order polynomial $P^e$. We have seen in Proposition 10 that the probability that a random $c \in V$ has order polynomial $P^e$ is

  $$\begin{aligned} 1 - \frac{1}{2^{\deg P}}. \end{aligned}$$

  Then, since the $t$ constants are independent, the probability that none of the $t$ constants has minimal polynomial $P^e$ equals $(2^{-\deg P})^t$, implying that

  $$\begin{aligned} \mathrm {Pr}_{c_1, \ldots , c_t \overset{\$}{\leftarrow } V}[W_L(c_1,\cdots ,c_t)=V] = 1-\frac{1}{2^{t\deg (P)}}. \end{aligned}$$

• Induction step. We now assume that the result holds for any linear application with $(r-1)$ invariant factors and whose minimal polynomial is a power of an irreducible polynomial. Let us consider $L$ with $r$ invariant factors. If $W_L(c_1,\cdots ,c_t)=V$, then at least one of the $t$ constants satisfies $W_L(u_{i,1}) = V_1$. This occurs with probability $1-\frac{1}{2^{t\deg (P)}}$. Once we found the constant, say $c_1$, such that $W_L(u_{1,1})=V_1$, we need to focus on the application defined on the quotient space, $L'=V/W_L(c_1)$. Since the order polynomial of $c_1$ is the minimal polynomial of L, then the invariant factors of $L'$ are $P^{e_2}$, ..., $P^{e_r}$ (see e.g., [8, Fact 2.2]). Then we have

  $$\begin{aligned} \mathrm {Pr}[W_L(c_1,\cdots ,c_t)=\mathbb {F}_2^n]=\left( 1-\frac{1}{2^{t\deg (P)}}\right) \Pr [W_{L'}(c'_2,\cdots ,c'_{t})=V/V_1] \end{aligned}$$

  where $c'_{i} = (c_i)_{\mathbb {F}_2^n/V_1}$. The result then follows from the induction hypothesis applied to $L'$, which has $(r-1)$ invariant factors.    $\square$

The general case can now be tackled thanks to the following lemma.

Lemma 6

Let L be a linear permutation of $\mathbb {F}_2^n$. Suppose that there exist two subspaces of $\mathbb {F}_2^n$, $V_1$ and $V_2$, invariant under $L$ such that $V_1 \oplus V_2 = \mathbb {F}_2^n$ and the minimal polynomials of the linear transformations induced by $L$ on $V_1$ and on $V_2$ are coprime. Then, for any $c_1, \ldots , c_t \in \mathbb {F}_2^n$,

$$\begin{aligned} W_L(c_1, \ldots , c_t) = W_L(a_1, \ldots , a_t) \oplus W_L(b_1, \ldots , b_t) \end{aligned}$$

where $(a_i,b_i)$ is the unique pair in $V_1 \times V_2$ such that $c_i =a_i + b_i$.

Proof

First we observe that $W_L(a_1, \ldots , a_t) \cap W_L(b_1, \ldots , b_t) =\{0\}$. Indeed, $W_L(a_1, \ldots , a_t) \subseteq V_1$ and $W_L(b_1, \ldots , b_t) \subseteq V_2$ because $V_1$ and $V_2$ are invariant under $L$.

It is easy to check that $W_L(c_1, \ldots , c_t) \subseteq W_L(a_1, \ldots , a_t) \oplus W_L(b_1, \ldots , b_t)$. Actually, any $x \in W_L(c_1, \ldots , c_t)$ can be expressed as

$$\begin{aligned} x = \sum _{\ell \in \mathbb {N}} \sum _{i=1}^t \lambda _{i,\ell } L^\ell (c_i) = \left( \sum _{\ell \in \mathbb {N}} \sum _{i=1}^t \lambda _{i,\ell } L^\ell (a_i) \right) + \left( \sum _{\ell \in \mathbb {N}} \sum _{i=1}^t \lambda _{i,\ell } L^\ell (b_i) \right) . \end{aligned}$$

We now need to show that $W_L(a_1, \ldots , a_t) \oplus W_L(b_1, \ldots , b_t) \subseteq W_L(c_1, \ldots , c_t)$. Let $P_1$ and $P_2$ respectively denote the minimal polynomials of the applications $L_1$ and $L_2$ induced by $L$ on $V_1$ and on $V_2$. Let $d_1$ and $d_2$ denote the degree of $P_1$ and $P_2$ respectively. Let us consider the following subspace of $\mathbb {F}_2^n$:

$$\begin{aligned} W = \Big \langle P_2(L^j) (c_i), 1 \le i \le t, 0 \le j< d_1 \Big \rangle + \Big \langle P_1(L^j) (c_i) , 1 \le i \le t, 0 \le j < d_2 \Big \rangle . \end{aligned}$$

Since each $P_1(L^j) (c_i)$ (resp. each $P_2(L^j) (c_i)$) is a linear combination of elements of the form $L^\ell (c_i)$, it is clear that $W \subseteq W_L(c_1, \ldots , c_t)$. On the other hand, for any $1 \le i \le t$ and any $0 \le j < d_1$, we have

$$\begin{aligned} P_2(L^j) (c_i) = P_2(L^j) (a_i + b_i) = P_2(L^j) (a_i) + P_2(L^j)(b_i) = P_2(L^j) (a_i), \end{aligned}$$

since $b_i \in V_2$ and $P_2(X^j)$ is a multiple of the minimal polynomial of $L_2$. Similarly,

$$\begin{aligned} P_1(L^j) (c_i) = P_1(L^j) (b_i), \end{aligned}$$

implying that

$$\begin{aligned} W = \Big \langle P_2(L^j) (a_i), 1 \le i \le t, 0 \le j< d_1 \Big \rangle + \Big \langle P_1(L^j) (b_i) , 1 \le i \le t, 0 \le j < d_2 \Big \rangle . \end{aligned}$$

Moreover, the following mapping

$$\begin{aligned} \begin{array}{rrcl} \phi _1: &{} V_1 &{} \rightarrow &{} V_1\\ &{} x &{} \mapsto &{} P_2(L)(x) \end{array} \end{aligned}$$

is a bijection since it is linear and its kernel is equal to the all-zero vector. Indeed, if $P_2(L)(x)=0$, then $\mathsf {ord}_L(x)$ is a divisor of $P_2$. But, since $x \in V_1$, we know that $\mathsf {ord}_L(x)$ is a divisor of $P_1$. Using that $P_1$ and $P_2$ are coprime, we get that $x$ is the all-zero vector. Moreover, $W_L(a_1, \ldots , a_t)$ is invariant under $\phi _1$. It follows that

$$\begin{aligned} \Big \langle P_2(L^j) (a_i), 1 \le i \le t, 0 \le j< d_1 \Big \rangle= & {} P_2(L) \left( \Big \langle L^j (a_i), 1 \le i \le t, 0 \le j < d_1 \Big \rangle \right) \\= & {} \phi _1 (W_L(a_1, \ldots , a_t)) = W_L(a_1, \ldots , a_t). \end{aligned}$$

Similarly,

$$\begin{aligned} \Big \langle P_1(L^j) (b_i), 1 \le i \le t, 0 \le j < d_2 \Big \rangle = W_L(b_1, \ldots , b_t). \end{aligned}$$

We eventually deduce that

$$\begin{aligned} W = W_L(a_1, \ldots , a_t) \oplus W_L(b_1, \ldots , b_t). \end{aligned}$$

Combined with the fact that $W \subseteq W_L(c_1, \ldots , c_t)$, it leads to

$$\begin{aligned} {}W_L(a_1, \ldots , a_t) \oplus W_L(b_1, \ldots , b_t) \subseteq W_L(c_1, \ldots , c_t).\quad \square \end{aligned}$$

The combination of the previous two results leads to the proof of Theorem 2.

Proof

(of Theorem 2 ). Let us decompose the minimal polynomial of $L$ as

$$\begin{aligned} \mathsf {Min}_L(X) = M_1(X)^{e_1} M_2(X)^{e_2} \ldots M_k(X)^{e_k} \end{aligned}$$

where all $M_i$ are irreducible. Then, from the decomposition based of the elementary divisors [11, p. 308], we know that there exist $k$ subspaces $U_1$, ...$U_k$ invariant under $L$ such that $\mathbb {F}_2^n = U_1 \oplus U_2 \ldots \oplus U_k$ and the minimal polynomial of the linear application $L_i$ induced by $L$ on each $U_i$ equals $M_i^{e_i}$. Let us consider $t$ randomly chosen $c_1, \ldots , c_t \in \mathbb {F}_2^n$. Then, Lemma 6 implies that

$$\begin{aligned} W_L(c_1, \ldots c_t) = \bigoplus _{i=1}^k W_L(u_{i,1}, \ldots , u_{i,t}) \end{aligned}$$

where $(u_{1,j}, \ldots , u_{k,j})$ is the unique $k$-tuple in $U_1 \times \ldots \times U_k$ such that $c_j = \sum _{i=1}^k u_{i,j}$. We deduce:

$$\begin{aligned} \mathrm {Pr}_{c_1, \ldots , c_t \overset{\$}{\leftarrow } \mathbb {F}_2^n}[W_L(c_1,\cdots ,c_t) = \mathbb {F}_2^n] = \prod _{i=1}^k \mathrm {Pr}_{u_{i,1}, \ldots , u_{i,t} \overset{\$}{\leftarrow } U_i}[W_{L_i}(u_{i,1},\cdots ,u_{i,t}) = U_i] \end{aligned}$$

Proposition 11 shows that, for any $1 \le i \le k$,

$$\begin{aligned} \mathop {\Pr }\limits _{u_{i,1}, \ldots , u_{i,t} \overset{\$}{\leftarrow } V_i}[W_{L_i}(u_{i,1},\cdots ,u_{i,t})= V_i] = \prod _{j=0}^{r_i-1} \left( 1-\frac{1}{2^{(t-j)\deg (M_i)}}\right) , \end{aligned}$$

where $r_i$ is the number of invariant factors of $L$ which are multiples of $M_i$. The result then directly follows.    $\square$

C Proof of Proposition 5 on the Invariants for Midori-64

The characterization of the invariants $g$ of the S-box layer of Midori-64 which satisfy $\{0000,0001\}^{16} \subseteq \mathsf {LS}(g)$ exploits the following general lemma.

Lemma 7

Let S be a mapping from $\mathbb {F}_2^n$ to itself, and $W$ be a linear subspace of $\mathbb {F}_2^n$. If $g \in \mathcal {U}(S)$ and $W \subseteq \mathsf {LS}(g)$, then $g$ is constant on the sets

$$\begin{aligned} \mathcal {E}_{S,W}(x) = \bigcup _{i \in \mathbb {N}} \tilde{S}_W^i (\{x\}), \; x \in \mathbb {F}_2^n \end{aligned}$$

where

$$\begin{aligned} \begin{array}{rcl} \tilde{S}_W: \mathcal {P}(\mathbb {F}_2^n) &{}\rightarrow &{} \mathcal {P}(\mathbb {F}_2^n) \\ X &{}\mapsto &{} \mathop {\bigcup }\nolimits _{w \in W} \{S(S(x) +w)+w , \;\;x\in X\}. \end{array} \end{aligned}$$

Moreover, if $S$ is an involution, then there exists $k \in \mathbb {N}$ such that $\mathcal {E}_{S,W}(x)= \tilde{S}_W^k (\{x\})$ for all $x \in \mathbb {F}_2^n$.

Proof

Let $g \in \mathcal {U}(S)$. Then, there exists $\varepsilon _1 \in \mathbb {F}_2$ such that $g(S(x)) = g(x) + \varepsilon _1$ for all $x \in \mathbb {F}_2^n$. Let $w \in W$. Then, $w$ is a $\varepsilon _2$-linear structure of $g$ for some $\varepsilon _2 \in \mathbb {F}_2$. It follows that, for any $x \in \mathbb {F}_2^n$,

$$\begin{aligned} \begin{array}{lll} g(S(S(x) +w)+w) &{} = &{} g(S(S(x) +w)) + \varepsilon _2 = g(S(x) +w) + \varepsilon _1 + \varepsilon _2 \\ &{} = &{} g(S(x)) + \varepsilon _2 + \varepsilon _1 + \varepsilon _2 = g(x) + \varepsilon _1 + \varepsilon _2 + \varepsilon _1 + \varepsilon _2 = g(x). \end{array} \end{aligned}$$

Then, $g$ is constant on the sets $\mathcal {E}_{S,W}(x)$. If $g$ is an involution, then $X \subseteq \tilde{S}_W (X)$ for any set $X$. Indeed, since $0 \in W$, we have

$$\begin{aligned} \tilde{S}_W (X) \supseteq \{S(S(x)), x\in X\} = X. \end{aligned}$$

It follows that the sequence $(\tilde{S}_W^i(\{x\}))_{i \in \mathbb {N}}$ is an increasing sequence for inclusion. Then, there exists $k_x$ such that $\mathcal {E}_{S,W}(x) = \tilde{S}_W^{k_x}(\{x\})$. We get the result by choosing $k = \max _x k_x$.    $\square$

In Midori-64 the sets $\mathcal {E}_{S,W}(x)$ have a simple form because $S$ consists of 16 copies of the same $4$-bit S-box, $\mathtt {Sb}$, and $W$ also corresponds to $16$-th Cartesian power of a subspace of $\mathbb {F}_2^4$, namely $W=V^{16}$ with $V = \{0000, 0001\}$. Then, we can deduce the characterization given in Proposition 5.

Proof

(of Proposition 5 ). Using that $S$ consists of 16 copies of $\mathtt {Sb}$ and that $W = V^{16}$ with $V=\{0000,0001\}$, we deduce that, for any $x_0, \ldots , x_{15} \in \mathbb {F}_2^4$,

$$\begin{aligned}&\tilde{S}_W(\{(x_0, \ldots , x_{15})\}) \\= & {} \{\mathtt {Sb}(\mathtt {Sb}(x_0)+w_0)+w_0, \ldots \mathtt {Sb}(\mathtt {Sb}(x_{15})+w_{15})+w_{15} , \; w_i \in V\} \\= & {} \tilde{\mathtt {Sb}}_V(\{x_0\}) \times \ldots \times \tilde{\mathtt {Sb}}_V(\{x_{15}\}). \end{aligned}$$

Then, for any $k \in \mathbb {N}$,

$$\begin{aligned} \tilde{S}_W^k(\{(x_0, \ldots , x_{15})\}) = \tilde{\mathtt {Sb}}^k_V(\{x_0\}) \times \ldots \times \tilde{\mathtt {Sb}}^k_V(\{x_{15}\}). \end{aligned}$$

Since the S-box layer is an involution, we deduce from the previous lemma that

$$\begin{aligned} \mathcal {E}_{S,W}((x_0, \ldots , x_{15})) = \mathcal {E}_{\mathtt {Sb},V}(x_0) \times \ldots \times \mathcal {E}_{\mathtt {Sb},V}(x_{15}). \end{aligned}$$

Now, for the Midori S-box, any $\mathcal {E}_{\mathtt {Sb},V}(x)$ correspond to one of the following sets

$$\begin{aligned} H_{00} = \{8\}, H_{10}=\{9\}, H_{01}= \{0,3,5, 6, \mathtt {b}, \mathtt {c}, \mathtt {f}\} \text{ and } H_{11} = \{1,2,4,7, \mathtt {a} , \mathtt {d} , \mathtt {e}\}. \end{aligned}$$

Moreover, all these four sets satisfy that, for any $x \in H_{ab}$, $\tilde{\mathtt {Sb}}^k(\{x\})=H_{ab}$ for all $k \ge 6$. Therefore, for any $x=(x_0 \ldots x_{15})\in \mathbb {F}_2^{16}$,

$$\begin{aligned} \mathcal {E}_{S,W}(x) = H_{b_0b_1} \times H_{b_2b_3} \times \ldots \times H_{b_{30}b_{31}} \end{aligned}$$

for some $b \in \mathbb {F}_2^{32}$. Since any $g \in \mathcal {U}(S)$ with $W \subseteq \mathsf {LS}(g)$ must be constant on all $\mathcal {E}_{S,W}(x)$, we deduce that its support must be a union of such sets, i.e.,

$$\begin{aligned} \mathsf {Supp}(g) = \bigcup _{b_0 \ldots b_{31} \in \mathcal {A}} H_{b_0b_1} \times H_{b_2b_3} \times \ldots \times H_{b_{30}b_{31}} \end{aligned}$$

where $\mathcal {A}$ is a subset of $\mathbb {F}_2^{32}$. It is worth noticing that, since all the sets $\mathcal {H}_{b_0\ldots b_{31}}=H_{b_0b_1} \times H_{b_2b_3} \times \ldots \times H_{b_{30}b_{31}}$ are disjoint, this equivalently means that $g$ is a linear combination of the $2^{32}$ functions of $64$ variables

$$\begin{aligned} g_{b_0 \ldots b_{31}} = \prod _{i=0}^{15} f_{b_{2i}b_{2i+1}} \text{ where } \mathsf {Supp} f_{b_{2i}b_{2i+1}} = H_{b_{2i}b_{2i+1}}. \end{aligned}$$

Let us now characterize the sets $\mathcal {A}$ which guarantee that $W \subseteq \mathsf {LS}(g)$. Let $h$ denote the Boolean function of $32$ variables whose support equals $\mathcal {A}$. We observe that, for any $b_0b_1 \in \mathbb {F}_2^2$, $00001 + H_{b_0b_1} = H_{b_0+1b_1}$. It follows that, for any $w \in W$ and any $b \in \mathbb {F}_2^{32}$, the image of the translation of $\mathcal {H}_{b}$ by $w$ is equal to $\mathcal {H}_{b+\pi (w)}$ where $\pi (w)$ is the $32$-bit word defined by $\pi (w)_i=00$ if $w_i=0000$ and $\pi (w)_i=10$ if $w_i=0001$ for all $0 \le i \le 15$. Therefore, if $w \in W$ is a $0$-linear structure for $g$, we have that $b \in \mathbb {F}_2^{32}$ belongs to $\mathsf {Supp}(h)$ if and only if $(b+\pi (w)) \in \mathsf {Supp}(h)$. This equivalently means that $\pi (w)$ is a $0$-linear structure for $h$. Similarly, if $w \in W$ is a $1$-linear structure for $g$, we have that $b \in \mathbb {F}_2^{32}$ belongs to $\mathsf {Supp}(h)$ if and only if $(b+\pi (w)) \not \in \mathsf {Supp}(h)$. This means that $\pi (w)$ is a $1$-linear structure for $h$. We then conclude that $\pi (W)=\{00,10\}^{16} \subseteq \mathsf {LS}(h)$.

Conversely, it is easy to check that all functions $g$ such that

$$\begin{aligned} \mathsf {Supp}(g) = \bigcup _{b_0 \ldots b_{31} \in \mathsf {Supp}(h)} H_{b_0b_1} \times H_{b_2b_3} \times \ldots \times H_{b_{30}b_{31}} \end{aligned}$$

with $\pi (W) \subseteq \mathsf {LS}(h)$ are invariants for the nonlinear layer of Midori-64. Indeed, each set $H_{b_0b_1}$ is invariant under $\mathtt {Sb}$. This property is closed under addition, implying that any such $g$ is an invariant for $S$. Moreover, any $w \in \{0000,0001\}^{16}$ is a linear structure for $g$ because $\pi (w)$ is a linear structure for $h$.    $\square$

D Sage Code of the Algorithms