Fast Secure Two-Party ECDSA Signing

Abstract

ECDSA is a standard digital signature schemes that is widely used in TLS, Bitcoin and elsewhere. Unlike other schemes like RSA, Schnorr signatures and more, it is particularly hard to construct efficient threshold signature protocols for ECDSA (and DSA). As a result, the best-known protocols today for secure distributed ECDSA require running heavy zero-knowledge proofs and computing many large-modulus exponentiations for every signing operation. In this paper, we consider the specific case of two parties (and thus no honest majority) and construct a protocol that is approximately two orders of magnitude faster than the previous best. Concretely, our protocol achieves good performance, with a single signing operation for curve P-256 taking approximately 37 ms between two standard machine types in Azure (utilizing a single core only). Our protocol is proven secure under standard assumptions using a game-based definition. In addition, we prove security by simulation under a plausible yet non-standard assumption regarding Paillier.

Y. Lindell—Much of this work was done for Dyadic Security Ltd.

1 Introduction

1.1 Background

In the late 1980s and the 1990s, a large body of research emerged around the problem of threshold cryptography; cf. [3, 7, 9, 10, 13, 20, 23, 24]. In its most general form, this problem considers the setting of a private key shared between n parties with the property that any subset of t parties may be able to decrypt or sign, but any set of less than t parties can do nothing. This is a specific example of secure multiparty computation, where the functionality being computed is either decryption or signing. Note that trivial solutions like secret sharing the private key and reconstructing to decrypt or sign do not work since after the first operation the key is reconstructed, and any single party can decrypt or sign by itself from that point on. Rather, the requirement is that a subset of t parties is needed for every private-key operation.

Threshold cryptography can be used in applications where multiple signators are needed to generate a signature, and likewise where highly confidential documents should only be decrypted and viewed by a quorum. Furthermore, threshold cryptography can be used to provide a high level of key protection. This is achieved by sharing the key on multiple devices (or between multiple users) and carrying out private-key operations via a secure protocol that reveals nothing but the output. This provides key protection since an adversary needs to breach multiple devices in order to obtain the key. After intensive research on the topic in the 1990s and early 2000s, threshold cryptography received considerably less interest in the past decade. However, interest has recently been renewed. This can be seen by the fact that a number of startup companies are now deploying threshold cryptography for the purpose of key protection [25,26,27]. Another reason is due to the fact that ECDSA signing is used in bitcoin, and the theft of a signing key can immediately be translated into concrete financial loss. Bitcoin has a multisignature solution built in, which is based on using multiple distinct signing keys rather than a threshold signing scheme. Nevertheless, a more general solution may be obtained via threshold cryptography (for the more general t-out-of-n threshold case).

Fast threshold cryptography protocols exist for a wide variety of problems, including RSA signing and decryption, ElGamal and ECIES encryption, Schnorr signatures, Cramer-Shoup, and more. Despite the above successes, and despite the fact that DSA/ECDSA is a widely-used standard, DSA/ECDSA has resisted attempts at constructing efficient protocols for threshold signing. This seems to be due to the need to compute k and ${k^{-1}}$ without knowing k. We explain this by comparing ECDSA signing to EC-Schnorr signing. In both cases, the public verification key is an elliptic curve point Q and the private signing key is x such that $Q=x\cdot G$, where G is the generator point of an EC group of order q.

Observe that Schnorr signing can be easily distributed since the private key x and the value k are both used in a linear equation. Thus, two parties with shares $x_1,x_2$ such that $Q=(x_1+x_2)\cdot G$ can each locally choose $k_1,k_2$, and set $R=k_1\cdot G+k_2\cdot G = (k_1+k_2)\cdot G$. Then, each can locally compute e and $s_i = k_i - x_i \cdot e \bmod q$ and send to each other, and each party can sum $s=s_1+s_2 \bmod q$ and output a valid signature (s, e). In the case of malicious adversaries, some zero knowledge proofs are needed to ensure that R is uniformly distributed, but these are highly efficient proofs of knowledge of discrete log. In contrast, in ECDSA signing, the equation for computing s includes $k^{-1}$. Now, given shares $k_1,k_2$ such that $k_1+k_2 = k \bmod q$ it is very difficult to compute $k_1',k_2'$ such that $k_1'+k_2'=k^{-1} \bmod q$.

As a result, beginning with [20] and more lately in [14], two-party protocols for ECDSA signing use multiplicative sharing of x and of k. That is, the parties hold $x_1,x_2$ such that $x_1\cdot x_2 = x\bmod q$, and in each signing operation they generate $k_1,k_2$ such that $k_1\cdot k_2 = k\bmod q$. This enables them to easily compute $k^{-1}$ since each party can locally compute $k_i' = k_i^{-1}\bmod q$, and then $k_1',k_2'$ are multiplicative shares of $k^{-1}$. The parties can then use additively homomorphic encryption – specifically Paillier encryption [21] – in order to combine their equations. For example, $P_1$ can compute $c_1=\mathsf{Enc}_{pk}((k_1)^{-1}\cdot H(m))$ and $c_2 = \mathsf{Enc}_{pk}(k_1^{-1} \cdot x_1 \cdot r)$. Then, using scalar multiplication (denoted $\odot$) and homomorphic addition (denoted $\oplus$), $P_2$ can compute $(k_2^{-1} \odot c_1) \oplus [(k_2^{-1} \cdot x_2) \odot c_2]$ which will be an encryption of

$$ k_2^{-1} \cdot (k_1^{-1} \cdot H(m)) + k_2^{-1} \cdot x_2 \cdot (k_1^{-1} \cdot x_1 \cdot r) = k^{-1} \cdot (H(m) + r\cdot x), $$

as required. However, proving that each party worked correctly is extremely difficult. For example, the first party must prove that the Paillier encryption includes $k_1^{-1}$ when the second party only has $R_1=k_1\cdot G$, it must prove that the Paillier encryptions are to values in the expected range, and more. This can be done, but it results in a protocol that is very expensive.

1.2 Our Results

As in previous protocols, we use Paillier homomorphic encryption (with a key generated by $P_1$), and multiplicative sharing of both the private key x and the random value k. However, we make the novel observation that if $P_2$ already holds a Paillier encryption $c_{key}$ of $P_1$’s share of the private key $x_1$, then $P_1$ need not do anything except participate in the generation of $R=k\cdot G$. Specifically, assume that the parties $P_1$ and $P_2$ begin by generating $R=k_1\cdot k_2 \cdot G$ (this is essentially accomplished by just running a Diffie-Hellman key exchange with basic knowledge-of-discrete-log proofs which are highly efficient). Then, given $c_{key}=\mathsf{Enc}_{pk}(x_1)$, R and $k_2,x_2$, party $P_2$ can singlehandedly compute an encryption of $k_2^{-1} \cdot H(m) + k_2^{-1} \cdot r \cdot x_2 \cdot x_1$ using the homomorphic properties of Paillier encryption. This ciphertext can be sent to $P_1$ who decrypts and multiplies the result by $k_1^{-1}$. If $P_2$ is honest, then the result is a valid signature.

The crucial issue that must be dealt with is what happens when $P_1$ or $P_2$ is corrupted. If $P_1$ is corrupted, it cannot do anything since the only message that it sends $P_2$ is in the generation of R which is protected by an efficient zero-knowledge proof. Thus, no expensive proofs are needed. Furthermore, if $P_2$ is corrupted, then the only way it can cheat is by encrypting something incorrect and sending it to $P_1$. However, here we can utilize the fact that we are specifically computing a digital signature that can be publicly verified. That is, since all $P_1$ does is locally decrypt the ciphertext received from $P_2$ and multiply by $k_1^{-1}$, it can locally check if the signature obtained is valid. If yes, it outputs it, and if not it detects $P_2$ cheating. Thus, no zero-knowledge proofs are required for $P_2$ either (again, beyond the zero-knowledge proof in the generation of R).

As a result, we obtain a signing protocol that is extremely simple and efficient. As we show, our protocol is approximately two orders of magnitude faster than the previous best. Before proceeding, we remark that there are additional elements needed in the protocol (like $P_2$ adding random noise in the ciphertext it sends), but these have little effect on the efficiency.

We remark that since the security of the signing protocol rests upon the assumption that $P_2$ holds an encryption of $x_1$, which is $P_1$’s share of the key, this must be proven in the key generation phase. Thus, the key generation phase of our protocol is more complicated than the signing phase, and includes a proof that $P_1$ generated the Paillier key correctly and that $c_{key}$ is an encryption of $x_1$, given $R_1=x_1\cdot G$. This latter proof is of interest since it connects between Paillier encryption and discrete log, and we present a novel efficient proof in the paper. We remark that since key generation is run only once, having a more expensive key-generation phase is a worthwhile tradeoff. This is especially the case since it is still quite reasonable (concretely taking about 5 s between standard single-core machines in Azure, which is much faster than the key-generation phase of [14]). Furthermore, it can easily be parallelized to further bring down the cost.

DSA vs ECDSA. In this paper, we refer to ECDSA throughout and we use Elliptic curve (additive group) notation. However, our entire protocol translates easily to the DSA case, since we do nothing but standard group operations.

Caveat. The only caveat of our work is that it focuses specifically on the two-party case, whereas prior works considered general thresholds as well. The two-party case is in some ways the most difficult case (since there is no honest majority), and we therefore believe that our techniques may be useful for the general case as well. We leave this for future research.

1.3 Related Work and a Comparison of Efficiency

The first specific protocol for threshold DSA signing with proven security was presented in [13]. Their protocol works as long as more than of the parties are honest. The two party case (where there is no honest majority) was later dealt with by [20]. The most recent protocol by [14] contains efficiency improvements for the two-party case, and improvements regarding the thresholds for the case of an honest majority.

Efficiency comparison with [14]. The previous best DSA/ECDSA threshold signing protocol is due to [14]. Their signing protocol requires the following operations by each party: 1 Paillier encryption, 5 Paillier homomorphic scalar multiplications, 5 Paillier homomorphic additions, and 46 exponentiations (the vast majority of these modulo N or $N^2$ for the Paillier modulus). Furthermore, they require the Paillier modulus to be greater than $q^8$ where q is the group order. Now, for P-256, this makes no difference since anyway a 2048-bit modulus is minimal. However, for P-384 and P-521 respectively, this requires a modulus of size 3072 and 4168 respectively, which severely slows down the computation. Regarding the key generation phase, [14] need to run a protocol for distributed key generation for Paillier. This outweighs all other computations and is very expensive for the case of malicious adversaries. (They did not implement this phase in their prototype, but the method they refer to [17] has a reported time of 15 min for generating a 2048-bit modulus for the semi-honest case alone.)

In contrast, the cost of our key-generation protocol is dominated by approximately 350 Paillier encryptions/exponentiations by each party; see Sect. 3.3 for an exact count. Furthermore, as described in Sect. 3.3, in the signing protocol, party $P_1$ computes 7 Elliptic curve multiplications and 1 Paillier decryption, and party $P_2$ computes 5 Elliptic curve multiplications and 1 Paillier encryption, 1 homomorphic scalar multiplication and 1 Paillier homomorphic addition. Furthermore, the Paillier modulus needs only to be greater than $2q^4+q^3$, where q is the ECDSA group order. Thus, a 2048-bit modulus can be taken for P-256 and P-384, and a 2086-bit modulus only is needed for P-521. We therefore conclude that the cost of our signing protocol is approximately two orders of magnitude faster than their protocol.¹ This theoretical estimate is validated by our experimental results.

Experimental results and comparison. The running-time reported for the protocol of [14] for curve P-256 is approximately 12 s per signing operation between a mobile and PC. An improved optimized implementation using parallelism and 4 cores on a 2.4 GHz machine achieves approximately 1 s per signing operation (these measurements are only for the computation time and do not include communication). In contrast, as we describe in Sect. 3.3, for curve P-256 our signing protocol takes approximately 37ms, using a single core (measuring the actual full running time, including communication). This validates the theoretical analysis of approximately two orders of magnitude difference, when taking into account the use of multiple cores. Specifically, on 4 cores, we can achieve a throughput of over 100 signatures per second, in contrast to a single signing operation for [14]. Full details of our experiments, for curves P-256, P-384 and P-521 appear in Sect. 3.3.

Finally, the key generation phase of our protocol for curve P-256 takes approximately 5 s, using a single core. In contrast, [14] requires distributed Paillier key generation which is extremely expensive, as described above.

2 Preliminaries

The ECDSA signing algorithm. The ECDSA signing algorithm is defined as follows. Let ${\mathbb {G}}$ be an Elliptic curve group of order q with base point (generator) G. The private key is a random value $x\leftarrow {\mathbb {Z}}_q$ and the public key is $Q=x\cdot G$.

The ECDSA signing operation on a message $m\in \{0,1\}^*$ is defined as follows:

• 1. Compute $m'$ to be the |q| leftmost bits of SHA256(m), where |q| is the bit-length of q

• 2. Choose a random $k\leftarrow {\mathbb {Z}}_q^*$

• 3. Compute $R\leftarrow k\cdot G$. Let $R=(r_x,r_y)$.

• 4. Compute $r= r_x \bmod q$. If $r=0$, go back to Step 2.

• 5. Compute $s\leftarrow k^{-1} \cdot (m'+r \cdot x) \bmod q$.

• 6. Output (r, s)

It is a well-known fact that for every valid signature (r, s), the pair $(r,-s)$ is also a valid signature. In order to make (r, s) unique (which will help in formalizing security), we mandate that the “smaller” of $s,-s$ is always output (where the smaller is the value between 0 and $\frac{q-1}{2}$.)

The ideal commitment functionality $\mathcal{F}_\mathsf{com}$. In one of our subprotocols, we assume an ideal commitment functionality $\mathcal{F}_\mathsf{com}$, formally defined in Functionality 2.1. Any UC-secure commitment scheme fulfills $\mathcal{F}_\mathsf{com}$; e.g., [1, 12, 18]. In the random-oracle model, $\mathcal{F}_\mathsf{com}$ can be trivially realized with static security by simply defining $\mathsf{Com}(x)=H(x,r)$ where $r\leftarrow \{0,1\}^n$ is random.

The ideal zero knowledge functionality $\mathcal{F}_\mathsf{zk}$. We use the standard ideal zero-knowledge functionality defined by $((x,w),\lambda )\rightarrow (\lambda ,(x,R(x,w)))$, where $\lambda$ denotes the empty string. For a relation R, the functionality is denoted by $\mathcal{F}_\mathsf{zk}^R$. Note that any zero-knowledge proof of knowledge fulfills the $\mathcal{F}_\mathsf{zk}$ functionality [16, Sect. 6.5.3]; non-interactive versions can be achieved in the random-oracle model via the Fiat-Shamir paradigm [11]; see Functionality 2.2 for the formal definition.

The committed non-interactive zero knowledge functionality $\mathcal{F}_\mathsf{com\text {-}zk}$. In our protocol, we will have parties send commitments to non-interactive zero-knowledge proofs. We model this formally via a commit-zk functionality, denoted $\mathcal{F}_\mathsf{com\text {-}zk}$, defined in Functionality 2.3. Given non-interactive zero-knowledge proofs of knowledge, this functionality is securely realized by just having the prover commit to such a proof using the ideal commitment functionality $\mathcal{F}_\mathsf{com}$.

Paillier encryption. Denote the public/private key pair by (pk, sk), and denote encryption and decryption under these keys by $\mathsf{Enc}_{pk}(\cdot )$ and $\mathsf{Dec}_{sk}(\cdot )$, respectively. We denote by $c_1 \oplus c_2$ the “addition” of the plaintexts in $c_1,c_2$, and by $a \odot c$ the multiplication of the plaintext in c by scalar a.

Security, the hybrid model and composition. We prove the security of our protocol under a game-based definition with standard assumptions (in Sect. 4), and under the simulation-based ideal/real model definition with a non-standard ad-hoc assumption (in Sect. 5). In all cases, we prove our protocols secure in a hybrid model with ideal functionalities that securely compute $\mathcal{F}_\mathsf{com},\mathcal{F}_\mathsf{zk},\mathcal{F}_\mathsf{com\text {-}zk}$. The soundness of working in this model is justified in [5] (for stand-alone security) and in [6] (for security under composition). Specifically, as long as subprotocols that securely compute the functionalities are used (under the definition of [5] or [6], respectively), it is guaranteed that the output of the honest and corrupted parties when using real subprotocols is computationally indistinguishable to when calling a trusted party that computes the ideal functionalities.

3 Two-Party ECDSA

In this section, we present our protocol for distributed ECDSA signing. We separately describe the key generation phase (which is run once) and the signing phase (which is run multiple times).

Our protocol is presented in the $\mathcal{F}_\mathsf{zk}$ and $\mathcal{F}_\mathsf{com\text {-}zk}$ hybrid model. We use the zero-knowledge functionalities $\mathcal{F}_\mathsf{zk}^{R_P}$, $\mathcal{F}_\mathsf{zk}^{R_{D_L}}$ and $\mathcal{F}_\mathsf{zk}^{R_{PDL}}$ based on the following three different relations:

• 1. Proof that a Paillier public-key was generated correctly: define the relation

  $${R_{P}}=\{(N,(p_1,p_2)) \mid N=p_1\cdot p_2 \mathrm{~and~} p_1,p_2 \mathrm{~are~prime}\}$$

  of valid Paillier public keys. We use the protocol described in Sect. 3.3 in the full version of [17]. The cost of this protocol is 3t Paillier exponentiations by each of the prover and verifier for statistical error $2^{-t}$, as well as 3t GCD computations by the prover.

• 2. Proof of knowledge of the discrete log of an Elliptic-curve point: define the relation

  $${R_{DL}}=\{({\mathbb {G}},G,q,P,w) \mid P = w\cdot G\}$$

  of discrete log values (relative to the given group). We use the standard Schnorr proof for this [22].

• 3. Proof of encryption of a discrete log in a Paillier ciphertext: define

  

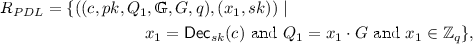
  where pk is a given Paillier public key and sk is its associated private key. (We will actually prove a slightly relaxed variant which is that completeness holds for $x_1\in {\mathbb {Z}}_{q/3}$. This suffices for our needs.)

A novel contribution of our result is a highly efficient proof for relation $R_{PDL}$; this is of interest since it bridges between two completely different worlds (Paillier encryption and Elliptic curve groups). This proof appears in Sect. 6.

For the sake of clarity of notation, we omit the group description $({\mathbb {G}},G,q)$ within calls to the $\mathcal{F}_\mathsf{zk}$ functionalities, since this is implicit. In addition, throughout, we assume that all values (Elliptic curve points) received are not equal to 0, and if zero is received then the party receiving the value aborts immediately.

3.1 Distributed Key Generation

The idea behind the distributed key generation protocol is as follows. The parties run a type of “simulatable coin tossing” in order to generate a random group element Q. This coin tossing protocol works by $P_1$ choosing a random $x_1$ and computing $Q_1=x_1\cdot G$, and then committing to $Q_1$ along with a zero-knowledge proof of knowledge of $x_1$, the discrete log of $Q_1$ (for technical reasons that will become apparent in Sect. 6, $P_1$ actually chooses $x\in {\mathbb {Z}}_{q/3}$, but this makes no difference). Then, $P_2$ chooses a random $x_2$ and sends $Q_2 = x_2\cdot G$ along with a zero-knowledge proof of knowledge to $P_1$. Finally, $P_1$ decommits and $P_2$ verifies the proof. The output is the point $Q=x_1\cdot Q_2 = x_2 \cdot Q_1$. This is fully simulatable due to the extractability and equivocality of the proof and commitment. In particular, assume that $P_1$ is corrupted. Then, a simulator receiving Q from the trusted party can cause the output of the coin-toss to equal Q. This is because it receives $Q_1,x_1$ from $P_1$ (who sends these values to the proof functionality) and can define the value sent by $P_2$ to be $Q_2 = (x_1)^{-1}\cdot Q$. Noting that $x_1 \cdot Q_2 = Q$, we have the desired property. Likewise, if $P_2$ is corrupted, then the simulator can commit to anything and then after seeing $(Q_2,x_2)$ as sent to the proof functionality, it can define $Q_1 = (x_2)^{-1}\cdot Q$. The fact that the $P_1$ is supposed to already be committed is solved by using an equivocal commitment scheme (modeled here via the $\mathcal{F}_\mathsf{com\text {-}zk}$ ideal functionality). Beyond generating Q, the protocol concludes with $P_2$ holding a Paillier encryption of $x_1$, where $Q_1=x_1\cdot G$. As described, this is used to obtain higher efficiency in the signing protocol, and is guaranteed via a zero-knowledge proof. See Protocol 3.1 for a full description.

3.2 Distributed Signing

The idea behind the signing protocol is as follows. First, the parties run a similar “coin tossing protocol” as in the key generation phase in order to obtain a random point R that will be used in generating the signature; after this, the parties $P_1$ and $P_2$ hold $k_1$ and $k_2$, respectively, where $R=k_1\cdot k_2 \cdot G$. Then, since $P_2$ already holds a Paillier encryption of $x_1$ (under a key known only to $P_1$), it is possible for $P_1$ to singlehandedly compute r from $R=(r_x,r_y)$ and an encryption of $s'=(k_2)^{-1}\cdot m' + (k_2)^{-1}\cdot r \cdot x_2 \cdot x_1$; this can be carried out by $P_2$ since it knows all the values involved directly except for $x_1$ which is encrypted under Paillier. Observe that this is “almost” a valid signature since in a valid signature $s=k^{-1}\cdot m' + k^{-1} \cdot r \cdot x$ (and here $x=x_1\cdot x_2$). Indeed, $P_2$ can send the encryption of this value to $P_1$, who can then decrypt and just multiply by $(k_1)^{-1}$. Since $k=k_1\cdot k_2$ we have that the result is a valid ECDSA signature. The only problem with this method is that the encryption of $(k_2)^{-1}\cdot m' + (k_2)^{-1}\cdot r \cdot x_2 \cdot x_1$ may reveal information to $P_1$ since no reduction modulo q is carried out on the values (because Paillier works over a different modulus). In order to prevent this, we have $P_2$ add $\rho \cdot q$ to the value inside the encryption, where $\rho$ is random and “large enough”; in the proof, we show that if $\rho \leftarrow {\mathbb {Z}}_{q^2}$, then this value is statistically close to $k_1 \cdot s$, where s is the final signature. Thus, $P_1$ can learn nothing more than the result (and in fact its view can be simulated). Note that since $s=k_1^{-1}\cdot s'$, it holds that $s'=k_1\cdot s$ and so $s'$ reveals no more information to $P_1$ than the signature s itself (this is due to the fact that $P_1$ can compute $s'$ from the signature s and from its share $k_1$).

The only problem that remains is that $P_2$ may send an incorrect $s'$ value to $P_1$. However, since we are dealing specifically with digital signatures, $P_1$ can verify that the result is correct before outputting it. Thus, a corrupt $P_2$ cannot cause $P_1$ to output incorrect values. However, it is conceivable that $P_2$ may be able to learn something from the fact that $P_1$ output a value or aborted. Consider, hypothetically, that $P_2$ could generate an encryption of a value $s'$ so that $(k_1)^{-1}\cdot s'$ is a valid signature if $LSB(x_1)=0$ and $(k_1)^{-1}\cdot s'$ is not a valid signature if $LSB(x_1)=1$. In such a case, the mere fact that $P_1$ aborts or not can leak a single bit about $P_1$’s private share of the key. In the proof(s) of security below, we show how we deal with this issue. See the formal definition of the signing phase in Protocol 3.2 (and a graphical representation in Fig. 1).

Offline/Online. Observe that the message to be signed is only used in $P_2$’s second message and by $P_1$ to verify that the signature is valid. Thus, it is possible to run the first three steps in an offline phase. Then, when m is received, all that is required to generate a signature is for $P_2$ to send a single message to $P_1$.

Output to both parties. Observe that since the validity of the signature can be checked by $P_2$, it is possible for $P_1$ to send $P_2$ the signature if it verifies it and it’s valid. This will not affect security at all.

Fig. 1.

The 2-Party ECDSA signing protocol

Correctness. Denoting $k=k_1\cdot k_2$ and $x=x_1\cdot x_2$, we have that $c_3$ is an encryption of $s'= \rho \cdot q + (k_2)^{-1} \cdot m' + (k_2)^{-1} \cdot r \cdot x_2 \cdot x_1 = \rho \cdot q + (k_2)^{-1} \cdot (m' + r \cdot x)$ (assuming that all is done correctly). Thus, $s = (k_1)^{-1} \cdot s' = k^{-1} \cdot (m'+rx) \bmod q$.

3.3 Efficiency and Experimental Results

We now analyze the theoretical complexity of our protocol, and describe its concrete running time based on our implementation.

Theoretical complexity – key-distribution protocol. Leaving aside the ZK proofs for now, $P_1$ carries out 2 Elliptic curve multiplications, 1 Paillier public-key generation and 1 Paillier encryption, and $P_2$ carries out two Elliptic curve multiplications. In addition, the parties run two discrete log proofs (each playing as prover once and as verifier once), and $P_1$ proves that N is a valid Paillier public key and runs the PDL proof described in Sect. 3.1. The cost of these proofs is as follows:

• Discrete log: the standard Schnorr zero-knowledge proof of knowledge for discrete log requires a single multiplication by the prover and two by the verifier.

• Paillier public-key validity [17]: For a statistical error of $2^{-40}$ this costs 120 Paillier exponentiations by each of the prover and the verifier (but 40 of these are “short”). In addition, the prover $P_1$ carries out 120 GCD computations.

• PDL proof (Sect. 6 ): This proof in Protocol 6.1 also involves running two executions of a range proof, and one execution of the zero-knowledge proof of Sect. 6.2. The cost is computed as follows:

  • The instructions within Protocol 6.1 for the prover $P_1$ cost 1 Paillier encryption, 1 Paillier (40-bit) scalar multiplication and 1 Elliptic curve multiplication. The cost for the verifier $P_2$ is 1 Paillier (40-bit) scalar multiplication and 2 Elliptic curve multiplications.

  • As described in the beginning of Sect. 6, each range proof is dominated by 2t Paillier encryptions for a statistical soundness error of $2^{-t}$. Setting $t=40$, we have 80 Paillier encryptions each.

  • The instructions within Sect. 6.2 require the prover $P_1$ to carry out 40 Paillier encryptions, and 40 Paillier exponentiations. The verifier $P_2$ computes on average 20 Paillier encryptions and 80 Paillier exponentiations.

Theoretical complexity – signing protocol. We now count the complexity of the signing protocol. We count the number of Elliptic curve multiplications and Paillier operations since this dominates the computation. As above, the zero-knowledge proof of knowledge for discrete log requires a single multiplication by the prover and two by the verifier, and ECDSA signature verification requires two multiplications. Thus, $P_1$ computes 7 Elliptic curve multiplications and a single Paillier decryption. In contrast, $P_2$ computes 5 Elliptic curve multiplications, 1 Paillier encryptions, 1 Paillier homomorphic scalar multiplication (which is a single “short” exponentiation) and one Paillier homomorphic addition (which is a single multiplication). Observe that unlike previous work, the length of the Paillier key need only be 5 times the length of the order of the Elliptic curve group (and not 8 times). Regarding rounds of communication, the protocol has only four rounds of communication (two in each direction). Thus, the protocol is very fast even on a slow network.

Implementation and running times. We implemented our protocol in C++ and ran it on Azure between two Standard_DS3_v2 instances. Although these instances have 4 cores each, we utilized a single core only with a single-thread implementation (note that key generation can be easily parallelized, if desired).

We ran our implementation on the standard NIST curves P-256, P-384 and P-521; the times for key generation and signing appear in Tables 1 and 2.

Table 1. Running times for key generation (average over 20 executions)

Table 2. Running times for signing (average over 1,000 executions)

We remark that the size of the Paillier key has a great influence on the running time. We know this since in our initial manuscripts, our analysis required $N>q^5$ (instead of $N>2q^4+q^3$). This seemingly small difference meant that for P-521, the Paillier key needed to be of size 2560 (instead of 2086). For this mildly larger key, the running time was 110ms for signing and 15,776ms for key generation. This is explained by the fact that Paillier operations have cubic cost, and thus the cost doubles when the key size increases by just 25%.

4 Proof of Security – Game-Based Definition

4.1 Definition of Security

We begin by presenting a game-based definition for the security of a digital signature scheme $\pi =(\mathsf{Gen},\mathsf{Sign},\mathsf{Verify})$. This will be used when proving the security of our protocol and thus is presented for the sake of completeness and a concrete reference.

Definition 4.2

A signature scheme $\pi$ is existentially unforgeable under chosen-message attacks if for every probabilistic polynomial-time oracle machine $\mathcal{A}$ there exists a negligible function $\mu$ such that for every n,

$$\mathrm{Pr}[\mathsf{Expt}\text {-}\mathsf{Sign}_{\mathcal{A},\pi }(1^n)=1]\le \mu (n).$$

We now proceed to define security for a distributed signing protocol. In the experiment $\mathsf{Expt}\text {-}\mathsf{DistSign}_{\mathcal{A},\varPi }^b$, we consider $\mathcal{A}$ controlling party $P_b$ in protocol $\varPi$ for two-party signature generation. Let $\varPi _b(\cdot ,\cdot )$ be a stateful oracle that runs the instructions of honest party $P_{3-b}$ in protocol $\varPi$. The adversary $\mathcal{A}$ can choose which messages will be signed, and can interact with multiple instances of party $P_{3-b}$ to concurrently generate signatures. Note that the oracle is defined so that distributed key generation is first run once, and then multiple signing protocols can be executed concurrently.

Formally, $\mathcal{A}$ receives access to an oracle that receives two inputs: the first input is a session identifier and the second is either an input or a next incoming message. The oracle works as follows:

• Upon receiving a query of the form (0, 0) for the first time, the oracle initializes a machine M running the instructions of party $P_{3-b}$ in the distributed key generation part of protocol $\varPi$. If party $P_{3-b}$ sends the first message in the key generation protocol, then this message is the oracle reply.

• Upon receiving a query of the form (0, m), if the key generation phase has not been completed, then the oracle hands the machine M the message m as its next incoming message and returns M’s reply. (If the key generation phase has completed, then the oracle returns $\bot$.)

• If a query of the form (sid, m) is received where $sid\ne 0$, but the key generation phase with M has not completed, then the oracle returns $\bot$.

• If a query (sid, m) is received and the key generation phase has completed and this is the first oracle query with this identifier sid, then the oracle invokes a new machine $M_{sid}$ running the instructions of party $P_{3-b}$ in protocol $\varPi$ with session identifier sid and input message m to be signed. The machine $M_{sid}$ is initialized with the key share and any state stored by M at the end of the key generation phase. If party $P_{3-b}$ sends the first message in the signing protocol, then this message is the oracle reply.

• If a query (sid, m) is received and the key generation phase has completed and this is not the first oracle query with this identifier sid, then the oracle hands $M_{sid}$ the incoming message m and returns the next message sent by $M_{sid}$. If $M_{sid}$ concludes, then the output obtained by $M_{sid}$ is returned.

The experiment for defining security is formalized by simply providing $\mathcal{A}$ who controls party $P_b$ with oracle access to $\varPi _b$. Adversary $\mathcal{A}$ “wins” if it can forge a signature on a message not queried in the oracle queries. Observe that $\mathcal{A}$ can run multiple executions of the signing protocol concurrently. We remark that we have considered only a single signing key; the extension to multiple different signing keys is straightforward and we therefore omit it. (This is due to the fact since signing keys are independent, one case easily simulate all executions with other keys.)

Definition 4.4

A protocol $\varPi$ is a secure two-party protocol for distributed signature generation for $\pi$ if for every probabilistic polynomial-time oracle machine $\mathcal{A}$ and every $b\in \{1,2\}$, there exists a negligible function $\mu$ such that for every n, $\mathrm{Pr}[\mathsf{Expt}\text {-}\mathsf{DistSign}^b_{\mathcal{A},\varPi }(1^n)=1]\le \mu (n)$.

4.2 Proof of Security

In this section, we prove that $\varPi$ comprised of Protocols 3.1 and 3.2 for key generation and signing, respectively, constitutes a secure two-party protocol for distributed signature generation of ECDSA.

Theorem 4.5

Assume that the Paillier encryption scheme is indistinguishable under chosen-plaintext attacks, and that ECDSA is existentially-unforgeable under a chosen message attack. Then, Protocols 3.1 and 3.2 constitute a secure two-party protocol for distributed signature generation of ECDSA.

Proof

We prove the security of the protocol in the $\mathcal{F}_\mathsf{com\text {-}zk},\mathcal{F}_\mathsf{zk}$ hybrid model. Note that if the commitment and zero-knowledge protocols are UC-secure, then this means that the output in the hybrid and real protocols is computationally indistinguishable. In particular, if $\mathcal{A}$ can break the protocol with some probability $\epsilon$ in the hybrid model, then it can break the protocol with probability $\epsilon \pm \mu (n)$ for some negligible function $\mu$. Thus, this suffices.

We separately prove security for the case of a corrupted $P_1$ and a corrupted $P_2$. Our proof works by showing that, for any adversary $\mathcal{A}$ attacking the protocol, we construct an adversary $\mathcal{S}$ who forges an ECDSA signature in Experiment 4.1 with probability that is negligibly close to the probability that $\mathcal{A}$ forges a signature in Experiment 4.3. Formally, we prove that if Paillier has indistinguishable encryptions under chosen-plaintext attacks, then for every PPT algorithm $\mathcal{A}$ and every $b\in \{1,2\}$ there exists a PPT algorithm $\mathcal{S}$ and a negligible function $\mu$ such that for every n,

$$\begin{aligned} \left| \mathrm{Pr}[\mathsf{Expt}\text {-}\mathsf{Sign}_{\mathcal{S},\pi }(1^n)=1]-\mathrm{Pr}[\mathsf{Expt}\text {-}\mathsf{DistSign}^b_{\mathcal{A},\varPi }(1^n)=1]\right| \le \mu (n), \end{aligned}$$

(1)

where $\varPi$ denotes Protocols 3.1 and 3.2, and $\pi$ denotes the ECDSA signature scheme. Proving Eq. (1) suffices, since by the assumption in the theorem that ECDSA is secure, we have that there exists a negligible function $\mu '$ such that for every n, $\mathrm{Pr}[\mathsf{Expt}\text {-}\mathsf{Sign}_{\mathcal{S},\pi }(1^n)=1]\le \mu '(n)$. Combining this with Eq. (1), we conclude that $\mathrm{Pr}[\mathsf{Expt}\text {-}\mathsf{DistSign}^b_{\mathcal{A},\varPi }(1^n)=1]\le \mu (n)+\mu '(n)$ and thus $\varPi$ is secure by Definition 4.4. We prove Eq. (1) separately for $b=1$ and $b=2$.

Proof of Eq. (1) for $b=1$ – corrupted $P_1$ : Let $\mathcal{A}$ be a probabilistic polynomial-time adversary in $\mathsf{Expt}\text {-}\mathsf{DistSign}^1_{\mathcal{A},\varPi }(n)$; we construct a probabilistic polynomial-time adversary $\mathcal{S}$ for $\mathsf{Expt}\text {-}\mathsf{Sign}_{\mathcal{S},\pi }(n)$. The adversary $\mathcal{S}$ essentially simulates the execution for $\mathcal{A}$, as described in the intuition behind the security of the protocol. Formally:

• 1. In $\mathsf{Expt}\text {-}\mathsf{Sign}$, adversary $\mathcal{S}$ receives $(1^n,Q)$, where Q is the public verification key for ECDSA.

• 2. $\mathcal{S}$ invokes $\mathcal{A}$ on input $1^n$ and simulates oracle $\varPi$ for $\mathcal{A}$ in $\mathsf{Expt}\text {-}\mathsf{DistSign}$m, answering as described in the following steps:

  • (a) $\mathcal{S}$ replies $\bot$ to all queries $(sid,\cdot )$ to $\varPi$ by $\mathcal{A}$ before the key-generation subprotocol is concluded. $\mathcal{S}$ replies $\bot$ to all queries from $\mathcal{A}$ before it queries (0, 0).

  • (b) After $\mathcal{A}$ sends (0, 0) to $\varPi$, adversary $\mathcal{S}$ receives $(0,m_1)$ which is $P_1$’s first message in the key generation subprotocol (any other query is ignored). $\mathcal{S}$ computes the oracle reply as follows:

    • i. $\mathcal{S}$ parses $m_1$ into the form $(\mathsf{com\text {-}prove},1,Q_1,x_1)$ that $P_1$ sends to $\mathcal{F}_\mathsf{com\text {-}zk}^{R_{DL}}$ in the hybrid model.

    • ii. $\mathcal{S}$ verifies that $Q_1 = x_1\cdot G$. If yes, then it computes $Q_2 = (x_1)^{-1}\cdot Q$ (using the value Q received as the verification key in experiment $\mathsf{Expt}\text {-}\mathsf{Sign}$ and the value $x_1$ from $\mathcal{A}$’s prove message); if no, then $\mathcal{S}$ just chooses a random $Q_2$.

    • iii. $\mathcal{S}$ sets the oracle reply of $\varPi$ to be $(\mathsf{proof},2,Q_2)$ and internally hands this to $\mathcal{A}$ (as if sent by $\mathcal{F}_\mathsf{zk}^{R_{DL}}$).

  • (c) The next message of the form $(0,m_2)$ received by $\mathcal{S}$ (any other query is ignored) is processed as follows:

    • i. $\mathcal{S}$ parses $m_2$ into the following three messages: (1) $(\mathsf{decom\text {-}proof},$ $sid\Vert 1)$ as $\mathcal{A}$ intends to send to $\mathcal{F}_\mathsf{com\text {-}zk}^{R_{DL}}$; (2) $(\mathsf{proof},1,N,(p_1,p_2))$ as $\mathcal{A}$ intends to send to $\mathcal{F}_\mathsf{zk}^{R_{P}}$; and (3) $(\mathsf{proof},1,(c_{key},pk,Q_1),(x_1,r))$ as $\mathcal{A}$ intends to send to $\mathcal{F}_\mathsf{zk}^{R_{PDL}}$.

    • ii. $\mathcal{S}$ verifies that $pk=N=p_1 \cdot p_2$ and that the length of $pk=N$ is as specified, and generates the oracle response to be $P_2$ aborting if they are not correct.

    • iii. Likewise, $\mathcal{S}$ generates the oracle response to be $P_2$ aborting if $Q_1 \ne x_1\cdot G$ or $c_{key}\ne \mathsf{Enc}_{pk}(x_1;r)$ or $x_1\notin {\mathbb {Z}}_q$.

    • iv. If $\mathcal{S}$ simulates an abort, then the experiment concludes (since the honest $P_2$ no longer participates in the protocol and so all calls to $\varPi _b$ are ignored). $\mathcal{S}$ does not output anything in this case since no verification key vk is output by $P_2$ in this case.

      Otherwise, $\mathcal{S}$ stores $(x_1,Q,c_{key})$ and the distributed key generation phase is completed.

  • (d) Upon receiving a query of the form (sid, m) where sid is a new session identifier, $\mathcal{S}$ queries its signing oracle in experiment $\mathsf{Expt}\text {-}\mathsf{Sign}$ with m and receives back a signature (r, s). Using the ECDSA verification procedure, $\mathcal{S}$ computes the Elliptic curve point R. (Observe that the ECDSA verification works by constructing a point R and then verifying that this defines the same r as in the signature.) Then, queries received by $\mathcal{S}$ from $\mathcal{A}$ with identifier sid are processed as follows:

    • i. The first message $(sid,m_1)$ is processed by first parsing the message $m_1$ as $(\mathsf{com\text {-}prove},sid\Vert 1,R_1,k_1)$. If $R_1=k_1\cdot G$ then $\mathcal{S}$ sets $R_2 = (k_1)^{-1}\cdot R$; else it chooses $R_2$ at random. $\mathcal{S}$ sets the oracle reply to $\mathcal{A}$ to be the message $(\mathsf{proof},sid\Vert 2,R_2)$ that $\mathcal{A}$ expects to receive. (Note that the value $R_2$ is computed using R from the ECDSA signature and $k_1$ as sent by $\mathcal{A}$.)

    • ii. The second message $(sid,m_2)$ is processed by parsing the message $m_2$ as $(\mathsf{decom\text {-}proof},sid\Vert 1)$ from $\mathcal{A}$. If $R_1 \ne k_1\cdot G$ then $\mathcal{S}$ simulates $P_2$ aborting and the experiment concludes (since the honest $P_2$ no longer participates in any executions of the protocol and so all calls to $\varPi _b$ are ignored).

      Otherwise, $\mathcal{S}$ chooses a random $\rho \leftarrow {\mathbb {Z}}_{q^2}$, computes the ciphertext $c_3\leftarrow \mathsf{Enc}_{pk}([k_1 \cdot s \bmod q] + \rho \cdot q)$, where s is the value from the signature received from $\mathcal{F}_{\textsc {ecdsa}}$, and sets the oracle reply to $\mathcal{A}$ to be $c_3$.

• 3. Whenever $\mathcal{A}$ halts and outputs a pair $(m^*,\sigma ^*)$, adversary $\mathcal{S}$ outputs $(m^*,\sigma ^*)$ and halts.

We proceed to prove that Eq. (1) holds. First, observe that the public-key generated by $\mathcal{S}$ in the simulation with $\mathcal{A}$ equals the public-key Q that it received in experiment $\mathsf{Expt}\text {-}\mathsf{Sign}$. This is due to the fact that $\mathcal{S}$ defines $Q_2=(x_1)^{-1}\cdot Q$ when $\mathcal{A}$ is committed to $Q_1=x_1\cdot G$. Thus, the public key is defined to be $x_1\cdot Q_2 = x_1\cdot (x_1)^{-1}\cdot Q = Q$, as required. We now proceed to show that $\mathcal{A}$’s view in the simulation by $\mathcal{S}$ is identical to its view in a real execution of Protocols 3.1 and 3.2. (Note that the view is identical when taking $\mathcal{F}_\mathsf{zk}$ and $\mathcal{F}_\mathsf{com\text {-}zk}$ as ideal functionalities; the real protocol is computationally indistinguishable.) This suffices since it implies that $\mathcal{A}$ outputs a pair $(m^*,\sigma ^*)$ that is a valid signature with the same probability in the simulation and in $\mathsf{Expt}\text {-}\mathsf{DistSign}$ (otherwise, the views can be distinguished by just verifying if the output signature is correct relative to the public key). Since the public key in the simulation is the same public key that $\mathcal{S}$ receives in $\mathsf{Expt}\text {-}\mathsf{Sign}$, a valid forgery generated by $\mathcal{A}$ in $\mathsf{Expt}\text {-}\mathsf{DistSign}$ constitutes a valid forgery by $\mathcal{S}$ in $\mathsf{Expt}\text {-}\mathsf{Sign}$. Thus, Eq. (1) follows.

In order to see that the view of $\mathcal{A}$ in the simulation of the key generation phase is identical to its view in a real execution of Protocol 3.1 (as in $\mathsf{Expt}\text {-}\mathsf{DistSign}$), note that the only difference between the simulation by $\mathcal{A}$ and a real execution with an honest $P_2$ is the way that $Q_2$ is generated: $P_2$ chooses a random $x_2$ and computes $Q_2 \leftarrow x_2 \cdot G$, whereas $\mathcal{S}$ computes $Q_2 \leftarrow (x_1)^{-1} \cdot Q$, where Q is the public verification key received by $\mathcal{S}$ in $\mathsf{Expt}\text {-}\mathsf{Sign}$. We stress that in all other messages and checks, $\mathcal{S}$ behaves exactly as $P_2$ (note that the zero-knowledge proof of knowledge of the discrete log of $Q_2$ is simulated by $\mathcal{S}$, but in the $\mathcal{F}_\mathsf{zk},\mathcal{F}_\mathsf{com\text {-}zk}$-hybrid model this is identical). Now, since Q is chosen randomly, it follows that the distributions over $x_2\cdot G$ and $(x_1)^{-1} \cdot Q$ are identical. Observe finally that if $P_2$ does not abort then the public-key defined in both a real execution and the simulation by $\mathcal{S}$ equals $x_1 \cdot Q_2 = Q$. Thus, the view of $\mathcal{A}$ is identical and the output public key is Q.

In order to see that the view of $\mathcal{A}$ in the simulation of the signing phase is computationally indistinguishable to its view in a real execution of Protocol 3.2 (as in $\mathsf{Expt}\text {-}\mathsf{DistSign}$), note that the only difference between the view of $\mathcal{A}$ in a real execution and in the simulation is the way that $c_3$ is chosen. Specifically, $R_2$ is distributed identically in both cases due to the fact that R is randomly generated by $\mathcal{F}_{\textsc {ecdsa}}$ in the signature generation and thus $(k_1)^{-1} \cdot R$ has the same distribution as $k_2 \cdot G$ (this is exactly the same as in the key generation phase with Q). The zero-knowledge proofs and verifications are also identically distributed in the $\mathcal{F}_\mathsf{zk},\mathcal{F}_\mathsf{com\text {-}zk}$-hybrid model. Thus, the only difference is $c_3$: in the simulation it is an encryption of $[k_1 \cdot s \bmod q] + \rho \cdot q$, whereas in a real execution it is an encryption of $s'=(k_2)^{-1}\cdot (m' + r x) + \rho \cdot q$, where $\rho \in {\mathbb {Z}}_{q^2}$ is random (we stress that all additions here are over the integers and not $\bmod \ q$, except for where it is explicitly stated in the protocol description).

We therefore prove that $\mathcal{A}$’s view is indistinguishable by showing that despite this difference, the values are actually statistically close. In order to see this, first observe that by the definition of ECDSA signing, $s=k^{-1}\cdot (m'+rx)=(k_1)^{-1}\cdot (k_2)^{-1}\cdot (m+rx) \bmod q$. Thus, $(k_2)^{-1}\cdot (m'+r x) = k_1 \cdot s \bmod q$, implying that there exists some $\ell \in {\mathbb {N}}$ with $0\le \ell <q$ such that $(k_2)^{-1}\cdot (m'+r x) = k_1 \cdot s + \ell \cdot q$. The reason that $\ell$ is bound between 0 and q is that in the protocol the only operations without a modular reduction are the multiplication of $[(k_2)^{-1}\cdot r\cdot x_2 \bmod q]$ by $x_1$, and the addition of $[(k_2)^{-1}\cdot m'\bmod q]$. This cannot increase the result by more than $q^2$. Therefore, the difference between the real execution and simulation with $\mathcal{S}$ is:

• 1. Real: the ciphertext $c_3$ encrypts $[k_1 \cdot s \bmod q] + \ell \cdot q + \rho \cdot q$

• 2. Simulated: the ciphertext $c_3$ encrypts $[k_1 \cdot s \bmod q] + \rho \cdot q$

We show that for all $k_1,s,\ell$ with $k_1,s,\ell \in {\mathbb {Z}}_q$, the above values are statistically close (for a random choice of $\rho \in {\mathbb {Z}}_{q^2}$). In order to see this, fix $k_1,s,\ell$, and let v be a value. If $v \ne [k_1 \cdot s \bmod q] + \zeta \cdot q$ for some $\zeta$, then neither the real or simulated values can equal v. Else, if $v = [k_1 \cdot s \bmod q] + \zeta \cdot q$ for some $\zeta$, then there are three cases:

• 1. Case $\zeta < \ell$ : in this case, v can be obtained in the simulated execution for $\rho <\ell$, but can never be obtained in a real execution.

• 2. Case $\zeta > q^2-1)$ : in this case, v can be obtained in the real execution for $\rho \ge q^2-1-\ell$, but can never be obtained in a simulated execution.

• 3. Case $\ell \le \zeta < q^2-1$ : in this case, v can be obtained in both the real and simulated executions, with identical probability (observe that in both the real and simulated executions, $\rho$ is chosen uniformly in ${\mathbb {Z}}_{q^2}$).

Recall that the statistical distance between two distributions X and Y over a domain $\mathcal{D}$ is defined to be:

$$\begin{aligned} \varDelta (X,Y)=\max _{T\subseteq D}\Big |\mathrm{Pr}[X\in T]-\mathrm{Pr}[Y\in T]\Big | \end{aligned}$$

Let X be the values generated in a real execution of the protocol and let Y be the values generated in the simulation with $\mathcal{S}$. Then, taking T to be set of values v for which $\zeta <\ell$, we have that $\mathrm{Pr}[X\in T]=0$ whereas $\mathrm{Pr}[Y\in T]\le \frac{q}{q^2}=\frac{1}{q}$ (this holds since $0\le \ell <q$ and $\rho \in {\mathbb {Z}}_{q^2}$). Thus, $\varDelta (X,Y)=\frac{1}{q}$, which is negligible. (Taking T to be the set of values v for which $\zeta >q^2-1$ would give the same result and are both the maximum since any other values add no difference.) We therefore conclude that the distributions over $c_3$ in the real and simulated executions are statistically close. This proves that Eq. (1) holds for the case that $b=1$.

Proof of Eq. (1) for $b=2$ – corrupted $P_2$ : We follow the same strategy as for the case that $P_1$ is corrupted, which is to construct a simulator $\mathcal{S}$ that simulates the view of $\mathcal{A}$ while interacting in experiment $\mathsf{Expt}\text {-}\mathsf{Sign}$. This simulation is easy to construct and similar to the case that $P_1$ is corrupted, with one difference. Recall that the last message from $P_2$ to $P_1$ is an encryption $c_3$. This ciphertext may be maliciously constructed by $\mathcal{A}$, and the simulator cannot detect this. (Formally, there is no problem for $\mathcal{S}$ to decrypt, since as will be apparent below, it generates the Paillier public key. However, this strategy will fail since in order to prove computational indistinguishability it is necessary to carry out a reduction to the security of Paillier, meaning that the simulation must be designed to work without knowing the corresponding private key.) We solve this problem by simply having $\mathcal{S}$ simulate $P_1$ aborting at some random point. That is, $\mathcal{S}$ chooses a random $i\in \{1,\ldots ,p(n)+1\}$ where p(n) is an upper bound on the number of queries made by $\mathcal{A}$ to $\varPi$. If $\mathcal{S}$ chose correctly, then the simulation is fine. Now, since $\mathcal{S}$’s choice of i is correct with probability $\frac{1}{p(n)+1}$, this means that $\mathcal{S}$ simulates $\mathcal{A}$’s view with probability $\frac{1}{p(n)+1}$ (note that $\mathcal{S}$ can also choose $i=p(n)+1$, which is correct if $c_3$ is always constructed correctly). Thus, $\mathcal{S}$ can forge a signature in $\mathsf{Expt}\text {-}\mathsf{Sign}$ with probability at least $\frac{1}{p(n)+1}$ times the probability that $\mathcal{A}$ forges a signature in $\mathsf{Expt}\text {-}\mathsf{DistSign}$.

Let $\mathcal{A}$ be a probabilistic polynomial-time adversary; $\mathcal{S}$ proceeds as follows:

• 1. In $\mathsf{Expt}\text {-}\mathsf{Sign}$, adversary $\mathcal{S}$ receives $(1^n,Q)$, where Q is the public verification key for ECDSA.

• 2. Let $p(\cdot )$ denote an upper bound on the number of queries that $\mathcal{A}$ makes to $\varPi$ in experiment $\mathsf{Expt}\text {-}\mathsf{DistSign}$. Then, $\mathcal{S}$ chooses a random $i\in \{1,\ldots ,p(n)+1\}$.

• 3. $\mathcal{S}$ invokes $\mathcal{A}$ on input $1^n$ and simulates oracle $\varPi$ for $\mathcal{A}$ in $\mathsf{Expt}\text {-}\mathsf{DistSign}$, answering as described in the following steps:

  • (a) $\mathcal{S}$ replies $\bot$ to all queries $(sid,\cdot )$ to $\varPi$ by $\mathcal{A}$ before the key-generation subprotocol is concluded. $\mathcal{S}$ replies $\bot$ to all queries from $\mathcal{A}$ before it queries (0, 0).

  • (b) After $\mathcal{A}$ sends (0, 0) to $\varPi$, adversary $\mathcal{S}$ computes the oracle reply to be $(\mathsf{proof\text {-}receipt},1)$ as $\mathcal{A}$ expects to receive.

  • (c) The next message of the form $(0,m_1)$ received by $\mathcal{S}$ (any other query is ignored) is processed as follows:

    • i. $\mathcal{S}$ parses $m_1$ into the form $(\mathsf{prove},2,Q_2,x_2)$ that $P_2$ sends to $\mathcal{F}_\mathsf{com\text {-}zk}^{R_{DL}}$ in the hybrid model.

    • ii. $\mathcal{S}$ verifies that $Q_2$ is a non-zero point on the curve and that $Q_2=x_2\cdot G$; if not, it simulates $P_1$ aborting, and halts (there is no point outputting anything since no verification key is output by $P_1$ in this case and so the output of $\mathsf{Expt}\text {-}\mathsf{DistSign}$ is always 0).

    • iii. $\mathcal{S}$ generates a valid Paillier key-pair (pk, sk), computes $c_{key}=\mathsf{Enc}_{pk}(\tilde{x}_1)$ for a random $\tilde{x}_1\in {\mathbb {Z}}_{q/3}$.

    • iv. $\mathcal{S}$ sets the oracle response to $\mathcal{A}$ to be the messages $(\mathsf{decom\text {-}proof},1,Q_1)$, $(\mathsf{proof},1,N)$ and $(\mathsf{proof},1,(c_{key},N,Q_1))$, where $Q_1 = (x_2)^{-1}\cdot Q$ with Q as received by $\mathcal{S}$ initially.

    $\mathcal{S}$ stores $(x_2,Q,c_{key})$ and the key distribution phase is completed.

  • (d) Upon receiving a query of the form (sid, m) where sid is a new session identifier, $\mathcal{S}$ computes the oracle reply to be $(\mathsf{proof\text {-}receipt},sid\Vert 1)$ as $\mathcal{A}$ expects to receive, and hands it to $\mathcal{A}$.

    Next, $\mathcal{S}$ queries its signing oracle in experiment $\mathsf{Expt}\text {-}\mathsf{Sign}$ with m and receives back a signature (r, s). Using the ECDSA verification procedure, $\mathcal{S}$ computes the Elliptic curve point R. Then, queries received by $\mathcal{S}$ from $\mathcal{A}$ with identifier sid are processed as follows:

    • i. The first message $(sid,m_1)$ is processed by first parsing the message $m_1$ as $(\mathsf{prove},sid\Vert 2,R_2,k_2)$ that $\mathcal{A}$ sends to $\mathcal{F}_\mathsf{zk}^{R_{DL}}$. $\mathcal{S}$ verifies that $R_2 = k_2 \cdot G$ and that $R_2$ is a non-zero point on the curve; otherwise, it simulates $P_1$ aborting. $\mathcal{S}$ computes $R_1 = (k_2)^{-1} \cdot R$ and sets the oracle reply to be $(\mathsf{decom\text {-}proof},sid\Vert ,R_1)$ as if coming from $\mathcal{F}_\mathsf{com\text {-}zk}^{R_{DL}}$.

    • ii. The second message $(sid,m_2)$ is processed by parsing $m_2$ as $c_3$. If this is the ith call by $\mathcal{A}$ to the oracle $\varPi$, then $\mathcal{S}$ simulates $P_1$ aborting (and not answering any further oracle calls). Otherwise, it continues.

• 4. Whenever $\mathcal{A}$ halts and outputs a pair $(m^*,\sigma ^*)$, adversary $\mathcal{S}$ outputs $(m^*,\sigma ^*)$ and halts.

As in the case that $P_1$ is corrupted, the public-key generated by $\mathcal{S}$ in the simulation with $\mathcal{A}$ equals the public-key Q that it received in experiment $\mathsf{Expt}\text {-}\mathsf{Sign}$. Now, let j be the first call to oracle $\varPi$ with $(sid,c_3)$ where $c_3$ is such that $P_1$ does not obtain a valid signature (r, s) with respect to Q. Then, we argue that if $j=i$, then the only difference between the distribution over $\mathcal{A}$’s view in a real execution and in the simulated execution by $\mathcal{S}$ is the ciphertext $c_{key}$. Specifically, in a real execution $c_{key}=\mathsf{Enc}_{pk}(x_1)$ where $Q_1=x_1\cdot G$, whereas in the simulation $c_{key}=\mathsf{Enc}_{pk}(\tilde{x}_1)$ for a random $\tilde{x}_1$ and is independent of $Q_1=x_1\cdot G$.² Observe, however, that $\mathcal{S}$ does not use the private-key for Paillier at all in the simulation. Thus, indistinguishability of this simulation follows from a straightforward reduction to the indistinguishability of the encryption scheme, under chosen-plaintext attacks.

This proves that

$$ \left| \mathrm{Pr}[\mathsf{Expt}\text {-}\mathsf{Sign}_{\mathcal{S},\pi }(1^n)=1 \mid i=j]-\mathrm{Pr}[\mathsf{Expt}\text {-}\mathsf{DistSign}^2_{\mathcal{A},\varPi }(1^n)=1]\right| \le \mu (n), $$

and so

$$\begin{aligned} \mathrm{Pr}[\mathsf{Expt}\text {-}\mathsf{DistSign}^2_{\mathcal{A},\varPi }(1^n)=1]\le & {} \frac{\mathrm{Pr}[\mathsf{Expt}\text {-}\mathsf{Sign}_{\mathcal{S},\pi }(1^n)=1 \wedge i=j]}{\mathrm{Pr}[i=j]} + \mu (n)\\\le & {} \frac{\mathrm{Pr}[\mathsf{Expt}\text {-}\mathsf{Sign}_{\mathcal{S},\pi }(1^n)=1]}{1/(p(n)+1)} + \mu (n) \end{aligned}$$

and so

$$ \mathrm{Pr}[\mathsf{Expt}\text {-}\mathsf{Sign}_{\mathcal{S},\pi }(1^n)=1] \ge \frac{\mathrm{Pr}[\mathsf{Expt}\text {-}\mathsf{DistSign}^2_{\mathcal{A},\varPi }(1^n)=1]}{p(n)+1} - \mu (n). $$

This implies that if $\mathcal{A}$ forges a signature in $\mathsf{Expt}\text {-}\mathsf{DistSign}^2_{\mathcal{A},\varPi }$ with non-negligible probability, then $\mathcal{S}$ forges a signature in $\mathsf{Expt}\text {-}\mathsf{Sign}_{\mathcal{S},\pi }$ with non-negligible probability, in contradiction to the assumed security of ECDSA.

5 Simulation Proof of Security (With a New Assumption)

There are advantages to full simulation based proofs of security (via the real/ideal paradigm). Observe that we proved the security of our protocol in Sect. 4 by simulating the view of $\mathcal{A}$ in a real execution. In fact, our simulation can be used to prove the security of our protocol under the real/ideal world paradigm except for exactly one place. Recall that when $P_2$ is corrupted, $\mathcal{S}$ cannot determine if $c_3$ is correctly constructed or not. Thus, $\mathcal{S}$ simply chooses a random point and “hopes” that the jth value $c_3$ generated is the first badly constructed $c_3$. This suffices for a game-based definition, but it does not suffice for simulation-based security definitions. Thus, in order to be able to prove our protocol using simulation, we need to be able to determine if $c_3$ was constructed correctly. Of course, we could add zero-knowledge proofs to the protocol, but these would be very expensive. Alternatively, we consider a rather ad-hoc but plausible assumption that suffices. The assumption is formalized in Appendix A, along with a full proof of security under this assumption.

6 Zero-Knowledge Proof for Relation $R_{PDL}$

6.1 The Main Zero-Knowledge Proof

In this section, we present an efficient construction of a zero-knowledge proof for the relation ${R_{PDL}}$, defined by:

$$ {R_{PDL}}= \{((c,pk,Q_1,{\mathbb {G}},G,q),(x_1,r)) \mid c=\mathsf{Enc}_{pk}(x_1;r) \mathrm{~and~} Q_1 = x_1\cdot G \mathrm{~and~} x_1\in {\mathbb {Z}}_q\}. $$

Intuitively, this relation means that c is a valid Paillier encryption of the discrete log of $Q_1$.

Our proof contains a new zero-knowledge protocol for proving that $c=\mathsf{Enc}_{pk}(x_1)$ and $Q_1 = x_1\cdot G$, while calling an existing zero-knowledge protocol for proving that $x_1\in {\mathbb {Z}}_q$. It is possible to prove that $x_1\in {\mathbb {Z}}_q$ by using the proof of non-negativity of [19] on the ciphertext $c'=c\ominus \mathsf{Enc}_{pk}(q)$. This works, but such proofs are quite expensive. In contrast, there exist much more simple and efficient proofs if $x_1\in {\mathbb {Z}}_{q/3}$ [4]. This suffices for our use since a random $x_1$ would be in this range anyway with probability 1 / 3, and so this cannot adversely affect the security. We therefore prove that $x_1\in {\mathbb {Z}}_{q/3}$ using the proof of [4]. Formally, this proof guarantees completeness when $x\in {\mathbb {Z}}_{q/3}$ and soundness for $x\in {\mathbb {Z}}_q$. This means that an honest prover will succeed in proving as long as $x\in {\mathbb {Z}}_{q/3}$ and a cheating prover will fail if $x\notin {\mathbb {Z}}_q$, except with negligible probability. We use the version of the proof as described in [2, Sect. 1.2.2]. With statistical soundness error of $2^{-t}$, the cost of this proof is dominated by computing 2t Paillier encryptions.

The idea behind the proof that $c=\mathsf{Enc}_{pk}(x_1)$ and $Q_1 = x_1\cdot G$ is as follows. The prover chooses a random r, and sends the verifier $r\cdot G$ along with a Paillier encryption $c_r$ of r. Then, for a random challenge e, the prover sends $z=r + e\cdot x_1$, and proves the $c_r \oplus (e\odot c)$ encrypts the value z. The verifier checks this proof and also checks that $z\cdot G=R+e\cdot Q_1$. Now, if $c\ne \mathsf{Enc}_{pk}(x_1)$ then the probability that z will fulfill both that $z\cdot G = R+e\cdot Q_1$ and $\mathsf{Enc}_{pk}(z) = c_r \oplus (e\odot c)$ is negligible, due to the random choice of e. Intuitively, this holds since the check that $c_r \oplus (e\odot c)$ encrypts z together with the check that $z\cdot G = R+e\cdot Q_1$ ensures that the same $x_1$ is used to compute $Q_1$ and is encrypted in c. This is shown formally in the proof.

We remark that the above is not enough since $z=r+e\cdot x_1$ may potentially reveal information about $x_1$ (note that there is no modular reduction carried out here and the computation is over the integers; this is necessary since there is no mod q inside Paillier). The prover therefore also adds to z the value $\rho \cdot q$ for a large-enough random $\rho$, and proves that $\mathsf{Enc}_{pk}(z) - c_r \oplus (e\odot c)$ is a multiple of q. Observe that the addition of $\rho \cdot q$ makes no difference to the check of $z\cdot G = R+e\cdot Q_1$ since this is all modulo q and so $\rho \cdot q$ disappears. The proof contains additional checks regarding the size of z and more; this is needed to ensure that values are in the appropriate range so that no modulo N operations happen inside Paillier.

Theorem 6.2

If Paillier encryption is indistinguishable under chosen-plaintext attacks and $N>2q^4+q^3$, then Protocol 6.1 is a zero-knowledge proof of knowledge of the relation $\mathcal{F}_\mathsf{zk}^{R_{PDL}}$ in the $\mathcal{F}_\mathsf{com}$-hybrid model with soundness error $2^{-t}$.

Proof

We prove completeness, soundness and zero knowledge, and that the proof is a proof of knowledge. Regarding completeness, it is easy to see that if both parties follow the protocol then $q^2< z < q^3+q^2$. In addition, $c_q$ is an encryption of $z - r - e \cdot x_1 = \rho \cdot q$ and thus V accepts the proof in the final step.

We now proceed to prove soundness. First, if $x_1\notin {\mathbb {Z}}_q$ then V rejects due to the range-ZK phase. It thus remains to prove that V rejects unless $c=\mathsf{Enc}_{pk}(x_1;r)$ and $Q_1 = x_1 \cdot G$. Let $c=\mathsf{Enc}_{pk}(x_1;r)$ and assume that $Q_1\ne x_1\cdot G$.

First, consider the subcase that P sends $(c_r,R)$ such that $c_r=\mathsf{Enc}_{pk}(r)$ and $R=r\cdot G$. It then follows that $c_q$ as computed by V is an encryption of $v=z - r - e \cdot x_1$. If v is not a multiple of q then V outputs 0 in the ciphertext-ZK phase.³ However, if v is a multiple of q then this implies that $z = r + e \cdot x_1 + \rho \cdot q$ for some integer $\rho$. Thus, $z'= r + e \cdot x_1 \bmod q$ and $z' \cdot G = r \cdot G + e \cdot x_1 \cdot G$. By the assumption that $R = r\cdot G$ we have that $z' \cdot G = R + e \cdot (x_1 \cdot G) \ne R + e \cdot Q_1$ since $Q_1 \ne x_1 \cdot G$. Thus, V outputs 0.

Next, consider the subcase that $c_r=\mathsf{Enc}_{pk}(r)$ but $R \ne r \cdot G$. As before, if v is not a multiple of q then V outputs 0 and so we have that $z=r+e\cdot x_1 + \rho \cdot q$ for some integer $\rho$. Now, V outputs 0 unless $z'\cdot G = R + e \cdot Q_1$. Thus, V outputs 0 unless $(r+e\cdot x_1)\cdot G = R + e \cdot Q_1$, which holds if and only if $r\cdot G + e \cdot (x_1 \cdot G) = R + e \cdot Q_1$ which in turn holds if and only if $r \cdot G - R = e \cdot (Q_1 - x_1 \cdot G)$. By the assumption, $R\ne r\cdot G$ and $Q_1 \ne x_1 \cdot G$. Thus, both $r \cdot G - R$ and $Q_1 - x_1 \cdot G$ are non-zero points on the curve. Since the curve is of prime order, $Q_1-x_1 \cdot G$ is a generator of the group and thus there exists a single w such that $w \cdot (Q_1 - x_1 \cdot G) = r\cdot G-R$. However, $e\in {\mathbb {Z}}_{2^t}$ is chosen uniformly at random and so the probability that equality holds is at most $2^{-t}$, as required.

The fact that the proof is a proof of knowledge follows from the proof of knowledge in the range-ZK phase. In particular, it is possible to extract the value $x_1$ from the proof that c is an encryption of a value in ${\mathbb {Z}}_q$. This suffices since the fact that the extracted $x_1$ fulfills the conditions of the relation follows from the proof of soundness above.

Finally, we prove that the protocol is zero knowledge by constructing a simulator $\mathcal{S}$. Intuitively, $\mathcal{S}$ can work since it can know the value of e before sending R to $V^*$ (by extracting e from $\mathcal{F}_\mathsf{com}$). Let $V^*$ be an adversarial verifier. Upon input $(c,pk,Q_1,{\mathbb {G}},G,q)$, simulator $\mathcal{S}$ works as follows:

• 1. $\mathcal{S}$ receives $(\mathsf{commit},sid,e)$ from $V^*$ as it intends to send to $\mathcal{F}_\mathsf{com}$.

• 2. $\mathcal{S}$ chooses a random $z\in {\mathbb {Z}}_{q^2}$, computes $z'=z\bmod q$, and computes $R=z'\cdot G - e \cdot Q_1$. In addition, $\mathcal{S}$ computes $c_r = \mathsf{Enc}_{pk}(0)$.

• 3. $\mathcal{S}$ internally hands $V^*$ the pair $(c_r,R)$ and receives back its decommitment. If it does not decommit, then $\mathcal{S}$ simulates P aborting.

• 4. $\mathcal{S}$ internally hands $V^*$ the value z it chose above.

• 5. $\mathcal{S}$ simulates the zero-knowledge proofs of the range-ZK and ciphertext-ZK phases.

We prove that the simulation is computationally indistinguishable from a real zero-knowledge proof of knowledge by constructing a hybrid simulator $\mathcal{S}'$ who is given the witness $(x_1,r)$. Then, $\mathcal{S}'$ works in exactly the same way as $\mathcal{S}$ except that it computes z as the real prover does. Clearly, the only difference between the output of $\mathcal{S}$ and $\mathcal{S}'$ is in the distribution over z: $\mathcal{S}$ chooses z randomly in ${\mathbb {Z}}_{q^2}$ and $\mathcal{S}'$ sets $z=r+e\cdot x_1 + \rho \cdot q$ where $\rho \in {\mathbb {Z}}_{q^2}$ is random. We argue that these distributions over z are statistically close. In order to see this, fix $r\in {\mathbb {Z}}_q,e\in {\mathbb {Z}}_{2^t},x_1\in {\mathbb {Z}}_q$ and let $z\in {\mathbb {Z}}_{q^2}$ be a value. We have the following cases:

• 1. Case 1 – $z < r + e\cdot x_1$ : In this case, z cannot be generated in a real execution, but can be generated in the simulation.

• 2. Case 2 – $z > q^2-1$ : In this case, z cannot be generated in the simulation, but can be generated in a real execution (note that the maximum value of z in a real execution is $r + e\cdot x_1 + q^2-1$).

• 3. Case 3 – $r + e\cdot x_1 \le z \le q^2-1$ : In this case, the probability that z is obtained in the simulation is exactly $1/(q^2-1)$ since z is randomly chosen in ${\mathbb {Z}}_{q^2}$. Likewise, the probability that z is obtained in a real execution is also exactly $1/(q^2-1)$ since this is obtained if and only if $\rho = \frac{r+e\cdot x_1}{q}$ and $\rho$ is randomly chosen in ${\mathbb {Z}}_{q^2}$.

Recall that the statistical distance between two distributions X and Y over a domain $\mathcal{D}$ is defined to be:

$$\begin{aligned} \varDelta (X,Y)=\max _{T\subseteq D}\Big |\mathrm{Pr}[X\in T]-\mathrm{Pr}[Y\in T]\Big | \end{aligned}$$

Let X be the real execution values and let Y be the simulation values. Then, taking T to be set of values z for which $z<r+e\cdot x_1$, we have that $\mathrm{Pr}[X\in T]=0$ whereas $\mathrm{Pr}[Y\in T]<\frac{q+2^t \cdot q}{q^2}<\frac{1}{\sqrt{q}}$ (this holds since $0 \le r,x_1 < q$ and $e\in {\mathbb {Z}}_{2^t}$ where $2^t<\sqrt{q}$). (Taking T to be the set of values z for which $z>q^2-1$ would give the same result and are both the maximum since any other values add no difference.) We therefore conclude that $\varDelta (X,Y)<\frac{1}{\sqrt{q}}$, and so the distributions over z in the real execution and simulation are statistically close. Since the only difference between $\mathcal{S}$ and $\mathcal{S}'$ is that $\mathcal{S}$ is the simulation and $\mathcal{S}'$ generates z as in a real execution, we have that the outputs of $\mathcal{S}$ and $\mathcal{S}'$ are statistically close.

Now, the only difference between $\mathcal{S}'$ and a real execution is that the proofs in the range-ZK and ciphertext-ZK phases are simulated by $\mathcal{S}'$ and are not real proofs. However, note that the statement is correct in both cases and this is the only difference. Thus, computational indistinguishability follows from the zero knowledge property of the proofs used in these phases.

We conclude by remarking that the requirement that $N>2q^4+q^3$ is needed for the zero knowledge proof that $c_q$ encrypts a multiple of q. This is because $z=r+ex_1+\rho q$ and it is crucial that no modulo N operation takes place. Since $\rho <q^2$ we have that $\rho q< q^3$. However, in Sect. 6.2, the proof further multiplies this be q and so it can be up to $q^4$ (as we will see below, the guarantee is that it is less than $2q^4+q^3$ and thus we need N to be greater than this value). This completes the proof.

It has been proven formally in [16] that any proof of knowledge securely computes the ideal zero-knowledge functionality. We therefore conclude:

Corollary 6.3

If Paillier encryption is indistinguishable under chosen-plaintext attacks and $N>2q^4+q^3$, then Protocol 6.1 securely computes the functionality $\mathcal{F}_\mathsf{zk}^{R_{PDL}}$ in the $\mathcal{F}_\mathsf{com}$-hybrid model, in the presence of malicious, static adversaries.

6.2 A Proof that c Encrypts a Multiple of q

In this section, we present a zero-knowledge proof of knowledge of the following relation R:

$$ R_q = \left\{ \left( (pk,c,q),(sk,L)\right) \mid \exists w : c=\mathsf{Enc}_{sk}(L\cdot q; w))\right\} $$

In actuality, our proof will only be sound and zero knowledge for the case that $0\le L\le q^2+q$. We do not include this in the relation definition for simplicity. However, formally, this is a promise problem and the guarantee that the promise holds is due to the fact that V checks that $q^2<z<q^3+q^2$ inside Protocol 6.1. Now, since in Protocol 6.1 we also prove that $x_1\in {\mathbb {Z}}_q$ and $r\in {\mathbb {Z}}_q$ and we know that $e<<q$, we have that $r+e\cdot x_1 < q^2$. Thus, $L=z-r-e\cdot x_1 >0$ and no modulo N operations happens inside the Paillier subtraction. We therefore conclude that the input L to this proof is such that $0\le L\cdot q < q^3+q^2$, as required.

Security. We prove that if $N>2q^4+q^3$ and we have a promise that $L<q^2+q$, then the protocol is a zero-knowledge proof. Completeness is straightforward (note that since $L<q^2+q$ it holds that $(L+r_i)\cdot q<(q^3+q^2+q^3)\cdot q =2q^4+q^3$ and so $M_i$ is in the appropriate range). We informally argue security.

We begin by proving soundness with error $2^{-t}$; assume that $c=\mathsf{Enc}_{pk}(x)$ for some x that is not a multiple of q. Denote $x=L\cdot q + v$ for $1<v<q$.

First, assume that there exists an i such that $e_i=1$ and $c_i=\mathsf{Enc}_{pk}(r_i\cdot q)$ for some $r_i\in {\mathbb {Z}}_{q^3}$. In such a case, $C=c \oplus c_i \ominus \mathsf{Enc}_{pk}(M_i)$ is an encryption of $L\cdot q + v + r_i\cdot q - M_i$. Now, V accepts only if $L\cdot q + v + r_i\cdot q - M_i=0 \bmod N$, by the soundness of the zero-knowledge proof at the end (this computation is modulo N since it happens inside the Paillier encryption). Clearly, it cannot hold that $L\cdot q + v + r_i\cdot q - M_i=0$ (over the integers) since this would imply that $M_i=L\cdot q + r_i\cdot q + v$, but $M_i$ is divisible by q (since otherwise V rejects) and $0<v<q$. Furthermore, it cannot hold that $L\cdot q + v + r_i\cdot q - M_i=-N$ since this implies that $M_i = L\cdot q + v + r_i\cdot q + N$, but V checks that $M_i<2q^4+q^3$ and N is greater than this value. Finally, it cannot hold that $L\cdot q + v + r_i\cdot q - M_i=N$. In order to see this, note that V checks that $r_i<q^3$ and that $M_i > q^2$. Thus, $N=L\cdot q + v + r_i\cdot q - M_i$ would imply that $N < L \cdot q + q + q^4 - q^2$ and so $L\cdot q > N - q^4 + q^2 -q$. However, the promise is that $L\cdot q < q^3+q^2$; since $N>2q^4+q^3$, this is a contradiction. The same arguments hold for any multiple of N and $-N$.

Thus, if the statement is incorrect, then V will reject unless for every i such that $e_i=1$ it holds that $c_i$ does not encrypt a value that is a multiple of q. Since V checks that $c_i$ does encrypt a value that is a multiple of q for every i such that $e_i=0$, it follows that a cheating prover can only succeed if it guesses the exact e before it sends $c_1,\ldots ,c_t$ (observe that there is exactly one e that will enable it to cheat). However, this occurs with probability $2^{-t}$ only.

Regarding zero knowledge, a simulator $\mathcal{S}$ follows the honest P’s instructions up to the final proof, and runs the zero-knowledge simulator for that proof. Since P doesn’t use the witness until the final proof, the simulator can work in this way. Computational indistinguishability thereby follows from a straightforward reduction to the zero knowledge property of the final proof.

A Simulation-Based Proof of Security (Using a New Assumption)

1.1 A.1 Definition of Security

We show how to securely compute the functionality $\mathcal{F}_{\textsc {ecdsa}}$. The functionality is defined with two functions: key generation and signing. The key generation is called once, and then any arbitrary number of signing operations can be carried out with the generated key. The functionality is defined in Fig. A.1.

We defined $\mathcal{F}_{\textsc {ecdsa}}$ using Elliptic curve (additive) group notation, although all of our protocols work for any prime-order group.

Security in the presence of malicious adversaries. We prove security according to the standard simulation paradigm with the real/ideal model [5, 15]. We prove security in the presence of malicious adversaries and static corruptions. As is standard for the case of no honest majority, we consider security with abort meaning that a corrupted party can learn output while the honest party does not. In our definition of functionalities, we describe the instructions of the trusted party. Since we consider security with abort, the corrupted party receives output first and then sends either continue or abort to the trusted party to determine whether or not the honest party also receives output.

We remark that when all of the zero-knowledge proofs are UC secure [6], then our protocol can also be proven secure in this framework.

1.2 A.2 Background and New Assumption

In Sect. 4, we proved the security of our protocol under a game-based definition. In some sense, proving security via simulation-based definitions (following the ideal/real model paradigm) is preferable. In particular, it guarantees security under composition. Following our proof in Sect. 4.2 closely, one may observe that $\mathcal{S}$ is essentially a simulator for an ideal functionality that securely computes ECDSA. Indeed, $\mathcal{S}$ is invoked with a public-key, and can use its oracle in $\mathsf{Expt}\text {-}\mathsf{Sign}$ to obtain a signature on any value it wishes. This is very similar to an ideal functionality that generates a public key and can be used to generate signatures. The only problem with the simulation strategy used in Sect. 4.2 is that in the case that $P_2$ is corrupted, $\mathcal{S}$ just guesses if $c_3$ is correctly constructed. Needless to say, this is not allowed in a simulation-based proof. One may be tempted to solve this problem by saying that since $\mathcal{S}$ generates the Paillier key-pair (pk, sk) when playing $P_1$, it can decrypt $c_3$ and check if the value is generated as expected. However, when trying to formally prove this, one needs to show a reduction to the indistinguishability of the encryption scheme (since the simulator does not know $x_1$ and so cannot provide $c_{key}=\mathsf{Enc}_{pk}(x_1)$). In this reduction, the simulator is given pk externally and does not know sk (see the proof of the key generation subprotocol in Sect. 4.2). Thus, in this reduction, it is not possible to decrypt $c_3$ and the appropriate distributions cannot be generated.

In this section, we introduce a new assumption under which it is possible to prove the full simulation-based security of Protocol 3.2 without any modifications. The assumption is non-standard, but very plausible. Consider an adversary who is given a Paillier encryption of a (high-entropy) secret value w; denote $c=\mathsf{Enc}_{pk}(w)$. Then, the adversary can always randomize c to generate an encryption $c'$ of the same w, but without anyone but itself and the secret-key owner knowing whether c and $c'$ encrypt the same value. In addition, the adversary can always generate an encryption $c'$ of a plaintext value that it knows but without knowing whether c and $c'$ encrypt the same value. Now, consider a setting where an adversary is given an oracle $\mathcal{O}_c(c')$ that outputs 1 if and only if $\mathsf{Dec}_{sk}(c')=\mathsf{Dec}_{sk}(c)$, where $c=\mathsf{Enc}_{pk}(w)$ is the challenge ciphertext, and the adversary’s task is to learn w. Clearly, the adversary can use this oracle to try and guess the value encrypted in c one at a time (just guess $x'$, compute $c'=\mathsf{Enc}_{pk}(x')$ and query $\mathcal{O}_c(c')$). However, since w has high entropy, this seems to be futile. Furthermore, it seems that the oracle $\mathcal{O}_c$ cannot help in any other way.

Extending the above a further step, the adversary can generate any affine function of w by choosing scalars $\alpha$ and $\beta$ and computing $c' = \alpha \odot (\mathsf{Enc}_{pk}(\beta )\oplus c)$ $= \mathsf{Enc}_{pk}(\alpha + \beta \cdot x)$. Then, as before, $\mathcal{A}$ tries to output w given an oracle $\mathcal{O}_c(c',\alpha ,\beta )$ that outputs 1 if and only if $\mathsf{Dec}_{sk}(c') = \alpha + \beta \cdot \mathsf{Dec}_{sk}(c)$. The adversary can use this oracle to try to guess w one value at a time, but it does not seem that it can help beyond this.

In order to formally define a security experiment including such an oracle, one must consider the task of the adversary. Since w must be a high-entropy random value one cannot consider the standard indistinguishability game. Rather, one could formalize a simple task where some w is randomly chosen and the adversary is given $(pk,\mathsf{Enc}_{pk}(w))$ and oracle access to $\mathcal{O}$ above, and its task is to output w (in entirety). This is very plausible since without the oracle it is clearly hard, and the oracle only answers queries $(c',\alpha ,\beta )$ by determining if “$c'$ encrypts $\alpha +\beta \cdot x$”, which essentially gives a single guess on the value of w. However, requiring that the adversary output the entire w turns out to not be very helpful for us. This is due to the fact that w must maintain some property of secrecy. We therefore extend this experiment by giving the adversary either $(pk,f(w_0),\mathsf{Enc}_{pk}(w_0))$ or $(pk,f(w_0),\mathsf{Enc}_{pk}(w_1))$, where $w_0,w_1$ are random and f is a one-way function. The adversary’s task is to guess which input type it received (with the input to the one-way function equal to what is encrypted or independent of it), and it is given the oracle $\mathcal{O}$ above to help it. Note that f may reveal some information about $w_0$ (since it is only a one-way function), but if f is somehow unrelated of the encryption scheme, then it still seems that this should not help very much.

For our actual experiment, we will define the one-way function to be the computation $w_0\cdot G$ in a group where the discrete log is hard. Observe that here the one-way function is related to the discrete log problem over Elliptic curve groups, whereas the encryption is Paillier and thus seems completely unrelated. Thus, we conjecture that this problem is hard. Since we consider a group, the equality that is actually checked by the oracle is modulo q, where q is the order of the group.

Formal assumption definition. The above description leads to the following experiment. Let G be a generator of a group ${\mathbb {G}}$ of order q. Consider the following experiment with an adversary $\mathcal{A}$, denoted $\mathsf{Expt}_{\mathcal{A}}(1^n)$:

• 1. Generate a Paillier key pair (pk, sk).

• 2. Choose random $w_0,w_1 \in {\mathbb {Z}}_q$ and compute $Q=w_0 \cdot G$.

• 3. Choose a random bit $b\in \{0,1\}$ and compute $c=Enc_{pk}(w_b)$.

• 4. Let $b' = \mathcal{A}^{\mathcal{O}_c(\cdot ,\cdot ,\cdot )}(pk,c,Q)$, where $\mathcal{O}_c(c',\alpha ,\beta )=1$ if and only if $Dec_{sk}(c') = \alpha + \beta \cdot w_b \bmod q$.

• 5. The output of the experiment is 1 if and only if $b'=b$.

We define the following:

Definition A.2

We say that the Paillier-EC assumption is hard if for every probabilistic polynomial-time adversary $\mathcal{A}$ there exists a negligible function $\mu$ such that $\mathrm{Pr}[\mathsf{Expt}_{\mathcal{A}}(1^n)=1] \le \frac{1}{2} + \mu (n)$.

The assumption in Definition A.2 is rather ad-hoc and tailored to the problem at hand. However, it is very plausible and enables us prove full simulation without modifying the protocol. In particular, an adversary for the above experiment can run the protocol simulator and can verify whether or not $c_3$ was constructed correctly. This is because $c_3$ is supposed to be an encryption of $\alpha + \beta \cdot x_1$ for $\alpha = (k_2)^{-1} \cdot m' \bmod q$ and $\beta = (k_2)^{-1} \cdot r \cdot x_2 \bmod q$, where the simulator knows all of the values $k_2,r,x_2$. Thus, the adversary can use its oracle to verify the validity of the ciphertext sent by the adversary who controls $P_2$. This means that the simulation can be run while interacting in this experiment, and if the result of the simulation can be distinguished from a real execution then this can be used to win the experiment.

In the full version of this paper we formally prove Theorem A.3 below. We assume only that the Paillier-EC assumption is hard, since this trivially implies that the Paillier encryption scheme is indistinguishable under chosen-plaintext attacks.

Theorem A.3

Assume that the Paillier-EC assumption is hard. Then, Protocol 3.2 securely computes $\mathcal{F}_{\textsc {ecdsa}}$ in the $(\mathcal{F}_\mathsf{zk},\mathcal{F}_\mathsf{com\text {-}zk})$-hybrid model in the presence of a malicious static adversary (under the full ideal/real definition).