Abstract
Two recent works [Lin, EUROCRYPT 2016, Lin and Vaikuntanathan, FOCS 2016] showed how to construct Indistinguishability Obfuscation (IO) from constant degree multilinear maps. However, the concrete degrees of multilinear maps used in their constructions exceed 30. In this work, we reduce the degree of multilinear maps needed to 5, by giving a new construction of IO from asymmetric L-linear maps and a pseudo-random generator (PRG) with output locality L and polynomial stretch. When plugging in a candidate PRG with locality-5 (e.g., [Goldreich, ECCC 2010, Mossel, Shpilka, and Trevisan, FOCS 2013, O’Donnald and Wither, CCC 2014]), we obtain a construction of IO from 5-linear maps.
Our construction improves the state-of-the-art at two other fronts: First, it relies on “classical” multilinear maps, instead of their powerful generalization of graded encodings. Second, it comes with a security reduction to (i) the SXDH assumption on algebraic multilinear maps [Boneh and Silverberg, Contemporary Mathematics, Rothblum, TCC 2013], (ii) the security of PRG, and (iii) sub-exponential LWE, all with sub-exponential hardness. The SXDH assumption is weaker and/or simpler than assumptions on multilinear maps underlying previous IO constructions. When noisy multilinear maps [Garg et al., EUROCRYPT 2013] are used instead, security is based on a family of more complex assumptions that hold in the generic model.
H. Lin—Partially supported by NSF grants CNS-1528178, CNS-1514526, CNS-1652849 (CAREER).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Pseudorandom Generator (PRG)
- Multilinear Maps
- Graded Encoding
- Security Reduction
- Inner-product Encryption (IPE)
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Indistinguishability obfuscation, defined first in the seminal work of Barak et al. [11], aims to transform programs into “unintelligible” ones while preserving functionality. IO is an extradinarily powerful object and has been used as a central tool for obtaining a plethora of new cryptographic constructions, solutions to long-standing open problems, and techniques enabling new cryptographic goals.
Unfortunately, so far, the existence of IO remain uncertain. Most known candidate IO schemes [5, 7, 10, 17, 25, 27, 30, 33, 46, 49, 53] are built from the so-called graded encoding schemes [26], a framework of complex algebraic structures that, in essence, enables evaluating polynomial-degree polynomials on secret encoded values and revealing whether the output is zero or not. The security of most IO candidates are either analyzed in the ideal model or based on strong uber assumptions [49], with only one exception [33]. On the front of instantiating graded encodings from concrete mathematical objects, the state of affairs is even more worrisome: Vulnerabilities have been demonstrated in all instantiations proposed so far [21, 22, 26, 31, 39]. Of course, this does not mean that the resulting IO constructions are insecure. In fact, this has motivated the search for IO constructions that withstand all existing attacks [29].
The state-of-affairs motivates the following natural question.
Two recent works [41, 44] have made significant progress towards answering the question: Lin [41] showed that to construct IO, we do not need full-fledged graded encodings that support evaluation of all polynomial-degree polynomials, instead, it suffices to start with graded encodings for only constant-degree polynomials, called constant-degree graded encodings. Following that, Lin and Vaikuntanathan [44] further weakened the assumption on constant-degree graded encodings from a uber assumption in [41] to the so-called joint-SXDH assumption, which is a stronger variant of the classical SXDH assumption. Besides from multilinear maps, their IO constructions additionally rely on PRGs in \(\mathsf {NC} ^0\) and sub-exponential LWE.
The trajectory of recent developments points towards the holly grail of “building IO from bilinear maps”. In this work, we make new strides in this direction: We give a new construction of IO from asymmetric L-linear maps and a PRG with output locality L (i.e., every output bit depends on at most L input bits). When plugging in a candidate PRG with locality-5 in the literature [34, 47, 48], we obtain a construction of IO from 5-linear maps. This gets the degree of multilinear maps needed for IO much closer to the dream version of 2. In comparison, previous IO constructions [41, 44] rely on multilinear maps with degree at least 30. On the other hand, no PRGs with locality 4 exist [23, 47]. Thus, our approach hits a barrier and cannot base IO on multilinear maps with degree \(L \le 4\). This barrier is common to recent IO constructions [41, 44] and suggests that we need new techniques circumventing the lower bound on locality of PRGs.
In addition to reducing the degree of multilinear maps, our IO construction improves the state-of-the-art at two other fronts. First, our construction uses the classical asymmetric multilinear maps introduced in [15, 50], which are direct generalization of bilinear pairing groups to higher degree. Previous constructions rely on graded encodings, which are enhanced versions of multilinear maps with more powerful functionalities (such as, supporting complex label structures). Second, the security of our IO scheme is based on the sub-exponential SXDH assumption on L-linear maps, the sub-exponential security of PRGs, and sub-exponential LWE. The SXDH assumption on multilinear maps is much simpler and/or weaker than the assumption on graded encodings underlying previous IO constructions, for instance, the joint-SXDH assumption in [44] and the multilinear subgroup elimination assumption in [33].
1.1 Our Results
We start with defining the SXDH assumption on multilinear maps and then describe our results.
SXDH on Multilinear Maps. Asymmetric multilinear pairing groups introduced in [15, 50] generalize asymmetric bilinear pairing maps to a collection of source groups \(G_1, \cdots , G_D\), whose elements can be paired to produce elements in a target group \(G_T\) via a multilinear map \(e(g_1^{a_1}, \cdots , g_D^{a_D}) = g^{a_1\cdots a_D}_{T}\). The degree (a.k.a. multilinearity) of the multilinear map is the number of elements that can be paired together, which equals to the number of source groups D. We say that the multilinear pairing groups have prime order if all source groups and the target group have the same prime order, and composite order if all groups have the same composite order. In this work, we consider constant-degree multilinear paring groups, and in particular 5-linear pairing groups, with either prime or composite order. We omit specifying the order of groups below.
The SXDH assumption on asymmetric multilinear pairing groups is a natural generalization of the standard symmetric external Diffie-Hellman (SXDH) assumption on asymmetric bilinear pairing groups, introduced first in [50]. In short, SXDH states that the decisional Diffie-Hellman assumption holds in every source group: It postulates that the distribution of \(g_d^a, g_d^b, g_d^{ab}\) in any source group d should be indistinguishable to that of \(g_d^a, g_d^b, g_d^r\). Formally, for all \(d \in [D]\),

where \(\{ {g_i} \}\) is the set of generators in all groups. When \(D = 2\), this gives the SXDH assumption on bilinear pairing groups.
Multilinear Maps v.s. Graded Encodings. The interface of (asymmetric) multilinear pairing groups is much simpler than that of graded encoding schemes introduced by [26]. First, graded encoding schemes support graded multiplication over a collection of groups \(\{ {G_l} \}\): Graded multiplication can pair elements of two groups \(G_{l_1}, G_{l_2}\), indexed by two labels \(l_1, l_2\), to produce an element in the group \(G_{l_1 + l_2}\), indexed by label \(l_1+l_2\) Footnote 1. In particular, the output element in \(G_{l_1+l_2}\) can be further paired with elements in other groups to produce elements in group \(G_{l_1 + l_2 + l_3 + \cdots }\) and so on. In contrast, multilinear map allows only “one-shot” multiplication, where the output element belongs to the target group \(G_T\) that cannot be paired anymore. Second, graded encoding schemes support the notion of “pairable groups” in the sense that only elements from groups \(G_{l_1}, G_{l_2}\) that satisfy a “pairable” relation can be paired.Footnote 2
The support for graded multiplication between pairable groups provides powerful capabilities. In essence, GES allows one to “engineer” the labels of a set of group elements \(\{ {g^{a_i}_{l_i}} \}\), so that, only polynomials of certain specific forms can be evaluated on values in the exponent. In contrast, the simple interface of multilinear maps does not provide such capabilities.
SXDH v.s. Joint-SXDH. Lin and Vaikuntanathan introduced the joint-SXDH assumption on graded encoding schemes, and showed that IO for \(\mathsf {P/poly} \) can be based on sub-exponential joint-SXDH and PRG in \(\mathsf {NC} ^0\). Their joint-SXDH assumption strengthens the SXDH assumption as follows: It considers the joint distribution of elements \((g_l^a, g_l^b, g_l^{ab})_{l \in S}\) in a set S of groups. The intuition is that as long as no pairs of groups \(G_{l_1}, G_{l_2}\) in the set S are pairable, in the same spirit as SXDH, the distribution is possibly indistinguishable to the joint distribution of elements \((g_l^a, g_l^b, g_l^{r})_{l \in S}\) in the same set of groups.Footnote 3 The joint-SXDH assumption is more complex and potentially stronger than the SXDH assumption.
Our Main Result: IO from SXDH on L -Linear Maps and Local-L PRG
Theorem 1
(Main Theorem). Let L be any positive integer. Assume the sub-exponential hardness of LWE with sub-exponential modulus-to-noise ratio. Then, IO for \(\mathsf {P/poly} \) is implied by the sub-exponential SXDH assumption on L-linear pairing groups, and the existence of a sub-exponentially secure locality-L PRG with polynomial \(n^{1+\varepsilon }\)-stretch for some \(\varepsilon > 0\).
We note that the sub-exponential hardness of SXDH and PRG required by our theorem is weaker than standard notions of sub-exponential hardness of decisional problems, in the sense that we only require the distinguishing gap to be sub-exponentially small against polynomial time adversaries, as opposed to sub-exponential time adversaries.
Our result establishes a direct and tight connection between the degree D of multilinear maps needed for constructing IO and the locality L of PRGs—they are the same \(D = L\)—assuming sub-exponential LWE. In comparison, the previous state-of-the-art [44] requires the degree of the multilinear map to be much larger, namely \(D > 6L\). Thus, when plugging-in a PRG of locality-5, their construction requires at least 30-linear maps, whereas our construction relies on 5-linear maps.
Step 1: Bootstrapping IO from Locality- L PRG and Degree- L FE. We follow the same two-step approach in all previous IO constructions: First, construct IO for \(\mathsf {P/poly} \) from some simpler primitives—call this the bootstrapping step—and then instantiate the primitives needed, using graded encodings or multilinear maps. In the literature, previous bootstrapping theorems have shown that general purpose IO can be built from one of the following: (i) IO for \(\mathsf {NC} ^1\) [27], or (ii) sub-exponentially secure FE for \(\mathsf {NC} ^1\) [2, 3, 13, 14], or (iii) sub-exponentially secure IO for constant degree computations and PRG in \(\mathsf {NC} ^0\) [41], or (iv) sub-exponentially secure FE for \(\mathsf {NC} ^0\) and PRG in \(\mathsf {NC} ^0\) [44].Footnote 4
In this work, we strengthen the bootstrapping theorem of [44], and show how to build IO from PRGs with locality-L and FE for computing degree L polynomials in some ring \(\mathcal {R}\) (which eventually corresponds to the exponent space of multilinear maps used for instantiating the FE).
Theorem 2
(Bootstrapping Theorem). Let L be any positive integer. Assume the sub-exponential hardness of LWE with sub-exponential modulus-to-noise ratio. IO for \(\mathsf {P/poly} \) is implied by the existence of sub-exponentially secure (collusion resistant) secret-key FE schemes for computing degree-L polynomials in some ring \(\mathcal {R}\) with linear efficiency, and a sub-exponentially secure locality-L PRG with \(n^{1+\varepsilon }\)-stretch for some \(\varepsilon >0\).
(In the case that the FE schemes are public-key, the assumption of sub-exponential LWE is not needed.)
Above, the linear efficiency of FE schemes means that encryption time is linear in the input length \(N(\lambda )\), that is, \(\mathsf{Time}_{\mathsf{FE.Enc}} = N(\lambda )\mathrm {poly}(\lambda )\). In fact, we only need the FE scheme to achieve the weaker functionality of revealing whether the output of a degree-L polynomial is zero in \(\mathcal {R}\). Below, we refer to such FE schemes as degree-L FE in \(\mathcal {R}\) with linear efficiency.
In comparison, with locality-L PRG, the bootstrapping theorem in [44] needs to start with FE for computing polynomials with higher degree \(3L+2\). We here reduce the degree of FE to exactly L, by proposing a new pre-processing idea: At a very high-level, we let the encryptor pre-process the input to be encrypted to perform part of the degree-\((3L+2)\) computations, and encrypt the processed values, so that later, the decryptor only need to perform a degree-L computation, and hence degree-L FE suffices. An overview of our bootstrapping step is given in Sect. 2.1.
Step 2: Degree Preserving Construction of FE. Next, we construct degree-L FE based on the SXDH assumption on L-linear maps.
Theorem 3
Let D be any positive integer and \(\mathcal {R}\) any ring. Assuming SXDH on D-linear maps over ring \(\mathcal {R}\), there exist secret key FE schemes for degree-D polynomials in \(\mathcal {R}\), with linear efficiency.
This new FE scheme is our main technical contribution. Previous constructions of FE for \(\mathsf {NC} ^1\) either relies on IO for \(\mathsf {NC} ^1\) or high degree multilinear maps [27, 28], whose degree is polynomial in the circuit-size of the computations. In [44], Lin and Vaikuntanathan constructed FE for \(\mathsf {NC} ^0\) from constant-degree graded encodings. Their construction, however, is not degree-preserving: To compute \(\mathsf {NC} ^0\) functions that can be evaluated in degree D, they require degree 2D graded encodings. Our FE construction is the first one that supports degree-D computations using only degree-D multilinear maps.
It turns out that removing a factor of 2 in the degree requires completely new techniques for constructing FE. The reason is that the factor of 2 increase in degree allows the FE construction in [44] to evaluate instead of a degree-D computation directly, an arithmetic randomized encodings of the computation. The benefit is that they can rely on the security of randomized encoding to argue the security of FE. In our case, since the degree is exactly D, we cannot afford to “embed” any cryptographic primitives in the FE construction, and must come up with ways of encoding inputs and intermediate computation values using multilinear maps that directly guarantee security. For this reason, our construction share similar flavor with constructions of inner product encryptions based on bilinear maps. See Sects. 2.2 and 2.3 for an overview of our degree-preserving FE construction.
Additional Contributions. Along the way of designing our degree-preserving FE construction, we also construct the following primitives that are of independent interests.
Simple Function Hiding IPE Schemes from SXDH on Bilinear Maps. Without using the heavy hammers of multilinear maps or IO, the state-of-the-art collusion resistant FE schemes can only compute inner products, they are called Inner Product Encryption (IPE). In the literature, Abdalla et al. (ABDP) [1] came up with a public key IPE scheme based on one of a variety of assumptions, such as, DDH, Paillier, and LWE.
Bishop et al. [12] (BJK) constructed the first secret-key IPE scheme based on the SXDH assumption over asymmetric bilinear pairing groups. Their scheme achieves a stronger security notion, called weak function-hiding, and is improved by [24] to achieve full function hiding. Lin and Vaikuntanathan [44] further showed that any weakly function hiding IPE scheme can be generically transformed into a function hiding IPE scheme. Here, (weak) function hiding requires the FE scheme to hide both inputs and functions (revealing only outputs), and is much harder to achieve than standard security that hides only inputs.
While the ABDP public-key IPE scheme is simple, the secret-key (weak) function hiding IPE schemes [12, 24] are much more complex. In this work, we give a simple construction of weak function hiding IPE from SXDH on bilinear maps, which can then be transformed to function hiding IPE using [44]. Our IPE scheme is built from the ABDP public-key IPE scheme in a modular way, and inherits its efficiency and simplicity: Ciphertexts and secret keys of length-N vectors consists of \((N+2)\) group elements, and the construction and security proof of our scheme fits within 2 pages (reducing to the security of the ABDP IPE scheme). In addition, the new scheme satisfies certain special properties that are important for our construction of degree-L FE schemes, which are not satisfied by previous IPE schemes [12, 24]. See Sect. 2.5 for an overview of our simple function hiding IPE.
High-Degree IPE. We also generalize IPE to the notion of high-degree IPE, or HIPE for short. They are multi-input FE schemes [35] for computing, so called, degree-D inner product defined as
We construct HIPE for degree-D inner products from degree-D multilinear maps, which is then used to build degree-D FE schemes. We believe that this notion is interesting on its own and may have other applications. See Sect. 2.3 for an overview of HIPE.
Algebraic v.s. Noisy Multilinear Maps. Our results and proofs are described w.r.t. algebraic multilinear maps. However, finding algebraic multilinear maps with degree above 2 is still a major open problem. Can our IO and FE schemes be instantiated with known noisy multilinear map candidates [21, 22, 26, 31, 39]? The answer is nuanced: The constructions can be instantiated as-is with noisy multilinear maps and correctness holds, but the security proof fails, for (1) the SXDH assumption does not hold on known candidates, and (2) the current security reduction relies on the homomorphic scalar multiplication functionality, which is not supported by known candidates. (The latter is shared with all previous reductions that base security on a laconic and instance-independent assumption [33, 44].) Nevertheless, the security proof of the degree-L FE scheme (the only component that relies on multilinear maps) can be adapted into a proof in the degree-5 ideal multilinear map model without homomorphic scalar multiplication. Security in the ideal model does not imply security against known cryptanalytic attacks [6, 16, 18,19,20, 26, 32, 46]. It is unclear whether these instantiations are secure against them—we have no concrete attacks nor formal arguments that validate their security against known attacks, such as, a security proof in the weak multilinear map model [29]. See Sect. 2.6 for a more detailed discussion.
1.2 Concurrent and Independent Work
In a concurrent work, Ananth and Sahai [4] (AS) showed a similar result. Both works convey the same high-level message that “IO can be constructed from 5-linear maps and locality-5 PRG, assuming sub-exponential LWE”. But, the concrete theorem statements differ. First, while our construction relies on the classical 5-linear maps, the AS construction uses degree-5 set-based graded encodings, which, as discussed above, is more powerful. Second, a main contribution of this paper is basing security of IO on the SXDH assumption, which is laconic and instance dependent. In comparison, the AS construction is proven secure based on two assumptions on graded encodings that are tailored to their construction and justified in the ideal model, and the security of their FE scheme follows immediately from the assumptions. In terms of techniques, both works follow the paradigm of IO construction in [44]. The two works propose different notions of FE for low-degree polynomials, and use completely different methods to construct them.
1.3 Subsequent Works
Given that locality 4 PRGs do not exist [47], the approach (in this and recent works [4, 44]) of using local PRGs to reduce the degree of multilinear maps used in IO constructions hits a barrier at degree 5. In a subsequent work, Lin and Tessaro [43] overcame this barrier and further reduced the degree of multilinear maps needed to 3. More specifically, they showed that assuming sub-exponential LWE, IO can be based on the SXDH assumption on L-linear maps and PRGs with a new notion of block-wise locality L. Roughly speaking, a PRG has block-wise locality L if every output bit depends on at most L input blocks, each containing up to \(\log \lambda \) bits. Their result crucially relies on our IO construction, with the modification of replacing locality L PRGs with block-wise locality L PRGs in the first bootstrapping step (the rest of the construction, such as, the low-degree FE scheme, is kept the same). They further initiated the study of block-wise local PRGs based on Goldreich’s local functions and their (in)security. In particular, they showed that the security of candidates with block-wise locality \(L \ge 3\) is backed by similar validation as candidates with (conventional) locality 5. Soon after their work, two exciting cryptanalytic works [9, 45] showed that, unfortunately, (polynomial-stretch) PRGs with block-wise locality 2 do not exist.
Summarizing the new state-of-the-art: Assuming sub-exponential LWE, there is a construction of IO from trilinear maps and PRGs with block-wise locality 3—we are one degree away from the dream statement of “building IO from bilinear maps”.
Organization. Next, we proceed to give an overview of our FE and IO constructions and their security proofs. Due to the lack of space, we leave the formal description of constructions and proofs to the full version [42]. In Sect. 2.6, we discuss in more detail issues related to instantiating our schemes with noisy multilinear maps.
2 Overview
In this work, scalars are written in normal font, such as a, b, and vectors are written in boldface, such as \({{\mathbf {v}}}, {{\mathbf {w}}}\).
2.1 Bootstrapping
Our bootstrapping theorem follows the same two step approach as [41, 44]. To construct IO for \(\mathsf {P/poly} \),
-
Step 1. First, construct sub-exponentially secure single-key FE schemes \(\mathbf{CFE}\) for \(\mathsf {NC} ^1\) that are weakly compact, meaning that encryption time scales polynomially in the security parameter \(\lambda \) and the input length N, but also scales sublinearly in the maximal size S of the circuits for which secret keys are generated. More precisely, a FE scheme is said to be \((1-\varepsilon )\)-weakly-compact if its encryption time is \(\mathrm {poly}(\lambda ,N)S^{1-\varepsilon }\).
-
Step 2. If the FE schemes obtained from Step 1 are public-key schemes, invoke the result of [2, 14] that any public-key (single-key) weakly-compact FE schemes (for any \(\varepsilon > 0\)) imply IO for \(\mathsf {P/poly} \).
Otherwise, if the FE schemes obtained are secret-key schemes, then invoke the recent result of [13] that any secret-key weakly-compact FE schemes also imply IO for \(\mathsf {P/poly} \), assuming additionally sub-exponential LWE.
The challenging task is constructing (public-key or secret-key) weakly-compact FE schemes for \(\mathsf {NC} ^1\) from simpler primitives. In [44] (LV), they constructed such schemes from (public key or secret key respectively) collusion resistant FE schemes for \(\mathsf {NC} ^0\) with linear efficiency, assuming the existence of a polynomial-stretch PRG in \(\mathsf {NC} ^0\). We observe that in their construction, if the PRG has locality L, the \(\mathsf {NC} ^0\)-FE scheme is used to compute polynomials with low degree \(3L+2\). In this work, we show that the degree of the FE schemes (i.e., the degree of the polynomials supported) can be reduced to L. Below, we start with reviewing the LV construction of weakly-compact FE for \(\mathsf {NC} ^1\), and then modify their construction to reduce the degree of the underlying FE scheme. (In the exposition below, we do not differentiate public-key vs secret-key schemes, since they are handled in the same way.)
The LV Weakly-Compact FE for \(\mathsf {NC} ^1\) . To construct weakly-compact FE schemes for \(\mathsf {NC} ^1\) from FE schemes for \(\mathsf {NC} ^0\), LV uses Randomized Encodings (RE) [8, 37] to represent every \(\mathsf {NC} ^1\) function \(f({{\mathbf {x}}})\), as a simpler \(\mathsf {NC} ^0\) randomized function \(\hat{f} ({{\mathbf {x}}}; \ {{\mathbf {r}}})\). Then, to enable computing \(f({{\mathbf {x}}})\), it suffices to publish a secret key for \(\hat{f} \in \mathsf {NC} ^0\), and a ciphertext of \(({{\mathbf {x}}}, {{\mathbf {r}}})\), which can be done using the \(\mathsf {NC} ^0\)-FE scheme. But, the resulting ciphertext is not compact, since the randomness \({{\mathbf {r}}}\) for computing the randomized encoding is at least of length \(S(\lambda )\mathrm {poly}(\lambda )\), where \(S(\lambda )\) is the size of the circuit computing f. The key idea of LV is using a polynomial-stretch PRG \(\mathbf{PRG}\!:\{0,1\}^{n}\rightarrow \{0,1\}^{n^{1+\alpha }}\) in \(\mathsf {NC} ^0\) to generate pseudo-randomness for RE, that is, computing instead \(g({{\mathbf {x}}}, {{\mathbf {s}}}) = \hat{f} ({{\mathbf {x}}}; \mathbf{PRG}({{\mathbf {s}}}))\). Now the input of the function becomes \(({{\mathbf {x}}}, {{\mathbf {s}}})\), whose length is sublinear in \(S(\lambda )\) thanks to the fact that the PRG has polynomial stretch. Since the \(\mathsf {NC} ^0\)-FE scheme has linear efficiency, the ciphertext size is also sublinear in \(S(\lambda )\). In addition, the function g can still be computed in \(\mathsf {NC} ^0\).
Observe that if g can be computed by a degree-D polynomial in some ring \(\mathcal {R}\), then one can instantiate the LV construction with degree-D FE schemes in \(\mathcal {R}\). The question is how large is the degree D? Plug in the randomized encoding scheme by Applebaum et al. [8], whose encodings \(\hat{f} ({{\mathbf {x}}}; {{\mathbf {r}}})\) are computable in \(\mathsf {NC} ^0_4\) and has degree 1 in \({{\mathbf {x}}}\) and degree 3 in \({{\mathbf {r}}}\). Then, the degree of g is determined by the degree \(D_{\mathrm {PRG}}\) of the PRG (i.e., the minimal degree of polynomials that computes PRG in \(\mathcal {R}\)), namely, \(D = 3 D_{\mathrm {PRG}} + 1\). As the degree of PRG is upper bounded by its locality \(D_{\mathrm {PRG}} \le L\), the degree of g is bounded by \(3L+1\). For the security proof to work out, the actual functions used in the LV construction are more complicated and has degree \(3L+2\). For simplicity of this overview, it is convenient to ignore this issue, as it does not affect understanding the main ideas.
A formal description of the LV weakly-compact FE scheme \(\mathbf{CFE}^{N,D,S}\) for \(\mathsf {NC} ^1\) circuits with input-length \(N = N(\lambda )\), depth \(D = D(\lambda )\), and size \(S = S(\lambda )\) can be found in Fig. 1; it relies on the following tools:
-
A (collusion resistant) FE scheme for degree-\((3D+2)\) polynomials \(\{\mathbf{FE}= (\mathsf{FE.Setup}, \mathsf{FE.KeyGen},\mathsf{FE.Enc},\mathsf{FE.Dec})\}\) in some ring \(\mathcal {R}\) with linear efficiency.
-
A pseudorandom generator \(\mathbf{PRG}\) with \(n^{1+\alpha }\)-stretch for any \(\alpha > 0\) that is computable in degree D in ring \(\mathcal {R}\).
-
A weak PRF \({\mathsf {F}}\) in \(\mathsf {NC} ^1\).
-
A specific randomized encoding scheme, which is the composition of Yao’s garbling scheme [51, 52] and the AIK randomized encoding scheme in \(\mathsf {NC} ^0\) [8]. Denote by \(\hat{C}_x = \mathsf {Yao}(C, {{\mathbf {x}}};\ {{\mathbf {r}}})\) Yao’s garbling algorithm that compiles a circuit C and an input \({{\mathbf {x}}}\) into a garbled circuit \(\hat{C}_x\), and by \(\varPi = \mathsf {AIK}(f, {{\mathbf {x}}}\ ; \ {{\mathbf {r}}})\) the AIK encoding algorithm.
We refer the reader to [44] for the correctness and security of the scheme, and to our full version [42] for the analysis of compactness and degree.
Relying on Degree- L FE. To reduce the degree of polynomials computed using the low-degree FE, our key idea is pre-processing the input \(({{\mathbf {x}}}, {{\mathbf {s}}})\), so that, part of the computation of the function g is already done at encryption time. To illustrate the idea, recall that g is linear in \({{\mathbf {x}}}\). Thus, if one pre-computes \({{\mathbf {x}}}\,\otimes \,{{\mathbf {s}}}\) (where \({{\mathbf {x}}}\,\otimes \,{{\mathbf {s}}}\) is the tensor product of \({{\mathbf {x}}}\) and \({{\mathbf {s}}}\)), then g can be computed with one degree less. More specifically, there exists another function \(g'\) that takes input \(({{\mathbf {x}}}, {{\mathbf {s}}}, {{\mathbf {x}}}\,\otimes \,{{\mathbf {s}}})\) and computes \(g({{\mathbf {x}}}, {{\mathbf {s}}})\) in degree 3L, by replacing every monomial of form \(x_i s_{i_1}s_{i_2}\cdots \) with \((x_is_{i_1})\ s_{i_2} \cdots \), where \(x_is_{i_1}\) is taken directly from \({{\mathbf {x}}}\,\otimes \,{{\mathbf {s}}}\). Therefore, we can modify the LV construction to encrypt \(({{\mathbf {x}}}, {{\mathbf {s}}}, {{\mathbf {x}}}\,\otimes \,{{\mathbf {s}}})\), whose length is still sublinear in \(S(\lambda )\), and generate keys for functions \(g'\) that have degree 3L.
The more tricky part is how to further reduce the degree of g in \({{\mathbf {s}}}\). The naive method of pre-computing \({{\mathbf {s}}}\,\otimes \,{{\mathbf {s}}}\) at encryption time would not work, since it would make encryption time exceed \(S(\lambda )\), losing compactness. To avoid this, consider a simple case where the \(\mathsf {NC} ^1\) function f to be computed is decomposable, in the sense that it has \(I = S(\lambda )/\mathrm {poly}(\lambda )\) output bits, and every output bit \(i \in [I]\) can be computed by a function \(f_i\) of fixed polynomial size \(\mathrm {poly}(\lambda )\). (In fact, it is w.l.o.g. to assume this, since every function f can be turned into one that is decomposable using Yao’s garbled circuits.) Then, the AIK randomized encoding of f consists of \(\{ {\hat{f}_i({{\mathbf {x}}}, {{\mathbf {r}}}[i])} \}_{i \in [I]}\), where the random tape \({{\mathbf {r}}}[i]\) for every encoding has a fixed polynomial length \(Q= poly(\lambda )\), since \(|f_i| = poly(\lambda )\).
Single-key compact FE \(\mathbf{CFE}\) by [44]
In LV, all the random tapes \(\{ {{{\mathbf {r}}}[i]} \}\) are generated by evaluating a PRG on a single seed \({{\mathbf {r}}}= \mathbf{PRG}({{\mathbf {s}}})\). We first modify how these random tapes are generated. Parse \({{\mathbf {s}}}\) as Q equally-long seeds, \({{\mathbf {s}}}_1, \cdots {{\mathbf {s}}}_Q\), and use \({{\mathbf {s}}}_q\) to generate the \(q^\mathrm{th}\) bit in all the random tapes, that is,
where \(\mathbf{PRG}_i\) is the function that computes the \(i^\mathrm{th}\) output bit of the PRG, which depends on at most L seed bits with indexes \(\gamma \in \Gamma (i)\). \(\mathbf{PRG}({{\mathbf {s}}}_q)\) is a length-I string, and hence the length \(|{{\mathbf {s}}}_q|\) of each seed \({{\mathbf {s}}}_q\) is sublinear in \(S(\lambda )\). Since each encoding \(\hat{f}_i\) has degree 3 in its random tape \({{\mathbf {r}}}[i]\), consider an arbitrary degree 3 monomial \({{\mathbf {r}}}[i]_{q_1}{{\mathbf {r}}}[i]_{q_2}{{\mathbf {r}}}[i]_{q_2}\).
where \(\Gamma (i) = \{ {\gamma _1, \cdots , \gamma _L} \}\). Now, suppose that for every index \(\gamma \in [|{{\mathbf {s}}}_q|]\) in all seeds, the encryptor pre-compute all the degree \(\le 3\) monomials over the \(\gamma ^\mathrm{th}\) bits in all Q seeds; denote this set as
Note that given \(M^3({{\mathbf {s}}},\gamma )\) for every \(\gamma \in \Gamma (i)\), the above monomial \({{\mathbf {r}}}[i]_{q_1}{{\mathbf {r}}}[i]_{q_2}{{\mathbf {r}}}[i]_{q_2}\) can be computed in just degree L. Therefore, given \(M^3({{\mathbf {s}}}, \gamma )\) for every \(\gamma \in [|{{\mathbf {s}}}_q|]\), the function g can be computed in degree L (with additionally the above-mentioned trick for reducing the degree in \({{\mathbf {x}}}\)). More precisely, there exists a degree-L polynomial \(g''\) that, on input \({{\mathbf {x}}}\), \(\{ {M^3({{\mathbf {s}}}, \gamma )} \}_\gamma \), and their tensor product, computes \(g({{\mathbf {x}}}, {{\mathbf {s}}})\).
Finally, we need to make sure that the total number of such degree \(\le 3\) monomials is sublinear in \(S(\lambda )\), so that, encryption remains weakly-compact. Note that, for each \(\gamma \in [|{{\mathbf {s}}}_q|]\), the number of degree \(\le 3\) monomials over the \(\gamma ^\mathrm{th}\) bits in these Q seeds is bounded by \((Q+1)^3 = \mathrm {poly}(\lambda )\). Moreover, the length of each seed \(|s_q|\) is still sublinear in \(S(\lambda )\). Thus, the total number of monomials to be pre-computed is sublinear in \(S(\lambda )\).
A formal description of our weakly-compact FE scheme can be found in Fig. 2. Important difference from the LV scheme is highlighted with red underline.
2.2 Quadratic Secret-Key FE
Before proceeding to constructing degree-D FE schemes from SXDH on degree-D MMaps, we describe a self-contained construction of FE for quadratic polynomials from SXDH on bilinear maps. The degree-D scheme is a generalization of the quadratic scheme.
We start with reviewing the tool, Inner Product Encryption (IPE), for constructing quadratic FE. A (public key or secret key) IPE scheme allows to encode vectors \({\mathbf {y}}\) and \({\mathbf {x}}\) in a ring \(\mathcal {R} \), in a function key \(\mathsf {iSK}({{\mathbf {y}}})\) and ciphertext \(\mathsf{iCT}({{\mathbf {x}}})\) respectively, and decryption evaluates the inner product \(\left\langle {{\mathbf {y}}, {\mathbf {x}}} \right\rangle \). In this work (like in [44]), we use specific IPEs that compute the inner product in the exponent, which, in particular, allows the decryptor to test whether the inner product is zero, or whether it falls into any polynomial-sized range.Footnote 5
Given IPE schemes, it is trivial to implement FE for quadratic polynomials, or quadratic FE schemes for short: Simply write a quadratic function f as a linear function over quadratic monomials \(f(x) = \Sigma _{i,j} c_{i,j} x_ix_j = \left\langle {{\mathbf {c}}, {\mathbf {x}} \otimes {\mathbf {x}}} \right\rangle \). Then, generate an IPE secret key \(\mathsf {iSK}({{\mathbf {c}}})\), and an IPE ciphertext \(\mathsf {iSK}({{\mathbf {x}}}\otimes {{\mathbf {x}}})\), from which the function output can be computed. However, such a scheme has encryption time quadratic in the input length \(N = |{{\mathbf {x}}}|\). The key challenge is improving the encryption time to be linear in the input length under standard assumptions (e.g. bilinear maps).
In this work, we do so based on SXDH on bilinear maps, where the exponent space \(\mathcal {R}\) of the bilinear map is the ring in which quadratic polynomials are evaluated. At a high-level, our key idea is “compressing” the encryption time of the above trivial quadratic FE schemes from quadratic to linear, by publishing some “compressed information” of linear size at encryption time, which can be expanded to an IPE ciphertext of \({{\mathbf {x}}}\,\otimes \,{{\mathbf {x}}}\) at decryption time. To make this idea work, we will use, as our basis, the public key IPE scheme by Abdalla et al. (ABDP) [1] based on the DDH assumption; we briefly review their scheme.
The ABDP Public Key IPE Scheme. The ABDP scheme \(\mathbf{IPE}\) resembles the El Gamal encryption and is quite simple. Let G be a cyclic group of order p with generator g, in which DDH holds. A master secret key of the ABDP scheme is a random vector  , and its corresponding public key is \(\mathsf {iMPK}= g^{s_1}, \cdots g^{s_N}\). A ciphertext encrypting a vector \({{\mathbf {x}}}= x_1, \cdots , x_N\) looks like \(\mathsf{iCT}= g^{-r}, \ g^{rs_1 + x_1},\ \cdots ,\ g^{rs_N + x_N}\), where r is the random scalar “shared” for encrypting every coordinate. It is easy to see that it follows from DDH that this encryption is semantically secure.
, and its corresponding public key is \(\mathsf {iMPK}= g^{s_1}, \cdots g^{s_N}\). A ciphertext encrypting a vector \({{\mathbf {x}}}= x_1, \cdots , x_N\) looks like \(\mathsf{iCT}= g^{-r}, \ g^{rs_1 + x_1},\ \cdots ,\ g^{rs_N + x_N}\), where r is the random scalar “shared” for encrypting every coordinate. It is easy to see that it follows from DDH that this encryption is semantically secure.
To turn the above scheme into an IPE, observe that given a vector \({{\mathbf {y}}}\in \mathbb {Z}_p^N\), and in addition the inner product \(\left\langle {{{\mathbf {y}}}, {{\mathbf {s}}}} \right\rangle \) in the clear, one can homomorphically compute inner product in the exponent to obtain \(g^{-r \left\langle {{{\mathbf {y}}},{{\mathbf {s}}}} \right\rangle } g^{r\left\langle {{{\mathbf {s}}}, {{\mathbf {y}}}} \right\rangle + \left\langle {{{\mathbf {x}}}, {{\mathbf {y}}}} \right\rangle } = g^{\left\langle {{{\mathbf {x}}}, {{\mathbf {y}}}} \right\rangle }\), which reveals whether the inner product \(\left\langle {{{\mathbf {x}}}, {{\mathbf {y}}}} \right\rangle \) is zero or not. Therefore, the ABDP scheme sets the secret key to be \(\mathsf {iSK}= \left\langle {{{\mathbf {s}}}, {{\mathbf {y}}}} \right\rangle ||{{\mathbf {y}}}\).
In this work, we will use the bracket notation  to represent elements in group \(G_l\), and omit l when there is no need to specify the group. Under this notation, the ABDP scheme can be written as,
to represent elements in group \(G_l\), and omit l when there is no need to specify the group. Under this notation, the ABDP scheme can be written as,

where \(a{\mathbf {u}}\) denotes coordinate-wise multiplication with a scalar a and \({\mathbf {u}}+ {{\mathbf {v}}}\) denotes coordinate-wise addition between two vectors. We will also refer to  as an encoding of x in group \(G_l\).
as an encoding of x in group \(G_l\).
 The first difficulty with “compressing” a ciphertext
The first difficulty with “compressing” a ciphertext  is that it contains information of the master secret key \({{\mathbf {s}}}\) of quadratic length, which is truely random and cannot be “compressed”.
is that it contains information of the master secret key \({{\mathbf {s}}}\) of quadratic length, which is truely random and cannot be “compressed”.
Our idea is replacing the truly random secret key \({{\mathbf {s}}}\) with the tensor product of two length-N vectors \({{\mathbf {s}}}^1\,\otimes \,{{\mathbf {s}}}^2\), so that, the new ciphertext depends only on information, namely \((r, {{\mathbf {s}}}^1, {{\mathbf {s}}}^2, {{\mathbf {x}}})\), of linear size. The reason that we use the tensor product \({{\mathbf {s}}}^1 \,\otimes \, {{\mathbf {s}}}^2\) as the secret key is that under DDH, encodings  is indistinguishable to encodings of \(N^2\) truely random elements, and hence there is hope that \({{\mathbf {s}}}^1 \,\otimes \, {{\mathbf {s}}}^2\) is “as good as” a truly random master secret key. As we will see later, this hope is true, however through complicated security proof.
is indistinguishable to encodings of \(N^2\) truely random elements, and hence there is hope that \({{\mathbf {s}}}^1 \,\otimes \, {{\mathbf {s}}}^2\) is “as good as” a truly random master secret key. As we will see later, this hope is true, however through complicated security proof.
Now, it is information theoretically possible to compress \(\mathsf{iCT}({{\mathbf {x}}}\,\otimes \, {{\mathbf {x}}})\). However, simply publishing \((r, {{\mathbf {s}}}^1, {{\mathbf {s}}}^2, {{\mathbf {x}}})\) would blatantly violate security. We need a way to securely and succinctly encode them so that only the ciphertext \(\mathsf{iCT}\) is revealed. Classical cryptographic tools for hiding computation like garbled circuits or randomized encodings do not help here, since the output length is quadratic, and garbled circuits or randomized encodings have at least quadratic size too. Instead, we leverage the special structure of \(\mathsf{iCT}\): Each of the last \(N^2\) encodings of \(\mathsf{iCT}\) encodes an element that is the inner product of two length-2 vectors,

Here, for convenience, we use 0 and \(\{ {(i, j)} \}\) to index different encodings in \(\mathsf{iCT}\).
Suppose that we have a (secret key) IPE scheme \({\mathbf{cIPE}}\) that is function hiding (defined shortly) from bilinear maps, and has certain canonical form: In particular, its ciphertexts and secret keys encodes the input and function vectors in different source groups \(G_1, G_2\) of the bilinear map, and decryption simply uses pairing to produce an encoding of the output inner product in the target group \(G_3\). (Unfortunately, off-the-shelf function hiding IPEs [12, 24, 44] do not have the canonical form and we discuss how to construct such a scheme later.)
Then, we can use a canonical function hiding IPE, to generate the last \(N^2\) encodings \(\{ {\mathsf{iCT}[i,j]} \}\): Publish N ciphertext \(\{ {\mathsf{cCT}_i} \}\) where each \(\mathsf{cCT}_i\) encrypts vector \((x_i||s^1_i)\), and N secret keys \(\{ {\mathsf {cSK}_j} \}\) where each \(\mathsf {cSK}_j\) encrypts vector \((x_j||r s_j^2)\). To obtain the \((i, j)^\mathrm{th}\) encoding, one can simply decrypt the \(i^\mathrm{th}\) ciphertext using the \(j^\mathrm{th}\) secret key, which produces

In order to hide r, \(x_j\)’s, and \(s_j^1,s_j^2\)’s, it is necessary that the IPE scheme is function hiding, which guarantees that secret keys and ciphertexts for two sets of vectors \(\{ {{\mathbf {u}}_i, {\mathbf {v}}_i} \}\) and \(\{ {{\mathbf {u}}'_i, {\mathbf {v}}'_i} \}\) are indistinguishable if they produce identical inner products \(\left\langle {{\mathbf {u}}_i, {\mathbf {v}}_j} \right\rangle = \langle {\mathbf {u}}'_i, {\mathbf {v}}'_j\rangle \). The hope is that function hiding is also sufficient, as, intuitively, it ensures that only the set of possible outputs \(\{ {\mathsf{iCT}[i,j]} \}\) is revealed, and all other information of \((r, {{\mathbf {x}}}, {{\mathbf {s}}}^1, {{\mathbf {s}}}^2)\) is hidden. (This intuition is not precise, as the IPE scheme is not simulation-secure, but is a good starting point.)
In summary, we now have the first version of our quadratic FE schemes.
-
Version 1 of Our Secret Key Quadratic FE scheme \(\mathbf{qFE}\)
-
– Setup: A master secret key \(\mathsf{msk}\) consists of two random vectors \({{\mathbf {s}}}^1, {{\mathbf {s}}}^2\) of length N.
-
– Key Generation: A secret key \(\mathsf {SK}({{\mathbf {c}}})\) of a function \(f_{{\mathbf {c}}}({{\mathbf {x}}}) = \left\langle {{{\mathbf {c}}}, {{\mathbf {x}}}\,\otimes \, {{\mathbf {x}}}} \right\rangle \) consists of
$$\begin{aligned} \mathsf {SK}({{\mathbf {c}}}) = \left( \ \left\langle {{{\mathbf {s}}}^1 \,\otimes \, {{\mathbf {s}}}^2, {{\mathbf {c}}}} \right\rangle , \ {{\mathbf {c}}}\ \right) . \end{aligned}$$ -
– Encryption: Sample a random scalar
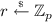 . A ciphertext \(\mathsf{CT}({{\mathbf {x}}})\) of input vector \({{\mathbf {x}}}\) contains
. A ciphertext \(\mathsf{CT}({{\mathbf {x}}})\) of input vector \({{\mathbf {x}}}\) contains  (1)
(1)and \(\{ {\mathsf {cSK}_j,\ \mathsf{cCT}_i} \}\) are generated using a freshly sampled master secret key \(\mathsf {cMSK}\) of a canonical function hiding IPE \({\mathbf{cIPE}}\).
-
– Decryption: For every \((i, j) \in [N]^2\), decrypt \(\mathsf{cCT}_i\) using \(\mathsf {cSK}_j\) to obtain
 (2)
(2)Homomorphically compute
 , and \(\varLambda _2 = \left\langle {\{ {\mathsf{iCT}[i,j]} \} ,\ {{\mathbf {c}}}} \right\rangle \). Homomorphically add \(\varLambda _1 + \varLambda _2\) to produce an encoding of the output
, and \(\varLambda _2 = \left\langle {\{ {\mathsf{iCT}[i,j]} \} ,\ {{\mathbf {c}}}} \right\rangle \). Homomorphically add \(\varLambda _1 + \varLambda _2\) to produce an encoding of the output 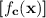 .
.
-
Next, we move to describing ideas for the security proof. As we develop the proof ideas, we will need to make several modifications to the above scheme.
Selective IND-Security of Our Quadratic FE Scheme. We want to show that ciphertexts of \(\mathbf{qFE}\) of one set of inputs \(\{ {{\mathbf {u}}_i} \}\) is indistinguishable from that of another \(\{ {{{\mathbf {v}}}_i} \}\), as long as all the secret keys published are associated with functions \(\{ {f_{{{\mathbf {c}}}_j}} \}\) that do not separate these inputs, that is, \(f_{{{\mathbf {c}}}_j}({\mathbf {u}}_i) = f_{{{\mathbf {c}}}_j}({{\mathbf {v}}}_i)\) for all i, j. For simplicity of this overview, we restrict our attention to the simpler case where only a single ciphertext and many secret keys are published. The security proof for the general case with many ciphertexts follows from a hybrid argument where the encrypted vectors are switched one by one from \({\mathbf {u}}_i\) to \({{\mathbf {v}}}_i\), and the indistinguishability of each step is proven using the same ideas to the single-ciphertext case.
Naturally, we want to reduce the security of \(\mathbf{qFE}\) the security of the ABDP IPE scheme \(\mathbf{IPE}\) and the function hiding of \({\mathbf{cIPE}}\). Our intuition is that given a ciphertext \(\mathsf{CT}({{\mathbf {x}}})\) for \({{\mathbf {x}}}= {\mathbf {u}}\) or \({{\mathbf {v}}}\), the security of \({\mathbf{cIPE}}\) ensures that the N ciphertexts and secret keys \(\{ {\mathsf{cCT}_i} \}, \{ {\mathsf {cSK}_j} \}\) contained in ciphertext \(\mathsf{CT}({{\mathbf {x}}})\) reveals only the output encodings \(\{ {\mathsf{iCT}[i,j]} \}\) and nothing else. Then, the security of the ABDP scheme ensures that the derived ciphertext \(\mathsf{iCT}\) encrypting either \({\mathbf {u}}\,\otimes \, {\mathbf {u}}\) or \({{\mathbf {v}}}\,\otimes \, {{\mathbf {v}}}\) is indistinguishable, at the presence of secret keys for vectors \(\{ {{{\mathbf {c}}}_j} \}\) that do not separate them. This intuition would go through if the two building blocks \({\mathbf{cIPE}}\) and \(\mathbf{IPE}\) provide very strong security guarantees: Naturally, \({\mathbf{cIPE}}\) has simulation security, so that, its ciphertexts and secret keys \(\{ {\mathsf{cCT}_i} \}, \{ {\mathsf {cSK}_j} \}\) can be simulated from the set of output encodings \(\{ {\mathsf{iCT}[i,j]} \}\), and second, the ABDP scheme is secure even when the master secret keys are generated as a tensor product \({{\mathbf {s}}}^1 \,\otimes \, {{\mathbf {s}}}^2\) as opposed to be truely random. Unfortunately, our building blocks do not provide such strong security guarantees, which leads to the following challenges.
-
Challenge 1—Relying only on indistinguishability-based function hiding of \({\mathbf{cIPE}}\) . The simulation security of \({\mathbf{cIPE}}\) essentially allows one to easily reduce the security of \(\mathbf{qFE}\) to that of \(\mathbf{IPE}\). With only indistinguishability-based security of \({\mathbf{cIPE}}\), the reduction to security of \(\mathbf{IPE}\) becomes significantly harder. Typically, one build a black-box security reduction that receives from its challenger \(\mathbf{IPE}\) secret keys and a ciphertext, in this case \(\{ {\mathsf {SK}_j} \}, \mathsf{iCT}\), and embeds them in the view of the adversary attacking the \(\mathbf{qFE}\) scheme. However, the ciphertext \(\mathsf{CT}\) of \(\mathbf{qFE}\) has only linear size, but \(\mathsf{iCT}\) has quadratic size—there is not enough space for embedding.Footnote 6
To resolve this problem, our idea is to embed \(\mathsf{iCT}\) in “piecemeal”. Observe that the ABDP scheme encrypts its input vector element by element using different master secret key elements, and a shared random scalar. Thus, we can flexibly view its ciphertext \(\mathsf{iCT}\) either as a single ciphertext, or as a list of many ciphertexts encrypting a list of vectors of shorter length. In particular, we will “cut” the ciphertext into N pieces, each of length N and indexed by \(i \in [N]\).
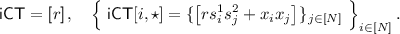
Since the \(i^\mathrm{th}\) ciphertext-piece can be viewed as an \(\mathbf{IPE}\) ciphertext of vector \(x_i{{\mathbf {x}}}\), generated with master secret key \(s^1_i{{\mathbf {s}}}^2\) and shared random scalar r. Our idea is gradually switching the values of \(x_i{{\mathbf {x}}}\) from \(u_i{\mathbf {u}}\) to \(v_i{{\mathbf {v}}}\) piece by piece in N steps. In each step, we first apply the function hiding of \({\mathbf{cIPE}}\) to move to a hybrid distribution where the challenge-piece \(\mathsf{iCT}[i, \star ]\) is directly hardwired in the \(\mathbf{qFE}\) ciphertext; since \(|\mathsf{iCT}[i, \star ]| = N\), there is enough space for it. Then, we rely on the indistinguishability-security of \(\mathbf{IPE}\) to argue that switching the plaintext-piece underlying \(\mathsf{iCT}[i, \star ]\) from \(u_i {\mathbf {u}}\) to \(v_i {{\mathbf {v}}}\) is indistinguishable.
-
Challenge 2—Relying on the security of the ABDP scheme under correlated randomness. Arguing the indistinguishability of switching the vectors underlying each ciphertext-piece \(\mathsf{iCT}[i, \star ]\) from \(u_i{\mathbf {u}}\) to \(v_i{{\mathbf {v}}}\) turns out to be tricky. First, An acute reader might have already noticed the problem that changing pieces in the tensor product would affect the function output, which is noticeable. For example, after switching the first plaintext piece to \(v_i{{\mathbf {v}}}\), the function output changes to \(\left\langle {{{\mathbf {c}}}_j, {\mathbf {u}}\,\otimes \, {\mathbf {u}}} \right\rangle \ne \left\langle {{{\mathbf {c}}}_j, v_1{{\mathbf {v}}}|| {\mathbf {u}}_{\ge 1}\,\otimes \, {\mathbf {u}}} \right\rangle \). To resolve this problem, we modify the scheme to build in an offset value \(\varDelta _j\) in every secret key \(\mathsf {SK}_j\) to ensure that the function output remains the same throughout all steps.
Second, the challenge ciphertext-piece is generated with master secret key \(s^1_i{{\mathbf {s}}}^2\), which is not truly random, since the vector \({{\mathbf {s}}}^2\) is used for generating the master secret keys \(s_{k}^1{{\mathbf {s}}}^2\) of other ciphertext-pieces for \(k \ne i\). We overcome this by relying on the SXDH assumption to argue that encodings of \(s^1_i{{\mathbf {s}}}^2\), given encodings of \(s^1_i\) and \({{\mathbf {s}}}^2\), are indistinguishable to encodings of random elements, and hence as good as a truly random master secret key. Similar idea was used in [44].
Next, we discuss in more detail how to overcome these two challenges.
Overcoming Challenge 1—Embed ABDP IPE ciphertext in piecemeal. Our goal is switching piece by piece the tensor product underlying the derived \(\mathbf{IPE}\) ciphertext from \({\mathbf {u}}\,\otimes \, {\mathbf {u}}\) to \({{\mathbf {v}}}\,\otimes \, {{\mathbf {v}}}\), which corresponds to changing the encrypted input from \({\mathbf {u}}\) to \({{\mathbf {v}}}\). To do so, we build a sequence of 2N hybrids \(\{ {H_\rho ^b} \}_{\rho \in [N], b \in \{0,1\}}\) satisfying the following desiderata:
-
1.
In \(H_\rho ^b\), the \(\rho ^\mathrm{th}\) ciphertext-piece \(\mathsf{iCT}[\rho , \star ]\) is embedded in the \(\mathbf{qFE}\) ciphertext \(\mathsf{CT}\),
-
2.
The derived \(\mathbf{IPE}\) ciphertext \(\mathsf{iCT}\) encrypts the following “hybrid” vectors.

To build such hybrids, we need to modify our \(\mathbf{qFE}\) scheme to build in more “redundant space” in its ciphertext.
-
Version 2 of Our Secret Key Quadratic FE scheme \(\mathbf{qFE}\)
-
– Encryption: A ciphertext \(\mathsf{CT}({{\mathbf {x}}})\) consists of
 (3)
(3)where \(\{ {\mathsf{cCT}_i} \}\) and \(\{ {\mathsf {cSK}_j} \}\) encode vectors \(\varvec{\chi }^d_i\) like before, but now padded with 3 zeros.
-
We refer to the first 4 elements in \({{\mathbf {X}}}\)’s as the first slot, which holds two vectors of length 2, and the last element as the second slot. In the honest executions, these vectors \(\{ {{{\mathbf {X}}}^d_i} \}\) are set to either \((\varvec{\mu }^d||\mathbf {0}, 0)\) if \({\mathbf {u}}\) is encrypted, or \((\varvec{\nu }^d||\mathbf {0}, 0)\) if \({{\mathbf {v}}}\) is encrypted, with \(\varvec{\mu }\) and \(\varvec{\nu }\) defined as \(\varvec{\chi }\) in Eq. 1 but replacing \(x_i\) with \(u_i\) or \(v_i\) respectively.
 Hybrid \(H_\rho ^b\) uses the following set of vectors \({{\mathbf {X}}}\)’s, which leverages the “space” of the additional zeros to satisfy the above desiderata.
Hybrid \(H_\rho ^b\) uses the following set of vectors \({{\mathbf {X}}}\)’s, which leverages the “space” of the additional zeros to satisfy the above desiderata.
Let us first see how the challenge ciphertext-piece \(\mathsf{iCT}[\rho , \star ]\) is hardwired. Observe that the last slots of \({{\mathbf {X}}}^2_j\)’s contain exactly the values encoded in \(\mathsf{iCT}[\rho , \star ]\): In \(H_\rho ^0\), they are set to \(\{ {\left\langle {\varvec{\mu }^1_\rho , \varvec{\mu }^2_j} \right\rangle = r s^1_\rho s^2_j + u_\rho u_j} \}_{j\in [N]}\) (see Eq. 2), corresponding to encrypting \(u_\rho {\mathbf {u}}\), while in \(H_\rho ^1\), they are set to \(\{ {\left\langle {\varvec{\nu }^1_\rho , \varvec{\nu }^2_j} \right\rangle = r s^1_\rho s^2_j + v_\rho v_j} \}_j\), encrypting \(v_\rho {{\mathbf {v}}}\). By the fact that \({\mathbf{cIPE}}\) encodes its function vectors, \({{\mathbf {X}}}^2_j\)’s here, in a bilinear source group,  is effectively embedded in \(\mathsf {cSK}_j\)’s and hence so is \(\mathsf{iCT}[\rho , \star ]\). Next, we check that the \(\mathbf{IPE}\) ciphertext derived by decrypting every pair \((\mathsf{cCT}_i,\mathsf {cSK}_j)\) indeed encrypts the right hybrid vector.
is effectively embedded in \(\mathsf {cSK}_j\)’s and hence so is \(\mathsf{iCT}[\rho , \star ]\). Next, we check that the \(\mathbf{IPE}\) ciphertext derived by decrypting every pair \((\mathsf{cCT}_i,\mathsf {cSK}_j)\) indeed encrypts the right hybrid vector.

In the case \(i = \rho \), \(\mathsf{iCT}[\rho ,\star ]\) encodes exactly the values hardwired in the last slot, which as argued above encrypts \(u_\rho {\mathbf {u}}\) in \(H_\rho ^0\) and \(v_\rho {{\mathbf {v}}}\) in \(H_\rho ^1\) as desired. In the case \(i < \rho \), the derived ciphertext-piece \(\mathsf{iCT}[i, \star ]\) encodes values \(\{ {\left\langle {\varvec{\nu }^1_i, \varvec{\nu }^2_j} \right\rangle } \}_j\), corresponding to encrypting \(v_i {{\mathbf {v}}}\); and similarly, when \(i > \rho \), the ciphertext-piece \(\mathsf{iCT}[i, \star ]\) encrypts \(u_i{\mathbf {u}}\) as desired. Therefore, all desiderata above are satisfied.
Now, to show the security of \(\mathbf{qFE}\), it suffices to argue that every pair of neighboring hybrids is indistinguishable. Note that the only difference between different hybrids lies in the values of the \({{\mathbf {X}}}\) vectors encoded in the ciphertexts and secret keys of \({\mathbf{cIPE}}\). Observe first that in hybrids \(H_\rho ^1\) and \(H^0_{\rho +1}\), every pair of vectors \(({{\mathbf {X}}}^1_i, {{\mathbf {X}}}^2_j)\) produce the same inner products, and hence the indistinguishability of \(H_\rho ^1\) and \(H^0_{\rho +1}\) follows immediately from the function hiding property of \({\mathbf{cIPE}}\). This is, however, not the case in hybrids \(H^0_\rho \) and \(H^1_\rho \), where for the special index \(\rho \), the challenge ciphertext-piece change from encrypting \(u_\rho {\mathbf {u}}\) to \(v_\rho {{\mathbf {v}}}\). Next, we show how to reduce the indistinguishability of \(H_\rho ^0\) and \(H_\rho ^1\) to the security of the ABDP IPE scheme, which turns out to be quite tricky.
Overcoming Challenge 2: Indistinguishability of \(H^0_{\rho }\) and \(H^1_\rho \) from IPE security. The goal is relying on the security of \(\mathbf{IPE}\) to argue that the embedded challenge ciphertext-pieces in \(H^0_\rho \) and \(H^1_\rho \) are indistinguishable, and hence so are the hybrids. But, we immediately encounter a problem: The function outputs obtained when decrypting the derived ciphertext \(\mathsf{iCT}\) using secret keys \(\mathsf {SK}_j\)’s are different in \(H^0_\rho \) and \(H^1_\rho \), namely

This means the hybrids are clearly distinguishable. To fix this, we modify our \(\mathbf{qFE}\) scheme to build in an offset value \(\varDelta \) in its secret keys, which will be added to the decryption output. In the honest execution, the offsets are set to zero, whereas in hybrid \(H^b_\rho \), they are set to \(\varDelta ^b_j(\rho )\) in each secret key \(\mathsf {SK}_j\), so that, the above inner products when added with \(\varDelta ^0_j(\rho )\) in the left hand side and \(\varDelta ^1_j(\rho )\) in the right hand side become equal. Clearly, whether the offset values \(\varDelta \) are used (set to non-zero) at all and their values must be hidden, we do so by encoding it using \({\mathbf{cIPE}}\), as described below.
-
Version 3 of Our Secret Key Quadratic FE schemes \(\mathbf{qFE}\)
-
– Setup: A master secret key \(\mathsf{msk}= ({{\mathbf {s}}}^1, {{\mathbf {s}}}^2, \mathsf {cMSK}')\) contains additionally
 .
. -
– Key Generation: In the secret key \(\mathsf {SK}({{\mathbf {c}}})\), the inner product \(\left\langle {{{\mathbf {s}}}^1 \,\otimes \, {{\mathbf {s}}}^2, {{\mathbf {c}}}} \right\rangle \) is now encoded, together with an offset value \(\varDelta \), using \(\mathsf {cMSK}'\) of \({\mathbf{cIPE}}\):

-
– Encryption: In the ciphertext \(\mathsf{CT}({{\mathbf {x}}})\), the random scalar r is now encrypted, with an additional 0, using \(\mathsf {cMSK}'\) of \({\mathbf{cIPE}}\):
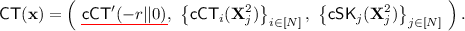
-
– Decryption: Decryption proceeds as before, except that now encoding \(\varLambda _1\) is obtained by decrypting \(\mathsf{cCT}'\) using \(\mathsf {cSK}'\), which yields
 as desired.
as desired.
-
With the new offset value in secret key, we can now fix our hybrids so that the function outputs always stay the same.
 In hybrid \(H_\rho ^b\), not only that the vectors \({{\mathbf {X}}}\)’s are set differently as above, the \({\mathbf{cIPE}}\) ciphertext \(\mathsf{cCT}'\) in ciphertext \(\mathsf{CT}\) encrypts (0||1) instead of \((-r||0)\) and the corresponding \({\mathbf{cIPE}}\) secret key \(\mathsf {cSK}'_{j}\) in \(\mathsf {SK}_j\) encodes vector \(( \left\langle {{{\mathbf {s}}}^1 \,\otimes \, {{\mathbf {s}}}^2, {{\mathbf {c}}}} \right\rangle \ ||\ r \left\langle {{{\mathbf {s}}}^1 \,\otimes \, {{\mathbf {s}}}^2, {{\mathbf {c}}}} \right\rangle + \varDelta _j^b(\rho ) )\), instead of \(( \left\langle {{{\mathbf {s}}}^1 \,\otimes \, {{\mathbf {s}}}^2, {{\mathbf {c}}}} \right\rangle || 0)\). At decryption time, the offset \(\varDelta _j^b(\rho )\) is added to the inner product between \({{\mathbf {c}}}_j\) and hybrid vector underlying \(\mathsf{iCT}\). Setting \(\varDelta _j^b(\rho )\) appropriately ensures that
In hybrid \(H_\rho ^b\), not only that the vectors \({{\mathbf {X}}}\)’s are set differently as above, the \({\mathbf{cIPE}}\) ciphertext \(\mathsf{cCT}'\) in ciphertext \(\mathsf{CT}\) encrypts (0||1) instead of \((-r||0)\) and the corresponding \({\mathbf{cIPE}}\) secret key \(\mathsf {cSK}'_{j}\) in \(\mathsf {SK}_j\) encodes vector \(( \left\langle {{{\mathbf {s}}}^1 \,\otimes \, {{\mathbf {s}}}^2, {{\mathbf {c}}}} \right\rangle \ ||\ r \left\langle {{{\mathbf {s}}}^1 \,\otimes \, {{\mathbf {s}}}^2, {{\mathbf {c}}}} \right\rangle + \varDelta _j^b(\rho ) )\), instead of \(( \left\langle {{{\mathbf {s}}}^1 \,\otimes \, {{\mathbf {s}}}^2, {{\mathbf {c}}}} \right\rangle || 0)\). At decryption time, the offset \(\varDelta _j^b(\rho )\) is added to the inner product between \({{\mathbf {c}}}_j\) and hybrid vector underlying \(\mathsf{iCT}\). Setting \(\varDelta _j^b(\rho )\) appropriately ensures that

Now \(H_\rho ^0\) and \(H_\rho ^1\) have the same function outputs. But, to formally reduce their indistinguishability to the security of \(\mathbf{IPE}\), we need a way to incorporate the offsets \(\varDelta \)’s into the challenge \(\mathbf{IPE}\) ciphertexts. We do so by viewing \(\varDelta _j\)’s as extension of the plaintext. More specifically, we implicitly switch from encrypting \({\mathbf {U}} = u_\rho {\mathbf {u}}||\varDelta ^0_1(\rho )||\cdots ||\varDelta _L^0(\rho )\) to \({\mathbf {V}} = v_\rho {{\mathbf {v}}}||\varDelta _1^1(\rho )||\cdots ||\varDelta _L^1(\rho )\) using master secret key \({\mathbf {S}} = s_\rho ^1{{\mathbf {s}}}^2 || t_1 || \cdots ||t_L\), at the presence of secret keys for vectors \({{\mathbf {Y}}}_j = \{ {{{\mathbf {c}}}_j[\rho ,\star ]||e_j} \}_j\), where L is the total number of keys, \(t_j\)’s are implicitly sampled secret key elements, and \(e_j\) is the unit vector of length L with a single one at index j. Observe that from such ciphertexts and secret keys, one can extract the challenge ciphertext-piece \(\mathsf{iCT}[\rho , \star ]\) encrypting \(u_\rho {\mathbf {u}}\) or \(v_\rho {{\mathbf {v}}}\), and obtain an encoding of \(-r\left\langle {{{\mathbf {s}}}^1 \,\otimes \, {{\mathbf {s}}}^2, {{\mathbf {c}}}} \right\rangle + \varDelta _j^b(\rho )\) embedded in each secret key \(\mathsf {cSK}'_j\)—these are the only parts that hybrids \(H_\rho ^0\) and \(H_\rho ^1\) differ at. Given that \(\left\langle {{\mathbf {U}}, {{\mathbf {Y}}}_j} \right\rangle = \left\langle {{\mathbf {V}}, {{\mathbf {Y}}}_j} \right\rangle \) for every j, we are almost done: Apply the security of \(\mathbf{IPE}\) to argue that \(H_\rho ^0\) and \(H_\rho ^1\) are indistinguishable, except that we must overcome one last hurdle—the master secret key for encrypting \(u_i{\mathbf {u}}\) or \(v_i{{\mathbf {v}}}\) is not truely random.
Pseudorandomness from SXDH. The master secret key of the challenge ciphertext-piece is \(s_\rho ^1{{\mathbf {s}}}^2\). It is not truely random since \({{\mathbf {s}}}^2\) is also used for generating the master secret keys of other ciphertext-pieces. But, observe that both the challenge ciphertext-piece and \({{\mathbf {s}}}^2\) are embedded in secret keys \(\{ {\mathsf {cSK}_j} \}\), and hence encoded in the same bilinear map source group. Furthermore, thanks to the fact that in \(H_\rho ^b\), the \(\rho ^\mathrm{th}\) ciphertext \(\mathsf{cCT}_\rho \) encrypts the vector \((\mathbf {0}||\mathbf {0}, 1)\), the key element \(s^1_\rho \) does not appear in the other source group. Therefore, we can apply the SXDH assumption to argue that encodings of \(s_\rho ^1{{\mathbf {s}}}^2\) is indistinguishable to that of a truly random vector \({{\mathbf {w}}}\)—in other words, the master secret key \(s_\rho ^1{{\mathbf {s}}}^2\) is pseudorandom, inside encodings. Therefore, the security of \(\mathbf{IPE}\) applies, and we conclude that hybrid \(H_\rho ^0\) and \(H_\rho ^1\) are indistinguishable.
2.3 Degree-D Secret-Key FE
Generalizing from quadratic FE to degree-D secret key FE, the natural idea is again starting from the trivial \(\mathbf{IPE}\)-based construction that encrypts all degree-D monomials, denoted as  , and compressing the \(N^D\)-size ciphertext into linear size. Naturally, instead of compressing a ciphertext generated using a truly random master secret key, we will use a structured master secret key
, and compressing the \(N^D\)-size ciphertext into linear size. Naturally, instead of compressing a ciphertext generated using a truly random master secret key, we will use a structured master secret key  . Thus the \(\mathbf{IPE}\) ciphertext to be compressed looks like:
. Thus the \(\mathbf{IPE}\) ciphertext to be compressed looks like:

The challenge is how to generate the \(N^D\) encodings \(\mathsf{iCT}[I]\) from just linear-sized information?
Key Tool: High-Degree IPE. We generalize IPE to the notion of high-degree IPE, or HIPE for short. More precisely, a degree-D HIPE is a multi-input functional encryption scheme for degree-D inner product defined as follows,
Introduced by [35], a multi-input functional encryption allows one to encrypt inputs at different coordinates, and generate secret keys associated with multi-input functions, so that, decryption computes the output of the function evaluated on inputs encrypted at different coordinates. In the context of HIPE, a degree-D HIPE encryption scheme \({\mathbf{hIPE}}\) allows one to generate a ciphertext \(\mathsf{hCT}^d({{\mathbf {x}}}^d)\) encrypting an input vector \({{\mathbf {x}}}^d\) at a coordinate \(d \in [D-1]\), and a secret key \(\mathsf {hSK}({{\mathbf {x}}}^D)\) at coordinate D, so that, decryption reveals whether the degree-D inner product \(\left\langle {{{\mathbf {x}}}^1 \cdots {{\mathbf {x}}}^D} \right\rangle \) is zero or not. Under this generalization, standard IPE is a special case of HIPE for degree \(D = 2\).
In terms of security, the notion of function hiding also generalizes naturally, HIPE is function hiding, if ciphertexts and keys \(\{ {\mathsf{hCT}^1_i, \cdots , \mathsf{hCT}^{D-1}_i, \mathsf {hSK}_i} \}_{i \in [L]}\) encoding two sets of vectors \(\{ {{\mathbf {u}}^1_i, \cdots , {\mathbf {u}}^{D-1}_i, {\mathbf {u}}^D_i} \}_{i \in [L]}\) and \(\{ {{{\mathbf {v}}}^1_i, \cdots , {{\mathbf {v}}}^{D-1}_i, {{\mathbf {v}}}^D_i} \}_{i \in [L]}\) are indistinguishable, whenever all degree-D inner products that can be computed from them are identical, that is,
In this work, we give a construction of function hiding degree-D HIPE scheme from the SXDH assumption on degree-D multilinear maps. Our construction starts from a canonical function hiding IPE scheme (for \(D = 2\)), and inductively build degree-\((D+1)\) HIPE scheme, by composing a degree-D HIPE scheme and a special-purpose function hiding IPE scheme. Our HIPE schemes have canonical form (similar to the canonical form for standard IPE): Ciphertexts (or secret keys) at coordinate d (or D) consist of encodings in the \(d^\mathrm{th}\) (or \(D^\mathrm{th}\) respectively) MMap source group, and decryption uses degree-D pairing to produce an encoding of the degree-D inner product. That is,

From Degree-D HIPE to Degree-D FE. HIPE works perfectly for our goal of compressing the ciphertext \(\mathsf{iCT}\). Generalizing \(\mathbf{qFE}\), our degree-D FE scheme \(\mathbf{dFE}\) generates ciphertexts as follows:
From such a ciphertext, a decryptor can “expand” out a size-\(N^D\) \(\mathbf{IPE}\) ciphertext \(\mathsf{iCT}\) by decrypting every combination of HIPE ciphertexts and secret keys. Namely, for every \(I \in [N]^D\),

where \(\mathsf{iCT}[I]\) encrypts the \(I^\mathrm{th}\) degree-D monomial \(\prod _{d \in [D]}x_{I_d}\), using the \(I^\mathrm{th}\) key element \(\prod _{d \in [D]}s^d_{I_d}\).
To show security of \(\mathbf{dFE}\), we, again, switch the degree-D monomials encrypted in the \(\mathbf{IPE}\) ciphertext \(\mathsf{iCT}\) in piecemeal. In each step, we can still only embed a size-N ciphertext-piece; naturally we embed \(\mathsf{iCT}[\rho , \star ]\) for a prefix \(\rho \in [N]^{D-1}\) of length \(D-1\). Thus, the \(N^D\) encrypted monomials are changed piece by piece in \(N^{D-1}\) steps, where in the \(\rho ^\mathrm{th}\) step, all monomials with index I smaller than \(\rho \) (i.e., \(I_{\le D-1} < \rho \)) have already been switched to \(\prod _{d \in [D]}v_{I_d}\), monomials with index I larger than \(\rho \) (i.e., \(I_{\le D-1}> \rho \)) remain to be \(\prod _{d \in [D]} u_{I_d}\), and monomials with index I that agrees with \(\rho \) (i.e., \(I_{\le D-1} = \rho \)) are being switched from \(\prod _{d \in [D]} u_{I_d}\) in \(H_\rho ^0\) to \(\prod _{d \in [D]} v_{I_d}\) in \(H_\rho ^1\).
Creating a sequence of hybrids that carry out these steps is more complex than the case for degree 2. First, we need more space in the ciphertext to make sure that the right monomials are encrypted for every index I; thus, the vectors \({{\mathbf {X}}}\)’s are padded to length \(2D-1\). Second, it becomes significantly harder to argue that the key elements \((\prod _{d \in [D-1]}s^d_{\rho _d}) {{\mathbf {s}}}^{\le D}\) are pseudorandom, as the shares \(s^d_i\)’s are encoded in different MMap source groups, and unlike the degree 2 case, we cannot eliminate the appearance of all shares \(\{ {s^d_{\rho _d}} \}\) since they are also used for generating the master secret keys of other ciphertext-pieces (whereas in the degree 2 case, \(s^1_\rho \) is only used for generating \(s^1_\rho {{\mathbf {s}}}^2\)). To resolve this, we apply the SXDH assumption iteratively to gradually replace every partial product \(\prod _{d \in [d^\star ]} s^d_{\rho _d}\) with an independent and random element \(w^d_\rho \), so that, the master secret keys for other ciphertext-pieces are generated using independent w elements.
2.4 Construction of HIPE
We construct function hiding HIPE schemes by induction in the degree D.
-
For the base case of \(D = 2\), function hiding degree-2 HIPE is identical to function hiding IPE, which we give a new construction discussed shortly in the next subsection.
-
For the induction step, we show that for any \(D \ge 2\), if there exist a function hiding degree-D HIPE scheme, denoted as \({\mathbf{dIPE}}\), from SXDH on degree-D MMap, then there exist a function-hiding degree-\((D+1)\) HIPE scheme, denoted as \({\mathbf{hIPE}}\), from SXDH on degree-\((D+1)\) MMap. Our induction keeps the invariant that both \({\mathbf{dIPE}}\) and \({\mathbf{hIPE}}\) have canonical form.
In the induction step, we construct the degree-\(D+1\) scheme \({\mathbf{hIPE}}\), by combining the degree-D scheme \({\mathbf{dIPE}}\), with a special purpose IPE scheme \({\mathbf{sIPE}}\). Denote by \((\mathsf{hCT}^1, \cdots , \mathsf{hCT}^D)\) and \(\mathsf {hSK}\) the ciphertexts and secret key of \({\mathbf{hIPE}}\), \((\mathsf{dCT}^1, \cdots , \mathsf{dCT}^{D-1})\) and \({\mathsf {dSK}}\) that of \({\mathbf{dIPE}}\), and \(\mathsf{sCT}\) and \(\mathsf {sSK}\) that of \({\mathbf{sIPE}}\).
To achieve functionality, we need to specify how to generate ciphertexts and secret key for input vectors \({{\mathbf {x}}}^1, \cdots , {{\mathbf {x}}}^{D}\) and \({{\mathbf {x}}}^{D+1}\), so that,

Observe that a degree-\((D+1)\) inner product of \({{\mathbf {x}}}^1, \cdots {{\mathbf {x}}}^{D+1}\), can be computed as the inner product between \({{\mathbf {x}}}^{D+1}\) and the coordinate-wise product of the first D vectors \(\prod _{d\in [D]}{{\mathbf {x}}}^{d}\), denoted as \({{\mathbf {x}}}^{\le D}\), that is,
Therefore, if the decryptor obtains a pair of \({\mathbf{sIPE}}\) ciphertext and secret key \((\mathsf{sCT}, \mathsf {sSK})\) for \(({{\mathbf {x}}}^{\le D}, {{\mathbf {x}}}^{D+1})\), he/she can decrypt to obtain  . To do so, our new scheme \({\mathbf{hIPE}}\) simply publishes \(\mathsf {sSK}\) as its secret key,
. To do so, our new scheme \({\mathbf{hIPE}}\) simply publishes \(\mathsf {sSK}\) as its secret key,
However, it cannot directly publish a ciphertext of \({{\mathbf {x}}}^{\le D}\), as \({{\mathbf {x}}}^{\le D}\) is the product of D input vectors, but each encryption algorithm \({\mathsf{hIPE}\mathsf{.Enc}}^{d}\) receives only a single vector \({{\mathbf {x}}}^d\) as input and cannot compute \({{\mathbf {x}}}^{\le D}\). The idea is to include in the D ciphertexts \(\mathsf{hCT}^1, \cdots , \mathsf{hCT}^D\) of \({\mathbf{hIPE}}\), ciphertexts and secret keys of the degree-D scheme, so that the decryptor can combine them to generate a ciphertext \(\mathsf{sCT}\) of \({{\mathbf {x}}}^{\le D}\).
Towards this end, we rely on the first property of \({\mathbf{sIPE}}\) that its ciphertext \(\mathsf{sCT}\) consists of many encodings \(\{ {\mathsf{sCT}_l} \}_{l \in [L]}\). Suppose that the element encoded \(\mathrm {sct}_l\) in every encoding \(\mathsf{sCT}_l\) can be expressed as the inner product of D vectors
Then, it suffices to encode these vectors in a tuple \((\mathsf{dCT}_l^1, \cdots \mathsf{dCT}_l^{D-1}, {\mathsf {dSK}}_l)\) of ciphertexts and secret key of \({\mathbf{dIPE}}\) using an independently sampled master secret key \({\mathsf {dMSK}}_l\), from which the decryptor can obtain exactly \(\mathsf{sCT}_l\). Thus, the D ciphertexts \(\mathsf{hCT}^1, \cdots , \mathsf{hCT}^D\) of our new scheme \({\mathbf{hIPE}}\) consists of exactly one such tuple (\(\mathsf{dCT}_l^1, \cdots \mathsf{dCT}_l^{D-1}, {\mathsf {dSK}}_l\)) for every l, namely,
Given \((\mathsf{hCT}^1, \cdots , \mathsf{hCT}^{D})\) and \(\mathsf {hSK}\) as specified above, the decryptor proceeds in two steps:
-
1.
First, decrypt for every l, the tuple \((\mathsf{dCT}_l^1, \cdots \mathsf{dCT}_l^{D-1}, {\mathsf {dSK}}_l)\) using the decryption algorithm of \({\mathbf{dIPE}}\) to obtain \(\mathsf{sCT}_l\); put them together to get a ciphertext \(\mathsf{sCT}\) of \({{\mathbf {x}}}^{\le D}\).
-
2.
Then, decrypt the obtained ciphertext \(\mathsf{sCT}\) using the decryption algorithm of \({\mathbf{sIPE}}\) and secret key \(\mathsf {hSK}= \mathsf {sSK}\) of \({{\mathbf {x}}}^{D+1}\) to obtain an encoding of the final inner product y, as illustrated below.

Setting Condition C – A First Attempt. We now argue that Condition C above indeed holds. This relies on a second property of the special-purpose IPE scheme \({\mathbf{sIPE}}\) that the elements \(\{ {\mathrm {sct}_l} \}\) encoded in its ciphertext \(\mathsf{sCT}\), depends linearly in the encrypted vector \({{\mathbf {x}}}^{\le D}\) and randomness \({{\mathbf {r}}}\) of encryption. More specifically, when the master secret key \(\mathsf {sMSK}\) is fixed, each element \(\mathrm {sct}_l\) is the output of a linear function \(h^{(\mathsf {sMSK})}_l\) on input \(({{\mathbf {x}}}^{\le D}, {{\mathbf {r}}})\),

where \({{{\mathbf {c}}}}^{(\mathsf {sMSK})}_l\) is the coefficient vector of \(h^{(\mathsf {sMSK})}_l\). Then, since \({{\mathbf {x}}}^{\le D} = {{\mathbf {x}}}^1 \cdots {{\mathbf {x}}}^D \), we can represent \(\mathrm {sct}_l\) as the inner product of D vectors \(\varvec{\chi }_l^1, \cdots , \varvec{\chi }_l^D\), each depending on only one input vector \({{\mathbf {x}}}^D\), as follows:

Therefore, as discussed above, encrypting the vectors \(\{ {\varvec{\chi }_l^d} \}\) in the ciphertexts of \({\mathbf{hIPE}}\) guarantees that the decryptor can obtain \(\mathsf{sCT}\) from the ciphertexts, and decrypting the ciphertext \(\mathsf{sCT}\) further produces an encoding of the correct output y.
A Security Issue. The above way of setting the vectors \(\{ {\varvec{\chi }^d_l} \}_{d, l}\) achieves functionality, but, does not guarantee security. A security issue stems from the fact that the randomness \({{\mathbf {r}}}\) used for generating the ciphertext \(\mathsf{sCT}\) is hardcoded entirely in the input vectors \(\{ {\varvec{\chi }_l^1} \}_l\) encrypted at the first coordinate. Consider a simple scenario where a single ciphertext of \({\mathbf{hIPE}}\) at the first coordinate, two ciphertexts at each other coordinate, and a single secret key, are published:
Since the randomness \({{\mathbf {r}}}\) is embedded in \(\mathsf{hCT}^1\), different combinations of ciphertexts, say \(\mathsf{hCT}^1\) and \(\mathsf{hCT}^2_{b_2}\cdots \) \(\mathsf{hCT}_{b_D}^{D}\), produce \({\mathbf{sIPE}}\) ciphertexts encrypting different vectors, \({{\mathbf {x}}}^1{{\mathbf {x}}}^2_{b_2}\cdots {{\mathbf {x}}}^D_{b_D}\), but using the same random coins \({{\mathbf {r}}}\). The security of \({\mathbf{sIPE}}\) does not hold when attackers can observe ciphertexts with shared randomness, and in particular, information of the encrypted vector \({{\mathbf {x}}}^1{{\mathbf {x}}}^2_{b_2}\cdots {{\mathbf {x}}}^D_{b_D}\) may be revealed. On the other hand, the function hiding property requires that only the final degree-\((D+1)\) inner products \({{\mathbf {x}}}^1{{\mathbf {x}}}^2_{b_2}\cdots {{\mathbf {x}}}^D_{b_D} {{\mathbf {x}}}^{D+1}\) are revealed, and nothing else.
Setting Condition C, Right. To address this security issue, we need to ensure that ciphertexts \(\mathsf{sCT}\) produced by different combinations of ciphertexts of \({\mathbf{hIPE}}\) correspond to (at the very least) distinct randomness. To do so, we embed fresh randomness \({{\mathbf {r}}}^d\) in ciphertexts at every coordinate by modifying the encrypted vectors \(\varvec{\chi }^d_l\) to the following:

Note that the inner products of these vectors correspond to a ciphertext \(\mathsf{sCT}\) generated using random coins \({{\mathbf {r}}}^{\le D} = \prod _{d \in [D]} {{\mathbf {r}}}^d\). That is,

In the simple scenario above, combining \(\mathsf{hCT}^1, \mathsf{hCT}^2_{b_2}\cdots , \mathsf{hCT}_{b_D}^{D}\) now produces \(\mathsf{sCT}\) with randomness \({{\mathbf {r}}}^1{{\mathbf {r}}}^2_{b_2}\cdots {{\mathbf {r}}}^D_{b_D}\), which is distinct for each combination.
Having distinct randomness is still not enough for applying the security of \({\mathbf{sIPE}}\), which requires independently and uniformly sampled randomness. We will rely on the SXDH assumption to argue that they are indeed pseudorandom. The security analysis of the above scheme turns out to be quite complicated, and in fact for security to hold, the scheme needs to further pad the vectors \(\varvec{\chi }_l^d\) with zeros, serving as redundant space for hardwiring information in different hybrids in the security proof.
2.5 Simple Function Hiding IPE
As described above, our construction of degree-D FE crucially relies on a canonical function hiding IPE. However, known secret-key IPE schemes [12, 24, 44] do not have the canonical form, in particular, their decryption does not produce an encoding of the output inner product  , but produce the inner product masked by a scalar
, but produce the inner product masked by a scalar  together with
together with  , where the scalar \(\theta \) is determined by the randomness used in key generation and encryption. In this work, we give a construction of a canonical function hiding IPE. Our construction is extremely simple and may be of independent interests. We now summarize the idea of the construction in one paragraph.
, where the scalar \(\theta \) is determined by the randomness used in key generation and encryption. In this work, we give a construction of a canonical function hiding IPE. Our construction is extremely simple and may be of independent interests. We now summarize the idea of the construction in one paragraph.
Lin and Vaikuntanathan [44] give a simple transformation from IPE with weak function hiding to IPE with full function hiding. Our construction starts from the ABDP public key IPE scheme, whose secret key for a vector \({{\mathbf {y}}}\) reveals \({{\mathbf {y}}}\) and its inner product with the master secret key \(\left\langle {{{\mathbf {s}}}, {{\mathbf {y}}}} \right\rangle \) in the clear. To achieve weak function hiding, we need to hide \({{\mathbf {y}}}\). Our idea is to simply encrypt the secret key as an input vector using the ABDP scheme itself, with an independently sampled master secret key \({{\mathbf {s}}}'\) of length \(N+1\), which yields the new secret key  . Recall that decryption of the ABDP scheme simply computes (homomorphically) the inner product between its secret key and ciphertext. Now that the original secret key is encrypted, we correspondingly encode the original ciphertext in a secret key using \({{\mathbf {s}}}'\), which gives the new ciphertext
. Recall that decryption of the ABDP scheme simply computes (homomorphically) the inner product between its secret key and ciphertext. Now that the original secret key is encrypted, we correspondingly encode the original ciphertext in a secret key using \({{\mathbf {s}}}'\), which gives the new ciphertext  . Computing the “inner product” of \(\mathsf{iCT}'\) and \(\mathsf {iSK}'\) using paring simultaneously decrypts both “layers” of ABDP encryption, and produce exactly an encoding of the output inner product.
. Computing the “inner product” of \(\mathsf{iCT}'\) and \(\mathsf {iSK}'\) using paring simultaneously decrypts both “layers” of ABDP encryption, and produce exactly an encoding of the output inner product.
We have described ideas underlying our FE and IO constructions; due to the lack of space, we refer the reader to the full version [42] for their formal description and proofs. With a better view of the constructions and security proofs, next, we revisit the topic of instantiating our schemes with known noisy multilinear map candidates in more detail.
2.6 On Instantiation with Noisy Multilinear Maps
As mentioned in the introduction when replacing algebraic multilinear maps with noisy ones [21, 22, 26, 31, 39], the constructions work as-is, but not the security proofs. Nevertheless, the security proof can be modified into an ideal model proof, or a proof based on a family of more complex assumptions.
The FE Security Proof Fails. The only component in our IO construction that relies on MMaps is the low-degree FE scheme. When using known noisy MMap candidates, its security proofs fail for two reasons:
-
1.
The SXDH assumption does not hold on known noisy MMap candidates. Roughly speaking, a noisy multilinear map scheme can encode a ring element a and a label l with some noise. Let L be a set of labels that correspond to the set of source groups in algebraic MMaps. Translating the SXDH assumption to the noisy setting would require for every label \(l \in L\), the distribution of randomly sampled encodings of a, b, ab with label l to be indistinguishable to that of a, b, r, for random ring elements a, b, r, even when low-level encodings of 1 with each label \(l \in L\) is published. Unfortunately, given these encodings of 1, known noisy MMap candidates can be completely broken.
-
2.
The security reduction uses the homomorphic scalar multiplication functionality of algebraic MMaps, which is not support by current candidates.
The reason that encodings of 1 is needed in the assumption and homomorphic scalar multiplication is needed for the reduction is as follows. The security of the FE scheme is based on the SXDH assumption, via a security reduction that turns FE attackers to SXDH distinguishers. To do so, given a challenge sampled according to (one of the two distributions specified in) the SXDH assumption, our reduction internally simulates the view of the attacker in the FE security game, and appropriately embeds the challenge into the view. Since the challenge is “laconic”—containing only a constant number of encodings. To concoct the attacker’s view, the reduction needs to (i) generate new encodings and (ii) randomize some encodings in the challenge for embedding. It does so using encodings of 1 in the challenge and homomorphic scalar multiplication. It seems (to us) that any reduction to a laconic and/or instance-independent assumption (i.e., one that is independent of the scheme and the attacker) necessarily needs the capabilities of generating and randomizing encodings. This is indeed the case for previous such reductions [33, 44] and they also require homomorphic scalar multiplication. Designing a reduction that does not rely on homomorphic scalar multiplication, or rely only on homomorphic scalar multiplication with small scalars is an interesting open question.
Security Proofs to Non-laconic Assumptions, and in Ideal MMap Model. Above problems can be eliminated if we give up on having a security reduction to a laconic and instance-independent assumption. In particular, our security proof presents a sequence of hybrids that gradually “morph” from one honest execution of the FE scheme to another (where the attacker receives secret keys and ciphertexts of different functions and inputs as specified in the security definition of FE). Each pair of neighboring hybrids defines an indistinguishability assumption that simply states that the attacker’s views in these two hybrids are indistinguishable, and the security of FE can be based on such a family of non-laconic and instance-dependent assumptions, without using encodings of 1 and homomorphic scalar multiplication. Such a security proof is non-trivial since the assumptions only require indistinguishability of distributions that are almost identical modulo the difference induced by switching a single DDH tuple to a random tuple. Moreover, since these assumptions hold in the ideal model, such a proof also gives a proof in degree-5 ideal multilinear map model.
Instantiating the Construction with Noisy Multilinear Maps. We can instantiate our FE scheme with noisy MMaps and correctness holds. The above-discussed issues w.r.t. the security proof do not appear when instantiating the construction. This is because the secret keys and ciphertexts of our FE scheme do not contain any low-level encodings of 0 or 1, in fact, they contain only encodings of large randomized elements, and its algorithms do not rely on homomorphic scalar multiplication. We note, however, decryption may generate top-level encodings of 0 or 1 for correctness. It is unclear (to us) whether these instantiations are secure against known cryptanalytic attacks. We do not know whether known attacks can be adapted to break their security, nor have formal arguments that validate their security against known attacks. Obtaining a concrete attack or give some formal proof, such as, a security proof in the weak MMap model [29], are interesting open problems.
Notes
- 1.
The operation is according to some well-defined addition operation over the labels; for example, if labels are integers, \(+\) is integer addition, and if labels are sets, \(+\) is set union.
- 2.
For instance, if labels are sets, then two groups are pairable, if their label-sets \(l_1, l_2\) are disjoint.
- 3.
Note that in both distributions, the same exponents, a, b, r, are used in all groups in S.
- 4.
- 5.
Such IPEs should be contrasted with functional encryption for testing the orthogonality of two vectors (see, e.g., [38, 40] and many others), which reveals only whether the inner product is zero and nothing else. In particular, they do not compute the inner product in the exponent in a way that allows for further computation, which is needed for our quadratic FE construction.
- 6.
Non-black-box security reduction may get around this difficulty, but is unclear how one can design a non-black-box reduction here.
References
Abdalla, M., Bourse, F., De Caro, A., Pointcheval, D.: Simple functional encryption schemes for inner products. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 733–751. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46447-2_33
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_15
Ananth, P., Jain, A., Sahai, A.: Achieving compactness generically: indistinguishability obfuscation from non-compact functional encryption. IACR Cryptology ePrint Archive, vol. 2015, p. 730 (2015)
Ananth, P., Sahai, A.: Projective arithmetic functional encryption and indistinguishability obfuscation from degree-5 multilinear maps. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 152–181. Springer, Cham (2017). doi:10.1007/978-3-319-56620-7_6
Ananth, P.V., Gupta, D., Ishai, Y., Sahai, A.: Optimizing obfuscation: avoiding Barrington’s theorem. In: ACM CCS 2014, Scottsdale, AZ, USA, pp. 646–658, 3–7 November 2014
Apon, D., Döttling, N., Garg, S., Mukherjee, P.: Cryptanalysis of indistinguishability obfuscations of circuits over GGH 2013. In: ICALP 2017. LNCS. Springer, Heidelberg (2017)
Applebaum, B., Brakerski, Z.: Obfuscating circuits via composite-order graded encoding. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 528–556. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_21
Applebaum, B., Ishai, Y., Kushilevitz, E.: Cryptography in nc\(^{\text{0}}\). In: FOCS, pp. 166–175 (2004)
Barak, B., Brakerski, Z., Komargodski, I., Kothari, P.K.: Limits on low-degree pseudorandom generators (or: sum-of-squares meets program obfuscation). Cryptology ePrint Archive, Report 2017/312 (2017). http://eprint.iacr.org/2017/312
Barak, B., Garg, S., Kalai, Y.T., Paneth, O., Sahai, A.: Protecting obfuscation against algebraic attacks. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 221–238. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_13
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S., Yang, K.: On the (im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_1
Bishop, A., Jain, A., Kowalczyk, L.: Function-hiding inner product encryption. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 470–491. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48797-6_20
Bitansky, N., Nishimaki, R., Passelègue, A., Wichs, D.: From cryptomania to obfustopia through secret-key functional encryption. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 391–418. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53644-5_15
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: IEEE 56th Annual Symposium on Foundations of Computer Science, FOCS 2015, 17–20 October 2015, Berkeley, CA, USA, pp. 171–190 (2015)
Boneh, D., Silverberg, A.: Applications of multilinear forms to cryptography. Contemp. Math. 324, 71–90 (2002)
Boneh, D., Wu, D.J., Zimmerman, J.: Immunizing multilinear maps against zeroizing attacks. Cryptology ePrint Archive, Report 2014/930 (2014). http://eprint.iacr.org/2014/930
Brakerski, Z., Rothblum, G.N.: Virtual black-box obfuscation for all circuits via generic graded encoding. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 1–25. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_1
Chen, Y., Gentry, C., Halevi, S.: Cryptanalyses of candidate branching program obfuscators. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 278–307. Springer, Cham (2017). doi:10.1007/978-3-319-56617-7_10
Cheon, J.H., Han, K., Lee, C., Ryu, H., Stehlé, D.: Cryptanalysis of the multilinear map over the integers. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 3–12. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46800-5_1
Coron, J.-S., et al.: Zeroizing without low-level zeroes: new MMAP attacks and their limitations. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 247–266. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_12
Coron, J.-S., Lepoint, T., Tibouchi, M.: Practical multilinear maps over the integers. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 476–493. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40041-4_26
Coron, J.-S., Lepoint, T., Tibouchi, M.: New multilinear maps over the integers. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 267–286. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_13
Cryan, M., Miltersen, P.B.: On pseudorandom generators in NC0. In: Sgall, J., Pultr, A., Kolman, P. (eds.) MFCS 2001. LNCS, vol. 2136, pp. 272–284. Springer, Heidelberg (2001). doi:10.1007/3-540-44683-4_24
Datta, P., Dutta, R., Mukhopadhyay, S.: Functional encryption for inner product with full function privacy. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9614, pp. 164–195. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49384-7_7
Döttling, N., Garg, S., Gupta, D., Miao, P., Mukherjee, P.: Obfuscation from low noise multilinear maps. Cryptology ePrint Archive, Report 2016/599 (2016). http://eprint.iacr.org/2016/599
Garg, S., Gentry, C., Halevi, S.: Candidate multilinear maps from ideal lattices. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 1–17. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38348-9_1
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2013, 26–29 October 2013, Berkeley, CA, USA, pp. 40–49 (2013)
Garg, S., Gentry, C., Halevi, S., Zhandry, M.: Functional encryption without obfuscation. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9563, pp. 480–511. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49099-0_18
Garg, S., Miles, E., Mukherjee, P., Sahai, A., Srinivasan, A., Zhandry, M.: Secure obfuscation in a weak multilinear map model. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 241–268. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53644-5_10
Garg, S., Mukherjee, P., Srinivasan, A.: Obfuscation without the vulnerabilities of multilinear maps. IACR Cryptology ePrint Archive, vol. 2016, p. 390 (2016)
Gentry, C., Gorbunov, S., Halevi, S.: Graph-induced multilinear maps from lattices. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 498–527. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_20
Gentry, C., Halevi, S., Maji, H.K., Sahai, A.: Zeroizing without zeroes: cryptanalyzing multilinear maps without encodings of zero. Cryptology ePrint Archive, Report 2014/929 (2014). http://eprint.iacr.org/2014/929
Gentry, C., Lewko, A.B., Sahai, A., Waters, B.: Indistinguishability obfuscation from the multilinear subgroup elimination assumption. In: Guruswami [36], pp. 151–170 (2015)
Goldreich, O.: Candidate one-way functions based on expander graphs. In: Electronic Colloquium on Computational Complexity (ECCC), vol. 7, no. 90 (2000)
Goldwasser, S., et al.: Multi-input functional encryption. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 578–602. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_32
Guruswami, V. (ed.) IEEE 56th Annual Symposium on Foundations of Computer Science, FOCS 2015, 17–20 October 2015. IEEE Computer Society, Berkeley (2015)
Ishai, Y., Kushilevitz, E.: Perfect constant-round secure computation via perfect randomizing polynomials. In: Widmayer, P., Eidenbenz, S., Triguero, F., Morales, R., Conejo, R., Hennessy, M. (eds.) ICALP 2002. LNCS, vol. 2380, pp. 244–256. Springer, Heidelberg (2002). doi:10.1007/3-540-45465-9_22
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78967-3_9
Langlois, A., Stehlé, D., Steinfeld, R.: GGHLite: more efficient multilinear maps from ideal lattices. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 239–256. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_14
Lewko, A., Okamoto, T., Sahai, A., Takashima, K., Waters, B.: Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 62–91. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_4
Lin, H.: Indistinguishability obfuscation from constant-degree graded encoding schemes. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 28–57. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49890-3_2
Lin, H.: Indistinguishability obfuscation from DDH on 5-linear maps and locality-5 PRGs. Cryptology ePrint Archive, Report 2016/1096 (2016). http://eprint.iacr.org/2016/1096
Lin, H., Tessaro, S.: Indistinguishability obfuscation from trilinear maps and block-wise local PRGs. In: CRYPTO 2017 (2017, to appear)
Lin, H., Vaikuntanathan, V.: Indistinguishability obfuscation from DDH-like assumptions on constant-degree graded encodings. In: IEEE 57th Annual Symposium on Foundations of Computer Science, FOCS 2016, New Brunswick, NJ, USA, 9–11 October 2016
Lombardi, A., Vaikuntanathan, V.: On the non-existence of blockwise 2-local PRGs with applications to indistinguishability obfuscation. Cryptology ePrint Archive, Report 2017/301 (2017). http://eprint.iacr.org/2017/301
Miles, E., Sahai, A., Zhandry, M.: Annihilation attacks for multilinear maps: cryptanalysis of indistinguishability obfuscation over GGH13. IACR Cryptology ePrint Archive, vol. 2016, p. 147 (2016)
Mossel, E., Shpilka, A., Trevisan, L.: On e-biased generators in NC0. In: 44th Symposium on Foundations of Computer Science (FOCS 2003), 11–14 October 2003, Cambridge, MA, USA, Proceedings, pp. 136–145 (2003)
O’Donnell, R., Witmer, D.: Goldreich’s PRG: evidence for near-optimal polynomial stretch. In: IEEE 29th Conference on Computational Complexity, CCC 2014, Vancouver, BC, Canada, 11–13 June 2014, pp. 1–12 (2014)
Pass, R., Seth, K., Telang, S.: Indistinguishability obfuscation from semantically-secure multilinear encodings. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 500–517. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_28
Rothblum, R.D.: On the circular security of bit-encryption. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 579–598. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36594-2_32
Yao, A.C.: Protocols for secure computations (extended abstract). In: 23rd Annual Symposium on Foundations of Computer Science, 3–5 November 1982, Chicago, Illinois, USA, pp. 160–164 (1982)
Yao, A.C.-C.: How to generate and exchange secrets (extended abstract). In: FOCS, pp. 162–167 (1986)
Zimmerman, J.: How to obfuscate programs directly. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 439–467. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_15
Acknowledgements
The author thanks Benny Applebaum, Nir Bitansky, Stefano Tessaro, and Vinod Vaikuntanathan for many helpful and insightful discussions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Lin, H. (2017). Indistinguishability Obfuscation from SXDH on 5-Linear Maps and Locality-5 PRGs. In: Katz, J., Shacham, H. (eds) Advances in Cryptology – CRYPTO 2017. CRYPTO 2017. Lecture Notes in Computer Science(), vol 10401. Springer, Cham. https://doi.org/10.1007/978-3-319-63688-7_20
Download citation
DOI: https://doi.org/10.1007/978-3-319-63688-7_20
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63687-0
Online ISBN: 978-3-319-63688-7
eBook Packages: Computer ScienceComputer Science (R0)







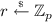 . A ciphertext
. A ciphertext 

 , and
, and 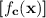 .
.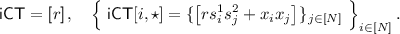

 .
.
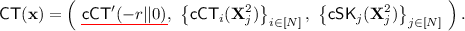
 as desired.
as desired.
