Abstract
Consensus algorithms are fundamental building blocks for fault-tolerant distributed systems and their correctness is critical. However, there are currently no fully-automated methods for their verification. The main difficulty is that the algorithms are parameterized: they should work for any given number of processes. We provide an expressive language for consensus algorithms targeting the benign asynchronous setting. For this language, we give algorithm-dependent cutoff bounds. A cutoff bound B reduces the parameterized verification of consensus to a setting with B processes. For the algorithms in our case studies, we obtain bounds of 5 or 7, enabling us to model check them efficiently. This is the first cutoff result for fault-tolerant distributed systems.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Cut-off Boundary
- Consensus Algorithm
- Small Scope Hypothesis
- Communication Predicate
- Fault-tolerant Distributed Algorithms
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Fault-tolerant distributed systems are hard to get right: processes can stall, crash, or recover, and the network might lose, delay, or duplicate messages [6]. As the number and the cost of failures of these systems increase, industry is increasingly applying push-button verification methods to them, such as model checking [41] and testing [31]. These methods analyze individual system configurations with a small, fixed number of participating processes. However, many real distributed systems are intended to work for any given number of processes, i.e., they are parameterized in this number. The deployed instances are often larger than the analyzed ones, and the analyses then offer no a priori guarantees for the deployed system. Still, an informal observation known as the small-scope hypothesis [25] states that analyzing small system instances suffices in practice. Empirical studies [4, 42, 49] support this hypothesis in different settings. For example, in the distributed setting, a recent study [49] of 198 bug reports for several popular distributed systems found that 98% of those bugs could be triggered by three or fewer processes.
A crucial question is then: can we state and formally prove this hypothesis? That is, given a parameterized system and a property \(\psi \), can we determine a cutoff bound: a number B such that whenever all systems with parameter values of B or less satisfy \(\psi \), then systems with arbitrary parameter values also satisfy \(\psi \)? The answer is no in general as the parametric verification problem is undecidable even when we can decide the system’s correctness for each parameter instance [5, 45]. The best we can hope for is to find cutoff bounds for interesting classes of systems and properties. While such results exist [15,16,17, 20, 29, 30], none apply to fault-tolerant distributed systems in general, and to algorithms for solving the distributed consensus problem in particular. Consensus algorithms are fundamental building blocks for distributed systems [22]: they are required whenever multiple processes want to maintain, in a fault-tolerant way, a consistent shared state or a consistent order of operations (for instance, in a database).
In addition to the lack of cutoff results, no fully automated method exists for the parametric verification of consensus algorithms. The invariant verification approach of [13] comes the closest, but it is not fully automated as the user must find inductive invariants that are automatically checked. Also, while the authors report good practical results, their main algorithm is only a semi-decision procedure. Other reported results have either performed bounded verification (e.g., [12, 47, 48]) or used interactive verification methods (e.g., [11, 21, 27, 35, 44]).
Contributions. Our main contribution is to prove the small scope hypothesis for an expressive class of consensus algorithms. In more detail:
-
1.
We define a language \( ConsL \) (Sect. 3), capable of expressing numerous consensus algorithms that target the asynchronous and partially synchronous setting with benign (i.e., non-Byzantine) failures. The central feature of \( ConsL \) are guards based on fractional thresholds and selection predicates. These guards capture algorithm constructs such as “if messages have been received from more than \(\frac{2}{3}\) of the processes, then select the smallest received value”. We have specified the following algorithms in \( ConsL \): Paxos [36], Chandra-Toueg [8], Ben-Or [7], \(\frac{1}{3}\)-rule and three algorithms from the Uniform Voting family [10], and the algorithm from [38].
-
2.
For \( ConsL \) algorithms, we prove a zero-one principle for consensus (Sect. 4): the algorithm’s correctness for binary inputs (from the set \(\{0,1\}\)) entails the algorithm’s correctness for inputs from any ordered set, finite or infinite. This is an analogue of the same principle for sorting networks [32].
-
3.
We give cutoff bounds for algorithms run on binary inputs (Sect. 5): given a \( ConsL \) algorithm \(\mathcal {A}\), we show that \(\mathcal {A}\) solves consensus on binary inputs if it solves it for exactly \(B=2d+1\) processes, where d is the least common denominator of the fractional thresholds in \(\mathcal {A}\)’s guards. Together with Step 2, this proves the small scope hypothesis for \( ConsL \) algorithms.
-
4.
The bounds we obtain for real-world algorithms are indeed small: 5 or 7 processes for all algorithms considered in this paper. We can thus leverage model checking to provide the first fully automated decision procedure applicable to a range of consensus algorithms, and we provide a tool (Sect. 6) that generates Promela/Spin [23] models from \( ConsL \) algorithms. The resulting verification times are competitive with the semi-automated method of [13].
2 Preliminaries
We start with set-theoretic preliminaries and briefly review the consensus problem and the Heard-Of (HO) model [10] for fault-tolerant distributed algorithms.
A multiset M over a set S is a function \(S \rightarrow \mathbb {N}\), where M(x) is the multiplicity of x in M. We define \(\left| M\right| = \sum _{s \in S} M(s)\) and the multiset \(M \setminus X\) for a set X by \((M\setminus X)(x) = 0\) if \(x \in X\) and \((M\setminus X)(x) = M(x)\) otherwise. Note that this operation removes all occurrences of X’s elements from M. The multiset image of a partial function \(f\!: A \rightharpoonup B\), is the multiset \(\#[f]\!: B \rightarrow \mathbb {N}\) defined by \(\#[f](y) = \left| f^{-1}(y)\right| \). We introduce notation for specifying multisets. For example, \(M = \{m_x \times x, m_y \times y\}\) denotes the multiset M where \(M(x) = m_x\), \(M(y) = m_y\), and \(M(z) = 0\) for \(z \notin \{x, y\}\). We also define \([a,b)_\mathbb {Q}=\{c \in \mathbb {Q}\mid a \le c < b\}\).
2.1 Consensus
The consensus problem assumes a fixed set \(\varPi = \{1,\ldots , n\}\) of communicating processes. Usually, we want an algorithm that solves this problem for any \(n > 0\), i.e., an algorithm parameterized by n. Each process in \(\varPi \) receives an input from the value domain \(\mathcal {V}\), and the goal is to have all processes decide on a common output. More precisely, a system solves the consensus problem [10] if it provides:
- Uniform Agreement::
-
No two processes ever decide on two different values.
- Termination::
-
Every process eventually decides on a value.
- Non-triviality::
-
Any value decided upon was input to some process.
- Stability::
-
Once a process decides, it never reverts to an undecided state.
Note that the termination requirement says nothing about execution stopping. In fact, to simplify modeling, we assume that all processes run forever. Furthermore, the requirements make no exemption for failed processes. We follow [10] where failed processes continue receiving and processing messages, and can thus still decide. However, the messages they send are no longer received by the other processes. We next explain this model in more detail.
2.2 The Heard-Of Model
We will define the semantics of our language via a translation into the HO model. This model characterizes round-based algorithms, where every process performs the following actions in each round: (1) send messages to other processes; (2) wait and collect messages from other processes; and (3) update the local state. The rounds must be communication-closed, such that the only messages collected in a round are the messages that are sent in that round.
A salient point of the HO model is that message collection (Step 2) is assumed to be performed by a lower-level messaging layer outside of the model. This layer ensures communication closedness (for example, by buffering early and dropping late messages) and handles issues such as message duplication. It decides when to stop the collection and advance the round (for instance, using a timeout), and hands over the received messages to the algorithm. Environment effects such as crashed or late senders or message loss or delay might prevent the delivery of some messages. The possible causes are indistinguishable to the receivers. The HO model chooses to uniformly model all such effects, including process crashes, as message loss. The environment effects are thus encapsulated in the heard-of sets \(HO_p^r \subseteq \varPi \), where \(HO_p^r\) models the set of processes whose messages are collected by the messaging layer for process p in round r.
Let \(\mathcal {M}\) denote the message space. An algorithm in the HO model is specified by the following three elements, indexed by processes p and rounds r:
-
1.
\(I_p \subseteq S_p\) is the set of initial states of p (contained in p’s state space \(S_p\)).
-
2.
The send function \(\texttt {{send}}_p^r : S_{p} \times \varPi \rightarrow \mathcal {M}\), where \(\texttt {{send}}_p^r(s_p, q)\) determines the message p sends to q in round r, based on p’s current state \(s_p\). This function is total; not sending a message is modeled by a special dummy message \(\star \).
-
3.
The update function \(\texttt {{next}}_p^r : S_{p} \times (\varPi \rightharpoonup \mathcal {M}) \rightarrow 2^{S_{p}}\). Let \(\mu _p^r: \varPi \rightharpoonup \mathcal {M}\) model the messages p receives in round r, i.e., given \(HO_p^r\) and \(s_q\), let \(\mu _p^r(q) = \texttt {{send}}_q^r(s_q, p)\) if \(q \in HO_p^r\) and let it be undefined otherwise. Then \(\texttt {{next}}_p^r(s_p, \mu _p^r)\) determines the set of possible successor states of p’s current state \(s_p\).
Example 1
Figure 1 shows the pseudo-code for the HO model of the \(\frac{1}{3}\)-rule consensus algorithm [10], where the state of each process consists of the fields \( inp \) and \( dec \) and \(\texttt {{send}}_p^r\) and \(\texttt {{next}}_p^r\) are the same for all processes p and rounds r. The updates of the \( inp \) and \( dec \) fields in \(\texttt {{next}}_p^r\) are done simultaneously. We do not explain here why this algorithm works; we just use it to showcase the HO model and motivate the design of our specification language, described shortly.
The semantics of an algorithm in the HO model is defined as the transition system \((S, \rightarrow , I)\), where each state \(s\in S\) (respectively \(s \in I\)) consists of the local states \(s_p \in S_p\) (respectively \(s_p \in I_p\)) of each process \(p\in \varPi \) and a value \(s. rnd \in \mathbb {N}\) recording the current round (initially 0). Given an HO collection \(\{HO_p^r\}_{p \in \varPi }^{r \in \mathbb {N}}\), there is a transition \(s \rightarrow s'\) in round \(r=s. rnd \) if and only if \(s'. rnd = r + 1\) and, for all processes \(p \in \varPi \) and \(\mu _p^r\) defined as above, \(s_p' \in \texttt {{next}}_p^r(s_p, \mu _p^r)\), i.e., all processes simultaneously execute an update. Each HO collection induces a set of infinite state sequences, called traces. The width of states and traces is \(\left| \varPi \right| \). This lockstep semantics models HO algorithm executions in synchronous settings in an obvious way. But crucially, for consensus properties and communication-closed algorithms, it also soundly abstracts the fine-grained semantics [9, 14], which models executions in asynchronous environments where processes progress independently of each other. Hence, we can verify consensus properties in the lockstep semantics of the HO model and conclude that they carry over to an asynchronous environment.
Solving consensus requires assumptions on the environment [18]; for instance, message loss can prevent consensus even with full synchrony [43]. As the HO model encapsulates environment effects in the HO collections, each algorithm states its environment assumptions using a communication predicate, a set of allowed HO collections. These then induce the algorithm’s set of traces. To be useful, a predicate must reflect realistic assumptions on distributed systems, i.e., be implementable by a messaging layer using these assumptions. Two of the most important such assumptions can be reflected in two types of round formulas \(\phi _{ th }\) and \(\phi _{ uf }\) of the forms:
The threshold formula \(\phi _{ th }(c,r)\) requires that, in round r, all processes receive messages from at least the fraction \(c \in [0, 1)_\mathbb {Q}\) of processes, reflecting the assumptions about the number of failures and timeouts in round r. The uniformity formula \(\phi _{ uf }(r)\) requires that all processes receive messages from the same set of processes in round r. This reflects the partial synchrony assumption of a stable period that spans an entire round. In stable periods, no crashes or recoveries occur, and all messages from non-crashed processes are delivered in a timely way. For example, the communication predicate for the \(\frac{1}{3}\)-rule algorithm is given by \(\exists r_1, r_2.\; r_2 > r_1 \wedge \phi _{ th }(\frac{2}{3}, r_1) \wedge \phi _{ uf }(r_1) \wedge \phi _{ th }(\frac{2}{3}, r_2)\).
While the modular construction of messaging layers implementing such predicates is an open question, provably correct ad-hoc implementations for partially synchronous environments exist [14, 24], with modest proof complexity.
3 Specification Language
The HO model leverages the round structure present in many distributed algorithms to create a simple model for them. However, similarities between consensus algorithms for the asynchronous setting with benign failures run deeper than just their round structure. In this section, we exploit these similarities to define \( ConsL \), a language that captures many algorithms for this setting.
3.1 Structural Commonalities Between Algorithms
To motivate the syntactic choices for \( ConsL \), we use the \(\frac{1}{3}\)-rule algorithm to highlight the typical structural characteristics of consensus algorithms:
-
1.
All processes are fully symmetric, i.e., execute the same code.
-
2.
The state of each process p contains two distinguished fields \( inp \) (the input p receives) and \( dec \) (p’s decision). Initially, \( dec \) is set to the distinguished value \(\bot \), indicating that no decision has been made.
-
3.
The \(\texttt {{send}}\) function always sends the value of a single state field.
-
4.
In the \(\texttt {{next}}\) function, each state field is either left unchanged or is updated to some received value. No new values are produced; instead, values are simply propagated between fields. Moreover, their origins are irrelevant. The map \(\mu _p^r : \varPi \rightharpoonup \mathcal {M}\) of received messages can hence be replaced by the multiset \(R_p^r = \#[\mu _p^r]\). A field f is then updated to a value v from \(R_p^r\) if:
-
(a)
\(\left| R_p^r\right| \) is strictly larger than some threshold, expressed as a fraction of the total number of processes; in the example, this fraction is \(\frac{2}{3}\) for the updates to both \( inp \) and \( dec \), and
-
(b)
v fulfills a particular predicate with respect to the set of received messages. In the example, the predicate for the \( dec \) update is that all messages in \(R_p^r\) equal v, and for the \( inp \) update that v is a value with the highest multiplicity in \(R_p^r\) and is the smallest such value.
-
(a)
3.2 Syntax
The above observations motivate the syntax for the basic building block of \( ConsL \), the specification of a single round (Fig. 2a). Here, we focus on the core language, typeset in normal font; the greyed out parts are extensions (Sect. 3.4). A round specification starts with the state field that is sent in the round, followed by the communication pattern. In the  pattern, all process pairs exchange messages. The specification ends with a list of update instructions.
pattern, all process pairs exchange messages. The specification ends with a list of update instructions.
An instruction instr consists of a guard and the updated field. We assume that each upd-field appears at most once in the instruction list. The guard consists of a threshold \(th \in [0,1)_\mathbb {Q}\), and a predicate pred. Intuitively, if messages are received from more than the given threshold of processes, the target field is updated with some value satisfying the predicate. The predicates are:
-
\(\texttt {{any}}\): any received value,
-
\(\texttt {{smor}}\): the smallest most often received value,
-
\(\texttt {{min}}\): the smallest received value, and
-
\(\texttt {{all=}}\): satisfied by v if all the received values equal v.
We will use the grammar symbols as projections where convenient; for example, given a guard G, we write th(G) for its threshold. Figure 2b shows the (single) round specification of the \(\frac{1}{3}\)-rule algorithm.
While the \(\frac{1}{3}\)-rule algorithm repeats the same round indefinitely, many algorithms use finite sequences of rounds, called phases, as units of repetition.Footnote 1 A ConsL algorithm \(\mathcal {A}\) consists of a finite set of phases, a phase sequence, specified by an infinite word w over this set, and a communication predicate, specified as below. The phase sequence determines the infinite sequence of round specifications to execute, reflecting our assumption that processes run forever. While our theorems also hold for arbitrary phase sequences, to obtain finite-state systems and enable model-checking, we require \(w = uv^\omega \), for finite words u and v.
Communication Predicates. As we use an HO model semantics, \( ConsL \) algorithms must express their environment assumptions using communication predicates. Arbitrary predicates could make cutoff bounds unobtainable, so we provide a restricted but sufficient way to specify them. The building blocks are the round formulas \(\phi _{ th }(c, r)\) and \(\phi _{ uf }(r)\) from Sect. 2.2. Abusing notation, we associate the round labels \(\phi _{ th }(c)\) and \(\phi _{ uf }\) with the corresponding round formulas. Let \(L = \{\phi _{ uf }\} \cup \{\phi _{ th }(c) \mid c \in [0,1)_\mathbb {Q}\}\) be the set of all round labels. A \( ConsL \) communication predicate is then specified by a language of infinite words over the alphabet \(\varSigma = \mathcal {P}(L)\). Again, to ensure a finite representation, we require the language to be \(\omega \)-regular. For example, the communication predicate of the \(\frac{1}{3}\)-rule algorithm is now specified as \(\varSigma ^* \varLambda _1 \varSigma ^* \varLambda _2 \varSigma ^\omega \), with \(\varLambda _1 = \{\phi _{ th }(\frac{2}{3}), \phi _{ uf }\}\) and \(\varLambda _2 = \{\phi _{ th }(\frac{2}{3})\}\).
Restrictions. To ensure that cutoff bounds exist, \( ConsL \) has several syntactic restrictions. They are technical in nature and we provide some intuition for the two main ones here.
First, we constrain the data flow within a phase. Intuitively, a phase of a consensus algorithm is a single attempt to reach a decision on one of the input values. We exploit this by assuming that all data within a phase originates from the \( inp \) field, and that \( inp \) and \( dec \) are updated at most once. We formalize this using the notion of a phase graph. First, given a phase \(\varPhi = [rs_1, rs_2, \ldots , rs_n]\), and a field f, let f’s latest update before i, denoted lu(f, i), be the largest j, with \(j < i\), such that f is updated in \(rs_j\), and 0 if no such j exists. The phase graph is then a directed graph whose nodes are pairs (i, f) such that either the field f is updated in \( rs _i\), or \(i = 0\) and f is sent in some \( rs _j\) with \(lu(f, j)=0\). An edge \((i,f) \rightarrow (j,g)\) exists in the graph iff f is sent in \( rs _j\), g is updated in \( rs _j\), and \(i=lu(f,j)\). Figure 2c shows \(\frac{1}{3}\)-rule’s phase graph. Our first restriction is then:
-
(R1)
The phase graph of each phase is a tree rooted at \((0, inp )\). For \(f \in \{ inp , dec \}\), at most one node (i, f) with \(i > 0\) exists, and it must be a leaf. Moreover, these are the only leaves of the graph.
Hence, each phase has at most one round where two fields are simultaneously updated. In the phase graph, these rounds correspond to fork points, where the \( dec \) -path \((0, inp ) \leadsto (j, dec )\) forks off from the \( inp \) -path \((0, inp ) \leadsto (i, inp )\) (see Figs. 2c and 4). Handling these is the most challenging part of our proofs, as discussed later.
The second main restriction is based on the observation that, to ensure agreement, consensus algorithms require that decided values get stored as inputs for future phases. Hence, at the fork point, an update on the \( dec \)-path must imply an update on the \( inp \)-path. Therefore, the guard of the update on the \( dec \)-path must be stronger than the guard of the update on the \( inp \)-path. We exploit this and require a total ordering of the update guards in an algorithm. We start by defining a partial order \(\mathrel {\sqsubseteq _{\mathcal {P}}}\) on the predicates by \(\texttt {{any}}\mathrel {\sqsubseteq _{\mathcal {P}}}P\), \(P \mathrel {\sqsubseteq _{\mathcal {P}}}P\), and \(P \mathrel {\sqsubseteq _{\mathcal {P}}}\texttt {{all=}}\), for all predicates P. Hence, \(P_1 \mathrel {\sqsubseteq _{\mathcal {P}}}P_2\) iff whenever a value v satisfies \(P_2\), then it also satisfies \(P_1\). We extend this order to guards such that \(G_1 \mathrel {\sqsubseteq }G_2\) iff \(th(G_1) \le th(G_2)\) and \( pred (G_1) \mathrel {\sqsubseteq _{\mathcal {P}}} pred (G_2)\). The associated restriction is (R2), which we list along with the remaining restrictions (R3) and (R4):
-
(R2)
The set of all guards used in the algorithm is totally ordered.
-
(R3)
\(\texttt {{min}}\) and \(\texttt {{smor}}\) predicates only appear in instructions where send-field is \( inp \).
-
(R4)
If \(th(G) = 0\), then \( pred (G) = \texttt {{any}}\).
3.3 Semantics
Guards. We assume in the rest of the paper that the system is parameterized by a set \(\varPi \) of processes and a totally ordered set \(\mathcal {V}\) of values. Given a multiset M of elements from the message space \(\mathcal {M}\triangleq \mathcal {V}\cup \{\bot ,\star \}\), define \(\textit{vs}(M) \triangleq M \setminus \{\bot ,\star \}\). Then, given a guard \(G = (t, p)\), a multiset M (of received messages), and a value \(v \in \mathcal {V}\), we write \(M \models G(v)\) if \(\left| \textit{vs}(M)\right| > t \cdot \left| \varPi \right| \), and one of the following four conditions holds:
-
1.
\(p = \texttt {{any}}\) and \(\textit{vs}(M)(v) > 0\),
-
2.
\(p = \texttt {{all=}}\) and \(\textit{vs}(M)(v) = \left| \textit{vs}(M)\right| \),
-
3.
\(p = \texttt {{min}}\) and v is the smallest value in \(\textit{vs}(M)\), or
-
4.
\(p = \texttt {{smor}}\) and v is the smallest most frequent value in \(M'= \textit{vs}(M)\), i.e., \(\forall v'.\ M'(v) \ge M'(v') \wedge (M'(v) = M'(v') \Longrightarrow v \le v')\).
Send and Next Functions. As mentioned earlier, the phase sequence of a \( ConsL \) algorithm uniquely determines a round specification \( rs (r)\) for each round \(r \in \mathbb {N}\) to be executed. We give an HO model semantics to such an algorithm by (1) specifying the same set of initial states for each process: \( inp \) takes an arbitrary value from \(\mathcal {V}\) and all other fields are \(\bot \); and (2) translating each round specification \( rs (r)\) into a pair \((\texttt {{send}}_p^r, \texttt {{next}}_p^r)\) as follows:
-
\(\texttt {{send}}_p^r\) returns process p’s current (in round r) value of the send-field of \( rs (r)\).
-
\(\texttt {{next}}_p^r\) updates process p’s state by selecting new values for all fields in the instruction list of \( rs (r)\). Given an instruction \({G} \; \triangleright \; {f}\) and the partial function \(\mu _p^r: \varPi \rightharpoonup \mathcal {M}\) of messages received by the process p, let \(R_p^r = \#[\mu _p^r]\). The set of possible new values of the field f of process p is determined as follows:
-
For all \(v \in \mathcal {V}\) such that \(R_p^r \models G(v)\), v is a possible new value for f.
-
If no such value \(v \in \mathcal {V}\) exists, the only possible value is the fallback value: the old value of f of process p if \(f \in \{ inp , dec \}\), and \(\bot \) otherwise.
-
We call fields other than \( inp \) and \( dec \) ephemeral since their fallback value \(\bot \) and the restriction (R1) jointly imply that they do not keep state between successive phases. Example 2 below presents an algorithm using ephemeral fields. Moreover, the semantics ensures that the \( dec \) field never reverts from a value in \(\mathcal {V}\) to \(\bot \). Hence, the stability requirement of consensus holds by construction for all \( ConsL \) algorithms, including those using the language extensions described later. We therefore do not further discuss this requirement.
Labeled Transition System Semantics. In Sect. 2.2 we introduced the unlabeled transition system semantics of the HO model. To restrict reasoning to those traces satisfying the communication predicates, we label the traces with round labels from \(\varSigma \) (Sect. 3.2). The r-th unlabeled transition \(s \rightarrow s'\) of a trace generated by an HO collection \(\{HO_p^r\}_{p \in \varPi }^{r \in \mathbb {N}}\) gives rise to a set of labeled transitions \(s \xrightarrow {\varLambda } s'\), where \(\varLambda \in \varSigma \), such that:
-
1.
\(\phi _{ uf }\in \varLambda \) implies that the formula \(\phi _{ uf }(r)\) holds for \(\{HO_p^r\}_{p \in \varPi }^{r \in \mathbb {N}}\).
-
2.
\(\phi _{ th }(c) \in \varLambda \) implies that \(\phi _{ th }(c,r)\) holds, and that c appears as the threshold of some guard in the algorithm. For technical reasons, we also require that for all guards G in the transition, \(th(G) = 0 \vee th(G) = c\).
A labeled trace includes both states and labels. The semantics of a \( ConsL \) algorithm \(\mathcal {A}\) is the set of infinite traces whose labels form a word in the communication predicate of \(\mathcal {A}\). Property satisfaction is relative to this semantics.
3.4 Extensions
To cover additional algorithms, we increase the expressiveness of \( ConsL \) by including three additional features: leaders (l), timestamps (t), and randomness (r). We write \( ConsL ^E\) for a given set \(E \subseteq \{l, t, r\}\) to denote the language with the corresponding extensions. An algorithm must specify the extensions it uses. As we do not know of any algorithms combining randomness and timestamps, for simplicity we assume \(\{r, t\} \not \subseteq E\). The leaders and timestamp extensions are also subject to some syntactic restrictions required for our proofs. The restrictions and extensions’ formal semantics are detailed in [39]; for space reasons, we only provide an informal overview here.
Leaders. Leaders are distinguished processes that act as coordinators: they collect the possible inputs and select one of them. Leaders add two new communication patterns:
-
 , where only the leader broadcasts a message in a round, and
, where only the leader broadcasts a message in a round, and -
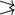 , where all processes send a message exclusively to the leader.
, where all processes send a message exclusively to the leader.
To prevent a failed leader from blocking progress, we assume that leaders can switch arbitrarily between phases. We also assume that the leader of each round is known in advance, as given by a function \( ldr : \mathbb {N} \rightarrow \varPi \). This assumption is common (e.g., [8, 36]). Still, many algorithms work without it [10] as long as all processes eventually agree on the phase leader. We believe that our results also hold without the assumption, but we have not yet proved this. Next, to ensure progress, we add two new round formulas:
-
a leader send formula \(\phi _{ls}(r) \triangleq \forall p.\ ldr (r) \in HO^r_p\), requiring that all processes hear from the round leader, and
-
a leader receive formula \(\phi _{lr}(c,r) \triangleq |HO^r_{ ldr (r)}| > c \cdot n\), requiring that the leader receives a sufficient number of messages in round r.
These formulas ensure that the algorithm is not stuck with a leader that has failed or is partitioned from the other processes. We also extend the set L of transition labels with the set \(\{\phi _{ls}\} \cup \{\phi _{lr}(c) \mid c \in [0,1)_\mathbb {Q}\}\).
Timestamps. A timestamped field stores a value together with the time of its last update, thereby recording information about the execution history. Time is logical, expressed by round numbers. When sending out a timestamped field, both the value and the timestamp are transmitted. A new predicate, \(\texttt {{maxts}}\), then selects a value with the highest timestamp; to break ties, the smallest such value is selected. In \( ConsL \), timestamps only make sense with the \( inp \) field, since the other fields are either never sent out or do not persist between phases.
Example 2
To showcase the use of leaders and timestamps, Fig. 3 shows our \( ConsL \) model of the Paxos algorithm [36], or more precisely, its Synod part. The single four-round phase is repeated forever. Compared to [36], (1) our phases (called “ballots” there) appear to start automatically (by conceptually moving the \( NextBallot \) message of [36] to the messaging layer), (2) we assume that all processes receive an input instead of just the leader, and (3) we replace phase numbers by round numbers in \( inp \)’s timestamps (these are isomorphic by (R1)).
Randomness. Randomization is an alternative to partial synchrony for making consensus solvable [7]. Randomized algorithms normally have a probabilistic termination guarantee: all processes eventually decide with probability 1. The termination proof usually relies on an almost-sure “lucky toss”, where all processes draw the same favorable randomness. We turn this into a standard termination guarantee by (1) modeling randomness as non-determinism: processes non-deterministically choose a bit for the fallback values; (2) providing a way to specify lucky tosses, inspired by the Ben-Or algorithm; and (3) extending the set L of transition labels with a special label \(\lambda \), indicating that a lucky toss occurred. For randomized algorithms, we make the usual assumption that \(\mathcal {V}= \{0,1\}\).
4 The Zero-One Principle
The zero-one principle for sorting networks [32] is a well-known result stating that a sorting network correctly sorts all sequences of inputs if and only if it correctly sorts all sequences of elements from \(\mathbb {B}\triangleq \{0,1\}\). We prove an analogous result for our language and the consensus problem. We call the consensus problem for the binary domain \(\mathcal {V}=\mathbb {B}\) the binary consensus problem. Since the randomization extension already assumes this domain, we restrict our attention here to non-randomized algorithms. We also need a further restriction on \( ConsL \), listed separately as we need it only for the termination part of the 0-1 principle. The other results hold without this restriction.
-
RT
\(\texttt {{min}}\) and \(\texttt {{all=}}\) guards do not appear in the same round specification.
Theorem 1
An algorithm expressed in \( ConsL ^E\) (with \(r \notin E\)) that additionally obeys (RT) solves the consensus problem for an arbitrary value domain \(\mathcal {V}\) if and only if it solves the binary consensus problem.
There are intuitive reasons why the principle should hold. Since we assumed \(r \notin E\), \( ConsL \)’s semantics immediately implies that all algorithms guarantee non-triviality (in addition to stability). We thus only have to consider agreement and termination, for which we prove that their violations are preserved when \(\mathcal {V}= \mathbb {B}\). By definition, agreement requires only two values to disprove. We combine this with the earlier observation that \( ConsL \) algorithms simply propagate values between the processes’ fields. Then it suffices to ensure that whenever two different values can be propagated in a multi-valued agreement counterexample, both 0 and 1 can be propagated when \(\mathcal {V}= \mathbb {B}\). This is in general possible as the values themselves are irrelevant and only their relative ordering matters. Disproving termination requires showing that, whenever guards (in particular, those for updating \( dec \)) can fail in a multi-valued setting, they can fail in the binary setting. From the language semantics (Sect. 3.3), there are two ways for a guard to fail. The first way is to have the process receive insufficiently many non-\(\bot \) messages. As this is independent of the size of \(\mathcal {V}\), we can mimic this cause of failure in the binary setting. The second way is to have the process receive different values when the update is guarded by an \(\texttt {{all=}}\) predicate. In this case, two values also suffice.
Unfortunately, the proof (given in [39]) is more complex than this intuition might suggest. One example of its intricacies is the restriction (RT). The following problematic example shows why this restriction is necessary.
Example showing the necessity of (RT)
Example 3
Consider the algorithm in Fig. 5. Note that the phase sequence is \(\varPhi _1\varPhi _2\varPhi _3^\omega \) and the communication predicate demands that all processes receive messages from a majority of processes in each round. Consequently, every round’s threshold guard is satisfied. This algorithm violates termination in a three-valued setting, but not in the binary setting. To see this, first consider the binary setting. Assume that some process p is still undecided after \(\varPhi _3\). This requires that p receives both 0’s and 1’s in \(\varPhi _3\). Hence, some majority \(P \subseteq \varPi \) of processes had \( inp \) set to 1 at the start of phase \(\varPhi _2\). It follows that all processes in P have updated both \( inp \) and \( vote \) to 1 in the first round of \( \varPhi _1\). Due to the communication predicate, in the second round of \(\varPhi _1\), p must have seen a message from at least one process from P and thus decided, which is a contradiction. Therefore, this algorithm terminates after at most four rounds in the binary setting.
In the multi-valued setting, the algorithm may not terminate. Consider a run of the algorithm where all processes have pairwise distinct values in their \( inp \) fields. In the first round, it is then possible that each process receives at least two different values and that there is no majority for a particular value in the \( inp \) fields at the end of the round. As a result, no process decides in the second round of phase \(\varPhi _1\). Moreover, it is possible that different values still exist after phase \(\varPhi _2\). Hence, phase \(\varPhi _3\) does not guarantee termination.
The crux of the problem is round 1 of phase \(\varPhi _1\), which (RT) prohibits. There, in a multi-valued setting, two processes p and q can update \( inp \) to two different values v and \(v'\), while the updates to \( vote \) fail at both p and q. However, in the binary setting, any process p that updates \( inp \) to 1 must update \( vote \) as well.
5 Cutoff Bounds for Binary Consensus
The zero-one principle shows that it suffices to verify consensus algorithms for the binary domain \(\mathcal {V}= \mathbb {B}\). We now complete our proof of the small scope hypothesis by proving it for the binary case. For an algorithm \(\mathcal {A}\) with the set of guards \(\mathcal {G}\), let \(T_\mathcal {A}= \{th(G) \mid G \in \mathcal {G} \wedge pred(G)\ne \texttt {{smor}}\} \cup \{\frac{th(G)}{2} \mid G \in \mathcal {G} \wedge pred(G) = \texttt {{smor}}\}\).
Theorem 2
Let \(\mathcal {A}\) be an algorithm written in \( ConsL ^E\) for some E. Let d be the least common denominator of the (reduced-form) fractions in \(T_\mathcal {A}\). Then, \(\mathcal {A}\) solves binary consensus for any number of processes if and only if \(\mathcal {A}\) solves binary consensus for exactly \(2d + 1\) processes.
As an example, Theorem 2 yields a cutoff bound of 7 for the \(\frac{1}{3}\)-rule algorithm (Fig. 2) and a cutoff bound of 5 for Paxos (Fig. 3). Like with the 0-1 principle, we only sketch the main proof ideas; the details are in [39].
We start by giving an overview of our proof technique and providing intuition for the choice of our cutoff bound \(B = 2d + 1\). The details differ slightly depending on the consensus property considered. We first explain the general approach, which is same for all the properties, and focus on the differences afterwards. We show that, given a (labeled) counterexample trace \(\tau _l\) of a large width \(k > B\) that violates a consensus property, we can create a counterexample \(\tau _s\) of the small width B, with the same labels as \(\tau _l\). A trace inflation lemma allows us to ignore systems of widths below B by inflating small counterexamples.
Our proof is based on simulations in the style of [37]. These rely on a simulation relation R relating states \(s_l\) of the large system to states \(s_s\) of the small system. The main proof obligation for simulation requires that \(s_s\) can mimic all possible transitions from \(s_l\); formally, given any \(s_s\), \(s_l\), \(s_l'\), and \(\varLambda \), we must prove:
To define the relation R, we observe that guards, and thus also transitions, are agnostic to the absolute numbers of processes; they only use fractional thresholds and compare the relative frequencies of values. Hence, we relate states of different sizes based on the frequencies of values from \(\mathcal {V}_\bot \), expressed as fractions of the number of processes. We discretize these fractions into size-independent slots \(\{0, \frac{1}{d}, \frac{2}{d}, \ldots \frac{d-1}{d}\}\), since only d-denominated fractions appear in the algorithm’s guards. The state \(s_s\) must then be wide enough to accommodate the \(s_l\)-slot of each value from \(\mathcal {V}_\bot \). In [39], we show that \(2d+1\) is the smallest such width. We now give more details of the simulation relation and our proof under the assumption that \(\mathcal {V}= \mathbb {B}\).
5.1 Core Elements of the Simulation Relation
Given two natural numbers n (the system’s width) and d (with \(d \ge 2\)), we define two sets \(T \triangleq \{0, \frac{1}{d}, \ldots , \frac{d-1}{d}\}\) and \(T_0 \triangleq T \cup \{-\frac{1}{3d}\}\), and a function \(\gamma _{n}\! : \{0, \ldots , n\} \rightarrow T_0\), with \(\gamma _{n}(c) = \frac{\lceil {\frac{d}{n} c\rceil } - 1}{d}\) when \(c > 0\), and \(\gamma _{n}(0) = -\frac{1}{3d}\). The function \(\gamma _n\) maps process counts to slots, where \(\gamma _{n}(c)\) yields the smallest threshold in \(T_0\) exceeded by the count c. These counts typically arise as \(c=\#[s(f)](v)\), i.e., the number of processes holding value v in field f, where we write s(f) for the function defined by \(s(f)(p)=s_p.f\) for all \(p\in \varPi \). If state s has width n, then \(\gamma _{n}(\#[s(f)](v))\) denotes the corresponding slot in \(T_0\). Given two multisets \(M_s\) and \(M_l\) of sizes B and k respectively, we define the following relations:
The first relation requires the slot of each value from \(\mathcal {V}_\bot \) to be exactly the same in both multisets. Sometimes this will be too strong a requirement, and we will switch to the other two relations, which are weaker (the first two relations can be expressed in terms of the last one, but we retain them for convenience).
Example 4
For the \(\frac{1}{3}\)-rule algorithm, we have \(B = 7\) and \(T = \{0, \frac{1}{3}, \frac{2}{3}\}\). Take \(k = 13\) and consider the multisets M in the first column of Table 1. The second column of the table indicates their size and the remaining columns display for each of them the slots \(\gamma _{\left| M\right| }(c)\) of the indicated counts c. Then, we have
-
\((M_s^1, M_l^1) \in cntMS _=\),
-
\((M_s^1, M_l^2) \in cntMS _\ge (\mathcal {V}) \cap cntMS _{\sum \ge }(\mathcal {V})\), but \((M_s^1, M_l^2) \notin cntMS _=\), and
-
\((M_s^1, M_l^3) \in cntMS _{\sum \ge }(\mathcal {V})\), but \((M_s^1, M_l^3) \notin cntMS _\ge (\mathcal {V})\).
These relations form the basis of our simulation relation R. For space reasons, we focus on just the salient points of R. For example, we require:
for all \((s_s, s_l) \in R\). Similar conditions relate the other fields. The exact relation used depends on both the property we are proving, and on the field’s position in the phase graph. The next subsection provides additional details, focusing on the core language \( ConsL \) (without extensions) for simplicity.
5.2 Simulating Transitions
Given a transition \(s \xrightarrow {\varLambda } s'\) in a trace, define \(U\) to be the set of all upd-fields appearing in the transition’s instructions, and the global update associated with the transition to be a function \(\mathcal {U}: U\rightarrow \varPi \rightarrow \mathcal {V}_\bot \), where \(\mathcal {U}(f)(p)\) is \(v \in \mathcal {V}\) if p updates the field f with v, and \(\bot \) if p updates f with a fallback value. We let \(u_p(f) = \mathcal {U}(f)(p)\) and call \(u_p\) the local update of the process p. Our simulation proofs proceed in three stages:
-
1.
Simulate local updates: for any local update \(u_p\) possible from \(s_l\), prove that there exists a set \(P \subseteq \varPi \) such that any process whose HO set is P can also perform the local update \(u_p\) from \(s_s\).
-
2.
Simulate global updates: given any global update \(\mathcal {U}_l\) associated with a transition \(s_l \xrightarrow {\varLambda } s_l'\), combine the local updates from the previous stage to construct a global update \(\mathcal {U}_s\) associated with a transition \(s_s \xrightarrow {\varLambda } s_s'\), such that \(\mathcal {U}_s\) is similar to \(\mathcal {U}_l\). For example, for all fields f updated in a transition before the fork point, we require that \((\#[\mathcal {U}_s(f)], \#[\mathcal {U}_l(f)]) \in cntMS _=\).
-
3.
Simulate state updates: given \(s_l \xrightarrow {\varLambda } s_l'\), \(\mathcal {U}_l\), and \(\mathcal {U}_s\) as above, show that applying \(\mathcal {U}_s\) to \(s_s\) yields an \(s_s'\) with \(s_s \xrightarrow {\varLambda } s_s'\) and \((s_s', s_l') \in R\). When \(\mathcal {U}_l\) updates \( inp \), i.e., \( inp \in U\), this is not always the case. The reason is that \(\mathcal {U}_s\) alone does not completely determine \(\#[s_s'( inp )]\), as the old values are used as a fallback. For instance, if \(\#[s_s( inp )] = M_s^1 = \{4 \times 0, 3 \times 1\}\), we can construct two global updates \(\mathcal {U}_1\) and \(\mathcal {U}_2\) with \(\#[\mathcal {U}_1( inp )] = \#[\mathcal {U}_2( inp )] = \{3 \times 0, 4 \times \bot \}\), such that applying \(\mathcal {U}_1\) to \(s_s\) yields a state \(s_s'\) with \(\#[s_s'( inp )] = \{7 \times 0\}\) (\(\mathcal {U}_1\)’s \(3 \times 0\) overwrite all 1’s in \(s_s( inp )\)), and \(\mathcal {U}_2\) leaves \(s_s\) intact (\(\mathcal {U}_2\)’s \(3 \times 0\) overwrite three 0’s in \(s_s( inp )\)). Hence, to obtain the desired \(s_s'\) with \((s_s', s_l') \in R\), we might first have to transform \(\mathcal {U}_s\) into some appropriate \(\mathcal {U}_s'\) with \(\#[\mathcal {U}_s( inp )] = \#[\mathcal {U}_s'( inp )]\) by permuting the processes’ local updates. This is achieved by permuting their round HO sets. Note that this preserves the step label \(\varLambda \).
Stage 1 is relatively straightforward, whereas the next two stages are significantly more involved. Stage 2 is complicated by the fork points (Sect. 3.2), which make constructing similar global updates a non-trivial combinatorial problem. The restriction (R2) is crucial in solving this problem. In Stage 3, a problem arises when the \( inp \) field is updated as the following example illustrates.
Example 5
Consider states \(s_s\) and \(s_l\) such that \(\#[s_s( inp )] = M_s^1 = \{4 \times 0, 3 \times 1\}\) and \(\#[s_l( inp )] = M_l^1 = \{5 \times 0, 8 \times 1\}\). There is an update \(\mathcal {U}_l\) with \(\#[\mathcal {U}_l( inp )] = \{1 \times 0, 1 \times 1, 11 \times \bot \}\) that yields a state \(s_l'\) with \(\#[s_l'( inp )] = M_l^3 = \{4 \times 0, 9 \times 1\}\). The updates \(\mathcal {U}_s\) with \(\#[\mathcal {U}_s( inp )] = \{1 \times 0, 1 \times 1, 5 \times \bot \}\) are the only ones satisfying \((\#[\mathcal {U}_s( inp )], \#[\mathcal {U}_l( inp )]) \in cntMS _=\). However, none of these can be applied to \(s_s\) to yield a state \(s_s^{\prime }\) such that (inp-rel) holds for \(s^{\prime }_l\) and \(s^{\prime }_s\), since attaining a fraction \(\gamma _{13}(\#[s_l'( inp )](1))=\gamma _{13}(9)=\frac{2}{3}\) of 1’s in \(s_s^{\prime }\) would require \(\#[s_s^{\prime }( inp )](1) \ge 5\). Hence, we might be forced to use a \(\mathcal {U}_s\) such that \((\#[\mathcal {U}_s( inp )], \#[\mathcal {U}_l( inp )]) \notin cntMS _=\), which in turn might cause \((\#[\mathcal {U}_s(f)], \#[\mathcal {U}_l(f)]) \notin cntMS _=\) for the other fields updated by \(\mathcal {U}_s\).
After the fork point, we therefore weaken the Stage 2 relation to
for an appropriate \(W \subset \mathcal {V}_\bot \). For ephemeral fields, this also implies that the simulation relation must use \( cntMS _\ge (W)\) and \( cntMS _{\sum \ge }(W)\) instead of \( cntMS _=\). The choice of W depends on the property whose violation we want to preserve.
Agreement and Non-triviality. Preserving agreement and non-triviality violations requires the small system to make decisions whenever the large system makes them. Thus, we choose \(W = \mathcal {V}\). This suffices to show that whenever a value \(v \in \mathcal {V}\) satisfies a guard (in particular, for updating \( dec \)) in the large system, v also satisfies that guard in the small system. Our choice of W might force updates to happen in the small system where none happened in the large system, but this is acceptable for the violations we wish to preserve.
Termination. Preserving termination violations requires exactly the opposite: whenever an update guard (in particular, for updating \( dec \)) fails in the large system, its failure must also be possible in the small system. Recalling the semantics of \( ConsL \), guards fail for two reasons: an insufficient number of non-\(\bot \) messages have been received, or different values have been received and the guard uses an \(\texttt {{all=}}\) predicate. Choosing \(W = \{\bot \}\) preserves the first cause of failure, but not the second. Choosing \(W = \mathcal {V}\) preserves the second cause, but not the first. Thus, the correct choice depends on the transition \(s_l \rightarrow s_l'\), and cannot be determined in advance. This is a well-known problem with forward simulation, the type of simulation that we described in (s-trans). To overcome this problem, we resort to backward-forward simulations [37], which enable us to switch between the two choices of W on-the-fly. As our transition systems are all finitely-branching, backward-forward simulation ensures the inclusion of infinite traces.
6 Experimental Results
We combine Theorems 1 and 2, the finite representations of the phase sequence and the communication predicates, and the techniques from [46] for handling unbounded timestamps to turn model checking into a decision procedure for \( ConsL \) algorithms and consensus. Given a \( ConsL \) algorithm \(\mathcal {A}\) with a cutoff bound B, one encodes the HO model of \(\mathcal {A}\) for \(\left| \varPi \right| = B\) and \(\mathcal {V}= \mathbb {B}\) in the model checker’s input language and verifies it. We have built a tool that automatically translates a \( ConsL \) algorithm into the appropriate Promela model and LTL properties for the Spin model checker [23]. As case studies, we generated models of different algorithms from the literature (Table 2). Our verification times confirm that the above decision procedure is applicable in practice, with modest resources.
The tool and the generated models are available for download [40]. For simplicity, our tool handles only a subset of phase sequence and communication predicate specifications described in Sect. 3.2. To improve performance, the tool implements two optimizations. First, it reduces the model’s branching factor. In a naive modeling approach, in every round in which the uniformity formula \(\phi _{ uf }\) does not hold, each of the B processes first chooses its HO set independently and then performs a local update based on this HO set, yielding a branching factor of \(2^{B^2}\). Instead, the tool-generated models first calculate the possible local updates and let each process pick one of them, lowering the branching factor to typically 2 or 3. Second, the tool reduces the state space by exploiting symmetry in the system and applying a counter abstraction. The abstraction is sound and complete. For leaderless algorithms this is immediate since guard satisfaction (Sect. 3.3) is defined exactly on multisets; for leader-based algorithms, we need an additional variable to track the leader process’ state in the abstraction.
7 Related Work
The general parametric verification problem was shown to be undecidable by Apt and Kozen [5]. Suzuki [45] showed that this holds also when the parameter is the number of replicated processes, each having a fixed state space. The small scope hypothesis is folklore, implicitly formulated by Jackson and Damon [26], and empirically studied for Java data structures by Andoni et al. [4], for answer-set programs by Oetsch et al. [42], and for distributed systems by Yuan et al. [49].
Cutoff Bounds. Cutoff bounds have been devised for several classes of algorithms and properties: for token-ring systems by Emerson and Namjoshi [17]; for systems with existential guards and systems with universal guards by Emerson and Kahlon [15]; for cache coherence protocols by Emerson and Kahlon [16]; for rectangular hybrid automata by Johnson and Mitra [29]; and for software transactional memories by Guerraoui et al. [20]. Kaiser et al. [30] devise a method for determining cutoff bounds for the thread-state reachability problem dynamically, by performing a partial search of the state space. Abdulla et al. [2] use similar ideas, but their results apply to a larger class of systems. None of these results applies to consensus algorithms or other types of fault-tolerant distributed systems. The only cutoff result that we are aware of in this area is by Delzanno et al. [12]. They derive cutoff bounds for the proposer and learner roles of Paxos, but not the acceptor role, for which they perform only bounded verification. We adopt the more common model where all processes play all the roles.
Other (Semi-)Automated Methods. Backward reachability analysis of well-quasi-ordered systems [1] and regular model checking [3] are two general approaches to the verification of parametric systems. Regular model checking has been used to verify some simple fault-tolerant algorithms [19]. However, no suitable well-quasi-ordering or regular transition relations are known to exist for fault-tolerant distributed systems that rely on threshold guards. Two recent works have explored alternative approaches for the parametric verification of such systems.
Konnov et al. [28] introduce an abstraction for systems based on a type of threshold guards, roughly similar to \( ConsL \) guards. Their technique yields a sound, but incomplete (due to abstraction) verification procedure for next-free LTL properties, and they successfully apply it to several simpler fault-tolerant algorithms. In [33, 34] they propose additional verification methods for the abstraction and also apply them to a simplified version of the consensus problem.
Drăgoi et al. [13] introduce the consensus logic \(\mathbb {CL}\), aimed at verifying the properties of round-based consensus algorithms, and a domain specific language for it [14]. \(\mathbb {CL}\) is strictly more expressive than \( ConsL \), and can encode algorithms for the synchronous and Byzantine settings. They provide a semi-decision procedure for invariant checking, which performs well in their experiments, and a full decision procedure for invariant checking for a fragment \(\mathbb {CL}_ dec \) whose expressive power is incomparable to \( ConsL \). Their method is only semi-automated, since the user must find the appropriate invariants, and is not guaranteed to give an answer for \(\mathbb {CL}\) (outside of \(\mathbb {CL}_ dec \)), since it is based on a semi-decision procedure.
8 Conclusions
Our main contribution is the specification language \( ConsL \) for consensus algorithms, for which we derive a zero-one principle and cutoff bounds for verifying consensus properties. This language covers a relevant and non-trivial class of consensus algorithms. Our bounds are algorithm-dependent, but fairly small, either 5 or 7 for our case studies. This formally proves the small scope hypothesis for this class, and lends additional credibility to the hypothesis for other fault-tolerant distributed algorithms. Moreover, the bounds are small enough to be within the reach of standard model-checking methods, yielding the first fully automated verification procedure for consensus algorithms.
We see two directions for future work. The first is to extend our results to other algorithms. One possible extension is to Byzantine-tolerant algorithms. However, as these algorithms typically use thresholds with denominators in the range of 3 to 7, model checking them could become infeasible with \(B=2d+1\). While lowering the factor 2 in B might be possible, we suspect that B’s dependency on d is fundamental since in systems with fewer than \(d+1\) processes the notions “more than \(\frac{d-1}{d}\) processes” and “all processes” coincide. Another possible extension is to target higher-level primitives that build on consensus algorithms in a white-box fashion, such as atomic (also called total-order) broadcast.
The second direction is to focus on the 0-1 principle. Putting aside the cutoff bounds might help to remove some of the more ad-hoc \( ConsL \) features (such as the restrictions in Sect. 3.2) and yield a simpler class of algorithms with hopefully simpler proofs. If such a class is obtained, one might consider generalizing the principle; for example, a 0-k principle could help decide k-set agreement. Furthermore, we believe that the unbounded growth of the input (and thus also message) space with the increasing system width is a key obstacle for applying the method of [28] to general consensus algorithms, and that the 0-1 principle could provide the missing link.
Notes
- 1.
Some authors exchange the meanings of phases and rounds; we follow [10].
References
Abdulla, P., Cerans, K., Jonsson, B., Tsay, Y.-K.: General decidability theorems for infinite-state systems. In: LICS, pp. 313–321 (1996)
Abdulla, P., Haziza, F., Holík, L.: Parameterized verification through view abstraction. Int. J. Softw. Tools Technol. Transf., pp. 1–22 (2015)
Abdulla, P.A.: Regular model checking. Int. J. Softw. Tools Technol. Transf. 14(2), 109–118 (2012)
Andoni, A., Daniliuc, D., Khurshid, S., Marinov, D.: Evaluating the “small scope hypothesis”. In: POPL, vol. 2 (2003)
Apt, K.R., Kozen, D.C.: Limits for automatic verification of finite-state concurrent systems. Inf. Process. Lett. 22(6), 307–309 (1986)
Bailis, P., Kingsbury, K.: The network is reliable. ACM Queue 12(7), 20:20–20:32 (2014)
Ben-Or, M.: Another advantage of free choice: completely asynchronous agreement protocols. In: PODC, pp. 27–30 (1983)
Chandra, T.D., Toueg, S.: Unreliable failure detectors for reliable distributed systems. J. ACM (JACM) 43(2), 225–267 (1996)
Chaouch-Saad, M., Charron-Bost, B., Merz, S.: A reduction theorem for the verification of round-based distributed algorithms. In: Bournez, O., Potapov, I. (eds.) RP 2009. LNCS, vol. 5797, pp. 93–106. Springer, Heidelberg (2009). doi:10.1007/978-3-642-04420-5_10
Charron-Bost, B., Schiper, A.: The Heard-Of model: computing in distributed systems with benign faults. Distrib. Comput. 22(1), 49–71 (2009)
Debrat, H., Merz, S.: Verifying fault-tolerant distributed algorithms in the heard-of model. Archive of Formal Proofs (AFP) (2012). https://www.isa-afp.org/entries/Heard_Of.shtml
Delzanno, G., Tatarek, M., Traverso, R.: Model Checking Paxos in Spin. Electron. Proc. Theoret. Comput. Sci. 161, 131–146 (2014)
Drăgoi, C., Henzinger, T.A., Veith, H., Widder, J., Zufferey, D.: A logic-based framework for verifying consensus algorithms. In: McMillan, K.L., Rival, X. (eds.) VMCAI 2014. LNCS, vol. 8318, pp. 161–181. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54013-4_10
Drăgoi, C., Henzinger, T. A., Zufferey, D.: PSync: a partially synchronous language for fault-tolerant distributed algorithms. In: POPL, pp. 400–415 (2016)
Emerson, E.A., Kahlon, V.: Reducing model checking of the many to the few. In: McAllester, D. (ed.) CADE 2000. LNCS (LNAI), vol. 1831, pp. 236–254. Springer, Heidelberg (2000). doi:10.1007/10721959_19
Emerson, E.A., Kahlon, V.: Exact and efficient verification of parameterized cache coherence protocols. In: Geist, D., Tronci, E. (eds.) CHARME 2003. LNCS, vol. 2860, pp. 247–262. Springer, Heidelberg (2003). doi:10.1007/978-3-540-39724-3_22
Emerson, E.A., Namjoshi, K.S.: On reasoning about rings. Int. J. Found. Comput. Sci. 14(04), 527–549 (2003)
Fischer, M.J., Lynch, N.A., Paterson, M.S.: Impossibility of distributed consensus with one faulty process. J. ACM 32(2), 374–382 (1985)
Fisman, D., Kupferman, O., Lustig, Y.: On verifying fault tolerance of distributed protocols. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 315–331. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78800-3_22
Guerraoui, R., Henzinger, T.A., Jobstmann, B., Singh, V.: Model checking transactional memories. In: PLDI, pp. 372–382 (2008)
Hawblitzel, C., Howell, J., Kapritsos, M., Lorch, J.R., Parno, B., Roberts, M.L., Setty, S., Zill, B.: IronFleet: proving practical distributed systems correct. In SOSP, pp. 1–17 (2015)
Herlihy, M.: Wait-free synchronization. ACM Trans. Program. Lang. Syst. 13(1), 124–149 (1991)
Holzmann, G.J.: The SPIN Model Checker - Primer and Reference Manual. Addison-Wesley, Boston (2004)
Hutle, M., Schiper, A.: Communication predicates: a high-level abstraction for coping with transient and dynamic faults. In: 37th Annual IEEE/IFIP International Conference on Dependable Systems and Networks, 2007, DSN 2007, pp. 92–101. IEEE (2007)
Jackson, D.: Software Abstractions: Logic, Language, and Analysis. MIT Press, Cambridge (2012)
Jackson, D., Damon, C.A.: Elements of style: analyzing a software design feature with a counterexample detector. IEEE Trans. Softw. Eng. 22(7), 484–495 (1996)
Jaskelioff, M., Merz, S.: Proving the correctness of Disk Paxos. Archive of Formal Proofs (AFP) (2005). https://www.isa-afp.org/entries/DiskPaxos.shtml
John, A., Konnov, I., Schmid, U., Veith, H., Widder, J.: Parameterized model checking of fault-tolerant distributed algorithms by abstraction. In: FMCAD, pp. 201–209 (2013)
Johnson, T.T., Mitra, S.: A small model theorem for rectangular hybrid automata networks. In: Giese, H., Rosu, G. (eds.) FMOODS/FORTE -2012. LNCS, vol. 7273, pp. 18–34. Springer, Heidelberg (2012). doi:10.1007/978-3-642-30793-5_2
Kaiser, A., Kroening, D., Wahl, T.: Dynamic cutoff detection in parameterized concurrent programs. In: Touili, T., Cook, B., Jackson, P. (eds.) CAV 2010. LNCS, vol. 6174, pp. 645–659. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14295-6_55
Kingsbury, K.: Jepsen: Testing the Partition Tolerance of PostgreSQL, Redis, MongoDB and Riak (2013). http://www.infoq.com/articles/jepsen
Knuth, D.E.: The Art of Computer Programming, Vol III: Sorting and Searching. Addison-Wesley, Boston (1973)
Konnov, I., Veith, H., Widder, J.: On the completeness of bounded model checking for threshold-based distributed algorithms: reachability. In: Baldan, P., Gorla, D. (eds.) CONCUR 2014. LNCS, vol. 8704, pp. 125–140. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44584-6_10
Konnov, I., Veith, H., Widder, J.: SMT and POR beat counter abstraction: parameterized model checking of threshold-based distributed algorithms. In: Computer Aided Verification, pp. 85–102, July 2015
Küfner, P., Nestmann, U., Rickmann, C.: Formal verification of distributed algorithms. In: Baeten, J.C.M., Ball, T., Boer, F.S. (eds.) TCS 2012. LNCS, vol. 7604, pp. 209–224. Springer, Heidelberg (2012). doi:10.1007/978-3-642-33475-7_15
Lamport, L.: The part-time parliament. ACM Trans. Comput. Syst. 16(2), 133–169 (1998)
Lynch, N., Vaandrager, F.: Forward and backward simulations part I: untimed systems. Inf. Comput. 121, 214–233 (1995)
Marić, O., Sprenger, C., Basin, D.: Consensus Refined. In: DSN, pp. 391–402 (2015)
Marić, O.: Formal Verification of Fault-Tolerant Systems. Ph.D. thesis, Department of Computer Science, ETH Zurich (2017). http://dx.doi.org/10.3929/ethz-a-010892776
Marić, O.: The Consensus Verifier, May 2017. http://www.infsec.ethz.ch/research/software/consl-verifier
Newcombe, C.: Why Amazon Chose TLA\(^+\). In: Ait, A.Y., Schewe, K.D. (eds.) Abstract State Machines, Alloy, B, TLA, VDM, and Z. ABZ 2014. LNCS, vol. 8477, pp. 25–39. Springer, Berlin (2014)
Oetsch, J., Prischink, M., Pührer, J., Schwengerer, M., Tompits, H.: On the small-scope hypothesis for testing answer-set programs. In: KR (2012)
Santoro, N., Widmayer, P.: Time is not a healer. In: Monien, B., Cori, R. (eds.) STACS 1989. LNCS, vol. 349, pp. 304–313. Springer, Heidelberg (1989). doi:10.1007/BFb0028994
Schiper, N., Rahli, V., van Renesse, R., Bickford, M., Constable, R.: Developing correctly replicated databases using formal tools. In: DSN, pp. 395–406 (2014)
Suzuki, I.: Proving properties of a ring of finite-state machines. Inf. Process. Lett. 28(4), 213–214 (1988)
Tsuchiya, T., Schiper, A.: Model checking of consensus algorithms. In: SRDS, pp. 137–148, October 2007
Tsuchiya, T., Schiper, A.: Using bounded model checking to verify consensus algorithms. In: Taubenfeld, G. (ed.) DISC 2008. LNCS, vol. 5218, pp. 466–480. Springer, Heidelberg (2008). doi:10.1007/978-3-540-87779-0_32
Tsuchiya, T., Schiper, A.: Verification of consensus algorithms using satisfiability solving. Distrib. Comput. 23(5–6), 341–358 (2010)
Yuan, D., Luo, Y., Zhuang, X., Rodrigues, G.R., Zhao, X., Zhang, Y., Jain, P.U., Stumm, M.: Simple testing can prevent most critical failures: an analysis of production failures in distributed dataintensive systems. In: OSDI (2014)
We would like to thank the anonymous reviewers and Ralf Sasse for their useful feedback on the paper.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Marić, O., Sprenger, C., Basin, D. (2017). Cutoff Bounds for Consensus Algorithms. In: Majumdar, R., Kunčak, V. (eds) Computer Aided Verification. CAV 2017. Lecture Notes in Computer Science(), vol 10427. Springer, Cham. https://doi.org/10.1007/978-3-319-63390-9_12
Download citation
DOI: https://doi.org/10.1007/978-3-319-63390-9_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63389-3
Online ISBN: 978-3-319-63390-9
eBook Packages: Computer ScienceComputer Science (R0)







 , where only the leader broadcasts a message in a round, and
, where only the leader broadcasts a message in a round, and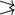 , where all processes send a message exclusively to the leader.
, where all processes send a message exclusively to the leader.

