Keywords

Introduction

The magnetoimpedance (MI) implies a change in the impedance of a magnetic conductor with the variation of an external magnetic field. The nature of the MI effect can be explained in the framework of the classical electrodynamics and is related to changes in the permeability and skin depth with the external field. The interest in the MI is supported by the possible use of the effect for the development of sensors of a weak magnetic field (see, for example, [1, 2]). From the point of view of the sensor miniaturization and integration with modern microelectronic technologies, thin-film structures are one of the most attractive materials for sensitive elements of MI sensors.

The linearity and sensitivity for the external magnetic field are the most important parameters in applications of the MI effect. However, for most of the materials, the MI response exhibits nonlinear behavior in the vicinity of zero field, and this is unfavorable for sensor applications. To improve the linear features of the MI response, the asymmetric field dependence of the impedance is promising. The asymmetric magnetoimpedance (AMI) may be obtained by applying the direct bias current or alternating magnetic field to the soft magnetic conductor [3,4,5]. Note that these methods have some limitations in applications due to an increase in the power consumption.

Another approach of producing the AMI consists in the use of materials with asymmetric static magnetic configuration arising from the magnetostatic interactions or exchange bias. This type of the AMI has been observed initially in field-annealed amorphous ribbons [6, 7]. For film structures, the AMI has been studied extensively in the exchange bias multilayers [8, 9]. It was found that the linear behavior of the MI response can be tuned by modifying the angle between the external field and exchange bias field or by changing the frequency.

The AMI effect has been also observed in three-layered NiFe/Cu/Co film structures [10]. The measured field dependence of the film impedance exhibited asymmetry within a wide frequency range. It was shown that the film structures have biphase magnetic behavior, and the origin of the AMI can be ascribed to the magnetostatic coupling between the soft and hard magnetic layers. The linear behavior of the MI response in bimagnetic films can be tuned by varying the copper spacer thickness and current frequency [10]. A model to describe the AMI effect in three-layered bimagnetic films has been proposed recently [11]. The MI response was found by means of a simultaneous solution of Maxwell equations together with Landau–Lifshitz equation, and the magnetostatic coupling between the hard and soft magnetic layers was described in terms of an effective bias field appearing in the permalloy layer. The model allows one to explain qualitatively the field and frequency dependences of the AMI effect observed in NiFe/Cu/Co film structures.

Note that the field sensitivity of the impedance in the three-layered films is sufficiently low [10]. This fact is related to the small thickness of the film structure, where the skin depth is much larger than the film thickness. To enhance the sensitivity of the AMI, the multilayers consisting of a repetition of the base bimagnetic three-layered film structure have been proposed [12]. It was found that these multilayers exhibit bimagnetic behavior, and the AMI sensitivity increases, which is promising for sensor design. In this work, we extend the approach proposed in [11] to the case of the bimagnetic multilayers and study the effect of the number of layers on the AMI.

Model

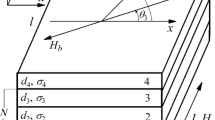
Figure 1 shows schematically the studied film structure having the length l and width w < l. The structure consists of the soft magnetic layer 1, highly conductive non-magnetic spacer 2, hard magnetic layer 3, and buffer layer 4. The corresponding values of the layer thickness are d 1, d 2, d 3, and d 4. The number of repetitions of the first three layers is denoted as N. The total number of layers equals to 4N − 1, and the multilayer thickness D = N(d 1 + d 2 + d 3) + (N − 1)d 4.

Fig. 1
figure 1

A sketch of the bimagnetic multilayer geometry and coordinate system used for analysis

Full size image

The multilayered film is subjected to the alternating current I = I 0exp(−iωt), and the external magnetic field H e is parallel to the current. Neglecting edge effects, we assume that the electromagnetic fields depend only on the coordinate perpendicular to the sample plane. Furthermore, we neglect the longitudinal alternating magnetic field arising in the soft magnetic layers due to the cross-magnetization process [13]. In this approximation, the solution of Maxwell equations for the amplitudes of the longitudinal electric field \(e_{k}^{(j)}\) and transverse magnetic field \(h_{k}^{(j)}\) is given by

$$e_{k}^{(j)} = (c\lambda_{k} /4\pi \sigma_{k} )[A_{k}^{(j)} \cosh (\lambda_{k} z) + B_{k}^{(j)} \sinh (\lambda_{k} z)],$$
(1)
$$h_{k}^{(j)} = A_{k}^{(j)} \sinh (\lambda_{k} z) + B_{k}^{(j)} \cosh (\lambda_{k} z).$$
(2)

Here k = 1, 2, 3, and 4 is the layer number; j = 1, … N is the number of the base structure repetition; \(A_{k}^{(j)}\) and \(B_{k}^{(j)}\) are the constants; λ k  = (1 − i)/δ k ; δ k  = c/(2πωσ k μ k )1/2; c is the velocity of light; σ k and μ k are the conductivity and the transverse permeability of the layer k, respectively. For the non-magnetic layers, k = 2 and k = 4, the transverse permeability is equal to unity, μ 2 = μ 4 = 1.

The amplitudes of the electric and magnetic field satisfy the continuity conditions at the layer interfaces [11]. In addition, the amplitude of the magnetic field at the multilayer surfaces, z = 0 and z = D, is governed by the following excitation conditions:

$$\begin{aligned} h_{1}^{(1)} (0) & = - 2\pi I_{0} /cw, \\ h_{3}^{(N)} (D) & = 2\pi I_{0} /cw. \\ \end{aligned}$$
(3)

Thus, the boundary conditions allow one to find the 2(4N − 1) constants in Eqs. (1) and (2). The multilayer impedance Z can be expressed in terms of the surface impedance tensor [2]:

$$Z = \frac{\pi l}{cw} \times \left[ {\frac{{e_{3}^{(N)} (D)}}{{h_{3}^{(N)} (D)}} - \frac{{e_{1}^{(1)} (0)}}{{h_{1}^{(1)} (0)}}} \right].$$
(4)

Further, it is assumed that the values of the permeability in the magnetic layers are governed by the magnetization rotation only. This approximation is valid at sufficiently high frequencies, when the domain-wall motion is strongly damped [14]. We assume that the magnetic layers have the uniaxial in-plane anisotropy. During the deposition of the multilayer, a constant magnetic field was applied along the short side of the film [12]. Therefore, the direction of the anisotropy axes in the magnetic layers is close to the transverse one. The magnetostatic coupling between the hard and soft magnetic layers induces the effective bias field H b in the soft magnetic layers. It is assumed that the bias field does not vary over the soft magnetic layer thickness and has the opposite direction with respect to the magnetization in the hard magnetic layers. Note that a similar approach has been used previously to study the AMI effect in amorphous ribbons [15, 16].

The distribution of the magnetization in the magnetic layers can be found by minimizing the free energy. In the hard magnetic layers, the free energy can be presented as a sum of the uniaxial anisotropy energy and Zeeman energy. The minimization procedure results in the following equation for the magnetization angle θ 3 in the hard magnetic layer:

$$H_{3} \sin (\theta_{3} - \psi_{3} )\cos (\theta_{3} - \psi_{3} ) = H_{e} \cos \theta_{3} .$$
(5)

Here ψ 3 is the anisotropy axis angle with respect to the transverse direction and H 3 is the anisotropy field in the hard magnetic layers.

For the equilibrium magnetization angle θ 1 in the soft magnetic layers, we obtain [11]

$$H_{1} \sin (\theta_{1} - \psi_{1} )\cos (\theta_{1} - \psi_{1} ) - H_{b} \sin (\theta_{1} - \theta_{3} ) - H_{e} \cos \theta_{1} = 0.$$
(6)

Here ψ 1 is the anisotropy axis angle and H 1 ≪ H 3 is the anisotropy field in the soft magnetic layers.

It should be noted that there is a difference in magnetic properties between the first soft magnetic layer and the inner soft magnetic layers. This is due to the first soft magnetic layer interacts only with one hard magnetic layer, whereas the other soft magnetic layers are sandwiched between two hard magnetic layers [12]. To take into account this fact, we assume that the bias field in the first soft magnetic layer is two times lower than H b .

The transverse permeability in the magnetic layers can be found by means of the solution of the linearized Landau–Lifshitz equation. To simplify calculations, we use the so-called electromagnetic approximation [2, 14], where the contribution of the exchange energy is neglected. More rigorous theoretical treatment requires the including of the exchange-conductivity effect in the model [17,18,19]. However, the contribution of the exchange-conductivity effect to the magnitude of the impedance is relatively low within the high-frequency range studied.

The solution of the linearized Landau–Lifshitz equation leads to the following expression for the transverse permeability in the magnetic layers [11]:

$$\mu_{k} = 1 + \frac{{\gamma 4\pi M_{k} [\gamma 4\pi M_{k} + \omega_{k} - i\kappa \omega ]\sin^{2} \theta_{k} }}{{[\gamma 4\pi M_{k} + \omega_{k} - i\kappa \omega ][\omega_{k} - \gamma H_{k} \sin^{2} (\theta_{k} - \psi_{k} ) - i\kappa \omega ] - \omega^{2} }}.$$
(7)

Here k = 1 and k = 3 corresponds to the soft and hard magnetic layers, respectively, M k are the values of the saturation magnetization in the layers, γ is the gyromagnetic constant, and κ is the Gilbert damping parameter. The characteristic frequencies ω 1 and ω 3 can be expressed as

$$\omega_{1} = \gamma [H_{1} \cos^{2} (\theta_{1} - \psi_{1} ) - H_{b} \cos (\theta_{1} - \theta_{3} ) + H_{e} \sin \theta_{1} ],$$
(8)
$$\omega_{3} = \gamma [H_{3} \cos^{2} (\theta_{3} - \psi_{3} ) + H_{e} \sin \theta_{3} ].$$
(9)

Results and Discussion

To investigate the effect of the magnetostatic coupling and number of layers on the MI ratio, we use geometrical parameters of the bimagnetic multilayers studied experimentally [12]. The MI ratio ΔZ/ Z 0 is defined as follows:

$$\Delta Z/Z_{0} = (Z - Z_{0} )/Z_{0} ,$$
(10)

where Z 0 is the DC resistance of the multilayered film:

$$Z_{0} = \frac{l}{{w[N(\sigma_{1} d_{1} + \sigma_{2} d_{2} + \sigma_{3} d_{3} ) + (N - 1)\sigma_{4} d_{4} ]}} \cdot$$
(11)

The dependence of the MI ratio of the multilayered film (N = 5) on the external field is shown in Fig. 2 for different values of the bias field H b . In the presence of the bias field, the impedance field dependence shifts with respect to zero field, and there is a difference between the maximum impedance values at the positive and negative fields. The asymmetry growths with the bias field, the negative field peak increases and the positive field peak decreases. The AMI in multilayered films is caused by the fact that the bias field changes the static magnetization distribution and transverse permeability in the soft magnetic layers [11].

Fig. 2
figure 2

The multilayer impedance ratio as a function of the external field at N = 5 and f = ω/2π = 0.5 GHz for different values of H b . Parameters used for calculations are d 1 = 25 nm, d 2 = 7 nm, d 3 = 50 nm, d 4 = 10 nm, M 1 = 800 G, M 3 = 1000 G, H 1 = 5 Oe, H 3 = 30 Oe, ψ 1 = −0.1π, ψ 3 = 0, σ 1 = 1016s−1, σ 2 = 5 × 1017s−1, σ 3 = 1.5 × 1017s−1, σ 4 = 7 × 1016s−1 and κ = 0.02

Full size image

Note that the AMI response in multilayers is very sensitive to the anisotropy axis angle in the soft magnetic layers. It was shown for three-layered bimagnetic film structures that the asymmetry in the MI response is maximal at low values of ψ 1 and decreases with an increase of ψ 1 [11]. The asymmetry between the impedance values at the peaks disappears, if the anisotropy in the soft magnetic layer has the transverse direction, ψ 1 = 0. The deviation of the easy axis from the transverse direction may be attributed to peculiarities of the bimagnetic multilayer preparation [10].

The variation in the field dependence of the MI ratio with the frequency is presented in Fig. 3. At not very high frequencies, the peak positions in the field dependence of ΔZ/Z remain nearly the same, and the maximal values of the impedance increase due to the decrease of the skin depth. At frequencies of the order of 1 GHz, the peak positions shift toward higher fields due to the ferromagnetic resonance. In this case, the asymmetry between peaks almost vanishes.

Fig. 3
figure 3

The multilayer impedance ratio as a function of the external field at N = 5 and H b  = 1 Oe for different f (GHz). Parameters used for calculations are the same as in Fig. 2

Full size image

Although the results of modeling describe main features of the AMI effect in bimagnetic multilayered films [12], some experimental data cannot be explained in the framework of the model proposed. It was observed that at frequencies above 1.5 GHz the shape of the impedance field dependence changes. The MI response becomes nonlinear at the low external field, and an additional peak in the impedance field dependence was observed near zero field [12]. At the same time, the model predicts a monotonic behavior of the film impedance within this field range. The disagreement between theoretical and experimental results may be ascribed to approximations of the model.

The influence of a number of layers on the field dependence of the MI ratio is illustrated in Fig. 4. The MI ratio increases with the number of repetitions N of the base structure, since the skin effect is more pronounced in thick multilayered films. It follows from Fig. 4 that the impedance peak positions shift slightly toward higher fields with an increase of N. However, the shape of the impedance field dependence is not affected by the number of layers. Similar results are obtained for the whole frequency range studied.

Fig. 4
figure 4

The multilayer impedance ratio as a function of the external field at f = 0.5 GHz and H b  = 1 Oe for different N. Parameters used for calculations are the same as in Fig. 2

Full size image

The AMI response of the bimagnetic multilayered film shows nearly linear behavior at low fields. To analyze the impedance variation, let us introduce the impedance field sensitivity S, which is defined as follows

$$S = \frac{{Z(H_{e} = - H_{1} ) - Z(H_{e} = 0)}}{{H_{1} Z_{0} }} \cdot 100\% \cdot$$
(12)

Figure 5 shows the frequency dependence of the impedance sensitivity calculated by means of Eq. (12) for a different number of repetitions of the base structure. The field sensitivity increases at relatively low frequencies and attains peak at the frequency of the order of 0.5 GHz. The highest field sensitivity is 1.3%/Oe at 0.55 GHz for N = 1, whereas for N = 7 it increases up to 22.7%/Oe at 0.45 GHz. Thus, the use of bimagnetic multilayers allows one to raise significantly the AMI effect, and these film structures may be promising for the development of miniature sensors of a weak magnetic field.

Fig. 5
figure 5

The frequency dependence of the impedance field sensitivity at H b  = 1 Oe for different N. Parameters used for calculations are the same as in Fig. 2

Full size image

In conclusion of this section, note that much attention is paid to the MI effect in multilayered nanostructured films. These films consist of soft magnetic layers separated by thin highly conductive non-magnetic layers. In particular, recently the non-symmetric multilayered films were attracted interest in connection with a development of magnetic biosensors [20]. Although the MI effect in the multilayers was studied experimentally quite well, its theoretical explanation is still missing. The approach presented in this work seems to be useful for the analysis of the MI effect in the non-symmetric multilayered nanostructured films.

Conclusion

A model to describe the AMI effect in bimagnetic multilayer is proposed. The MI response is calculated by means of a solution of Maxwell equations with Landau–Lifshitz equation. The asymmetry in the field dependence of the impedance is related to the magnetostatic coupling between the magnetic layers. As a result of the magnetostatic coupling, the bias field is induced in the soft magnetic layers, which leads to changes in the static magnetization distribution in the layers. It is demonstrated that the AMI effect increases significantly in bimagnetic multilayers in comparison with the base three-layered film structure. The obtained field and frequency dependences of the impedance are in a qualitative agreement with results of the experimental study of the AMI effect in bimagnetic multilayers [12]. The analysis shows that the bimagnetic multilayers may be attractive sensitive elements for the design of miniature sensors of a weak magnetic field.