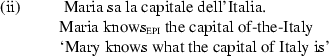Abstract
This article proposes an account of knowing-who constructions within a generalisation of Hintikka’s (Knowledge and belief. Cornell UP, Ithaca, MA, [10]) quantified epistemic logic employing the notion of a conceptual cover Aloni PhD thesis [1]. The proposed logical system captures the inherent context-sensitivity of knowing-wh constructions Boër and Lycan (Knowing Who. MIT Press, Cambridge, MA, [5]), as well as expresses non-trivial cases of so-called concealed questions Heim (Semantics from different points of view. Springer, Berlin, [9]). Assuming that quantifying into epistemic contexts and knowing-who are linked in the way Hintikka had proposed, the context dependence of the latter will translate into a context dependence of de re attitude ascriptions and this will result in a ready account of a number of traditionally problematic cases including Quine’s well-known double vision puzzles Quine (The ways of Paradox and other essays. Random House, New York, [16]).
Notes
- 1.
If we consider also non-serial, non-transitive and non-euclidean frames, the principle is valid only if \(\phi \) does not contain any modal operator.
- 2.
Definite descriptions will be translated as (non-rigid) individual constants until Sect. 4.4.2.
- 3.
- 4.
Notice that (8-b) above is stronger than the negation of (10-b) (if \(|D|>2\)). Embedded questions have been observed to exhibit so-called homogeneity effects [15]: “a knows who \(\phi \)” is intuitively true if a is fully informed about who \(\phi \), whereas its negation “a doesn’t know who \(\phi \)” conveys that a has pretty much no idea who \(\phi \). A compositional account of the semantics of the English examples would have to account for these facts (among others). Such a compositional analysis, however, is outside the scope of this article.
- 5.
It is well known that English know also allows acquaintance readings.

In languages like Italian and Dutch, where epistemic know and acquaintance know are lexically distinct, the CQ reading can be forced by using the verb for epistemic know (sapere in Italian and weten in Dutch), as shown by (ii) for Italian, which does not allow acquaintance interpretations.
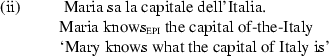
- 6.
References
Aloni M (2001) Quantification under conceptual covers. PhD thesis, ILLC, University of Amsterdam
Aloni M (2005a) A formal treatment of the pragmatics of questions and attitudes. Linguist Philos 28(5):505–539
Aloni M (2005b) Individual concepts in modal predicate logic. J Philos Log 34(1):1–64
Aloni M (2008) Concealed questions under cover. Grazer Philos Stud 77:191–216. Special issue on ‘Knowledge and Questions’ edited by Franck Lihoreau
Boër S, Lycan W (1985) Knowing Who. MIT Press, Cambridge, MA
Carlson L (1988) Quantified Hintikka-style epistemic logic. Synthese 74(2):223–262
Frege G (1892) Über Sinn und Bedeutung. Z für Philos und philos Krit 100:25–50
Groenendijk J, Stokhof M (1984) Studies on the semantics of questions and the pragmatics of answers. PhD thesis, University of Amsterdam
Heim I (1979) Concealed questions. In: Bäuerle R, Egli U, von Stechow A (eds) Semantics from different points of view. Springer, Berlin
Hintikka J (1962) Knowledge and belief. Cornell UP, Ithaca, MA
Hintikka J (1972) Knowledge by acquaintance-individuation by acquaintance. In: Pears D (ed) Bertrand Russell: A collection of critical essays. Doubleday, Anchor Books
Holliday WH, Perry J (2014) Roles, rigidity, and quantification in epistemic logic. In: Baltag A, Smets S (eds) Johan van Benthem on logic and information dynamics, Outstanding Contributions to Logic. Springer
Hughes GE, Cresswell MJ (1996) A new introduction to modal logic. Routledge, London and New York
Kaplan D (1969) Quantifying in. In: Davidson D, Hintikka J (eds) Words and objections: Essays on the work of W. V. Quine. Reidel, Dordrecht, pp 221–243
Križ M (2015) Homogeneity, trivalence, and embedded questions. In: Proceedings of the 20th Amsterdam Colloquium
Quine WV (1956) Quantifiers and propositional attitudes. J Philos 53:101–111. Reprinted. In: Quine WV (1966) The ways of paradox and other essays. Random House, New York
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
Let \(M=\langle W, R, D, I, C \rangle \) be a CC-model and \(M'=\langle W, R, D, I \rangle \) be the corresponding classical QEL-model. And given a CC-assignment g and a world \(w \in W\), let \(h_{g,w}\) be an element of \(D^{{\mathscr {V}}_N} \) such that for all \(v \in {\mathscr {V}}_N: h(v) = g(v)(w)\). We prove the following theorem for any closed \(\phi \) in \({\mathscr {L}}_{CC}\):
Theorem 4.3
Proof
The proof is by induction on the construction of \(\phi \). We start by showing that the following holds for all terms t:

Suppose t is a variable. Then \([\![t ]\!]_{M,w,g}= g(t)(w)\). By definition of \(h_{g,w}\), \(g(t)(w)=h_{g,w}(t)\), which means that \( [\![t ]\!]_{M,w,g} = [\![t ]\!]_{M', w, h_{g,w}}\). Suppose now t is a constant. Then \([\![t ]\!]_{M,w,g}= I(t)(w)=[\![t ]\!]_{M', w, h_{g,w}} \). We can now prove the theorem for atomic formulae.
Suppose \(\phi \) is \(Pt_1,...,t_n\). Now \(M , w, g\models _{CC} Pt_1,...,t_n\) holds iff (a) holds:

By (A), (a) holds iff (b) holds:

which means that \(M', w, h_{g,w} \models _{QEL} Pt_1,...,t_n\).
Suppose now \(\phi \) is \(t_1=t_2\). \(M , w, g\models _{CC} t_1=t_2\) holds iff (c) holds:

By (A) above, (c) holds iff (d) holds:

which means that \(M', w, h_{g,w}\models _{QEL} t_1=t_2\).
Suppose now \(\phi \) is \(\Box \psi \). \(M , w, g\models _{CC} \Box \psi \) holds iff (e) holds:

By induction hypothesis, (e) holds iff (f) holds:

And (f) holds iff (g) holds:

Since \(\psi \) does not contain any free variable, (g) is equivalent to \(M' , w, h_{g,w} \models _{QEL} \Box \psi \).
Suppose now \(\phi \) is \(\exists x_n \psi \). \(M , w, g\models _{CC} \exists x_n \psi \) holds iff (h) holds:

By induction hypothesis, (h) holds iff (i) holds:

By definition \(h_{g[x_n/c],w}= h_{g,w}[x_n/c(w)]\), and \(c(w)\in D\). But then (i) holds iff (j) holds:

which means \(M' , w, h_{g,w} \models _{QEL} \exists x_n \psi \). The induction for \(\lnot \) and \(\wedge \) is immediate. \(\square \)
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG
About this chapter
Cite this chapter
Aloni, M. (2018). Knowing-Who in Quantified Epistemic Logic. In: van Ditmarsch, H., Sandu, G. (eds) Jaakko Hintikka on Knowledge and Game-Theoretical Semantics. Outstanding Contributions to Logic, vol 12. Springer, Cham. https://doi.org/10.1007/978-3-319-62864-6_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-62864-6_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-62863-9
Online ISBN: 978-3-319-62864-6
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)