1 Introduction

Local site conditions influence the significant characteristics of ground motion, such as amplitude, frequency content and duration. The magnitude of this influence depends on the material and geometrical properties of the underlying soil profile at the site and the characteristics of input motion.

Approximation of site-specific dynamic response of layered soil deposit is denoted as a site-specific response analysis. Time histories rendered from ground response analysis constitute the ground surface motions. A case study of ground response analysis of a site in Ahmedabad city during the Bhuj earthquake was carried out by Raju et al. (2004) to determine the varying degree of damage in multi-storey buildings in the close proximity of the Sabarmati river area due to amplification of ground motion. Similar study was carried out by Uthayakumar and Naesgaard (2004) to determine the significant amplification in the earthquake motion in Fraser river delta, British Columbia. Ground response analysis using the SHAKE2000 software was carried out by Roy and Sahu (2012) to determine the local site effects for the Kolkata Metropolitan District area. This study also stated the engineering importance of site-specific ground response analysis, difficulties faced in conducting a complete ground response analysis and steps to be followed in conducting a meaningful site amplification study.

It’s the usual practice to analyse buildings by considering the base to be fixed. Nevertheless, in reality, sub layer soil property influences the response of the structure to a greater extent by its natural ability to deform. The possible severities of omitting the effects of SSI in seismic design of buildings were noted by many researchers such as Mylonakis et al. (1997) and Roy and Dutta (2001a, b) etc. Flexibility of soil causing the lengthening of lateral natural period of the structure due to the reduction in overall lateral stiffness was shown in the studies carried out by Bielak (1975) and Stewart et al. (1999a, b). Seismic soil-structure interaction study of massive concrete structures supported over raft foundation using finite element software to determine the stress resultants in the raft was carried out by Rajasankar et al. (2007) Finite element transient analysis of segmental retaining walls using Ramberg-Osgood model to simulate the nonlinear hysteretic behaviour of soil was carried out by Helwany et al. (2001) using computer program DYNA3D and the results were further compared with laboratory shake table tests. Nonlinear time-domain soil-structure interaction analysis of embedded reactor structures subjected to earthquake loads using a simple hysteretic soil model based on the Ramberg-Osgood formulation was carried by Solberg and Hossain (2013).

In the present study, site specific ground motion was generated from ground response analysis using ProSHAKE software. To suffice this, geotechnical data from twenty bore holes at the site with depth varying between 7–15 m below ground level were considered. Time history record of Elcentro earthquake motion was scaled down to a peak acceleration of 0.1 g and was used in the ground response analysis due to the unavailability of recorded strong ground motion data in the study area. Ground motion, thus generated possessing the highest PGA was further used in the finite element soil-structure interaction analysis of multi-storey shear wall buildings. To simulate the nonlinear hysteretic behaviour of soil, Ramberg-Osgood soil model was employed in SSI analysis. The effects of local site conditions in varying the seismic response of the buildings were evaluated. Position of shear walls, drawing the least earthquake forces on the buildings was also identified.

2 Ground Response Analysis

Ground response analysis was carried out for the geological study area covering latitude 12o87’N and longitude 74o88’E, located at Mangalore, Karnataka state, India. This study area is one of the major cities of Karnataka coastal belt surrounded by the Western Ghats in the east and the Arabian Sea in the west. Mangalore comes under seismic Zone III, zonal classification as per Indian seismic code IS1893:2002. Lateritic soil is found in abundance in this region. The location of the site is as shown in Fig. 1. Borehole data of the study area were used in ground response analysis. Typical borehole log of the site showing the peak ground acceleration is as shown in Fig. 2. Ground response analysis was carried out using the one dimensional equivalent linear ground response analysis program ProSHAKE. The necessary inputs for the analysis are shear wave velocity, bedrock acceleration time history, damping curves and shear modulus reduction curve of soil layers at the site.

Fig. 1.
figure 1

Spatial variation of mean PHA (g) values at bedrock in study area

Full size image
Fig. 2.
figure 2

Typical borehole log of site

Full size image

Shear wave velocity (Vs) in the study area was estimated using SPT (N) values obtained from geotechnical investigation by adopting the empirical relation stated by Seed and Idriss (1981).

$$ V_{s} = 61N^{0.5} $$
(1)

Where,

Vs :

is the shear wave velocity and

N:

is the standard penetration test value of soil.

Shear modulus reduction curve and damping curve of the soil layer was assumed as the upper bound curve of sand given by Seed et al. (1986). The acceleration time history of input motion and peak acceleration time history at the ground level of borehole 18 are as shown in Figs. 3 and 4 respectively.

Fig. 3.
figure 3

Typical input acceleration time history

Full size image
Fig. 4.
figure 4

Acceleration time history of free field motion at borehole 18

Full size image

3 Soil-Structure Interaction Analysis

When structure is held on soil deposit, the inability of foundation to respond to the deformations of soil stratum as in free field motion causes the movement of the base of structure to vary from the free field motion. As well, the dynamic responses of the structure itself cause deformation of the supporting soil. This phenomenon, in which the response of soil influences the motion of the structure and response of the structure influences the motion of the soil, is referred as soil-structure interaction (SSI). In the analysis of integrated structure-foundation-soil system, present study adopts the direct method of SSI and the soil is represented by elastic continuum finite element model with nonlinear material behavior.

3.1 Structural Idealization

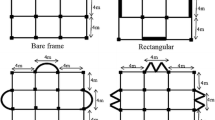
Multi-storey reinforced concrete shear wall buildings with symmetry in plan and of aspect ratio (h/d) ranging from 1 to 4 resting on raft foundation were considered. The shear walls were placed symmetrically along the exterior frames (SWE), core (SWI) and all four corners of the exterior frames (SWC). Building frames were of 3 bays in each direction with equal bay length. The storey height and length of each bay were chosen as 3 m and 4 m respectively. Schematic representation of the plan of idealized 3 bay × 3 bay building frame with various shear wall locations is shown in Fig. 5. The dimensions of building components were arrived on the basis of structural design, adopting the respective Indian standard codes for the design of reinforced concrete structures IS456:2000 and IS13920:1993. Dimensions of building components are as shown in Table 1. The effects of infill were neglected. Thicknesses of shear wall were varied from 150–250 mm depending on the building heights. M20 grade concrete and Fe 415 grade steel were chosen for the design of structural elements.

Fig. 5.
figure 5

Plan of building frames with various shear wall locations

Full size image
Table 1. Geometric properties of building components
Full size table

3.2 Geotechnical Idealization

Soil is treated as a homogenous, isotropic and an elastic half space medium. Non cohesive materials generally show hysteretic energy dissipation with nonlinear behaviour when subjected to cyclic loading. To simulate the nonlinear hysteretic behaviour of non-cohesive soil the elasto-plastic model, Ramberg-Osgood model, was adopted. The properties of soil are given in Table 2. Soil domain is practically infinite compared to the structure. In analyzing soil-structure interaction problems it is essential that both the structure and soil are to be brought in the computational domain. Therefore, perfectly matched layer (PML) (Basu and Chopra (2003)) concept was followed to represent the infinite soil domain in an effective manner. PML layer form a cuboid box throughout the bounded domain of soil.

Table 2. Details of soil parameters
Full size table

3.3 Finite Element Model

Finite element multiphysics simulation software LS DYNA was used in the modeling and analyses of three dimensional SSI system in this study. In modelling of 3D space frames, Belytschko-Schwer resultant beam elements possessing three translational and three rotational degrees of freedom at each node were used. For modelling of slabs at various storey levels, shear wall and raft, Belytschko-Tsay shell element having both bending and membrane capabilities with four-nodes were used. Belytschko-Tsay shell elements have six degrees of freedom at each node. In modelling the three dimensional soil stratum, fully integrated S/R solid having three translational degrees of freedom at each node was employed. Node incompatibility occurring at the interface of raft foundation and the soil medium due to varying degrees of freedom at nodes was overcome by INTERFACE_SSI card which identify the soil-structure interface. Three dimensional finite element model of idealized soil–foundation–structure system with PML is as shown in Fig. 6. Application of PML model was possible only if the material in bounded domain near PML was linear. Thus the soil layer adjacent to the structure was elasto- plastic and layer adjacent to PML was elastic (Reheman and Shiojiri 2011).

Fig. 6.
figure 6

Idealized 3D finite element model of soil-foundation-structure system

Full size image

4 Methodology

The following analyses were carried out to identify the best location of shear wall in symmetric buildings at a specific site.

  • One dimensional equivalent linear ground response analysis was executed using ProSHAKE program to determine the amplification of ground motion due to local site condition.

  • Eigen value analysis to determine the fundamental natural period of the building which forms the significant element in determining the seismic loads coming on structures.

  • Finite element soil-structure interaction (SSI) analysis of multi-storeyed concrete shear wall buildings at the site was performed to determine the responses in building due to the effect of soil flexibility and varying shear wall locations employing surface ground motion with highest peak ground acceleration (PGA) generated using ProSHAKE software.

Damping ratio equivalent to 5% of critical damping was presumed for both the structure and soil. Acceleration time histories were applied at the interface in the global X direction of the integrated SSI system.

5 Results and Discussions

Site specific SSI analyses were carried out on three-dimensional finite element integrated soil-foundation-structure models to determine the response of the system during ground motion. Multistorey buildings of different aspect ratios with three different shear wall positions were considered. The variations in responses of buildings due to the effect of soil flexibility and various positions of shear wall are expressed in terms of variation in natural period, base shear and roof deflection.

5.1 Natural Period

Fundamental natural period has a significant role to play in determining the seismic response of structures. Variation of natural period determined from free vibration analysis of buildings with varying aspect ratio on account of the effect of soil flexibility and position of shear walls is shown in Fig. 7. This variation, (natural period of buildings with SSI as compared with conventional fixed base) reduces with increase in aspect ratio showing that the influence of soil flexibility is more on buildings with low aspect ratio.

Fig. 7.
figure 7

Comparison of lateral natural period of building with fixed base and SSI

Full size image

Highest variation in the value of natural period is found in SWI shear wall configuration, i.e., shear wall at the core and the lowest in bare frame buildings revealing that the influence of soil on bare frame buildings is less than that on the shear wall buildings at this site.

5.2 Base Shear

Seismic base shear is the maximum anticipated lateral force that is probable to occur at the base of the structure due to seismic ground motion. Variation of base shear in buildings with various shear wall position by incorporating the effect of soil flexibility is as shown in Figs. 8 and 9 respectively.

Fig. 8.
figure 8

Base shear in various building configurations

Full size image
Fig. 9.
figure 9

Comparison of seismic base shear of building with fixed base and SSI

Full size image

Buildings with shear wall at the core (SWI) show the least value of base shear as compared to the other shear wall configurations considered. The least variation in base shear is also found in SWI shear wall configuration for all buildings except for aspect ratio of 1. Base shear for bare frame buildings are lower that in shear wall buildings, due to lower seismic weight of the bare frame building. Seismic weight forms the vital component in the base shear generation. Base shear values obtained by conventional fixed base analysis are higher than SSI analysis making conventional analysis results as more conservative.

5.3 Roof Deflection

Deflection of the roof of the building with reference to the base of the structure is roof deflection. The variation in roof deflection of buildings with various shear wall position by incorporating the effect of soil flexibility and the variation obtained between the conventional fixed base analysis and SSI analysis is shown in Figs. 10 and 11 respectively. Values of roof deflection are considerably reduced by the inclusion of shear wall in buildings.

Fig. 10.
figure 10

Roof deflection in various building configurations

Full size image
Fig. 11.
figure 11

Comparison of roof deflection of buildings with fixed base and SSI

Full size image

Roof deflection is found to be the least in shear wall buildings with shear wall placed at core (SWI) and the highest in shear wall buildings with shear wall at corners of exterior frame (SWC). Roof deflections of buildings incorporating SSI effect are higher than the conventional fixed base condition due to the inclusion of flexibility in the structural system.

6 Conclusions

Following general conclusions are drawn from the present study.

  • Natural period variation between the conventional fixed base analysis and SSI analysis is less for bare frame buildings and it increases with increase in stiffness of building by the addition of shear walls. In shear wall buildings, natural period is the highest in shear wall buildings with shear wall placed at corners of exterior frame and the lowest in shear wall building with shear wall at the core.

  • In general with SSI effect, base shear is the least in shear wall buildings with shear wall placed at core. Base shear values found by conventional fixed base condition for all buildings are higher than those considering SSI effects and hence conservative.

  • Roof deflections are considerably reduced by inclusion of shear walls in buildings and increased by inclusion of soil flexibility in structural systems. Buildings with shear wall placed at the core have the least roof deflection for this specific site.