Abstract
This study focused on the probabilistic risk assessment of reinforced concrete piers bridges subjected to ground motion excitation. In order to assess the vulnerability of Piers Bridge, a case study of a typical Algerian highway bridge is presented, illustrating the seismic performance and damage evaluation method. Pushover and incremental dynamic analysis using several earthquake records is implanted to determine the fragility curves reflecting the probability of various damage occurrences. These fragility curves provide the probability of exceeding the multiple damage states for a given intensity of ground motion excitation. To develop the fragility curves, a nonlinear static pushover and incremental dynamic time-history analysis have been performed using the SeismoStruct nonlinear analysis program for bridge model to develop fragility curve, this study includes comparison between real or artificial ground motions selection, IDA is performed using a set of 18 real ground acceleration records and 8 artificial ground acceleration records of similar seismo/geological origins. Finally, the developed fragility curves can be used to assess the seismic performance of Piers Bridge and help to decision making for effective retrofitting technique.
Similar content being viewed by others
1 Introduction
Seismic vulnerability assessment and development of fragility curves for existing bridges are a matter of great concern among the researchers in the recent years (Kurian et al. (2006); SeongKwan et al. (2007). Fragility curves of bridges can be developed empirically as well as analytically. Empirical fragility curves are usually developed based on the damage reports from past earthquakes. When actual bridge damage and ground motion data are not available, analytical fragility curves can be used to assess the performance of bridges (Nielson and DesRoches (2007), Choi et al. (2004)).
In Algeria, neither bridge damages nor their performances have been reported during the previous earthquakes that have struck the country, aside from those observed during the 2003 Zemmouri earthquake. According to the ASCE post-earthquake investigation report (ASCE 2004), the most significant bridge damages were due to the superstructure moving off their bearings and dropping onto the bents caps, columns damage observed in old bridges, shear key at some metallic girders, superstructure rotation, vertical movement, girder movement and buckling as well as some damage at seat-type abutment and to bin-type wing wall. Nevertheless, the bridges have performed well and no long interruption of their serviceability was noticed during the earthquake. In this respect, due to the lack of information from past earthquakes damage on bridges, it is not possible to derive fragility curves empirically for the typical bridge piers in Algeria. Therefore, fragility curves have been developed analytically from nonlinear dynamic analyses of typical bridge piers. Since damage states are mostly related to structural capacity (C) and the ground motion intensity parameter is related to structural demand (D), the probability of failure (pf) gives the probability that the seismic demand will exceed the structural capacity. Mander and Basoz (1999) have presented the theory of fragility curves for highway bridges based on uncertainties in various bridge parameters to evaluate seismic vulnerability of typical bridges. While Ghobarah et al. (1997) have quantified numerically the damage states from the dynamic responses of the bridges under various levels of ground motion excitation; Hwang et al. (2001) described a detailed procedure for analytical development of fragility curves.
The main objective of this study is to develop analytical fragility curves for typical Algerian reinforced concrete bridge piers based on a numerical approach taking into account, the structural parameters and the variation of the input ground motion. Prior to the newly established Algerian seismic regulation code for bridge structures RPOA (2008), the bridge piers have been designed using the seismic design coefficient method. In this respect, seismic coefficients equal to 10% of the total weight in the horizontal direction and 7% of the total weight in the vertical direction have been used to design the bridge piers. By using the Incremental Dynamic Analysis (IDA) Vamvatsikos and Cornell (2002), this analysis method which can be used for more detailed seismic performance predictions of structures subjected to different seismic excitation levels. It involves numerous inelastic times history analyses performed using a set of ground motion records, each scaled (up or down), and to study different seismic intensity levels. IDA provides valuable information regarding possible structural responses, required for the probabilistic seismic performance assessment of structures and seismic risk analysis (e.g., development of fragility curves and prediction of the annual rate of collapse, etc.).
2 Bridge Properties and Modeling Assumptions
A typical structural bridge pier in Algeria has been selected for the fragility analysis, considering these typical RC bridge piers. As it deals with piers that are not designed according to the 2008 new Algerian seismic design code for bridges, it is assumed that only the size and the reinforcement of the piers can be changed with other conditions such as their height, the length and the weight of the superstructure.
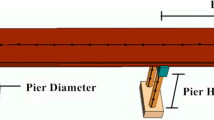
The structures studied include regular 4-span bridge with an overall length of 116.80 m. The superstructure consists of a longitudinally reinforced concrete deck slab of 10 m wide and it is supported by three sets of columns and by an abutment at each end. Each set has three columns with a circular cross section of 1.20 m diameter.
The substructure of bridge consists of rigid abutments at the ends in additional to reinforcement concrete piers. The longitudinal view of the bridge and the cross section can be seen in Fig. 1.
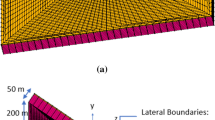
The bridge is modeled with finite elements using Sismostruct software (Sismostruct 2015). A three-dimensional view of the model is shown in Fig. 2. The bridge is constructed of linear beam column elements representing the superstructure and nonlinear column fiber section elements for the columns, the superstructure is assumed to behave linearly and P-delta effects are included in the analysis.
The bridge columns are assumed to behave nonlinearly and defined as fiber section elements. For core and cover concrete, abutment is modeled by using springs in longitudinal axis of superstructure and fixed supports against rotation and vertical translation.
For the dynamic time history analysis of the pier model, fiber modeling technique (Martinez-Rueda and Elnashai (1997) was used to incorporate the material inelasticity and geometric nonlinearity. The complete pier section was subdivided into approximately 200–300 section fibers each provided with the uniaxial material properties, as shown in Fig. 3. The sectional stress-strain state of the pier is achieved by integrating the nonlinear uniaxial stress-strain response of the individual fibers.
Concrete model was defined using the constitutive relationship proposed by Mander et al. (1988) and the cyclic response theory proposed by Martinez-Rueda and Elnashai (1997). The steel stress strain relationship proposed by Menegotto and Pinto (1973) and the isotropic hardening rules by Filippou et al. (1983) were used in the modeling. The confinement provided by transverse and cross tie reinforcement was modeled with a confinement factor, defined as the ratio between the confined and unconfined compressive stress of concrete. In SeismoStruct (Sismostruct 2015), the confinement factor is calculated using the confinement model proposed by Mander et al. (1988). For the cover concrete, the confinement factor was considered to be 1.0 or defined as non-confined concrete.
3 Ground Motions
In order to perform IDA, in this previous study two analyses were developed, the first analyze used a real ground motion records and the other use a suite of artificial ground motion records.
18 ground motion records are used and adopted for this study to order to provide a sufficient accuracy of seismic demands. These earthquakes have Richter magnitudes in the range of 5.6–7.6. Figure 4 shows response spectra for each of the 18 earthquake ground motions; these ground motions are used in the analysis listed in Table 1. In this study PGA is considered as the Intensity Measure (IM) for its efficacy, utility and adequacy in vulnerability assessment. The PGA of the ground motions range from PGA 0.194 to PGA 0.781.
For the second analyze a series of artificial acceleration records was created for Incremental dynamic analysis. These records are determined to follow the RPOA (2008) design spectrum spectral acceleration curve (see in Fig. 5) within a defined range. According to RPOA (2008), the 5%-damped elastic response spectrum of the design seismic action shall be used for the fitting and the defined period range.
4 Damage Levels
The probability of entering a damage state an input ground motion intensity parameter is expressed by fragility curves. Different forms of Engineering Demand Parameter (EDPs) are used to measure the DS of the bridge components.
Several damage states were considered in the seismic evaluation of the bridges under study including yielding, serviceability, bar-buckling and collapse. The yielding and serviceability damage states for the bridge columns were predicted using the method described by Priestley et al. (2007). A study by Berry and Eberhard (2007) provides some empirical equations to estimate the engineering demand parameters including drift ratio, plastic rotation, and strain in the longitudinal bars for circular bridge columns based on the properties of typical columns.
In this study damage levels were considered in accordance with ATC (1996) and FEMA 273 (1997) guidelines and limit drift ratio was accepted as the damage measure. For RC Piers Bridge limit drift ratio are summarized in Table 2.
5 Incremental Nonlinear Dynamic Analysis IDA
Incremental nonlinear dynamic analysis (IDA) is a parametric analysis method that is useful for estimating structural performance under several ground motions. It mainly involves producing one or more curves of damage measure versus intensity measure under the effect of scaled ground motions as a result of several non-linear dynamic analyses. These ground motions can be selected from real records of earthquakes or can be generated artificially. Real records are more realistic since they include all ground motions characteristics such as amplitude, frequency, duration, energy content, number of cycles and phase. For this study, the maximum drift ratio is assumed as the best damage indicator and peak ground acceleration (PGA) is selected as the ground motion intensity measure. Under each ground motion, nonlinear time history analyses were conducted while scaling the PGA; of chosen ground motion incrementally every 0.1 g, until structural instability is obtained.
The SeismoStruct computer program (Sismostruct 2015) was utilized for non-linear dynamic analysis and the maximum drift ratio is recorded at the end of each analysis. The relationship between the maximum drift ratio and the corresponding PGA was obtained, which creates the IDA curves for a certain structure under the specified ground motion. The IDA curves of sample frames are shown in Fig. 6.
6 Fragility Curves
Fragility is modelled by a lognormal cumulative distribution function where the structural demand and capacity are assumed to be log-normally or normally distributed. In this study, probabilistic seismic demand models are used to derive the fragility curves. The ground motions are scaled to selective intensity levels and an Incremental Dynamic Analysis (IDA) is conducted at each level of the intensity. A regression analysis is carried out to obtain the mean and standard deviation for each limit state by assuming the power law function (Cornell et al. (2002), which gives a logarithmic correlation between median EDP and selected IM:
Where, a and b are unknown coefficients which can be estimated from a regression analysis of the response data collected from the nonlinear time history analysis. In order to create sufficient data for the cloud approach incremental dynamic analysis is carried out instead of nonlinear time history analysis. The dispersion of the demand, βEDP/IM, conditional upon the IM can be estimated from Eq. (3), (Ramanathan et al. (2012)
With the probability seismic demand models and limit states corresponding to various damage states, it is now possible to generate the fragilities using Eq. (4),
Ln(IMn) is defined as the median value of the intensity measure for the chosen damage state (slight, moderate, extensive, collapse), a and b are the regression coefficients and the dispersion component is presented in Eq. (6), (Ramanathan et al. (2012)).
Where Sc is the median and βc is the dispersion value for the damage states of the bridge pier (Madas and Elnashai (1992)). Figure 7 shows the typical lognormal probability plot for RC Piers Bridge considering both two cases 18 real ground motions and 8 artificial ground motions.
The fragility curves for Sample Bridge associated with those damage states are plotted in Fig. 8. Fragility curves is obtained by considering both two cases 18 real ground motions and 8 artificial ground motions. It can be observed that for involved seismic intensity levels, the fragility curves obtained show that the probability associated with the appearance of concrete cracks of piers bridge is very high, while that associated with the yielding is lower. It is also observed that the probabilities associated spalling and crushing of rebar are very low even for very high seismic intensity levels.
Figure 9 shows the plots of analytical fragility curves of both real and artificial ground motions (dotted lines), for example, for a level of acceleration of 0.4 g, the probability of failure of concrete cracking is in the order of 100% for both real and artificial ground motions. As for yielding, for a level of acceleration of 0.6 g, the probability of failure is 39% and 0% with artificial accelerations. For other damage (spalling and crushing of rebar), the State of exceeds of damage is very low even for very high seismic intensity levels.
7 Conclusions
Highway bridges are critical component for transportation network and play a significant role in the economic development of a country. Failure of a single link will have catastrophic impact on the whole transportation network as well as country’s economy.
This paper illustrates the results of the seismic vulnerability study aimed to develop the analytical fragility curves for typical Algerian bridge piers based on numerical simulations.
Bridge piers designed with the simplified seismic design method for bridges in Algeria are analyzed, and a large number of worldwide accelerometer records from which, Algerian strong motion records and earthquake records from some major event, e.g., the 1995 Kobe, the 1994 Northridge were selected in order to get a wide range of the variation of input ground motions.
The bridge was modeled using fiber elements in SeismoStruct software. The nonlinear time dynamic analysis of the bridge was made in two stages, first considering 18 real strong motions, and then 8 artificial strong motions calibrated on seismic RPOA 2008 design spectra corresponding to the bridge site.
The displacements obtained from seismic analyzes were related to the intensity of earthquakes and damage of the structure and fragility curves was build.
For involved seismic intensity levels, the fragility curves obtained show that the probability associated with the appearance of concrete cracks of piers bridge is very high, while that associated with the yielding is lower. It is also observed that the probabilities associated spalling and crushing of rebar are very low even for very high seismic intensity levels.
The results and of this study apply only to the bridge examined in this article, depending on the assumptions that have been adopted. These conclusions cannot be generalized to other works or other sites without prior analyses.
References
Kurian, S.A., Deb, S.K. and Dutta, A.: Seismic vulnerability assessment of a railway over bridge using fragility curves. In: Proceedings of 4th International Conference on Earthquake Engineering, p. 317 (2006)
Seongkwan, M.L., Tschangho, J.K., Seung, L.K.: Development of fragility curves for bridges in Korea. KSCE J. Civ. Eng. 3(11), 165–174 (2007)
Padgett, J.E., DesRoches, R.: Methodology for the development of analytical curves for retrofitted bridges. Earthq. Eng. Struct. Dyn. 37, 1157–1174 (2008)
Choi, E., DesRoches, R., Nielson, B.: Seismic fragility of typical bridges in moderate seismic zones. Eng. Struct. 26, 187–199 (2004)
Nielson, B., DesRoches, R.: Analytical seismic fragility curves for typical bridges in the central and south eastern United States. Earthq. Spectra 3(23), 615–633 (2007)
Mander, J.B., Basoz, N.: Seismic fragility curves theory for highway bridges. In: Proceedings of 5th US Conference of Lifeline Earthquake Engineering, pp. 31–40. ASCE (1999)
Ghobarah, A., Aly, N.M., El-Attar, M.: Performance level criteria and evaluation. In: Proceedings of the International Workshop on Seismic Design Methodologies for the Next Generation of Codes, 207–215. Balkema, Rotterdam (1997)
Hwang, H., Jing, B.L., Chiu, Y.: Seismic Fragility Analysis of Highway Bridges. Center for Earthquake Research Information, Memphis. Ref. No. MAEC RR-4 (2001)
RPOA: Algerian seismic regulation code for bridge structures, Document Technique Règlementaire. Ministère des Travaux Publics, Algiers (2008)
Vamvatsikos, D., Cornell, A.: Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 31(3), 491–514 (2002)
Seismosoft: SeismoStruct v7.0.6 - A computer program for static and dynamic nonlinear analysis of framed structures (2015). http://www.seismosoft.com
Mander, J.B., Priestley, M.J.N., Park, R.: Theoretical stress-strain model for confined concrete. J. Struct. Eng. ASCE 114(8), 1804–1826 (1988)
Martinez-Rueda, J.E., Elnashai, A.S.: Confined concrete model under cyclic load. Mater. Struct. 30(197), 139–147 (1997)
Menegotto, M., Pinto, P.E.: Method of analysis for cyclically loaded RC plane frame including in geometryand non-elastic behavior of elements under combined normal force and bending. In: Symposium on the Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads, International Association for Bridge and Structural Engineering, pp. 15–22, Zurich, Switzerland (1973)
Filippou, F.C., Popov, E.P., Bertero, V.V.: Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints. Report EERC 83-19, Earthquake Engineering Research Center, University of California, Berkeley (1983)
Priestley, M.J.N., Calvi, G.M., Kowalsky, M.J.: Displacement Based Seismic Design of Structures. IUSS Press, Pavia, Italy (2007)
Berry, M., Eberhard, M.O.: “Damage Analysis,” Chapter 4 in “Application of the PEER PBEE Methodology to the I-880 Viaduct.” In: Kunnath, S.K. (ed.) Pacific Earthquake Engineering Research Center Report PEER-2006-10. University of California, Berkeley, pp. 45–54 (2007)
ATC: Seismic evaluation and retrofit of concrete buildings. Report no. ATC-40. Applied Technology Council, Redwood City, CA (1996)
FEMA-273: NEHRP Guidelines for Seismic Rehabilitation of Buildings. Building Seismic Safety Council, FEMA, Washington, D.C (1997)
Cornell, A.C., Jalayer, F., Hamburger, R.O.: Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. J. Struct. Eng. 128(4), 526–532 (2002)
Ramanathan, K., DesRoches, R., Padgett, J.E.: A comparison of pre- and post-seismic design considerations in moderate seismic zones through the fragility assessment of multispan bridge classes. Eng. Struct. 45, 559–573 (2012)
Madas, P., Elnashai, A.S.: A new passive confinement model for transient analysis of reinforced concrete structures. Earthq. Eng. Struct. Dyn. 21, 409–431 (1992)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG
About this paper
Cite this paper
Fouad, K., Mustapha, R., Abderrahmane, K. (2018). Seismic Assessment of Algerian Bridge. In: Rodrigues, H., Elnashai, A., Calvi, G. (eds) Facing the Challenges in Structural Engineering. GeoMEast 2017. Sustainable Civil Infrastructures. Springer, Cham. https://doi.org/10.1007/978-3-319-61914-9_24
Download citation
DOI: https://doi.org/10.1007/978-3-319-61914-9_24
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-61913-2
Online ISBN: 978-3-319-61914-9
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)