Abstract
Tarski investigates in [109] partial commutative monoids constructed from partial bijections on a given set. In Kudryavtseva et al. [71], this study is conveniently formalized in the language of inverse semigroups. Further connections can be found in works on K-theory of rings, such as Ara and Exel [7].
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
The right skew join of x and y could of course be defined as
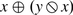 , that is, \(y \triangledown x\).
, that is, \(y \triangledown x\). - 2.
Although strictly speaking, the operation symbols should not be denoted the same way as their interpretations (in a given structure), that confusion is widespread and harmless.
- 3.
Often transliterated as “Vagner”.
- 4.
This set can be endowed with a well studied structure of topological groupoid , which will however not be of concern in the present work.
- 5.
Bibliography
Ara, P., Exel, R.: Dynamical systems associated to separated graphs, graph algebras, and paradoxical decompositions. Adv. Math. 252, 748–804 (2014). MR 3144248
Ara, P., Goodearl, K.R.: Tame and wild refinement monoids. Semigroup Forum 91(1), 1–27 (2015). MR 3369375
Ara, P., Goodearl, K.R., O’Meara, K.C., Pardo, E.: Separative cancellation for projective modules over exchange rings. Israel J. Math. 105, 105–137 (1998). MR 1639739 (99g:16006)
Clifford, A.H., Preston, G.B.: The Algebraic Theory of Semigroups. Vol. II. Mathematical Surveys, vol. 7. American Mathematical Society, Providence, RI (1967). MR 0218472 (36 #1558)
Exel, R.: Tight representations of semilattices and inverse semigroups. Semigroup Forum 79(1), 159–182 (2009). MR 2534230
Freese, R., Nation, J.B.: Congruence lattices of semilattices. Pac. J. Math. 49, 51–58 (1973). MR 0332590 (48 #10916)
Grätzer, G.: Lattice Theory: Foundation. Birkhäuser/Springer, Basel AG, Basel (2011). MR 2768581 (2012f:06001)
Howie, J.M.: An Introduction to Semigroup Theory. London Mathematical Society Monographs, vol. 7. Academic/Harcourt Brace Jovanovich Publishers, London/New York (1976). MR 0466355 (57 #6235)
Jónsson, B.: On the representation of lattices. Math. Scand. 1, 193–206 (1953). MR 0058567 (15,389d)
Kudryavtseva, G., Lawson, M.V., Lenz, D.H., Resende, P.: Invariant means on Boolean inverse monoids. Semigroup Forum 92(1), 77–101 (2016). MR 3448402
Lawson, M.V.: Enlargements of regular semigroups. Proc. Edinb. Math. Soc. (2) 39(3), 425–460 (1996). MR 1417688 (97k:20104)
Lawson, M.V.: Inverse Semigroups: The Theory of Partial Symmetries. World Scientific Publishing Co., Inc., River Edge, NJ (1998). MR 1694900 (2000g:20123)
Lawson, M.V.: A noncommutative generalization of Stone duality. J. Aust. Math. Soc. 88(3), 385–404 (2010). MR 2827424 (2012h:20141)
Lawson, M.V.: Non-commutative Stone duality: inverse semigroups, topological groupoids and C ∗-algebras. Int. J. Algebra Comput. 22(6), 1250058, 47 pp. (2012). MR 2974110
Lawson, M.V., Lenz, D.H.: Pseudogroups and their étale groupoids. Adv. Math. 244, 117–170 (2013). MR 3077869
Lawson, M.V., Scott, P.: AF inverse monoids and the structure of countable MV-algebras. J. Pure Appl. Algebra 221(1), 45–74 (2017). MR 3531463
Leech, J.: Skew Boolean algebras. Algebra Univers. 27(4), 497–506 (1990). MR 1387897 (97a:06018)
Leech, J.: Inverse monoids with a natural semilattice ordering. Proc. Lond. Math. Soc. (3) 70(1), 146–182 (1995). MR 1300843
Mal’cev, A.I.: On the general theory of algebraic systems. Mat. Sb. N.S. 35(77), 3–20 (1954). MR 0065533 (16,440e)
McKenzie, R.N., McNulty, G.F., Taylor, W.F.: Algebras, Lattices, Varieties. Vol. I. The Wadsworth & Brooks/Cole Mathematics Series. Wadsworth & Brooks/Cole Advanced Books & Software, Monterey, CA (1987). MR 883644 (88e:08001)
Munn, W.D.: Some recent results on the structure of inverse semigroups. In: Semigroups (Proceedings of a Symposium, Wayne State Univeristy, Detroit, MI, 1968), pp. 107–123. Academic, New York (1969). MR 0262404 (41 #7012)
O’Meara, K.C.: The exchange property for row and column-finite matrix rings. J. Algebra 268(2), 744–749 (2003). MR 2009331 (2004i:16040)
Resende, P.: A note on infinitely distributive inverse semigroups. Semigroup Forum 73(1), 156–158 (2006). MR 2277324 (2007j:20094)
Schein, B.M.: On the theory of generalized groups (Russian). Dokl. Akad. Nauk SSSR 153, 296–299 (1963). English translation in Soviet Math. Dokl. 4, 1680–1683 (1963). MR 0170966 (30 #1200)
Schein, B.M.: Completions, translational hulls and ideal extensions of inverse semigroups. Czechoslov. Math. J. 23(98), 575–610 (1973). MR 0325820 (48 #4166)
Solomon, L.: Representations of the rook monoid. J. Algebra 256(2), 309–342 (2002). MR 1939108 (2003m:20091)
Tarski, A.: Cardinal Algebras. With an Appendix: Cardinal Products of Isomorphism Types, by Bjarni Jónsson and Alfred Tarski. Oxford University Press, New York, NY (1949). MR 0029954 (10,686f)
Vagner, V.V.: On the theory of antigroups. Izv. Vysš. Učebn. Zaved. Matematika 4(107), 3–15 (1971). MR 0294544 (45 #3614)
Vagner, V.V.: t-Simple representations of antigroups. Izv. Vysš. Učebn. Zaved. Matematika 9(112), 18–29 (1971). MR 0289678 (44 #6866)
Wallis, A.R.: Semigroup and category-theoretic approaches to partial symmetry, Ph.D. thesis. Heriot-Watt University, Edinburgh (2013)
Zhitomirskiy, G.I.: Inverse semigroups and fiberings. In: Semigroups (Luino, 1992), pp. 311–321. World Scientific Publishing, River Edge, NJ (1993). MR 1647275
Zhitomirskiy, G.I.: Topologically complete representations of inverse semigroups. Semigroup Forum 66(1), 121–130 (2003). MR 1939670 (2003h:20113)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Wehrung, F. (2017). Boolean Inverse Semigroups and Additive Semigroup Homomorphisms. In: Refinement Monoids, Equidecomposability Types, and Boolean Inverse Semigroups. Lecture Notes in Mathematics, vol 2188. Springer, Cham. https://doi.org/10.1007/978-3-319-61599-8_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-61599-8_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-61598-1
Online ISBN: 978-3-319-61599-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


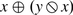 , that is,
, that is,