Keywords

1 Introduction

The numbers of hand-held devices have dramatically increased over the past decade [1] followed by a tremendous traffic growth brought along by the emerging spectrum consumers [2]. This trend is expected to be continued towards new growing markets of wearable electronics that integrate into the next generation (5G) communications paradigm [3, 4] and embrace direct device-to-device (D2D) connectivity as part of it [5]. At the same time, International Telecommunications Union (ITU) has recently provided 5G requirements including several novel scenarios [6] and offered some considerations on the mobility support [7].

While the communications quality in conventional outdoor scenarios could be improved by increasing the density of wireless infrastructure nodes [8], the indoor case is much more sensitive to wireless interference [9]. It is particularly important for the enclosed offices, corridors within their premises, and shopping malls [10]. The typical environments of this type could be described as cubical areas with different sizes where the user movement is fairly predictable [11, 12].

The mobility pattern of a user in the indoor premises depends on a number of factors dictating the movement trajectory, that is, it is not an entirely “random” process. A typical example of the corresponding mobility model could be described as a relatively slow movement of users inside the shops and faster movement between them. Similar behavior is observed in the dynamics of fractal sets, see, e.g., [13, 14]. The analysis of stable connectivity between mobile devices in such a scenario could be considered as a challenging task in the context of 5G communications systems [15,16,17,18].

A conventional way to study the performance of wireless networks is to utilize the tools of stochastic geometry. According to this approach, the locations of communicating entities are represented by employing a static spatial point process. The metrics of interest, such as the signal-to-interference ratio (SIR) moments and distributions, are then obtained by analyzing the distances between a receiver, a transmitter, and other communicating stations [19, 20]. This approach is however limited to static time-averaged measures. At the same time, accounting for the fact that communication sessions are always of finite durations, time-dependent metrics are often of interest.

In this work, a model for analyzing the dynamics of the connection quality indicator, the so-called SIR, is developed. We consider the case, where the movement of transceivers is considered as a set of paths that are random on a fractal set process. The proposed model is a representative abstraction for the aforementioned office or shopping mall scenario, where the fractal set represents the attraction points of a shopping mall (specific areas inside the shops). The analysis is based on the Fokker-Planck equation with fractional spatial derivatives. The model considers the distribution of coordinates for the receiver, the transmitter, and the interfering stations, as well as the level of mobility, and translates them into the average SIR evolution in time. The use of fractal sets allows to explicitly include the effects of spatial movement correlation thus adequately representing the real-life scenarios. We illustrate the application of the proposed model and demonstrate that the behavior of SIR is generally varying for different types of fractals, that is, spatial correlation of the movement process.

The rest of this work is organized as follows. The system model, metrics of interest, and SIR trajectory modeling are introduced in Sect. 2. The formulation for the time evolution of SIR is derived in Sect. 3. The numerical results and the conclusions are drawn in the last section.

2 System Model and Preliminaries

2.1 Random Walks over Fractal Sets

We consider a set of users moving over the fractal set. We focus on a tagged receiver and N interfering stations. The random movement trajectory of a user is represented as a random walk on the three-dimensional fractal set [17]. Fokker-Planck equation with fractional derivatives that represents the distribution function on such sets has been studied in [21]. One of the crucial assumptions in our model is that the motion of each spatial coordinate is small movements independent. With this assumption at hand, the evolution equation in the one-dimensional coordinate space can be considered as a basic model. This equation is the following

$$\begin{aligned} \frac{\delta f (x,t)}{\delta t} + \frac{\delta (u(x,t)f(x,t))}{\delta x} = B(t)\frac{\delta ^{2\alpha }f(x,t)}{\delta x^{2 \alpha }}, \end{aligned}$$
(1)

where f(x, t) is a continuously-differentiable function of the coordinates and time, u(x, t) is the so-called drift velocity, which is defined as the average velocities of the respective two-dimensional distribution [17], that is,

$$\begin{aligned} u(x,t)f(x,t)=\int F(x,v,t)vdv, \end{aligned}$$
(2)

where the integration is performed over the entire mobility domain by considering the boundary conditions.

The non-negative diffusion coefficient B(t) is determined as

$$\begin{aligned} B(t) = \frac{1}{2} \frac{d \sigma ^2}{dt}-cov_{x,u}(t), \end{aligned}$$
(3)

where

$$\begin{aligned} \sigma ^2(t)=\int (x-\overline{x}(t))^2f(x,t)dx,\,\overline{x}(t)=\int xf(x,t)dx. \end{aligned}$$
(4)

The value of the fractal derivative \(\alpha \), \(\alpha \in {}(0,1)\) is a parameter of the model. This fractional order derivative has several different interpretations. It can be considered in terms of Riemann-Liouville, Riesz-Feller, Caputo-Gerasimov, Grunwald-Letnikov considerations, see, e.g.  [22] for further details. The function f is required to belong to \(L_p\), \(p>1\) class with respect to x. For example, a symmetric Riesz-Feller derivative on [a, b] is represented as

$$\begin{aligned} \frac{\delta ^{2\alpha }f(x)}{\delta x^{2\alpha }} = \frac{1}{2cos\pi \alpha } \Big [ \big ( D^{2\alpha }_{a+}f \big )(x) +\big (D^{2\alpha }_{b-}f \big )(x)\Big ], \end{aligned}$$
(5)

where

$$\begin{aligned} \begin{aligned}&\big ( D^{2\alpha }_{a+}f \big )x = \frac{1}{\varGamma (m-2\alpha )}\frac{d^m}{dx^m}\int ^x_a f(y)(x-y)^{m-2\alpha -1}dy, \\&\big ( D^{2\alpha }_{b+}f \big )x = \frac{(-1)^m}{\varGamma (m-2\alpha )}\frac{d^m}{dx^m}\int ^b_x f(y)(y-z)^{m-2\alpha -1}dy, \end{aligned} \end{aligned}$$
(6)

and \(m=[Re(2\alpha )]+1\). We consider the special case, \(m=2\), in (1).

The fractional derivative term is conventionally represented as a convolution with an appropriate (usually singular) kernel as

$$\begin{aligned} \frac{\delta ^{2\alpha }f(x)}{\delta x^{2\alpha }}=\int K_\alpha (x-y)f(y)dy. \end{aligned}$$
(7)

We consider the following kernel

$$\begin{aligned} K_\alpha (z)=\frac{1}{\varGamma (1-2\alpha )} \frac{1}{z^{2\alpha }}. \end{aligned}$$

The kinematic Eq. (1) can be solved numerically for any initial condition \(f(x,t)|_{t=0}=p(x)\) and boundary conditions. We choose the probability of zero flow at the border as the latter.

The coordinates density distribution of users corresponding to the motion over a fractal random trajectory is described in the n-dimensional space \((n=1,2,3)\) by the following equation

$$\begin{aligned} \frac{\delta f(x,t)}{\delta t}+div_x\big ( u(x,t)f(x,t)\big ) = B(t)\int K\big ( |x-y| \big )f(y,t)dy, \end{aligned}$$
(8)

where u(x, t), B(t), and K(z) are known.

In the following sections, we study the dependence of the mean SIR value, when the mobility trajectories are samples generated from the distribution evolving according to (8).

2.2 SIR Trajectories

Observe that SIR is a functional depending on the distance between the moving points at consecutive time instants. The coordinates \((x_i(t),y_i(t),z_i(t))\) determine the position of the \(i^{th}\) point of the trajectory in a convex three-dimensional region, \(V\subset \mathfrak {R}^3\). The distance between the points on two randomly chosen trajectories in three-dimensional space is defined by

$$\begin{aligned} r^2_{ij}=\big ( x_i(t)-x_j(t)\big )^2+\big ( y_i(t)-y_j(t)\big )^2+\big ( z_i(t)-z_j(t)\big )^2. \end{aligned}$$
(9)

Let the function of interest, depending on the distance between the spatial points and belonging to different trajectories, be denoted as \(\phi _{ij}=\phi (r_{ij})\). In wireless networks, this function is known as the path loss model. In this paper, we assume the commonly accepted power law path loss model [23], i.e.,

$$\begin{aligned} \phi _{ij} \equiv \phi (r_{ij})=\frac{1}{r^2_{ij}}. \end{aligned}$$
(10)

In a field of \(N+2\) moving users, let us tag two users – one receiver and one transmitter. The remaining nodes are considered as interfering stations. The mean SIR at the tagged receiver at each time instance is given by

$$\begin{aligned} S(r_1,r_2) = \frac{\phi _{ij}}{\sum _{j=3}^{N+2}\phi _{1j}}, \end{aligned}$$
(11)

where the sum in the denominator is the average value of the interference defined by using the distances between the receiver and the interfering stations, i.e.,

$$\begin{aligned} U(r,t) = \int _V \phi \big ( |r-r'|\big )f(r',t)dr', \end{aligned}$$
(12)

and \(f(r',t)\) is the density function of distances.

Then, the mean SIR in (11) can be written as

$$\begin{aligned} q(t)=\int S(r,t)f(r,t)dr. \end{aligned}$$
(13)

The mean value of SIR in (13) depends on the average environmental field U(r, t) in (12). This value is a non-linear function over the trajectory sample.

2.3 Examples

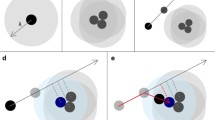
The typical movement trajectories in the example obtained for the fractal walk on a two-dimensional ternary Cantor set are shown in Fig. 1(a). The modeling algorithm is described in [17]. As one may observe, the mobility process of users comprises many short travels around the attractor points as well as occasional long-distant movements. This process closely resembles the basic properties of real measurements of user mobility in shopping malls, see, e.g., [24].

The associated SIR trajectory produced by using (13) for a randomly tagged receiver is shown in Fig. 1(b). For this illustration, the number of interfering stations, N, was set to 100. Note that the autocorrelation being a result of spatial correlation caused by a fractal set is clearly observed.

Fig. 1.
figure 1

Ternary Cantor set in \(\mathfrak {R}^2\).

Full size image

3 Formulation for Evolution of Average SIR

In this section, we derive the main result of this paper, which is the evolution equation for the average value of SIR as specified in (13). Recall that the coordinates density of the communicating users evolves according to (8). Using (12)–(13), we obtain

$$\begin{aligned} N\frac{dq}{dt}=\int _V\frac{\phi (r)}{U(r,t)}\frac{\delta f(r,t)}{\delta t}dr- \int _V\frac{\phi (r)}{U^2(r,t)}\frac{\delta U(r,t)}{\delta t}f(r,t)dr. \end{aligned}$$
(14)

Substituting the first term of (14) with the derivative \(\frac{\delta f (r,t)}{\delta t}\) obtained from (8), we proceed as

$$\begin{aligned} \begin{aligned} \int \frac{\phi (x)}{U(x,t)}\frac{\delta f(x,t)}{\delta t}&=-\int \frac{\phi (x)}{U(x,t)}div_x\big (u(x,t)f(x,t)\big )dx +\\&+ B(t)\int \frac{\phi (x)}{U(x,t)} \int K \big (|x-y|\big )f(y,t)dydx =\\&=\int grad_x\Big ( \frac{\phi (x)}{U(x,t)} \Big )u(x,t)f(x,t)dx + \\&+B(t)\int \frac{\phi (x)}{U(x,t)}\int K\big ( |x-y|\big )f(y,t)dydx. \end{aligned} \end{aligned}$$
(15)

The Eq. (15) is obtained by using the integration by parts if the distribution function vanishes on the boundary of the region. We further denote the result of the scalar product \(u(x,t)grad_x\Big (\frac{\phi (x)}{U(x,t)}\Big )\) by P(x, t). Due to the SIR heterogeneity and the existence of non-zero density function for the speed change, the offset in the average value of SIR is estimated by the scalar product. The second term with the altered integration order from the last line of (15) is obtained in the form of SIR fractal derivative by applying Fubini’s theorem as \(R(y,t)=D^{2\alpha }\Big (\frac{\phi }{U}\Big )(y,t)\). Hence, we now have

$$\begin{aligned} \int \frac{\phi (x)}{U(x,t)}\frac{\delta f(x,t)}{\delta t}dx = \int \Big ( P(x,t)+B(t)D^{2 \alpha }\Big (\frac{\phi }{U}\Big )(x,t) \Big )f(x,t)dx. \end{aligned}$$
(16)

The second term in (8) can be treated similarly. Particularly, substituting derivative in (12) with \(\delta f/\delta t\) of (8), the derivative \(\delta U/\delta t\) becomes

$$\begin{aligned} \begin{aligned} \frac{\delta U(r,t)}{\delta t}&= \int \phi \big (|r-r'|\big )\frac{\delta f(r',t)}{\delta t}dr'= \\&-\int \phi \big (|r-r'|\big )div_{r'}\big (u(r',t)f(r',t)\big )dr'+\\&+B(t)\int \phi \big (|r-r'|\big )K\big (|r'-r''|\big )f(r'',t)dr'dr''. \end{aligned} \end{aligned}$$
(17)

Integrating the first term by parts, we have

$$\begin{aligned} \begin{aligned} \int \phi \big (|r-r'|\big )&div_{r'}\big (u(r',t)f(r',t)\big )dr'=\\&=\int grad_{r'}\phi \big (|r-r'|\big )\big (u(r',t)f(r',t)\big )dr'= \\&=\int grad_{r}\phi \big (|r-r'|\big )\big (u(r',t)f(r',t)\big )dr'= \\&=div_r\int grad_{r}\phi \big (|r-r'|\big )\big (u(r',t)f(r',t)\big )dr'=div_rJ(r,t). \end{aligned} \end{aligned}$$
(18)

The resulting equation is obtained by replacing the derivative of \(\phi (|r-r'|)\) with respect to \(r'\) by the derivative with respect to r. The second term in (8) for the fractional derivative of the \(L_p([a,b])\) class of functions is represented as [22]

$$\begin{aligned} \int ^b_ah(x) \big (D_{a+}^{2\alpha }g\big )(x)dx = \int ^b_ah(x) \big (D_{b-}^{2\alpha }h\big )(x)dx. \end{aligned}$$

As a result, we obtain

$$\begin{aligned} \int \phi \big (|r-r'|\big )K\big (|r'-r''|\big )f(r'',t)dr'dr'' = \Big (D^{2\alpha }U\Big )(x,t). \end{aligned}$$
(19)

Next, by combining (17) and (19), we arrive at

$$\begin{aligned} \frac{\delta U(x,t)}{\delta t}=B(t)\Big (D^{2\alpha }U\Big )(x,t)-div_xJ(x,t). \end{aligned}$$
(20)

The latter result demonstrates that the average SIR changes over time in the same manner as the distribution function of coordinates defined in (8). Note that these changes occur with the same coefficients as in (8).

The final equation for the evolution of the mean value of SIR is obtained with (14) and (16)–(20), thus resulting in

$$\begin{aligned} \begin{aligned} N\frac{dq}{dt}&= \int \Big (P(x,t)+B(t)D^{2\alpha }\big (\frac{\phi }{U}\big )(x,t)\Big )f(x,t)dx - \\&-B(t)\int \frac{\phi (x)}{U^2(x,t)}\Big (\big (D^{2\alpha }U\big )(x,t)\Big )f(x,t)dx+\\&+\int \frac{\phi (x)}{U^2(x,t)}\big (div_xJ(x,t)\big )f(x,t)dx. \end{aligned} \end{aligned}$$
(21)

Observe that the above equation non-linearly depends on the distribution function of the coordinates of points. Therefore, to quantitatively assess each contribution of the term in (21) to the SIR values, the numerical simulations are required. The result in (21) is a general model of the average SIR values evolution in diffusion approximation, and it is valid not only for fractal but also for the general non-stationary random walks.

Despite the complex structure of (21), it still provides a possibility to make qualitative conclusions regarding the contributions of each component. In the scenario with \(\alpha = 1\) in (8), there is an interesting special case of the so-called zero-flow average SIR. Recall that in the classic Fokker-Planck equation, the term \(f(r,t)u grad\big (\frac{\phi }{U}\big )\) after integration over the region of interest represents the drift. Here, the term \(\frac{\phi }{U^2}div (J)\) corresponds to the similar effect, but it affects the average field U(r, t). These two terms have different signs, i.e., the total transport effect of the drift \(u\nabla \frac{\phi }{U}+\frac{\phi }{U^2}div(J)\) after integration with the density f(r, t) might be negligible, e.g., the average scalar product of the drift and the radius-vector ur is equal to zero. In this case, the SIR changes are due to the diffusion effect only.

4 Numerical Results and Conclusions

The result in (21) offers an opportunity for faster modeling of the average SIR values. In our numerical illustration, we consider two empirical density functions corresponding to two various Hausdorff dimensions of the fractal sets, Cantor square with \(2\alpha _1=\ln {8}/\ln {3}\) and Sierpinski triangle with \(2\alpha _2=\ln {3}/\ln {2}\). As one may observe in Fig. 2(a), these functions exhibit drastically different properties.

Fig. 2.
figure 2

SIR densities and average SIR evolution in time for two fractals.

Full size image

The average SIR values for the sample lengths of 100 are demonstrated in Fig. 2(b). The number of interfering nodes in this example is \(N=10\). Note that the Cantor fractal results have much more variability implying that an appropriate choice of the underlying model is of paramount importance.

In this paper, starting from the kinematic equation that describes the evolution of the coordinates density of users, we obtained the equation for the time evolution of the average SIR value experienced at the receiver of interest that moves in a field of N interfering stations. The proposed formalism allows to address a wide variety of specific movement patterns including non-stationary ones. We then proceeded with obtaining the kinematic equation for the average SIR value. The resulting expression, although being complex, can be solved in special cases of interest, e.g., when the stationary density of the coordinates is considered. However, even in the general case of non-stationary movement, it allows for the qualitative assessment.

Our numerical illustration highlights that the average SIR evolution is drastically affected by the choice of the fractal set. One practical problem emphasized by our study is to determine the appropriate value of \(\alpha \) for different environments. In realistic scenarios, i.e., for applications in shopping malls, stadiums, etc., there is not only non-zero time-dependent drift corresponding to e.g., a lunch break or other intermissions when the flow of people changes significantly, but also specific collective effects with non-local interaction.