Abstract
Over the past several decades, maize yields in the US Midwest have risen at about 17% per decade as a result of steady technological progress. Although the trend is expected to remain positive, climate change is expected to have an increasing countervailing effect. In this chapter, I compute the yield growth rates necessary to fully offset the potential negative effects of a warming climate. Relying on a statistical model allowing for nonlinear effects of temperature on yield, I find that maize yields would decrease by −4.2, −21.8 and −46.1% around the trend, under uniform warming scenarios of 1 °C, 3 °C and 5 °C, respectively. I find that an increase of 6.6%/decade in maize yields is required to fully offset the detrimental effects of a severe but still plausible 3 °C warming in the next three decades. This indicates that future maize yield trends could – all else equal – be substantially curtailed due to the climate change. This case study illustrates how agricultural policy analysts can assess the magnitude of potential climate change impacts relative to historical yield trends to help identify targets for agricultural research.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
Climate change is resulting in shifting rainfall patterns and rising temperatures that will increasingly challenge agricultural producers across the globe, including in temperate regions with high agricultural productivity such as the United States (US) Midwest region. Various statistical studies have found a strong longitudinal relationship between exposure to high temperature (>30 °C) and lower-than-average crop yields (Schlenker and Roberts 2009; Lobell et al. 2011). This historical evidence presages lower yields in the region under a warmer climate relative to a world without climate change .Footnote 1 At the same time, Midwest maize yields have risen at about 17% per decade in recent times as a result of steady technological progress. This chapter analyzes the extent to which these secular maize yield trends can help offset the projected relative decline of maize yields resulting from a warming climate.Footnote 2 This case study illustrates how agricultural policy analysts can assess the magnitude of potential climate change impacts relative to historical yield trends to help identify targets for agricultural research and investments.
The case study is organized as follows. First, I estimate a statistical model of maize yields regressed on weather variables for the US Midwest. The model allows for nonlinear temperature effects on yield following the approach developed by Schlenker and Roberts (2009). This model accounts for distinct effects of temperature exposure to various temperature bins within each day of the growing season. The model is based on panel data and exploits the longitudinal covariance of maize yields and weather conditions at the county level. Second, I use the estimated climate sensitivity parameters to developed maize yield change projections under three uniform warming scenarios (1, 3 and 5 °C). Third, I use these projections to answer the following question. What yield growth rate would be necessary to fully offset the projected yield effects under warming scenario? Obviously, the answer depends on the time horizon of the warming, so I explore time frames ranging from one decade to a century. Finally, I discuss the magnitude of potential climate change impacts on maize yields in light of historical yield trends.
The chapter is organized as follows. First, I describe the data sources and provide summary statistics for key variables in the analysis. I also provide an overview of the warming scenarios. In the subsequent section I present the crop statistical model and describe how climate change impact projections are computed. I then present the model results and the associated impacts from a uniform warming and provide a discussion of the findings. I then conclude the chapter.
2 Data Sources and Summary Statistics
The empirical analysis in this chapter relies on agricultural and climate data. The agricultural data was obtained from Quick Stats, the US Department of Agriculture’s (USDA) online database. This database provides data from historical surveys on county-level agricultural production variables such as acres planted and harvested as well as production. The dependent variable in the study, maize yield, is obtained by dividing total maize production by acres planted. For the 1929–2014 period, this information is complete for 644 counties in 13 Midwest states. This constitutes the set of counties in the study.
The climate data is obtained from the PRISM Climate Group, which provide USDA’s official climatological data. The PRISM data is a detailed gridded dataset providing daily measurements of minimum, average and maximum temperature and total precipitation for each 4-by-4 km grid over the entire contiguous US since 1981. Because the data is gridded, it needs to be aggregated to the county level to match the agricultural observations. I perform this aggregation by weighting each PRISM grid by the amount of cropland it contains based on USDA’s Cropland Data Layer (CDL). The CDL provides 30-m resolution land cover pixels corresponding to over 100 classes. The weights were based on cropland pixel counts falling within each PRISM data grid and the average of CDL cropland counts for years 2008–2014 were used. Note that temperature exposure to each temperature “bin” or interval is computed by fitting a double sine curve going through the minimum and maximum temperature of each consecutive day for each PRISM grid and subsequently counting the time spent within each degree bin over the growing season in each year. The temperature exposure was then aggregated to county using the aforementioned approach.
Key summary statistics are presented in Table 1 and correspond to a balanced panel of 644 counties over the 1981–2014 study period. This period is confined to years with complete climate data. The table shows maize yields vary considerably, ranging from 17.0 to 210.8 bu./acre. This variation obviously encompasses both cross-sectional (across counties) and longitudinal (within counties) dimensions. There is also a wide range of variation for precipitation over this time period with minimum and maximum levels of 110 and 1254 mm for the April–September period. Following conventional practice, these months correspond were chosen to approximate the maize growing season in the region.
Regarding air temperature , the present study relies on measurements of the temperature distribution across the entire growing season rather than average monthly temperature . In other words, the temperature variables correspond to the time spent within each temperature bin over the April–September period. This approach is arguably better suited to capture exposure to extreme temperatures than monthly average temperatures . Although the statistical analysis makes use of exposure data to each bin ranging from 0 to 36 °C, I only present summary statistics for aggregated contiguous bins in Table 1. The table shows that the most frequent temperature range is between 15 and 25 °C, which corresponds to the bins with the highest mean exposures.
In this chapter I seek to compare the potential effects of a warming climate relative to historical yields trends. Figure 1 illustrates the rise in maize yields in the Midwest since 1929. Panel A shows the yield trend has roughly doubled in absolute terms between 1929–1960 and 1961–2014. However, this obscures the fact that the rate of this trend has slowed down by almost 40% during this period, as shown in panel B.Footnote 3 I will refer to these growth rates later on in the analysis. Also, it is worth noting that I do not detect a statistically significant trend in weather variables over the study period (1981–2014). This suggests that these yield trends are mostly a reflection of technological progress and not really of parallel climate trends.
Corn yield trends in the US Midwest (Notes: Observations correspond to acreage-weighted maize yields for each year. The trend lines were fitted assuming a linear trend for years 1929–1960 and 1961–2014. The sample corresponds to a balanced panel of 644 counties across 13 states over the 1929–2014 period)
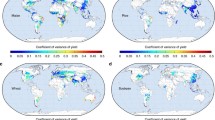
Regarding climate change data, I adopt 3 uniform warming scenarios of 1, 3 and 5 °C with no precipitation change. The reason I focus on temperature rather than precipitation changes is that previous studies (e.g. Lobell et al. 2008; Schlenker and Roberts 2009) have found that temperature changes are the major explanatory factor explaining crop yield fluctuations in the US Midwest (and elsewhere). A possible reason is that high temperatures capture the effect of dry summer spells, which are crucial for maize production, but are not captured by the season-long precipitation variables. Figure 2 provides an overview of the temperature distribution for the baseline climate as well as under the warming scenarios (lower row). The maps illustrate the mean exposure above 30 °C in each county during the growing season. Under the baseline climate, very few counties have mean exposure exceeding 30 days over the April–September period (total of 183 days). However, exposure above this threshold substantially increases under the most severe warming scenario. This will have a major effect on the projected yield impacts as we will see shortly.
Exposure to extreme temperature under varying uniform warming scenarios (Notes: The upper row shows the yearly mean exposure (in days) to temperatures exceeding 30 °C during the April–September growing season for each county in 13 Midwest states for baseline and 3 uniform warming scenarios. The lower row presents the temperature distribution across the sample for each temperature bin. Each box represents the median and the first and third quantiles of the distribution. The whiskers extent to data extremes. The dotted vertical line indicates the 30 °C threshold for illustrative purposes)
3 Crop Yield Model and Climate Change Impacts
Crop statistical models have re-emerged as an alternative approach to the traditional biophysical models for assessing the potential impacts of climate change on crop yields . A statistical crop yield model is basically a regression analysis of crop yields on weather variables. Early examples can be traced back to the early part of the last century (Wallace 1920; Hodges 1931). In this chapter, I adopt the approach developed more recently by Schlenker and Roberts (2009). These authors developed an innovative approach that separately estimates the effect of the cumulative exposure (over the growing season) to different temperature bins on crop yield .Footnote 4 Mathematically, the nonlinear effect of temperature on yield may be represented by a function of temperature h, denoted g(h). Logged maize yield y it in county i and year t can thus be represented as:
where ϕ it (h) is the time distribution of temperature for April–September, p it is precipitation, z it is a quadratic time trend and the c i are county fixed-effects that capture time-invariant factors explaining yields level across counties (e.g. soil quality, etc). However, Eq. (1) cannot be estimated directly because of the integral. To make this model tractable one needs to approximate the integral with a summation over discrete temperature bins:
where Φ it (h + 1) − Φ it (h) represents the time spent over the [h; h + 1] interval, and g(h + 0.5) is a parameter to estimate. However, given the high number of temperature bins, collinearity between exposures to contiguous bins might create noisy estimates. As a result I assume that g(h) is a smooth function over temperature bins which I can approximate with cubic B-spline with 8 degrees of freedom evaluated at each temperature bin. This can be written as:
where B j is the jth column of the basis matrix of the natural cubic spline. The model effectively regresses yield on eight temperature variables, x it, j . The model is estimated via Least Squares and errors are clustered by county and by year to account for heteroscedasticity and contemporaneous error dependence. Once parameters γ j are estimated, one can derive the marginal effects of temperature exposure by pre-multiplying estimated coefficients by the basis matrix. These marginal effects correspond to the marginal effects of each temperature bin on crop yield .
Obtaining climate change projections based on these marginal effects is straightforward and simply requires multiplying the marginal effects for each temperature bin by the change in exposure to each bin under a given warming scenario. The log yield changes can then transformed into percentage changes using well-known formulas.
4 Results and Discussion
4.1 Model Results and Warming Impacts
The main result of the model is the nonlinear effect of temperature on maize yields which is illustrated in Fig. 3. The effects of precipitation are not presented here because the scenarios do not alter the level of precipitation. Exposure to temperatures above 30 °C appear detrimental to maize yields. The response function reflects the fact that years with higher exposure to high temperature tend to be associated with lower than average maize yields in the study region. This is in line with previous findings in the literature.
The lower part of the Fig. 3 represents the baseline temperature distribution across temperature bins. This is somewhat similar to the distribution within bins illustrated in Fig. 2. Again, for the baseline climate, exposure beyond 30 °C is not very common. However, a uniform warming scenario shifts the temperature distribution to the right, which increases the frequency of high temperatures . The anticipated consequence is that maize yields would decrease as exposure to detrimental temperature levels rises.
Figure 4 illustrates the maize yields impacts for all counties in the sample (top row) as well as the distribution of impacts (bottom row) for each warming scenario. Because the statistical model regresses the log yield on weather variables conditional on a time trend, these impacts reflect percentage changes around the yield trend. A warming scenario of 1 °C has a relatively small effect with some northern counties experiencing small positive effects. However, more severe warming scenarios generate increasing crop yield losses. Interestingly, the model predicts rising heterogeneous effects across the sample as illustrated by the higher variance of projected impacts for the most severe warming scenario. The reason is that warming results in a disproportionately higher increase in the frequency of extreme temperatures in region that were warmer in the baseline climate.
Maize yield impacts under alternative warming scenarios (Notes: The top row represents the projected effect of the corresponding warming scenario for each county in the sample. Grey counties are not in the sample. Some of these effects are not statistically significant when close to zero. The bottom row represents the distributions of these county-level effects)
The acreage-weighted maize yield impacts for the sample are −4.2%, −21.8% and −46.1% for the 1 °C, 3 °C, and 5 °C warming scenarios, respectively. Again, these impacts are around the trend so they do not represent net effects on yields. These impacts from uniform scenarios, however, do not provide information about their timing or the pace of warming.
4.2 Warming Impacts Against Technological Progress
To provide some context for the magnitude of these yield impacts, I compute the yield growth rate necessary to fully compensate these warming effects. This rate is computed as r = 1/t (( y0 − yt)/y0 + 1) where t is the time allowed for yield growth (in decades), and ( y0 − yt)/y0 is the share of acreage-weighted average yields loss in the projected climate relative to the baseline climate (y t < y 0).
I present these rates based on the historical yield sensitivity to temperature in panel A of Table 1. The table naturally shows that in order to compensate the impacts of a warming climate the growth rate in maize yields needs to be higher, the sooner this warming occurs. This explains the higher rates for lower time horizons (upper rows). Obviously, the rate needs to be even higher, to compensate larger damages from a more warming. This explains why higher rates are also found under more severe scenarios. Panel A shows that to compensate for a 3 °C warming within the next 3 decades (mid-century) the maize yield growth rate needs to be 6.56%/decade. This warming scenario approximately corresponds to climate change projections under higher emissions scenarios toward the middle of the century for the continental US. Recall that the recent historical yield trend shown in Fig. 1 is about 17.4%/decade. This is greater than the required growth rate to offset the warming impacts. However, these results show that climate change would have a sizable countervailing impact even if relatively high secular yield growth rates are maintained. More precisely, if the secular trend continues at this historical rate, the net yield growth might be reduced to about 17.4−6.6 = 10.8%/decade. This is a 38% reduction, which seems considerable.
The previous discussion assumed that only an increase in average yields is considered to counterbalance potential yield losses from a warming climate. However, breeding programs may be designed to reduce the vulnerability of maize yield to extreme conditions. This can be graphically represented as a reduction in the slope of the marginal effect of high temperature on crop yield in Fig. 3. I consider a case in which these marginal effects for temperatures exceeding 30 °C are reduced by half. Projected yield impacts will naturally be lower. Similarly, the required maize yield growth rates need to compensate a warming climate would also be lower. These rates are represented in panel B of Table 1. Indeed, with reduced extreme temperature sensitivity, the offsetting rates could be lower.
Panel C presents the difference between the compensating rates in the case based on historical heat sensitivity and with reduced heat sensitivity. These rates can be interpreted as the “secular yield growth rate equivalent” of an immediate reduction by half in extreme temperature sensitivity. In other words, the comparison of panels A and C provide insights into the tradeoff of combatting projected yield losses from warming by increasing average yield trends or by reducing the sensitivity of yields to extreme conditions. It is clear that the sooner and the more severe the warming is, the more appealing reducing the sensitivity to extreme becomes. Alternatively, if warming is mild or very distant, reducing yield sensitivity to high temperature present relatively small advantages (Table 2).
5 Conclusion
In this chapter I illustrate how to assess the yield growth rate requirements to fully compensate yield losses due to climate change based on statistical techniques. The crop statistical model employed allows for nonlinear effects of temperature on yields. In line with results in the literature, the statistical model suggests that exposure to temperature exceeding 30 °C is detrimental to maize yields in the US Midwest. A warming climate would therefore entail an increase in exposure to detrimental conditions and reduce yields. Indeed, I find sample-wide yield impacts around the yield trend of −4.2%, −21.8% and −46.1% for the 1 °C, 3 °C, and 5 °C uniform warming scenarios, respectively. The middle of the road-scenario is plausible by mid-century.
I find that a historical rate in maize yield growth in the US Midwest of 17.4%/decade exceeds the rate (6.56%/decade) needed to compensate a plausible warming of 3 °C within the next 3 decades. However, the net yield trend would be substantially diminished under this scenario due to the countervailing effect of a warming climate. In addition, I explore how the reduction in half of yield sensitivity to extreme temperature reduces the yield growth requirements to offset detrimental warming effects. I find that reducing sensitivity to extreme condition is a more attractive option when warming is imminent and severe. This case study highlights how agricultural policy analysis can assess the magnitude of potential yield losses due to climate change relative to historical yield trends.
The analysis could be extended with a cost-benefit analysis of alternative mean-increasing or variance-reducing technological change. The study also has important limitations including the fact that crop yield models cannot account for CO2 fertilization or detailed management information that may be explicitly modeled with biophysical approaches. Other limitations include the assumptions about time separability of temperature effects as well as the omission of confounded effects of other inputs with weather conditions.
Notes
- 1.
Evidence suggests that temperature affects yield by lowering the water supply in rainfed environments (see Lobell et al. 2013).
- 2.
Although crop yield does not directly reflect agricultural productivity , it provides a useful metric that is easily understood by a wide audience interested in agriculture and food security concerns.
- 3.
The 1929–1960 period corresponds to the period of hybrid corn varieties adoption across the US.
- 4.
This approach assumes that temperature effects on yield are cumulative and substitutable over time. This assumption may be relaxed.
References
Hodges, J. A., “The Effect of Rainfall and Temperature on Corn Yields in Kansas,” Journal of Farm Economics, April 1931, 13 (2), 305–318.
Lobell, David B., Graeme L. Hammer, Greg McLean, Carlos Messina, Michael J. Roberts, and Wolfram Schlenker, “The critical role of extreme heat for maize production in the United States,” Nature Climate Change, 2013, 3 (5), 497–501.
Lobell, David B., Marshall B. Burke, Claudia Tebaldi, Michael D. Mastrandrea, Walter P. Falcon, and Rosamond L. Naylor, “Prioritizing Climate Change Adaptation Needs for Food Security in 2030,” Science, February 2008, 319 (5863), 607–610.
Lobell, David B., Wolfram Schlenker, and Justin Costa-Roberts, “Climate Trends and Global Crop Production Since 1980,” Science, July 2011, 333 (6042), 616–620.
Schlenker, Wolfram and Michael J. Roberts, “Nonlinear temperature effects indicate severe damages to U.S. crop yields under climate change,” Proceedings of the National Academy of Sciences, September 2009, 106 (37), 15594–15598.
Wallace, H. A., “Mathematical inquiry into the effect of weather on corn yield in the eight corn belt states,” Monthly Weather Review, 1920, 48, 439.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike 3.0 IGO license (https://creativecommons.org/licenses/by-nc-sa/3.0/igo/), which permits any noncommercial use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the Food and Agriculture Organization of the United Nations (FAO), provide a link to the Creative Commons license and indicate if changes were made. If you remix, transform, or build upon this book or a part thereof, you must distribute your contributions under the same license as the original. Any dispute related to the use of the works of the FAO that cannot be settled amicably shall be submitted to arbitration pursuant to the UNCITRAL rules. The use of the FAO’s name for any purpose other than for attribution, and the use of the FAO’s logo, shall be subject to a separate written license agreement between the FAO and the user and is not authorized as part of this CC-IGO license. Note that the link provided above includes additional terms and conditions of the license.
The images or other third party material in this chapter are included in the chapter’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 FAO
About this chapter
Cite this chapter
Ortiz-Bobea, A. (2018). U.S. Maize Yield Growth and Countervailing Climate Change Impacts. In: Lipper, L., McCarthy, N., Zilberman, D., Asfaw, S., Branca, G. (eds) Climate Smart Agriculture . Natural Resource Management and Policy, vol 52. Springer, Cham. https://doi.org/10.1007/978-3-319-61194-5_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-61194-5_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-61193-8
Online ISBN: 978-3-319-61194-5
eBook Packages: Economics and FinanceEconomics and Finance (R0)