Abstract
Identity-based encryption (IBE) has been extensively studied and widely used in various applications since Boneh and Franklin proposed the first practical scheme based on pairing. In that seminal work, it has also been pointed out that providing an efficient revocation mechanism for IBE is essential. Hence, revocable identity-based encryption (RIBE) has been proposed in the literature to offer an efficient revocation mechanism. In contrast to revocation, another issue that will also occur in practice is to combine two or multiple IBE systems into one system, e.g., due to the merge of the departments or companies. However, this issue has not been formally studied in the literature and the naive solution of creating a completely new system is inefficient. In order to efficiently address this problem, in this paper we propose the notion of mergeable and revocable identity-based encryption (MRIBE). Our scheme provides the first solution to efficiently revoke users and merge multiple IBE systems into a single system. The proposed scheme also has several nice features: when two systems are merged, there is no secure channel needed for the purpose of updating user private keys; and the size of the user private key remains unchanged when multiple systems are merged. We also propose a new security model for MRIBE, which is an extension of the security model for RIBE, and prove that the proposed scheme is semantically secure without random oracles.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
Boldyreva, A., Goyal, V., Kumar, V.: Identity-based encryption with efficient revocation. In: Ning, P., Syverson, P.F., Jha, S. (eds.) CCS, pp. 417–426. ACM (2008)
Boneh, D., Boyen, X.: Efficient selective-ID secure identity-based encryption without random oracles. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 223–238. Springer, Heidelberg (2004). doi:10.1007/978-3-540-24676-3_14
Boneh, D., Franklin, M.: Identity-based encryption from the Weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_13
Dodis, Y., Fazio, N.: Public key broadcast encryption for stateless receivers. In: Feigenbaum, J. (ed.) DRM 2002. LNCS, vol. 2696, pp. 61–80. Springer, Heidelberg (2003). doi:10.1007/978-3-540-44993-5_5
Gentry, C.: Practical identity-based encryption without random oracles. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 445–464. Springer, Heidelberg (2006). doi:10.1007/11761679_27
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions (extended abstract). In: FOCS, pp. 464–479. IEEE (1984)
Halevy, D., Shamir, A.: The LSD broadcast encryption scheme. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 47–60. Springer, Heidelberg (2002). doi:10.1007/3-540-45708-9_4
Hanaoka, Y., Hanaoka, G., Shikata, J., Imai, H.: Identity-based hierarchical strongly key-insulated encryption and its application. In: Roy, B. (ed.) ASIACRYPT 2005. LNCS, vol. 3788, pp. 495–514. Springer, Heidelberg (2005). doi:10.1007/11593447_27
Lee, K., Lee, D.H., Park, J.H.: Efficient revocable identity-based encryption via subset difference methods. IACR, 2014:132 (2014)
Liang, K., Liu, J.K., Wong, D.S., Susilo, W.: An efficient cloud-based revocable identity-based proxy re-encryption scheme for public clouds data sharing. In: Kutyłowski, M., Vaidya, J. (eds.) ESORICS 2014. LNCS, vol. 8712, pp. 257–272. Springer, Cham (2014). doi:10.1007/978-3-319-11203-9_15
Libert, B., Vergnaud, D.: Adaptive-ID secure revocable identity-based encryption. In: Fischlin, M. (ed.) CT-RSA 2009. LNCS, vol. 5473, pp. 1–15. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00862-7_1
Naor, D., Naor, M., Lotspiech, J.: Revocation and tracing schemes for stateless receivers. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 41–62. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_3
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). doi:10.1007/11426639_27
Seo, J.H., Emura, K.: Efficient delegation of key generation and revocation functionalities in identity-based encryption. In: Dawson, E. (ed.) CT-RSA 2013. LNCS, vol. 7779, pp. 343–358. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36095-4_22
Seo, J.H., Emura, K.: Revocable identity-based encryption revisited: security model and construction. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 216–234. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36362-7_14
Seo, J.H., Emura, K.: Adaptive-ID secure revocable hierarchical identity-based encryption. In: Tanaka, K., Suga, Y. (eds.) IWSEC 2015. LNCS, vol. 9241, pp. 21–38. Springer, Cham (2015). doi:10.1007/978-3-319-22425-1_2
Seo, J.H., Emura, K.: Revocable hierarchical identity-based encryption: history-free update, security against insiders, and short ciphertexts. In: Nyberg, K. (ed.) CT-RSA 2015. LNCS, vol. 9048, pp. 106–123. Springer, Cham (2015). doi:10.1007/978-3-319-16715-2_6
Shamir, A.: How to share a secret. ACM 22(11), 612–613 (1979)
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). doi:10.1007/3-540-39568-7_5
Waters, B.: Efficient identity-based encryption without random oracles. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 114–127. Springer, Heidelberg (2005). doi:10.1007/11426639_7
Yang, Y., Liu, J.K., Liang, K., Choo, K.-K.R., Zhou, J.: Extended proxy-assisted approach: achieving revocable fine-grained encryption of cloud data. In: Pernul, G., Ryan, P.Y.A., Weippl, E. (eds.) ESORICS 2015. LNCS, vol. 9327, pp. 146–166. Springer, Cham (2015). doi:10.1007/978-3-319-24177-7_8
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
A Security Proof
A Security Proof
Proof
The proof is similar to that of [1], except we meed to handle multiple systems and the mergeable algorithms. We construct an adversary \(\mathcal {B}\) for the DBDH problem associated with \(\mathcal {G}\). \(\mathcal {B}\) gets \((k,\mathbb {G},p,g,X,Y,Z,W)\) as input and it has to return a bit d. It is going to use \(\mathcal {A}\). For answering oracles, we define the following four functions. For \(i,j,l,r\in \mathbb {Z}_p, S=\{0,j\}\) define
Setup: \(\mathcal {B}\) receives the challenging message \((k,\mathbb {G},p,g,X,Y,Z,W)\) and sets the system parameters as follows.
-
\(\mathcal {B}\) chooses the \(N,N_S\in \mathbb {N}\) and sends the security parameter \((k,N,N_S)\) to \(\mathcal {A}\). \(\mathcal {A}\) generates the challenging identity \(\omega ^*\), the challenging time \(t^*\), the subscript of challenging public key \(i^*\) and the state for some related information about \((\omega ^*,t^*,i^*)\), then sends \((\omega ^*,t^*,i^*,state)\) to \(\mathcal {B}\).
-
\(\mathcal {B}\) chooses a random bit \(b\leftarrow \{0,1\}\) and initializes the database \(\mathcal {D},\mathcal {D_{SK}},\) \(\mathcal {D_{MSK}}\) \(\leftarrow \emptyset \), where \(\mathcal {D}\) is used to record the historical information of the challenging identity \(\omega ^*\), and \(\mathcal {D_{SK}},\mathcal {D_{MSK}}\) records information of the challenging identity \(\omega ^*\) to verify whether to abort.
-
\(\mathcal {B}\) simulates the system parameters for all \(N_S\) systems. \(\mathcal {B}\) sets public parameter \(pp=(\mathbb {G},p,g)\) and randomly picks a value \(i_r\leftarrow \{1,2,...,N_S\}\), where the challenging identity \(\omega ^*\) is initialized in the system with public key \(pk_{i_r}\). Then, \(\mathcal {B}\) updates the database \(\mathcal {D}\leftarrow (\vec {pk_{\omega ^*}},\omega ^*)\), where \(\vec {pk_{\omega ^*}}\leftarrow \vec {pk_{\omega ^*}}\cup \{pk_{i_r}\}\). \(\forall j\in \{1,2,...,N_S\}\) then:
-
1.
Randomly pick and store \(r_j,r_{1,j}, r_{2,j}\leftarrow \mathbb {Z}_p^*\) in the system j and generate the parameters \(g_{1,j}\) and \(g_{2,j}\).
$$\begin{aligned} g_{1,j}\leftarrow X^{r_{1,j}}, g_{2,j}\leftarrow Y^{r_{2,j}}. \end{aligned}$$ -
2.
Pick random second-degree polynomials f(x), u(x) with coefficients in \(\mathbb {Z}_p\) s.t. \(u(x)=-x^2\) for \(x=\omega ^*,t^*\), o.w. \(u(x)\ne -x^2\). \(\forall i=\{1,2,3\}\) then: set \(h_{i,j}\leftarrow g_{2,j}^{u(i)}g^{f(i)}\).
-
3.
Set the public key \(pk_j\leftarrow (g,g_{1,j},g_{2,j},h_{1,j},h_{2,j},h_{3,j})\).
-
1.
-
\(\mathcal {B}\) sends the public parameter pp and public keys \(\{pk_i\}_{i\in \{1,2,...,N_S\}}\) to \(\mathcal {A}\).
-
\(\mathcal {B}\) simulates the revocation list and the binary tree. \(\forall j=\{1,2,...,N_S\}\) then: let \(rl_j\) be an empty set and \(\mathsf{T}_j\) be a binary tree with at least N leaf nodes. \(\mathcal {B}\) picks a leaf node \(v^*\) from \(\mathsf{T}_{i_r}\), where the challenging identity \(\omega ^*\) is assigned to the leaf \(v^*\), and chooses a random bit \(rev\leftarrow \{0,1\}\), where 0 means \(\omega ^*\) is a non-revoked user, otherwise, he is a revoked user.
\(\mathcal {O_{SK}}(pk_i,\omega )\): \(\mathcal {A}\) issues up to \(q_p\) private key generation queries. \(\mathcal {B}\) responds to a query on message \((pk_i,\omega )\) as follows.
-
If \(\omega =\omega ^*\), \(\mathcal {B}\) simulates the private key \(sk_{\omega ,i}\) for the challenging identity \(\omega ^*\).
-
1.
If \(rev=0\), set \(\mathcal {D_{SK}}\leftarrow \mathcal {D_{SK}}\cup \{pk_i\}\) and abort if \(\mathcal {A}\) is able to obtain the secret key \(sk_{\omega ^*,i^*}\) by checking the transactions in database \(\mathcal {D_{SK}}\) and \(\mathcal {D_{MSK}}\) in Fig. 1.
-
2.
Else set \(v\leftarrow v^*\). \(\forall x\in \mathsf{Path}(v)\) then:
-
(a)
Set \(r_x\leftarrow \mathsf{F}_{r_i}(\omega ^*\Vert x)\), where \(msk_i=(a_i,r_i)\).
-
(b)
If \(\not \exists l_x\) then randomly choose \(l_x\leftarrow \mathbb {Z}_p\) and store \(l_x\) in node x.
-
(c)
Set \((D_x,d_x)\) and update private key \(sk_{\omega ^*,i}\leftarrow sk_{\omega ^*,i}\cup (x,D_x,d_x)\).
$$\begin{aligned} D_x\leftarrow F_1(g_{2,i},h_{1,i},h_{2,i},h_{3,i},\omega ^*,l_x,r_x), d_x\leftarrow F_2(r_x). \end{aligned}$$
-
(a)
-
1.
-
If \(\omega \ne \omega ^*\), \(\mathcal {B}\) simulates the private key \(sk_{\omega ,i}\) for the identity \(\omega \). \(\forall x\in \mathsf{Path}(v)\) then:
-
1.
Set \(r_x\leftarrow \mathsf{F}_{r_i}(\omega \Vert x)\), where \(msk_i=(a_i,r_i)\).
-
2.
If \(\not \exists l_x\) then randomly choose \(l_x\leftarrow \mathbb {Z}_p\) and store \(l_x\) in node x.
-
3.
If \(rev=0\), set \((D_x,d_x)\) and update private key \(sk_{\omega ,i}\leftarrow sk_{\omega ,i}\cup (x,D_x,d_x)\).
$$\begin{aligned} D_x\leftarrow F_3(g_{1,i},g_{2,i},\omega ,t^*,l_x,r_x), d_x\leftarrow F_4(g_{1,i},g_{2,i},\omega ,r_x). \end{aligned}$$ -
4.
If \(rev=1\), simulate the private key \(sk_{\omega ,i}\) depends on the \(\mathsf{Path}(v)\) and \(\mathsf{Path}(v^*)\).
-
(a)
\(\forall x\in (\mathsf{Path}(v)\setminus \mathsf{Path}(v^*))\) then: set \((D_x,d_x)\) and update private key \(sk_{\omega ,i}\leftarrow sk_{\omega ,i}\cup (x,D_x,d_x)\).
$$\begin{aligned} D_x\leftarrow F_3(g_{1,i},g_{2,i},\omega ,t^*,l_x,r_x), d_x\leftarrow F_4(g_{1,i},g_{2,i},\omega ,r_x). \end{aligned}$$ -
(b)
\(\forall x\in (\mathsf{Path}(v)\cap \mathsf{Path}(v^*))\) then: set \((D_x,d_x)\) and update private key \(sk_{\omega ,i}\leftarrow sk_{\omega ,i}\cup (x,D_x,d_x)\).
$$\begin{aligned} D_x\leftarrow F_3(g_{1,i},g_{2,i},\omega ,\omega ^*,l_x,r_x), d_x\leftarrow F_4(g_{1,i},g_{2,i},\omega ,r_x). \end{aligned}$$
-
(a)
-
1.
-
Return the private key \(sk_{\omega ,i}=\{(x,D_x,d_x)\}_{x\in \mathsf{Path}(v)}\).
\(\mathcal {O_R}(\omega ,t)\): \(\mathcal {A}\) issues up to \(q_r\) revocation queries. \(\mathcal {B}\) responds to a query on message \((\omega ,t)\) as follows. If \((\cdot ,\omega )\in \mathcal {D}\), for all leaf nodes v associated with identity \(\omega \) add (v, t) to revocation list \(rl_i\leftarrow rl_i\cup (v,t)\), then return \(rl_i\) else return \(\bot \).
\(\mathcal {O_{KU}}(pk_i,t)\): \(\mathcal {A}\) issues up to \(q_k\) key update generation queries. \(\mathcal {B}\) responds to a query on message \((pk_i,t)\) as follows.
-
If \(t\ne t^*\), \(\mathcal {B}\) simulates the key update \(ku_{t,i}\) for the system i.
-
1.
If \(rev=0\), \(\forall x\in \mathsf{KUNodes}(\mathsf{T},rl,t)\) then: \({r_x}\leftarrow \mathbb {Z}_p^*\), set \(E_x\) and \(d_x\) and update \(ku_{t,i}\leftarrow ku_{t,i}\cup (x,E_x,e_x)\).
$$\begin{aligned} E_x\leftarrow F_3(g_{1,i},g_{2,i},t,t^*,l_x,r_x), e_x\leftarrow F_4(g_{1,i},g_{2,i},t,r_x). \end{aligned}$$ -
2.
If \(rev=1\), simulate the key \(ku_t\) depends on the \(\mathsf{Path}(v)\) and \(\mathsf{Path}(v^*)\).
-
(a)
\(\forall x\in (\mathsf{KUNodes}(\mathsf{T},rl,t)\setminus \mathsf{Path}(v^*))\) then: \({r_x}\leftarrow \mathbb {Z}_p^*\), set \(E_x\) and \(d_x\) and update \(ku_{t,i}\leftarrow ku_{t,i}\cup (x,E_x,e_x)\).
$$\begin{aligned} E_x\leftarrow F_3(g_{1,i},g_{2,i},t,t^*,l_x,r_x), e_x\leftarrow F_4(g_{1,i},g_{2,i},t,r_x). \end{aligned}$$ -
(b)
\(\forall x\in (\mathsf{KNodes}(\mathsf{T},rl,t)\cap \mathsf{Path}(v^*))\) then: \({r_x}\leftarrow \mathbb {Z}_p^*\), set \(E_x\) and \(d_x\) and update \(ku_{t,i}\leftarrow ku_{t,i}\cup (x,E_x,e_x)\).
$$\begin{aligned} E_x\leftarrow F_3(g_{1,i},g_{2,i},t,\omega ^*,l_x,r_x), e_x\leftarrow F_4(g_{1,i},g_{2,i},t,r_x). \end{aligned}$$
-
(a)
-
1.
-
If \(t=t^*\), \(\mathcal {B}\) simulates the key update \(ku_{t,i}\) in the challenging time \(t^*\) for the system i.
-
1.
If \(rev=1\) and \(\forall t\le t^*\) we have that \((\omega ^*,t)\not \in rl_{i^*}\) then abort since challenging identity \(\omega ^*\) must be revoked when \(rev=1\).
-
2.
Else, \(\forall x\in \mathsf{KUNodes}(\mathsf{T},rl,t)\) then: \({r_x}\leftarrow \mathbb {Z}_p^*\), set \(E_x\) and \(d_x\) and update \(ku_{t,i}\leftarrow ku_{t,i}\cup (x,E_x,e_x)\).
$$\begin{aligned} E_x\leftarrow F_1(g_{2,i},h_{1,i},h_{2,i},h_{3,i},t^*,l_x,r_x), e_x\leftarrow F_2(r_x). \end{aligned}$$
-
1.
-
Return the key update \(ku_{t,i}=\{(x,E_x,e_x)\}_{x\in \mathsf{KUNodes}(\mathsf{T},rl,t)}\).
\(\mathcal {O_{MP}}(pk_\alpha ,pk_\beta )\): \(\mathcal {A}\) issues up to \(q_m\) merge parameter generation queries. \(\mathcal {B}\) responds to a query on message \((pk_\alpha ,pk_\beta )\) by updating the revocation list \(rl_\beta \), state \(st_\beta \) and the database \(\mathcal {D}\) as follows.
-
Update the revocation list and state \(rl_\beta \leftarrow rl_\alpha \cup rl_\beta , st_\beta \leftarrow st_\beta \cup st_\alpha \setminus \mathsf{T}_{\alpha }\).
-
If \(\omega ^*\) is involved in the system with \(pk_\alpha \), then updating the database \(\mathcal {D}\).
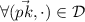 then set
then set  , if \(pk[len]=pk_\alpha \),
, if \(pk[len]=pk_\alpha \),  .
. -
Return the updated revocation list \(rl_\beta \) and state \(st_\beta \).
\(\mathcal {O_{MSK}}(\omega ,pk_\alpha ,pk_\beta )\): \(\mathcal {A}\) issues up to \(q_{mp}\) merge private key generation queries. \(\mathcal {B}\) responds to a query on message \((\omega ,pk_\alpha ,pk_\beta )\).
-
If \(\omega =\omega ^*\), \(\mathcal {B}\) simulates the private key \(sk_{\omega ,\alpha ,\beta }\) for challenging identity \(\omega \).
-
1.
If \(rev=0\), set \(\mathcal {D_{MSK}}\leftarrow \mathcal {D_{MSK}}\cup \{(pk_\alpha ,pk_\beta )\}\) and abort if \(\mathcal {A}\) is able to obtain the secret key \(sk_{\omega ^*,i^*}\) by checking the transactions in database \(\mathcal {D_{SK}}\) and \(\mathcal {D_{MSK}}\) in Fig. 1.
-
2.
Else set \(v\leftarrow v^*\). \(\forall x\in \mathsf{Path}(v)\) then:
-
(a)
Set \(r_{x,\alpha }\leftarrow G_{r_\alpha }(\omega \Vert x)\) and \(r_{x,\beta }\leftarrow \mathsf{F}_{r_\beta }(\omega \Vert x)\).
-
(b)
Set \((D_{x,\alpha ,\beta },d_{x,\alpha ,\beta })\) and update private key \(sk_{\omega ,\alpha ,\beta }\leftarrow sk_{\omega ,\alpha ,\beta }\cup (x,D_{x,\alpha ,\beta },d_{x,\alpha ,\beta })\), where the union symbol is used to combine the secret keys since this algorithm will return secret keys belong to \(\mathsf{Path}(v)\).
$$\begin{aligned} D_{x,\alpha ,\beta }=\frac{F_1(g_{2,\beta },h_{1,\beta },h_{2,\beta },h_{3,\beta },\omega ,l_{x,\beta },r_{x,\beta })}{F_1(g_{2,\alpha },h_{1,\alpha },h_{2,\alpha },h_{3,\alpha },\omega ,l_{x,\alpha },r_{x,\alpha })},d_{x,\alpha ,\beta }=\frac{F_2(r_{x,\beta })}{F_2(r_{x,\alpha })}. \end{aligned}$$
-
(a)
-
1.
-
If \(\omega \ne \omega ^*\), \(\mathcal {B}\) simulates the private key \(sk_{\omega ,\alpha ,\beta }\) for the identity \(\omega \). \(\forall x\in \mathsf{Path}(v)\) then:
-
1.
Set \(r_{x,\alpha }\leftarrow G_{r_\alpha }(\omega \Vert x)\) and \(r_{x,\beta }\leftarrow G_{r_\beta }(\omega \Vert x)\).
-
2.
If \(rev=0\), set \((D_x,d_x)\) and update private key \(sk_\omega \leftarrow sk_\omega \cup (x,D_x,d_x)\), where the union symbol is used for the same reason in previous section.
$$\begin{aligned} D_{x,\alpha ,\beta }=\frac{F_3(g_{1,\beta },g_{2,\beta },\omega ,t^*,l_{x,\beta },r_{x,\beta })}{F_3(g_{1,\alpha },g_{2,\alpha },\omega ,t^*,l_{x,\alpha },r_{x,\alpha })}, d_{x,\alpha ,\beta }=\frac{F_4(g_{1,\beta },g_{2,\beta },\omega ,r_{x,\beta })}{F_4(g_{1,\alpha },g_{2,\alpha },\omega ,r_{x,\alpha })}. \end{aligned}$$ -
3.
If \(rev=1\), simulate the private key \(sk_\omega \) depends on the \(\mathsf{Path}(v)\) and \(\mathsf{Path}(v^*)\).
-
(a)
\(\forall x\in (\mathsf{Path}(v)\setminus \mathsf{Path}(v^*))\) then: set \((D_x,d_x)\) and update private key \(sk_\omega \leftarrow sk_\omega \cup (x,D_x,d_x)\).
$$\begin{aligned} D_{x,\alpha ,\beta }=\frac{F_3(g_{1,\beta },g_{2,\beta },\omega ,t^*,l_{x,\beta },r_{x,\beta })}{F_3(g_{1,\alpha },g_{2,\alpha },\omega ,t^*,l_{x,\alpha },r_{x,\alpha })}, d_{x,\alpha ,\beta }\!=\!\frac{F_4(g_{1,\beta },g_{2,\beta },\omega ,r_{x,\beta })}{F_4(g_{1,\alpha },g_{2,\alpha },\omega ,r_{x,\alpha })}. \end{aligned}$$ -
(b)
\(\forall x\in (\mathsf{Path}(v)\cap \mathsf{Path}(v^*))\) then: set \((D_x,d_x)\) and update private key \(sk_\omega \leftarrow sk_\omega \cup (x,D_x,d_x)\).
$$\begin{aligned} D_{x,\alpha ,\beta }=\frac{F_3(g_{1,\beta },g_{2,\beta },\omega ,\omega ^*,l_{x,\beta },r_{x,\beta })}{F_3(g_{1,\alpha },g_{2,\alpha },\omega ,\omega ^*,l_{x,\alpha },r_{x,\alpha })}, d_{x,\alpha ,\beta }\!=\!\frac{F_4(g_{1,\beta },g_{2,\beta },\omega ,r_{x,\beta })}{F_4(g_{1,\alpha },g_{2,\alpha },\omega ,r_{x,\alpha })}. \end{aligned}$$
-
(a)
-
4.
Return the private key \(sk_{\omega ,\alpha ,\beta }=\{(x,D_{x,\alpha ,\beta },d_{x,\alpha ,\beta })\}_{x\in \mathsf{Path}(v)}\).
-
1.
Output: \(\mathcal {A}\) outputs two message \(m_0\) and \(m_1\). \(\mathcal {B}\) picks a random bit \(b\leftarrow \{0,1\}\) and generates the challenging ciphertext \(c^*=(c_1^*,c_2^*,c_{\omega ^*},c_{t^*})\) and then sends \(c^*\) to \(\mathcal {A}\). \(\mathcal {A}\) outputs a bit d. If \(b=d\), \(\mathcal {B}\) outputs 1 else output 0.
If any oracles abort, \(\mathcal {B}\) outputs 1.
1.1 A.1 Analysis
Let \(\mathsf{sreal, srand}\) denote the events that none of the oracles abort in \(\mathsf{Exp}_{\mathcal {G,B}}^{dbdh-real}(k)\), \(\mathsf{Exp}_{\mathcal {G,B}}^{dbdh-rand}(k)\) respectively. Then
The probability that \(\mathcal {O_{SK}}(pk_i,\omega )\), \(\mathcal {O_{MSK}}(\omega ,pk_\alpha ,pk_\beta )\) and \(\mathcal {O_{KU}}(pk_i,t)\) oracles abort depends on the bit rev which are chosen independently from whether \(\mathcal {B}\) is in \(\mathsf{Exp}_{\mathcal {G,B}}^{dbdh-real}(k)\) or \(\mathsf{Exp}_{\mathcal {G,B}}^{dbdh-rand}(k)\). So, \(\Pr [\mathsf{sreal}]=\Pr [\mathsf{srand}]\).
\(\mathcal {O_{SK}}(pk_i,\omega )\) and \(\mathcal {O_{MSK}}(\cdot ,\cdot ,\omega ^*)\) oracles can be queried on \(\omega ^*\) without constrain only if \(\mathcal {O_R}(\omega ,t)\) oracle was queried on \((\omega ^*,t)\) for any \(t\le t^*\). Thus, we have
We see that \(\mathcal {O_{SK}}(pk_i,\omega )\) oracles abort if \(\omega =\omega ^*\) and \(\mathcal {O_{KU}}(t)\) oracle aborts if \(rev=1, t=t^*\) and \(\exists t\le t^*\ (\omega ^*,t)\not \in rl_{\omega ^*}\). Thus,
\(\mathcal {B}\) simulates the exact experiment \(\mathsf{Exp}_{\mathcal {MRIBE,A},N,N_S}^{smrid-cpa}(k)\) for \(\mathcal {A}\) when \(\mathcal {B}\) is in \(\mathsf{Exp}_{\mathcal {G,B}}^{dbdh-real}(k)\) and none of the oracles abort. So,
When \(\mathcal {B}\) is \(\mathsf{Exp}_{\mathcal {G,B}}^{dbdh-rand}(k)\) and none of the oracles abort then as explained earlier bit b is information-theoretically hidden from \(\mathcal {A}\). So,
Also, since \(\mathcal {B}\) outputs 1 when either of the oracles aborts, so
Thus,
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Xu, S., Yang, G., Mu, Y., Susilo, W. (2017). Mergeable and Revocable Identity-Based Encryption. In: Pieprzyk, J., Suriadi, S. (eds) Information Security and Privacy. ACISP 2017. Lecture Notes in Computer Science(), vol 10342. Springer, Cham. https://doi.org/10.1007/978-3-319-60055-0_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-60055-0_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-60054-3
Online ISBN: 978-3-319-60055-0
eBook Packages: Computer ScienceComputer Science (R0)


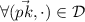 then set
then set  , if
, if  .
.