Abstract
We construct a compact public-key encryption with tight CCA security in the multi-user, multi-challenge setting, where the reduction loss is a constant. Our scheme follows the Hofheinz-Jager framework but is compressed in the sense that only one of the underlying two-tier signatures needs to be committed. Considering the virtually unbounded simulations, e.g., \(2^{80}\), the ciphertext size of our scheme decreases to about 256 group elements, whereas the best known solution provided by Blazy et al. required about 625 group elements under the same standard assumptions. In particular, we formalize a new notion called simulatable two-tier signature, which plays a central role in the construction of our tree-based signature and public-key encryption. Combining simulatable two-tier signatures with additional “ephemeral” signatures, we provide a method of constructing commitments to a tree-based signature, where most parts of the tree-based signature can be simulated and sent in the clear. Our method can reduce the length of the commitments and the related proofs of knowledge in previous works by 60%.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The concrete ciphertext size of PKE in [10] is not explicit in their paper. We compute the ciphertext size according to the appendix of [10] when \(d=2\), \(f=1\) and \(\lambda =80\). Note that (d, f) are the parameters related to the underlying d-time two-tier signatures and \(2^{\lambda }\) denotes the maximal number of signatures.
- 2.
The simulatable two-tier signature is different from the notion simulatable signature introduced in [2]. The latter is defined in the common reference string (CRS) model and allows to create valid signatures using the trapdoor associated with the CRS, while our simulatable two-tier signature does not require the CRS and the trapdoor.
- 3.
For simplicity, we omit the description of state information. Indeed, we need to store the state information, such as \(v_h\), \((\widehat{\textsf {ppk}},\widehat{\textsf {psk}})\), and the secondary public/secret key pairs and corresponding two-tier signatures generated so far.
- 4.
For more details on the definition of IND-CCA security in the multi-user/-challenge setting, we refer to [19].
- 5.
k in the left side of Eq. (6).
- 6.
References
Abe, M., David, B., Kohlweiss, M., Nishimaki, R., Ohkubo, M.: Tagged one-time signatures: tight security and optimal tag size. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 312–331. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36362-7_20
Abe, M., Fuchsbauer, G., Groth, J., Haralambiev, K., Ohkubo, M.: Structure-preserving signatures and commitments to group elements. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 209–236. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_12
Attrapadung, N., Hanaoka, G., Yamada, S.: A framework for identity-based encryption with almost tight security. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 521–549. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48797-6_22
Bader, C., Hofheinz, D., Jager, T., Kiltz, E., Li, Y.: Tightly-secure authenticated key exchange. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 629–658. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46494-6_26
Bader, C., Jager, T., Li, Y., Schäge, S.: On the impossibility of tight cryptographic reductions. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 273–304. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_10
Belenkiy, M., Camenisch, J., Chase, M., Kohlweiss, M., Lysyanskaya, A., Shacham, H.: Randomizable proofs and delegatable anonymous credentials. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 108–125. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03356-8_7
Bellare, M., Boldyreva, A., Micali, S.: Public-key encryption in a multi-user setting: security proofs and improvements. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 259–274. Springer, Heidelberg (2000). doi:10.1007/3-540-45539-6_18
Bellare, M., Shoup, S.: Two-tier signatures, strongly unforgeable signatures, and fiat-shamir without random oracles. In: Okamoto, T., Wang, X. (eds.) PKC 2007. LNCS, vol. 4450, pp. 201–216. Springer, Heidelberg (2007). doi:10.1007/978-3-540-71677-8_14
Blazy, O., Kiltz, E., Pan, J.: (Hierarchical) identity-based encryption from affine message authentication. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 408–425. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44371-2_23
Blazy, O., Kakvi, S.A., Kiltz, E., Pan, J.: Tightly-secure signatures from chameleon hash functions. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 256–279. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46447-2_12
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28628-8_3
Canetti, R., Halevi, S., Katz, J.: Chosen-ciphertext security from identity-based encryption. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 207–222. Springer, Heidelberg (2004). doi:10.1007/978-3-540-24676-3_13
Chen, J., Wee, H.: Fully, (almost) tightly secure IBE and dual system groups. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 435–460. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_25
Dodis, Y., Haralambiev, K., López-Alt, A., Wichs, D.: Efficient public-key cryptography in the presence of key leakage. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 613–631. Springer, Heidelberg (2010). doi:10.1007/978-3-642-17373-8_35
ElGamal, T.: A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theor. IT–31(4), 469–472 (1985)
Gay, R., Hofheinz, D., Kiltz, E., Wee, H.: Tightly CCA-secure encryption without pairings. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 1–27. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49890-3_1
Goldreich, O.: Two remarks concerning the goldwasser-micali-rivest signature scheme. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 104–110. Springer, Heidelberg (1987). doi:10.1007/3-540-47721-7_8
Groth, J.: Simulation-sound NIZK proofs for a practical language and constant size group signatures. In: Lai, X., Chen, K. (eds.) ASIACRYPT 2006. LNCS, vol. 4284, pp. 444–459. Springer, Heidelberg (2006). doi:10.1007/11935230_29
Hofheinz, D., Jager, T.: Tightly secure signatures and public-key encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 590–607. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_35
Hofheinz, D.: Algebraic partitioning: fully compact and (almost) tightly secure cryptography. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 251–281. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49096-9_11
Hofheinz, D., Koch, J., Striecks, C.: Identity-based encryption with (almost) tight security in the multi-instance, multi-ciphertext setting. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 799–822. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46447-2_36
Kiltz, E., Pan, J., Wee, H.: Structure-preserving signatures from standard assumptions, revisited. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 275–295. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_14
Krawczyk, H., Rabin, T.: Chameleon hashing and signatures. In: Proceedings of NDSS 2000, pp. 143–154 (2000)
Libert, B., Joye, M., Yung, M., Peters, T.: Concise multi-challenge CCA-secure encryption and signatures with almost tight security. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8874, pp. 1–21. Springer, Heidelberg (2014). doi:10.1007/978-3-662-45608-8_1
Libert, B., Peters, T., Joye, M., Yung, M.: Compactly hiding linear spans. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 681–707. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48797-6_28
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen cipher-text attacks. In: STOC 1990, pp. 427–437. ACM, New York (1990)
Rackoff, C., Simon, D.R.: Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 433–444. Springer, Heidelberg (1992). doi:10.1007/3-540-46766-1_35
Acknowledgements
We would like to thank the reviewers for helpful comments. Puwen Wei and Wei Wang were supported by NSFC (No. 61502276 and No. 61672019) and the Foundation of Science and Technology on Communication Security Laboratory (No. 9140c110207150c11050). Bingxin Zhu was supported by the Fundamental Research Funds of Shandong University (No. 2016JC029).
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Appendices
A Examples of Simulatable Two-Tier Signatures
In this section, we briefly describe some examples of simulatable two-tier signatures based on schemes in [10]. The validity proof of the corresponding SimTTSign algorithms is easy to check and thus omitted.
-
Simulatable two-tier signatures based on f -CDHI [10]
- \(\bullet \) :
-
\(\textsf {PriGen}(1^{\lambda },d)\): \(g\mathop {\leftarrow }\limits ^{R}\mathbb {G}\), \((x_0,\dots ,x_c)\mathop {\leftarrow }\limits ^{R}\mathbb {Z}_p\), \(\textsf {psk}=(x_0,\dots ,x_c)\), \(\textsf {ppk}=(g,(h_0,\dots ,h_c))\), where \(c\cdot f=d\) and \(h_i=g^{x_i}\) for \(i=0,\dots ,c\).
- \(\bullet \) :
-
SecGen(ppk, psk): \(k\mathop {\leftarrow }\limits ^{R}\mathbb {G}\), \(\textsf {spk}=k\), \(\textsf {ssk}\) is empty.
- \(\bullet \) :
-
TTSign(psk, ssk, m, j): \(j=\alpha f+\beta \), where \(j\in \{1,\dots ,d\}, \alpha \in \{0,\dots ,c\}\) and \(\beta \in \{0,\dots ,f-1\}\). Output \(\sigma =(g^mk)^{1/(x_{\alpha }+\beta )}\).
- \(\bullet \) :
-
TTVrfy(ppk,spk,\(m,\sigma ;j\)): Check if \(e(\sigma ,h_{\alpha }g^{\beta })=e(g^{m}k,g)\).
- \(\bullet \) :
-
\(\textsf {SimTTSign}(\textsf {ppk}, m)\): \(r\mathop {\leftarrow }\limits ^{R}\mathbb {Z}_p\), \(\sigma '\leftarrow g^r\) and \(\textsf {spk}'=(h_{\alpha }g^{\beta })^rg^{-m}\), where \(j=\alpha f+\beta \). Output \((\textsf {spk}',\sigma ')\).
-
Simulatable two-tier signatures based on DLOG [10]
- \(\bullet \) :
-
\(\textsf {PriGen}(1^{\lambda })\): \(x\mathop {\leftarrow }\limits ^{R}\mathbb {Z}_p\), \(g\in \mathbb {G}\), \(\textsf {psk}=x\), \(\textsf {ppk}=y=g^x\).
- \(\bullet \) :
-
SecGen(ppk, psk): \(r\mathop {\leftarrow }\limits ^{R}\mathbb {Z}_p\), \(\textsf {ssk}=r\), \(\textsf {spk}=y^0g^r\).
- \(\bullet \) :
-
TTSign(psk, ssk, m): Output \(\sigma =r-xm\).
- \(\bullet \) :
-
TTVrfy(ppk, spk, \(m,\sigma \)): Check if \(y^mg^{\sigma }=\textsf {spk}\).
- \(\bullet \) :
-
\(\textsf {SimTTSign}(\textsf {ppk}, m)\): \(\sigma '\mathop {\leftarrow }\limits ^{R}\mathbb {Z}_p\) and \(\textsf {spk}'=y^mg^{\sigma '}\). Output \((\textsf {spk}',\sigma ')\).
Structure of TreeSig. \((\widehat{\textsf {spk}_{v_i||0}},\widehat{\textsf {spk}_{v_i||1}})\) are authenticated by signature \(\sigma _{v_i}\) that verifies under \(\textsf {spk}_{v_i}\), and \(\textsf {spk}_{v_{i+1}}\) with \(v_{i+1}=v_i||\beta _ij_i\) is authenticated by signature \(\widehat{\sigma _{v_i||\beta _i}}\) that verifies under \(\widehat{\textsf {spk}_{v_i||\beta _i}}\).
B Illustration of TreeSig
C Proof of Theorem 1
Proof
Suppose \(\mathcal {A}\) is a PPT adversary that \((\epsilon _{\textsf {Tree}},t_{\textsf {Tree}},q_{\textsf {Tree}})\)-breaks the EUF-NCMA security of TreeSig. We show how to construct a PPT algorithm \(\mathcal {B}\) that \((\epsilon _{\textsf {TTSig}},t_{\textsf {TTSig}},q_{\textsf {TTSig}})\)-breaks the EUF-NCMA security of TTSig or a PPT algorithm \(\hat{\mathcal {B}}\) that \((\epsilon _{\widehat{\textsf {TTSig}}},t_{\widehat{\textsf {TTSig}}},\) \(q_{\widehat{\textsf {TTSig}}})\)-breaks the EUF-NCMA security of \(\widehat{\textsf {TTSig}}\). Construction of \(\mathcal {B.}\) When receiving \((m^{(1)},\dots ,m^{(q)})\), \(\mathcal {B}\) computes \((\widehat{\textsf {ppk}},\widehat{\textsf {psk}})\leftarrow \widehat{\textsf {PriGen}}(1^{\lambda })\) and generates the signature \(\sigma ^{(j)}\) on \(m^{(j)}\) as below, for \(j=1,\dots ,q\).
-
Authentication for
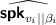 and nodes generation. Choose the leftmost unused leaf \(N_{v_h}\). For \(i=0,1,\dots ,h-1\), if the related keys associated to \(N_{v_{i}}\) have not been defined, compute \((\widehat{\textsf {spk}_{v_i||0}},\widehat{\textsf {ssk}_{v_i||0}})\leftarrow \widehat{\textsf {SecGen}}(\widehat{\textsf {ppk}},\) \(\widehat{\textsf {psk}})\) and \((\widehat{\textsf {spk}_{v_i||1}},\widehat{\textsf {ssk}_{v_i||1}})\leftarrow \widehat{\textsf {SecGen}}(\widehat{\textsf {ppk}},\widehat{\textsf {psk}})\), query the signing oracle \(\mathcal {O}_{\textsf {TTSig}}(\cdot )\) with message \(\widehat{\textsf {spk}_{v_i||0}}||\widehat{\textsf {spk}_{v_i||1}}||\widehat{\textsf {ppk}}\) and get \((\textsf {spk}_{v_i},\sigma _{v_i})\). For the leaf \(N_{v_h}\), query the signing oracle \(\mathcal {O}_{\textsf {TTSig}}(\cdot )\) with message \(m^{(j)}\), and get \((\textsf {spk}_{v_h^{(j)}},\sigma _{v_h^{(j)}})\).
and nodes generation. Choose the leftmost unused leaf \(N_{v_h}\). For \(i=0,1,\dots ,h-1\), if the related keys associated to \(N_{v_{i}}\) have not been defined, compute \((\widehat{\textsf {spk}_{v_i||0}},\widehat{\textsf {ssk}_{v_i||0}})\leftarrow \widehat{\textsf {SecGen}}(\widehat{\textsf {ppk}},\) \(\widehat{\textsf {psk}})\) and \((\widehat{\textsf {spk}_{v_i||1}},\widehat{\textsf {ssk}_{v_i||1}})\leftarrow \widehat{\textsf {SecGen}}(\widehat{\textsf {ppk}},\widehat{\textsf {psk}})\), query the signing oracle \(\mathcal {O}_{\textsf {TTSig}}(\cdot )\) with message \(\widehat{\textsf {spk}_{v_i||0}}||\widehat{\textsf {spk}_{v_i||1}}||\widehat{\textsf {ppk}}\) and get \((\textsf {spk}_{v_i},\sigma _{v_i})\). For the leaf \(N_{v_h}\), query the signing oracle \(\mathcal {O}_{\textsf {TTSig}}(\cdot )\) with message \(m^{(j)}\), and get \((\textsf {spk}_{v_h^{(j)}},\sigma _{v_h^{(j)}})\). -
Authentication for
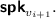 For \(i=0,1,\dots ,h-1\), if \(\textsf {spk}_{v_{i+1}}\) has not been authenticated, compute \(\widehat{\sigma _{v_{i}||\beta _i}}\leftarrow \widehat{\textsf {TTSign}}(\widehat{\textsf {psk}},\widehat{\textsf {ssk}_{v_{i}||\beta _i}},\) \(\textsf {spk}_{v_{i+1}};j_i),\) where \(v_{i+1}=v_i||\beta _ij_i\).
For \(i=0,1,\dots ,h-1\), if \(\textsf {spk}_{v_{i+1}}\) has not been authenticated, compute \(\widehat{\sigma _{v_{i}||\beta _i}}\leftarrow \widehat{\textsf {TTSign}}(\widehat{\textsf {psk}},\widehat{\textsf {ssk}_{v_{i}||\beta _i}},\) \(\textsf {spk}_{v_{i+1}};j_i),\) where \(v_{i+1}=v_i||\beta _ij_i\).
Hence the signature \(\sigma ^{(j)}\) on message \(m^{(j)}\) can be generated without knowing \(\textsf {sk}_{tree}\). Return \(\textsf {vk}_{tree}=(\textsf {ppk},\textsf {spk}_{v_0})\) and \((\sigma ^{(1)},\dots ,\sigma ^{(q)})\) to \(\mathcal {A}\). Note that \(\mathcal {B}\) perfectly simulates the signing oracle of TreeSig and the resulting distribution is identical to that of the real one. Suppose \(\mathcal {A}\) outputs a forgery \((m^*,\sigma ^{(*)})\) and \(\delta \) is the largest index such that \(\textsf {spk}_{v_\delta ^{(*)}}=\textsf {spk}_{v_\delta ^{(i)}}\) for some (i). Here, variables with \((*)\) (or (i)) denote the corresponding parts of \(\sigma ^{(*)}\) (or \(\sigma ^{(i)}\)). Consider the following cases.
-
If \(\widehat{\textsf {ppk}}^{(*)}\ne \widehat{\textsf {ppk}}\), \(\mathcal {B}\) outputs \((\widehat{\textsf {spk}_{v_{0}||0^{(*)}}}||\widehat{\textsf {spk}_{v_{0}||1^{(*)}}}||\widehat{\textsf {ppk}}^{(*)}, \sigma _{v_{0}^{(*)}}, i_{v_{0}})\), where \(i_{v_{0}}\) denotes the \(i_{v_{0}}\)-th query to \(\mathcal {O}_{\textsf {TTSig}}\) and corresponds to the secondary public key \(\textsf {spk}_{v_{0}}\).
-
If \(\widehat{\textsf {ppk}}^{(*)}= \widehat{\textsf {ppk}}\),
-
\(\delta =h\). \(\mathcal {B}\) outputs \((m^*,\sigma _{v_h^{(*)}},i_{v_h^{(i)}})\), where \(i_{v_h^{(i)}}\) denotes the \(i_{v_h^{(i)}}\)-th query to \(\mathcal {O}_{\textsf {TTSig}}\) and corresponds to \(\textsf {spk}_{v_h^{(i)}}\).
-
\(\delta <h\).
-
* \(\beta _{\delta }^{(*)}\ne \beta _{\delta }^{(i)}\) and \(\widehat{\textsf {spk}_{v_\delta || \beta _{\delta }^{(*)}}}\ne \widehat{\textsf {spk}_{v_\delta || (\beta _{\delta }^{(i)}\oplus 1)}}\). \(\mathcal {B}\) outputs \((\widehat{\textsf {spk}_{v_{\delta }||0^{(*)}}}||\) \(\widehat{\textsf {spk}_{v_{\delta }||1^{(*)}}}||\widehat{\textsf {ppk}}^{(*)}, \sigma _{v_\delta ^{(*)}},i_{v_\delta ^{(i)}})\), where \(i_{v_\delta ^{(i)}}\) denotes the \(i_{v_\delta ^{(i)}}\)-th query to \(\mathcal {O}_{\textsf {TTSig}}\) and corresponds to \(\textsf {spk}_{v_\delta ^{(i)}}\).
-
* \(\beta _{\delta }^{(*)}= \beta _{\delta }^{(i)}\) and \(\widehat{\textsf {spk}_{v_\delta || \beta _{\delta }^{(*)}}}\ne \widehat{\textsf {spk}_{v_\delta || \beta _{\delta }^{(i)}}}\). \(\mathcal {B}\) outputs \((\widehat{\textsf {spk}_{v_{\delta }||0^{(*)}}}||\widehat{\textsf {spk}_{v_{\delta }||1^{(*)}}}\) \(||\widehat{\textsf {ppk}}^{(*)}, \sigma _{v_\delta ^{(*)}},i_{v_\delta ^{(i)}})\).
-
* Otherwise, \(\mathcal {B}\) aborts. More precisely, \(\mathcal {B}\) aborts if \(((\beta _{\delta }^{(*)}\ne \beta _{\delta }^{(i)})\wedge (\widehat{\textsf {spk}_{v_\delta || \beta _{\delta }^{(*)}}}= \widehat{\textsf {spk}_{v_\delta || (\beta _{\delta }^{(i)}\oplus 1)}}))\) or \(((\beta _{\delta }^{(*)}= \beta _{\delta }^{(i)}) \wedge (\widehat{\textsf {spk}_{v_\delta || \beta _{\delta }^{(*)}}}= \widehat{\textsf {spk}_{v_\delta || \beta _{\delta }^{(i)}}}))\). Denote this event as Bad.
-
-
By the perfect simulation of \(\mathcal {B}\),
where \(q_{\textsf {Tree}}=q\). So we have
Construction of \(\mathcal {\hat{B}.}\) Next, we will show that \(\Pr [\textsf {Exp}_{\textsf {TreeSig},\mathcal {A},q_{\textsf {Tree}}}^{\textsf {EUF-NCMA}}(\lambda )=1\wedge \textsf {Bad}]\le \epsilon _{\widehat{\textsf {TTSig}}}\) by constructing a PPT algorithm \(\hat{\mathcal {B}}\), which breaks the security of \(\widehat{\textsf {TTSig}}\). \(\mathcal {\hat{B}}\) takes as input \(\widehat{\textsf {ppk}}\) and simulates \(\textsf {Exp}_{\textsf {TreeSig},\mathcal {A},q_{\textsf {Tree}}}^{\textsf {EUF-NCMA}}(\lambda )\) as follows. Upon receiving \(m^{(1)},\ldots ,m^{(q)}\), \(\hat{\mathcal {B}}\) compute \((\textsf {vk}_{tree},\textsf {sk}_{tree}) \leftarrow \textsf {TreeSig.Gen}(1^{\lambda })\) where \(\textsf {vk}_{tree}=(\textsf {ppk},\textsf {spk}_{v_0})\) and \(\textsf {sk}_{tree}=(\textsf {psk},\textsf {ssk}_{v_0})\).
-
1.
Authentication for
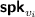 and nodes generation. Choose the leftmost unused node \(N_{v_h}\). For \(i=1,\ldots ,h\), if the related keys associated to the node \(N_{v_i}\) have not been defined, run \(\textsf {SecGen}(\textsf {ppk},\textsf {psk})\) 2d times to generate \((\textsf {spk}_{v_{i-1}||01},\) \(\textsf {ssk}_{v_{i-1}||01}),\) ...,\((\textsf {spk}_{v_{i-1}||0d},\textsf {ssk}_{v_{i-1}||0d})\) and \((\textsf {spk}_{v_{i-1}||11},\textsf {ssk}_{v_{i-1}||11})\), ..., \((\textsf {spk}_{v_{i-1}||1d},\) \(\textsf {ssk}_{v_{i-1}||1d})\), query \(\mathcal {O}_{\widehat{\textsf {TTSig}}}(\cdot )\) with \((\textsf {spk}_{v_{i-1}||01},\ldots , \textsf {spk}_{v_{i-1}||0d})\) and \((\textsf {spk}_{v_{i-1}||11},\ldots ,\) \(\textsf {spk}_{v_{i-1}||1d})\) respectively, and get \((\widehat{\textsf {spk}_{v_{i-1}||0}};\widehat{\sigma _{v_{i-1}||01}}^1,\ldots ,\) \(\widehat{\sigma _{v_{i-1}||0d}}^d)\) and \((\widehat{\textsf {spk}_{v_{i-1}||1}};\) \(\widehat{\sigma _{v_{i-1}||11}}^1,\ldots ,\) \(\widehat{\sigma _{v_{i-1}||1d}}^d)\). Then, \((\textsf {spk}_{v_{i-1}||01},\ldots ,\) \(\textsf {spk}_{v_{i-1}||0d})\) and \((\textsf {spk}_{v_{i-1}||11},\ldots ,\textsf {spk}_{v_{i-1}||1d})\) are assigned to nodes \(N_{v_{i-1}||01},\dots ,\) \(N_{v_{i-1}||0d}\) and \(N_{v_{i-1}||11},\) \(\dots , N_{v_{i-1}||1d}\), respectively. For message \(m^{(j)}\), compute \(\sigma _{v_h} \leftarrow \textsf {TTSign}(\textsf {psk},\textsf {ssk}_{v_h},\) \(m^{(j)})\).
and nodes generation. Choose the leftmost unused node \(N_{v_h}\). For \(i=1,\ldots ,h\), if the related keys associated to the node \(N_{v_i}\) have not been defined, run \(\textsf {SecGen}(\textsf {ppk},\textsf {psk})\) 2d times to generate \((\textsf {spk}_{v_{i-1}||01},\) \(\textsf {ssk}_{v_{i-1}||01}),\) ...,\((\textsf {spk}_{v_{i-1}||0d},\textsf {ssk}_{v_{i-1}||0d})\) and \((\textsf {spk}_{v_{i-1}||11},\textsf {ssk}_{v_{i-1}||11})\), ..., \((\textsf {spk}_{v_{i-1}||1d},\) \(\textsf {ssk}_{v_{i-1}||1d})\), query \(\mathcal {O}_{\widehat{\textsf {TTSig}}}(\cdot )\) with \((\textsf {spk}_{v_{i-1}||01},\ldots , \textsf {spk}_{v_{i-1}||0d})\) and \((\textsf {spk}_{v_{i-1}||11},\ldots ,\) \(\textsf {spk}_{v_{i-1}||1d})\) respectively, and get \((\widehat{\textsf {spk}_{v_{i-1}||0}};\widehat{\sigma _{v_{i-1}||01}}^1,\ldots ,\) \(\widehat{\sigma _{v_{i-1}||0d}}^d)\) and \((\widehat{\textsf {spk}_{v_{i-1}||1}};\) \(\widehat{\sigma _{v_{i-1}||11}}^1,\ldots ,\) \(\widehat{\sigma _{v_{i-1}||1d}}^d)\). Then, \((\textsf {spk}_{v_{i-1}||01},\ldots ,\) \(\textsf {spk}_{v_{i-1}||0d})\) and \((\textsf {spk}_{v_{i-1}||11},\ldots ,\textsf {spk}_{v_{i-1}||1d})\) are assigned to nodes \(N_{v_{i-1}||01},\dots ,\) \(N_{v_{i-1}||0d}\) and \(N_{v_{i-1}||11},\) \(\dots , N_{v_{i-1}||1d}\), respectively. For message \(m^{(j)}\), compute \(\sigma _{v_h} \leftarrow \textsf {TTSign}(\textsf {psk},\textsf {ssk}_{v_h},\) \(m^{(j)})\). -
2.
Authentication for
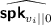 and
and  . For \(i=0,1,\ldots ,h-1\), if \(\widehat{\textsf {spk}_{v_i||0}}\) and \(\widehat{\textsf {spk}_{v_i||1}}\) has not been authenticated, compute \(\sigma _{v_i} \leftarrow \textsf {TTSign}(\textsf {psk},\) \(\textsf {ssk}_{v_i},\) \(\widehat{\textsf {spk}_{v_i||0}}||\widehat{\textsf {spk}_{v_i||1}}||\widehat{\textsf {ppk}})\).
. For \(i=0,1,\ldots ,h-1\), if \(\widehat{\textsf {spk}_{v_i||0}}\) and \(\widehat{\textsf {spk}_{v_i||1}}\) has not been authenticated, compute \(\sigma _{v_i} \leftarrow \textsf {TTSign}(\textsf {psk},\) \(\textsf {ssk}_{v_i},\) \(\widehat{\textsf {spk}_{v_i||0}}||\widehat{\textsf {spk}_{v_i||1}}||\widehat{\textsf {ppk}})\).
So the signature \(\sigma ^{(j)}\) on message \(m^{(j)}\) can be generated for \(j=1,\dots ,q\). Note that, for simplicity, we denote \(\widehat{\sigma _{v_i}}\) as the corresponding signature of \(N_{v_i}\), where \(v_i=v_{i-1}||\beta _{i-1}j_{i-1}\). \(\hat{\mathcal {B}}\) returns \(\textsf {vk}_{tree}=(\textsf {ppk},\textsf {spk}_{v_0})\) and \((\sigma ^{(1)},\ldots ,\sigma ^{(q)})\) to \(\mathcal {A}\).
Finally, \(\mathcal {A}\) outputs a forgery \((m^*,\sigma ^{(*)})\). Suppose \(\delta \) is the largest index such that \(\textsf {spk}_{v_\delta ^{(*)}}=\textsf {spk}_{v_\delta ^{(i)}}\) for some \(i\in \{1,\dots ,q\}\). \(\hat{\mathcal {B}}\) outputs \((\textsf {spk}_{v_{\delta +1}^{(*)}},\widehat{\sigma _{v_\delta ||\beta _{\delta }^{(*)}}}, i_{v_\delta ||\beta _{\delta }^{(*)}},\) \(j_{\delta }^{(*)})\) if either one of the following conditions holds:
-
\((\beta _{\delta }^{(*)}\ne \beta _{\delta }^{(i)})\wedge (\widehat{\textsf {spk}_{v_\delta || \beta _{\delta }^{(*)}}}= \widehat{\textsf {spk}_{v_\delta || (\beta _{\delta }^{(i)}\oplus 1)}})\),
-
\((\beta _{\delta }^{(*)}= \beta _{\delta }^{(i)}) \wedge (\widehat{\textsf {spk}_{v_\delta || \beta _{\delta }^{(*)}}}= \widehat{\textsf {spk}_{v_\delta || \beta _{\delta }^{(i)}}})\),
where \(i_{v_\delta ||\beta _{\delta }^{(*)}}\) denotes the \(i_{v_\delta ||\beta _{\delta }^{(*)}}\)-th query to \(\mathcal {O}_{\widehat{\textsf {TTSig}}}\) and corresponds to \(\widehat{\textsf {spk}_{v_\delta ||\beta _{\delta }^{(*)}}}\). Otherwise, \(\hat{\mathcal {B}}\) aborts. Note that the above conditions correspond to the event Bad. Since \(\hat{\mathcal {B}}\) perfectly simulates Exp\(_{\textsf {TreeSig},\mathcal {A},q_{\textsf {Tree}}}^{\textsf {EUF-NCMA}}(\lambda )\), we have
where \(q_{\textsf {Tree}}=q\). By (8) and (9), we have \(\epsilon _{\textsf {Tree}}\le \epsilon _{\textsf {TTSig}}+\epsilon _{\widehat{\textsf {TTSig}}}\). Since \(\mathcal {B}\) has to make at most \(h+1\) queries to \(\mathcal {O}_{\textsf {TTSig}}(\cdot )\) for each \(m^{(j)}\), we have \(t_{\textsf {Tree}}= t_{\textsf {TTSig}}-O(hq_{\textsf {Tree}})\), \(q_{\textsf {Tree}}\le q_{\textsf {TTSig}}\). Similarly, for the construction of \(\hat{\mathcal {B}}\), \(t_{\textsf {Tree}}= t_{\widehat{\textsf {TTSig}}}-O(hq_{\textsf {Tree}})\), \(q_{\textsf {Tree}}\le q_{\widehat{\textsf {TTSig}}}\). Therefore, \(t_{\textsf {Tree}}=\max \{ t_{\textsf {TTSig}},t_{\widehat{\textsf {TTSig}}}\}-O(hq_{\textsf {Tree}})\) and \(q_{\textsf {Tree}}\le \max \{q_{\textsf {TTSig}},q_{\widehat{\textsf {TTSig}}}\}\).
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Wei, P., Wang, W., Zhu, B., Yiu, S.M. (2017). Tightly-Secure Encryption in the Multi-user, Multi-challenge Setting with Improved Efficiency. In: Pieprzyk, J., Suriadi, S. (eds) Information Security and Privacy. ACISP 2017. Lecture Notes in Computer Science(), vol 10342. Springer, Cham. https://doi.org/10.1007/978-3-319-60055-0_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-60055-0_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-60054-3
Online ISBN: 978-3-319-60055-0
eBook Packages: Computer ScienceComputer Science (R0)



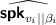 and nodes generation. Choose the leftmost unused leaf
and nodes generation. Choose the leftmost unused leaf 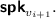 For
For 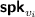 and nodes generation. Choose the leftmost unused node
and nodes generation. Choose the leftmost unused node 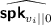 and
and  . For
. For