Abstract
As was mentioned before, we do not know what quantum gravity is. In this final chapter we will explain why it is so difficult to quantize it. Then I will say what most people now think about the directions where the solution to this hard problem should be sought and finally abuse your patience by sharing with you my own heretical and irresponsible guesses.
Notes
- 1.
It was introduced into quantum field theories in 1971 by Kenneth Wilson.
- 2.
In real QCD chiral-symmetry applications, the coefficients \(\sigma _{1,2}\) can be determined phenomenologically. Then loop calculations for not too large energies become possible. The corresponding technique was developed by Jürg Gasser and Heinrich Leutwyler in 1984.
- 3.
One can also write down the invariant \(R_{\mu \nu \alpha \beta } R^{\mu \nu \alpha \beta }\), but it is not independent. One can show that
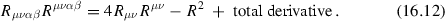
This is the so-called Gauss–Bonnet identity .
- 4.
It is the bispinor (9.40) with \(\xi \equiv \eta \).
- 5.
We managed to get along without defining \( \mathcal{D}_\mu \) in the previous classical chapter. In principle we need to define it now, and not only when it acts on the vectors and tensors, but also for the spinors, explaining why the spin connection \(\omega _\rho ^{ab}\) entering \(\mathcal{D}_\rho \psi _\sigma \) depends in this case not only on the vierbein field \(e^a_\mu \), but also on \(\psi _\mu \) (this brings about the term \({\sim }\psi ^4\) in the Lagrangian). However, I shall conceal from the reader all these important details.
- 6.
That was confirmed by explicit calculations. One does see logarithmic divergences in the 3-loop scattering amplitudes in the theory (16.14).
- 7.
The corresponding counterterm of canonical dimension \(d=18\) was written back in 1981 by Renata Kallosh and independently by Paul Howe and Ulf Lindström.
- 8.
This is especially clear in the path integral approach, see Sect. 8.3.
- 9.
The field is even stronger inside the hole, but whatever is created there cannot escape.
- 10.
\(\xi ^\alpha \) have nothing to do with \(x^\mu \). The latter are the coordinates in flat Minkowski space-time, where the string lives and which theorists call usually the bulk .
- 11.
In fact, string theory was first formulated as one of the phenomenological models describing hadron physics and at that time did not attract so much attention. It was only after the superstring revolution of 1984–1985 that string (or rather superstring) theory began to be considered as a serious candidate for the role of the ToE.
- 12.
An additional important remark is that this accurate quantization cannot be carried out for every bulk. Purely bosonic strings can only be embedded in 26-dimensional space-time. Otherwise, certain bad anomalies do not cancel...
- 13.
It belongs to the adjoint representation of SO(25, 1).
- 14.
André Neveu, John Schwarz, Pierre Ramond, Michael Green, Edward Witten, Alexander Polyakov and many others.
- 15.
They carry magnetic charge and are known as ’t Hooft–Polyakov monopoles.
- 16.
The first line in (16.30) represents the left-hand side of the generalized Lagrange equation for a generic function \(L(q, \dot{q}, \ddot{q})\). In our particular case, \(\delta L/\delta \dot{q} = 0\).
- 17.
Mikhail Ostrogradsky showed how to derive Hamiltonians for higher-derivative Lagrangian systems back in 1850. He did so in a remarkable paper published in Memoires de l’Académie Impériale des Sciences de St. Pétersbourg, where he in fact derived the Hamiltonian formalism independently of William Hamilton. He applied this method to generic Lagrangians \(L(q_i, \dot{q_i}, \ddot{q_i}, \ldots )\).
This paper did not attract much attention in his time (it was not written in an optimal pedagogical way), but is often cited nowadays. However, the observation that the Hamiltonian functions for higher-derivative systems are not bounded either from below or from above, what is called by many people “Ostrogradsky instability”, belongs not to Ostrogradsky (he only derived general formulas and did not study particular dynamical systems), but to Abraham Pais and George Uhlenbeck, who studied the classical and quantum dynamics of the system (16.29) in a paper published exactly a hundred years after Ostrogradsky’s paper.
- 18.
It is more tricky if \(\Omega _1 = \Omega _2\) — the case that we will not consider here.
- 19.
For any energy E and for any \(\epsilon > 0\), one can find an eigenstate \(|nm\rangle \) with \(|E - E_{nm}| < \epsilon \).
- 20.
An interested reader can consult arXiv:1710.11538 [hep-th] and references therein.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Smilga, A. (2017). Mysterious Quantum Gravity. In: Digestible Quantum Field Theory. Springer, Cham. https://doi.org/10.1007/978-3-319-59922-9_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-59922-9_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-59920-5
Online ISBN: 978-3-319-59922-9
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)