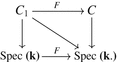Abstract
The aim of this course is to provide an introduction to Mori’s Minimal Model Program (MMP) on smooth projective varieties. We review classical results on Weil and Cartier divisors and define ample and nef divisors. We explain how an asymptotic Riemann–Roch theorem gives a general definition for the intersection number of Cartier divisors. We also go through the construction of the moduli space of morphisms from a fixed curve to a fixed smooth variety, define free curves and uniruled varieties, and state Mori’s bend-and-break lemmas. We finish with a proof of Mori’s cone theorem for smooth projective varieties and explain the basic steps of the MMP.

Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The definitions can be given for any scheme, but they take a slightly more complicated form.
- 2.
This is because in a unique factorization domain, prime ideals of height 1 are principal.
- 3.
Let i be the inclusion of D in X. Since this is an exact sequence of sheaves on X, the sheaf on the right should be \(i_{{\ast}}\mathcal{O}_{D}\) (a sheaf on X with support on D). However, it is customary to drop i ∗. Note that as far as cohomology calculations are concerned, this does not make any difference [8, Lemma III.2.10].
- 4.
If \(s \in H^{0}(X,\mathcal{L})\), the subset \(X_{s} =\{ x \in X\mid \mathsf{ev}_{x}(s)\neq 0\}\) is open. A family (s i ) i ∈ I of sections generates \(\mathcal{L}\) if and only if \(X =\bigcup _{i\in I}X_{s_{i}}\). If X is noetherian and \(\mathcal{L}\) is globally generated, it is generated by finitely many global sections.
- 5.
This is the traditional notation for the tensor product \(\mathcal{F} \otimes \mathcal{O}_{\mathbf{P}_{\mathbf{k}}^{n}}(m)\), which is also the same as \(\mathcal{F}(mH)\).
- 6.
The very important fact that a projective morphism with finite fibers is finite is deduced in [8] from the difficult Main Theorem of Zariski. In our case, it can also be proved in an elementary fashion.
- 7.
This should really be called the Hirzebruch–Riemann–Roch theorem (or a (very) particular case of it). The original Riemann–Roch theorem is our Theorem 2.39 with the dimension of \(H^{1}(X,\mathcal{L})\) replaced with that of its Serre-dual \(H^{0}(X,\omega _{X} \otimes \mathcal{L}^{-1})\).
- 8.
This acronym comes from “numerically effective,” or “numerically eventually free” (according to [17, D.1.3]).
- 9.
The number \(\deg (\pi )\) is the degree of the field extension π∗: K(X) ↪ K(Y ) if this extension is finite, and 0 otherwise.
- 10.
For any affine open subset U ⊂ Y, the ring extension \(H^{0}(U,\mathcal{O}_{Y }) \subset H^{0}(U,\pi _{{\ast}}\mathcal{O}_{X})\) is finite because π is projective and the quotient fields are the same because k(Y ) = k(X). Since \(H^{0}(U,\mathcal{O}_{Y })\) is integrally closed in k(Y ), these rings are the same.
- 11.
In general, one needs to require that the generic fiber of π be geometrically integral. In positive characteristic, u might very well be a bijection without being an isomorphism (even if Y is normal: think of the Frobenius morphism).
- 12.
In particular, a sufficient (but not necessary!) condition for \(\mathop{\mathrm{Mor}}\nolimits (C,X)\) to be smooth at [ρ] is H 1(C, ρ ∗ T X ) = 0.
- 13.
We are using here a generalization of Theorem 2.39 to locally free sheaves of any rank.
- 14.
When X is only quasi-projective, embed it into some projective variety \(\overline{X}\). There is an evaluation morphism
$$\displaystyle{\mathsf{ev}: \mathbf{P}_{\mathbf{k}}^{1} \times \mathop{\mathrm{Mor}}\nolimits (\mathbf{P}_{\mathbf{ k}}^{1},\overline{X})\longrightarrow \overline{X}}$$and \(\mathop{\mathrm{Mor}}\nolimits (\mathbf{P}_{\mathbf{k}}^{1},X)\) is the complement in \(\mathop{\mathrm{Mor}}\nolimits (\mathbf{P}_{\mathbf{k}}^{1},\overline{X})\) of the image by the (proper) second projection of the closed subscheme \(\mathsf{ev}^{-1}(\overline{X}\setminus X)\).
- 15.
This is automatic if dim(M) = dim(X) − 1 and we can always reduce to that case, but the seemingly more general definition we gave is more flexible.
- 16.
If F: k → k is the Frobenius morphism, the k-scheme C 1 fits into the Cartesian diagram
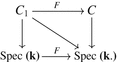
In other words, C 1 is the scheme C, but k acts on \(\mathcal{O}_{C_{1}}\) via pth powers.
- 17.
This ring was Z in the brief description of the proof before the statement of the theorem.
- 18.
A constructible subset is a finite union of locally closed subsets.
- 19.
The “universal” bound on the degree of the rational curve is essential for the proof.
For those who know some elementary logic, the statement that there exists a rational curve of (−K X )-degree at most some constant on a projective Fano variety X is a first-order statement, so the Lefschetz principle tells us that if it is valid on all algebraically closed fields of positive characteristics, it is valid over all algebraically closed fields.
- 20.
To be consistent with our previous definition of “curve on X”, we should perhaps say instead that C is a smooth projective curve with a morphism C → X which is birational onto its image.
- 21.
For once, we follow Grothendieck’s notation: for a locally free sheaf \(\mathcal{E}\), the projectivization \(\mathbf{P}(\mathcal{E})\) is the space of hyperplanes in the fibers of \(\mathcal{E}\).
- 22.
This situation is very subtle: although the completion of the local ring \(\mathcal{O}_{Y,q}\) is not factorial (it is isomorphic to k[[x, y, z, u]]∕(xy − zu), and the equality xy = zu is a decomposition into a product of irreducibles in two different ways) the fact that L 1 is numerically equivalent to L 2 implies that the ring \(\mathcal{O}_{Y,q}\) is factorial (see [16, (3.31)]).
- 23.
This is the case for any desingularization of the quotient X of an abelian variety of dimension 3 by the involution x ↦ − x [18, 16.17]; a minimal model here is X itself, but it is singular.
References
C. Birkar, Existence of flips and minimal models for 3-folds in char p. Ann. Sci. Éc. Norm. Supér. 49, 169–212 (2016)
C. Birkar, P. Cascini, C.D. Hacon, J.M. McKernan, Existence of minimal models for varieties of log general type. J. Am. Math. Soc. 23, 405–468 (2010)
O. Debarre, Higher-Dimensional Algebraic Geometry. Universitext (Springer, New York, 2001)
S. Druel, Existence de modèles minimaux pour les variétés de type général (d’après Birkar, Cascini, Hacon et McKernan), Séminaire Bourbaki, Exp. 982, 2007/2008. Astérisque 326, 1–38 (2009)
A. Grothendieck, Eléments de géométrie algébrique III, 1. Inst. Hautes Études Sci. Publ. Math. 11 (1966)
A. Grothendieck, Eléments de géométrie algébrique IV, 3. Inst. Hautes Études Sci. Publ. Math. 28 (1966)
A. Grothendieck, Techniques de construction et théorèmes d’existence en géométrie algébrique IV: les schémas de Hilbert, Séminaire Bourbaki. Exp. 221 (1960/61). Astérisque hors série 6, Soc. Math. Fr. (1997)
R. Hartshorne, Algebraic Geometry. Graduate Texts in Mathematics vol. 52 (Springer, New York, 1977)
Y. Kawamata, K. Matsuda, K. Matsuki, Introduction to the minimal model problem, in Algebraic Geometry, Sendai, 1985, ed. by T. Oda. Advanced Studies in Pure Mathematics, vol. 10 (North-Holland, Amsterdam, 1987), pp. 283–360
S. Kleiman, Towards a numerical theory of ampleness. Ann. Math. 84, 293–344 (1966)
J. Kollár, Nonrational hypersurfaces. J. Am. Math. Soc. 8, 241–249 (1995)
J. Kollár, Rational Curves on Algebraic Varieties. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 32 (Springer, Berlin, 1996)
H. Matsumura, Commutative Ring Theory, Cambridge Studies in Advanced Mathematics, 2nd edn., vol. 8 (Cambridge University Press, Cambridge/New York, 1989)
Y. Miyaoka, S. Mori, A numerical criterion for uniruledness. Ann. Math. 124, 65–69 (1986)
S. Mori, Projective manifolds with ample tangent bundles. Ann. Math. 110, 593–606 (1979)
S. Mori, Threefolds whose canonical bundles are not numerically effective. Ann. Math. 116, 133–176 (1982)
M. Reid, Chapters on algebraic surfaces, in Complex Algebraic Geometry (Park City, UT, 1993), IAS/Park City Mathematics Series, vol. 3 (American Mathematical Society, Providence, RI, 1997), pp. 3–159
K. Ueno, Classification Theory of Algebraic Varieties and Compact Complex Spaces. Springer Lecture Notes, vol. 439 (Springer, New York, 1975)
Acknowledgements
These are notes for the five 1-hour lectures I gave for the CIMPA-CIMAT-ICTP School “Moduli of Curves,” which took place at the Centro de Investigación en Matemáticas (CIMAT) in Guanajuato, México, 22 February–4 March 2016. I would like to thank the organizers, and especially Leticia Brambila-Paz, for making this event possible in this very warm place and for attracting a great number of students from all over the world.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 The Author(s)
About this chapter
Cite this chapter
Debarre, O. (2017). Higher-Dimensional Varieties. In: Brambila Paz, L., Ciliberto, C., Esteves, E., Melo, M., Voisin, C. (eds) Moduli of Curves. Lecture Notes of the Unione Matematica Italiana, vol 21. Springer, Cham. https://doi.org/10.1007/978-3-319-59486-6_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-59486-6_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-59485-9
Online ISBN: 978-3-319-59486-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)