SVM Kernel Configuration and Optimization for the Handwritten Digit Recognition

Abstract

The paper presents optimization of kernel methods in the task of handwritten digits identification. Because such digits can be written in various ways (depending on the person’s individual characteristics), the task is difficult (subsequent categories often overlap). Therefore, the application of kernel methods, such as SVM (Support Vector Machines), is justified. Experiments consist in implementing multiple kernels and optimizing their parameters. The Monte Carlo method was used to optimize kernel parameters. It turned out to be a simple and fast method, compared to other optimization algorithms. Presented results cover the dependency between the classification accuracy and the type and parameters of selected kernel.

1 Introduction

The automated character recognition is the important part of the content extraction from handwritten documents. Multiple approaches were applied to this task so far. Many of them belong to the Artificial Intelligence (AI) domain. Advancement in computer technologies allows for introducing more computationally demanding approaches to the problem, being the sub domain of the pattern recognition methodology. Methods applied there include statistical approaches and Artificial Neural Networks (ANN) (see Ref. [19]). Because the particular characters are written differently by various people, any AI method should consider the uncertainty (various handwriting characteristics, noise, etc.). This way Support Vector Machines (SVM) (see Ref. [1]) or Fuzzy Logic (FL) (see Ref. [9]) gain importance. Both are considered as theoretically optimal classifiers in the uncertainty conditions. However, only the former approach is able to automatically learn from the available data sets. Therefore, it is often applied to the image and speech recognition (see Ref. [10]), or in the diagnostics of analog systems (see Ref. [5]).

The paper presents kernel-based learning methods used to the handwritten digits recognition. As the classifier, SVM were applied. The presented problem is the classical pattern recognition task, aiming at categorizing objects of different types. In the presented research handwritten digits are analyzed and identified. As the same digit is written differently by various people (may be bolder or thicker, askew, etc.), the task requires sophisticated approaches for data processing. To correctly apply SVM to the task, the proper kernel with adjusted parameters must be used. Despite numerous approaches, this problem still is challenging for researchers. In this paper the systematic overview of kernel functions implementation (with optimized parameters) for the SVM classifier is performed.

The structure of the paper is as follows. Section 2 contains the problem statement and related work. Application of SVM to the classification of digits is described in Sect. 3. Section 4 contains experimental results, in which comparison of SVM kernels for classification is demonstrated, and where influence of the regularization coefficient on the classification accuracy are verified. Conclusions and directions for further research are presented in Sect. 5.

2 Problem Statement and Related Work

The handwritten digit recognition (Fig. 1) is a difficult task and attempts to solve it have been made since the seventies of the last century. The importance of the task is related with the writer identification, automated extraction of information from scanned papers and other applications.

Fig. 1.

Digits to recognize (see Ref. [10]).

Details of the considered problem are as follows:

In the text present on the scanned sheet of paper, analyzed characters are located. The task is to distinguish digits from all other symbols (including noisy components) and subsequently identify particular digits with the minimum sample error, defined as the percentage of incorrectly classified objects. In the numerical approach, the identification task requires introducing the separating hyperplane with the minimal error. As the subsequent digits may be similar to each other, their categories overlap, making flawless separation impossible. Formally, the following target function is to be minimized:

$$\begin{aligned} f( \varepsilon , w )=\frac{1}{2} \left\| w \right\| ^{2} + C \sum _{i=1}^{n} \varepsilon _{i}, \end{aligned}$$

where:

$\varepsilon _{i}$- elements on the incorrect half of the separating hyperplane,

C- regularization coefficient,

w- the SVM weights vector. They must be adjusted so the error is minimal.

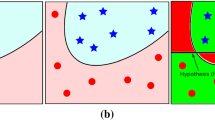
In such a case approaches considering the separation margin (with two weights of support vectors $w_1$ and $w_2$ in Fig. 2) are preferred.

Fig. 2.

Feature space with the margin of error (see Ref. [10]).

The problem of the handwritten digits recognition has been extensively studied during the last few years, leading to more or less successful solutions. Methods used for this purpose belong to both image recognition and artificial intelligence domains (see Ref. [7] ). To solve the task, three steps must be performed, all influencing the classification accuracy. These are selection of features, selection of the classifier and its optimization. The first problem leads to multiple sets of characteristic values describing the image, starting from pixel maps (see Ref. [20]) through the block wise histograms of local digit orientations (see Ref. [17]) and histogram-oriented gradients (see Ref. [8]), up to Freeman codes (see Ref. [3]), Zernike moments, Fourier descriptors or Karhunen-Loeve features (see Ref. [6]). The classifiers applied involve in most cases various types of Artificial Neural Networks (ANN), such as Multilayered Perceptron (MLP) (see Ref. [18]). Other approaches include the Random Forest (RF) (see Ref. [4]) or linear classifiers (see Ref. [16]).

Because of popularity and confirmed efficiency of SVM, they were used in the presented work. The main challenges involving their exploitation to the presented task are the classifier’s optimization and its adjustment to available data to maximize the accuracy. To solve the problem, the proper kernel must be selected and its parameters adjusted. Presented works are usually based on the typical SVM kernels: Radial Basis Function (RBF), polynomial, linear and sigmoidal (see Ref. [8]). Additionally, minimum kernel was used (see Ref. [17]). In (Ref. [15]) the intersection kernel was introduced. Selection of kernel parameters often involves the designer$'$s experience. Alternatively, optimization methods are used, such as simulated annealing (see Ref. [5]), Genetic Algorithm (GA) (see Ref. [11]) or Particle Swarm Optimization (PSO) (see Ref. [2]). Although ready-made solutions for particular problems are available, the procedures have to be repeated for every new analyzed object. This justifies searching for novel algorithms and their configuration. In the following work the original approach to the classifier optimization is presented. First, the wide set of kernels is applied, including multiple functions ensuring the potentially high accuracy of SVM. Secondly, the Monte Carlo stochastic search is used to select kernel parameters. This approach is simple compared to currently applied algorithms, hopefully giving comparable results with smaller computational effort.

3 Application of SVM to the Classification of Digits

The SVM classifier is a useful tool for solving difficult real-world problems, performing well in uncertainty conditions (such as noise and inseparable examples belonging to different categories). This is a classical extension of neural networks, robust to noise and uncertainty in data. Its application requires solving multiple configuration problems, such as selection of the proper kernel and setting its parameters (depending on the particular kernel type). Although in the literature this problem was widely considered, there was no thorough investigation conducted for the handwritten digit recognition. This section contains information about SVM details required for the optimization of the identification process.

3.1 Description of Applied Kernels

In most computing environments (such as Matlab) and programming languages (such as Java), the SVM toolbox or library is present. It usually contains a couple of the most popular kernels (such as linear, RBF and polynomial), which proven their usefulness in multiple applications. Because many other functions can be used for this purpose, it is reasonable to apply them as well, in hope of increasing the classification accuracy. This section introduces all implemented functions with their parameters.

The introduced kernels (see Ref. [12]) were tested on both synthetic and real-world data sets. The first one is related with the binary XOR problem, while the second one consists of features extracted from optically scanned digits. This way it is twice verified if selected functions are capable of solving the linearly non-separable problem.

The exploited real-world set contains ten thousand examples, each with 76 attributes. Original data vectors contained 171 attributes, extracted from the black-and-white picture. They were first preprocessed to eliminate quasi-stationary features (i.e. the ones with the smallest variance). Then, 50 percent of remaining attributes were eliminated, giving 76 attributes processed by classifiers.

Mathematical description of kernels uses the following notation:

$\left\langle x,y \right\rangle =x^{T}y$ - scalar product,

$\left| x - y \right| =\sum _{i=1}^{n} \left| x_{i}-y_{i} \right|$ - the first norm,

$\left\| x - y \right\| ^{2}= \sum _{i=1}^{n} \left| x_{i}-y_{i}\right| ^{2}$ - the second norm squared,

$\left\| x - y \right\| ^{d}= \sum _{i=1}^{n} \left| x_{i}-y_{i}\right| ^{d}$ - d norm to the power d.

The standard kernels widely used were tested:

• Linear - the simplest one with small computational requirements, not ensuring linear separability of objects in the original feature space. It is not parametrized.

  $$\begin{aligned} K(x,y)= \left\langle x,y \right\rangle +c \end{aligned}$$

  (1)

• Radial basis function (RBF), being the fundamental positive-valued kernel, used because of usually high classification scores. Its parameter is the width of the Gaussian curve $\gamma$.

  $$\begin{aligned} K(x,y) = exp\left( - \gamma \left\| x - y \right\| ^{2} \right) \end{aligned}$$

  (2)

• Polynomial kernel is preferred for problems with normalized data. Its parameter is the polynomial degree d.

  $$\begin{aligned} K(x,y)= \left( \gamma \left\langle x,y \right\rangle +c \right) ^{d} \end{aligned}$$

  (3)

• The hyperbolic tangent (sigmoid) is applied as the activation function of ANN. The SVM with such a function is expected to have at least comparable (if not better) classification accuracy. Its parameter is the steepness of the curve $\gamma$.

  $$\begin{aligned} K(x,y)= tanh \left( \gamma \left\langle x,y \right\rangle +c \right) \end{aligned}$$

  (4)

The calibration coefficient c determines the position of the kernel function in the feature space. It is initially set to 0.

Additional kernels were considered in experiments. Although they are well-known, their usefulness for the handwritten digit recognition was not verified so far. They are the following:

• The Laplacian kernel

  $$\begin{aligned} K(x,y) = exp\left( - \gamma \left| x - y \right| \right) \end{aligned}$$

  (5)

  is equivalent to the exponential one $K(x,y) = exp\left( - \frac{\left| x - y \right| }{2 \gamma ^{2}} \right) ,$ but is less susceptible to changes of the $\gamma$ parameter.

• The sinc wave kernel (sinc) is symmetric and non-negative.

  $$\begin{aligned} K(x,y)= sinc\left| x - y \right| =\frac{sin\left| x - y \right| }{\left| x - y \right| } \end{aligned}$$

  (6)

• The sinc2 kernel has characteristics similar to sinc.

  $$\begin{aligned} K(x,y)= sinc\left\| x - y \right\| ^{2}=\frac{sin\left\| x - y \right\| ^{2}}{\left\| x - y \right\| ^{2}} \end{aligned}$$

  (7)

• The quadratic kernel is less computationally costly than the Gaussian one and should be applied when the training time is significant.

  $$\begin{aligned} K(x,y)= 1-\frac{\left\| x - y \right\| ^{2}}{\left\| x - y \right\| ^{2} + c} \end{aligned}$$

  (8)

• The non-positive and definite multiquadratic kernel is applied in the same fields as the quadratic one.

  $$\begin{aligned} K(x,y)= -\sqrt{ \left\| x - y \right\| ^{2} +c^{2}} \end{aligned}$$

  (9)

• The inverse multiquadric kernel.

  $$\begin{aligned} K(x,y)=\frac{1}{\sqrt{ \left\| x - y \right\| ^{2} +c^{2}}} \end{aligned}$$

  (10)

• The log kernel is conditionally positive definite.

  $$\begin{aligned} K(x,y)= -log \left( \left\| x - y \right\| ^{d} +1 \right) \end{aligned}$$

  (11)

• The Cauchy kernel comes from the Cauchy distribution. It can be used in the analysis of multidimensional spaces.

  $$\begin{aligned} K(x,y)= \frac{1}{1+\frac{\left\| x - y \right\| ^{2} }{c^{2}}} \end{aligned}$$

  (12)

• The generalized T-Student kernel has a positive semi-definite kernel matrix.

  $$\begin{aligned} K(x,y)= \frac{1}{1+ \left\| x - y \right\| ^{d}} \end{aligned}$$

  (13)

4 Experimental Results

The experiments consisted in training and testing the SVM with the selected kernel on the synthetic and real-world data. Parameters of each kernel were optimized to maximize the object classification accuracy. In the handwritten digit recognition task experiments were divided into two steps: optimization of kernel parameter with the constant regularization coefficient and optimization of the regularization coefficient for the optimal (previously determined) value parameter. Also, the real-world data (further called original set) was disturbed randomly to obtain object more difficult to identify (further called modified set). The data set was divided into the training L and testing T one in the 7:3 ratio. The division process was repeated ten times to ensure objectivity of the obtained results.

Processing of the XOR problem set was successful for most kernels. However, the ‘minimum’ $K(x,y)=\sum _{i=1}^{n} min(x_{i}, y_{i})$ and the ‘power’ $K(x,y)= - \left\| x - y \right\| ^{d}$ kernels failed to satisfactorily learn on this set. Below experimental results are presented.

4.1 Digit Identification

In Table 1, optimal results of the original data identification for the applied kernels are shown. All experiments were conducted for the constant regularization coefficient ($C=16$). The column v represents the number of generated support vectors, $a_{L}$ is the classification accuracy for the training set, while $a_{T}$ is the accuracy on the testing set.

Table 1. Classification efficiency comparison between optimal kernel parameters.

Rows in bold refer to kernel configurations giving better classification results than the reference RBF kernel. Large number of support vectors suggests overlearning, which is confirmed by the low classification score for the testing set T. In such a situation the SVM efficiency for the training set is high (usually close to 100 percents), but performance on the testing set is much lower. The Gaussian function with the $\gamma =\frac{1}{n}$ is the best of all standard function. However, the Laplacian kernel with the $\gamma =0.01$ coefficient outperforms it, which justifies its usage. In general, smaller values of kernel parameters usually give better classification results. This is because the separating hyperplane is relatively simple and has better generalization abilities.

Random modification of the original data set consisted in disturbing the selected number of features. Each one was changed by adding the value up to $\pm 10$ percent of the original value. The process was repeated for three, ten, twenty and all 76 features, obtaining four versions of the modified set, respectively $T_{3}$, $T_{10}$, $T_{20}$ and $T_{76}$. In Table 2 results of classification for different kernels (with optimized parameters) on the modified set are presented.

Table 2. Comparison of optimal kernel configurations efficiency to modified data sets.

Change in three randomly selected attributes in general does not influence the classification accuracy. The SVM is able to select other features, for which distinguishing between digits is still possible. Classification results are then identical as for original sets. Again, the Laplacian kernel (with $\gamma =0.01$) is globally the best for modified data sets. On the other hand, the sigmoidal kernel has the lowest accuracy. Results for the minimum and power kernels are identical, regardless of the applied data sets. The same is for the quadratic (with c = 100) and Cauchy (with c = 10) kernels.

In most of kernel functions, disturbance in the attributes’ values decreases the classification accuracy. On the other hand, in some cases (like sinc and sinc2 kernels) the operation slightly increases the classification accuracy. For the sigmoidal function, the classification accuracy remains unchanged (and still too low to be considered in practice).

4.2 Influence of the Regularization Coefficient on the Classification Accuracy

In this experiment, we checked the relation between the penalty parameter C and the error term, and how the regularization coefficient influences results. The selected values were used to measure the influence of C on the digit classification accuracy. Measurements were conducted for $C=5,10,15,16,17,20,30$. In Table 3 results of the classification for different kernels (with optimized parameters) for the regularization coefficient $C=10$ are presented.

Table 3. Classification efficiency comparison for parameters C.

For the majority of kernels (without linear and inversemultiquadric kernels) the regularization coefficient $C=10$ leads to the best results of classification. However, the original value (i.e. $C=16$) gives the multiquadratic kernel advantage over the RBF. Again, results for the minimum and power kernels are identical, regardless the regularization coefficient. The same is for the quadratic and Cauchy kernels. For all cases, the regularization coefficient C, the Laplacian kernel (with $\gamma =0.01$) is globally the best. It is the most likely related with dimensions of feature space after the kernel transformation. In the case when the same results were obtained by two different kernels (for instance, minimum and power with d = 1, or quadratic with c = 100 and Cauchy for c = 10), the transformation is virtually identical. For some kernels (sigmoidal, sinc, sinc2, log, tstudent, power, minimum) the regularization coefficient C did not influence results of classification (for all values of C, identical outcomes were obtained).

4.3 Optimization of Kernels’ Parameters

The standard operation during the classifier configuration is the kernel parameters’ configuration. Multiple heuristic algorithms exist, useful for this purpose (see Refs. [13, 14]).

Firstly, we chose parameters of all kernels intuitively. The obtained results are in Tables 4 and 5.

Table 4. Results of the SVM classification for various configurations of the rbf kernel.

Table 5. Results of the SVM classification for various configurations of the Laplacian kernel.

Fig. 3.

Results of the SVM classification for various configurations of the Laplacian kernel and the RBF kernel.

Secondly, in the presented research the relatively simple Monte Carlo approach was exploited. It consists in the repeated random selection of values from the predefined range according to the selected probability distribution. This approach is effective for optimization of the single parameter, faster than, for instance, simulated annealing of the evolutionary algorithm. Kernel parameters were selected according to the uniform distribution and the range of values adjusted for each kernel individually. The optimization was implemented with the constant value of the regularization coefficient ($C=16$). The obtained results for kernels with similar ranges of the parameter (i.e. RBF and Laplacian) are presented in Fig. 3. In both cases, similar behavior of the function for changed values can be observed. The Laplacian kernel is better in the whole range, its maximal classification outcome was obtained for the $\gamma =0.01$ coefficient.

5 Conclusions

The paper presented application of the SVM classifier tree to the identification of the handwritten digits in the presence of noise. The standard configuration of the multi-class SVM classifier was used for the task of the digit identification. Experiments with multiple kernels showed that although the most popular Gaussian function performs properly, other choices, such as the Laplacian kernel may perform even better. The processed data sets are easy to classify, as the performance of SVM for most kernels is above 90 percent. The best outcomes were obtained for kernel parameters selected according to the Monte Carlo approach. It gives comparable results to other methods, such as the simulated annealing (see Ref. [5]) or the evolutionary approach), presenting greater simplicity. The disadvantage of the presented approach is overlearning, observed for most kernels. This is the effect of excessive adjusting the classifier to the training data, leading to the low generalization ability. Future research require introducing more real-world data to verify the SVM performance against samples of digits produced by various groups of people (children, disabled, etc.). The amount of available data for the classifier training influences its efficiency. The open question is, what is the minimal amount of training samples, ensuring the maximum classification accuracy. Also, implementation of additional kernels for the symbol classification would be advisable.