Abstract
We consider the Newtonian paradigm of physics: its laws and in particular the status of time, space and frames therein. These conform to many ‘everyday intuitions’ about time and space, which, however, do not however apply in subsequent chapters’ quantum, special relativity and especially general relativity paradigms. For now, we consider some differences between Newton, Galileo and Aristotle’s world-views, and also the forms taken by various force laws in the Newtonian paradigm. We finally outline two tools: tensors and the principles of dynamics; these tools are very useful including through variants of these transcending to special and general relativity.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
This book capitalizes subject areas, specific laws of nature, specific theorems, lemmas and similar, specific principles, and the names of the Problem of Time facets, underlying Background Independence aspects and strategies for resolving these which form the main topic of this book. This is used to keep track of which phrasings refer to specific concepts that have already been introduced in the book, rather than being merely colloquial uses of the words in question.
- 2.
Calculus was also founded by Newton, and concurrently by Leibniz. However, in the great treatise Principia Mathematica [676], Newton himself proved each Mechanics proposition by pictorially laid out rigorous Euclidean Geometry (including use of limiting processes).
- 3.
Let us use \(I\)-indices to run over particle labels, currently 1 and 2, and \(\underline{\mbox{r}}_{IJ} := \underline{x}_{I} - \underline{x}_{J}\), and small hats for unit vectors.
- 4.
This contradicts the Aristotelian doctrine that heavy bodies fall faster than lighter ones. On the other hand, another Ancient Greek philosopher—Epicurus—did entertain such a concept [520].
- 5.
Most usually this is \(\mathbb{R}^{3}\), but some issues are sufficiently well-illustrated by ℝ or \(\mathbb{R}^{2}\), and \(\mathbb{R}^{p}\) for \(p > 3\) also enter at the level of configuration space. Moreover, there is no extra complication in treating this in arbitrary dimension.
- 6.
See Appendix A.2 for an outline of Group Theory. \(\mathit{Tr}(p)\) and \(\mathit{Rot}(p)\) are continuous transformations. \(Ref\) are discrete. Let us call \(\mathit{Eucl}(p)\) as defined here the proper alias special Euclidean group, whereas including \(Ref\) would involve a full Euclidean group) ‘Proper’ and ‘special’ are more widely used of cases excluding discrete reflection transformations. See also Appendix B as regards other types of Flat Geometry corresponding to the preservation of other combinations of the previous paragraph’s quantities.
- 7.
My capital sans-serif indices are general indices, many of which are reserved for particular uses in this book. This book also uses bold font for index-free presentations, so e.g. the
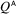 are denoted more succinctly by \(\boldsymbol{Q}\).
are denoted more succinctly by \(\boldsymbol{Q}\).
References
Barbour, J.B.: Absolute or Relative Motion? Vol 1: The Discovery of Dynamics. Cambridge University Press, Cambridge (1989)
Courant, R., Hilbert, D.: Methods of Mathematical Physics, vols. 1 and 2. Wiley, Chichester (1989)
Ehlers, J.: Survey of general relativity theory. In: Israel, W. (ed.) Relativity, Astrophysics and Cosmology. Reidel, Dordrecht (1973)
Jammer, M.: Concepts of Mass in Contemporary Physics and Philosophy. Princeton University Press, Princeton (2000)
Jammer, M.: Concepts of Simultaneity. From Antiquity to Einstein and Beyond. Johns Hopkins University Press, Baltimore (2006)
Lanczos, C.: The Variational Principles of Mechanics. University of Toronto Press, Toronto (1949)
Muga, G., Sala Mayato, R., Egusquiza, I. (eds.): Time in Quantum Mechanics, vol. 1. Springer, Berlin (2008)
Muga, G., Sala Mayato, R., Egusquiza, I. (eds.): Time in Quantum Mechanics, vol. 2. Springer, Berlin (2010)
Newton, I.: Philosophiae Naturalis Principia Mathematica [Mathematical Principles of Natural Philosophy]. (1686); For an English translation, see e.g. Cohen, I.B., Whitman, A.: University of California Press, Berkeley, (1999). In particular, see the Scholium on Time, Place, Space and Motion therein
Stewart, J.M.: Advanced General Relativity. Cambridge University Press, Cambridge (1991)
Taylor, E.F., Wheeler, J.A.: Spacetime Physics. Freeman, San Francisco (1966)
Will, S.C.M.: The confrontation between general relativity and experiment. Living Rev. Relativ. 17, 4 (2014). arXiv:1403.7377
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Anderson, E. (2017). Time, Space and Laws in Newtonian Mechanics. In: The Problem of Time. Fundamental Theories of Physics, vol 190. Springer, Cham. https://doi.org/10.1007/978-3-319-58848-3_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-58848-3_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-58846-9
Online ISBN: 978-3-319-58848-3
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


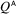 are denoted more succinctly by
are denoted more succinctly by