Some Computational Limits of Trellis Automata

Abstract

We investigate some computational limits of trellis automata. Reusing a counting argument introduced in [4], we show that:

$$\{x_1\dots x_ny_1\dots y_n: x_iy_i\in \{ab,ba,bb\}\;\text { for } i=1,\dots ,n\}$$

is not a trellis language.

1 Introduction

Trellis automata are one of the simplest parallel language recognizer. Introduced by Dyer [3], as real-time one-way bounded cellular automata, they represent a significant class of formal languages with low complexity. Notably, they are equivalent to the linear conjunctive grammars [5]. In spite of their simplicity, they have a rich computational ability and recognize various languages. In this regard, the linear context free, the visible pushdown, the poly-slender context free languages are known to be all recognized by trellis automata [1, 2, 6, 8, 11].

On the other side, some limits are known. Trellis automata are not closed under concatenation and do not contain all (and even deterministic) context-free languages. To support these claims, several languages have been shown not to be trellis languages [8,9,10]:

• the context free language $L_1L_1$ square of $L_1=\{1^k0u10^k:k>0, u\in \{0,1\}^*\}$

• the language $\{uvu:u,v\in \{0,1\}^*, |u|>1\}$,

• the deterministic context free (and LL(1)) language $\{c^ma^{l_0}ba^{l_1}b\cdots a^{l_m}b\cdots a^{l_z}bd^n:m,n,l_i\ge 0,z\ge 1,l_m=n\}$.

The proofs rely on counting arguments which set conditions on the structure of trellis languages.

Here we will reuse another counting argument introduced in [4] in the context of functional computation, which demonstrated that the reverse operation is not realizable in minimal time on cellular automata. This argument will allow to exhibit some new prerequisite for a language to be recognized by trellis automata. As an application, we will prove that the language

$$\{x_1\dots x_ny_1\dots y_n: x_iy_i\in \{ab,ba,bb\}\;\text { for } i=1,\dots ,n\}$$

is not a trellis language.

The paper is organized as follow. Section 2 recalls the basic definitions about trellis automata. Section 3 describes the notion of language factors diagram which can be interpreted as the language counterpart of trellis computation. Section 4 considers the patterns which may occur in the trellis computation and the ones which may occur in the factors diagrams, and also their correlation. Section 5 states a necessary condition regarding the patterns for a language to be recognizable by trellis automata. Section 6 shows that the language $\{x_1\dots x_ny_1\dots y_n: x_iy_i\in \{ab,ba,bb\}\;\text { for } i=1,\dots ,n\}$ does not fulfill such a condition.

2 Trellis Automaton

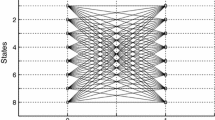
A trellis automaton is one of the simplest parallel language recognizer. Its underlying structure is a triangular array with sites arranged in staggered rows, as shown below.

Formally, a trellis automaton is specified by a tuple $(Q,\varSigma ,Q_{acc},\delta )$ where

• Q is the finite set of states

• $\varSigma \subset Q$ is the input alphabet

• $Q_{acc}\subset Q$ is the set of accepting states

• $\delta :Q^2\rightarrow Q$ is the transition function

If n is the length of w, the trellis has height n and contains on its i-th row, the $n+1-i$ values

$$\delta (x_1\dots x_{i}),\delta (x_2\dots x_{1+i}),\dots ,\delta (x_{n+1-i}\dots x_n)$$

A trellis automaton is said to accept (resp. reject) a word $w\in \varSigma ^*$, if on input w the topmost cell enters an accepting (resp. non-accepting) state.

Definition 1

(Trellis language). A language L over an alphabet $\varSigma$ is a trellis language if there exists some trellis automaton $(Q,\varSigma ,Q_{acc},\delta )$ which accepts exactly the words $w\in L$.

Example 1

The trellis automaton $(\{a,b,c\},\{a,b\},\{a\},\delta )$ accepts the set of strings of odd length whose middle symbol is a: $\mathtt{Mi}_a=\{uav:u,v\in \{a,b\}^*\text { and } |u|=|v|\}$

The accepting state marks the topmost cell of every triangle whose basis is a factor in $\mathtt{Mi}_a$.

Example 2

The trellis automaton $(\{a,b,d,r\},\{a,b\},\{d\},\delta )$ recognizes the set of Dyck words over $\{a,b\}$

The accepting state marks the Dyck words, marks the proper prefixes of Dyck words, marks the proper suffixes of Dyck words, marks all the other words.

A fundamental feature of trellis automata has been noticed by Čulík:

Property 1

(Outside-context independence [1]). The computation of any word contains the computations of all its factors.

As it can be seen in Example 1 or 2, the automaton which tests the input w processes together all its factors.

3 Factors Diagram for a Language

As a matter of fact, Property 1 has strong implications on the structure of languages recognized by trellis automata. To make them explicit, let us first introduce the language counterpart of trellis computation.

Definition 2

(Factors diagram). Let L be a language on an alphabet $\varSigma$.

The indicator function of L, noted $\mathbbm {1}_L$, is defined by

$$\begin{array}{rccl} \mathbbm {1}_L:&{}\varSigma ^* &{} \rightarrow &{} \{0,1\}\\ &{}w &{} \rightarrow &{}\left\{ \begin{array}{ccc} 1 &{} \,\,{if}\,\, &{} w\in L\\ 0 &{} \,\,{if}\,\, &{} w\notin L \end{array}\right. \end{array}$$

Let $w=x_1\dots x_n$ be a word. The factors diagram of w for the language L, denoted $\varGamma _L(w)$, is a triangular array which records the values of all slices of w.

If n is the length of w, the factors diagram has height n and contains on its i-th row, the $n+1-i$ values

$$\mathbbm {1}_L(x_1\dots x_{i}),\mathbbm {1}_L(x_2\dots x_{1+i}),\dots ,\mathbbm {1}_L(x_{n+1-i}\dots x_n)$$

Fig. 1.

Factors diagram $\varGamma _{\mathcal {L}}(w)$ on word $w=aababbabaababb$ for the language $\mathcal {L}$

Example 3

Looking at Examples 1 and 2 where the automata evolutions on the same string are drawn, we observe that the above factors diagrams are simply projections of these automata computations. Indeed, a trellis automaton which recognizes a language L, must enter accepting states exactly on the factors belonging to L.

Fig. 2.

The factors diagram is the projection of the automaton computation

The following proposition formally describes the relationship between automaton evolutions and factors diagrams.

Proposition 1

Let $\mathcal {A}=(Q,\varSigma ,Q_{acc},\delta )$ be any trellis automaton, L be the language accepted by $\mathcal {A}$ and $\mathbbm {1}_{acc}$ be the indicator function of the set of accepting states:

$$\begin{array}{cccl} \mathbbm {1}_{acc}: &{}Q &{}\rightarrow &{}\{0,1\}\\[3pt] &{}q &{} \rightarrow &{}\left\{ \begin{array}{ccc} 1 &{} \,\,if\,\, &{} q\in Q_{acc}\\ 0 &{} \,\,if\,\, &{} q\notin Q_{acc} \end{array}\right. \end{array}$$

For any word $w\in \varSigma ^*$, given its automaton computation $C_{\mathcal {A}}(w)$ and its factors diagram $\varGamma _L(w)$, we have:

$$\mathbbm {1}_{acc}(C_{\mathcal {A}}(w))=\varGamma _L(w)$$

4 Trellis Automaton Patterns and Language Patterns

Therefore, a prerequisite for a language to be a trellis one, is the following. All patterns which occur in the factors diagrams of such a language, must arise in the evolutions of some trellis automaton. Let us focus at the patterns of triangular shape.

Definition 3

(Characteristic pattern). Let L be a language. A characteristic pattern of height h is any triangle of height h extracted from a factors diagram of L.

$P_L(h)$ will refer to the set of all distinct characteristic patterns of height h.

Example 4

Consider $\mathtt{Mi}_a$ the language of strings with a in the middle. The factors diagrams of $\mathtt{Mi}_a$ consist of vertical stripes of only 0 or only 1.

By instance, is a characteristic pattern of height 3, but not

We may describe the automaton patterns in the same way:

Definition 4

(Automaton patterns). Let $\mathcal {A}=(Q,\varSigma ,Q_{acc},\delta )$ be a trellis automaton. An automaton pattern of height h is any triangle of height h extracted from a computation of $\mathcal {A}$.

$P_{\mathcal {A}}(h)$ will refer to the set of all distinct automaton patterns of height h.

However, trellis automata are deterministic local devices. So, for an automata pattern, the bottom row completely determines the subsequent rows. In other words, an automata pattern of height h can be viewed as a row pattern of length h complemented with its consequences.

Example 5

The automaton pattern extracted from the computation of Example 2, is entirely defined by its bottom row (and, of course, by the automaton rules).

As shown earlier in [9], it entails a necessary condition for a language to be recognizable by a trellis automaton, regarding to the number of its characteristic patterns:

Lemma 1

If L is a trellis language then the number of characteristic patterns of height h, $|P_L(h)|$, is in $2^{O(h)}$.

Proof

Assume that L is a language accepted by some trellis automaton $\mathcal {A}=(Q,\varSigma ,Q_{acc},\delta )$. According to Proposition 1, the characteristic patterns match the projection of the automaton patterns: $P_L(h)=\mathbbm {1}_{acc}(P_{\mathcal {A}}(h))$. In terms of cardinal, it means that $|P_L(h)|\le |P_{\mathcal {A}}(h)|$. Moreover, the number of automaton patterns of height h is bounded by the number of distinct rows of length h where values range in Q: $|P_{\mathcal {A}}(h)|\le |Q|^h$.

Now, as the area of a characteristic pattern of height h is in $\varTheta (h^2)$ and its values are 0 or 1, we can find languages whose set of characteristic patterns grows larger than $2^{O(h)}$. Using this counting argument, it has been shown that the following languages are not trellis ones:

• The context-free language $L_1L_1$, square of the linear language $L_1=\{1^k0u10^k:k>0, u\in \{0,1\}^*\}$, since $|P_{L_1L_1}(h)|\in 2^{\varTheta (h^2)}$. See [9].

• The deterministic context-free language (and even LL(1) language) $L=\{c^ma^{l_0}ba^{l_1}b\cdots a^{l_m}b\cdots a^{l_z}bd^n: m,n,z\ge 1, l_i \ge 0, l_m = n\}$, since $|P_L(h) | \in \varOmega (h!)$. See [8].

Of course, this criterion is only a necessary condition and not a sufficient one. Another drawback of this approach is that to estimate the growth rate of the characteristic patterns number of height h as h grows large, is not usually an easy task. By the way, the previous witness languages are ad hoc languages to fulfill the counting requirement. And the status of more common languages remains as yet unknown. Two candidates are currently mentioned:

• The balanced language over $\{a,b\}$ defined as the set of strings with the same number of symbols a and b:

  $$\mathtt{Eq}=\{w\in \{a,b\}^*:\sharp _a(w) = \sharp _b(w)\}$$

• The copy language defined as the set of words repeated twice:

  $$\mathtt{Copy}=\{ww:w\in \{a,b\}^*\}$$

Here we will look at the language $\mathtt{Mi}_a\mathtt{Mi}_a$ and the variant $\mathtt{Mi}_a\mathtt{Mi}_b$ where $\mathtt{Mi}_a$ (resp. $\mathtt{Mi}_b$) stands for the set of odd length words with a (resp. b) in the middle:

$$\mathtt{Mi}_a=\{xay\in \{a,b\}^*: |x|=|y|\}$$

Making use of an approach introduced in [4], we will show that $\mathtt{Mi}_a\mathtt{Mi}_a$ and $\mathtt{Mi}_a\mathtt{Mi}_b$ are not trellis languages. But although they are closely related to the $\mathtt{Copy}$ language and its negative variant:

$$\mathtt{Copy}=(\mathtt{Mi}_a\mathtt{Mi}_b)^\complement \cap (\mathtt{Mi}_b\mathtt{Mi}_a)^\complement \cap \{aa,ab,ba,bb\}^*$$

$$\{w\overline{w}:w\in \{a,b\}^*\}=(\mathtt{Mi}_a\mathtt{Mi}_a)^\complement \cap (\mathtt{Mi}_b\mathtt{Mi}_a)^\complement \cap \{aa,ab,ba,bb\}^*= \mathtt{Eq}\cap (\mathtt{Mi}_a\mathtt{Mi}_a)^\complement $$

it will not allow us to determine whether they are trellis languages or not.

5 Counting Argument

Here we will focus on a subfamily of the characteristic patterns composed of horizontal stripes.

Definition 5

(Stripes patterns). A stripes pattern is a characteristic pattern such that all the values within each row are equal. The characteristic string of a stripes pattern of height h is the binary string $c=c_1\cdots c_h$ of length h where $c_i$ is the 0 or 1 value of the i-th row of the stripes pattern.

An automaton pattern $\pi$ would be said to have a characteristic string c if its projection $\mathbbm {1}_{acc}(\pi )$ is a stripes pattern of characteristic c.

Note that the characteristic string completely characterizes the stripes pattern. And so, whatever the language, the number of its stripes patterns of height h is bounded by $2^h$. Regardless of the fact that the subfamily of stripes patterns is not so large and even within the bound defined in Lemma 1, it has been proved that any trellis automaton could not display all of them:

Proposition 2

(Grandjean, Richard, Terrier [4]). For any trellis automaton $\mathcal {A}$, there exist some stripes patterns which never occur in the space-time diagrams of $\mathcal {A}$.

Along the same lines, Proposition 2 could be refined to deal with languages exhibiting not necessarily all stripes patterns.

Definition 6

For any language L, $\mathcal {C}_L$ will refer to the set of characteristic strings whose corresponding stripes patterns occur in L.

Give, any subset $\mathcal {F}\subset \mathcal {C}_L$, the integer $\alpha _h^{\mathcal {F}}$ will refer to the minimal number of double length extensions of every string of length $2^h$ within $\mathcal {F}$:

$$\alpha _h^{\mathcal {F}}=\min \limits _{c\in \mathcal {F},|c|=2^h}(|\{d\in \mathcal {F}: c \,\, is \,\, a \,\, prefix \,\, of \,\, d \,\, and \,\, |d|=2|c|\}|)$$

Proposition 3

  If L is a language which admits a subset $\mathcal {F}$ of characteristic strings such that the sequence $(\alpha _h^{\mathcal {F}})$ is monotonic and divergent, then L is not a trellis language.

The counting argument used to prove the proposition is based on the next technical fact.

Fact 1

Let $(\alpha _h)$ be any monotonic sequence of positive integers which is divergent: $\alpha _{h+1}\ge \alpha _h$ for all h, and $\lim \limits _{h\rightarrow \infty }\alpha _h\rightarrow \infty$. Let C be any positive constant.

Then the sequence $(u_h)$ defined recursively by:

$$u_0=C\quad \,\, and \,\,\quad u_{h+1}=\frac{u_h^2}{\alpha _h}$$

converges to 0.

Proof

First, observe that

$$u_h=C^{2^h}{/}\prod \limits _{i=0}^{h-1} \alpha _i^{2^{h-i-1}}$$

Second, by assumption, there exists an index H such that $\alpha _h\ge C+1$, for all $h\ge H$. Then for $h\ge H$,

$$u_h\le C^{2^h}{/}\prod \limits _{i=H}^{h-1} (C+1)^{2^{h-i-1}}=C^{2^h}{/}(C+1)^{2^{h-H}}$$

So the sequence $(u_h)$ converges to 0.

Proof

(Proposition 3 ). Assume that L is a language accepted by some trellis automaton $\mathcal {A}=(Q,\varSigma ,Q_{acc},\delta )$. We will construct a sequence of strings $w_i$ of length $2^{i}$ belonging to $\mathcal {F}$ such that the number of automaton patterns with characteristic $w_i$ is bounded by $u_i$. Then, according to Fact 1, we will have $u_I<1$ for I large enough. That means there will be no automaton pattern with characteristic $u_I$ and hence $w_I$ would not be a characteristic string of L. Thus the assumption that L is a trellis language, would lead to a contradiction.

The construction of the sequence of strings $w_i$ is done by recurrence:  

The base case.:

For $i=0$, the automaton patterns of height 1 are reduced to one site and their number is bounded by the cardinal of Q. So there are at most $C = |Q|$ automaton patterns with characteristic string 0 or 1. Let set $w_0$ be a string of length 1 belonging to $\mathcal {F}$ and $u_0$ be |Q|.

The inductive step.:

Consider all automaton patterns of height $2^{i+1}$ having a characteristic string within $\mathcal {F}$ which is a double length extension of $w_i$. As depicted in Fig. 3, we can divide such a kind of pattern in four sub-patterns X, Y, Z and T where X, Y and Z are of height $2^i$ and also where X and Y share the characteristic $w_i$. By recurrence assumption, the number of automaton patterns of characteristic $w_i$ is bounded by $u_i$ and so the number of couples (X, Y) is at most $u_i^2$. Furthermore the sub-patterns Z and T depend only on X and Y. That is to say the number of automaton patterns whose characteristic strings are extensions of $w_i$ is bounded by $u_i^2$. Now, since the minimal number of extensions of $w_i$ within $\mathcal {F}$ is $\alpha _i$, the average number of automaton patterns per extension is bounded by $u_{i+1}=u_i^2/\alpha _i$. In other words, there is one extension $w_{i+1}$ of $w_i$ with length $2^{i+1}$ and belonging to $\mathcal {F}$ such that the number of automaton patterns with characteristic $w_{i+1}$ is bounded by $u_{i+1}$.

 

Fig. 3.

Subdivision of an automaton pattern in four patterns X, Y, Z and T

6 Some Non Trellis Language

Now we will apply the previous criterion to show that the language $\mathtt{NO}_{aa} = \{x_1\dots x_ny_1\dots y_n: x_iy_i\in \{ab,ba,bb\}\;\text { for } i=1,\dots ,n\}\cup \{w\in \{a,b\}^*: w\text { is of odd length}\}$ is not a trellis language. As an aside, notice that $\mathtt{NO}_{aa}$ is not a context-free language although its complement $\mathtt{Mi}_a\mathtt{Mi}_a$ is a context-free one.

As preliminary, let us look at an example. Figure 4 depicts the factors diagram on the input word $^{\omega }bab^{12}abbbabaaabbab^{\omega }$. The dark sites mark the 0 values (i.e., the factors not in $\mathtt{NO}_{aa}$), the light sites mark the 1 values. We observe that the black horizontal stripes in the upper part match the symbols a of the input.

Fig. 4.

The factors diagram on $^{\omega }bab^{12}abbbabaaabbab^{\omega }$ for the language $\mathtt{NO}_{aa}$

More generally, the $\mathtt{NO}_{aa}$ factors diagrams exhibit the following stripes patterns:

Fact 2

For any binary string $c_1c_2\dots c_k$, there exists a stripes pattern of $\mathtt{NO}_{aa}$ with characteristic string $c_11c_21\dots 1c_k1$.

Proof

Given any binary string $c_1c_2\dots c_k$ of length k, we consider the word $w = b^{m+k-1} a b^m x_1\cdots x_kb^{m+k-1}$ where m is any integer greater than k and, the symbols $x_i$ are a if $c_i=0$ and b otherwise. As it is defined, each symbol $x_i$ decides whether the $m+i$ factors with length $2(m+i)$ of $b^{m+i-1} a b^m x_1\cdots x_kb^{m+2i-k-1}$ are all in $\mathtt{NO}_{aa}$ (in case of $x_i=b$) or are all outside of $\mathtt{NO}_{aa}$ (in case of $x_i=a$). Therefore the factors diagram of w contains on its $2(m+i)$-row a sequence of $m+i$ consecutive values $c_i$ and that for all $i=1,\cdots ,k$. Besides, all values of the odd rows are 1 since any odd length factor is in $\mathtt{NO}_{aa}$. At last, choosing m large enough, we can extract from the factors diagram of w a stripes pattern of characteristic $c_11c_21\dots 1c_k1$.

Proposition 4

The language $\mathtt{NO}_{aa} = \{x_1\dots x_ny_1\dots y_n: x_iy_i\in \{ab,ba,bb\}~\text {for } i=1,\dots ,n\}\cup \{w\in \{a,b\}^*: w\text { is of odd length}\}$ is not a trellis language.

Proof

According to Fact 2, every string of $\mathcal {F}=\{01,11\}^*$ is a characteristic string of $\mathtt{NO}_{aa}$. Besides, within $\mathcal {F}$, every string $c_11\dots c_{2^{h-1}}1$ of length $2^h$ is the prefix of $2^{h-1}$ strings of double length: $\{c_11\dots c_{2^{h-1}}1e_11\dots e_{2^{h-1}}1: e_1,\dots , e_{2^{h-1}} \in \{0,1\}\}\subset \mathcal {F}$. Hence $\alpha _h^{\mathcal {F}}= 2^{h-1}$ and so the sequence $(\alpha _h^{\mathcal {F}})$ is monotonic and divergent. Then it follows from Proposition 3 that $\mathtt{NO}_{aa}$ is not a trellis language.

As a matter of fact, it can be shown in the same way that the language $\mathtt{NO}_{ab} = \{x_1\dots x_ny_1\dots y_n: x_iy_i\in \{aa,ba,bb\}\text { for } i=1,\dots ,n\}\cup \{w\in \{a,b\}^*: w\text { is of odd length}\}$ is not a trellis language. At the same time, neither $\mathtt{Mi}_a\mathtt{Mi}_a$ nor $\mathtt{Mi}_a\mathtt{Mi}_b$ are trellis languages.

7 Conclusion

As illustrated in this paper, to make explicit limitations on the computational ability of trellis automata, the analysis of the characteristic patterns associated to trellis languages, is a significant approach. But we are still far from having fully exploited such tools.

The language $\mathtt{Mi}_a\mathtt{Mi}_a$ and its derived forms have been shown not to be trellis ones. Despite the fact it gives us good reason to believe that the $\mathtt{Copy}$ language, coinciding with $(\mathtt{Mi}_a\mathtt{Mi}_b)^\complement \cap (\mathtt{Mi}_b\mathtt{Mi}_a)^\complement \cap \{aa,ab,ba,bb\}^*$, is not recognizable by trellis automata, the question remains still open. Regarding the Okhotin’s grammars hierarchy, another challenge would be to determine whether the language $(\mathtt{Mi}_a\mathtt{Mi}_a)^\complement$ is representable by a conjunctive grammar or not [7].