Privacy-Enhanced Profile-Based Authentication Using Sparse Random Projection

Abstract

In a profile-based authentication system, a user profile is stored at the verifier and later used to verify their authentication claim. A profile includes user-specific information that is privacy sensitive. In this paper we propose a non-cryptographic approach to providing privacy for user profile data in profile-based authentication systems, using an efficient construction of random projection: a linear dimension reducing transform that projects the profile and the verification data to a lower dimension space, while preserving relative distances of the vectors and so correctness of authentication. We define privacy measures for two types of profiles: a single vector profile and a multivector profile, derive theoretical bounds on the privacy and correctness of privacy enhanced systems, and verify the results experimentally on two profile-based authentication systems: a face-biometric system  and a behavioural based authentication system. We discuss our results and propose directions for future research.

1 Introduction

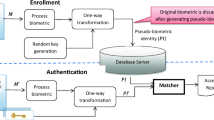
Traditional entity authentication systems that rely on secrets (e.g. passwords, secret keys), or hardware tokens, are vulnerable to credential theft and credential sharing. This latter vulnerability not only allows users to share their credentials with others to bypass security of subscription services (e.g. online games), but also has been used for delegation (subcontracting) of work to others [1] resulting in the breach of the company security policy. In a profile-based authentication system, a user’s authentication claim is compared with their stored profile that is constructed during a trusted registration process. A profile is one or more vectors of feature values, each sampling a feature that captures some user-specific property. The profile data is stored at the verifier and is used to accept or reject an authentication claim of a user that presents their verification data. The verifier uses a matching algorithm that compares the verification data with the stored profile and decides to accept, or reject, the claim. A traditional biometric system [2, 3] is a profile-based authentication system where the profile data and verification data are each a single vector, and matching is by measuring the distance between the two. A more recent type of profile-based authentication system, sometimes referred to as implicit authentication system (IA) [4], uses a user profile that is a vector of random variables whose distribution is specific to the user. A feature is stored as a set of samples that represent the distribution of the feature, and the verification (matching) algorithm compares the distribution of the verification data (represented by a second sample set) with the profile data to determine if they are from the same distribution.

Privacy. Profile data carry sensitive personal information that must be protected from the verifier. Ideally the verifier should only be able to use the profile data for the verification decision. In practice however profiles can be used to learn about users’ behaviour and interests for marketing and advertising, or track them across websites. Biometric profiles are uniquely identifying, and are of extreme sensitivity from privacy view point. Behavioural profiles also reveal user private information such as their health conditions, physical abilities or user skills and behaviour, as well as pattern of usage of applications and devices. Richer profiles (i.e. more behaviour data) lead to higher accuracy in authentication and this provides incentive to employ more user data, and “to keep it around for a longer period of time” [5].

An immediate solution to protecting privacy of profile data against the verifier is to store them in encrypted form and design the verification algorithm as a computation in encrypted domain, or use a secure two party computation protocol. These approaches in their general form [6] are computationally expensive and are primarily of theoretical interest. One can tailor more efficient secure computation systems for computationally simple verification algorithms, such as finding linear sums [7], but this cannot be easily extended to more general matching algorithms such as KS-test used in this paper (See Sect. 2). In [8] random projection of profile data was proposed to provide profile privacy for biometric data. Authors showed that, using a random transformation matrix whose elements are generated using a Gaussian distribution, one can project profile vectors to a lower dimension space, such that the correctness of the verification algorithm is maintained. Authors also showed that the approach allows changeability of the profile, which is a desirable security property. Our work builds on this result and strengthens and extends in a number of ways.

Our Work. The setting. We consider a profile-based authentication system with an honest-but-curious verifier who follows the protocol but would like to glean information about users from their stored data. We define correctness and security of the authentications system using Success Rate (SR), False Acceptance Rate (FAR) and False Rejection Rate (FRR) (See Definition 1).

To provide profile privacy, a trusted registration authority (RA) performs user registration during which the following two things happen: (i) after checking the user’s credentials, the RA generates a random matrix $R^{[u]}$ that will be stored on the user’s device, and (ii) use the user’s device (with the embedded transform) to generate their transformed profile $R^{[u]}\mathbf {X}^{[u]}$, where $\mathbf {X}^{[u]}$ is the original user profile. (Note that the user profile stays private to the RA also.) The user identifier and the transformed profile, $(u, R^{[u]}\mathbf {X}^{[u]})$, will be securely sent to the verifier. (The system can be designed such that the transform be generated by the device, and remain unknown to the RA.) In a user authentication session, verification data is generated by the device, transformed using the embedded transform, and sent to the verifier. For efficient computation we use discrete random matrices whose elements are generated according to Eq. (1) (Sect. 2).

Privacy model and theoretical results. We consider two cases: single-vector profiles, and multivector profiles. For single-vector profiles the adversary, denoted by $\mathcal{A}^{FV}$ adversary, wants to find the original Feature Values. Our notion of privacy in this case is in terms of the expected mean and variance of the adversary’ error in finding these values (See Definition 3, item (1)). For multivector profiles, the Feature Distribution adversary denoted by $\mathcal{A}^{FD}$ adversary, wants to learn the distribution of the feature. Definition 3, item (2) introduces the notion of $\pi$ -Distribution-Privacy, where $\pi$ is the fraction of features (in the feature vector) that remain “close” to their original distributions, given the adversary’s knowledge. We consider two types of adversary knowledge: (i) the adversary knows the distribution of random matrices, but does not know the random matrix $R^{[u]}$ that is assigned to the user, and (ii) the adversary knows $R^{[u]}$. This latter case corresponds to the extreme case that the user device has been compromised and $R^{[u]}$ has been leaked. These two types of knowledge are shown by subscripts D and R, respectively. Thus we have $\mathcal{A}^{FV}_D$, $\mathcal{A}^{FV}_R$, $\mathcal{A}^{FD}_D$ , and $\mathcal{A}^{FD}_R$ adversaries, where the superscripts show the goal, and the subscripts show the knowledge type.

Single vector profiles. Proposition 1 gives the mean and variance of error for the best (least expected error) $\mathcal{A}^{FV}$ adversary strategy for finding the profile vector. Theorem 2 uses this result to quantify the privacy level of the system against this adversary. When the projection matrix $R^{[u]}$ is known to the adversary, Proposition 1, item (ii), gives the expected mean and variance of error, and Theorem 2, item (ii), shows the privacy level against a $\mathcal{A}^{FV}_R$ adversary.

Multivector profiles. Using the best estimation strategy on each profile vector we obtain an estimate of the multivector profile, that is compared with the original one, and closeness of each estimated feature with the original one is determined. To quantify closeness of an estimated feature distribution to its original distribution, we use KS-test [9] for two one-dimensional probability distributions. Proposition 1, items (i) and (ii), show that the variance of the estimated values is high and so the original feature distribution cannot be recovered. In our experiments we will experimentally find the $\pi$ values of the adversaries $\mathcal{A}^{FD}_D$ and $\mathcal{A}^{FD}_R$.

We use the set of matrices that are generated using a discrete distribution. The correctness of authentication system in this case is shown in Sect. 3. Using a discrete distribution reduces the computation of profile transform to addition and subtraction only and so becomes very efficient (no multiplication).

Experimental results. To evaluate the above framework we considered the following profile-based authentication system.

Our profile-based authentication systems. For single-vector profiles we designed a simple face recognition algorithm with a matching algorithm that for verification uses k-Nearest-Neighbors (kNN) algorithm [10], with k = 1 (verification uses the closest profile in the profile database to the presented verification vector). This profile-based authentication was evaluated using the face-biometric data that was downloaded from AT&T Laboratories [11], and shown to have comparable performance to face-biometric system in [12].

For multivector system we used a profile-based behavioural biometric system called Draw a Circle (DAC) [13]. This is a challenge-response authentication system in which profile data and verification data consist of 30 and 20 profile vectors, respectively. The verification algorithm, for each feature, matches the distribution of the feature samples in the verification data against the corresponding distribution of feature samples in the profile data using Kolmogorov Smirnov-test (KS-test) [9], and then combines the results, using the meta-data analyzer VoteP [14], into a final accept, reject decision. More details about DAC is in Sect. 4. The success rate of the above systems, before using random projection, are 94.16% and 94.40%, respectively.

Profile projection. We assign a $m\times k$ random matrix $R^{[u]}$ that is generated using the distribution, described by Eq. (1), to each user. For correctness, our experimental results show that after projection, the FRR and FAR of both systems improve: in the case of face-biometric system, FRR and FAR both become close to 0.0, while for DAC, they are slightly lower than their original values. This is due to the combination of the distance preserving property of RP, and the fact that each user has an individual matrix. For privacy evaluation we use the same matrices and k values. For $\mathcal{A}^{FV}_D$ and $\mathcal{A}^{FV}_R$ adversaries in the face-biometric system, our results show that for higher k values, although the mean of estimated error becomes smaller, but as expected, because of large variance, the estimated value will be different from the original value. For DAC we used $\mathcal{A}^{FD}_D$ and $\mathcal{A}^{FD}_R$ adversaries that aim at feature distributions. We measured the similarity between the original and estimated profile and showed that feature distributions were not be preserved and this was even true for $\mathcal{A}^{FD}_R$ when the projection matrix is known. Details of experiments are given in Sect. 4.

Profile changeability. This property ensures that by changing user matrix, one can effectively refresh the stored (projected) profile. Although this is not the focus of this work, we report our experiment in Sect. 4.3. that shows perfect ability to refresh the profile.

The rest of the paper is organized as follows. Section 2 provides the background. Section 3 describes our setting, privacy attacks and measures for quantifying privacy, and provides privacy analysis for different attack scenarios, and Sect. 4 gives the experimental results. Section 5 summarizes related works, and Sect. 6 concludes the paper.

2 Preliminaries

A metric space $\mathcal {M}_m$ is a set of points equipped with a non-negative distance function $d: \mathcal {M}_m \times \mathcal {M}_m \rightarrow \mathbb {R}$ that satisfy, non-negativity, symmetry and triangular properties. We consider elements of $\mathcal {M}_m$ to be vectors of length m with components in $\mathbb {R}$, i.e. $\mathcal {M}_m \subset \mathbb {R}^m$. For two vectors $\mathbf {X}, \mathbf {Y} \in \mathcal {M}_m$, where $\mathbf {X}=\{ \mathbf {X}_1, \mathbf {X}_2, ..., \mathbf {X}_m\}$ and $\mathbf {Y}=\{ \mathbf {Y}_1, \mathbf {Y}_2, ..., \mathbf {Y}_m\}$, we consider the Euclidean distance $d(\mathbf {X},\mathbf {Y})= \sqrt{\sum _{i=1}^{m}(\mathbf {X}_i-\mathbf {Y}_i)^2}$.

For two subsets $\mathbf {A}$ and $\mathbf {B}$ of $\mathcal {M}_m$, we consider each set as samples of an underlying distribution, and use the distance between the two underlying distributions using Kolmogorov-Smirnov (KS) test in [9], as the distance $D(\mathbf {A},\mathbf {B})$ between the two subsets.

Two-sample Kolmogorov-Smirnov (KS) test [9] is a non-parametric hypothesis testing method for equality of two distributions, each represented by a set of points. For two sample sets of size n and $n'$, the test measures D, the maximum distance between two cumulative empirical distribution functions, and rejects the null hypothesis at level $\alpha$ if $D > c(\alpha )\sqrt{(n+n')/(nn')}$. The test outputs a P-value which is the confidence level of the test.

VoteP method [14] is a method of combining the results of multiple KS-tests, and obtain the combined P-value. We use this method to combine the result of feature similarity tests to obtain the verification decision. The method finds the number of P-values that are above a given threshold, and accepts the hypothesis if the fraction of these P-values (over all P-values) is above some specific threshold.

Performance Measures. Let fa, tr, fr and ta denote the number of false acceptance, true rejection, false rejection and true acceptance instances of an experiment (e.g. verification of claims). False Acceptance Rate (FAR), False Rejection Rate (FRR) and the Success Rate (SR) are defined as follows:

$$FAR=fa/(fa+tr),~ ~ FRR=fr/(fr+ta),~ SR=(ta+tr)/(ta+fr+tr+fa).$$

Random projection(RP) is a dimension reduction transformation that uses random matrices to project a vector $\mathbf {X} \in {\mathbb {R}}^m$, to a vector $\mathbf {X'}=\frac{1}{\sqrt{k}\sigma _r}R\mathbf {X}$, $\mathbf {X'} \in {\mathbb {R}}^k$, using a random matrix $R^{k \times m}, k < m$, where $\sigma _r$ is the standard deviation of entries of $R^{[u]}$. The important property of this transformation is that it preserves pair-wise Euclidean distances between the points in the metric space ${\mathbb {R}}^m$, up to an error that can be estimated for the dimension reduction parameter. Existence of distance-preserving dimension reduction transformations follows from the following Lemma.

Johnson-Lindenstrauss(JL) Lemma [15]. Let $\epsilon \in (0, 1)$ and $\mathcal {M}_m \subset \mathbb {R}^m$ be a set of n vectors and $k=\frac{4ln(n)}{\epsilon ^2/2-\epsilon ^3/3}$. There exists a Lipshcitz mapping $f: \mathbb {R}^m \rightarrow \mathbb {R}^k$ such that for all $u, v \in \mathcal {M}_m$:

$$(1-\epsilon ) d^2(u,v) \le d^2(f(u),f(v)) \le (1+\epsilon ) d^2(u,v) $$

For a given projected dimension k, to satisfy the above inequality for a small $\epsilon$ (i.e. to preserve distances up to $\epsilon$), one needs to have a sufficiently small n (sparse set). In profile-based authentication systems, sparseness of the profile vector space is a requirement for the correctness of the system (otherwise matching verification data against the profile will have high error) and so the required condition is satisfied.

The proof of JL Lemma constructs the RP transform using matrices whose entries are sampled from a Gaussian distribution [15]. It has been shown experimentally (e.g. in [16]) that the result also holds if R is generated by a zero mean and unit variance distribution. In [17], it is proved that the property will hold if the matrix entries are sampled individually and independently, from the following three-valued distribution,

$$\begin{aligned} \Pr (x=+1) = \frac{1}{2s},\;\;\; \Pr (x=0) = 1-\frac{1}{s},\;\;\; \Pr (x=-1) = \frac{1}{2s},\;\;\; \end{aligned}$$

(1)

Theorem 1

([17]). Suppose $\mathcal {M}_m \subset \mathbb {R}^m$ be a set of n vectors projected onto ${\mathbb {R}}^{k}$ using the transform $f: {\mathbb {R}}^{m} \rightarrow {\mathbb {R}}^k$ defined as $f(u)=\frac{1}{\sqrt{k}\sigma _r}Ru$ for $u \in \mathcal {M}_m$, where R is a $k \times m$ matrix generated using the distribution given in Eq. (1) and $\sigma _r$ is the standard deviation of entries of R. Given $\epsilon ,\beta >0$ let $k_0=\frac{4+2\beta }{\epsilon ^2/2-\epsilon ^3/3} log(n)$. If $k\ge k_0$ then with probability at least $1-n^{-\beta }$ for all $u,v \in \mathcal {M}_m$ we will have:

$$(1-\epsilon ) d^2(u,v) \le d^2(f(u),f(v)) \le (1+\epsilon ) d^2(u,v) $$

We use $s=3$ that results in many zeros in the matrix and speeds up the computation (only $\frac{1}{3}$ of the data are actually processed) and called it sparse random projection.

Minimum-norm solution. Let $\mathbf {X'}=R\mathbf {X}$, where $\mathbf {X'} \in {\mathbb {R}}^m$ and $R \in {\mathbb {R}}^{k \times m}$ and $k < m$. This system of linear equations has $m-k$ degrees of freedom. Among all solutions of the system, the solution $\mathbf {\hat{X}}=R^T(RR^T)^{-1}\mathbf {X'}$, known as the minimum-norm solution, minimizes the Euclidean norm of the solution $\Vert \mathbf {\hat{X}}\Vert =\sqrt{\sum _{t=1}^{m}\mathbf {\hat{X}}_i^2}$ [18]. In [19] the following result is proven about this solution.

For a fixed $\mathbf {X} \in {\mathbb {R}}^m$, let $\ell$ pairs $(\mathbf {X'_j},R_j), \text { } 1 \le j \le \ell$ be given, where $R_j \in {\mathbb {R}}^{k \times m}$ entries are generated using a Gaussian distribution with zero mean and $\mathbf {X'_j}=R_j \mathbf {X}$. Let $\mathbf {\hat{X}_j}$ denote the minimum-norm solution of the linear system $\mathbf {X'_j}=R_j \mathbf {X}$. Then, the mean of the estimation error of $\mathbf {X}$ will be zero. This suggests that, given the projected value $\mathbf {X'}$ of a vector $\mathbf {X}$, the minimum-norm solution of the system of linear equation that can be written for the projected profile, provides a good estimation of $\mathbf {X}$.

3 Privacy-Preserving Profile-Based Authentication Systems

A profile-based authentication system consists of three types of entities: (i) a group of users $\mathcal U$ that must be authenticated; (ii) a trusted registration authority (RA) that interacts with a user u and generates a profile $\mathbf {X}^{[u]}$ for them; and (iii) a verifier V that interacts with a user, and using the profile and the presented verification data decides if the user’s claim is valid or not. The set of user profiles is stored in a profile database DB at the verifier. There are two types of profile-based systems, depending on the nature of profile data (and verification data).

• (i) The profile of user u, $\mathbf {X}^{[u]}$, is a single vector $\mathbf {X}^{[u]}\in \mathcal {M}_m$, and can be represented as a $1 \times m$ vector with elements from $\mathbb R$. Biometric systems can generate such profiles (e.g. fingerprint data). In practice one may use multiple instances of the profile vector to achieve better accuracy in verification.

• (ii) The profile of user u, $\mathbf {X}^{[u]}$, is a set of n profile vectors ${\mathbf {X}_j^{[u]}}\in \mathcal {M}_m$ (for $1 \le j \le n$) where each ${\mathbf {X}_j^{[u]}}$ consists of m feature values, i.e. $\mathbf {X}^{[u]}_j=\{\mathbf {X}^{[u]}_{j1},\mathbf {X}^{[u]}_{j2},...,\mathbf {X}^{[u]}_{jm}\}$. We refer to these vectors as feature vectors. A profile thus can be represented as an $n \times m$ matrix with elements from $\mathbb R$. Behavioural authentication data (e.g. keystroke, mouse dynamics etc.) generate this kind of profile.

Note that in (i), the actual feature values provide information about the user, while in (ii), the distribution of a feature that is captured by a set of sample points, provide identifying information.

3.1 Correctness and Security

Correctness and security of profile-based authentication system is define by two parameters $\epsilon$ -FRR, and $\delta$ -FAR.

Definition 1

$(\epsilon , \delta )$ -security: A profile-based authentication system provides $(\epsilon , \delta )$-security if it satisfies the following:

For the claimed identity u and the verification data $\mathbf {Y}^{[v]}$, the matching algorithm outputs $M(\mathbf {X}^{[u]}, \mathbf {Y}^{[v]})=0$ (reject) with probability at most $\epsilon$, if $u=v$, and outputs $M(\mathbf {X}^{[u]}, \mathbf {Y}^{[v]})=1$ (accept) with probability at most $\delta$, when $u \ne v$.

$$Pr[M(\mathbf {X}^{[u]}, \mathbf {Y}^{[v]})=0 \text { }|\text { } u=v] \le \epsilon ; ~~ Pr[M(\mathbf {X}^{[u]}, \mathbf {Y}^{[v]})=1 \text { }|\text { } u \ne v] \le \delta ; $$

Changeability of a profile-based authentication captures the ability to refresh a user profile while maintaining correctness and security.

Definition 2

$\zeta$ -changeability: A privacy-preserving profile-based authentication system provides $\zeta$-changeability if it satisfies the following:

For transformed profile $\mathbf {X'}^{[u]}=R^u\mathbf {X}^{[u]}$ and the verification data $\mathbf {Y'}^{[v]}=R^v\mathbf {X}^{[u]}$, the matching algorithm outputs $M(\mathbf {X'}^{[u]}, \mathbf {Y'}^{[v]})=1$(accept) with probability at most $\zeta$, if $R^u \ne R^v$.

$$Pr[M(R^u\mathbf {X}^{[u]}, R^v\mathbf {X}^{[u]})=1 \text { }|\text { } R^u \ne R^v] \le \zeta . $$

3.2 Privacy Model

Privacy transform must not be significantly adversely affect the correctness of authentication, and must protect the profile data.

Correctness after applying privacy transform. Let a profile $\mathbf {X}^{[u]}$ be mapped to $\mathbf {X'}^{[u]}$, and the verification date $\mathbf {Y}^{[v]}$ be mapped to $\mathbf {Y'}^{[u]}$. To preserve correctness of authentication, ideally we must have, $M'(\mathbf {X'}^{[u]},\mathbf {Y'}^{[u]})=1$, if $M(\mathbf {X}^{[u]},\mathbf {Y}^{[v]})=1$, and $M'(\mathbf {X'}^{[u]},\mathbf {Y'}^{[u]})=0$, if $M(\mathbf {X}^{[u]},\mathbf {Y}^{[v]})=0$ where M() and $M'()$ are the matching algorithm used before applying the transform and the one used in the projected space.

Privacy Attacks. We define four types of adversaries $\mathcal {A^G_K}$ that are distinguished by their (i) attack goal ($\mathcal G$), and their (ii) prior knowledge ($\mathcal K$). The goal $\mathcal {G}\! \in \{ FV, FD\}$ where FV denotes Feature Value and FD denotes Feature Distribution. These goals are for single and multivector profiles, respectively. The prior knowledge of the adversary is denoted by $\mathcal K \! \in \{D, R \}$, where D denote the distribution that is used for the generation of the random matrices, and R denotes the actual user matrix. Thus we have $\mathcal{A}^{FV}_R$, $\mathcal{A}^{FD}_R$, $\mathcal{A}^{FV}_D$ and $\mathcal{A}^{FD}_D$ adversaries. Assume the adversary has the transformed profile of a user $\mathbf {X'}^{[u]}$ (or transformed verification data).

Definition 3

Let f be a random transformation. Our privacy notions are:

1. $(\mu , \lambda )$ -Value-Privacy: Let f applied to a profile vector $\mathbf {X}$ of length m, result in $\mathbf {X'}$. Then f provides $(\mu , \lambda )$-Value-Privacy for the ith feature in $\mathbf {X}$(i.e. $\mathbf {X}_{i}$), against an attacker $\mathcal{A}^{FV}$, if given $\mathbf {X'}$, the best strategy of $\mathcal{A}^{FV}$ for $\mathbf {X}_{i}$ satisfies, $E[{\mathbf {X}_{i}-\hat{\mathbf {X}}_{i}}] \le \mu \text { and } Var[{\mathbf {X}_{i}-\hat{\mathbf {X}}_{i}}] \le \lambda$, where $E[{\mathbf {X}_{i}-\hat{\mathbf {X}}_{i}}]$ and $Var[{\mathbf {X}_{i}-\hat{\mathbf {X}}_{i}}]$ are the expected value and the variance of the attacker’s normalized estimation error under the random transformation, respectively.

2. $\pi$ -Distribution-Privacy: Let f be applied to a multivector profile $\mathbf {X}$, resulting in $\mathbf {X'}$. Then f provides $\pi$-Distribution-Privacy against an attacker $\mathcal{A}^{FD}$ if the best strategy of $\mathcal{A}^{FD}$ results in an estimated profile in which at most $\pi$-percent of features pass a statistical closeness test with the corresponding features in the original profile.

3.3 Privacy Transform

We use the privacy transformation given in Eq. (1). A user u is associated with a $k \times m$ matrix $R^{[u]}$ that is generated using this distribution (in our experiments we use $s=3$). Correctness of the privacy enhanced authentication follows from Theorem 1, using $M'=M$.

3.4 Privacy Analysis

We have the following results.

Privacy adversaries $\mathcal{A}^{FV}$ . The system of linear equations $\mathbf {X'}^{[u]}=\frac{1}{\sqrt{k}\sigma _r}R^{[u]}\mathbf {X}^{[u]}$ is under-determined and has infinite number of solutions. For a fixed unknown $\mathbf {X}^{[u]}$ and the set of random $R^{[u]}$ matrices, the minimum-norm solution of the above system is known to be the best estimate in the sense that the estimation error of $\mathbf {X}^{[u]}$ will have a distribution with zero mean and small variance. We adopt this solution as the best estimate for $\mathcal{A}^{FV}_R$ attacker who knows $R^{[u]}$ and the projected profile.

In the case of $\mathcal{A}^{FV}_D$, they can generate an RP matrix $R'^{[u]}$ according to the distribution, and estimate $\mathbf {X}^{[u]}$ using minimum-norm solution, hoping that the estimated value is close to the real value. The following proposition gives the mean and variance of the best estimation for the cases, (i) attacker $\mathcal{A}^{FV}_R$ and (ii) attacker $\mathcal{A}^{FV}_D$. The proof is given in Appendix A.

Proposition 1

Let $R^{[u]}$ be a $k \times m$ RP matrix with entries sampled from Eq. 1 with parameter s. For the projected profile $\mathbf {X'}^{[u]}=\frac{1}{\sqrt{k}\sigma _r}R^{[u]}\mathbf {X}^{[u]}$, we have, (i) If $\mathbf {X'}^{[u]}$ and distribution of $R^{[u]}$ entries are known and $\mathbf {\hat{X}}^{[u]}_i$ is the best estimation for the ith component of $\mathbf {X}^{[u]}$ obtained using minimum-norm solution, the mean and variance of the estimation error ${\mathbf {X}^{[u]}_i-\mathbf {\hat{X}}^{[u]}_i}$ will be $\mu _i={\mathbf {X}^{[u]}_i}$, and ${\sigma _i}^2= \frac{1}{k}\sum _{t=1}^{m}{\mathbf {X}^{[u]}_{t}}^2$.

(ii) If $\mathbf {X'}^{[u]}$ and $R^{[u]}$ are known and $\mathbf {\hat{X}}^{[u]}_i$ is the estimation of the ith component of $\mathbf {X}^{[u]}$ obtained using minimum-norm solution, the mean and variance of the estimation error ${\mathbf {X}^{[u]}_i-\mathbf {\hat{X}}^{[u]}_i}$ will be, $\mu _i=0$, and $\sigma _i^2= \frac{1}{k}((s-1){\mathbf {X}^{[u]}_i}^2+\sum _{t \ne i}{\mathbf {X}^{[u]}_{t}}^2)$, respectively.

The above propositions lead to the following theorem.

Theorem 2

(i) Random projection as defined in Proposition 1 provides $(\mu _i, \lambda _i)$-Value-Privacy against $\mathcal{A}^{FV}_D$ for the ith component of $\mathbf {X}^{[u]}$, and we have $\mu _i={\mathbf {X}^{[u]}_i}$, and ${\lambda _i}^2= \frac{1}{k}\sum _{t=1}^{m}{\mathbf {X}^{[u]}_{t}}^2$.

(ii) Random projection as defined in Proposition 1 provides $(\mu _i, \lambda _i)$-Value-Privacy against $\mathcal{A}^{FV}_R$ for the ith component of $\mathbf {X}^{[u]}$, and we have $\mu _i=0$, and $\lambda _i^2= \frac{1}{k}((s-1){\mathbf {X}^{[u]}_i}^2+\sum _{t \ne i}{\mathbf {X}^{[u]}_{t}}^2)$.

Note that in both above cases, due to the large variance of the estimation error, the attacker’s best estimation will be highly unreliable.

Privacy adversaries $\mathcal{A}^{FD}$ . Proposition 1 shows that for $\mathcal{A}^{FD}_D$ the expected error and variance of the ith feature, when $s=3$, will be $\mu _i={\mathbf {X}^{[u]}_i}$, and ${\lambda _i}^2= \frac{1}{k}\sum _{t=1}^{m}{\mathbf {X}^{[u]}_{t}}^2$, respectively. The high variance of error, results in the estimation values to vary significantly from the mean, and so the original feature distributions will not be recovered by the attacker. For $\mathcal{A}^{FD}_R$, using Proposition 1 and $s=3$, we have $\mu _i=0$ and ${\lambda _i}^2=\frac{1}{k}(2{\mathbf {X}^{[u]}_i}^2+\sum _{t \ne i}{\mathbf {X}^{[u]}_t}^2)$. Again due to the large variance of the error, the probability that an estimated value be close to the original feature values will be negligible.

4 Experiments

We will use our privacy transform on a single vector, and a multivector, profile-based authentication system, referred to as face-biometric system and DAC, respectively. We will measure the correctness and privacy of the transformed systems against $\mathcal{A}^{FV}_D$, $\mathcal{A}^{FV}_R$, $\mathcal{A}^{FD}_D$, and $\mathcal{A}^{FD}_R$ adversaries. First we give a brief overview of the face-biometric system and DAC and their corresponding matching algorithms.

A face-biometric user authentication system. We use the face database used in the paper [12] and published in [11]. A face image is represented by a vector of length 10304 (each value [0,255]). The database has 40 users, each represented by 10 face images. We designed and implemented a simple matching algorithm that uses kNN algorithm with $k=1$. Using multiple sample face for each user we obtained success rate of 98.0%, FRR of 2.0% and FAR of 0.0%, which are comparable with the original results reported in [12].

Table 1. Comparison of correctness before and after projection. Random projection improve the system correctness a bit.

Fig. 1.

A Challenge from server side and the user’s response

DAC (Draw A Circle). DAC is a behavioural authentication for mobile devices. DAC is a challenge-response system that is implemented as a two level game: In Level 1, the challenge is a random circle that must be drawn from a given starting point. In Level 2, the challenge is a circle with a given starting point, that disappears after 3 s. There are 55 features in Level 1, and 56 in Level 2 (Table 1 in [13]). Figure 1 shows the system interface of DAC. Verification algorithm, for each feature, measures closeness of presented verification data with the corresponding profile feature data using KS-test, and combines the resulting P-values using VoteP method [14].

4.1 Correctness Experiments

Face-biometric. We measured the correctness of face-biometric system before and after RP, using FAR, FRR and SR metrics. We used, $k=\{56,66,110,355\}$. From the 10 available feature vectors for a user, one vector models their single vector profile and the remaining 9 vectors are used as verification claims. For this data-set kNN with $K=1$, the results are given in Table 1, showing that the privacy transform with individual user RP matrices, has improved the correctness, for all k values, making it close to 1.0. As discussed earlier this is because of the combination of distance preserving property, and the use of individual matrices that increases the distinguishability of the data of different users in the space.

DAC. For DAC we use a database of 39 users. Each profile consists of 30 feature vectors (collected during registration), and 20 other vectors for verification. We calculate FAR, FRR and SR of DAC, before and after projection, for $k=\{25,35, 45\}$. By reducing k, we expect FAR and FRR of the system to increase because more information will be lost. Table 1 shows that FAR and FRR will remain below 6.0% for different values of k, even when $k=25$. The success rate in all cases is higher than $94.0\%$, and again random projection improves the correctness results.

Fig. 2.

Comparison of theoretical and experimental mean of error $\mathbf {X}^{[u]}_i-\mathbf {\hat{X}}^{[u]}_i$ for k = 355 where distribution of $R^{[u]}$ is known to the attacker. The experimental mean and variance of the estimation error is large for all k.

4.2 Privacy Evaluation

Privacy Evaluation for the two systems are below.

Face-biometric system. We transformed each profile in the face-biometric system using 10,000 random matrices of size $k \times m$, where m is the length of the feature vector. Matrices are generated using the distribution in (1).

For $\mathcal{A}^{FV}_R$ attacker, for each projected profile we found the minimum-norm solution, $\mathbf {\hat{X}}^{[u]}$, as the best estimate of the original profile assuming the matrix was known. For $\mathcal{A}^{FV}_D$ we repeated the same process, using a random matrix that was generated according to the known distribution. We calculated the mean and the standard deviation of the estimation error for each feature i, $\mathbf {X}^{[u]}_i-\mathbf {\hat{X}}^{[u]}_i$, for each profile, and compared the results with Theorem 2, for $k=\{56,66,110,355\}$. Using Theorem 2, these choices of k correspond to $\epsilon = \{1, 0.75, 0.50, 0.25\}$ (accuracy of distance preservation) and $\beta =\{2.66, 2.64, 2.58, 2.62\},$ where $1-n^{-\beta }=0.99$ is the probability of successful distance preservation for n = 50. The first sub-figure of Fig. 2 gives the mean of estimation error for $k=355$ for each feature, assuming $\mathcal{A}^{FV}_D$. This conforms with our theoretical results showing that the mean of the estimated value is zero. The second sub-figure of Fig. 2 gives the results for the variance of the estimation error for $k=355$ and shows that the error has a very large variance of the order of $10^6$, hence very unreliable estimation for the attacker.

The first sub-figure of Fig. 3 shows the theoretical and experimental results for the mean of the error for $\mathcal{A}^{FV}_R$, and the last sub-figure of Fig. 3 show similar results for variances of the estimation error for every feature. It can be seen that the variance is large (of the order of $10^6$), indicating that even $\mathcal{A}^{FV}_R$ will obtain negligible information about feature values. For both cases, the results for other k values are given in the full version of the paper.

Fig. 3.

Comparison of theoretical and practical mean of error $\mathbf {X}^{[u]}_i-\mathbf {\hat{X}}^{[u]}_i$ for k = 355 where $R^{[u]}$ is known. The experimental mean and variance of the estimation error is large for all k.

In both attack scenarios, decreasing k results in higher error variance and so further reducing the dimension of data will improve privacy but this will be at the cost of correctness. Note that dimension reduction must maintain sparseness of the space and so the optimum value of k must be found experimentally.

DAC. We transformed each profile using 10,000 random matrices generated using the distribution given by Eq. (1). For $\mathcal{A}^{FD}_R$, we obtained the best estimate of the 30 transformed feature vectors by calculating the minimum-norm solutions, assuming the matrix is known. Then we used KS-test to measure the similarity between the distribution of features in the estimated set of vectors and the original ones, as the measure of the attacker’s success. For $\mathcal{A}^{FD}_D$ we performed the same experiment, using random matrices that were generated from the known distribution.

The first sub-figure of Fig. 4 shows the portion of features that passed the KS-test in game level 2, for 15 users, assuming $\mathcal{A}^{FD}_D$. The experiments are done with $k=\{25,35,45\}$ that according to Theorem 2 correspond to distance preserving parameters of $\epsilon =\{0.31, 0.26, 0.22\}$, and $\beta =1.17$ which indicates $1-n^{-\beta }=0.99$ for n = 10. The second sub-figure of Fig. 4 shows similar results for same parameters, assuming $\mathcal{A}^{FD}_R$.

Our results show that for both attack scenarios only in a small fraction of features distributions could be correctly estimated. For $k=\{25,35,45\}$, in the case of $\mathcal{A}^{FD}_D$ this fraction is $\{3.78, 3.51,3.24\}\%$. For $\mathcal{A}^{FD}_R$ the values increase to $\{7.80, 9.10, 10.19\}\%$. Thus, our approach achieves better than ($4\%)$-Distribution-Privacy for $\mathcal{A}^{FD}_D$ and better than ($11\%)$-Distribution-Privacy against the extreme attacker $\mathcal{A}^{FD}_R$. Similar results were obtained for game level 1 and are not presented due to limited space.

Fig. 4.

The distribution of $R^{[u]}$ and $R^{[u]}$ itself is known: distribution of less than (4%) and (11%) of features estimated close to the original one in game Level 2, for 15 different users.

4.3 Changeability Evaluation

In [8] authors evaluated changeability property of RP for single vector profile. We extend this result to multivector profile. For a profile $\mathbf {X}^{[u]}$, for each k, we used 1,000 random matrices to transform $\mathbf {X}^{[u]}$ into $\{\mathbf {X'}^{[u]}_1,\mathbf {X'}^{[u]}_2,....,\mathbf {X'}^{[u]}_{1000}\}$. We used our matching algorithm, to measure the similarity of every pair of profiles that are transformed using two different random matrices, to estimate the probability of $M(\mathbf {X'}^{[u]}_j, \mathbf {X'}^{[u]}_i), 1 \le i,j \le 1,000$ ($i \ne j$) return accept. From $999 \times 1,000$ claims for each $k=\{25,35,45\}$, none of the $(\mathbf {X'}^{[u]}_j, \mathbf {X'}^{[u]}_i)$ pairs was accepted. The average % of features that pass the KS-test ($\alpha$ = 0.05) for different k is as 15.26%, 14.70% and 14.46%, respectively.

5 Related Works

RP has been used for private data mining [19], and RP for profile privacy and achieving changeability of biometric data is considered in [8]. In this work the projection matrix uses continuous Gaussian distribution and a single matrix is used to transform all user’s biometric data. Authors analyse correctness and privacy and provide experimental results for an attack scenario where the attacker knows, or tries to recover, the random matrix. The paper does not consider the case that only the distribution of the matrix entries are known to the adversary. The paper focusses on biometric profiles (not behavioural) and does not consider distribution privacy attacks where the attacker’s goal is to recover the distribution of features. The accuracy results in [8] are worse than ours. This is because the same RP is used for all profiles. Using Gaussian distribution results in higher storage and computational overhead compared to discrete distribution that we use. Other non-cryptographic approaches to privacy includes data perturbation [20, 21], or adding noise to the data [22]. These approaches cannot be directly used for profile privacy because they will affect the output of the matching algorithm.

Behavioural authentication systems [23] come in many forms such as keystroke, touch dynamics or game playing [24, 25]. DAC is an active challenge-responses behavioural-based authentication system. Privacy protection of profiles can use cryptographic approaches [7], but this approach is limited to special matching algorithms.

6 Concluding Remarks

Profile-based authentication provides a powerful method of increasing confidence in authentication results, and protecting against a range of new attacks that defeat traditional authentication systems. Profile data is privacy sensitive and must be protected. We proposed a non-cryptographic approach, using RP, for privacy enhancement of profile-based authentication systems that rely on a single, or multivector, profiles. We provided a framework for analysing privacy enhancement of profile-based authentication systems, theoretically derived the privacy level that is offered by RP, and experimentally showed the effectiveness of RP as a privacy preserving transform. Our future work includes applying the transform to other profile-based authentication systems, and investigating optimal reduction of dimension such that the privacy is maximized while correctness results are maintained.

A Proof of Proposition 1

Proof of Proposition 1 (i)

Proof

Suppose $\sigma _r$ be the variance of the distribution used to generate entries of $R^{[u]}$. Let $\epsilon _{ij}$ be the ijth entry of ${R^{[u]}}^T{R^{[u]}}$. We have $\epsilon _{ij}=\sum _{t=1}^{k}r_{ti}r_{tj}$, and

$$\begin{aligned}&E[\epsilon _{ij}]=E[\sum _{t=1}^{k}r_{ti}r_{tj}]=\sum _{t=1}^{k}E[r_{ti}r_{tj}]=\Bigg \{ \begin{array}{ccccccccc} k{\sigma _r}^2&{}&{}&{}&{}&{}i = j\\ 0&{}&{}&{}&{}&{}i \ne j\\ \end{array} \end{aligned}$$

that means ${R^{[u]}}^T{R^{[u]}} \approx \frac{1}{k{\sigma _r}^2}I$. We know, the minimum-norm solution of the linear system of equations $\mathbf {X'}^{[u]}=\frac{1}{\sqrt{k}\sigma _r}R^{[u]}\mathbf {X}^{[u]}$ is given by $={R^{[u]}}^T(R^{[u]}{R^{[u]}}^T)^{-1}R^{[u]}\mathbf {X}^{[u]}$, which due to ${R^{[u]}}^T{R^{[u]}} \approx \frac{1}{k{\sigma _r}^2}I$ can be written as $\approx \frac{1}{k{\sigma _r}^2} {R^{[u]}}^T{R^{[u]}}\mathbf {X}^{[u]}=\frac{1}{\sqrt{k}{\sigma _r}} {R^{[u]}}^T\mathbf {X'}^{[u]}$.

Knowing the matrix $R^{[u]}$, the attacker can estimate the variance of the entries of $R^{[u]}$, $\hat{\sigma _r}$ and use it to calculate the minimum-norm solution as $\approx \frac{1}{\sqrt{k}{\hat{\sigma _r}}} {R^{[u]}}^T\mathbf {X'}^{[u]}$. Therefore we will have $E[\mathbf {\hat{X}}^{[u]}_i]=E[\frac{1}{k\sigma _r\hat{\sigma _r}}\sum _{t=1}^{m}\epsilon _{it}\mathbf {X}^{[u]}_{t}]=\frac{\sigma _r}{\hat{\sigma _r}}\mathbf {X}^{[u]}_i$, and

$$\begin{aligned} Var[\mathbf {\hat{X}}^{[u]}_i] =\,&E[{\mathbf {\hat{X}}^{[u]}_i}{^2}]-E^2[{\mathbf {\hat{X}}^{[u]}}_i]=\frac{1}{k^2\sigma _r^2\hat{\sigma _r}^2}E[(\sum _{t=1}^{m}\epsilon _{it}\mathbf {X}^{[u]}_{t})^2]-(\frac{\sigma _r}{\hat{\sigma _r}}\mathbf {X}^{[u]}_i)^2\\&=\frac{1}{k^2\sigma _r^2\hat{\sigma _r}^2}E[\sum _{t=1}^{m}{\epsilon _{it}}^2{\mathbf {X}^{[u]}_{t}}^2+\sum _{p,q=1\atop p\ne q}^{m}\epsilon _{ip}\mathbf {X}^{[u]}_{p}\epsilon _{iq}\mathbf {X}^{[u]}_{q}]-(\frac{\sigma _r}{\hat{\sigma _r}}\mathbf {X}^{[u]}_i)^2\\&=\frac{1}{k^2\sigma _r^2\hat{\sigma _r}^2}{\mathbf {X}^{[u]}_i}^2E[{\epsilon _{ii}}^2]+E[\sum _{t=1 \atop t\ne i}^{m}{\mathbf {X}^{[u]}_{t}}^2{\epsilon _{it}}^2]-(\frac{\sigma _r}{\hat{\sigma _r}}{\mathbf {\hat{X}}^{[u]}_i})^2\\&=\frac{1}{k^2\sigma _r^2\hat{\sigma _r}^2}\mathbf {X}^{[u]}_i)^2E[(\sum _{t=1}^{k}{r_{ti}}^2)^2]+\sum _{t=1 \atop t\ne i}^{m}{\mathbf {X}^{[u]}_{t}}^2E[(\sum _{f=1}^{k}r_{fi}r_{ft})^2])-(\frac{\sigma _r}{\hat{\sigma _r}}{\mathbf {X}^{[u]}_i})^2\\&=\frac{1}{k^2\sigma _r^2\hat{\sigma _r}^2}{\mathbf {X}^{[u]}_i})^2E[\sum _{t=1}^{k}{r_{ti}}^4+\sum _{p\ne q}^{k}{r_{pi}}^2{r_{qi}}^2]+\\&\sum _{t=1 \atop t\ne i}^{m}{\mathbf {X}^{[u]}_{t}}^2E[\sum _{f=1}^{k}{r_{fi}}^2{r_{ft}}^2+\sum _{p,q=1 \atop p\ne q}^{k}r_{pi}r_{pt}r_{qi}r_{qt}]) -(\frac{\sigma _r}{\hat{\sigma _r}}\mathbf {X}^{[u]}_i)^2\\&=\frac{1}{k^2\sigma _r^2\hat{\sigma _r}^2}({\mathbf {X}^{[u]}_i}^2(ks{\sigma _r}^4+k(k-1){\sigma _r}^4)+k{\sigma _r}^4\sum _{t=1 \atop t\ne i}^{m}{\mathbf {X}^{[u]}_{t}}^2)-(\frac{\sigma _r}{\hat{\sigma _r}}\mathbf {X}^{[u]}_i)^2 \end{aligned}$$

Assuming $\hat{\sigma _r}=\sigma _r$ we will have: $E[\mathbf {\hat{X}}^{[u]}_i-\mathbf {X}^{[u]}_i] \approx 0$ and $Var[\mathbf {X}^{[u]}_i-\mathbf {\hat{X}}^{[u]}_i]= \frac{s-1}{k}{\mathbf {X}^{[u]}_i}^2+\frac{1}{k}\sum _{t\ne i}(\mathbf {X}^{[u]}_{t})^2$ where s is the parameter of the distribution of $R^{[u]}$.

Proof of Proposition 1 (ii)

Proof

The attacker can generate a $k \times m$ matrix $\hat{R}^{[u]}$ using the known distribution (as an estimate for $R^{[u]}$) and use it to estimate $\mathbf {X}^{[u]}$ similar to the case of known $R^{[u]}$, as follows.

$\mathbf {\hat{X}}^{[u]}=\frac{1}{\sqrt{k}{\sigma _r}}\hat{R}^{[u]^T}\mathbf {X'}^{[u]}=\frac{1}{k{\sigma _r}^2}\hat{R}^{[u]^T}R^{[u]}\mathbf {X}^{[u]}$

Let $\hat{\epsilon }_{ij}$ be the ijth entry of ${\hat{R}^{[u]^T}}R^{[u]}$. That is $\hat{\epsilon }_{ij}=\sum _{t=1}^{k}\hat{r}_{ti}r_{tj}$ and $\mathbf {\hat{X}}^{[u]}_i=\frac{1}{k{\sigma _r}^2}\sum _{t=1}^{k}\hat{\epsilon }_{it}\mathbf {X}^{[u]}_{t}$.

We have $E[\hat{\epsilon }_{ij}]=E[\sum _{t=1}^{k}\hat{r}_{ti}r_{tj}]=0$ and $E[{\hat{\epsilon }_{ij}}^2]=E[(\sum _{t=1}^{k}\hat{r}_{ti}r_{tj})^2] =E[\sum _{t=1}^{k}{\hat{r}_{ti}}^2{r_{tj}}^2+\sum _{p,q=1 \atop p\ne q}^{k}\hat{r}_{pi}r_{pj}\hat{r}_{qi}r_{qj}]=k{{\sigma _r}}^4$

Therefore, we get $E[\mathbf {\hat{X}}^{[u]}_i]=\frac{1}{k{\sigma _r}^2}E[\sum _{t=1}^{m}\hat{\epsilon }_{it}\mathbf {X}^{[u]}_{t}]=0$ and

$$\begin{aligned} Var[\mathbf {\hat{X}}^{[u]}_i]&=E[\mathbf {\hat{X}}^{[u]}_i{^2}]-E^2[\mathbf {\hat{X}}^{[u]}_i]=\frac{1}{k^2{{\sigma _r}}^4}E[\sum _{t=1}^{m}\hat{\epsilon }_{it}{\mathbf {X}^{[u]}_t}{^2}]=\frac{1}{k^2{{\sigma _r}}^4}E[\sum _{t=1}^{m}{\hat{\epsilon }_{it}}^2{\mathbf {X}^{[u]}_t}{^2}+\\&\sum _{p,q=1 \atop p\ne q}^{m}{\hat{\epsilon }_{ip}}\mathbf {X}^{[u]}_{p} \hat{\epsilon }_{iq}{\mathbf {X}^{[u]}_q}]=\frac{1}{k}\sum _{t=1}^{m}{\mathbf {X}^{[u]}_t}{^2} \end{aligned}$$

Therefore we will have: $E[\mathbf {X}^{[u]}_i-{\mathbf {\hat{X}}^{[u]}_i}]=\mathbf {X}^{[u]}_i$ and $Var[\mathbf {X}^{[u]}_i-\mathbf {\hat{X}}^{[u]}_i]=\frac{1}{k}\sum _{t=1}^{m}{{\mathbf {X}^{[u]}_t}}^2$.