Election-Dependent Security Evaluation of Internet Voting Schemes

Abstract

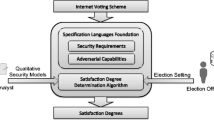
The variety of Internet voting schemes proposed in the literature build their security upon a number of trust assumptions. The criticality of these assumptions depends on the target election setting, particularly the adversary expected within that setting. Given the potential complexity of the assumptions, identifying the most appropriate Internet voting schemes for a specific election setting poses a significant burden to election officials. We address this shortcoming by the construction of an election-dependent security evaluation framework for Internet voting schemes. On the basis of two specification languages, the core of the framework essentially evaluates election-independent security models with regard to expected adversaries and returns satisfaction degrees for security requirements. These satisfaction degrees serve election officials as basis for their decision-making. The framework is evaluated against requirements stemming from measure theory.

1 Introduction

Significant research efforts have been made to establish security requirements for Internet voting schemes [8, 9, 14, 15]. Amongst the most prevalent requirements, there are vote secrecy (also referred to as vote privacy [6, 21]), i.e. an adversary must not be able to establish the link between the voter and her cast vote, vote integrity, i.e. an adversary must not be able to undetectably manipulate votes, and eligibility, i.e. an adversary must not be able to cast votes for abstaining voters. The numerous Internet voting schemes proposed in the literature, e.g. [1, 3, 5, 11, 21], implement these requirements by making certain assumptions. For example, the JCJ/Civitas [5, 11] scheme builds vote secrecy upon the assumption that the device used to cast a vote is trustworthy. Pretty Good Democracy [21] enforces vote secrecy in the presence of malicious voting devices, yet the scheme assumes that the voter can cast her vote without adversarial influence. The criticality of these assumptions, and therefore the security of Internet voting in general, differs within different election settings. To face this reality, our goal is to construct an election-dependent security evaluation framework for Internet voting schemes that measures to what extent an Internet voting scheme satisfies security requirements within concrete election settings.

Related Work. Several works have addressed the assessment of risks for electronic voting systems [2, 4, 12, 17, 19, 20] by deriving threats trees for these systems. The fine-grained threats considered in these works require decision makers to assign probabilities to specific threats. Reviewing threat trees for Internet voting systems poses a significant burden on election officials, e.g. [7] provides a 18-page threat tree for Internet voting. While this approach facilitates the interpretation of large and complex threat trees, the approach is tailored towards system analysts. Hence, the approach does not foresee the incorporation of election settings by election officials. Volkamer and Grimm [24] propose the concept of resilience terms to capture complex trust distributions of Internet voting schemes and to express which central entities have to be trusted in order to fulfill security requirements. These trust distributions do, however, not incorporate the election setting into the security evaluation and expression. Furthermore, adversaries might consider other attack targets to violate security requirements, for instance voting devices or influencing voters throughout the vote casting process. On the foundation of resilience terms, Schryen et al. [23] develop a quantitative trust metric upon propositional logic. As foundation for their quantification, the authors determine resilience terms for security requirements in distributed systems. Thereafter, they compute the probability that security requirements might be violated on the basis of failure probabilities of individual entities. The approach inherits one essential shortcoming of the resilience term evaluation, namely the fact that the evaluation focuses on central entities of the voting system.

Contribution. We build the election-dependent security evaluation framework upon two specification languages: The language of qualitative security models enables system analysts to specify the security of Internet voting schemes in an election-independent manner, i.e. system analysts specify canonical assumptions about adversarial capabilities under which the scheme enforces security requirements. Intuitively, these canonical assumptions indicate the weakest successful adversary (refer to Pamula et al.’s notion [18]) in terms of abstract capabilities. The language of election settings allows election officials to specify their election settings in terms of expected adversaries and the number of voters. Upon the specification of qualitative security models and an election setting, the framework computes satisfaction degrees of Internet voting schemes with regard to the security requirements within the concrete election setting. Before its actual construction, the requirements for the security evaluation framework are determined. Ultimately, the framework is evaluated against these requirements.

2 Requirements for the Security Evaluation Framework

By its nature, the envisioned framework closely relates to the mathematical concept of a measure (refer for instance to Salamon [22]). We therefore base the requirements for the construction upon the properties of a measure and adapt them to our context. The first property a measure possesses is that it must assign the empty set of the $\sigma$-algebra in the measure space, to the measurement 0. Transferring this property to our context, two requirements are derived:

First, if the Internet voting scheme under investigation faces an adversary that has no capabilities, then the scheme’s satisfaction degrees must be 1 with regard to all security requirements, unless the security requirement can be violated without any adversarial capabilities¹. We refer to this requirement as no capabilities – perfect security. Second, if the Internet voting scheme under investigation proves to be resistant against a specific adversarial capability, then in the presence of any two adversaries that differ only with regard to that capability, the scheme’s satisfaction degrees are equal. We refer to this requirements as capability resistance.

The second property a measure possesses is continuity. In measure theory, the property of continuity is defined by stating that (1) the measurement of the union of a countable infinite sequence of increasing sets $(E_n)_{n \in \mathbb N}$ is equal to the measurement of the last set of the infinite sequence and (2) the measurement of the intersection of an infinite sequence of decreasing sets $(E_n)_{n \in \mathbb N}$ is equal to the measurement of the last set of the infinite sequence. Transferring this property, we require that if the Internet voting scheme under investigation faces a sequence of adversaries, of which the capabilities converge towards the capabilities of a fixed adversary, then also the scheme’s satisfaction degrees in the presence of the sequence of adversaries converges towards the scheme’s satisfaction degree in the presence of the fixed adversary.

The third property a measure possesses is monotonicity. In terms of measure theory, the property ensures that the measurement of a subset of another set from the $\sigma$-algebra must be smaller than the measurement of the set. The fourth property a measure shall must possess is $\sigma$-additivity. In terms of measure theory, the property requires that the measurement of a union of disjoint subsets of the $\sigma$-algebra equals the sum of the measurement of the disjoint subsets. Both properties are transferred to the context of security evaluation for Internet voting schemes. Hence, we require that if the Internet voting scheme under investigation faces two adversaries, of which one is stronger than the other, then the scheme’s satisfaction degrees must not be larger when facing the stronger adversary as compared to the weaker adversary.

3 Construction of the Security Evaluation Framework

The section is dedicated to the construction of the security evaluation framework. We emphasize that the herein presented construction mainly builds upon our previous construction published in 2016 [16]. Before diving into the details of the construction, we provide the necessary definitions. We subsequently show how the security of Internet voting schemes is assessed by evaluating the election-independent security within the concrete election settings.

3.1 Definitions

Before presenting the construction of the security evaluation framework, we recall several definitions [16] while we slightly adapted the notations for this paper.

Definition 1 (Qualitative Adversary Model)

Let an Internet voting scheme A with the set of instantiated capabilities $C^A$ be given. An adversary model $\mathcal {A}^A$, or simply adversary, against scheme A is defined by a subset of instantiated capabilities $C^A$, i.e. $\mathcal {A}^A \subseteq C^A$.

Definition 2 (Qualitative Security Model)

Let an Internet voting scheme A with the set of instantiated capabilities $C^A$ be given. We say that

$$\begin{aligned} \mathcal {M}^{A,r,i}&= (\alpha _1^{A,r,i} \vee \dots \vee \alpha _{\xi ^{A,r,i}}^{A,r,i}) \\&\text { with } \alpha _j^{A,r,i} = (c_{j,1}^{A,r,i} \wedge \dots \wedge c_{j,\lambda _j^{A,r,i}}^{A,r,i}) \text { and } c_{j,k}^{A,r,i} \in C^A \end{aligned}$$

is a qualitative security model of A with regard to security requirement r and impact level i if there exists a set of adversaries $\mathcal S = \{\mathcal {A}_1, \dots , \mathcal {A}_{\xi ^{A,r,i}}\}$ where $\mathcal {A}_j$ is specified by capabilities $\{c_{j,1}^{A,r,i}, \dots , c_{j,\lambda _j^{A,r,i}}^{A,r,i}\}$, such that

• 1. all adversaries $\mathcal {A} \in \mathcal S$ are capable of causing impact i on r, and

• 2. for all adversaries $\mathcal {A} \in \mathcal S$, there is no adversary $\mathcal {A}^\prime \subset \mathcal {A}$ such that $\mathcal {A}^\prime$ is capable of causing impact i on r, and

• 3. for all adversaries $\mathcal {A}^\prime$ capable of causing impact i on r, there is an adversary $\mathcal {A} \in \mathcal S$, such that $\mathcal {A} \subseteq \mathcal {A}^\prime$.

Definition 3 (Resistance Against Abstract Capability)

Let an Internet voting scheme A with the set of instantiated capabilities $C^A$ and the qualitative security models $\mathcal {M}^{A,r,1}, \dots , \mathcal {M}^{A,r,n}$ be given. We say that the scheme A is resistant against capability $C_o \in C$ with regard to requirement r, if for all impact levels $1\le i \le n$ and for all $c^{A,r,i}_{j,k}$ in all $\alpha ^{A,r,i}_{j}$, capability $c^{A,r,i}_{j,k} \in C^A$ is not an instantiation of $C_o$.

Definition 4 (Election Setting)

Given probability distributions $\mathbb {P}_{C_1}, \dots , \mathbb {P}_{C_{l}}$ for all abstract capabilities $C_o \in C$, the number of eligible voters $n_{el}$, and the number of expected voters $n_{ex}$, a tuple of the form

$$E = (\mathbb {P}_{C_1}, \dots , \mathbb {P}_{C_l}, n_{el}, n_{ex})$$

is referred to as an election setting.

While being generous in definition, we simply require election officials to provide uniform distributions U(a, b) for adversarial capabilities probabilities.

3.2 Determination of Satisfaction Degrees in Election Settings

As baseline of the framework, we show how to evaluate qualitative security models within specific election settings. Therefore, it is first shown how the probability of an adversary violating a qualitative security model can be calculated. Thereafter, it is outlined how Monte-Carlo simulations [13] are adapted for the quantitative evaluation of qualitative security models against probabilistic adversaries. The herein described algorithms build upon our previous work [16, Sect. 7.3]. As we noticed that this description is difficult to understand, we present, in the following paragraphs, the algorithm in a more readable manner. We abbreviate the probability of the event that the adversary $\mathcal {A}$ satisfies a security model X or possesses a specific (abstract or instantiated) capability, i.e. $P_{\mathcal {A}} (X = 1)$, by P(X).

Determination of Satisfaction Degrees with Given Probabilities. To determine the satisfaction degree of an Internet voting scheme A with qualitative security models $\mathcal {M}^{A,r,i}$ under given probabilities $P(C_o)$ for all $C_o \in C$ and under n impact levels (the instantiation of impact levels will be explained in the following paragraph), the following function $f(P(C_1), \dots , P(C_l))$ is defined:

• 1. For each instantiated impact level $1\le i \le n$, the probability formula of the qualitative security model is evaluated based on the given probabilities. Note, we show in [16, Sect. 7.1] how to transform qualitative security models into probability formulas.

• 2. For each instantiated impact level $1\le i \le n$, a risk value is calculated by multiplying the normalized impact $\frac{i}{n}$ with the evaluated probability formula of the respective qualitative security model.

• 3. The largest risk value is identified.

• 4. The satisfaction degree estimator is the inverse of the largest risk value.

Extension Towards Probabilistic Adversaries. Rather than precise probabilities, election officials assign probability distributions to adversarial capabilities. While we currently assume that instantiated capabilities are independent, the framework is generated in a way that also caters for dependent instantiated capabilities. Therefore, to determine the satisfaction degree of an Internet voting scheme A with regard to a security requirement r within a specified election setting E, we build upon Monte-Carlo simulations [13]. Therefore, the following process is defined:

Instantiation of Impact Levels. The number of impact levels and probability formulas are instantiated by the number of eligible voters $n_{el}$ and the number of expected voters $n_{ex}$.

Generation of Monte-Carlo based Satisfaction Degree Estimators. The following steps are conducted m times (number Monte-Carlo iterations). The process steps are shown for the j-th Monte-Carlo iteration.

• 1. For each abstract adversarial capability $C_o \in C$, an estimator of the probability $P(C_o)$ is sampled according to the probability distribution $\mathbb {P}_{C_o}$.

• 2. For each vector of probability estimators $p_1^{(j)}, \dots , p_l^{(j)}$, f is called.

Conducting these two steps yields samples of the following random variable:

$$\begin{aligned} M:=f(P(C_1),P(C_2), \dots , P(C_l)) \end{aligned}$$

Processing of Satisfaction Degree Estimators. We define the statistical satisfaction degree of scheme A with regard to requirement r and election setting E as the expected value of random variable M, i.e. $\mathbb {E}(M)$.

• 3. To approximate $\mathbb {E}(M)$ by the m satisfaction degree estimators generated in step 2, namely $e_1, \dots , e_{m}$, the average of these estimators is calculated. Hence, the empirical satisfaction degree $\overline{M^m}$ (in the remainder simply referred to as satisfaction degree) of scheme A with regard to requirement r and election setting E is defined as:

  $$ \overline{M^m}:= \frac{1}{m} (e_1 + \dots + e_{m}) = \frac{1}{m}\sum _{k=1}^m f(p_1^{(k)},p_2^{(k)},\dots , p_{l}^{(k)}) $$

  By the weak law of large numbers, it holds that the empirical satisfaction degree converges in probability towards the statistical satisfaction degree, i.e. $\overline{M^m} \overset{m \rightarrow \infty }{\longrightarrow } \mathbb {E}[M]$.

To evaluate the quality of the empirical satisfaction degree with regard to the statistical satisfaction degree, a confidence interval is calculated. Within this work, we focus on the core of the framework and omit the confidence interval from further consideration (see [16] for further details).

4 Evaluation of the Security Evaluation Framework

After its construction, the security evaluation framework is evaluated with regard to the requirements determined in Sect. 2. The following proofs build upon the weak law of large numbers and hold therefore for a sufficiently large number of Monte-Carlo iterations.

No Capabilities – Perfect Security. The first requirement that the security evaluation framework shall possess is that the satisfaction degree of all schemes must be 1 with regard to all security requirements, if the adversary has no capabilities, unless the security requirement can be violated without any adversarial capabilities. This void of capabilities is equivalent to the absence of randomness as the adversary’s capability is determined. Hence the probability distributions that are passed by the election official, degenerate to deterministic functions. Within a probabilistic framework, such deterministic functions are called constant random variables. Their distribution function is the Dirac delta function $\delta _x$, where $x \in \mathbb {R}$ denotes the point of mass [10]. In particular, it holds $U(a,a + 1/n) \xrightarrow []{n \rightarrow \infty } \delta _a$. Hence, for each $C_o \in C$ the Dirac delta function $\delta _0$ is passed, as there is only one probability that can be assigned to the event that an adversary has capability $C_o$, namely zero.

Theorem 1

Let $\delta _0$ be the distribution function for all abstract capabilities $C_o \in ~C$. The satisfaction degree of scheme A is 1 for all security requirements r, unless the security requirement can be violated without any adversarial capabilities.

Proof

If the probability of having an abstract capability $C_o \in C$ is 0 for all $C_o \in C$, then all instantiated capabilities $c^{A,r,i}_{j,k}$, with $1 \le k \le \lambda ^{A,r,i}_{j}$ for the impact level i have probability 0, i.e. $P(c^{A,r,i}_{j,k})=0$. This leads to $P(\alpha _j^{A,r,i})=0$ and thus

$$P(\bigvee _{j=1}^{\xi ^{A,r,i}} \alpha _j^{A,r,i}) \le \sum _{j=1}^{\xi ^{A,r,i}} P(\alpha _j^{A,r,i})=0.$$

As this holds true for all impact levels, the maximum risk of all impact levels equals 0. Consequently, the satisfaction degree estimator results in 1. Given the fact that the random variables for capability probability have their entire density at 0, each Monte-Carlo iteration assigns the value 0 to all capability probabilities. Hence, the resulting random variable M has its entire density on the value 1, such that $\mathbb {E}(M)=1$.    $\square$

Capability Resistance. The second requirement refers to the resistance of Internet voting schemes against specific abstract adversarial capabilities.

Theorem 2

Let Internet voting scheme A be resistant against abstract capability $C_o$ with regard to requirement r. Let $P(C_1), P(C_2), \dots , P(C_o), \dots , P(C_{l})$ denote random variables for the probabilities of adversarial capabilities $C_1,C_2, \ldots C_o, \dots C_l$. If random variable $P(C_o)$ is replaced by a differently distributed random variable $P(C_o)^\prime$, then the resulting satisfaction degrees of scheme A with regard to requirement r do not differ.

Proof

For the random variables $P(C_{1}),P(C_{2}), \dots , P(C_{o})^\prime , \dots , P(C_{l})$, we denote the random variable generated by the Monte-Carlo simulations by:

$$\begin{aligned} M^\prime :=f(P(C_{1}),P(C_{2}), \dots , P(C_{o})^\prime , \dots , P(C_l)) \end{aligned}$$

Due to A’s resistance, it holds for all $c^{A,r,i}_{j,k}$ in all $\alpha ^{A,r,i}_{j}$ that $c^{A,r,i}_{j,k}$ is no instantiation of $C_o$. Consequently, function f is neither affected by random variable $P(C_o)$ nor by $P(C_o)^\prime$. As a consequence, it holds

$$\begin{aligned} M&= f(P(C_{1}),P(C_{2}), \dots , P(C_{o}), \dots , P(C_l)) \\&= f(P(C_{1}),P(C_{2}), \dots , P(C_{o})^\prime , \dots , P(C_l)) = M^\prime , \end{aligned}$$

and hence $\mathbb {E}(M) = \mathbb {E}(M^\prime ).$    $\square$

Continuity. Election officials provide uniform probability distributions for capability probabilities, e.g. distributions $P(C_i) \sim U(a_i, b_i), i=1,2,\ldots ,l$. To prove continuity of the framework with regard to the expected adversary, we study the framework’s result under sequences of random variables $(P(C_{i,n}))_{n \in \mathbb {N}}$ where $P(C_{i,n}) \sim U(a_i, b_i + 1/n)$ for $i=1,2,\ldots ,l$. We say that continuity is given if the framework’s results are identical under the random variables $P(C_i) \sim U(a_i, b_i)$ and $P(C_{i,n}) \sim U(a_i, b_i + 1/n)$ for n converging to infinity. Formally, this is expressed as follows:

$$\begin{aligned} \mathbb {E}(M_n)&= \mathbb {E}(f(P(C_{1,n}),P(C_{2,n}), \dots ,P(C_{l,n}))) \\&\overset{n \rightarrow \infty }{\longrightarrow } \mathbb {E}(f(P(C_1),P(C_2), \dots ,P(C_{l}))) = \mathbb {E}(M) \end{aligned}$$

Before proving the main theorem, we define two lemmata. Due to space limitations, we omit proofs of the lemmata herein².

Lemma 3

The satisfaction degree estimator for requirement r in scheme A is continuous with regard to a sample probability $P(C_o)$ for any $C_o \in C$.

Definition 5

A sequence of random variables $(X_n)_{n \in \mathbb N}$ weakly converges to a random variable X, if for every continuous function f, it holds

$$\begin{aligned} lim_{n \rightarrow \infty } \int _{X_n} f(x) \mathrm d \mathbb {P}_{X_n} = \int _X f(x) \mathrm d \mathbb {P}_X, \end{aligned}$$

where $\mathbb {P}_{X_n}$ denotes the probability distribution of $X_n$ and $\mathbb {P}_X$ the probability distribution of X, shortly $X_n \overset{d}{\longrightarrow } X$.

Lemma 4

Let $X \sim U(a,b)$ be a uniformly distributed random variable and let $(X_n)_{n \in \mathbb N} \sim U(a,b + 1/n)$ be a sequence of random variables. Then it holds $X_n\overset{d}{\rightarrow } X$.

Theorem 5

Let $P(C_i) \sim U(a_i, b_i), i = 1,2,\ldots ,l$ denote uniformly distributed random variables for the probabilities of adversarial capabilities $C_i$. The satisfaction degree of A with regard to requirement r is continuous with regard to any weakly convergent sequence of random variables $(P(C_{i,n}))_{n \in \mathbb {N}}$ where $P(C_{i,n}) \sim U(a_i, b_i + 1/n)$ for $i=1,2,\ldots ,l.$

Proof

Let $M_n$ denote a framework’s satisfaction degree calculation for a given sample of random variables $p_{i,n} \leftarrow P(C_{i,n}), i=1,2,\ldots l$. For the random variables $P(C_{1,n}),P(C_{2,n}), \dots , P(C_{l,n})$, we denote the resulting random variable generated by f as:

$$\begin{aligned} M_n:=f(P(C_{1,n}),P(C_{2,n}), ...,P(C_{l,n})). \end{aligned}$$

Analogously to $\overline{M^m}$, we define the satisfaction degree calculated by the framework as $\overline{M^m_n} =\frac{1}{m}\sum _{k=1}^m f(p_{1,n}^{(k)},p_{2,n}^{(k)},\dots , p_{l,n}^{(k)})$. By the law of large numbers, $\overline{M^m_n} \overset{m \rightarrow \infty }{\longrightarrow } \mathbb {E}[M_n]$ holds. Given the weak convergence of $P(C_{i,n}) \overset{n \rightarrow \infty }{\longrightarrow } P(C_i)$ (refer to Lemma 4) and the fact that the satisfaction degree estimator is continuous (refer to Lemma 3), it holds:

$$M_n = f(P(C_{1,n}),P(C_{2,n}), \dots ,P(C_{l,n})) \overset{d }{\longrightarrow } f(P(C_1),P(C_2), \dots ,P(C_l)) = M$$

For the sequence of expected values $(\mathbb {E}[M_n])_{n \in \mathbb N}$, it consequently holds:

$$\begin{aligned} | \mathbb {E}[M_n] - \mathbb {E}[M] | = | \mathbb {E}[M_n - M] | \overset{n \rightarrow \infty }{\longrightarrow } 0 \end{aligned}$$

   $\square$

Monotonicity. We study the framework’s result under the random variables $P(C_i) \sim U(a_i, b_i), i=1,2,\ldots ,o,\ldots l$, when $P(C_o)$ is exchanged by a random variable $P(C_o)^\prime \sim U(a^\prime _o,b^\prime _o)$ with $a_o^\prime \ge a_o$ and $b_o^\prime \ge b_o$. We say that monotonicity is given if the framework’s result is larger under $P(C_i) \sim U(a_i, b_i),i=1,2,\ldots ,c,\ldots l$ than under the same set where $P(C_o)$ is exchanged by a random variable $P(C_o)^\prime .$ Formally, this is expressed as follows:

$$\begin{aligned} \mathbb {E}(M^\prime )&= \mathbb {E}(f(P(C_1), P(C_2), \dots , P(C_o)^\prime , \dots , P(C_{l} ))) \\&\le \mathbb {E}(f(P(C_1), P(C_2), \dots , P(C_o), \dots , P(C_{l})) ) = \mathbb {E}(M) \end{aligned}$$

Before proving the main theorem, we define two lemmata. Due to space limitations, we omit proofs of the lemmata herein.

Lemma 6

The satisfaction degree estimator for requirement r in scheme A is non-increasing with regard to a sample probability $P(C_o)$ for any $C_o \in C$.

Lemma 7

Let two random variables $X \sim U(a,b)$ and $Y \sim U(c,d)$ with $c \ge a$ and $d \ge b$ be given. For any non-decreasing function f, it holds:

$$\mathbb {E}[f(X)] \le \mathbb {E}[f(Y)]$$

Theorem 8

Let $P(C_i) \sim U(a_i, b_i), i=1,2,\ldots ,c,\ldots ,l$ denote uniformly distributed random variables for the probabilities of adversarial capabilities $C_i$. The satisfaction degree of A with regard to requirement r is non-increasing with when random variable $P(C_o)$ is exchanged by $P(C_o)^\prime \sim U(a^\prime _o, b^\prime _o)$, with $a^\prime _o \ge a_o$ and $b^\prime _o \ge b_o$.

Proof

For $P(C_1), \dots , P(C_o)^\prime , \dots , P(C_l)$, we denote the resulting random variable generated by f by $M^\prime$, and the respective expected value by $\mathbb {E}[M^\prime ]$.

By Lemma 7 and the fact that the satisfaction degree estimator is non-increasing (refer to Lemma 6), we are able to conclude that

$$\begin{aligned} \mathbb {E}(M^\prime )&= \mathbb {E}(f(P(C_1), P(C_2), \dots , P(C_o)^\prime , \dots , P(C_{l} ))) \\&\le \mathbb {E}( f(P(C_1), P(C_2), \dots , P(C_o), \dots , P(C_{l}))) = \mathbb {E}(M). \end{aligned}$$

   $\square$

5 Conclusion

We constructed an evaluation framework for Internet voting schemes that incorporates the expertise of system analysts and election officials to evaluate schemes within concrete election settings. The framework’s internal consistency was evaluated against requirements derived from measure theory.

We summarize limitations of the constructed framework as basis for future research: The framework’s generic nature requires election officials to estimate probability distributions for abstract adversarial capabilities. Estimating presence probabilities on this level of abstraction might be more challenging than estimating probabilities of concrete capabilities for election officials and should be investigated in the future. Currently, the framework does not incorporate varying adversary motivations, i.e. probability distributions remain invariant over different election types and sizes. We assume adversaries specified by qualitative security models to always succeed. One might consider refining the constructed framework towards assigning success probabilities to qualitative security models.

In the future, the framework will be generalized further: Among these generalizations, the framework will be extended towards the case in which instantiated capabilities might be considered dependent. Based upon its actual concept, the framework will be extended to handle non-uniform probability distributions for abstract capabilities, i.e. normal distributions. Furthermore, we plan to publish the framework as collaborative platform: There, security experts are invited to discuss and jointly determine qualitative security models of Internet voting schemes. After specifying their election setting, the platform should support election officials to determine the most adequate voting scheme(s) for their setting.