Abstract
We propose a new framework for concurrently composable security that relaxes the security notion of UC security. As in previous frameworks, our notion is based on the idea of providing the simulator with super-polynomial resources. However, in our new framework simulators are only given restricted access to the results computed in super-polynomial time. This is done by modeling the super-polynomial resource as a stateful oracle that may directly interact with a functionality without the simulator seeing the communication. We call these oracles “shielded oracles”.
Our notion is fully compatible with the UC framework, i.e., protocols proven secure in the UC framework remain secure in our framework. Furthermore, our notion lies strictly between SPS and Angel-based security, while being closed under protocol composition.
Shielding away super-polynomial resources allows us to apply new proof techniques where we can replace super-polynomial entities by indistinguishable polynomially bounded entities. This allows us to construct secure protocols in the plain model using weaker primitives than in previous Angel-based protocols. In particular, we only use non-adaptive-CCA-secure commitments as a building block in our constructions.
As a feasibility result, we present a constant-round general MPC protocol in the plain model based on standard polynomial-time hardness assumptions that is secure in our framework. Our protocol can be made fully black-box. As a consequence, we obtain the first black-box construction of a constant-round concurrently secure general MPC protocol in the plain model based on polynomial-time hardness assumptions.
B. Broadnax and M. Nagel—This work was supported by the German Federal Ministry of Education and Research within the framework of the project “Sicherheit vernetzter Infrastrukturen (SVI)” in the Competence Center for Applied Security Technology (KASTEL).
N. Döttling—This work was supported by the DAAD (German Academic Exchange Service) under the postdoctoral program (57243032) and in part supported by European Research Council Starting Grant 279447. Research supported in part from a DARPA/ARL SAFEWARE award, AFOSR Award FA9550-15-1-0274, and NSF CRII Award 1464397. The views expressed are those of the author and do not reflect the official policy or position of the Department of Defense, the National Science Foundation, or the U.S. Government.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Cryptographic protocols typically run in a network where multiple protocols interact with each other. Some of them may even act in an adversarial manner. This makes designing protocols that are secure in such a general setting a complicated task. The universal composability (UC) framework [Can01] provides means for designing and analyzing cryptographic protocols in this concurrent setting. More specifically, it captures a security notion that implies two major properties: general concurrent security and modular analysis. The former means that a protocol remains secure even when run in an environment with multiple instances of arbitrary protocols. The latter implies that one can deduce the security of a protocol from its components. Unfortunately, there exist strong impossibility results [CF01, CKL03, Lin03, PR08, KL11] regarding the realizaility of cryptographic tasks in the UC framework: One requires trusted setup assumptions in order to design UC-secure protocols for many cryptographic tasks. UC-secure protocols have thus been constructed based on various setup assumptions [Can+02, Bar+04, Can+07, KLP07, Kat07, CPS07, LPV09, Dac+13]. However, if the trusted setup is compromised, all security guarantees are lost. In general, one would like to base the security of cryptographic protocols on as little trust as possible.
In order to drop the requirement for trusted setup, relaxed notions of security have been developed. One of the most prominent solutions is “UC security with super-polynomial time simulators” (SPS), introduced in [Pas03]. In this model, the simulator is allowed to run in super-polynomial time, thereby overcoming the impossibility results. Various multi-party computation protocols without trusted setup that satisfy this notion have been constructed, e.g., [Pas03, BS05, LPV09, LPV12, Gar+12, Dac+13, Ven14]. SPS security weakens the security of the UC framework because the simulator, being able to run in super-polynomial time, may now be able to carry out stronger attacks in the ideal setting. Still, this security notion is meaningful, since for many cryptographic tasks the ideal setting has an information-theoretic nature. Contrary to UC security, however, security in this model is not closed under protocol composition. As a consequence, this notion neither supports general concurrent security nor modular analysis.
“Angel-based security” [PS04] overcomes these issues. In this model, both the adversary and the simulator have access to an oracle called “(Imaginary) Angel” that provides super-polynomial resources for specific computational problems. Many general MPC protocols without setup have been constructed in the Angel-based framework [PS04, MMY06, CLP10, LP12, KMO14, Kiy14, Goy+15, HV16]. Like UC-security, this notion is closed under protocol composition. Furthermore, Angel-based security implies SPS security. In fact, it provides a stronger security notion since the simulator has only access to specific super- polynomial computations. [CLP10] later recast the Angel-based security model in the extended UC (EUC) framework [Can+07] and dubbed their notion “UC with super-polynomial helpers”. In contrast to the non-interactive and stateless Angels in previous works, the “helpers” in [CLP10] are highly interactive and stateful.
In this work, we take this framework a step further. In our new framework, simulators only have restricted access to the results computed in super-polynomial time. More specifically, we model the super-polynomial resources as stateful oracles that are “glued” to an ideal functionality. These oracles may directly interact with the functionality without the simulator observing the communication. The outputs of these oracles are therefore “shielded away” from the simulator. As with Angel-based security, our notion implies SPS security. Moreover, it can be shown that our notion is in fact strictly weaker than Angel-based security. Furthermore, our notion comes with a composition theorem guaranteeing general concurrent security. While modular analysis is not directly implied for technical reasons, using our composition theorem one can achieve modular analysis by constructing protocols with strong composition features. Protocols with these features can be “plugged” into large classes of UC-secure protocols in such a way that the composed protocol is secure in our framework. As a proof of concept, we construct a constant-round commitment scheme with such features.
In order to obtain a composable security notion, environments are “augmented” in our framework, i.e., they may invoke additional (ideal) protocols that include shielded oracles. Since the super-poly computations in these protocols are hidden away, these augmented environments have the unique property that they do not “hurt” protocols proven secure in the UC framework. Therefore, our notion is in fact fully compatible with the UC framework. Moreover, our concept of “shielding away” super-polynomial resources allows us to apply new proof techniques not applicable in previous frameworks: We are able to replace entities involving super-polynomial resources in our proofs by indistinguishable polynomially bounded entities. This allows us to construct (constant-round) protocols using weaker primitives than in previous Angel-based protocols.
1.1 Our Results
We propose a new framework that is based on the idea of granting simulators only restricted access to the results of a super-polynomial oracle. We have the following results:
-
New Composable Security Notion: Our notion of security is closed under general composition, it implies SPS security and is strictly weaker than Angel-based security (Theorem 9, Proposition 8, Theorem 17).
-
UC-compatibility: Protocols proven secure in the UC framework are also secure in our new framework (Theorem 12, Corollary 13).
-
Modular Composition: As a proof of concept, we present a constant-round commitment scheme in the plain model based on OWPs that is secure in our framework and can be “plugged” into a large class of UC-secure protocols, such that the composite protocol is secure in our framework. Furthermore, this construction can be made fully black-box based on homomorphic commitment schemes. To our best knowledge, this is the first constant-round (black-box) commitment scheme in the plain model based on a standard polynomial-time hardness assumption with such a composition feature (Theorem 21, Corollary 22, Corollary 23, Theorem 26, Corollary 30).
-
Constant-round (black-box) MPC: We present a modular construction of a constant-round general MPC protocol in the plain model based on standard polynomial-time hardness assumptions that is secure in our framework. This protocol can be made fully black-box based on homomorphic commitment schemes. As a consequence, we obtain the first black-box construction of a constant-round concurrently secure general MPC protocol in the plain model based on polynomial-time hardness assumptions (Theorem 31).
-
Building on non-adaptive CCA-commitments: Our constructions require weaker primitives than previous Angel-based protocols. Specifically, it suffices to use non-adaptive CCA-secure commitment schemes as a building block in our constructions instead of CCA-secure commitment schemes used previously (Theorem 21, Theorem 26).
2 Related Work
The frameworks most related to ours are SPS and Angel-based security.
SPS security, introduced by [Pas03], provides a meaningful security notion for many cryptographic tasks such as commitment schemes or oblivious transfer. However, SPS security does not come with a composition theorem. There exist many constructions (in the plain model) satisfying this notion, e.g., [Pas03, BS05, LPV09, LPV12, Gar+12, Dac+13, Ven14]. Notably, [LPV12, Gar+12] constructed (non-black-box) constant-round general MPC protocols based on standard polynomial-time hardness assumptions.
Angel-based security [PS04] implies SPS security and comes with a composition theorem. Various general MPC protocols without setup have been constructed in the Angel-based setting [PS04, MMY06, CLP10, LP12, KMO14, Kiy14, Goy+15, HV16]. Some rely on non-standard or super-polynomial time assumptions [PS04, MMY06, KMO14]. The construction in [CLP10] is the first one to rely on standard polynomial-time assumptions, but has non-constant round complexity. Later works [Goy+15, Kiy14] have improved the round-complexity, while also relying on standard assumptions. The most round-efficient construction based on standard polynomial-time assumptions is [Kiy14], which requires \(\widetilde{O}(\log ^{2}n)\) rounds and makes only black-box use of the underlying cryptographic primitive. Some Angels in the literature, e.g., [CLP10, KMO14, Kiy14, Goy+15] come with a feature called “robustness” which guarantees that any attack mounted on a constant-round protocol using this angel can be carried out by a polytime adversary with no angels. Protocols proven secure for robust Angels can be “plugged” into UC-secure protocols, resulting in Angel-secure protocols. All known constructions for robust Angels based on standard polytime assumptions require a super-constant number of rounds. Moreover, [CLP13] construct a (super-constant-round) protocol that is secure in the Angel-based setting and additionally preserves certain security properties of other protocols running in the system. They call such protocols “environmentally friendly”.
We want to note that other security notions in the concurrent setting have been proposed that are not based on the idea of simulators with super-polynomial resources. The “multiple ideal query model” [GJO10, GJ13, GGJ13, CGJ15] considers simulators that are allowed to make more than one output query per session to the ideal functionality. Another (not simulation-based) notion is “input indistinguishability” [MPR06, Gar+12] which guarantees that an adversary cannot decide which inputs have been used by the honest protocol parties. We note that this security notion is incomparable to ours.
3 Shielded Oracles
3.1 Definition of the Framework
Our model is based on the universal composability framework (UC). In this model, a protocol \(\pi \) carrying out a given task is defined to be secure by comparing it to an ideal functionality \(\mathcal {F}\), which is a trusted and incorruptible party that carries out a given task in an ideally secure way. \(\pi \) is said to be secure if it “emulates” \(\mathcal {F}\).
While the plain UC model leaves open how session identifiers and corruptions are organized, we follow the convention that both must be consistent with the hierarchical order of the protocols: The session identifier (\(\mathord { sid }\)) of a sub-protocol must be an extension of the session id of the calling protocol. Likewise, in order to corrupt a sub-party, an adversary must corrupt all parties that are above that sub-party in the protocol hierarchy.
We relax the UC security notion by introducing a super-polynomial time machine that may aid the simulator. This machine is modeled as a stateful oracle \(\mathcal {O}\) that is “glued” to an the ideal functionality \(\mathcal {F}\). \(\mathcal {O}\) may freely interact with the simulator and \(\mathcal {F}\). However, the simulator does not “see” the communication between \(\mathcal {O}\) and \(\mathcal {F}\). Since the output of the oracle is partially hidden from the simulator, we call \(\mathcal {O}\) a shielded oracle.
Definition 1
(Shielded oracles). A shielded oracle is a stateful oracle \(\mathcal {O}\) that can be implemented in super-polynomial time. By convention, the outputs of a shielded oracle \(\mathcal {O}\) are of the form  or
or  .
.
The simulator is allowed to communicate with the functionality only via the shielded oracle. This way, the shielded oracle serves as an interface that carries out specific tasks the simulator could not do otherwise. The communication between the shielded oracle and the functionality is hidden away from the simulator. The actions of the shielded oracle may depend on the session identifier (\(\mathord { sid }\)) of the protocol session as well as the party identifiers of the corrupted parties.
Definition 2
( \(\mathcal {O}\) -adjoined functionalities). Given a functionality \(\mathcal {F}\) and a shielded oracle \(\mathcal {O}\), define the interaction of the \(\mathcal {O}\) -adjoined functionality \(\mathcal {F}^{\mathcal {O}}\) in an ideal protocol execution with session identifier \(\mathord { sid }\) as follows:
-
\(\mathcal {F}^{\mathcal {O}}\) internally runs an instance of \(\mathcal {F}\) with session identifier \(\mathord { sid }\).
-
When receiving the first message x from the adversary, \(\mathcal {F}^{\mathcal {O}}\) internally invokes \(\mathcal {O}\) with input \((\mathord { sid }, x)\).
All subsequent messages from the adversary are passed to \(\mathcal {O}\).
-
Messages between the honest parties and \(\mathcal {F}\) are forwarded.
-
Corruption messages are forwarded to \(\mathcal {F}\) and \(\mathcal {O}\).
-
When \(\mathcal {F}\) sends a message y to the adversary, \(\mathcal {F}^{\mathcal {O}}\) passes y to \(\mathcal {O}\).
-
The external write operations of \(\mathcal {O}\) are treated as follows:
-
If \(\mathcal {O}\) sends
 , \(\mathcal {F}^{\mathcal {O}}\) sends y to \(\mathcal {F}\).
, \(\mathcal {F}^{\mathcal {O}}\) sends y to \(\mathcal {F}\). -
If \(\mathcal {O}\) sends
 , \(\mathcal {F}^{\mathcal {O}}\) sends y to the adversary.
, \(\mathcal {F}^{\mathcal {O}}\) sends y to the adversary.
-
Let \(\mathord {\mathrm {IDEAL}}(\mathcal {F}^{\mathcal {O}})\) be the ideal protocol with functionality \(\mathcal {F}^{\mathcal {O}}\) as defined in [Can01].
In order to obtain a composable security notion, we introduce the notion of augmented environments. Augmented environments are UC environments that may invoke, apart form the challenge protocol, polynomially many instances of \(\mathord {\mathrm {IDEAL}}(\mathcal {F}^{\mathcal {O}})\) for a given functionality \(\mathcal {F}^{\mathcal {O}}\). The only restriction is that the session identifiers of these instances as well as the session identifier of the challenge protocol are not extensions of one another.
Augmented environments may send inputs to and receive outputs from any invoked instance of \(\mathord {\mathrm {IDEAL}}(\mathcal {F}^{\mathcal {O}})\). In addition, augmented environments can play the role of any adversary via the adversary’s interface of the functionality. In particular, augmented environments may corrupt parties sending the corresponding corruption message as input to the functionality.
In what follows we give a definition of an execution experiment with an \(\mathcal {F}^{\mathcal {O}}\)-augmented environment. For simplicity and due to space constraints, the description is kept informal.
Definition 3
(The \(\mathcal {F}^{\mathcal {O}}\) -execution experiment). An execution of a protocol \(\sigma \) with adversary \(\mathcal {A}\) and an \(\mathcal {F}^{\mathcal {O}}\) -augmented environment \(\mathcal {Z}\) on input \(a\in \{0,1\}^{\mathord {*}}\) and with security parameter \(n \in \mathbb {N}\) is a run of a system of interactive Turing machines (ITMs) with the following restrictions:
-
First, \(\mathcal {Z}\) is activated on input \(a \in \{0,1\}^{*}\).
-
The first ITM to be invoked by \(\mathcal {Z}\) is the adversary \(\mathcal {A}\).
-
\(\mathcal {Z}\) may invoke a single instance of a challenge protocol, which is set to be \(\sigma \) by the experiment. The session identifier of \(\sigma \) is determined by \(\mathcal {Z}\) upon invocation.
-
\(\mathcal {Z}\) may pass inputs to the adversary or the protocol parties of \(\sigma \).
-
\(\mathcal {Z}\) may invoke, send inputs to and receive outputs from instances of \(\mathord {\mathrm {IDEAL}}(\mathcal {F}^{\mathcal {O}})\) as long as the session identifiers of these instances as well as the session identifier of the instance of \(\sigma \) are not extensions of one another.
-
The adversary \(\mathcal {A}\) may send messages to protocol parties of \(\sigma \) as well as to the environment.
-
The protocol parties of \(\sigma \) may send messages to \(\mathcal {A}\), pass inputs to and receive outputs from subparties and give outputs to \(\mathcal {Z}\).
Denote by \(\mathord {\mathrm {Exec}}\bigl (\sigma , \mathcal {A}, \mathcal {Z}[\mathcal {F}^{\mathcal {O}}]\bigr )(n, a)\) the output of the \(\mathcal {F}^{\mathcal {O}}\)-augmented environment \(\mathcal {Z}\) on input \(a \in \{0,1\}^{*}\) and with security parameter \(n \in \mathbb {N}\) when interacting with \(\sigma \) and \(\mathcal {A}\) according to the above definition.
Define \(\mathord {\mathrm {Exec}}\bigl (\sigma , \mathcal {A}, \mathcal {Z}[\mathcal {F}^{\mathcal {O}}]\bigr ) = \bigl \lbrace \mathord {\mathrm {Exec}}\bigl (\sigma , \mathcal {A}, \mathcal {Z}[\mathcal {F}^{\mathcal {O}}])(n, a)\bigr \rbrace _{n \in \mathbb {N}, a \in \{0,1\}^{\mathord {*}}}\)
We will now define security in our framework in total analogy to the UC framework:
Definition 4
(
\(\mathcal {F}^{\mathcal {O}}\)
-emulation). Let \(\pi \) and \(\phi \) be protocols. \(\pi \) is said to emulate \(\phi \) in the presence of \(\mathcal {F}^{\mathcal {O}}\)-augmented environments, denoted by  , if for any PPT adversary \(\mathcal {A}\) there exists a PPT adversary (called “simulator”) \(\mathcal {S}\) such that for every \(\mathcal {F}^{\mathcal {O}}\)-augmented PPT environment \(\mathcal {Z}\) it holds that
, if for any PPT adversary \(\mathcal {A}\) there exists a PPT adversary (called “simulator”) \(\mathcal {S}\) such that for every \(\mathcal {F}^{\mathcal {O}}\)-augmented PPT environment \(\mathcal {Z}\) it holds that
Throughout this paper, we only consider static corruptions.
3.2 Basic Properties and Justification
In this section, we show that that our security notion is transitive and that the dummy adversary is complete within this notion. As a justification for our notion, we show that it implies super-polynomial time simulator (SPS) security.
Definition 5
( \(\mathcal {F}^{\mathcal {O}}\) -emulation with respect to the dummy adversary). The dummy adversary \(\mathcal {D}\) is an adversary that when receiving a message \((\mathord { sid }, \mathord { pid }, m)\) from the environment, sends m to the party with party identifier \(\mathord { pid }\) and session identifier \(\mathord { sid }\), and that, when receiving m from the party with party identifier \(\mathord { pid }\) and session identifier \(\mathord { sid }\), sends \((\mathord { sid }, \mathord { pid }, m)\) to the environment.
Let \(\pi \) and \(\phi \) be protocols. \(\pi \) is said to emulate \(\phi \) in the presence of \(\mathcal {F}^{\mathcal {O}}\)-augmented environments with respect to the dummy adversary, if
Proposition 6
(Completeness of the dummy adversary). Let \(\pi \) and \(\phi \) be protocols. Then, \(\pi \) emulates \(\phi \) in the presence of \(\mathcal {F}^{\mathcal {O}}\)-augmented environments if and only if \(\pi \) emulates \(\phi \) in the presence of \(\mathcal {F}^{\mathcal {O}}\)-augmented environments with respect to the dummy adversary.
The proof is almost exactly the same as in [Can01], and therefore only given in the full version of this work. The proof of transitivity is omitted here, too.
Proposition 7
(Transitivity). Let \(\pi _{1},\pi _{2}, \pi _{3}\) be protocols. If  and
and  then it holds that
then it holds that  .
.
In order to justify our new notion, we prove that security with respect to \(\mathcal {F}^{\mathcal {O}}\)-emulation implies security with respect to SPS-emulation which we will denote by  . See the full version for a formal definition of
. See the full version for a formal definition of  . The proof is straightforward: View the oracle as part of the simulator. This simulator runs in super-polynomial time, hence can be simulated by an SPS-simulator.
. The proof is straightforward: View the oracle as part of the simulator. This simulator runs in super-polynomial time, hence can be simulated by an SPS-simulator.
Proposition 8
(
\(\mathcal {F}^{\mathcal {O}}\)
-emulation implies SPS-emulation). Let \(\mathcal {O}\) be a shielded oracle. Assume  . Then it holds that
. Then it holds that  .
.
3.3 Universal Composition
A central property of the UC framework is the universal composition theorem. This theorem guarantees that the security of a protocol is closed under protocol composition. This means that security guarantees can be given for a UC-secure protocol even if multiple other protocols interact with this protocol in a potentially adversarial manner. We prove a similar theorem in our framework. More specifically, we generalize the universal composition theorem to also include \(\mathcal {F}^{\mathcal {O}}\)-hybrid protocols.
Theorem 9
(Composition theorem). Let \(\mathcal {O}\) be a shielded oracle, \(\mathcal {F}\) and \(\mathcal {G}\) functionalities.
-
1.
(Polynomial hybrid protocols) Let \(\pi \), \(\rho ^{\mathcal {G}}\) be protocols. Assume
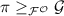 . Then it holds that
. Then it holds that 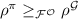 .
. -
2.
(\(\mathcal {F}^{\mathcal {O}}\) -hybrid protocols) Let \(\pi \) be a protocol, \(\rho ^{\mathcal {F}^{\mathcal {O}}}\) a protocol in the \(\mathcal {F}^{\mathcal {O}}\)-hybrid model. Assume
 . Then it holds that
. Then it holds that 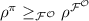 .
.
Proof
(of the second statement). For single instance composition (where \(\rho \) calls only a single instance of \(\pi \)), treat \(\rho \) as part of the environment and use the premise that  .
.
For the general case iteratively apply the single instance composition theorem. In each iteration a new instance of \(\mathord {\mathrm {IDEAL}}(\mathcal {F}^{\mathcal {O}})\) is replaced by an instance of \(\pi \), and the remaining instances of \(\pi \), \(\mathord {\mathrm {IDEAL}}(\mathcal {F}^{\mathcal {O}})\) and \(\rho \) are treated as part of the augmented environment. The claim then follows using transitivity. \(\square \)
The universal composition theorem in the UC framework has two important implications: general concurrent security and modular analysis. The former means that a protocol remains secure even when run in an environment with multiple instances of arbitrary protocols. The latter implies that one can deduce the security of a protocol from its components.
Theorem 9 directly implies general concurrent security (with super-polynomial time simulators). However, modular analysis is not directly implied by Theorem 9. This is because the oracle \(\mathcal {O}\) may contain all “complexity” of the protocol \(\pi \), i.e., proving security of \(\rho ^{\mathcal {F}^{\mathcal {O}}}\) may be as complex as proving security of \(\rho ^\pi \).
Still, one can use Theorem 9 to achieve modular analysis by constructing secure protocols with strong composition features. A protocol \(\pi \) with such composition features allows analyzing the security of a large class of protocols \(\rho ^{\mathcal {F}}\) in the UC framework and achieve security in our framework when replacing \(\mathcal {F}\) with \(\pi \). As a proof of concept, we will show, using Theorem 9, that a large a class of protocols in the \(\mathcal {F}_\text {com}\)-hybrid model can be composed with a commitment protocol presented in this paper (Theorem 26).
The following is a useful extension of Theorem 9 for multiple oracles. The reader is referred to the full version for a proof.
Corollary 10
(Composition theorem for multiple oracles). Let \(\mathcal {O}\), \(\mathcal {O}'\) be shielded oracles. Assume that  and
and  . Then there exists a shielded oracle \(\mathcal {O}''\) such that
. Then there exists a shielded oracle \(\mathcal {O}''\) such that  .
.
3.4 Polynomial Simulatability
We show a unique feature of our framework: For appropriate oracles to be defined below, augmented environments do not “hurt” UC-secure protocols. This means that a protocol that was proven secure in the UC framework is secure in our framework, too. This makes our security notion fully compatible with UC security.
Definition 11
(Polynomial simulatability). Let \(\mathcal {O}\) be a shielded oracle, \(\mathcal {F}\) a functionality. Say that \(\mathcal {O}\) adjoined to \(\mathcal {F}\) is polynomially simulatable if there exists a (PPT) functionality \(\mathcal {M}\) such that for all \(\mathcal {F}^{\mathcal {O}}\)-augmented environments \(\mathcal {Z}\) it holds that

If a functionality \(\mathcal {F}^{\mathcal {O}}\) is polynomially simulatable then the super-polynomial power of the oracle \(\mathcal {O}\) is totally “shielded away” from the environment. Note that in Definition 11, indistinguishability must hold for augmented environments not only for polynomial environments.
As a consequence, \(\mathcal {F}^{\mathcal {O}}\)-augmented environments can be replaced by efficient environments if \(\mathcal {F}^{\mathcal {O}}\) is polynomially simulatable.
Theorem 12
(Reduction to polynomial time environments). Let \(\mathcal {O}\) be a shielded oracle and \(\mathcal {F}\) a functionality such that \(\mathcal {F}^{\mathcal {O}}\) is polynomially simulatable. Let \(\pi \), \(\phi \) be protocols that are PPT or in the \(\mathcal {F}^{\mathcal {O}}\)-hybrid model. It holds that

where the right-hand side means that \(\pi \) emulates \(\phi \) in the presence of all \(\mathcal {F}^{\mathcal {O}}\)-augmented environments that never invoke an instance of \(\mathord {\mathrm {IDEAL}}(\mathcal {F}^{\mathcal {O}})\).
Proof
Poly-emulation implies \(\mathcal {F}^{\mathcal {O}}\) -emulation: Replace all instances of \(\mathord {\mathrm {IDEAL}}(\mathcal {F}^{\mathcal {O}})\) with instances of \(\mathcal {M}\) using the fact that \(\mathcal {F}^{\mathcal {O}}\) is polynomially simulatable. Treat all instances of \(\mathcal {M}\) as part of the environment. This new environment runs in polynomial time. Substitute \(\pi \) by \(\phi \) using the premise. Replace all instances of \(\mathcal {M}\) with instances of \(\mathord {\mathrm {IDEAL}}(\mathcal {F}^{\mathcal {O}})\) again. The statement follows.
The converse is trivial. \(\square \)
As augmented environments that never invoke instances of \(\mathord {\mathrm {IDEAL}}(\mathcal {F}^{\mathcal {O}})\) are identical to an UC-environment, the following corollary immediately follows.
Corollary 13
(Compatibility with the UC framework). Let \(\mathcal {O}\) be a shielded oracle and \(\mathcal {F}\) a functionality such that \(\mathcal {F}^{\mathcal {O}}\) is polynomially simulatable. It holds that

Note that this does not contradict the classical impossibility results for the plain UC framework (cp. [CF01]): If  for a polynomially simulatable \(\mathcal {F}^{\mathcal {O}}\), then this only means that
for a polynomially simulatable \(\mathcal {F}^{\mathcal {O}}\), then this only means that  , but it does not follow that
, but it does not follow that  . Although the super-polynomial power of \(\mathcal {O}\) is shielded away from the outside, it is indeed necessary.
. Although the super-polynomial power of \(\mathcal {O}\) is shielded away from the outside, it is indeed necessary.
Replacing augmented environments with efficient environments will be a key property in various proofs later in this paper. In particular, it will allow us to prove the security of protocols in our framework using relatively weak primitives such as non-adaptively-secure-CCA commitments as opposed to CCA-secure commitments, which are commonly used in Angel-based protocols.
Next, we show that by suitably tweaking a given oracle \(\mathcal {O}\) one can make \(\mathcal {F}^{\mathcal {O}}\) polynomially simulatable while preserving the security relation.
Lemma 14
(Derived oracle). Let \(\mathcal {O}\) be a shielded oracle such that  . Then there exists a shielded oracle \(\mathcal {O}'\) such that
. Then there exists a shielded oracle \(\mathcal {O}'\) such that  and additionally \(\mathcal {O}'\) adjoined to \(\mathcal {F}\) is polynomially simulatable.
and additionally \(\mathcal {O}'\) adjoined to \(\mathcal {F}\) is polynomially simulatable.
Proof
Since \(\pi \) emulates \(\mathcal {F}^{\mathcal {O}}\), there exists a simulator \(\mathcal {S}_{\mathcal {D}}\) for the dummy adversary \(\mathcal {D}\). Define the shielded oracle \(\mathcal {O}'\) as follows: \(\mathcal {O}'\) internally simulates \(\mathcal {S}_{\mathcal {D}}\) and \(\mathcal {O}\), passes each message \(\mathcal {S}_{\mathcal {D}}\) sends to \(\mathcal {F}\) to \(\mathcal {O}\), sends each  output from \(\mathcal {O}\) to \(\mathcal {F}\) and each
output from \(\mathcal {O}\) to \(\mathcal {F}\) and each  output from \(\mathcal {O}\) to \(\mathcal {S}_{\mathcal {D}}\), and forwards the communication between \(\mathcal {S}_{\mathcal {D}}\) and the environment. By construction, for all \(\mathcal {F}^{\mathcal {O}}\)-augmented environments \(\mathcal {Z}\) it holds that
output from \(\mathcal {O}\) to \(\mathcal {S}_{\mathcal {D}}\), and forwards the communication between \(\mathcal {S}_{\mathcal {D}}\) and the environment. By construction, for all \(\mathcal {F}^{\mathcal {O}}\)-augmented environments \(\mathcal {Z}\) it holds that

It follows from Proposition 6 that  and
and  . Since \(\mathcal {S}_{\mathcal {D}}\) runs in polynomial time, \(\mathcal {F}^{\mathcal {O}}\)-augmented environments can simulate \(\mathcal {F}^{\mathcal {O}'}\)-augmented environments. Therefore,
. Since \(\mathcal {S}_{\mathcal {D}}\) runs in polynomial time, \(\mathcal {F}^{\mathcal {O}}\)-augmented environments can simulate \(\mathcal {F}^{\mathcal {O}'}\)-augmented environments. Therefore,  and
and  . The theorem follows by defining \(\mathcal {M}\) to be the functionality that internally simulates the protocol \(\pi \). \(\square \)
. The theorem follows by defining \(\mathcal {M}\) to be the functionality that internally simulates the protocol \(\pi \). \(\square \)
The following corollary shows that UC-secure protocols can be used as sub-protocols in protocols proven secure in our framework, while preserving security.
Corollary 15
(Composition with UC-secure protocols). Let \(\pi \), \(\rho ^{\mathcal {F}}\) be protocols such that  and
and  . Then there exists a shielded oracle \(\mathcal {O}'\) such that
. Then there exists a shielded oracle \(\mathcal {O}'\) such that

Proof
Since \(\rho ^{\mathcal {F}}\) is PPT there exists a shielded oracle \(\mathcal {O}'\) such that \(\mathcal {G}^{\mathcal {O}'}\) is polynomially simulatable and  by Lemma 14. From Corollary 13 it follows that
by Lemma 14. From Corollary 13 it follows that  . The statement then follows from the composition theorem and the transitivity of \(\mathcal {G}^{\mathcal {O}'}\)-emulation. \(\square \)
. The statement then follows from the composition theorem and the transitivity of \(\mathcal {G}^{\mathcal {O}'}\)-emulation. \(\square \)
The last result demonstrates the compatibility of our framework with the UC framework again. While it is much more desireable to “plug” a protocol proven secure in our framework into a UC secure protocol—in order to obtain a secure protocol in the plain model (this will be addressed in Theorem 26 and Corollary 30)—doing it the other way around is still a convenient property. For instance, it allows one to instantiate “auxiliary” functionalities such as authenticated channels \(\mathcal {F}_{\text {auth}}\) or secure channels \(\mathcal {F}_{\text {SMT}}\), while preserving security.
3.5 Relation with Angel-Based Security
A natural question that arises is how our security notion compares to Angel-based security. We will prove that for a large class of Angels (which to our best knowledge includes all Angels that can be found in the literature), Angel-based security implies our security notion. However, assuming the existence of one-way functions, the converse does not hold. Thus, our notion is strictly weaker than Angel-based security.
In the following, we denote by  if \(\pi \) securely realizes \(\phi \) with respect to an angel \(\varGamma \). Note that the following results also hold for “UC with super-polynomial helpers” put forward by [CLP10].
if \(\pi \) securely realizes \(\phi \) with respect to an angel \(\varGamma \). Note that the following results also hold for “UC with super-polynomial helpers” put forward by [CLP10].
Definition 16
(Session-respecting Angel (informal)). (See the full version for a formal treatment.) An Angel is called session-respecting if its internal state can be regarded as a vector with independent components for each session the Angel is queried for.
Theorem 17
(Relation between angels and shielded oracles)
-
1.
Assume
 for an imaginary Angel \(\varGamma \). If \(\varGamma \) is session-respecting, then there exists a shielded oracle \(\mathcal {O}\) such that
for an imaginary Angel \(\varGamma \). If \(\varGamma \) is session-respecting, then there exists a shielded oracle \(\mathcal {O}\) such that 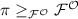 .
. -
2.
Assume the existence of one-way functions. Then there exists a protocol \(\rho \) (in the \(\mathcal {F}_\text {auth}\)-hybrid model), a functionality \(\mathcal {G}\) and a shielded oracle \(\mathcal {O}\) s.t.
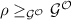 but no imaginary angel \(\varGamma \) can be found such that
but no imaginary angel \(\varGamma \) can be found such that  holds.
holds.
We give a proof sketch below. See the full version for a more formal treatment.
Proof
(Idea of proof)
-
1.
We consider the dummy adversary \(\mathcal {D}\) only. Since
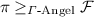 we have $$\begin{aligned} \exists \,\mathcal {S}_\mathcal {D}^\varGamma \ \forall \,\mathcal {Z}^\varGamma : \mathord {\mathrm {Exec}}( \pi , \mathcal {D}^\varGamma , \mathcal {Z}^\varGamma ) \equiv \mathord {\mathrm {Exec}}( \mathcal {F}, \mathcal {S}_\mathcal {D}^\varGamma , \mathcal {Z}^\varGamma ) \end{aligned}$$(8)
we have $$\begin{aligned} \exists \,\mathcal {S}_\mathcal {D}^\varGamma \ \forall \,\mathcal {Z}^\varGamma : \mathord {\mathrm {Exec}}( \pi , \mathcal {D}^\varGamma , \mathcal {Z}^\varGamma ) \equiv \mathord {\mathrm {Exec}}( \mathcal {F}, \mathcal {S}_\mathcal {D}^\varGamma , \mathcal {Z}^\varGamma ) \end{aligned}$$(8)Now, we consider the experiment with shielded oracle \(\mathcal {O}= \mathcal {S}_\mathcal {D}^\varGamma \), ideal functionality \(\mathcal {F}^{\mathcal {O}}\) and simulator \(\mathcal {S}= \mathcal {S}_\mathcal {D}\). Note that the code of \(\mathcal {S}_\mathcal {D}\) is executed twice: by \(\mathcal {O}\) and by \(\mathcal {S}\). As \(\varGamma \) is assumed to be session-respecting the operation of the Angel is split between \(\mathcal {O}\), that internally runs a copy of the Angel for all queries within the challenge session, and the simulator \(\mathcal {S}\), that handles all remaining queries having access to the global Angel \(\varGamma \). It follows
$$\begin{aligned} \mathord {\mathrm {Exec}}( \mathcal {F}, \mathcal {S}_\mathcal {D}^\varGamma , \mathcal {Z}^\varGamma ) \equiv \mathord {\mathrm {Exec}}( \mathcal {F}^{\mathcal {O}}, \mathcal {S}^\varGamma , \mathcal {Z}^\varGamma ) \end{aligned}$$(9)In order to prove
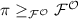 we need to show $$\begin{aligned} \exists \,\mathcal {S}\ \forall \,\mathcal {Z}: \mathord {\mathrm {Exec}}( \pi , \mathcal {D}, \mathcal {Z}[\mathcal {F}^{\mathcal {O}}] ) \equiv \mathord {\mathrm {Exec}}( \mathcal {F}^{\mathcal {O}}, \mathcal {S}, \mathcal {Z}[\mathcal {F}^{\mathcal {O}}] ) \end{aligned}$$(10)
we need to show $$\begin{aligned} \exists \,\mathcal {S}\ \forall \,\mathcal {Z}: \mathord {\mathrm {Exec}}( \pi , \mathcal {D}, \mathcal {Z}[\mathcal {F}^{\mathcal {O}}] ) \equiv \mathord {\mathrm {Exec}}( \mathcal {F}^{\mathcal {O}}, \mathcal {S}, \mathcal {Z}[\mathcal {F}^{\mathcal {O}}] ) \end{aligned}$$(10)and we claim that \(\mathcal {S}\) from above suffices. Assume that (10) does not hold, i.e. there is a \(\mathcal {Z}[\mathcal {F}^{\mathcal {O}}]\) that can distinguish between interacting with \(\pi \) and \(\mathcal {D}\) or with \(\mathcal {F}^{\mathcal {O}}\) and \(\mathcal {S}\). Then there exists an environment \(\mathcal {Z}^\varGamma \) that internally runs \(\mathcal {F}^{\mathcal {O}}\) simulating all augmented \(\mathcal {F}^{\mathcal {O}}\)-sessions by means of the global \(\varGamma \) and thus contradicts (9).
-
2.
Let \(\widetilde{\rho }\) be a commitment protocol such that
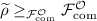 and \(\mathcal {O}\) adjoined to \(\mathcal {F}_\text {com}\) is poly-simulatable. One can find such a protocol using the Angel-based protocol in [CLP10], part 1 of this theorem and Lemma 14, assuming the existence of one-way functions. Define the protocol \(\rho \) to be identical to \(\widetilde{\rho }\) except for the following instruction:
and \(\mathcal {O}\) adjoined to \(\mathcal {F}_\text {com}\) is poly-simulatable. One can find such a protocol using the Angel-based protocol in [CLP10], part 1 of this theorem and Lemma 14, assuming the existence of one-way functions. Define the protocol \(\rho \) to be identical to \(\widetilde{\rho }\) except for the following instruction:Before the actual commit phase begins, the receiver chooses \(a_1, \ldots , a_n\) uniformly at random (n is the security parameter) and sends \(\mathord {\mathrm {Commit}}(a_i)\) \((i = 1, \ldots , n)\) to the sender (by running the program of the honest sender in \(\widetilde{\rho }\) with the pid of the sender). The sender replies with \((1, \ldots , 1) \in \lbrace 0, 1 \rbrace ^n\). The receiver then checks if the values he received from the sender equal \((a_1, \ldots , a_n)\). If yes, the receiver outputs “11” (2-bit string). Otherwise, the protocol parties execute the protocol \(\widetilde{\rho }\).
By construction, it holds that
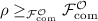 . This follows from the fact that every \(\mathcal {F}^{\mathcal {O}}\)-augmented environment can be replaced by an efficient environment (since \(\mathcal {O}\) attached to \(\mathcal {F}\) is polynomially simulatable) and efficient environments can guess the correct \(a_i\) only with negligible probability (otherwise \(\widetilde{\rho }\) would be insecure, contradicting
. This follows from the fact that every \(\mathcal {F}^{\mathcal {O}}\)-augmented environment can be replaced by an efficient environment (since \(\mathcal {O}\) attached to \(\mathcal {F}\) is polynomially simulatable) and efficient environments can guess the correct \(a_i\) only with negligible probability (otherwise \(\widetilde{\rho }\) would be insecure, contradicting 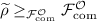 ).
).Assume for the sake of contradiction that there exists an imaginary angel \(\varGamma \) s.t.
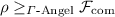 holds. Let the sender be corrupted. Since the adversary has access to \(\varGamma \), he can run the program of the simulator. The simulator must be able to extract commitments (because
holds. Let the sender be corrupted. Since the adversary has access to \(\varGamma \), he can run the program of the simulator. The simulator must be able to extract commitments (because  ). This enables the adversary to extract all \(a_i\) (by relaying the commitments from the receiver each to a different internal copy of the simulator), forcing the receiver to output “11” in the real model experiment. This cannot be simulated in the ideal model experiment, however. We have thus reached a contradiction. \(\square \)
). This enables the adversary to extract all \(a_i\) (by relaying the commitments from the receiver each to a different internal copy of the simulator), forcing the receiver to output “11” in the real model experiment. This cannot be simulated in the ideal model experiment, however. We have thus reached a contradiction. \(\square \)
Theorem 17 raises the question if it is possible to construct secure protocols with “interesting properties” in our framework that are not (known to be) secure in the Angel-based setting. We will answer this question in the affirmative, presenting a modular construction of a general MPC protocol in the plain model that is constant-round (and black-box) and based only on standard polynomial-time hardness assumptions (Theorem 31).
We would like to briefly note that by Theorem 17 we can already conclude that we can realize every (well-formed) functionality in our framework by importing the results of [CLP10].
Proposition 18
(General MPC in the plain model). Assume the existence of enhanced trapdoor permutations. For every (well-formed)Footnote 1 functionality \(\mathcal {F}\), there exists an extraction oracle \(\mathcal {O}\) and a protocol \(\rho \) (in the plain modelFootnote 2) such that

4 A Constant-Round Commitment Scheme
In this section we will construct a constant-round commitment scheme that is secure in our framework. We note that we assume authenticated channels and implicitly work in the \(\mathcal {F}_{\text {auth}}\)-hybrid model.
Let \(\langle C, R \rangle \) be a commitment scheme that we will use a building block for our bit commitment scheme \(\varPi \) later. We require \(\langle C, R \rangle \) to be tag-based. In a tag-based commitment scheme the committer and receiver additionally use a “tag”—or identity—as part of the protocol [PR05, DDN00]. Moreover we require \(\langle C, R \rangle \) to be “immediately committing” as in the following definition.
Definition 19
(Immediately committing). A commitment scheme \(\langle C, R \rangle \) is called immediately committing if the first message in the protocol comes from the sender and already perfectly determines the value committed to.
The above definition implies that the commitment scheme is perfectly binding and super-polynomially extractable, i.e., given the transcript an extractor can find the unique message of the commitment by exhaustive search.
For the discussion of our commitment scheme, we settle the following notation. Let \(s = ((s_{i, b})) \in \{ 0, 1\}^{2n}\) for \(i \in [n]\) and \(b \in \{0,1\}\) be a 2n-tuple of bits. For an n-bit string \(I = b_1 \cdots b_n\), we define \(s_I := (s_{1, b_1}, \ldots , s_{n, b_n})\). Thus I specifies a selection of n of the \(s_{i,b}\), where one of these is selected from each pair \(s_{i,0}, s_{i,1}\).
Construction 1
The bit commitment scheme \(\varPi \) is defined as follows. Whenever the basic commitment scheme \(\langle C, R \rangle \) is used, the committing party uses its \(\mathord { pid }\) and the \(\mathord { sid }\) as its tag. Let \(m\in \{0, 1\}\)
-
\(\mathord {\mathrm {Commit}}(m)\):
-
\(\mathrm {R}\): Choose a random n-bit string I and commit to I using \(\langle C, R \rangle \).
-
\(\mathrm {S}\): Pick n random bits \(s_{i,0}\) and compute \(s_{i,1} = s_{i,0} \oplus m\) for all \(i \in [n]\).
-
\(\mathrm {S}\) and \(\mathrm {R}\) run 2n sessions of \(\langle C, R \rangle \) in parallel in which \(\mathrm {S}\) commits to the \(s_{i,b_i}\) \((i \in [n], b_i \in \{0,1\})\).
-
-
\(\mathord {\mathrm {Unveil}}\):
-
\(\mathrm {S}\): Send all \(s_{i,b_i} \in \{0, 1\}\) \((i \in [n], b_i \in \{0,1\})\) to \(\mathrm {R}\).
-
\(\mathrm {R}\): Check if \(s_{1,0} \oplus s_{1,1} = \cdots = s_{n,0} \oplus s_{n,1}\). If this holds, unveil the string I to \(\mathrm {S}\).
-
\(\mathrm {S}\): If \(\mathrm {R}\) unveiled the string correctly, then unveil all \(s_I\).
-
\(\mathrm {R}\): Check if \(\mathrm {S}\) unveiled correctly. If yes, let \(s'_{1}, \ldots , s'_{n}\) be the unveiled values. Check if \(s'_{i}=s_{i, b_i}\) for all \(i \in [n]\). If so, output \(m := s_{1,0} \oplus s_{1,1}\).
-
The above construction is reminiscent of [DS13] who presented a compiler that transforms any ideal straight-line extractable commitment scheme into an extractable and equivocal commitment scheme.
Note that if an attacker is able to learn the index set I in the commit phase then he can easily open the commitment to an arbitrary message \(m'\) by sending “fake” shares \(t_{i,b}\), such that \(t_{I} = s_{I}\), and \(t_{\lnot I} = s_I \oplus (m', \ldots , m')\). (Here \(\oplus \) is interpreted element-wise.) Hence \(\varPi \) is equivocal for super-polynomial machines.
We claim that this protocol securely realizes \(\mathcal {F}_\text {com}^{\mathcal {O}}\) for a certain shielded oracle \(\mathcal {O}\). We first describe \(\mathcal {O}\), before we move to the theorem.
Construction 2
We define the actions of the shielded oracle \(\mathcal {O}\) as follows.Footnote 3
If the sender is corrupted
-
\(\mathcal {O}\) chooses a random n-bit string I, and commits to the string I to the adversary \(\mathcal {A}\) using \(\langle C, R \rangle \).
-
\(\mathcal {O}\) acts as honest receiver in 2n sessions of \(\langle C, R \rangle \) in parallel. After these sessions have completed, \(\mathcal {O}\) extracts each instance of \(\langle C, R \rangle \), obtaining the shares \((s_{i, b}\) for \(i \in [n])\) and \(b \in \{0,1\}\). (If a commitment cannot be extracted, the corresponding share is set to \(\bot \)).
-
\(\mathcal {O}\) computes \(m_i := s_{i,0} \oplus s_{i,1}\) for all \(i \in [n]\). (Indices i where one or both of the \(s_{i,b}\) is \(\bot \) are ignored.) Let \( m \in \{0,1\}\) be the most frequently occurring \(m_i\). (If there are multiple \(m_i\) occurring with the highest frequency, m chooses \(m=0\)). \(\mathcal {O}\) relays \((\mathord {\mathrm {Commit}}\), m) to \(\mathcal {F}_\text {com}\).
-
When \(\mathcal {A}\) sends shares \(s'_{1,0}, s'_{1,1}, \ldots , s'_{n,0}, s'_{n,1}\) in the unveil phase of \(\varPi \), \(\mathcal {O}\) acts as an honest receiver, unveiling I.
-
Finally, if \(\mathcal {A}\)’s unveil is accepting, \(\mathcal {O}\) instructs \(\mathcal {F}_\text {com}\) to unveil the message.
If the receiver is corrupted
-
\(\mathcal {O}\) acts as the sender in an execution of \(\varPi \), engaging in a commit session of \(\langle C, R \rangle \) with the adversary. If the adversary’s commitment is accepting, \(\mathcal {O}\) extracts this instance of \(\langle C, R \rangle \) obtaining a string I (If parts of this string cannot be extracted they are set to \(\bot )\).
-
\(\mathcal {O}\) picks n random bits \(s_{i,0}\), and lets \(s_{i,1} = s_{i,0}\) for all \(i \in [n]\), as if it were honestly committing to \(m = 0\). Next, it runs 2n instances of \(\varPi \) in parallel, committing to the \(s_{i,b}\).
-
In the unveil phase, when \(\mathcal {O}\) learns the message m, it computes “fake” shares \(t_{i,b}\) as follows: \(t_{I} = s_{I}\) and \(t_{\lnot I} = s_{\lnot I} \oplus (m, \ldots , m)\) (\(\oplus \) is interpreted element-wise.). \(\mathcal {O}\) sends these shares \(t_{i,b}\) to the adversary.
-
\(\mathcal {O}\) acts as the honest sender in the unveil phase of \(\varPi \). If \(\mathcal {A}\)’s unveil of I is accepting, then \(\mathcal {O}\) honestly executes the unveil phase for all bit shares \(t_I\). (Otherwise, \(\mathcal {O}\) outputs nothing and ignores all further inputs.)
If no parties are corrupted, \(\mathcal {O}\) simulates an honest execution of protocol \(\varPi \) on input 0, forwarding all messages to the adversary. Since \(\mathcal {O}\) knows the index string I (because \(\mathcal {O}\) has created it itself) it can create fake shares just like in the case of a corrupted receiver.
If both parties are corrupted, \(\mathcal {O}\) just executes the dummy adversary \(\mathcal {D}\) internally. (Note that \(\mathcal {Z}\) only interacts with \(\mathcal {D}\) in the real experiment if both parties are corrupted).
This concludes the description of the shielded oracle \(\mathcal {O}\). Observe that \(\mathcal {O}\) can be implemented in super-polynomial time. Also note that in the case of both or no party being corrupted, \(\mathcal {O}\) can be implemented in polynomial time.
Before we can state our theorem, we need another assumption about the commitment scheme \(\langle C, R \rangle \).
Definition 20
(pCCA-secure commitment schemes). Let \(\langle C, R \rangle \) be a tag-based commitment scheme. A pCCA-decommitment oracle \(\mathcal {E}\) interacts with an adversary \(\mathcal {A}\) in polynomial many parallel sessions of \(\langle C, R \rangle \) as an honest receiver with tags chosen by the adversary. After all sessions have been completed successfully, \(\mathcal {E}\) simultaneously reveals all committed values to \(\mathcal {A}\) (note that when a session has multiple compatible committed values, \(\mathcal {E}\) reveals only one of them. Hence, there might exist many decommitment oracles).
Consider the probabilistic experiment \(\mathord {\mathrm {IND}}_b( \langle C, R \rangle , \mathcal {A}^{\mathcal {E}}, 1^n, z)\) with \(b \in \{0, 1\}\):
On input \(1^n\) and auxiliary input z, the adversary \(\mathcal {A}\) adaptively chooses a pair of challenge values \(v_0, v_1\in \{0, 1\}\) together with a tag and sends them to the challenger. The challenger commits to \(v_b\) using \(\langle C, R \rangle \) with that tag. The output of the experiment is the output of \(\mathcal {A}^{\mathcal {E}}\). If any of the tags used by \(\mathcal {A}\) for queries to the pCCA-decommitment oracle equals the tag of the challenge, the output of the experiment is replaced by \(\bot \).
\(\langle C, R \rangle \) is said to be parallel-CCA-secure if there exists an \(\mathcal {E}\) s.t. for all PPT adversaries \(\mathcal {A}\) it holds that:Footnote 4
Note that previous protocols proven secure in the Angel-based framework required (adaptive) CCA-secure commitments schemes [CLP10, Goy+15, Kiy14]. For our notion it suffices to assume parallel-CCA-secure (i.e. non-adaptive) commitment schemes as a building block.
Theorem 21
Assume that \(\langle C, R \rangle \) is parallel-CCA-secure and immediately committing. Then  , where \(\varPi \) is as defined in Construction 1 and \(\mathcal {O}\) is the shielded oracle as defined in Construction 2.
, where \(\varPi \) is as defined in Construction 1 and \(\mathcal {O}\) is the shielded oracle as defined in Construction 2.
Proof
By Proposition 6 it suffices to find a simulator for the dummy adversary. By construction of \(\mathcal {O}\) the simulator in the ideal experiment can be chosen to be identical to the dummy adversary.
The main idea of the proof is to consider a sequence of hybrid experiments for a PPT environment \(\mathcal {Z}\) that may externally invoke polynomially many \(\mathcal {F}_\text {com}^{\mathcal {O}}\)-sessions and iteratively replace those sessions by the real protocol \(\varPi \) in a specific order utilizing the fact that the super-polynomial computations of \(\mathcal {O}\) are hidden away and thus the replacements are unnoticeable by \(\mathcal {Z}\), or otherwise we would obtain a PPT adversary against the hiding property of \(\langle C, R \rangle \).
Step 1: Let \(\mathcal {Z}\) be a PPT environment that may externally invoke polynomial many \(\mathcal {F}_\text {com}^{\mathcal {O}}\)-sessions. We denote the output of this experiment by the random variable \(\mathord {\mathrm {Exec}}\bigl (\mathcal {F}_\text {com}^{\mathcal {O}}, \mathcal {Z}\bigr )\). Let \(\mathord {\mathrm {Exec}}\bigl ( \varPi , \mathcal {Z}\bigr )\) be the output of \(\mathcal {Z}\) if all instances of \(\mathcal {F}_\text {com}^{\mathcal {O}}\) sessions are replaced by the instances of the protocol \(\varPi \). We show that for all environments \(\mathcal {Z}\) it holds that
Let \(\mathcal {Z}\) be an environment. By a standard averaging argument we can fix some random coins r for \(\mathcal {Z}\). Thus we can assume henceforth that \(\mathcal {Z}\) is deterministic.
We call instances of \(\mathcal {F}_\text {com}^{\mathcal {O}}\) (or \(\varPi )\) where the sender or receiver is corrupted sender sessions or receiver sessions, respectively. Since in the cases where both or no party is corrupted, the \(\mathcal {O}\)-adjoinded functionalities in this case can be treated as part of the environment. We therefore only need to consider \(\mathcal {F}^{\mathcal {O}}\)-augmented environments that only invoke either sender sessions or receiver sessions.
We say a discrepancy occurred, if in any ideal sender session of \(\mathcal {F}_\text {com}^{\mathcal {O}}\) \(\mathcal {O}\) extracts a value m, but later \(\mathcal {Z}\) correctly unveils a value \(m' \ne m\). First notice that unless a discrepancy happens, the output of an ideal sender session is identically distributed to the output of the real protocol \(\varPi \).
We will now distinguish two cases.
-
1.
The probability that \(\mathcal {Z}\) causes a discrepancy is negligible.
-
2.
The probability that \(\mathcal {Z}\) causes a discrepancy is non-negligible.
Case 1: We replace all sender sessions with instances of \(\varPi \), incurring only a negligible statistical distance. We are left with a hybrid experiment in which only the receiver sessions are still ideal. We will now iteratively replace ideal receiver sessions with the real protocol, beginning with the last session that is started.
Assume that there are at most q receiver sessions. Define hybrids \(\mathsf {H}_0, \ldots , \mathsf {H}_q\) as follows. Hybrid \(\mathsf {H}_i\) is the experiment where the first i receiver sessions are ideal and the remaining \(q-i\) receiver sessions are replaced by instances of \(\varPi \) (in which the receiver is corrupted). Clearly, \(\mathsf {H}_q\) is identical to the experiment where all receiver sessions are ideal, whereas \(\mathsf {H}_0\) is the experiment where all receiver sessions are real. The experiment \(\mathsf {H}_i\) outputs whatever \(\mathcal {Z}\) outputs. Let \(P_i = \Pr [ \mathsf {H}_i = 1 ]\) denote the probability that \(\mathcal {Z}\) outputs 1 in the hybrid game \(\mathsf {H}_i\). Assume now that \(\epsilon := \left|P_0 - P_q\right|\) is non-negligible, i.e., \(\mathcal {Z}\) has non-negligible advantage \(\epsilon \) in distinguishing \(\mathsf {H}_0\) from \(\mathsf {H}_q\). We will now construct an adversary \(\mathcal {A}_\varPi \) that breaks the hiding property of \(\varPi \) with advantage \(\epsilon / q\).
By the averaging principle, there must exist an index \(i^{\mathord {*}} \in [q]\) such that \(\left|P_{i^{\mathord {*}}-1} - P_{i^{\mathord {*}}}\right| \ge \epsilon / q\). By a standard coin-fixing argument, we can fix the coins selected by the \(\mathcal {O}\)-instances inside the first \(i^{\mathord {*}}-1\) (ideal) receiver sessions. Fixing these coins maintains \(\mathcal {Z}\)’s distinguishing advantage. Since we fixed the coins of \(\mathcal {Z}\) before, the experiment is now deterministic until the start of receiver session \(i^{\mathord {*}}\). Since \(\mathcal {Z}\) is fully deterministic up until this point, the first message of \(\mathcal {Z}\) in session \(i^{\mathord {*}}\), which is a commitment on the bit string I, is also computed deterministically.
We can now construct the non-uniform adversary \(\mathcal {A}\) against the hiding property of \(\langle C, R \rangle \). (We note that we do not construct an adversary \(\mathcal {A}\) for the standard hiding game but for a multi-instance variant.) As a non-uniform advice, \(\mathcal {A}\) receives a complete trace of all messages sent until this point. This includes all bit strings \(I_1, \ldots , I_{i^{\mathord {*}}}\) to which \(\mathcal {Z}\) committed to in all receiver sessions \(1, \ldots , i^{\mathord {*}}\) (it also includes \(\mathcal {Z}\)’s input). Note that all messages come from a deterministic process, and the corresponding \(I_i\) are uniquely determined by the first messages of each session i since \(\langle C, R \rangle \) is immediately committing.
\(\mathcal {A}\) now proceeds as follows. \(\mathcal {A}\) internally simulates \(\mathcal {Z}\) and all sessions invoked by \(\mathcal {Z}\). This simulation can be done in polynomial time, since all sender sessions and the subsequent receiver sessions \(i^{\mathord {*}} + 1\) through q have been replaced by instances of \(\varPi \), and \(\mathcal {A}\) knows the index strings \(I_i\) that are used in the (ideal) receiver sessions 1 through \(i^{\mathord {*}}\).
Let \(m^{\mathord {*}}\) be the message that \(\mathcal {Z}\) chooses as input for the sender in session \(i^{\mathord {*}}\). \(\mathcal {A}\) reads \(I \overset{\text {def}}{=}I_{i^{\mathord {*}}}\) from its non-uniform advice and samples a tuple \(s_I\) of n random strings. It then computes \(s_{\lnot I} = s_I \oplus (m^{\mathord {*}}, \ldots , m^{\mathord {*}})\) and \(s'_{\lnot I} = s_I\) for all \(i \in [n]\). \(\mathcal {A}\) sends the messages \((s_{\lnot I}, s_{\lnot I}')\) to the hiding experiment. It now forwards all the messages between the hiding experiment and \(\mathcal {Z}\) and simultaneously commits honestly on all values \(s_I\) to \(\mathcal {Z}\). When \(\mathcal {Z}\) requires that the commitments for all \(s_I\) be opened, \(\mathcal {A}\) honestly unveils these. When \(\mathcal {Z}\) terminates, \(\mathcal {A}\) outputs whatever \(\mathcal {Z}\) output in the experiment. This concludes the description of \(\mathcal {A}\).
We will now analyze \(\mathcal {A}\)’s advantage. If the challenger of the hiding game picks the messages \(s'_{\lnot I}\), \(\mathcal {Z}\) obtains a commitment on the all-zero string in \(\mathcal {A}\)’s simulation. Therefore, in this case the view of \(\mathcal {Z}\) is distributed identically to the view inside the hybrid \(\mathsf {H}_{i^{\mathord {*}}}\). If the challenger of the hiding game picks the messages \(s_{\lnot I}\), \(\mathcal {Z}\) obtains a commitment to the message m which is identical to the view of \(\mathcal {Z}\) inside the hybrid \(\mathsf {H}_{i^{\mathord {*}}-1}\). It follows
i.e. \(\mathcal {A}\) breaks the hiding property of protocol \(\langle C, R \rangle \) with advantage \(\epsilon / q\), which concludes case 1. (Note that in this case \(\mathcal {A}\) does not need the pCCA oracle.)
Case 2: We now turn to case 2. A first observation is that we only need to consider augmented environments that invoke exactly one external session where the sender is corrupted. This is because if a (general) environment \(\mathcal {Z}\) causes a discrepancy with non- negligible probability, then there exists a session \(j^{\mathord {*}}\) in which a discrepancy happens for the first time. An environment \(\mathcal {Z}'\) that invokes only one session where the sender is corrupted can then simulate \(\mathcal {Z}\), guess \(j^{\mathord {*}}\) and simulate all the other sessions where the sender is corrupted with the real protocol. It holds that \(\mathcal {Z}'\) also causes a discrepancy with non-negligible probability.
So we henceforth assume that \(\mathcal {Z}\) invokes at most q sessions and only one session where the sender is corrupted. In what follows, we will replace all ideal sessions where the receiver is corrupted with real protocols using the same strategy as in case 1. Define the hybrids \(\mathsf {H}_0, \dots , \mathsf {H}_q\) as in case 1 except that now \(\mathcal {Z}\) can additionally invoke exactly one sender session in all these hybrids. Clearly, \(\mathsf {H}_q\) is identical to the experiment where all sessions are ideal, whereas \(\mathsf {H}_0\) is the experiment where all receiver sessions are real. Let \(P_i = \Pr [ \mathsf {H}_i = 1 ]\) again.
Assume now that \(\mathcal {Z}\) can distinguish between \(\mathsf {H}_0\) and \(\mathsf {H}_q\) with non-negligible advantage \(\epsilon \). Then there exists an index \(i^{\mathord {*}} \in [q]\) such that \(\left| P_{i^{\mathord {*}}-1} - P_{i^{\mathord {*}}} \right| \ge \epsilon / q\). We can now fix the coins that are used in the first \(i^{\mathord {*}}-1\) ideal sessions until the point where session \(i^{\mathord {*}}\) starts, while maintaining \(\mathcal {Z}\)’s distinguishing advantage.
We will construct a non-uniform adversary \(\mathcal {A}'\) that breaks the parallel-cca-security of \(\langle C, R \rangle \) with advantage \(\epsilon / q\). As in case 1, \(\mathcal {A}'\) receives as a non-uniform advice a trace of a run of \(\mathcal {Z}\) which also includes all index sets \(I_i\) to which \(\mathcal {Z}\) committed in all sessions until session \(i^{\mathord {*}}\) and possibly the shares to which \(\mathcal {Z}\) committed in the only sender-session (again, it also includes \(\mathcal {Z}'\)s input).
\(\mathcal {A}'\) now proceeds the same way as in case 1. It internally runs \(\mathcal {Z}\) and simulates either hybrid \(\mathsf {H}_{i^{\mathord {*}}-1}\) or \(\mathsf {H}_{i^{\mathord {*}}}\) for \(\mathcal {Z}\) by embedding the challenge of the hiding game into the simulated session \(i^{\mathord {*}}\). The adversary \(\mathcal {A}'\) simulates all ideal receiver sessions for \(i \le i^{\mathord {*}}\) with the help of its advice while all subsequent receiver sessions for \(i > i^{\mathord {*}}\) have already been replaced by \(\varPi \). If \(\mathcal {Z}\) has already started to commit to the shares in the only sender session then (by definition) these shares are also part of \(\mathcal {A}'\)’s advice and \(\mathcal {A}'\) can simulate the sender session. (Note that \(\langle C, R \rangle \) is immediately committing, hence the first message of (the parallel executions of) \(\langle C, R \rangle \) uniquely determines the shares). If \(\mathcal {Z}\) has not yet started to commit to the shares in the sender session then \(\mathcal {A}'\) can use its parallel-cca oracle to extract them by forwarding the corresponding messages between the oracle and \(\mathcal {Z}\). After the experiment terminates, \(\mathcal {A}'\) outputs whatever \(\mathcal {Z}\) outputs.
The analysis of \(\mathcal {A}'\) is the same as in case 1 and we end up with the conclusion that \(\mathcal {A}'\) breaks the parallel-cca-security of protocol \(\langle C, R \rangle \) with advantage \(\epsilon / q\).
Hence, it remains to consider environments that invoke exactly one sender-session (all receiver sessions are real and hence can be treated as part of the environment). Assume that such an environment \(\mathcal {Z}\) causes a discrepancy with non-negligible probability \(\epsilon '\).
We will now construct a non-uniform adversary \(\mathcal {A}''\) that breaks the hiding property of the commitment scheme \(\langle C, R \rangle \). \(\mathcal {A}''\) takes part in a partial one-way hiding experiment where the challenger picks a random string \(I = b_1 \cdots b_n\) and commits to this string using the commitment scheme \(\langle C, R \rangle \). \(\mathcal {A}''\) then sends a vector \((a_1, \ldots , a_n)\) to the experiment where \(a_l \in \{ 0, 1, \bot \}\). Let \(M = \{ l \mid a_l \ne \bot \}\). \(\mathcal {A}''\) wins if \({{\mathrm{card}}}(M) \ge n/2\) and \(a_l = b_l\) for all \(l \in M\). It holds that since \(\langle C, R \rangle \) is hiding, \(\mathcal {A}''\) can win this experiment only with negligible probability.
\(\mathcal {A}''\) receives as non-uniform advice the input of \(\mathcal {Z}\). \(\mathcal {A}''\) now proceeds as follows: \(\mathcal {A}''\) forwards the commitment it receives in the experiment to \(\mathcal {Z}\) as in the commit phase of the one sender session that \(\mathcal {Z}\) can invoke. When \(\mathcal {Z}\) sends the commitments on the shares \(s_{l,b}\), \(\mathcal {A}''\) forwards them to its parallel-CCA-oracle, thus learning the values \(s_{l, b}\) that \(\mathcal {Z}\) committed to. \(\mathcal {A}\) can now simulate the oracle \(\mathcal {O}\) and reconstruct the message m defined by these shares (by defining m to be the most frequent value that occurs in \(\{s_{i,0} \oplus s_{i,1}\}_{i \in [n]}\) just like \(\mathcal {O}\)). When \(\mathcal {Z}\) sends the shares \(s_{l, b}'\) in the unveil phase of the sender session, \(\mathcal {A}''\) compares them to the originally extracted shares \(s_{l, b}\) and defines the vector \((a_1, \ldots , a_n)\) as

and sends \((a_{1}, \dots , a_{n})\) to the experiment.
We will now analyze \(\mathcal {A}''\)’s success probability. Let M be the set of indices l for that condition \((\star )\) holds. If \(\mathcal {Z}\) causes a discrepancy, it holds that all tuples of shares \((s'_{l, 0}, s'_{l, 1})\) define the same but different message \(m' \ne m\) than the majority of the original shares \((s_{l, 0}, s_{l, 1})\), i.e. \({{\mathrm{card}}}(M) \ge n/2\). Moreover, for each \(l \in M\) \(b_l\) equals the lth bit of I. Hence, by construction, \(\mathcal {A}''\) wins with non- negligible probability if \(\mathcal {Z}\) causes a discrepancy with non-negligible probability.
Step 2: We will now prove that for every \(\mathcal {F}^{\mathcal {O}}\)-augmented environment
If the sender is corrupted then nothing needs to be shown, as in this case the real and ideal experiment are statistically close. This follows from the fact that by step 1, case 2, an \(\mathcal {F}_\text {com}^{\mathcal {O}}\)-augmented environment can cause a discrepancy only with negligible probability.
If the receiver is corrupted then by step 1 the real and ideal experiment are both indistinguishable to an experiment where all instances of \(\mathcal {F}_\text {com}^{\mathcal {O}}\) invoked by the environment have been replaced by the real protocol. Hence the outputs of the real and ideal experiment are indistinguishable.
If no party is corrupted then one can first replace all sender sessions and receiver sessions with the real protocol using step 1, obtaining a polynomial time environment. Then one can prove indistinguishability by using a very similar reduction to the hiding property as in step 1, case 1.
If both parties are corrupted then the real and ideal experiment are identically distributed. \(\square \)
The premise of Theorem 21 can be further relaxed by using only a weakly pCCA oracle instead of a standard pCCA oracle. A weakly pCCA oracle returns \(\bot \) everywhere in case that at least one commitment is not accepting. Weakly pCCA suffices because a shielded oracle in a sender session (acting as the honest receiver) aborts if at least one commitment is not accepting in the commit phase.
The underlying commitment scheme \(\langle C, R \rangle \) can be instantiated with the 8-round construction in [Goy+14]. It is straightforward to see that this scheme is pCCA secure by using the extractor in its security proof. The Zero-Knowledge Argument of Knowledge inside [Goy+14] is instantiated with the Feige-Shamir protocol [FS90] and—deviating from the original work —the basic commitment scheme is instantiated by the Blum commitment [Blu81] because we require an immediately committing protocol. Since this scheme is constant-round, we obtain the following result:
Corollary 22
Assume the existence of one-way permutations. Then there is a constant-round protocol \(\varPi _{\text {com}}\) and a shielded oracle \(\mathcal {O}\) such that  .
.
The above construction is non-black-box since [Goy+14] (instantiated this way) is non-black-box. However, recall that the only non-black-box part of [Goy+14] is a ZK proof for proving knowledge of committed values and that these values satisfy linear relations. As already pointed out in [Goy+14], this can both be done making only black-box use of a homomorphic commitment scheme. Instantiating [Goy+14] with a perfectly binding homomorphic commitment scheme thus yields a fully black-box construction. Since we need an immediately committing scheme in the plain model for our protocol we let the sender (and not a trusted setup) generate the commitment key of the homomorphic commitment. This construction can be used as a building block in [Goy+14] if the homomorphic commitment scheme is “verifiable”. A verifiable homomorphic commitment scheme allows one to (non-interactively) verify that a commitment key is well-formed. For instance, the ElGamal commitment scheme [ElG84] (which is based on the DDH assumption) is a verifiable perfectly binding homomorphic commitment scheme [AIR01]. The Linear Encryption scheme [BBS04] (which is based on the DLin assumption) can also be viewed as a commitment scheme with these properties.
Corollary 23
Assume the existence of verifiable perfectly binding homomorphic commitment schemes. Then there exists a constant-round black-box protocol \(\varPi ^{BB}_{\text {com}}\) and a shielded oracle \(\mathcal {O}\) such that 
5 A Modular Composition Theorem for \(\varPi \)
We show that we can plug the protocol \(\varPi \) from Construction 1 into a large class of UC-secure protocols in the \(\mathcal {F}_\text {com}\)-hybrid model in such a way that the composite protocol is secure in our framework. We first define Commit-Compute protocols and parallel-CCA-UC-emulation.
Definition 24
(Commit-Compute protocols). Let \(\rho ^{\mathcal {F}_\text {com}}\) be a protocol in the \(\mathcal {F}_\text {com}\)-hybrid model. We call \(\rho ^{\mathcal {F}_\text {com}}\) a commit-compute protocol or CC protocol if it can be broken down into two phases: An initial commit phase, where the only communication allowed is sending messages to instances of \(\mathcal {F}_\text {com}\). After the commit phase is over, a compute phase begins where sending messages to instances of \(\mathcal {F}_\text {com}\) except for \(\mathtt {unveil}\)-messages is prohibited, but all other communication is allowed.
Definition 25
(pCCA-UC-emulation). We write \(\rho \mathchoice{\underset{\mathcal {E}\text {-pCCA}}{\ge }}{\mathrel {\ge _{\mathcal {E}\text {-pCCA}}}}{\mathrel {\ge _{\mathcal {E}\text {-pCCA}}}}{\mathrel {\ge _{\mathcal {E}\text {-pCCA}}}} \phi \) if a protocol \(\rho \) UC-emulates a protocol \(\phi \) in the presence of (non-uniform) environments that may interact with a pCCA-decommitment oracle \(\mathcal {E}\) as defined in Definition 20 for tags that are not extensions of the session identifier of the challenge protocol.
In the following, let \(\varPi \) be the protocol as in Construction 1 with an immediately committing and parallel-CCA secure commitment scheme \(\langle C, R \rangle \). Let \(\mathcal {E}\) be the (uniquely defined) pCCA-decommitment oracle of \(\langle C, R \rangle \).
We are now ready to state the theorem:
Theorem 26
Let \(\rho ^{\mathcal {F}_\text {com}}\) be a CC protocol and \(\mathcal {G}\) a functionality. If \(\rho ^{\mathcal {F}_\text {com}} \mathchoice{\underset{\mathcal {E}\text {-pCCA}}{\ge }}{\mathrel {\ge _{\mathcal {E}\text {-pCCA}}}}{\mathrel {\ge _{\mathcal {E}\text {-pCCA}}}}{\mathrel {\ge _{\mathcal {E}\text {-pCCA}}}} \mathcal {G}\) then there exists a shielded oracle \(\mathcal {O}'\) such that

Proof
Since \(\rho ^{\mathcal {F}_\text {com}} \mathchoice{\underset{\mathcal {E}\text {-pCCA}}{\ge }}{\mathrel {\ge _{\mathcal {E}\text {-pCCA}}}}{\mathrel {\ge _{\mathcal {E}\text {-pCCA}}}}{\mathrel {\ge _{\mathcal {E}\text {-pCCA}}}} \mathcal {G}\) there exists a dummy adversary simulator \(\mathcal {S}_\mathcal {D}\). Let \(\mathcal {O}\) be the shielded oracle from Construction 2, s.t.  . We define the shielded oracle \(\mathcal {O}'\) as follows. \(\mathcal {O}'\) internally simulates multiple instances of \(\mathcal {O}\) (one for each instance of \(\mathcal {F}_\text {com}\) in \(\rho \)) and \(\mathcal {S}_\mathcal {D}\), and forwards messages as follows.
. We define the shielded oracle \(\mathcal {O}'\) as follows. \(\mathcal {O}'\) internally simulates multiple instances of \(\mathcal {O}\) (one for each instance of \(\mathcal {F}_\text {com}\) in \(\rho \)) and \(\mathcal {S}_\mathcal {D}\), and forwards messages as follows.
-
Messages from the adversary addressed to an instance of \(\mathcal {F}_\text {com}\) are forwarded to the corresponding internal instance of \(\mathcal {O}\).
-
Messages from an internal instance of \(\mathcal {O}\) to an instance of \(\mathcal {F}_\text {com}\) are forwarded to the dummy adversary simulator \(\mathcal {S}_\mathcal {D}\).
-
Messages between \(\mathcal {S}_\mathcal {D}\) and the functionality \(\mathcal {G}\) are forwarded.
-
Messages from the dummy adversary simulator \(\mathcal {S}_\mathcal {D}\) addressed as coming from an instance of \(\mathcal {F}_\text {com}\) are forwarded to the respective instance of \(\mathcal {O}\).
-
Messages from the dummy adversary simulator \(\mathcal {S}_\mathcal {D}\) not addressed as coming from an instance of \(\mathcal {F}_\text {com}\) are output to the adversary (without forwarding them to an internal instance of \(\mathcal {O}\)).
We claim that for this oracle  holds. By Proposition 6 it is sufficient to find a simulator for the dummy adversary. The simulator will be the dummy adversary in the ideal world.
holds. By Proposition 6 it is sufficient to find a simulator for the dummy adversary. The simulator will be the dummy adversary in the ideal world.
Recall that we call instances of \(\mathcal {F}_\text {com}^{\mathcal {O}}\) (or \(\varPi )\) where the sender or receiver is corrupted sender sessions or receiver sessions, respectively.
We denote by \(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}\) the protocol \(\rho ^{\mathcal {F}_\text {com}^{\mathcal {O}}}\) where all ideal sender sessions have been replaced by the real protocol. Let \(\mathord {\mathrm {Exec}}(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}, \mathcal {Z})\) denote an execution of an environment \(\mathcal {Z}\) with (polynomially many) instances of \(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}\). Furthermore, denote by \(\mathord {\mathrm {Exec}}(\mathcal {G}^{\mathcal {O}'}, \mathcal {Z})\) an execution of an environment \(\mathcal {Z}\) where all instances of \(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}\) have been replaced by instances of \(\mathcal {G}^{\mathcal {O}'}\).
Let \(\mathcal {Z}\) be an environment in the experiment \(\mathord {\mathrm {Exec}}(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}, \mathcal {Z})\). By a standard averaging argument we can fix some random coins r for \(\mathcal {Z}\). Thus we can assume henceforth that \(\mathcal {Z}\) is deterministic.
In the following hybrid argument, we will have to globally order the main sessions by the ending of their commit-phase and (adaptively) invoke instances of \(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}\), \(\rho ^{\mathcal {F}_\text {com}^{\mathcal {O}}}\) or \(\mathcal {G}^{\mathcal {O}'}\) based on this order. Since the message scheduling may be random, however, this order is not determined a-priori.
In the following, we will therefore have the experiment in the hybrids implement the commit-phases of all invoked protocols “obliviously”, i.e., interact with the environment by running the programs of the shielded oracles and store the inputs of the honest parties without following their instructions in the commit-phases. Note that the only communication that is visible to the environment in the commit-phase is its interaction with the shielded oracles or the receiver in an instance of \(\varPi _{\mathrm {S}}\). The latter interaction is identical to an interaction with the shielded oracle in a sender session. Each time the adversary commits to a value, this value is extracted (by a super-polynomial computation) and stored. Note that the inputs of the honest parties have no effect on the messages the shielded oracles output to the adversary in the commit phase.
Once the commit phases of an instance of \( \rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}\) has ended, the experiment in the hybrids will invoke an instance of \(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}\), \(\rho ^{\mathcal {F}_\text {com}^{\mathcal {O}}}\) or \(\mathcal {G}^{\mathcal {O}'}\) depending on the position within the global order of sessions. The experiment will then invoke the honest parties with their respective inputs and follow their instructions (it will also invoke the simulator \(\mathcal {S}_\mathcal {D}\) with the extracted values if this session is \(\mathcal {G}^{\mathcal {O}'}\)). Messages from \(\mathcal {F}_\text {com}^{\mathcal {O}}\) or \(\mathcal {S}_\mathcal {D}\) to instances of \(\mathcal {O}\) (which are “\(\mathtt {ok}\)” messages) are suppressed. This way, the emulation is consistent with the messages in the commit phase and distributed identically as if one of the protocols \(\mathcal {G}^{\mathcal {O}'}\), \(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}\), or \(\rho ^{\mathcal {F}_\text {com}^{\mathcal {O}}}\) was executed from the beginning.
Step 1. We show that
Let q(n) be an upper bound on the number of instances of \(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}\) that \(\mathcal {Z}\) invokes. Consider the \(2q(n)+1\) hybrids \(\mathsf {H}_{00}, \mathsf {H}_{01}, \mathsf {H}_{10}, \mathsf {H}_{11}, \mathsf {H}_{20},\dots ,\mathsf {H}_{q(n)0}\) which are constructed as follows:
Definition of Hybrid \(\mathsf {H}_{ij}\) : Execute the commit phases of each session “without running the code of the parties” by invoking instances of \(\mathcal {O}\). Follow the instruction of each instance of \(\mathcal {O}\). Parties are only there as placeholders for the environment in the commit phase. Their instructions will be execute after the commit phase of the respective session is over. Note that this can be done since the actions of the parties in the commit phase have no effect on the view of the environment in this phase. Messages output from an instance of \(\mathcal {O}\) are stored as well. After the commit phase of a session is over do the following:
-
1.
If this is the kth session in which the commit phase has ended and \(k\le i\) then invoke an instance of the dummy adversary simulator and the functionality \(\mathcal {G}\). Hand the dummy parties their respective inputs and the dummy adversary simulator the messages output by the instances of \(\mathcal {O}\). Follow the instructions of the dummy adversary simulator and \(\mathcal {G}\). Ignore messages of the dummy adversary simulator to the environment if these messages are coming from an instance of \(\mathcal {F}_\text {com}\) in the commit phase (i.e. an “\(\mathtt {ok}\)” message). In the unveil phase, messages from the dummy adversary simulator mimicking an interaction with \(\mathcal {F}_\text {com}\) (which are messages of the form \((\mathtt {unveil}, b)\)) are forwarded to the respective instance of \(\mathcal {O}\) Messages from the dummy adversary simulator not mimicking an interaction with an instance of \(\mathcal {F}_\text {com}\) are output (without forwarding them to an internal instance of \(\mathcal {O}\)).
-
2.
If \(k=i+1\) and \(j=0\) or \(k>i+1\) then run the protocol parties of \(\rho ^{\mathcal {F}_\text {com}}\) with their inputs and follow their instructions. For all subsessions where the sender is corrupted invoke instances \(\varPi _{\mathrm {S}}\) and execute the commit phase of \(\varPi _{\mathrm {S}}\) using the same randomness for the receiver as the respective oracle (do not pass the messages to the environment). For all subsessions where the receiver or both or no party has been corrupted invoke instances of \(\mathcal {F}_\text {com}\) and adjoin the respective oracle. Send the outputs of the instances of \(\mathcal {O}\) to the respective instances of \(\mathcal {F}_\text {com}\). Ignore “\(\mathtt {ok}\)” messages from the instances of \(\mathcal {F}_\text {com}\).
-
3.
If \(k=i+1\) and \(j=1\) then run the parties of \(\rho ^{\mathcal {F}_\text {com}}\) with their inputs in the commit phase and follow their instructions. For all subsessions invoke an instance of \(\mathcal {F}_\text {com}\) and adjoin the respective oracle. Send the extracted committed values of the \(\mathcal {O}\)-instances in sender sessions to the respective \(\mathcal {F}_\text {com}\)-instance. Ignore “\(\mathtt {ok}\)” messages from the instances of \(\mathcal {F}_\text {com}\).
Observe that \(\mathsf {H}_{00} = \mathord {\mathrm {Exec}}(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}, \mathcal {Z})\) and \(\mathsf {H}_{q(n)0} = \mathord {\mathrm {Exec}}(\mathcal {G}^{\mathcal {O}'}, \mathcal {Z})\).
Let \(P_{ij}\) denote the probability that \(\mathcal {Z}\) outputs 1 in hybrid \(\mathsf {H}_{ij}\). Assume \(\left|P_{00}-P_{q(n)0}\right|\) is non-negligible. Then there exists an index \(i^{*}\) such that either \(\left|P_{i^{*}1}-P_{(i^{*}+1)0}\right|\) or \(\left|P_{i^{*}0}-P_{i^{*}1}\right|\) is also non-negligible.
Case 1: \(\left|P_{i^{*}1}-P_{(i^{*}+1)0}\right|\) is non-negligible. In this case, these neighboring hybrids are equal except that in the \((i^{*}+1)\)th session \(\rho ^{\mathcal {F}_\text {com}^{\mathcal {O}}}\) is replaced by \(\mathcal {G}^{\mathcal {O}'}\).
We fix the coins that are used in the experiment in all sessions until the point where the \((i^{*}+1)\)th commit phase has ended, while maintaining \(\mathcal {Z}\)’s distinguishing advantage.
We can now construct an environment \(\mathcal {Z}'\) that distinguishes \(\rho ^{\mathcal {F}_\text {com}}\) from \(\mathcal {G}\). As a non-uniform advice, \(\mathcal {Z}'\) receives a complete trace of all messages sent until this point, including all shares \(s_{i}\) and strings I that \(\mathcal {Z}\) committed to until the point where the \((i^{*}+1)\)th commit phase has ended. \(\mathcal {Z}'\) internally simulates the execution experiment with \(\mathcal {Z}\) using its advice. Messages to the \((i^{*}+1)\)th session are sent to the challenge protocol. \(\mathcal {Z}'\) may (tentatively) also invoke instances of \(\mathcal {F}_\text {com}^{\mathcal {O}}\) in order to simulate the instances of \(\mathcal {F}_\text {com}^{\mathcal {O}}\) that are invoked after the point where the \((i^{*}+1)\)th commit phase has ended.
Observe that the real execution corresponds to hybrid \(\mathsf {H}_{i^{*}1}\) and the ideal execution to hybrid \(\mathsf {H}_{(i^{*}+1)0}\). By construction, \(\mathcal {Z}'\) distinguishes \(\rho ^{\mathcal {F}_\text {com}}\) from \(\mathcal {G}\). Since \(\mathcal {F}_\text {com}^{\mathcal {O}}\) is polynomially simulatable, \(\mathcal {Z}'\) can be replaced by a polynomial time environment that also distinguishes \(\rho ^{\mathcal {F}_\text {com}}\) from \(\mathcal {G}\), using Theorem 12. This is a contradiction (to the definition of the dummy adversary simulator).
Case 2: \(\left|P_{i^{*}0}-P_{i^{*}1}\right|\) is non-negligible. In this case, these neighboring hybrids are equal except that in the \((i^{*}+1\))th session \(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}\) is replaced by \(\rho ^{\mathcal {F}_\text {com}^{\mathcal {O}}}\). Since \(\mathcal {Z}\) distinguishes these hybrids it holds that with non-negligible probability \(\mathcal {Z}\) causes a discrepancy in hybrid \(\mathsf {H}_{i^{*}1}\) as otherwise these hybrids would be statistically close. Let \(\widetilde{\mathcal {Z}}\) be the environment that internally runs \(\mathcal {Z}\) and outputs 1 as soon as a discrepancy occurs.Footnote 5 By construction, \(\widetilde{\mathcal {Z}}\) outputs 1 with non-negligible probability in \(\mathsf {H}_{i^{*}1}\). We will now consider \(i^{*}+1\) new hybrids \(\mathsf {h}_0, \ldots , \mathsf {h}_{i^{*}}\).
Definition of Hybrid \(\mathsf {h}_j\) : Execute the commit phases of each session “without running the code of the parties” as described in the description of the hybrids \(\mathsf {H}_{ij}\). After the commit phase of a session is over do the following (for a fixed \(j\in \{0, \ldots , i^{*}\}\)):
-
1.
If \(k\le i^{*}-j\) then invoke an instance of the dummy adversary simulator and the functionality \(\mathcal {G}\). Hand the dummy parties their respective inputs and the dummy adversary simulator the messages output by the instances of \(\mathcal {O}\). Follow the instructions of the dummy adversary simulator and \(\mathcal {G}\). Ignore messages of the dummy adversary simulator to the environment if these messages are coming from an instance of \(\mathcal {F}_\text {com}\) in the commit phase (i.e. an “\(\mathtt {ok}\)” message). In the unveil phase, messages from the dummy adversary simulator mimicking an interaction with \(\mathcal {F}_\text {com}\) (which are messages of the form \((\mathtt {unveil}, b)\)) are forwarded to the respective instance of \(\mathcal {O}\) (with the same SID). Messages from the dummy adversary simulator not mimicking an interaction with an instance of \(\mathcal {F}_\text {com}\) are output (without forwarding them to an internal instance of \(\mathcal {O}\))
-
2.
If this is the kth session in which the commit phase has ended and \(i^{*}-j+1\le k\le i^{*}+1\) then run the protocol parties of \(\rho ^{\mathcal {F}_\text {com}}\) with their inputs in the commit phase and follow their instructions. For all subsessions where the receiver or both or no party is corrupted invoke instances of \(\mathcal {F}_\text {com}\) and adjoin the respective oracle Send the outputs of the instances of \(\mathcal {O}\) to the respective instances of \(\mathcal {F}_\text {com}\). Ignore “\(\mathtt {ok}\)” messages from the instances of \(\mathcal {F}_\text {com}\).
-
3.
If \(k\ge i^{*}+2\) then run the protocol parties of \(\rho ^{\mathcal {F}_\text {com}}\) with their inputs in the commit phase and follow their instructions. For all subsessions invoke an instance of \(\mathcal {F}_\text {com}\) and adjoin the respective oracle. Send the extracted committed values of the \(\mathcal {O}\)-instances in sender sessions to the respective \(\mathcal {F}_\text {com}\)-instance. Ignore “\(\mathtt {ok}\)” messages from the instances of \(\mathcal {F}_\text {com}\).
Observe that \(\mathsf {h}_0 = \mathsf {H}_{i^{*}1}\). Let \(j^{*}\) be the largest index such that \(\widetilde{\mathcal {Z}}\) causes a discrepancy in hybrid \(\mathsf {h}_{j^{*}}\) with non-negligible probability. (\(j^{*}\) is well-defined, since there is an index for which this property holds, namely 0). Furthermore, \(j^{*}\le i^{*}-1\). This follows from the following argument. Observe that the last hybrid \(\mathsf {h}_{i^{*}}\) only contains instances of \(\rho ^{\mathcal {F}_\text {com}}\) (since all instance of \(\mathcal {G}\) have been replaced). Because \(\varPi \) emulates \(\mathcal {F}_\text {com}^{\mathcal {O}}\) and due to the composition theorem \(\mathord {\mathrm {Exec}}(\rho ^{\varPi }, \mathcal {Z})\) is indistinguishable from \(\mathsf {h}_{i^{*}}\). Since no discrepancy occurs in \(\mathord {\mathrm {Exec}}(\rho ^{\varPi }, \mathcal {Z})\) it follows that a discrepancy can occur in \(\mathsf {h}_{i^{*}}\) only with negligible probability.
By construction, \(\widetilde{\mathcal {Z}}\) distinguishes the hybrids \(\mathsf {h}_{j^{*}}\) and \(\mathsf {h}_{j^{*}+1}\) (in the first hybrid \(\widetilde{\mathcal {Z}}\) outputs 1 with non-negligible probability and in the second hybrid only with negligible probability).
We will now modify these hybrids. For \(k \in \lbrace j^{*}, j^{*}+1 \rbrace \) define the hybrid \(\mathsf {hyb}_{k-j^{*}}\) to be identical to \(\mathsf {h}_k\) except for the following: At the beginning, the experiment randomly selects one sender session in one of the commit phases \(1,\dots , i^{*}+1\). In all commit phases that end after the \((i^{*}-j^{*})\)th commit phase the real protocol \(\varPi _{\mathrm {S}}\) is invoked instead of \(\mathcal {F}^{\mathcal {O}_{\mathrm {S}}}\) in all sender sessions that have not been selected at the beginning. The one sender session that has been selected at the beginning always remains ideal.
It holds that \(\widetilde{\mathcal {Z}}\) also distinguishes \(\mathsf {hyb}_{0}\) from \(\mathsf {hyb}_{1}\). This is because \(\widetilde{\mathcal {Z}}\) still causes a discrepancy in \(\mathsf {hyb}_{0}\) with non-negligible probability because with high probability (\(1/\mathord { poly }\)) the first session in which \(\widetilde{\mathcal {Z}}\) causes a discrepancy is selected. Furthermore, \(\widetilde{\mathcal {Z}}\) causes a discrepancy in \(\mathsf {hyb}_{1}\) only with negligible probability.
We fix the coins that are used in the experiment in all sessions until the point where the \((i^{*}-j^{*})\)th commit phase has ended, while maintaining \(\widetilde{\mathcal {Z}}\)’s distinguishing advantage.
We can now construct an environment \(\mathcal {Z}''\) that distinguishes \(\rho ^{\mathcal {F}_\text {com}}\) from \(\mathcal {G}\). As a non-uniform advice, \(\mathcal {Z}''\) receives a complete trace of all messages sent until this point, including all shares \(s_{i}\) and index sets I that \(\widetilde{\mathcal {Z}}\) committed to until the point where the \((i^{*}-j^{*})\)th commit phase has ended. \(\mathcal {Z}''\) proceeds as follows: It internally simulates the execution experiment with \(\widetilde{\mathcal {Z}}\) using its advice, randomly picking a sender session at the beginning. Messages to the \((i^{*}-j^{*})\)th session are sent to the challenge protocol. \(\mathcal {Z}''\) can simulate the only instance of \(\mathcal {F}^{\mathcal {O}_{\mathrm {S}}}\) that may occur in a commit phase with its pCCA-oracle \(\mathcal {E}\). \(\mathcal {Z}''\) may (tentatively) also invoke ideal receiver sessions in order to simulate ideal receiver sessions that are invoked after the point where the \((i^{*}-j^{*})\)th commit phase has ended.
Observe that the real execution corresponds to hybrid \(\mathsf {hyb}_{1}\) and the ideal execution to hybrid \(\mathsf {hyb}_{0}\). By construction, \(\mathcal {Z}''\) distinguishes \(\rho ^{\mathcal {F}_\text {com}}\) from \(\mathcal {G}\). With the same argument as in the proof of Theorem 21, step 1, case 2, one can replace all ideal receiver sessions that \(\mathcal {Z}''\) invokes with instances of the real protocol. By construction, an environment \(\mathcal {Z}''\) was found that can query the pCCA-oracle \(\mathcal {E}\) and distinguish \(\rho ^{\mathcal {F}_\text {com}}\) and \(\mathcal {D}\) from \(\mathcal {G}\) and \(\mathcal {S}_{\mathcal {D}}\). We have thus reached a contradiction.
Step 2. We show that  , completing the proof.
, completing the proof.
Let \(\mathcal {Z}\) be a \(\mathcal {G}^{\mathcal {O}'}\)-augmented environments. By step 1, we can replace all instances of \(\mathcal {G}^{\mathcal {O}'}\) with instances of \(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}\). Since \(\varPi \) emulates \(\mathcal {F}_\text {com}^{\mathcal {O}}\), it follows from the composition theorem that we can replace (the challenge protocol) \(\rho ^{\varPi }\) also with \(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}\). Again by step 1, we can replace all instances of \(\rho ^{\varPi _{\mathrm {S}}, \mathcal {F}_\text {com}^{\mathcal {O}}}\) back with instances of \(\mathcal {G}^{\mathcal {O}'}\). The theorem follows. \(\square \)
If the following property holds for the commitment scheme \(\langle C, R \rangle \), the premise \(\rho ^{\mathcal {F}_\text {com}} \mathchoice{\underset{\mathcal {E}\text {-pCCA}}{\ge }}{\mathrel {\ge _{\mathcal {E}\text {-pCCA}}}}{\mathrel {\ge _{\mathcal {E}\text {-pCCA}}}}{\mathrel {\ge _{\mathcal {E}\text {-pCCA}}}} \mathcal {G}\) is automatically fulfilled.
Definition 27
( r -non-adaptive robustness). Let \(\langle C, R \rangle \) be a tag-based commitment scheme and \(\mathcal {E}\) a pCCA-decommitment oracle for it as in Definition 20. For \(r\in \mathbb {N}\), we say that \(\langle C, R \rangle \) is r -non-adaptively-robust w.r.t. \(\mathcal {E}\) if for every PPT adversary \(\mathcal {A}\), there exists a PPT simulator \(\mathcal {S}\), such that for every PPT r-round interactive Turing machine \(\mathcal {B}\), the following two ensembles are computationally indistinguishable:
-
\(\{\langle \mathcal {B}(y), \mathcal {A}^{\mathcal {E}}(z)\rangle (1^{n})\}_{n\in \mathbb {N}, y\in \{0,1\}^{*}, z\in \{0,1\}^{*}}\)
-
\(\{\langle \mathcal {B}(y), \mathcal {S}(z)\rangle (1^{n})\}_{n\in \mathbb {N}, y\in \{0,1\}^{*}, z\in \{0,1\}^{*}}\)
The above definition is a weakening of the (adaptive) robustness property put forward by [CLP10].
Corollary 28
If additionally the commitment scheme \(\langle C, R \rangle \) in \(\varPi \) is r-non-adaptively-robust, then for every r-round CC protocol \(\rho ^{\mathcal {F}_\text {com}}\) it holds that if  then there exists a shielded oracle \(\mathcal {O}'\) such that
then there exists a shielded oracle \(\mathcal {O}'\) such that
Up to now we could instantiate \(\langle C, R \rangle \) with a modified version of [Goy+14] as described above of Corollary 22. To additionally make this scheme r-non-adaptively-robust w.r.t. \(\mathcal {E}\) one can add “redundant slots” using the idea of [LP09] (the scheme needs to have at least \(r+1\) slots to be r-non-adaptively-robust).
In the following lemma we show that every UC-secure protocol \(\rho ^{\mathcal {F}_\text {com}}\) can be transformed into a UC-secure CC protocol.
Lemma 29
(CC compiler). Let \(\rho ^{\mathcal {F}_\text {com}}\) be a protocol in the \(\mathcal {F}_\text {com}\)-hybrid model. Then there exists a CC protocol \(\mathrm {Comp}(\rho )^{\mathcal {F}_\text {com}}\) such that  . Furthermore, if \(\rho ^{\mathcal {F}_\text {com}}\) is constant-round then so is \(\mathrm {Comp}(\rho )^{\mathcal {F}_\text {com}}\).
. Furthermore, if \(\rho ^{\mathcal {F}_\text {com}}\) is constant-round then so is \(\mathrm {Comp}(\rho )^{\mathcal {F}_\text {com}}\).
Proof
(Idea of proof). Replace each instance of \(\mathcal {F}_\text {com}\) with a randomized commitment where the sender commits to a bit b by sending a random value a to \(\mathcal {F}_\text {com}\) and \(a\oplus b\) to the receiver. Note that since the protocol is PPT the number of commitments of each party is polynomially bounded. Put all randomized calls to \(\mathcal {F}_\text {com}\) in a single commit phase. \(\square \)
Let \(\varPi _{r}\) be the constant-round protocol as in Construction 1 where \(\langle C, R \rangle \) is instantiated with the immediately committing, parallel-CCA secure and r-non-adaptively-robust modified version of [Goy+14] as described above. Furthermore, let \(\varPi ^{BB}_{r}\) be the same as \(\varPi _{r}\), except that [Goy+14] is instantiated with a verifiable perfectly binding homomorphic commitment scheme, thus making the construction fully black-box. Applying Corollary 28 and Lemma 29 one obtains the following:
Corollary 30
Assume the existence of one-way permutations. Let \(\rho ^{\mathcal {F}_\text {com}}\) be a constant-round protocol and \(\mathcal {G}\) a functionality. If  then there exists a shielded oracle \(\mathcal {O}'\) such that for sufficiently large r it holds that
then there exists a shielded oracle \(\mathcal {O}'\) such that for sufficiently large r it holds that
Furthermore, assuming the existence of verifable perfectly binding homomorphic commitment schemes, the same property holds for \(\varPi ^{BB}_{r}\).
6 Constant-Round (Black-Box) General MPC
We can now apply Corollary 30 to obtain a constant-round general MPC protocol based on standard polynomial-time hardness assumptions that is secure in our framework. [HV15] showed that for every well-formed functionality \(\mathcal {F}\) there exists a constant-round protocol \(\rho ^{\mathcal {F}_\text {com}}\) that UC-emulates \(\mathcal {F}\), assuming two-round semi-honest oblivious transfer. Plugging \(\varPi _r\) (for a sufficiently large r) into this protocol yields a constant-round general MPC protocol based on standard assumptions (e.g. enhanced trapdoor permutations). Furthermore, since the construction in [HV15] is black-box, plugging \(\varPi ^{BB}_r\) into [HV15] yields a fully black-box construction of a constant-round general MPC protocol based on polynomial-time hardness assumptions that is secure in our framework.
Theorem 31
(Constant-round general MPC in the plain model)
-
(a)
Assume the existence of enhanced trapdoor permutations. Then for every well-formed functionality \(\mathcal {F}\), there exists a constant-round protocol \(\pi _{\mathcal {F}}\) (in the plain model) and a shielded oracle \(\mathcal {O}\) such that
 (16)
(16) -
(b)
Assume the existence of verifiable perfectly binding homomorphic commitment schemes and two-round semi-honest oblivious transfer.
Then for every well-formed functionality \(\mathcal {F}\), there exists a constant-round protocol \(\pi ^{BB}_{\mathcal {F}}\) (in the plain model) and a shielded oracle \(\mathcal {O}\) such that
 (17)
(17)\(\pi ^{BB}_{\mathcal {F}}\) uses the underlying homomorphic commitment scheme and oblivious transfer only in a black-box way.
7 Conclusion
Shielded super-polynomial resources allow for general concurrent composition in the plain model while being compatible with UC security. As an application a secure constant-round (black-box) general MPC protocol was modularly designed and future work will be needed to make this proof of concept a general principle.
Notes
- 1.
See [Can+02] for a definition of well-formed functionalities.
- 2.
A model without any trusted setup except for authenticated communication channels.
- 3.
For ease of notation, we drop the prefixes
 and
and  in the messages output by \(\mathcal {O}\).
in the messages output by \(\mathcal {O}\). - 4.
In our special case the decommitment oracle \(\mathcal {E}\) is unique since we assume an immediately committing commitment scheme.
- 5.
To make the environment able to learn the committed value in a \(\mathcal {F}_\text {com}^{\mathcal {O}}\)-hybrid protocol, we redefine the shielded oracle \(\mathcal {O}\) for the case of a corrupted sender as follows: After the unveil phase is over, the oracle first outputs the extracted committed value to the simulator and after receiving a notification message from the simulator it sends an unveil message to the functionality. Denote this modified oracle by \(\widetilde{\mathcal {O}}\). Furthermore define \(\widetilde{\varPi }\) to be identical to \(\varPi \), except that before outputting the committed value, the receiver sends the committed value to the sender. The sender then sends a notification message to the receiver, who then outputs the committed value. It follows from the exact same arguments as in the proof of Theorem 21 that
 and that \(\widetilde{\mathcal {O}}\) adjoined to \(\mathcal {F}_\text {com}\) is polynomially simulatable. Using these modified versions in the above proof one obtains
and that \(\widetilde{\mathcal {O}}\) adjoined to \(\mathcal {F}_\text {com}\) is polynomially simulatable. Using these modified versions in the above proof one obtains  . Since \(\varPi \) unconditionally emulates \(\widetilde{\varPi }\) it holds that
. Since \(\varPi \) unconditionally emulates \(\widetilde{\varPi }\) it holds that  , hence
, hence  .
.
References
Aiello, B., Ishai, Y., Reingold, O.: Priced oblivious transfer: how to sell digital goods. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 119–135. Springer, Heidelberg (2001). doi:10.1007/3-540-44987-6_8
Barak, B., et al.: Universally composable protocols with relaxed set-up assumptions. In: 45th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2004, pp. 186–195. IEEE (2004)
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28628-8_3
Blum, M.: Coin flipping by telephone. In: Advances in Cryptology, CRYPTO 1981: IEEE Workshop on Communications Security. University of California, Santa Barbara, Department of Electrical and Computer Engineering, pp. 11–15 (1981)
Barak, B., Sahai, A.: How to play almost any mental game over the net - concurrent composition via super-polynomial simulation. In: 46th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2005, pp. 543–552. IEEE (2005)
Canetti, R., et al.: Universally composable two-party and multiparty secure computation. In: Proceedings of the 34th Annual ACM Symposium on Theory of Computing, STOC 2002, pp. 494–503. ACM (2002)
Canetti, R., Dodis, Y., Pass, R., Walfish, S.: Universally composable security with global setup. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 61–85. Springer, Heidelberg (2007). doi:10.1007/978-3-540-70936-7_4
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42th Annual IEEE Symposium on Foundations of Computer Science. FOCS 2001, pp. 136–145. IEEE (2001)
Canetti, R., Fischlin, M.: Universally composable commitments. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 19–40. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_2
Canetti, R., Goyal, V., Jain, A.: Concurrent secure computation with optimal query complexity. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 43–62. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_3
Canetti, R., Kushilevitz, E., Lindell, Y.: On the limitations of universally composable two-party computation without set-up assumptions. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 68–86. Springer, Heidelberg (2003). doi:10.1007/3-540-39200-9_5
Canetti, R., Lin, H., Pass, R.: Adaptive hardness and composable security in the plain model from standard assumptions. In: 51st Annual IEEE Symposium on Foundations of Computer Science, FOCS 2010, pp. 541–550. IEEE (2010)
Canetti, R., Lin, H., Pass, R.: From unprovability to environmentally friendly protocols. In: 54th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2013, pp. 70–79. IEEE (2013)
Canetti, R., Pass, R., Shelat, A.: Cryptography from sunspots: how to use an imperfect reference string. In: 48th Annual IEEE Symposium on Foundations of Computer Science. FOCS 2007, pp. 249–259. IEEE (2007)
Dachman-Soled, D., Malkin, T., Raykova, M., Venkitasubramaniam, M.: Adaptive and concurrent secure computation from new adaptive, non-malleable commitments. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 316–336. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42033-7_17
Dolev, D., Dwork, C., Naor, M.: Nonmalleable cryptography. SIAM J. Comput. 30(2), 391–437 (2000)
Damgård, I., Scafuro, A.: Unconditionally secure and universally composable commitments from physical assumptions. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 100–119. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42045-0_6
ElGamal, T.: A public key cryptosystem and a signature scheme based on discrete logarithms. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 10–18. Springer, Heidelberg (1985). doi:10.1007/3-540-39568-7_2
Feige, U., Shamir, A.: Witness indistinguishable and witness hiding protocols. In: Proceedings of the 22nd Annual ACM Symposium on Theory of Computing, STOC 1990, pp. 416–426. ACM (1990)
Garg, S., Goyal, V., Jain, A., Sahai, A.: Concurrently secure computation in constant rounds. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 99–116. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_8
Goyal, V., Gupta, D., Jain, A.: What information is leaked under concurrent composition? In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 220–238. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_13
Goyal, V., Jain, A.: On concurrently secure computation in the multiple ideal query model. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 684–701. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38348-9_40
Goyal, V., Jain, A., Ostrovsky, R.: Password-authenticated session-key generation on the internet in the plain model. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 277–294. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_15
Goyal, V., et al.: An algebraic approach to non-malleability. In: 55th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2014, pp. 41–50. IEEE (2014)
Goyal, V., Lin, H., Pandey, O., Pass, R., Sahai, A.: Round-efficient concurrently composable secure computation via a robust extraction lemma. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9014, pp. 260–289. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46494-6_12
Hazay, C., Venkitasubramaniam, M.: On black-box complexity of universally composable security in the CRS model. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9453, pp. 183–209. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48800-3_8
Hazay, C., Venkitasubramaniam, M.: Composable adaptive secure protocols without setup under polytime assumptions. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9985, pp. 400–432. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53641-4_16
Katz, J.: Universally composable multi-party computation using tamper-proof hardware. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 115–128. Springer, Heidelberg (2007). doi:10.1007/978-3-540-72540-4_7
Kiyoshima, S.: Round-efficient black-box construction of composable multi-party computation. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 351–368. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44381-1_20
Kidron, D., Lindell, Y.: Impossibility results for universal composability in public-key models and with fixed inputs. J. Cryptol. 24(3), 517–544 (2011). Cryptology ePrint Archive (IACR): Report 2007/478. Version 2010–06-06
Kalai, Y.T., Lindell, Y., Prabhakaran, M.: Concurrent composition of secure protocols in the timing model. J. Cryptol. 20(4), 431–492 (2007)
Kiyoshima, S., Manabe, Y., Okamoto, T.: Constant-round black-box construction of composable multi-party computation protocol. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 343–367. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_15
Lindell, Y.: General composition and universal composability in secure multi-party computation. In: 44th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2003, pp. 394–403. IEEE (2003)
Lin, H., Pass, R.: Non-malleability amplification. In: Proceedings of the 41st Annual ACM Symposium on Theory of Computing, STOC 2009, pp. 189–198. ACM (2009)
Lin, H., Pass, R.: Black-box constructions of composable protocols without set-up. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 461–478. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_27
Lin, H., Pass, R., Venkitasubramaniam, M.: A unified framework for concurrent security: universal composability from stand-alone non-malleability. In: Proceedings of the 41st Annual ACM Symposium on Theory of Computing, STOC 2009, pp. 179–188. ACM (2009)
Pass, R., Lin, H., Venkitasubramaniam, M.: A unified framework for uc from only OT. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 699–717. Springer, Heidelberg (2012). doi:10.1007/978-3-642-34961-4_42
Malkin, T., Moriarty, R., Yakovenko, N.: Generalized environmental security from number theoretic assumptions. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 343–359. Springer, Heidelberg (2006). doi:10.1007/11681878_18
Micali, S., Pass, R., Rosen, A.: Input-indistinguishable computation. In: 47th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2006, pp. 367–378. IEEE (2006)
Pass, R.: Simulation in quasi-polynomial time, and its application to protocol composition. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 160–176. Springer, Heidelberg (2003). doi:10.1007/3-540-39200-9_10
Pass, R., Rosen, A.: Concurrent non-malleable commitments. In: 46th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2005, pp. 563–572. IEEE (2005)
Prabhakaran, M., Rosulek, M.: Cryptographic complexity of multi-party computation problems: classifications and separations. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 262–279. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85174-5_15
Prabhakaran, M., Sahai, A.: New notions of security: achieving universal composability without trusted setup. In: Proceedings of the 36th Annual ACM Symposium on Theory of Computing, STOC 2004, pp. 242–251. ACM (2004)
Venkitasubramaniam, M.: On adaptively secure protocols. In: Abdalla, M., Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 455–475. Springer, Heidelberg (2014). doi:10.1007/978-3-319-10879-7_26
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Broadnax, B., Döttling, N., Hartung, G., Müller-Quade, J., Nagel, M. (2017). Concurrently Composable Security with Shielded Super-Polynomial Simulators. In: Coron, JS., Nielsen, J. (eds) Advances in Cryptology – EUROCRYPT 2017. EUROCRYPT 2017. Lecture Notes in Computer Science(), vol 10210. Springer, Cham. https://doi.org/10.1007/978-3-319-56620-7_13
Download citation
DOI: https://doi.org/10.1007/978-3-319-56620-7_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-56619-1
Online ISBN: 978-3-319-56620-7
eBook Packages: Computer ScienceComputer Science (R0)


 ,
,  ,
, 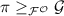 . Then it holds that
. Then it holds that 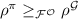 .
. . Then it holds that
. Then it holds that 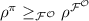 .
. for an imaginary Angel
for an imaginary Angel 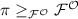 .
.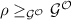 but no imaginary angel
but no imaginary angel  holds.
holds.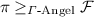 we have
we have 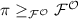 we need to show
we need to show 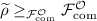 and
and 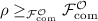 . This follows from the fact that every
. This follows from the fact that every 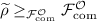 ).
).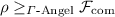 holds. Let the sender be corrupted. Since the adversary has access to
holds. Let the sender be corrupted. Since the adversary has access to  ). This enables the adversary to extract all
). This enables the adversary to extract all 

 and
and  in the messages output by
in the messages output by  and that
and that  . Since
. Since  , hence
, hence  .
.